| 一种基于非负绞杀的循环神经网络变量选择与结构优化算法 |
神经网络是一种学习能力很强的网络模型, 其较强的鲁棒性、容错性及适应系统的动态性, 使之成为复杂系统建模领域的研究热点。目前, BP神经网络[1]、RBF神经网络[2]、卷积神经网络[3]已被应用于多种工业场景以解决实际问题。
现有大量学习任务都需要处理序列信息, 如时间序列预测、机器翻译、语音识别等情境[4]。针对序列输入的需求, 循环神经网络(Recurrent Neural Network, RNN)[5]应运而生。RNN通过引入时序反馈机制, 使得某时刻的输出可以作为输入再次输入到神经元, 这种网络结构可以保持数据中的依赖关系, 非常适用于时间序列数据建模。文献[6]提出了一种基于RNN的动态反向传播(BP)算法模型, 并对北方某日光温室的温度和湿度进行了预测, 实验结果表明RNN-BP在各项性能指标均优于BP神经网络。文献[7]根据油田生产历史数据利用长短期记忆神经网络(LSTM)构建油田产量预测模型, 并进行了实验验证和应用效果分析, 该模型不仅考虑了产量指标与其影响因素之间的联系, 还兼顾了产量随时间变化的趋势和前后关联。文献[8]针对负荷数据时序性和非线性的特点, 提出了一种基于卷积神经网络(CNN)和长短期记忆(LSTM)网络的混合模型短期负荷预测方法, 将CNN提取的特征向量以时序序列方式构造并作为LSTM网络输入数据, 再采用LSTM网络进行短期负荷预测。
随着数据采集系统和硬件存储设备的飞速发展, 复杂系统过程数据呈现规模大、维度高、复杂性强等特点。为提高模型预测精度, 降低建模复杂性, 变量筛选显得尤为重要, NMI(Normalized Mutual Information)[9]、PCA(Principal Component Analysis)[10-11]、LASSO[12]等多种方法得到研究与应用。非负绞杀(Nonnegative Garrote, NNG)算法是由Breiman提出的一种基于约束函数的模型优化方法, 其通过对模型未知参数进行约束促使部分参数压缩为零, 进而实现变量选择, 得到参数估计值[13]。该类算法克服了传统方法计算复杂度高及稳定性差的缺点, 逐渐成为高维数据研究领域广受欢迎的一类方法。文献[14]将NNG用于训练良好的多层感知机(MLP)输入权值的精确收缩, 并以V折交叉验证确定最优绞杀参数s, 实验结果证明了该方法变量选择的有效性。文献[15]在NNG对MLP输入权值收缩的基础上, 利用EO算法进行进一步的局部优化, 通过对某电厂实际生产数据的仿真验证了算法性能。然而, 该方法所使用的MLP模型仅考虑过程的静态特性, 无法实现对时序数据的信息提取及动态过程建模。
为此, 本文提出一种基于RNN和NNG结合的变量选择和模型优化算法(NNG-RNN)。该算法一方面利用RNN带有反馈的网络结构处理并拟合时序数据, 从而在寻找与建模目标参数相关的特征时, 能够充分考虑到各变量在不同时间延迟上对预测目标的影响;另一方面, NNG算法对网络输入权重和循环节点的同时压缩达到高维数据的变量选择和循环层的结构简化。最后通过时序过程数据集对算法进行测试, 并与不同算法的性能对比验证了所提出算法的有效性。
1 理论背景 1.1 循环神经网络(RNN)RNN在前向神经网络基础上增加了时序反馈机制, 具体表现为在相邻时间步长内连接隐含层, 隐含层的值不仅取决于当前输入值, 还取决于前一时刻隐含层的值[16]。基于这一特殊结构, RNN可以“记住”前面的信息并将其应用于计算当前输出, 因此可以跨时间步传递信息, 其输出将涵盖每一个时间节点的信息。典型的RNN网络结构如图 1所示。
 |
| 图 1 RNN网络结构图 |
图中各参数意义如下: U是输入层到隐含层的权重矩阵, V是隐含层到输出层的权重矩阵, W是隐含层循环至自身下一时刻的权重矩阵, x是输入值, y是输出值, h是隐含层的状态, g与f表示激活函数, 网络输出值与隐含层状态表达式分别为:
| $ y_{t}=g\left(v h_{t}+b_{o}\right) $ | (1) |
| $ h_{t}=f\left(u x_{t}+w h_{t-1}+b_{h}\right) $ | (2) |
图 2是典型RNN网络结构的详细展开图, 则公式(1)(2)扩展可得:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;h_j^t = \\ f\left( {\left( {\sum\limits_{i = 1}^p {{u_{ij}}} {x_i}} \right) + \left( {\sum\limits_{\tau = 1}^T {\left( {\sum\limits_{l = 1}^q {{w_{lj}}} h_l^{t - \tau }} \right)} } \right) + b_j^h} \right) \end{array} $ | (3) |
| $ {y^t} = g\left( {\left( {\sum\limits_{j = 1}^q {{v_j}} h_j^t} \right) + {b^o}} \right) $ | (4) |
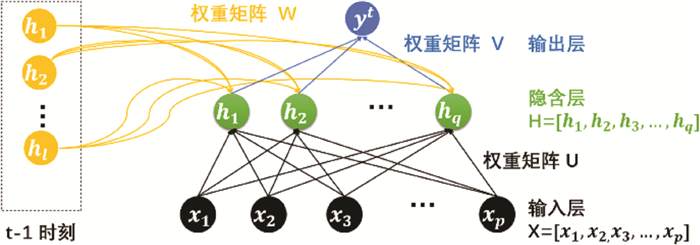 |
| 图 2 三层RNN网络结构图 |
其中,p和q分别代表候选输入变量与隐含层节点数量, τ代表时延步长。hjt表示第j个隐含层节点在t时刻的输出, y(t) 则表示t时刻网络输出。uij、wlj、vj(i=1, 2, ⋯, p; j=1, 2, ⋯, q; l=1, 2, ⋯, q) 分别表示输入变量xi与第j个隐含层节点的权重、第l个隐含节点上一时刻对第j个节点当前时刻的权重及隐含层节点与输出之间的权重。bjh、bo分别表示输入与隐含层的偏置及隐含层与输出层的偏置。
将式(3)代入式(4)可得RNN完整表达式:
| $ \begin{array}{l} \;\;\;\;\;\;\;{y^t} = g\left( {\left( {\sum\limits_{j = 1}^q {{v_j}} f\left( {\left( {\sum\limits_{i = 1}^p {{u_{ij}}} {x_i}} \right) + } \right.} \right.} \right.\\ \left. {\left. {\left. {\left( {\sum\limits_{\tau = 1}^T {\left( {\sum\limits_{l = 1}^q {{w_{lj}}} h_l^{t - \tau }} \right)} } \right) + b_j^h} \right)} \right) + {b^o}} \right) \end{array} $ | (5) |
变量选择主要是通过机器学习方法从输入变量集合中选择对响应变量有重大影响的解释变量, 这是统计分析和推理的重要组成部分。建模过程中若选入与响应无关的协变量, 不仅干扰对变量间关系的理解, 模型的泛化能力也会因而下降[17]。
变量选择方法通常包括最优子集法或正向(反向)逐步回归方法, 数学统计中最常用的方法之一是子集选择, 这意味着在给定数据集{(yn, x1n, ⋯⋯, xMn), n=1⋯⋯N}中消除x1, ⋯, xM中的冗余变量, 并根据其余变量集获得预测值y。在线性模型中, 每个x对应一个变量的子集, 非线性模型则更加复杂, 具有更多的变量子集。
Breiman提出NNG算法用以解决线性问题的子集回归问题, 其基本原理是在最大似然或最小二乘(Ordinary Least, OLS)估计参数的基础上添加关于模型复杂度的约束函数, 构造一个带约束的非线性优化表达式, 然后找到该目标函数的极值(极大值/极小值)以获取参数估计值。这种将一些变量的系数压缩为零的策略可同时完成变量选择和参数估计这两个任务, 从而大大降低了算法复杂度, 提高了子集选择的稳定性[18]。
在初始NNG中, 线性模型如下所示:
| $ y = \sum\limits_{i = 1}^p {{\beta _i}} {x_i} + \theta $ | (6) |
其中, x=[x1, x2, ⋯, xp] 和y分别表示输入和输出变量, β=[β1, β2, ⋯, βp] 是系数矩阵, θ是随机误差。令X∈Rn×p是输入变量矩阵, 则每一列代表一个解释变量, n为样本总数, Y∈Rn是输出样本矩阵。令
| $ \left\{ {\begin{array}{*{20}{l}} {c*(s) = argmin\left\{ {\sum\limits_{k = 1}^n {{{\left( {{y_k} - \sum\limits_{i = 1}^p {{c_i}} {{\hat \beta }_i}{x_{ik}}} \right)}^2}} } \right\}}\\ {s.t.{c_i} \ge 0, \sum\limits_{i = 1}^p {{c_i}} \le s} \end{array}} \right. $ | (7) |
其中, s是绞杀参数。假定
| $ \widetilde{\beta}_{i}=c_{i} \hat{\beta}_{i}, i=1, 2, \cdots, p $ | (8) |
由此可得输出预测值:
| $ \tilde{y}=\sum\limits_{i=1}^{p} \tilde{\beta}_{i} x_{i} $ | (9) |
如式(7)所示, NNG通过在给定s值的条件下求解二次规划问题获得最优压缩权重c*。本文使用有效集法求解二次规划问题, 其通过求解有限个等式约束问题来求解约束二次规划问题, 是一种可行点法, 具有良好的收敛性和稳定性[19-20]。设置不同绞杀参数s可获得不同程度的约束, 从而得到不同复杂程度的模型结构。s越小, 约束越大, 反之亦然。降低参数s可以使更多的c变为零, 同时其对应的乘积β也等于零, 即从候选变量集中删除相应变量, 从而达到变量选择的目的。
2 算法设计 2.1 NNG与RNN结合算法主要思想是将NNG引入RNN, 利用其出色的系数压缩能力, 实现RNN输入变量选择及结构参数优化。首先由先验知识配置网络初始参数, 训练得到一个较为完备的RNN初始模型, 记输入层-隐含层连接权重及隐含层循环至自身权重分别为
| $ \begin{array}{l} {y^t} = g\left( {\left( {\sum\limits_{j = 1}^q {{v_j}} f\left( {\left( {\sum\limits_{i = 1}^p {{c_i}} {{\hat u}_{ij}}{x_i}} \right) + } \right.} \right.} \right.\\ \left. {\left. {\left. {\left( {\sum\limits_{\tau = 1}^T {\left( {\sum\limits_{l = 1}^q {{c_r}} {{\hat w}_{lj}}h_l^{t - \tau }} \right)} } \right) + b_j^h} \right)} \right) + {b^o}} \right) \end{array} $ | (10) |
| $ \left\{ {\begin{array}{*{20}{l}} {c*(s) = {\mathop{\rm argmin}\nolimits} \left\{ {\sum\limits_{k = 1}^n {\left( {{y_k} - g\left( {\left( {\sum\limits_{j = 1}^q {{v_j}} f\left( {\sum\limits_{i = 1}^p {{c_i}} {{\hat u}_{ij}}{x_i}} \right) + } \right.} \right.} \right.} } \right.}\\ {\left. {{{\left. {\left. {\left. {\;\;\;\;\left( {\sum\limits_{\tau = 1}^T {\left( {\sum\limits_{l = 1}^q {{c_r}} {{\hat w}_{lj}}{h_l}(t - \tau )} \right)} + {b_j}} \right)} \right) + {b^0}} \right)} \right)}^2}} \right\}}\\ {s.t.{c_i}, {c_r} \ge 0, \sum\limits_{i = 1}^p {{c_i}} + \sum\limits_{\tau = 1}^T {\sum\limits_{j = 1}^q {{c_r}} } \le s} \end{array}} \right. $ | (11) |
NNG-RNN算法表达式如式(11)所示。显然, ci通过压缩输入层-隐含层权量实现变量选择, cr通过对隐含层循环至自身节点的压缩来筛选循环节点在不同时延长度上对预测目标的影响, 两者结合可以达到快速优化网络的目的。
更新后的输入权重
| $ {{\tilde u}_{ij}} = {c_i}{{\hat u}_{ij}}, i = 1, 2, \cdots , p;j = 1, 2, \cdots , q $ | (12) |
| $ {{\tilde w}_{lj}} = {c_r}{{\hat w}_{lj}}, l = 1, 2, \cdots , q;j = 1, 2, \cdots , q $ | (13) |
则模型输出yt可表达为:
| $ \begin{array}{l} \;\;\;\;\;\;{y^t} = g\left( {\left( {\sum\limits_{j = 1}^q {{v_j}} f\left( {\left( {\sum\limits_{i = 1}^p {{{\tilde u}_{ij}}} {x_i}} \right) + } \right.} \right.} \right.\\ \left. {\left. {\left. {\left( {\sum\limits_{\tau = 1}^T {\left( {\sum\limits_{l = 1}^q {{{\tilde w}_{lj}}h_l^{t - \tau }} } \right)} } \right) + b_j^h} \right)} \right) + {b^o}} \right) \end{array} $ | (14) |
在NNG-RNN算法中, s决定RNN权重的压缩程度。通常, s由向量S=[s1, s2, s3, ⋯, sg] 中的值枚举确定, 其中s1、sg分别是压缩阈值的下限与上限, g是向量个数。当s=0, 所有的权重都将约束为0, RNN的节点也不复存在;反之, 当s>p+qτ, 即输入变量个数与循环节点个数与步长乘积之和, 那么任何权重都未得到压缩, NNG将失去其存在的意义。在本文中, 交叉验证的方法将会用来确定最佳的参数s。
交叉验证是机器学习中建立模型和验证模型参数的常用方法。其基本原理为, 在建立模型的过程中, 从所有输入变量的样本中提取大部分数据作为训练集, 以此来构建模型, 其余部分作为验证集, 验证所建立模型的有效性。最常见的交叉验证方法有: 留一法、留P交叉验证法和V折交叉验证法[21]。
然而, 传统的交叉验证将分组数据随机定义为训练集和测试集, 破坏了原始数据的序列性。同时, RNN会根据设定的最大时滞长度配置网络的初始状态。当测试集位于数据中间, 训练集的时序性被割裂时, 会出现利用未来数据预测当前状态的不合理现象, 导致模型效果的偏差。为解决这一问题, 本文设计并使用一种滚动交叉验证方法, 其原理示意图如图 3所示。
 |
| 图 3 滚动交叉验证原理图 |
滚动交叉验证也被称为滚动原点评价[22]或滚动原点再校准评估[23]。首先, 只使用80%的数据进行训练, 寻找最优参数, 从而保留一部分未被模型学习到的数据来测试模型性能。对于用来确定最优参数的数据集, 将按照时间顺序分为多个模块。前一时段作为训练数据, 下一时段数据作为验证数据, 训练集不断增加, 验证集也依次向后滚动, 以此保留数据时序完整性。模型的预测精度由总训练次数的平均均方根误差决定。
本文选择不同参数对应预测模型的均方根误差(root mean square error, RMSE)作为评价性能的指标, 如式(15)所示。
| $ RMSE = \sqrt {\frac{{\sum\limits_{j = 1}^n {{{\left( {{y_j} - {{\hat y}_j}} \right)}^2}} }}{n}} $ | (15) |
其中,n是测试样本的数目;yj是真实值;
Step 1数据集划分。将数据前80%作为训练数据集, 剩余20%作为测试数据集。
Step 2超参数s寻优。
1) 令j=1, S=[s1, s2, ⋯, sg];
2) 初始化参数i=1, 将训练数据集分为V组进行滚动验证;
3) 以1至i组数据作为训练数据, 训练RNN获得网络初始权重;
4) 求解式(11)非线性约束二次函数优化表达式, 得到压缩系数
5) 由式(12)-(13)更新网络权重, 获得优化的RNN;
6) 使用第i+1组数据检验模型性能, 根据式(15)计算得当前RMSEi;
7) 令i=i+1, 若i < v则重复步骤3-6, 求得所有RMSEi平均值记作ARMSEj;
8) 令j=j+1, 若j < g, 则重复步骤2-7, 共计得g组ARMSE, 寻取最小ARMSE所对应s值作为最优超参数s确定值, 记作s*;
Step 3网络初始化。依据先验知识得到网络结构参数, 使用训练数据集训练RNN, 获得网络初始权重。
Step 4将s* 代入式(11)进行求解, 得到最优压缩系数c*(s*)=(c*1, c*2, ⋯, c*p)。
Step 5由式(12)-(13)更新网络权重, 获得优化的RNN, 并由式(14)输出网络表达式。
3 实验与结果分析本节通过数值算例对所提出的NNG-RNN算法进行评价, 并与NNG-MLP、LASSO-RNN、RNN和MLP的预测结果进行比较。其中, LASSO作为一种变量选择算法, 通过在回归基础上增加一个惩罚项, 对估计参数进行压缩, 当压缩参数缩小到一个阈值时无关变量被删除, 以达到变量选择的目的[24]。对比算法LASSO-RNN先采用LASSO对所有变量进行筛选, 再将筛选后的变量作为输入变量, 利用RNN进行建模。
3.1 仿真设定所有算法都在相同的仿真环境和参数设置下执行。仿真运行环境为深度学习服务器: Intel(R) Core(TM) i7-7700K CPU@4.20GHz处理器、64GB内存、64位Windows10操作系统下MATLAB R2020a。在这些实验中, MLP与RNN的网络设置相同, 均为3层网络结构, 隐含层有10个神经元, 输出层有1个神经元, 输入数量由数据中变量的样本数量决定, 此外, RNN最大时延步长τ=3。本文采用四种模型评价指标评估算法所建模型性能, 分别为: 模型规模(model size, M.S.)、正确率(C.R)、均方差(mean squared error, MSE)以及确定系数(coefficient of determination, R2)被定义如下:
1) 模型规模(M.S.): 算法选择的输入变量个数。
2) 正确率(C.R): 所选变量中正确变量的比例。
| $ C.R = \frac{{{n_c}}}{{M.S}} \times 100\% $ | (16) |
3) 均方差(MSE): 整个建模过程中使用的测试数据集中输出变量的实际值与预测值之间的均方差, 计算公式表示如下:
| $ MSE = \frac{{\sum\limits_{j = 1}^{{n_t}} {{{\left( {{y_j} - {{\hat y}_j}} \right)}^2}} }}{{{n_t}}} $ | (17) |
其中,yj和
4) 确定系数(R2): 预测值解释真实值的比例, 它衡量了预测值与真实值的吻合程度。
| $ {R^2} = 1 - \frac{{\sum\limits_j^n {{{\left( {{y_j} - {{\hat y}_j}} \right)}^2}} }}{{\sum\limits_j^n {{{\left( {{y_j} - \bar y} \right)}^2}} }} $ | (18) |
为验证所提出的NNG-RNN算法, 生成了一组具有时滞动态特性的Friedman数据集[25], 以模拟复杂过程数据集的多输入与时滞特征。本文使用的数据集有五个与输出变量相关的输入变量, 输出变量由下式决定:
| $ \begin{array}{l} \;\;\;\;\;\;\;{y^t} = 10\sin \left( {\pi \;x_1^t\;x_2^t} \right) + 20{\left( {x_3^t - 0.5} \right)^2} + \\ 10\left( {x_4^{t - 1} + x_4^{t - 2} + x_4^{t - 3}} \right) + 5x_5^t + \varepsilon \end{array} $ | (19) |
其中,自变量x由(0, 1)之间均匀分布的随机数组成, ε为高斯噪声。原始Friedman数据集由5个输入变量按式(19)运算得对应y值, 为测试算法性能, 随机生成25个无关变量[x5, x6, ⋯, x30] 作为输入变量一部分, 与5个相关变量一起构成30个变量加入建模过程;同时, 对4号输入变量x4增加延迟特性即将4号变量前3个时刻数据
在本例中, 共生成2 000组数据, 80%用于训练, 其余用于测试。具体的模型评价指标数值记录于表 1中。
| 表 1 数值仿真不同算法的结果对比 |
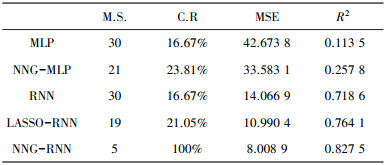 |
由表 1可以看出: RNN性能优于MLP, 这得益于其隐含节点的循环反馈功能, 使得RNN更能提取时序数据中的信息。此外, NNG算法的加入对两类网络均有优化和提高, 而NNG对RNN输入层至隐含层及隐含层循环权重的同时压缩和优化, 相较于MLP仅对输入层至隐含层的优化, 压缩力度更大, 对输入变量的筛选更加准确, 模型结构更简化, 预测性能也有显著提高。LASSO优化算法则在模型规模、正选率方面与NNG相差甚远, 均方差与确定系数也略逊于NNG。
图 4、图 5分别从误差与拟合效果两个角度对不同算法的性能进行展示。由图 4可得, 由MLP至NNG-RNN5种算法的误差范围逐渐缩小向0差值聚集, 并在NNG-RNN算法中达到顶峰, 且该算法预测误差的正态分布曲线所构成面积最小。图 5显而易见, NNG-RNN算法的拟合曲线, 红线几乎覆盖了所有的蓝线, 也就是说, 预测值与真实值高度重合, 且走势一致。综上, 本文所提出NNG-RNN算法预测偏差最小, 拟合程度最高, 均优于其他算法, 具有明显的有效性和优越性。
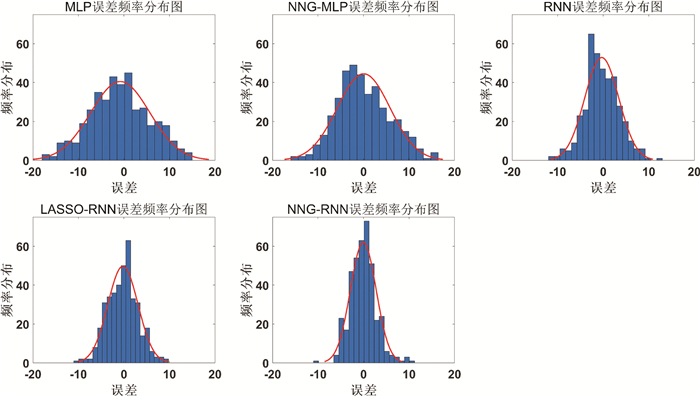 |
| 图 4 误差频率分布直方图及正态曲线 |
 |
| 图 5 不同算法拟合曲线图 |
4 结论
本文提出一种面向RNN的变量选择与结构优化算法, 用以解决RNN输入变量多、时序复杂, 结构冗余等问题。该算法充分利用RNN对时序信息的挖掘和处理能力, 结合NNG算法对RNN输入与循环层的约束压缩, 并利用滚动交叉验证策略确定绞杀参数, 从而得到了一种模型简化、泛化能力更强的动态神经网络。最后, 利用动态过程数据集对所提出算法进行仿真与性能测试, 实验结果表明, 本算法各项性能指标均优于其他算法, 具有更简化的动态模型结构和更强的泛化能力。
| [1] |
崔少华, 李素文, 汪徐德. BP神经网络和SVD算法联合的地震数据去噪方法[J]. 电子测量与仪器学报, 2020, 34(2): 12-19. |
| [2] |
范馨月, 王清青, 查筑红, 等. ICU患者感染发病率的RBF神经网络模型预测效果评价[J]. 中华医院感染学杂志, 2019, 29(11): 1727-1731. |
| [3] |
刘村, 李元祥, 周拥军, 等. 基于卷积神经网络的视频图像超分辨率重建方法[J]. 计算机应用研究, 2019, 36(4): 1256-1260, 1274. |
| [4] |
黄强娟. 时序网络结构建模与演化分析研究[D]. 长沙: 国防科技大学, 2019.
|
| [5] |
LIPTON ZC, BERKOWITZ J, ELKAN C. A critical review of recurrent neural networks for sequence learning[J]. arXiv preprint arXiv: 1506.00019, 2015.
|
| [6] |
HONGKANG W, LI L, YONG W, et al. Recurrent neural network model for prediction of microclimate in solar greenhouse[J]. IFAC-PapersOnLine, 2018, 51(17): 790-795. DOI:10.1016/j.ifacol.2018.08.099 |
| [7] |
王洪亮, 穆龙新, 时付更, 等. 基于循环神经网络的油田特高含水期产量预测方法[J]. 石油勘探与开发, 2020, 47(5): 1009-1015. |
| [8] |
陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137. |
| [9] |
SUN K, TIAN P, QI H, et al. An improved normalized mutual information variable selection algorithm for neural network-based soft sensors[J]. Sensors, 2019, 19(24): 5368. DOI:10.3390/s19245368 |
| [10] |
WANG Y, MA X, QIAN P. Wind turbine fault detection and identification through PCA-based optimal variable selection[J]. IEEE Transactions on Sustainable Energy, 2018, 9(4): 1627-1635. DOI:10.1109/TSTE.2018.2801625 |
| [11] |
LIU Y, SINGLETON A, ARRIBAS-BEL D. A principal component analysis (PCA)-based framework for automated variable selection in geodemographic classification[J]. Geo-spatial Information Science, 2019, 22(4): 251-264. DOI:10.1080/10095020.2019.1621549 |
| [12] |
UTAZIRUBANDA J C, M LEON T, NGOM P. Variable selection with group LASSO approach: application to cox regression with frailty model[J]. Communications in Statistics-Simulation and Computation, 2021, 50(3): 881-901. DOI:10.1080/03610918.2019.1571605 |
| [13] |
BREIMAN L. Better subset regression using the nonnegative garrote[J]. Technometrics, 1995, 37(4): 373-384. DOI:10.1080/00401706.1995.10484371 |
| [14] |
SUN K, LIU J, KANG J L, et al. Development of a variable selection method for soft sensor using artificial neural network and nonnegative garrote[J]. Journal of Process Control, 2014, 24(7): 1068-1075. DOI:10.1016/j.jprocont.2014.05.010 |
| [15] |
SUN K, WU X, XUE J, et al. Development of a new multi-layer perceptron based soft sensor for SO2 emissions in power plant[J]. Journal of Process Control, 2019, 84: 182-191. DOI:10.1016/j.jprocont.2019.10.007 |
| [16] |
杨丽, 吴雨茜, 王俊丽, 等. 循环神经网络研究综述[J]. 计算机应用, 2018, 38(S2): 1-6, 26. |
| [17] |
曾津, 周建军. 高维数据变量选择方法综述[J]. 数理统计与管理, 2017, 36(04): 678-692. |
| [18] |
王大荣, 张忠占. 线性回归模型中变量选择方法综述[J]. 数理统计与管理, 2010, 29(4): 615-627. |
| [19] |
XIA L, LING J, XU Z, et al. Application of sequential quadratic programming based on active set method in cleaner production[J]. Clean Technologies and Environmental Policy, 2021(prepublish): 1-10. DOI:10.1007/s10098-021-02207-8?utm_source=xmol |
| [20] |
FLETCHER R. A general quadratic programming algorithm[J]. IMA Journal of Applied Mathematics, 1971, 7(1): 76-91. DOI:10.1093/imamat/7.1.76 |
| [21] |
SAUD S, JAMIL B, UPADHYAY Y, et al. Performance improvement of empirical models for estimation of global solar radiation in India: a k-fold cross-validation approach[J]. Sustainable Energy Technologies and Assessments, 2020, 40: 100768. DOI:10.1016/j.seta.2020.100768 |
| [22] |
TASHMAN L J. Out-of-sample tests of forecasting accuracy: an analysis and review[J]. International Journal of Forecasting, 2000, 16(4): 437-450. DOI:10.1016/S0169-2070(00)00065-0 |
| [23] |
BERGMEIR C, BENITEZ J M. On the use of cross-validation for time series predictor evaluation[J]. Information Sciences, 2012, 191: 192-213. DOI:10.1016/j.ins.2011.12.028 |
| [24] |
LEE J H, SHI Z, GAO Z. On LASSO for predictive regression[J]. Journal of Econometrics, 2021(6). |
| [25] |
FRIEDMAN J H. Multivariate adaptive regression splines[J]. The Annals of Statistics, 1991, 1-67. |
 2021, Vol. 35
2021, Vol. 35


