| 变系数聚焦Manakov方程组的精确解 |
1970年以来,孤立子现象的研究受到物理学家和数学家的高度重视。孤立子可以保持其形状和速度不变,从而实现远距离保真通信[1-3],因此在光纤通信领域中有着非常重要的研究意义。纤维介质中多个脉冲的共同传播现象可以用聚焦Manakov方程组描述[4]。本文研究下述更一般的变系数聚焦Manakov方程组:
| $ \begin{array}{l} i\frac{{\partial {u_k}}}{{\partial t}} + r{\nabla ^2}{u_k} + 2nr\left( {\sum\limits_{j = 1}^m {{{\left| {{u_j}} \right|}^2}} } \right){u_k} + \\ \sum\limits_{i = 1}^n {\left( {{F_k} + \psi {x_i}} \right){u_k} = 0} \\ k = 1,2, \cdots ,m \end{array} $ | (1) |
方程中i为虚数单位,函数uk=uk(x1, x2, …, xn, t)是n+1维复函数,系数r=r(t), Fk=Fk(t), ψ=ψ(t)是t的任意实函数,拉普拉斯算子
设g(x, t), f(x, t)为变量t与x的可微函数,定义函数对(g, f)上的双线性微分算子[5]为:
| $ \begin{array}{l} D_t^mD_x^ng \cdot f = \frac{{{\partial ^m}}}{{\partial {s^m}}}\frac{{{\partial ^n}}}{{\partial {y^n}}}g(x + y,t + s)f(x + y,\\ t + s)\left| {_{y = 0,s = 0}} \right. \end{array} $ | (2) |
由定义可得双线性微分算子具有如下性质:
| $ \begin{array}{*{20}{l}} {{D_t}g \cdot f = gf - {f_t}g}\\ {{D_x}g \cdot f = {g_x}f - {f_x}g}\\ {D_x^2g \cdot f = {g_{xx}}f - 2{g_x}{f_x} + {f_{xx}}g}\\ {D_x^2f \cdot f = {f_{xy}}f - 2{f_x}{f_x} + {f_{xy}}f} \end{array} $ | (3) |
这里的下标表示偏导数。特别的,双线性微分算子还具有下列重要性质:
| $ D_t^mD_x^n\exp \delta \cdot \exp \delta = 0 $ | (4) |
为了求解方程组(1),我们先作如下有理变换:
| $ {u_k}\left( {{x_1},{x_2}, \cdots ,{x_n},t} \right) = \frac{{{g_k}\left( {{x_1},{x_2}, \cdots ,{x_n},t} \right)}}{{f\left( {{x_1},{x_2}, \cdots ,{x_n},t} \right)}} $ | (5) |
其中f(x1, x2, …, xn, t)是实函数,gk(x1, x2, …, xn, t)是复函数。
将有理变换(5)代入方程组(1)中,整理可得:
| $ \begin{array}{l} i\left( {\frac{{\partial {g_k}}}{{\partial t}}f - \frac{{\partial f}}{{\partial t}}{g_k}} \right) + \sum\limits_{i = 1}^n r \left( {\frac{{{\partial ^2}{g_k}}}{{\partial x_i^2}}f - 2\frac{{\partial {g_k}}}{{\partial {x_i}}}\frac{{\partial f}}{{\partial {x_i}}} + } \right.\\ \left. {\frac{{{\partial ^2}f}}{{\partial x_i^2}}{g_k}} \right) + \frac{1}{{{f^2}}}\left[ {\sum\limits_{i = 1}^n r \left( {2{g_k}f{{\left( {\frac{{{\partial ^2}f}}{{\partial {x_i}}}} \right)}^2} - 2{g_k}{f^2}\frac{{{\partial ^2}f}}{{\partial x_i^2}}} \right) + } \right.\\ \left. {2nr\left( {\sum\limits_{j = 1}^m {{g_j}} {g_j}} \right){g_k}f} \right] + \sum\limits_{i = 1}^n {\left( {{F_k} + \psi {x_i}} \right)} {g_k}f = 0\\ \;\;\;\;\;\;k = 1,2, \cdots ,m \end{array} $ | (6) |
借助双线性微分算子定义及其性质,可将方程组(6)写成如下两个双线性形式的方程:
| $ \begin{array}{l} \sum\limits_{i = 1}^n {D_{{x_i}}^2} f \cdot f - 2n\sum\limits_{j = 1}^m {\left( {{g_j}g_j^*} \right)} = 0\\ i{D_t}{g_k} \cdot f + r\left( {\sum\limits_{i = 1}^n {D_{{x_i}}^2{g_k}} \cdot f} \right) + \sum\limits_{i = 1}^n {\left( {{F_k} + } \right.} \\ \left. {\psi {x_i}} \right){g_k}f = 0\\ k = 1,2, \cdots ,m \end{array} $ | (7) |
通过Pade近似[6]的方法,将gk和f展成小参数ε的幂级数:
| $ \begin{array}{*{20}{l}} {f = 1 + {f_2}{\varepsilon ^2} + {f_4}{\varepsilon ^4} + \cdots }\\ {{g_k} = {g_{k1}}\varepsilon + {g_{k3}}{\varepsilon ^3} + \cdots } \end{array} $ | (8) |
将摄动展开式(8)代入到双线性形式(7)中,并对比ε的同次幂系数,可得如下系数方程组:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {i\frac{{\partial {g_{k1}}}}{{\partial t}} + r\sum\limits_{i = 1}^n {\frac{{\partial {g_{k1}}}}{{\partial {x_i}}}} + \sum\limits_{i = 1}^n {\left( {{F_k}(t) + \psi {x_i}} \right)} {g_{k1}} = 0}\\ {\sum\limits_{i = 1}^n {\frac{{{\partial ^2}{f_2}}}{{\partial x_i^2}}} - n\sum\limits_{j = 1}^m {\left( {{g_{j1}}g_{j1}^*} \right)} = 0} \end{array}\\ i\left( {\frac{{\partial {g_{k1}}}}{{\partial t}}{f_2} - {g_{k1}}\frac{{\partial {f_2}}}{{\partial t}} + \frac{{\partial {g_{k3}}}}{{\partial t}}} \right) + \sum\limits_{i = 1}^n {\left( {{F_k} + \psi {x_i}} \right)} \\ \begin{array}{*{20}{l}} {\left( {{g_{k1}}{f_2} + {g_{k3}}} \right) + r\sum\limits_{i = 1}^n {\left( {\frac{{{\partial ^2}{g_{k1}}}}{{\partial x_i^2}}{f_2} - 2\frac{{\partial {g_{k1}}}}{{\partial {x_i}}} + {g_{k1}}\frac{{{\partial ^2}{f_2}}}{{\partial x_i^2}} + } \right.} }\\ {\left. {\frac{{{\partial ^2}{g_{k3}}}}{{\partial x_i^2}}} \right) = 0} \end{array}\\ \;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\left( {\frac{{{\partial ^2}{f_4}}}{{\partial x_i^2}} + {f_2}\frac{{{\partial ^2}{f_2}}}{{\partial x_i^2}} - {{\left( {\frac{{\partial {f_2}}}{{\partial {x_i}}}} \right)}^2}} \right)} - n\sum\limits_{j = 1}^m {\left( {{g_{j1}}g_{j3}^* + } \right.} \\ \left. {{g_{j3}}g_{j1}^*} \right) = 0\\ \;\;\;\;\;\;\;\; \cdots \cdots \\ \;\;\;\;\;\;\;\;k = 1,2, \cdots ,m \end{array} $ | (9) |
对双线性形式(7)作摄动方法时,根据双线性微分算子的性质(4),选择指数函数解[5]作为解的N阶近似时,摄动展开(8)在有限项处截断,使得εi, i=N+1, N+2, …项的系数全为零,从而得到方程组(1)的精确解。这里得到的精确解在传播时不改变形状,即是一种孤立波解,称这样的解为方程组的N-孤子解。
3 精确解将系数方程组(9)中的函数展成指数函数的幂级数:
| $ {g_{k1}} = \sum\limits_{j = 1}^N {{a_{kj}}} \mathit{exp}\left( {{b_{kj}}\left( {{x_1},{x_2}, \ldots ,{x_n},t} \right)} \right) $ | (10) |
其中akj是任意非零常数,bkj(x1, x2, ..., xn, t)是待定的复函数,j=1, 2, …, N。将幂级数(10)代入系数方程组(9),求解得到方程组(1)的精确解:
| $ \begin{array}{l} {u_k} = \frac{{\sum\limits_{j = 1}^N {{a_{kj}}} \exp \left( {{b_{kj}}} \right) + \sum\limits_{j \in \Lambda } {\exp } \left( {\sum\limits_{l \in \Lambda } {{b_{kjl}}} + \sum\limits_{l \in \Lambda } {b_{kjl}^*} + \sum\limits_{l \in \Lambda } {{b_l}} } \right)}}{{1 + \sum\limits_{j = 1}^N {\exp } \left( {{b_{kj}} + b_{kj}^* + {b_j}} \right) + \sum\limits_{l \in \Lambda } {\exp } \left( {\sum\limits_{l \in \Lambda } {{b_{kjl}}} + \sum\limits_{l \in \Lambda } {b_{kjl}^*} + \sum\limits_{l \in \Lambda } {{b_l}} } \right)}}\\ \;\;\;\;\;\;\;k = 1,2, \cdots ,m \end{array} $ |
此解为方程组(1)的N-孤子解,其中Λ={1, 2, …, N}是指标集,
取常数N=1,即:
| $ {g_{k1}} = {a_{k1}}\mathit{exp}\left( {{\mu _{k1}} + i{\nu _{k1}}} \right) $ | (11) |
其中ak1是任意非零常数,bk1=μk1+iνk1是待求复函数。
将(11)代入系数方程组(9),可得f的幂级数展开系数,根据双线性微分算子的性质(4)得:
| $ \begin{array}{*{20}{l}} {{g_{kj}} = 0,k = 1,2, \cdots ,m,j = 3,5, \cdots }\\ {{f_j} = 0,j = 4,6, \cdots } \end{array} $ |
进而求得方程组(1)的单孤子解:
| $ \begin{array}{*{20}{l}} {{u_k} = \frac{{{a_{k1}}\mathit{exp}\left( {{\mu _{k1}} + i{\nu _{k1}}} \right)}}{{1 + \mathit{exp}\left( {2{\mu _{k1}} + {b_0}} \right)}}}\\ {k = 1,2, \cdots ,m} \end{array} $ | (12) |
其中:
| $ \begin{array}{l} \exp \left( {{b_0}} \right) = \frac{{\sum\limits_{i = 1}^n {a_{i1}^2} }}{{4C_1^2}}\\ {\mu _{k1}} = \sum\limits_{j = 1}^n {\left( {{C_1}{x_j} - 2{C_1}\int r \left( {\int \psi dt} \right)dt} \right)} \\ {\nu _{k1}} = \sum\limits_{j = 1}^n {\left( {\int {\left( {rC_1^2 + {F_j}(t) - r{{\left( {\int \psi dt} \right)}^2}} \right)dt} } \right.} \\ \left. { + {x_j}\int \psi dt} \right) \end{array} $ |
取定n=1, m=1, r=1/2, F=f(t)时,变系数聚焦Manakov方程组(1)即为:
| $ i{u_t} + \frac{1}{2}{u_{xx}} + {\left| u \right|^2}u + (f(t) + x \cdot \psi (t))u = 0 $ | (13) |
其中u=u(x, t),f(t)是任意实函数。
方程(13)又描述准一维Bose-Einstein凝聚孤子动力学的具有线性势的单分量非线性Schrödinger方程[7]。该方程的单孤子解为:
| $ u = \frac{{{e^{{C_1}x - 2{C_1}}}\int {\frac{1}{2}} \left( {\int \psi dt} \right)dt + i\left( {\int {\left( {\frac{1}{2}C_1^2 + f(t) - \frac{1}{2}{{\left( {\int \psi dt} \right)}^2}} \right)dt} + x\int \psi dt} \right)}}{{1 + {e^{2\left( {{C_1}x - 2{C_1}\int {\frac{1}{2}} \left( {\int \psi dt} \right)dt} \right) + \ln \frac{1}{{4C_1^2}}}}}} $ | (14) |
(a)若ψ(t)=0,此时方程(13)就是我们平常所讨论的非线性Schrödinger方程。取定常数
| $ |u{|^2} = \frac{{{e^{x + 1}}}}{{{{\left( {1 + {e^{x + 1}}} \right)}^2}}} $ |
(b)若ψ(t)=2(1+cost),取定常数C1=12,则:
| $ |u{|^2} = \frac{{{e^{2\cos t - {t^2} + x + 1}}}}{{{{\left( {1 + {e^{2\cos t - {t^2} + x + 1}}} \right)}^2}}} $ |
取定n=1, m=1, r=12·t, F=f(t)时,变系数聚焦Manakov方程组(1)变为:
| $ i{u_t} + \frac{1}{2}t{u_{xx}} + |u{|^2}u + (f(t) + x \cdot \psi (t))u = 0 $ | (15) |
其单孤子解为:
| $ u = \frac{{{e^{{C_1}x - 2{C_1}\int {\frac{1}{2}} t\left( {\int \psi dt} \right)dt + i\left( {\int {\left( {\frac{1}{2}tC_1^2 + f(t) - \frac{1}{2}t{{\left( {\int \psi dt} \right)}^2}} \right)} dt + x\int \psi dt} \right)}}}}{{1 + {e^{2\left( {{C_1}x - 2{C_1}\int {\frac{1}{2}} t\left( {\int \psi dt} \right)dt} \right) + \ln \frac{1}{{4C_1^2}}}}}} $ |
(c)若ψ(t)=3t2+2t+1,取定常数
| $ {\left| u \right|^2} = \frac{{{e^{x - \left( {\frac{1}{5}{t^5} + \frac{1}{4}{t^4} + \frac{1}{3}{t^3} + \frac{1}{2}{t^2}} \right)}}}}{{{{\left( {1 + {e^{x - \left( {\frac{1}{5}{t^5} + \frac{1}{4}{t^4}{t^4} + {{\frac{1}{3}}^3}{t^2} + {{\frac{1}{2}}^2}} \right)}}} \right)}^2}}} $ |
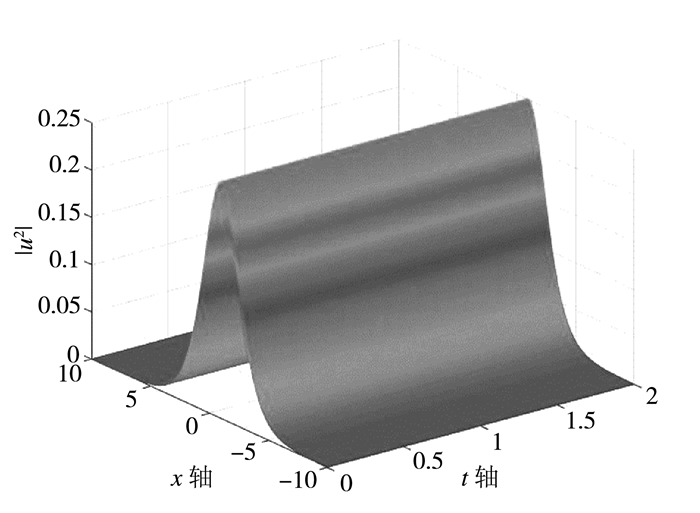 |
| 图 1 方程(a)的单孤子解图像 |
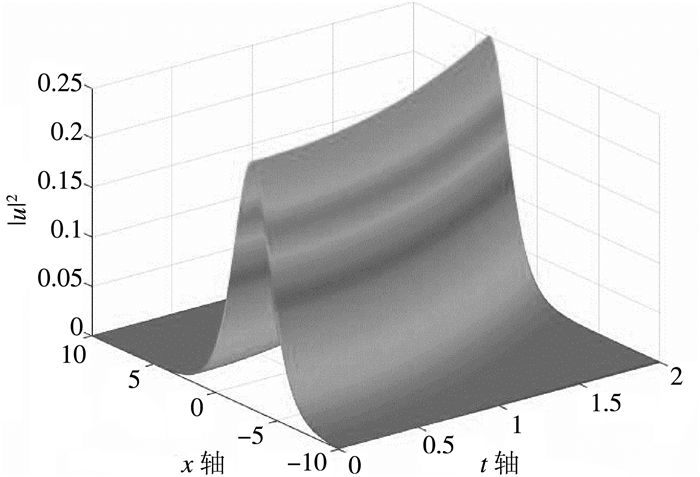 |
| 图 2 方程(b)的单孤子解图像 |
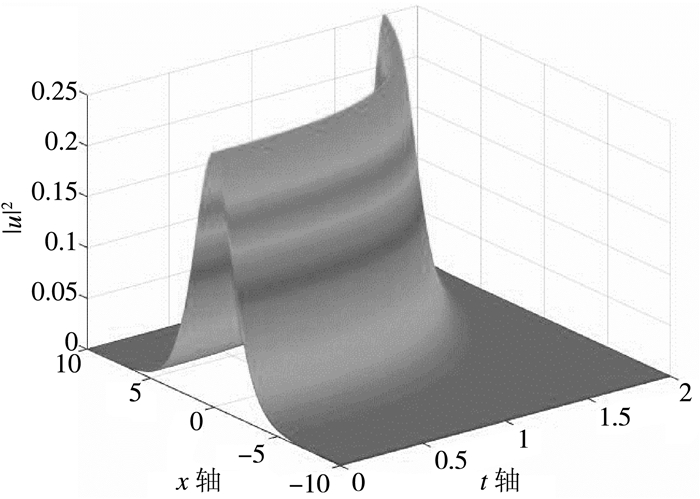 |
| 图 3 方程(c)的单孤子解图像 |
4 结语
本文利用双线性形式和摄动方法研究了更一般的变系数聚焦Manakov方程组,给出了方程组的N-孤子精确解的求解方法,最后又画出了单孤子解的图像,研究了解其动力学行为。该方程组在物理学中的更广泛应用还有待进一步研究。
| [1] |
HASEGAWA A. Opticalsolitons in Fibers[M]. Berlin: Springer-Verlag, 1989.
|
| [2] |
HASEGAWA A, KODAMA Y. Solitons in Optical Communication[M]. Oxford: Oxford University Press, 1995.
|
| [3] |
RADHAKRISHNAN R, LAKSHMANAN M. Bright and darksoliton solutions to coupled non-linear Schrödinger equations[J]. Journal of physics A General physics, 1995, 28(9): 2683-2692. |
| [4] |
WANG D S, CHEN J. New integrable variable-coefficient coupled nonlinear schrodinger equations and their soliton solutions[J]. Chinese Journal of Contemporary Mathematics, 2012, 33(2): 23-26. |
| [5] |
HIROTA R. The Direct Method in Soliton Theory[M]. Cambridge: Cambridge University Press, 2005.
|
| [6] |
BAKER G A, GAMMEL G L. The Pade Approximant in Theoretical Physics[M]. New York: Academic Press, 1970.
|
| [7] |
LI Z D, LI Q Y, HU X H, et al. Hirota method for the nonlinear Schrödinger equation with an arbitrary linear time-dependent potential[J]. Annals of Physics, 2007, 322(11): 2545-2553. DOI:10.1016/j.aop.2006.11.012 |
 2019, Vol. 33
2019, Vol. 33


