| 永磁同步电机双PI解耦控制 |
永磁同步电机是通过永磁体来发出励磁磁场, 以此来实现电能与机械能之间进行互相转换的一种电磁装置。我国相对于其他国家来说, 永磁体材料是比较多的, 尤其是一种新发现的稀土永磁材料——钕铁硼, 这种材料在我国的储量十分丰富, 这使得永磁同步电机在我国有极好的应用前景[1-3]。
将三相电流通入到永磁同步电机的定子之间, 这时在定子之间会产生一个旋转的磁场, 由于一个永磁体被插入电机的转子中间, 而在这个永磁体中间有着一个固定的磁极。根据磁极的基本原理, 电机的转子会跟着其定子中间的旋转磁场来转动。这样, 电机的转子转动的速度就会与旋转磁场的转速相似。
随着各种容量的电机被开发, 其被运用的范围也越来越广泛, 在不同的地方都占有极大的优势。永磁同步电动机的结构在一些地方是相似的, 电机的矢量控制时, 由于两相旋转坐标系之下的交直轴相互影响, 两相之间会存在耦合分量, 而当电机转速发生快速改变的时候, 会对电机的性能产生一些不必要的影响, 所以通常为避免这种情况, 需要进行必要的解耦控制, 因此提出了一种双PI解耦控制原理的新型解耦控制方法。
1 PMSM的矢量控制模型PMSM的A、B、C三相对称绕组被安装在其定子上。由于电机的定子与转子两者中间存在相对运动, 它们的位置关系也总是跟着时间的变化而不断的改变, 所以定子与转子的各个参数之间电磁耦合关系表现的尤为复杂。
分析PMSM的定转子的变化十分困难。在不会让电机分析出现误差的条件下, 为了简化对PMSM的分析, 需要对电机做出如下的一些假设[4]:1)忽略铁心饱和, 磁路饱和、磁滞和涡流影响;2)电机定子的铁心中间, 三个相会沿着其对称分布, 而在空间中, 三个相互差120°电角度;3)转子上没有阻尼绕组, 永磁体无阻尼作用;4)电机定子的电动势按正弦的变化规律产生变化, 定子电流在气隙中假定为只会正弦变化, 磁场中不计高谐波电势。
矢量控制广泛用于各类交流同步电机的调节速度的的系统中, 永磁同步电机的矢量控制, 它的基本原理是考虑在三种坐标系之间的坐标变化、电磁转矩的基础上, 对于永磁同步电机, 可以通过矢量变化来分解其定子电流, 让其与直流电机的结原理相类似。由于我们对直流电机的控制技术已经极为成熟, 因此我们把同步电机类似于直流电机, 我们就能很好的控制永磁同步电机[5-6]。在转子磁链定向的坐标系上, 把电机定子电流分解成两个相互垂直的分量——励磁电流分量、转矩电流分量, 两者的作用是用于产生磁场和电磁转矩[7], 然后可以将它们分别控制, 这样永磁同步电机的原理就可以接近直流电机。
PMSM矢量控制的基本原理是通过对定子电流的控制从而来进行对输出转矩的控制本文所研究的是id=0控制[8-9], 也称磁场定向控制。这种方法没有直轴电流, 只有控制输出转矩的交轴电流分量iq, 这时电机的电流全部来产生电磁转使得电流得到的控制效率极高。对于表贴式电机, 在id=0时, 电机的电流在这时会有最大的电磁力矩。
基于id=0的PMSM的矢量控制系统原理图如图 1所示。其采用的是双闭环结构, 一般为外环转速环与内环电流环。转速环可以根据对速度指令的追踪结果来消除各种影响最终结果负面因素, 而电流环则通过对速度指令ω的追踪来消除各种负面因素。
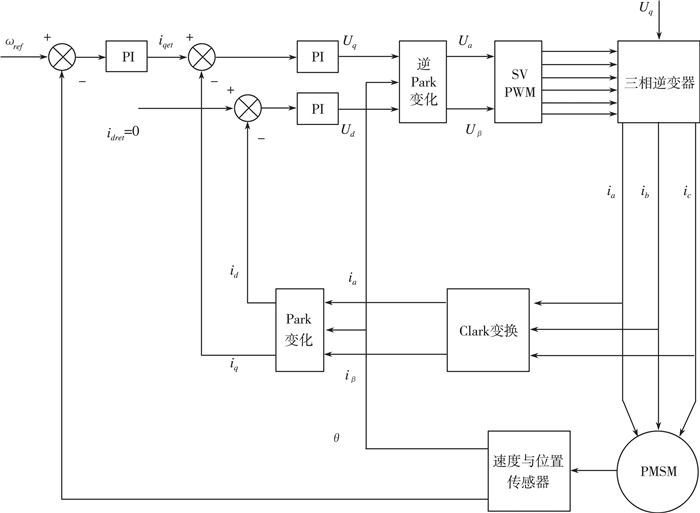 |
| 图 1 PMSM矢量控制框图 |
下列是基于矢量控制的对PMSM的调速控制:输出电压Udc, 通过三相逆变器得到ia、ib、ic。三相电流经过CLARK变换, 即可以得到两相静止坐标系下的电流iα、iβ, 两相静止电流再通过PARK变换, 则可以得到两相旋转坐标系下的电流id、iq。与此同时, 速度与位置传感器把转子的位置信号θ传递给逆PARK变换与PARK变换, 为两者的变换做好了角度基础;把转子速度外环实际所测值ω反馈给速度给定值ωref。
转子速度外环实际所测值ω与速度给定值ωref之差, 当成速度外环PI调节器的输入值, 经过PI调节之后得到转矩电流给定值iqref。由于是基于id=0矢量控制方法, 所以对于内环电流调节器中励磁电流给定值idref=0。转矩电流给定值iqref与q轴电流的反馈值id之差作为内环电流PI调节器的输入信号, 经过PI调节后得到两相旋转坐标系下的电压信号ua、ub[10]。两个电压值经过逆PARK变换得到uα、uβ作为SVPWM的输入信号, 经过三相逆变器, 产生三相正弦交流电输入PMSM的定子绕组, 发出磁场让转子转动来实现对电机的矢量控制。
2 PMSM的双PI解耦控制系统 2.1 PI控制器具有比例-积分控制规律的控制器称为PI控制器, 它是一种线性的控制器, 其输出信号同时成比例的反应输入信号及其积分, 根据实际指令值和和输出值之间的误差, 将构成控制量去对被控对象进行控制[11]。
PI控制器分为一个比例环节和一个积分环节, 两者分别有着不同的作用。比例环节将产生的误差信号进行控制, 以此降低输入信号与指令值的偏差大小。
而积分环节则可以让系统消除稳态误差, 而如果误差一直存在, 积分环节的调节作用就一直存在, 而积分调节的功能大小也是依据积分常数Ti的大小。拥有积分调节功能时, 系统性能可以更好被调节。
PI调节器可以消除或减小系统的稳态误差从而使系统的稳态性能更为完好, 所以它广泛用于各种具有大惯性的被控对象。
2.2 双PI解耦控制原理由前面的矢量控制框图可知, 因为一个电流环的电流产生, 导致电流环d轴与q轴电流之间有着一个影响它们的耦合电压产生[12]。所以我们利用双PI解耦控制, 在电流环的PI控制器后面额外各增添一个PI控制器, 这时我们可以通过对实时反馈得到的电流值来与给定值进行作差得出的值来调节这个耦合电压的大小[13]。
在PMSM矢量控制系统中, 可以依据电流和给定值两者的偏差, 在原本的电流环中新添两个PI调节器, 这样得出所需要的补偿电压的大小。通过计算我们可以得出所需要的补偿电压的大小, 把其添加到d、q轴的电压上面, 我们就可以对同步电机的耦合进行解耦[14]。
PMSM双PI解耦系统中的d轴电流与q轴电流的传递函数表示为
| $ R{i_d} + {L_d}s{i_d} - \omega {L_q}{i_q} = P{I_1}\left( {i_d^* - {i_d}} \right) - P{I_4}\left( {i_q^* - {i_q}} \right) $ | (1) |
| $ R{i_q} + {L_q}s{i_q} - \omega {L_d}{i_d} = P{I_2}\left( {i_q^* - {i_q}} \right) - P{I_3}\left( {i_d^* - {i_d}} \right) $ | (2) |
结合式(1)和(2), 可得
| $ {i_d}\left( {P{I_1} + R + s{L_d}} \right) + {i_q}\left( {P{I_4} - \omega {L_q}} \right) = P{I_1}i_d^* + P{I_4}i_q^* $ | (3) |
| $ {i_q}\left( {P{I_2} + R + s{L_q}} \right) + {i_d}\left( {P{I_3} + \omega {L_d}} \right) = P{I_3}i_d^* + P{I_2}i_q^* $ | (4) |
用矩阵表示即为
| $ \left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] = \frac{1}{\mathit{\Delta } }\left[ {\begin{array}{*{20}{c}} {{g_{dd}}}&{{g_{dq}}}\\ {{g_{qd}}}&{{g_{qq}}} \end{array}} \right] $ | (5) |
以上的矩阵中各个系数的值分别为
| $ {g_{dd}} = P{I_1}\left( {P{I_2} + R + s{L_q}} \right) - P{I_3}\left( {P{I_4} - \omega {L_q}} \right) $ |
| $ {g_{dq}} = P{I_4}\left( {P{I_2} + R + s{L_q}} \right) - P{I_2}\left( {P{I_4} - \omega {L_q}} \right) $ |
| $ {g_{qd}} = P{I_3}\left( {P{I_1} + R + s{L_q}} \right) - P{I_4}\left( {P{I_3} + \omega {L_d}} \right) $ |
| $ {g_{qq}} = P{I_2}\left( {P{I_1} + R + s{L_q}} \right) - P{I_4}\left( {P{I_3} + \omega {L_d}} \right) $ |
根据上列各式, 可以观察出系数gdq决定了q轴电流相对于d轴电流大小的影响, 而系数gqd决定了d轴电流相对于q轴电流大小的影响。让gdq=0、gqd=0, 可以得到四个控制器的关系如式(6)、(7)所示。
| $ P{I_4} = \frac{{\omega {{\hat L}_q}}}{{R + s{{\hat L}_q}}}P{I_2} $ | (6) |
| $ P{I_3} = \frac{{\omega {L_d}}}{{R + s{{\hat L}_d}}}P{I_1} $ | (7) |
由此可得双PI解耦控制系统的原理图如图 2所示。
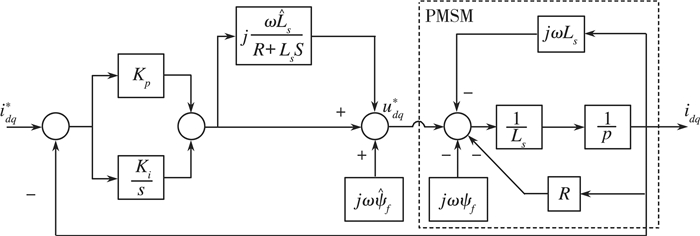 |
| 图 2 双PI解耦控制图 |
所以其开环传递函数是
| $ \begin{array}{l} G = \frac{{{K_p}s + {K_i}}}{s}\left( {1 + \frac{{j\omega {{\hat L}_s}}}{{\hat R + {{\hat L}_s}s}}} \right)\frac{1}{{s{L_s} + j\omega {L_s} + R}}\\ \;\;\; = \frac{{{K_p}s + {K_i}}}{{s\left( {\hat R + {{\hat L}_s}s} \right)}}\frac{{s{{\hat L}_s} + j\omega {{\hat L}_s} + R}}{{s{L_s} + j\omega {L_s} + R}} \end{array} $ | (8) |
通过图 1中PMSM的矢量结构原理框图我们可以看出, 它是一个内环为电流环, 外环为转速环的双闭环控制系统。我们在用双PI系统进行解耦控制时, 也是类似的设计时, 应该先将一个内环电流PI调节器当成外环的一部分, 先把另一个内环PI调节器设计成功, 再在其基础上设计外环[15-16]。
我们应该根据稳态和动态时的不同需求为主, 来设计电流环的结构, 让其在稳态时可以让电流无静差;在动态时可以快速的相应电机的实际电流。保证电机不会因为过流而损坏。
速度环在同步电机的矢量控制中, 也是有非常重要的作用, 它可以让电机实际的转速跟着目标的变化而快速变化。恰当的设计速度环可以使得同步电机的抗干扰性能大大提升。当设计恰当时, 其可以减小速度波形, 让电机系统达到无静差状态。
PMSM结构及电流环控制结构框图 3所示, 控制器输出电压为
| $ \left\{ {\begin{array}{*{20}{l}} {u_{sd}^* = \left( {{K_{P1}} + {K_{i1}}\frac{1}{s}} \right)\left( {i_{sd}^* - {i_{sd}}} \right)}\\ {u_{sq}^* = \left( {{K_{P2}} + {K_{i2}}\frac{1}{s}} \right)\left( {i_{sq}^* - {i_{sq}}} \right)} \end{array}} \right. $ | (9) |
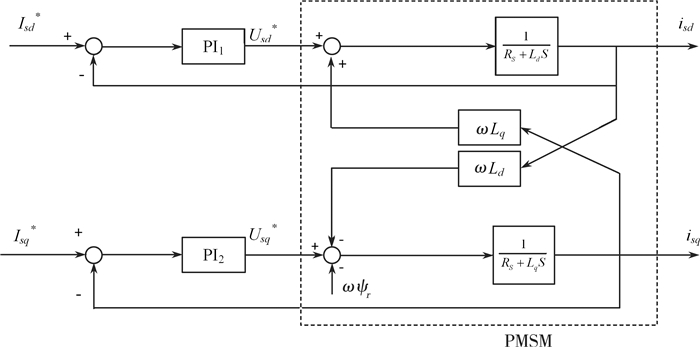 |
| 图 3 永磁同步电机电流环控制结构图 |
当使用电流反馈解耦的方法来对输出电压进行补偿时, 其方程为
| $ \left\{ {\begin{array}{*{20}{l}} {u_{sd}^* = \left( {{K_{P1}} + {K_{i1}}\frac{1}{s}} \right)\left( {i_{sd}^* - {i_{sd}}} \right) - \omega {{\hat L}_q}{i_{sq}}}\\ {u_{sq}^* = \left( {{K_{P2}} + {K_{i2}}\frac{1}{s}} \right)\left( {i_{sq}^* - {i_{sq}}} \right) + \omega {{\hat L}_d}{i_{sd}}}\\ { + \omega {{\mathit{\hat \Psi }}_r}} \end{array}} \right. $ | (10) |
因为当只有当参数的预想值与实际所得值相等时, 电机中的耦合电压才可能完全被消除。可是由于参数值的误差大小都在20%~30%之间, 因此这个方法不能够完全进行解耦控制。
PMSM的电流结构框图如图 3所示:
当同步电机仅仅使用转速双闭环控制系统时, 随着转速的增大, 系统中的耦合电流也随之增大, 所以我们进行解耦控制的时候, 需要把上面两式中的isq*分量和isd*分量都设为零, 所以有如(6)与(7)两式。
根据图 4我们可以得出
| $ \begin{array}{l} {i_{sd}} = \frac{1}{\Delta }\left\{ {i_{sd}^*\left[ {P{I_1}\left( {{R_s} + {L_q}s + P{I_2}} \right) + } \right.} \right.\\ \left. {P{I_3}\left( {\omega {L_q} + P{I_4}} \right)} \right] + {i_{sq}}P{I_2}\left( {\omega {L_q} + P{I_4}} \right) - P{I_4}(R\\ \left. { + {L_q}s + P{I_2}} \right) \end{array} $ | (11) |
| $ \begin{array}{l} {i_{sq}} = \frac{1}{\Delta }\left\{ {i_{sd}^*\left[ {P{I_3}\left( {{R_s} + {L_d}s + P{I_1}} \right)} \right.} \right.\\ \left. {P{I_1}\left( {\omega {L_d} + P{I_3}} \right)} \right] + {i_{sq}}\left[ {P{I_4}\left( {\omega {L_d} + P{I_3}} \right) + } \right.\\ \left. {\left. {P{I_2}\left( {{R_s} + {L_d}s + P{I_1}} \right)} \right]} \right\} \end{array} $ | (12) |
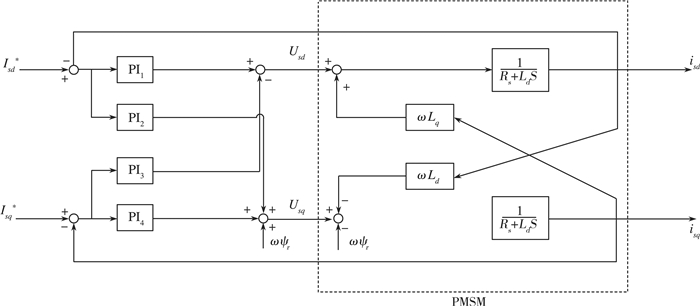 |
| 图 4 双PI解耦控制结构系统框图 |
然而, 在电机实际运行时, 因为一些因素, 我们需要把一些参数的估计值代替为实际值, 因此, 图 4变成如图 5所示。
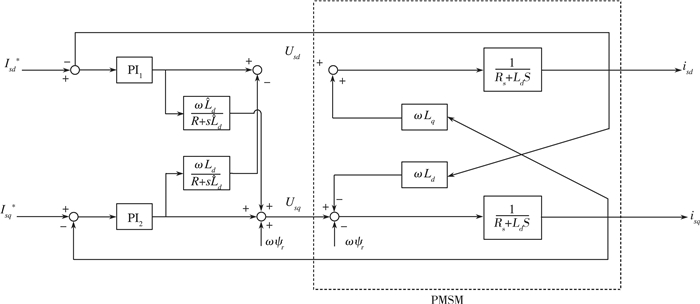 |
| 图 5 双PI解耦系统结构图 |
以励磁电流isd为例, 把永磁同步电机的耦合电压与补偿电压相减, 可得
| $ \Delta {u_{dc}} = {i_{sq}}\omega {L_q} - \left( {i_{sq}^* - {i_{sq}}} \right)P{I_4} $ | (13) |
在式(13)两边同时除isq*可得
| $ \frac{{\Delta {u_{dc}}}}{{i_q^*}} = \frac{{{i_{sq}}}}{{i_{sq}^*}}\left( {\omega {L_q} + P{I_4}} \right) $ | (14) |
式中
| $ \frac{{{i_{sq}}}}{{i_{sq}^*}} = \frac{F}{{1 + F}} $ | (15) |
| $ F = \frac{{P{I_2}}}{{R + {L_q}s}} $ | (16) |
所以
| $ \begin{array}{l} \frac{{\Delta {u_{dc}}}}{{i_{qq}^*}} = \frac{{\omega {L_q}F - P{I_4}}}{{1 + F}}\\ \;\;\;\;\;\;\;\; = \frac{{\omega {P_4}\left( {\frac{{{L_q}}}{{{R_s} + {L_q}s}} - \frac{{{{\hat L}_q}}}{{{{\hat R}_s} + {{\hat L}_q}s}}} \right)}}{{1 + F}} \end{array} $ | (17) |
因此, 由于参数估计而存在的误差补偿受到了负反馈的抑制, 极大的减少因为参数估计而引起的误差, 很好的解决了由于电机耦合带来的影响。
3 仿真实验结果在MATLAB中建立相应的仿真模型, 在同步电机的仿真模型中, 利用PI控制器来调节速度环和转速环; 建立了三个坐标变换模块:一个是三相坐标系变化到两相静止坐标系的的CLARK变换模块;一个是从两相静止坐标系到两相旋转坐标系下的PARK变换模块;另一个是从两相旋转到两相静止坐标系下的逆PARK变换模块; 构建一个输入为Ua、Ub、T、Udc, 输出为六个三相逆变器的门级驱动信号的SVPWM模块, 以上面几个模块为基础, 在于id=0的控制原理建立了永磁同步电机的仿真模型, 并对电机的未解耦和双PI解耦两种情况进行了仿真。电机的参数设置Ld=0.0085H, Lq=0.0085H, Rs=2.876 Ω。仿真的时间为0.3 s, 图 6未解耦情况下电机的交直轴的电流波形, 图 7为双PI解耦情况下电机的交直轴的电流波形。
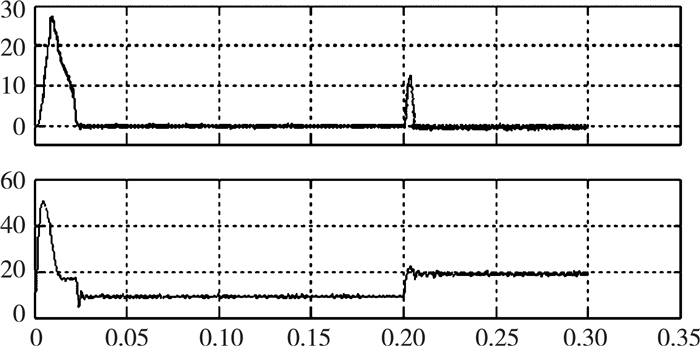 |
| 图 6 未解耦控制下电机直(上)交(下)电流波形 |
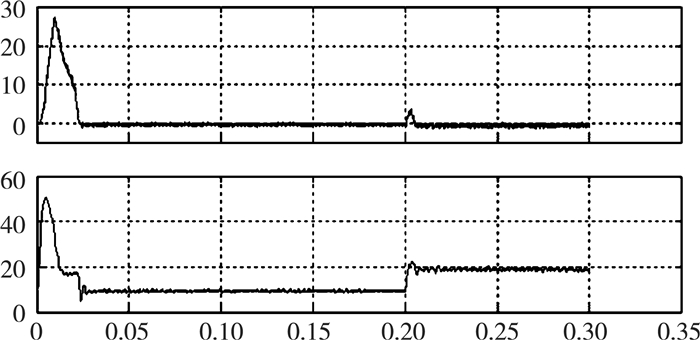 |
| 图 7 双PI解耦控制下电机直(上)交(下)电流波形 |
由图可以看出, 不加耦情况下, 当电机转速上升过程和交轴电流iq发生变化时, 直轴电流id也会相应的发生波动。与不加耦相比, 当电机进行双PI解耦时, 直轴电流id因为转速和转轴电流iq的变化而变化的影响很小, 这说明双PI解耦控制能对电机进行很好解耦控制。
4 结语对于永磁同步电机的强耦合、非线性等特点, 提出了用双PI解耦控制的方法, 在电流环的PI控制器后面额外各增添一个PI控制器来达到给电机耦合现象进行解耦的目标, 提高了永磁同步电机运行时的稳定性和精确性。仿真试验表明, 该解耦方法可以使永磁同步电机在参数发生变化时实现电机的动态解耦, 并使系统有良好的鲁棒性及稳定性。
| [1] |
林科振.低开关频率下永磁电机控制方法研究[D].北京: 北京交通大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10004-1014141156.htm
|
| [2] |
樊虎, 王恒东. 上海稀土永磁电机开发应用综述[J]. 电机技术, 1991(2): 24-27. |
| [3] |
LIXIN TANG, LIMIN ZHONG, RAHMAN M.F. A Novel direct torque controlled interior permanent magnet synchronous machine drive with low ripple in flux and torque and fixed switching frequency[J]. IEEE Transactions on Power Electronics, 2004, 19(2): 346-354. DOI:10.1109/TPEL.2003.823170 |
| [4] |
唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2004.
|
| [5] |
陈伯时. 电力拖动自动控制系统(运动控制系统)[M]. 北京: 机械工业出社, 2003.
|
| [6] |
谢宝昌, 任永德. 电机的DSP控制技术及其应用[M]. 北京: 北京航空航天大学出版, 2005.
|
| [7] |
肖有文, 夏长亮, 史婷娜. 四开关三相无刷直流电机两有效矢量调制电流控制策略[J]. 中国电机工程学报, 2014, 34(12): 1897-1904. |
| [8] |
TEXAS INSTRUMENTS. Implementation of a speed fieldOriented control of 3-phase PMSM using TMS320F240[M]. Literature Number: SPRA588, 1999.
|
| [9] |
YIFAN ZHAO, T.A.Lipo. Space vector PWM control of dual three-phase induction machine using vector space decomposition[J]. IEEE Transactions on Industry Applications, 1995, 31(5): 1100-1109. DOI:10.1109/28.464525 |
| [10] |
金光哲, 徐殿国, 高强. 高频注入电压预估同步电机转子位置检测方法[J]. 中国电机工程学报, 2014, 34(9): 1376-1383. |
| [11] |
周扬忠, 胡育文, 田蕉. 永磁同步电机控制系统中变比例系数转矩调节器设计研究[J]. 中国电机工程学报, 2004, 24(9): 204-208. DOI:10.3321/j.issn:0258-8013.2004.09.036 |
| [12] |
郭希铮, 游小杰, 王晓丹. 永磁同步电机电流调节器动态特改进方法分析[J]. 电力自动化设备, 2011, 31(6): 39-44. DOI:10.3969/j.issn.1006-6047.2011.06.009 |
| [13] |
BAO-jUN WANG, JIA-jUN Wang. Sliding mode control of surface-mount permanent-magnet synchronous motor based on error model with unknown load[J]. Journal of Software, 2011, 6(5): 819-825. |
| [14] |
周渊深. 异步电动机解耦控制策略综述[J]. 中小型电机, 2005, 32(6): 56-60. |
| [15] |
杨明, 付博, 李钊, 等. 永磁同步电动机矢量控制电压解耦控制研究[J]. 电气传动, 2010, 40(5): 24-28. DOI:10.3969/j.issn.1001-2095.2010.05.006 |
| [16] |
李路菁.基于DSP的永磁同步电机伺服系统的研究[D].南京: 南京航空航天大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10287-2005079285.htm
|
 2019, Vol. 33
2019, Vol. 33


