| 氦气示踪检测法在气密性检测系统中的应用 |
2. 山东劳动职业技术学院,济南 250354
2. Shandong Labor Vocational and Technical College, Jinan 250354, China
在这个快速发展的时代, 产品质量的好坏直接决定了产品的使用和发展前景, 不同行业生产的产品大都需要检测其气密性[1], 如汽车、管道、航天、飞机制造、医药等领域, 它们气体或液体的存储设备都必须有严格的质量检测, 尤其是产品的气密性的排查, 气密性不达标, 产品质量不合格, 不仅影响系统的操作、生产的发展, 还会导致大气的污染、材料的浪费、爆炸等安全事故的发生。
现如今, 气密性检测在使用不同的方式进行检测泄漏率常会遇到一些问题, 比如:检测点的压力高于检测设备可以测量的压力、待测物体内部压力不稳定致使检测设备的灵敏度不高[2-3], 本文设计出一种具有自动稳压功能的吸枪式氦气示踪检测法, 较快的维持容器内部压力的稳定, 提高检测效率。
1 氦气性质及特点气体示踪检测法, 目前采用二氧化碳作为示踪气体的比较多, 但二氧化碳气体排放过量易引起环境温度升高, 氨气、卤素有毒; 也有采用氦气作为示踪气体的, 无污染, 如2019年10月1日国家检阅部队典礼期间放飞的7万只彩色气球, 气球里面充的气体是氦气, 气球上升到一定高度后就会自动爆炸, 氦气对空气没有任何污染。
氦气的性质与特点:它是一种惰性气体; 在常温状态中无色无味; 燃点非常低近似不可燃, 气体比较安全; 它的化学性质活泼度特别低, 常态下不会与其他物质发生作用。另外, 氦气的密度非常小, 约为0.18 g/L, 很轻, 远远低于空气的密度(约为1.3 g/L), 所以氦气更容易从细微气孔中渗出, 作为气密性检测用气体非常合适, 会大大提高检测精度[4], 因此, 选用氦气作为气密性检测的示踪气体具有较高的推广价值。
2 氦气示踪检测法原理气体示踪检测法:将气体充入检测零部件内部, 用浓度传感器检测浓度变化或用吸枪缓慢在零部件表面来回移动, 采样通过砂孔、缝隙出来的气体, 来判断零部件的气密性; 或者容器内部抽真空后, 再用喷枪喷洒气体到物体表面, 检测容器内部进入氦气的流量来判断容器的气密性。氦气示踪检测法适合用在精密性要求较高的密闭容器上, 灵敏度较高, 检测精度(泄漏率)可以达到10-7 atm·cc3/s, 远高于冒泡法和压降法[5-6]。氦气示踪检测方法中采用的氦质谱检漏仪具有响应快、检测准确率高、可以定量检测的优点, 使用领域广泛。
2.1 氦气示踪检测法中检测方式的选用1) 需要标记泄漏位置的检测方式
吸枪式检测方式:首先往容器里面进行充氦气体, 然后再用吸枪慢慢的扫过容器的整个表面, 采样扩散出来的气体[7]。这种方式很方便找出泄漏位置, 容器不需要抽成真空状态, 检测装置如图 1所示。
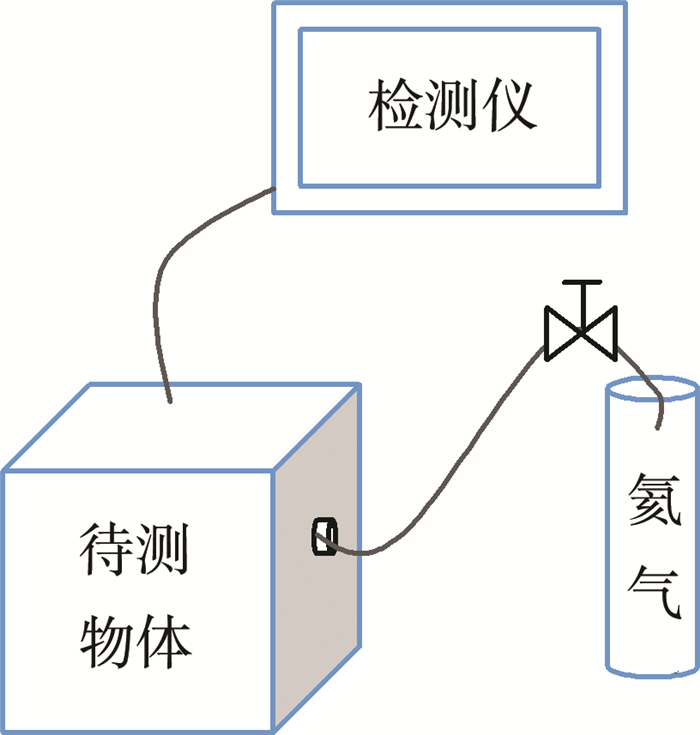 |
| 图 1 吸枪式检测装置示意图 |
喷枪式检测方式:首先需要把容器内部抽成真空状态, 然后用喷枪往容器表面进行喷洒气体, 采样容器内部的氦气的流量, 这种方式的灵敏度较高, 成本低。这两种方式都是逐步小面积的测试, 可以测试到出问题的具体位置, 方便标记。
2) 不需要标记泄漏位置的检测方式
真空式检测方式:需要准备真空室, 把待测物体放进去, 然后往物体里面充入氦气, 真空室与氦质谱检漏仪相连, 实时监测真空室里氦气浓度的变化, 这种方式灵敏度高, 并且可以连接一个辅助泵, 提高检测效率, 检测装置如图 2所示[8]。
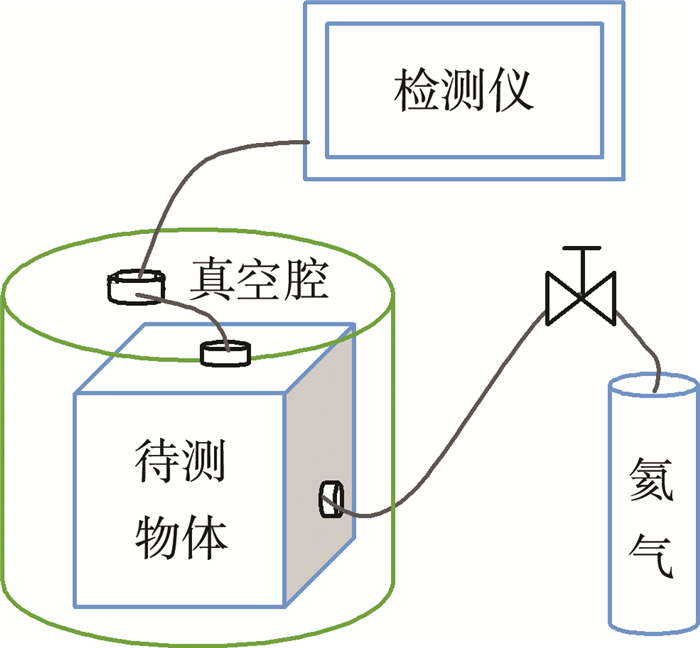 |
| 图 2 真空式检测装置示意图 |
吸枪累积式检测:首先对待测物体进行充氦, 然后把待测物体放在一个与吸枪探头相连的累积腔内, 通过监视累积腔内气体浓度数值的变化进行检测被测物体气密性的好坏[9], 这种方式可以实现总体泄露率的检测, 可靠性高, 成本相对较低, 检测装置如图 3所示。
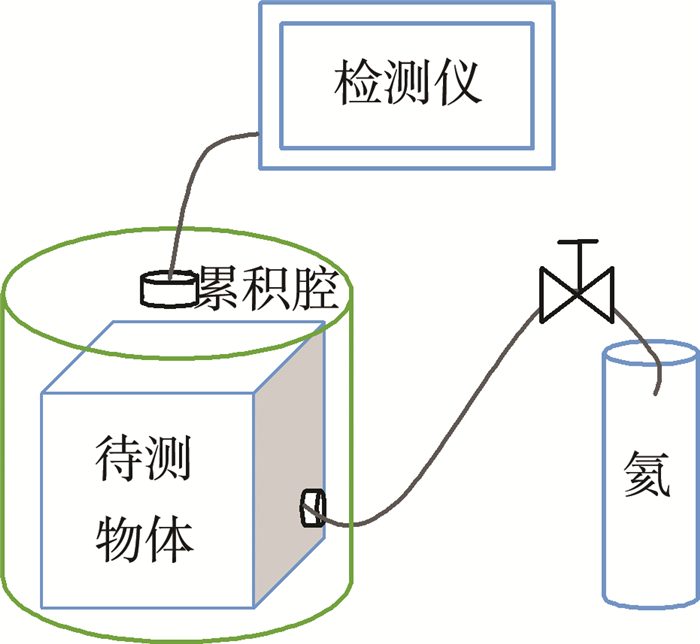 |
| 图 3 吸枪累积式检测装置示决图 |
背压式检测方式:首先将待测物体放在一个充氦气的容器腔内, 一定时间后, 再把待测物体拿出来放在通风处, 这样做的目的是将待测物体表面的氦气体去除掉, 防止残留的气体影响后续的检测任务, 最后再将待测物体放置在一个与吸枪探头相连的腔内, 测量其气密性, 这种方式也可以实现总体泄露率的测试, 成本较低。
2.2 检漏时间计算1) 容器内部抽成真空状态所需要的时间。这个时间指的是达到检漏仪测试压力所需要的最基本的时间, 如图 4所示。
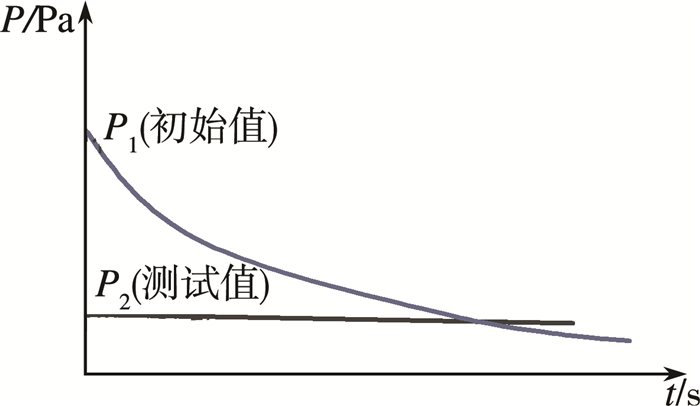 |
| 图 4 物体内部压力与抽气时间关系曲线 |
| $ {\rm{计算公式}}:t = 2.3\frac{V}{{{S_{air}}}}lg\frac{{{P_1}}}{{{P_2}}} $ | (1) |
式(1)中:V—被测件的体积, L
Sair—真空系统的有效抽速, L/s
2) 物体内充入氦气体时, 检测仪检测到氦信号需要的时间, 如图 5所示。
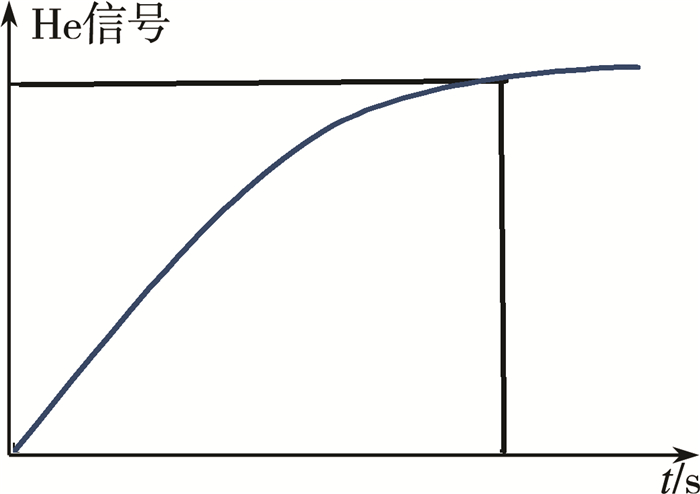 |
| 图 5 捕捉到氦信号的响应时间曲线 |
| $ {\rm{计算公式}}:t = 2.3V/{S_{He}} $ | (2) |
式(2)中:SHe—氦气体的抽速, L/s
3) 气密性检测完毕后进行释放氦气体过程中, 氦信号消失所需要的响应时间, 如图 6所示。
 |
| 图 6 He信号消失的响应时间曲线 |
| $ {\rm{计算公式}}:t = 2.3\frac{V}{{{S_{He}}}}lg\frac{{{F_1}}}{{{F_2}}} $ | (3) |
检测设备本身的因素包括:初抽的能力、检测允许的最大进气口压力、进入检测模式所需要的时间、氦气体的抽速、灵敏度, 最低可测的氦信号、响应时间及恢复时间[9]。通常, 缩短响应时间的方法就是增大抽速, 常用的方法是增加一台辅助泵或者选择更大氦气体抽速的检测仪器[10]。但是, 选用增加一台辅助泵来缩短响应时间的方法时, 要注意这种方法会造成氦气的分流, 计算公式如下:
| $ {t = 2.3V/({S_1} + {S_2})} $ | (4) |
| $ {Q = {Q_1} \times {S_1}/({S_1} + {S_2})} $ | (5) |
式(4)中:S1—检测仪的抽速, L/s
S2—辅助泵的抽速, L/s
式(5)中:Q—检测仪显示的泄漏率, L/s
Q1—实际泄漏率, L/s
3.2 外在因素对氦气示踪检测法检测的影响在日常工作中, 利用一些气密性检测设备检测时的结果不会是0, 根据PV=nRT可知, 产品气密性检测结果与压力、体积、温度(真空环境除外)等外界环境因素有关。
1) 温度变化产生的影响
设待测物体的测试压力为P1=5×105 Pa, 测试背景为2 Pa/s, 不合格背景为大于等于4 Pa/s, 假定温度在27 ℃的基础上每小时上升1 ℃时, 根据公式P1V1/T1=P2V2/T2, 经计算可得每分钟变化后的压力差为:
| $ \begin{array}{*{20}{l}} {△P = {P_2} - {P_1} = {P_1}({T_2}/{T_1} - 1)}\\ { = 5 \times {{10}^5} \times [(273 + 28)/(273 + 27) - 1]}\\ { = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 667{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Pa}}} \end{array} $ | (6) |
进而得到每秒钟变化的压力差:
| $ △P/3600 = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} 667/3{\kern 1pt} {\kern 1pt} {\kern 1pt} 600 = 0.46{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Pa}}/{\rm{s}} $ | (7) |
根据式(6)、式(7)的计算结果可知, 温度变化越大, 待测物体设定的压力越大, 对检测结果影响越大。温度越高, 气体密度会越大[11], 在温度有变化的场合, 要采取一些措施, 尽可能的使待测物体温度接近于外界气温。
2) 待测物体容积的变化
容积变大, 内部气体压力会减小, 气体从气眼、砂孔等处溢出率降低, 影响检测结果。非密封物体在气密性检测前, 需要对开口进行密封, 密封不严易引起开口处散气, 。对于机械加工产品, 密封开口处时可以选用与待测物体材质相近的材料加压封闭, 必要时使用橡胶密封圈, 保证密封良好[12-13]。
3) 待测物体内部气体压强的变化
假如待测物体气密性差, 当充入氦气达到设定压力后, 物体内部气体会从气眼、砂孔等位置溢出, 物体内部气体压强会逐渐降低, 气体压力随之减小, 氦气体溢出的压力进而减小, 以致于吸枪吸不到或者吸收到非常少的氦气, 致使检测仪显示不出数据, 导致泄漏气体位置查不出, 影响测量的准确率。
综上可知, 氦气示踪检测法中, 除了真空式检测外, 均要考虑这些外在因素的影响。温度和容积的变化均会引起待测物体内部压强的改变, 所以稳定待测物体内部压强也是必要的[14]。如吸枪式检测法, 可以通过增加一套自动稳压控制系统稳定内部气体压强的变化, 如图 7所示。
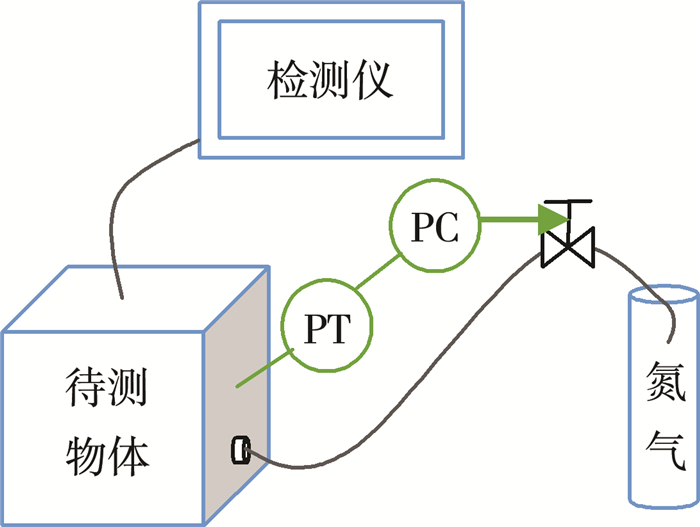 |
| 图 7 带自动稳压系统的吸枪式氦气示踪检测装置示意图 |
4 具有自动稳压功能的吸枪式氦气示踪检测系统建模与仿真
吸枪式氦气示踪检测法, 可以直接测出待测物体泄漏处的具体位置, 方便标记和后续的修补工作, 具有较高的研究价值。
4.1 系统被控对象数学模型的建立当待测物体内部充氦气至设定压强值后,对其压强的变化情况进行分析。
待测物体的泄露一般分为两类:大孔泄漏和小孔泄漏。当加工产品中有大孔泄漏时, 这种情况很容易检测出, 这里主要介绍小孔泄漏时的情况。小孔泄漏, 气体溢出的比较缓慢, 氦气属于惰性气体, 很难被液化, 常用的是压缩气体, 检测时可以近似看作是等温过程。
4.1.1 气体泄漏量的计算气体泄漏量计算公式为:
| $ {Q_2} = Y{C_d}AP{\left[ {\frac{{MK}}{{RT}}{{\left( {\frac{2}{{K + 1}}} \right)}^{(K + 1)/(K - 1)}}} \right]^{1/2}} $ | (8) |
式(8)中相关参数取值如下:
1) 气体绝热指数K。氦气的K值是5/3。
2) 气体膨胀因子Y
[2/(K+1)]K/(K-1)=0.49, 则当P0/P≤0.49时, 为临界流; 当P0/P>0.49时, 为次临界流[15], 其中, P0—环境压力, 单位Pa; P—容器内介质压力, 单位Pa。
而对细小气孔、砂眼等检测, 需要用到明显大于外界环境的压力, 即一般P>2×105 Pa。由此可知, 运用吸枪式检测法时泄漏氦气的流动状态为临界流状态, 则气体膨胀因子取值Y=1。
3) 气体泄漏系数Cd。当气孔、砂眼等为圆形孔时Cd取值为1, 为△形孔时Cd取值为0.95, 为矩形孔时Cd取值为0.9。一般待测物体的气孔等是不标准的, 取值范围为0.9~1, 这里为了容易计算, 取值Cd=1。
4) 泄漏位置处的面积A。
5) 摩尔质量M:氦气摩尔质量M为4 g/mol。
6) 通用气体常数R:取8.314 4 J/(mol·K)。
综上各参数分析, 把参数取值带入(10)式, 可得氦气的泄漏量计算公式为:
| $ {Q_2} = 0.5AP/{T^{1/2}} $ | (9) |
| $ {\rm{气容计算公式}}:C = dm/dP $ | (10) |
| $ {\rm{理想气体状态方程}}:PV = nRT = mRT/M $ | (11) |
氦气经细小孔溢出可以看作是等容等温状态, 在此状态下对式(11)方程两边求微分得:
| $ \begin{array}{*{20}{l}} {V \cdot dP = \frac{{RT}}{M}dm}\\ {{\rm{整理得 }}:dm/dP = VM/RT}\\ {{\rm{即 }}:{\rm{ 气容}}C = dm/dP = VM/RT} \end{array} $ | (12) |
待测物体内部气体的流动过程, 根据质量守恒定律可得:
| $ {△Q_1} - {△Q_2} = C \cdot \frac{{d△P}}{{dt}} $ | (13) |
其中:△Q1—氦气流入量的增量, △Q2—氦气泄漏量的增量, △P—待测物体内压强的增量。
将式(10)、式(13)带入式(14)得:
| $ {△Q_1} - \frac{{0.5A}}{{{T^{1/2}}}} \cdot △P = \frac{{VM}}{{RT}} \cdot \frac{{d△P}}{{dt}} $ | (14) |
由于一般盛装氦气的容器与气密性检测设备之间有一定的距离, 氦气的传输和压强的变化都需要一定的时间, 延滞时间用τ表示, 则系统的微分方程可写成:
| $ \frac{{VM}}{{RT}} \cdot \frac{{d△P}}{{dt}} + \frac{{0.5A}}{{{T^{1/2}}}} \cdot △P = {△Q_1}(t - \tau ) $ | (15) |
则系统对应的传递函数为:
| $ G(s) = \frac{{△P(s)}}{{{△Q_1}(s)}} = \frac{1}{{VMs/RT + 0.5A/{T^{1/2}}}}{e^{ - \tau s}} $ | (16) |
取A=4π×10-6 m2, V=(0.5)3=0.125 m3, 气温为25 ℃, 气管直径2 cm, 气管长度20 m, 根据压缩气体流速公式可以计算出延时时间τ=15 s。
把以上数值带入式(16)中, 得到具体的传递函数为:
| $ G(s) = \frac{{{{10}^6}}}{{1.675 \times {{10}^3}s + 0.364}}{e^{ - 15s}} $ | (17) |
细小孔泄漏量比较缓慢, 曲线变化不明显, 为了较好的观看模型仿真曲线, 将传递函数(17)缩小106倍进行调试, 建立如图 8所示的仿真模型。
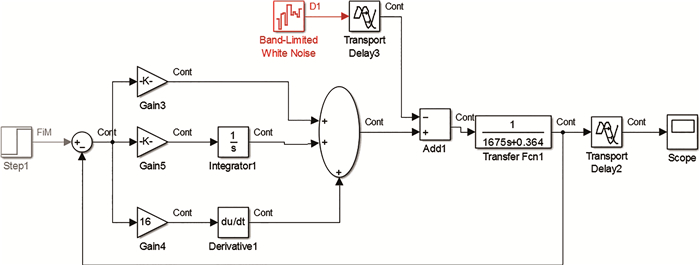 |
| 图 8 系统的MATLAB仿真模型 |
首先将Ki和Kd设为0, 有小到大改变Kp; 当出现较合适的比例度时, 接着由小到大调整Ki, 同时Kp也要有稍许的变化, 直至输出曲线稳定; 最后, 加入微分Kd, 改善系统性能, 但Kd不宜过大, 过大会降低系统的抗干扰能力, 最终实验得到的PID三个参数分别为Kp=145, Ki=0.4, Kd=16。
由式(9)可知, 泄漏量与泄漏孔的面积A成正比关系, 当A比较规则时, 泄漏量相对较为稳定, 此时系统的仿真曲线如图 9所示; 当A不规则或有所处泄漏位置时, 泄漏量不稳定, 泄漏量波动变化时系统的仿真曲线如图 10所示。由此说明, 这种方式的稳压控制系统具有可行性。
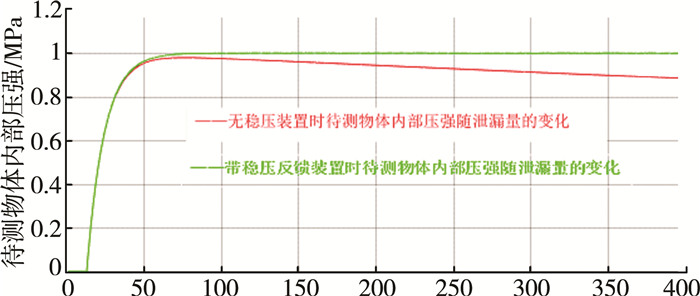 |
| 图 9 泄漏量稳定时的系统仿真曲线 |
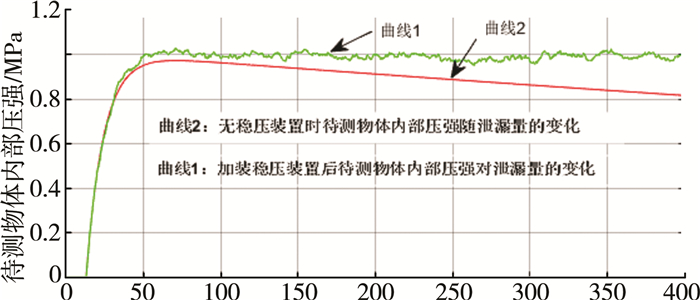 |
| 图 10 泄漏量波动变化时的系统仿真曲线 |
5 总结
氦气示踪检测法, 检漏精确度比较高, 可以满足工业中加工产品气密性的质量要求。文章中提到的真空检测法受外界影响甚微, 比较稳定, 但是需要准备真空环境; 吸枪式检测法, 不需要真空环境, 但是一般会受到压力、温度、体积等因素的影响, 本文给出了改进方法具有自动稳压功能的吸枪式氦气示踪检测法, 并在MATLAB中进行了仿真验证, 具有可行性。由于不确定性因素的影响, 建立的模型有待进一步的完善, 可以与智能控制技术相结合进行进一步的研究探索。
| [1] |
程利军, 张英堂, 李志宁, 等. 起动电流在发动机气密性检测中的应用[J]. 振动.测试与诊断, 2012, 32(06): 986-989, 1038-1039. |
| [2] |
刘春, 王兴, 李跃中. 一种高压容器检测仪的设计原理[J]. 仪表技术与传感器, 2009(S1): 384-387, 427. |
| [3] |
孔翔飞, 廉洁. 基于嵌入式系统的气密性检测仪[J]. 仪表技术与传感器, 2013(02): 28-30, 67. DOI:10.3969/j.issn.1002-1841.2013.02.010 |
| [4] |
毛芹, 王涛, 王军茹.气密性检测技术现状和典型方法[C]//RIZAESA.2011 International Conference on Future Computer Science and Application(FCSA 2011), Kota Kinabalu, Malaysia: International Industrial Electronic Center, 2011.
|
| [5] |
王佐勋, 徐德. LED晶圆贴片过程中压力的二阶段模糊决策与控制[J]. 控制与决策, 2016, 31(03): 403-409. |
| [6] |
于复生, 陈继文, 刘红艳, 等. 蓄电池气密性检测装置的研制[J]. 仪器仪表学报, 2006(S1): 277-278, 280. |
| [7] |
高磊. 复杂腔体零件差压式气密性检测建模与仿真[J]. 现代机械, 2016(05): 15-19. |
| [8] |
朱正德, 徐涛. 关于气门/缸盖阀座间气密性检测的几个技术问题[J]. 中国测试技术, 2003(06): 30-32, 20. |
| [9] |
李俊杰, 王宏伟, 王俊生. 基于DSP和LabVIEW的飞机气密性检测系统[J]. 仪表技术与传感器, 2010(11): 47-49, 52. DOI:10.3969/j.issn.1002-1841.2010.11.017 |
| [10] |
李启杰, 兰浩, 陈俊名, 等. 水质监测中气相色谱流量控制器的研发[J]. 仪表技术与传感器, 2016(06): 28-32. DOI:10.3969/j.issn.1002-1841.2016.06.009 |
| [11] |
刘一扬, 刘玲玲, 王雪梅. 驱动桥壳总成气密性自动检测试验台的设计[J]. 机械设计与制造, 2016(01): 151-153, 157. DOI:10.3969/j.issn.1001-3997.2016.01.042 |
| [12] |
周思林, 伍先达, 宋厚权, 等. 基于模糊推理的高压气密性检测仪的设计[J]. 仪器仪表学报, 2004(S1): 357-359, 381. |
| [13] |
李浩亮, 杨任农, 席茜, 等. 基于分布式PID控制的时变时延多智能体系统的一致性[J]. 控制与决策, 2019, 34(01): 189-197. |
| [14] |
周蓉, 韩文杰, 谭文. 线性自抗扰控制的适用性及整定[J]. 控制理论与应用, 2018, 35(11): 1654-1662. DOI:10.7641/CTA.2018.80249 |
| [15] |
郑克波, 栾小丽, 刘飞. 反向响应过程PID控制回路性能评估[J]. 控制工程, 2018, 25(03): 386-390. |
 2020, Vol. 34
2020, Vol. 34


