| 基于一类复混沌系统的图像加密研究 |
2. 山东凯迪欧电气有限公司, 泰安 271001
2. Shandong Kaidio Electricity co., Ltd, Taian 27100, China
地磁场在长期变化中会出现极性反转现象, 地磁学家们对此做了大量研究, 提出了很多模型, 比如圆盘发电机模型、运动学发电机反转模型、统计模型等等。在这些模型中, 圆盘发电机模型作为最早的地磁起源及反转模拟, 起过很重要的作用。圆盘发电机模型包含单盘发电机模型[1]、双盘发电机模型[2]、N圆盘耦合发电机模型[3]以及在这些模型的基础上得到的各种各样的圆盘发电机模型。双盘发电机模型是日本地磁学家Rikitake在1958年首次提出, 该模型在地磁起源及其反转模拟起到过很重要的作用, 且该模型具有良好的混沌特性[4]。基于Rikitake模型, 很多学者提出并研究了多种类型的双盘发电机模型, 比如:带摩擦的Rikitake系统[5-6], 变形的Rikitake双盘耦合发电机模型[7]等等。双盘发电机模型的动力学行为及其同步的研究[8]在机电控制等方面具有重要的理论基础和使用价值。
复混沌系统是指状态变量处于复空间的混沌动力系统, 与实混沌系统相比, 复混沌系统的动力学行为更加复杂, 产生的复混沌信号比实混沌系统产生的混沌信号更加复杂且难以预测, 是一种可靠的安全通信载体, 应用在网络信息安全中可以更好地提高保密性能; 而且比起实变量, 复变量更容易由电容和电感实现, 从而具有更广阔的应用前景。近几年, 复混沌系统的动力学特性、同步及其应用引起了学者们的极大关注[9-13]。目前, 基于复混沌系统的图像加密的研究[14]还不多, 还需要进一步的研究与应用。
本文拟建立一个新的复混沌模型, 该模型是双盘发电机模型的推广。利用分岔图、Lyapunov指数和庞加莱截面等方法研究了该系统的混沌特性。通过Matlab仿真对其进行验证, 仿真结果表明, 该混沌系统具有良好的混沌特性, 并且研究了新的复混沌系统在数字图像加密中的应用。
1 复变形Rikitake混沌系统的提出2014年, 雷腾飞等在研究工程中的耦合发电机时, 基于地磁学家Rikitake提出的Rikitake模型[2], 提出了新的发电机模型[7]如下:
| $ \left\{\begin{array}{l} \dot{m_{1}}=-a m_{1}+m_{2}\left(m_{3}-c\right) \\ \dot{m_{2}}=-b m_{2}+m_{1}\left(m_{3}-c\right) \\ \dot{m_{3}}=d m_{3}-m_{1} m_{2} \end{array}\right.。$ | (1) |
其中, a, b, c, d是正常数。当a=2, b=3, c=1, d=0.75时, 系统(1)是混沌的, 该系统称为变形Rikitake双盘耦合发电机系统。
当系统(1)中的变量m1, m2均为复变量时, 可以得到如下的复系统:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {{m_1}}\limits^. = - a{m_1} + {m_2}\left( {{m_3} - c} \right)}\\ {\mathop {{m_2}}\limits^. = - b{m_2} + {m_1}\left( {{m_3} - c} \right)}\\ {\mathop {{m_3}}\limits^. = d{m_3} - \frac{1}{2}\left( {{{\overline m }_1}{m_2} + {m_1}{{\overline m }_2}} \right)} \end{array}, } \right. $ | (2) |
其中, m1=x1+jx2和m2=x3+jx4是复状态变量; m3=x5是实状态变量。分离复变形Rikitake双盘耦合发电机系统(2)的实部和虚部, 可以得到与其等价的实变量形式为:
| $ \left\{\begin{array}{l} \dot{x}_{1}=-a x_{1}+x_{3}\left(x_{5}-c\right) \\ \dot{x}_{2}=-a x_{2}+x_{4}\left(x_{5}-c\right) \\ \dot{x}_{3}=-b x_{3}+x_{1}\left(x_{5}-c\right) \\ \dot{x}_{4}=-b x_{4}+x_{2}\left(x_{5}-c\right) \\ \dot{x}_{5}=d x_{5}-x_{1} x_{3}-x_{2} x_{4} \end{array}\right.。$ | (3) |
当参数取值为a=8, b=3, c=0.69, d=3.5时, 系统(3)是混沌的, 如图 1-2。下面具体分析系统(3)的动力学特性。
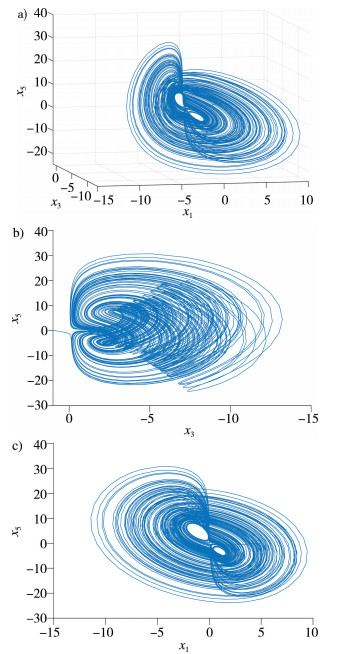 |
| 注:a) 吸引子在x1-x3-x5平面的侧视图; b) 吸引子在x3-x5平面的侧视图; c)吸引子在x1-x5平面的侧视图。 图 1 在x1, x3, x5坐标系上, 复变形Rikitake系统的混沌吸引子 |
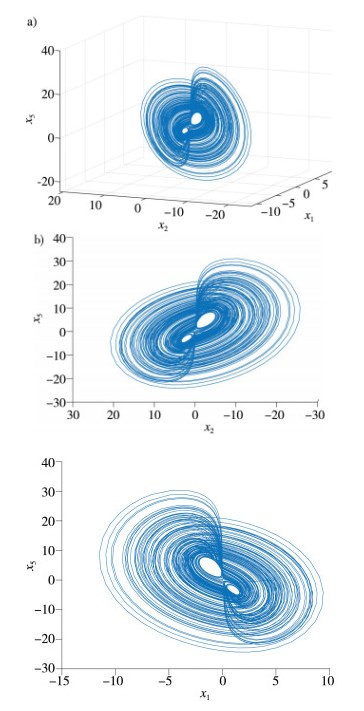 |
| 注:a)吸引子在x1-x2-x5平面的侧视图; b)吸引子在x2-x5平面的侧视图; c) 吸引子在x1-x5平面的侧视图。 图 2 在x1, x2, x5坐标系上, 复变形Rikitake系统的混沌吸引子 |
2 动力学分析 2.1 对称性和不变性
在系统(3)中引入下列坐标变换:
| $ \left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right) \rightarrow\left(-x_{1}, -x_{2}, -x_{3}\right.\\ \left.-x_{4}, x_{5}\right) $ |
系统保持不变, 则系统(3)关于x5轴呈现对称性, 而且这种对称性对所有参数a, b, c, d均成立。
2.2 耗散性在系统(3)中引入下列坐标变换:
| $ \left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right) \rightarrow\left(-x_{1}, -x_{2}, -x_{3}, \right.\\ \left.-x_{4}, x_{5}\right) $ |
因此, 当d-2(a+b) < 0时, 系统(3)是耗散的, 并以指数形式收敛。
| $ \frac{\mathrm{d} V}{\mathrm{~d} t}=(d-2(a+b)) \rightarrow V= \\ V_{0} e^{(d-2(a+b)) t}。$ |
系统(3)的所有轨迹线最终会被限制在一个体积为零的极限子集上, 其运动将被固定在一个吸引子上, 由此说明了系统(3)存在吸引子。
2.3 李雅普诺夫指数和分数维数系统(3)的Jacobian矩阵为:
| $ \boldsymbol{J}=\left(\begin{array}{ccccc} -a & 0 & x_{5}-c & 0 & x_{3} \\ 0 & -a & 0 & x_{5}-c & x_{4} \\ x_{5}-c & 0 & -b & 0 & x_{1} \\ 0 & x_{5}-c & 0 & -b & x_{2} \\ -x_{3} & -x_{4} & -x_{1} & -x_{2} & d \end{array}\right) $ |
根据Wolf算法, 计算可得到系统(3)在参数为a=8, b=3, c=0.69, d=3.5和初值为
x(0)=(1+2j, 0, 1)下的Lyapunov指数分别为:
λ1=1.014 713, λ2=0.012 757, λ3=-0.004 016,
λ4=-8.591 474, λ5=-10.840 152。
如图 3所示。此时, 可以计算出系统(3)的分数维数为:
| $ \begin{aligned} &D=l+\frac{1}{\left|\lambda_{l+1}\right|} \sum\limits_{k=1}^{l} \lambda_{k}=3+\frac{\lambda_{1}+\lambda_{2}+\lambda_{3}}{\left|\lambda_{4}\right|} \\ &=3.11912 。\end{aligned} $ |
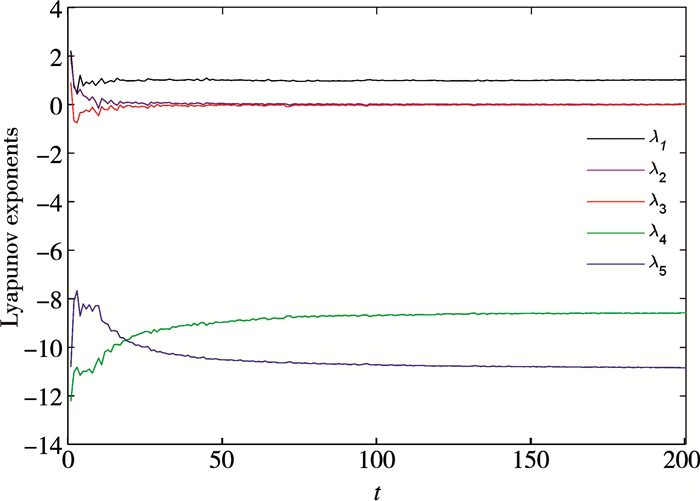 |
| 图 3 当a=8, b=3, c=0.69, d=3.5时, 系统(3)的Lyapunov指数 |
由此可见, 此系统具有两个正的Lyapunov指数, 且维数为分数维, 这就意味着系统(3)具有超混沌行为。
2.4 平衡点的稳定性求解方程组
| $ E_{0}=(0, 0, 0, 0, 0) $ |
| $ E_{\theta}=\left(\sqrt{\frac{b}{a}} r \sin \theta, \sqrt{\frac{b}{a}} r \cos \theta, r \sin \theta, r \cos \theta, x_{5}\right)。$ |
其中
下面讨论平衡点E0=(0, 0, 0, 0, 0)的稳定性。系统(3)在E0的Jacobian矩阵为
| $ \boldsymbol{J}_{E_{0}}=\left(\begin{array}{ccccc} -a & 0 & -c & 0 & 0 \\ 0 & -a & 0 & -c & 0 \\ -c & 0 & -b & 0 & 0 \\ 0 & -c & 0 & -b & 0 \\ 0 & 0 & 0 & 0 & d \end{array}\right) 。$ |
从而可得到矩阵JE0的特征方程为
| $ \begin{aligned} &(\lambda-d)\left(\lambda^{2}+(a+b) \lambda+a b-c^{2}\right)^{2} \\ &=0。\end{aligned} $ |
根据Routh-Hurwitz[15]判据定理知, 要使平衡点稳定, 其特征值必须满足Re[λ] < 0。因此, 当
d < 0和ab>c2时, E0是稳定的, 否则, E0是不稳定的。类似地, 可以分析平衡点Eθ的稳定性。
2.5 庞加莱截面通过分析庞加莱截面[16]上截点的分布情况, 可以确定系统的是否具有混沌特性, 当截面上仅有若干个离散的点时, 可判断系统是周期的; 当截面上是一封闭曲线时, 可判定系统是准周期的; 当截面上是成片的密集点, 并且具有层次结构时, 可判定系统处于混沌状态。
从图 4可以看出, 系统(3)在x1-x2方向、x1-x3方向、x1-x5方向和x3-x5方向上的庞加莱截面中, 均出现了成片的密集点, 并且具有层次结构, 表明系统(3)处于混沌状态。
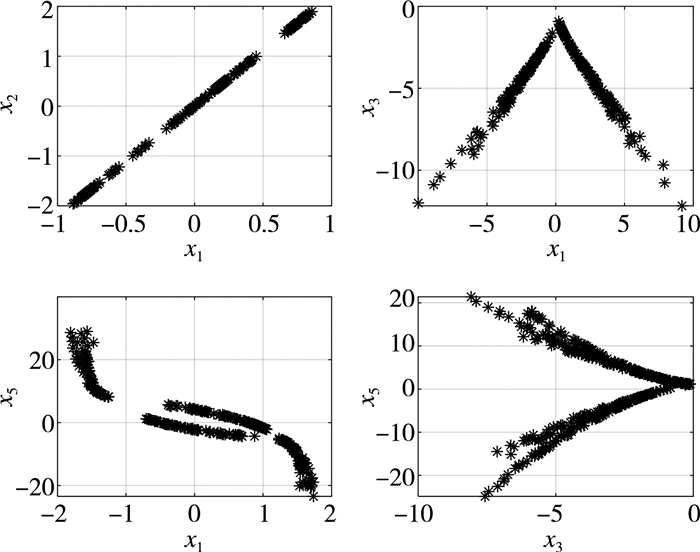 |
| 图 4 庞加莱截面图 |
2.6 初值敏感性
不改变系统(3)的参数, 仅改变状态变量x的初始值, x1由5变成5.000 1。图 5显示, 尽管状态变量x的初始值的改变量很小, 只改变了0.01%, 但是x仍然发生了巨大偏差, 由此可见系统(3)对初始条件敏感。
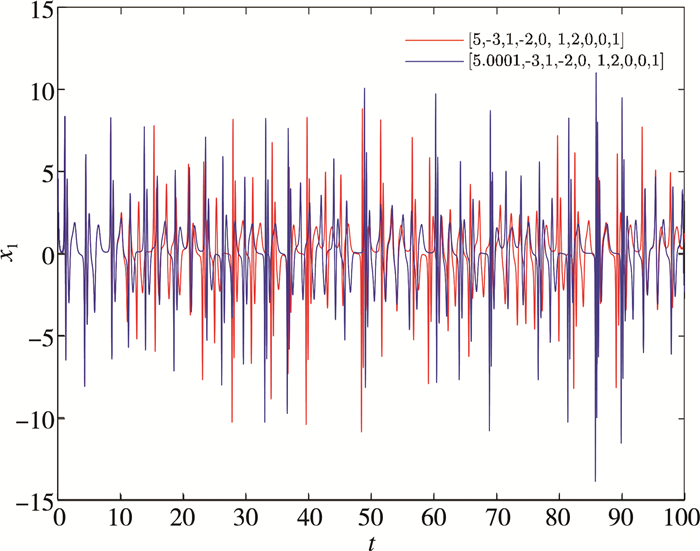 |
| 图 5 初值敏感性图 |
2.7 0-1测试
设x(j)(j=1, 2, …, N)为离散时间序列, 选取c为区间(0, π)的随机常数, 定义函数p(n)与q(n)[17]为:
| $ \begin{aligned} &p(n)=\sum\limits_{j=1}^{n} x(j) \cos (\theta(j)), n=1, 2, \cdots, N \\ &q(n)=\sum\limits_{j=1}^{n} x(j) \sin (\theta(j)), n=1, 2, \cdots, N \\ &\theta(j)=j c+\sum\limits_{i=1}^{j} x(j), j=1, 2, \cdots, n \end{aligned} $ |
如果函数p(n)与q(n)的轨迹是有界的, 时间序列是非混沌的; 如果函数p(n)与q(n)的轨迹表现为布朗运动, 则时间序列是混沌的。
对于第4个变量x4进行0~1测试, 得出p(n)与q(n)的运动轨迹, 如图 6所示, 故该系统(3)是混沌的。
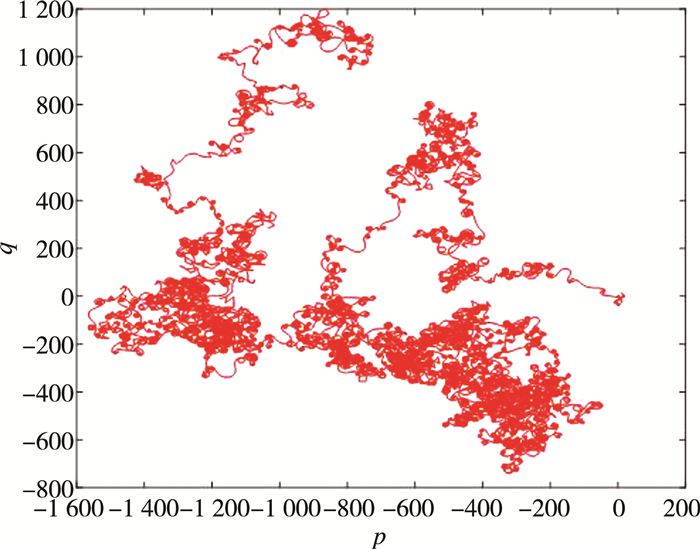 |
| 图 6 p(n)-q(n)运动轨迹图 |
3 图像加密实现
作为整个加密实现的基础, 本文先介绍置乱与扩散两种加密方式[18]。所谓置乱, 即将原图像的像素点打乱, 然后再以某种方式将像素点放回的过程。扩散是在不改变像素点位置的条件下, 将任一明文像素点的信息隐藏在尽可能多的密文像素点中。值得注意的是, 置乱方式是“单纯”加密方式, 仅用这一种加密方式显然是不靠谱的。所以, 本文用混沌系统产生的混沌序列作为伪随机数列, 应用到置乱与扩散算法中。先置乱, 这个过程可以重复几次, 再扩散, 将置乱后的图像用扩散算法重复几次, 这就构成一次加密, 多次加密后的结果就是最终要输出的密文图像。
另外, 加密图像采用非常著名的Lean图像, 主要原因是该图像包含很多适于图像处理方面的细节, 平滑区、阴影、纹理等, 非常适合测试各类图像处理算法。
加密算法流程如图 7所示:
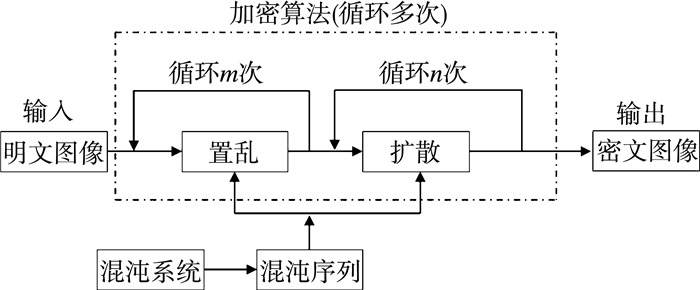 |
| 图 7 加密算法实现过程 |
3.1 混沌数字图像加密实现
下面介绍加密方案的具体实现。
首先, 置乱算法, 我们采用二维图像展成一维向量后的置乱方法, 将具有M×N像素点的Lena图像按行展成一维行向量, 记为α, 对于系统(3)产生的混沌序列, 将其作为伪随机数列A, 另外, 对于其中重复的伪随机数, 允以去除, 去除后的伪随机数列, 记为B。将行向量A中没有出现在B中的数值添加到B的末尾, 最后交换B中第i个与第MN-i+1个元素, 以此完成无重复的位置置乱。
解密算法只需取上面过程的逆过程, 相对比较容易实现。然后对置乱m次的图像进行扩散处理。本文基于GF(217)有限域来实现扩散处理, 因为在常见的GF(24)有限域上, 0作为乘数时有信息的损失, 所以不能将GF(24)域上的乘法运算直接用于扩散算法中。
| $ \left\{\begin{array}{l} C_{i, H}=C_{i-1, H} \times S_{i, H} \times P_{i, H} \\ C_{i, L}=C_{i-1, l} \times S_{i, L} \times P_{i, L} \\ C_{i}=\left(C_{i, H} \times 16+C_{i, L}\right) \end{array}\right., $ | (4) |
| $ \left\{\begin{array}{l} P_{i, H}=C_{i, H} \div C_{i-1, H} \div S_{i, H} \\ P_{i, L}=C_{i, L} \div C_{i-1, L} \div S_{i, L} \\ P_{i}=\left(P_{i, H} \times 16+P_{i, L}\right) \end{array}, \right. $ | (5) |
| $ \left\{\begin{array}{l} C_{i, H}=C_{i+1, H} \times S_{i, H} \times P_{i, H} \\ C_{i, L}=C_{i+1, L} \times S_{i, L} \times P_{i, L} \\ C_{i}=\left(C_{i, H} \times 16+C_{i, L}\right) \end{array}, \right. $ | (6) |
| $ \left\{\begin{array}{l} P_{i, H}=C_{i, H} \div C_{i+1, H} \div S_{i, H} \\ P_{i, L}=C_{i, L} \div C_{i+1, L} \div S_{i, L} \\ P_{i}=\left(P_{i, H} \times 16+P_{i, L}\right) \end{array}\right.。$ | (7) |
正向扩散时, 借助于式(4), 而式(5)是正向扩散的逆运算。
逆向扩散时, 借助于式(6), 而式(7)是逆向扩散的逆运算。
3.2 效果展示 |
| 图 8 Lean图像与无重复置乱后的图像 |
 |
| 图 9 对置乱图像进行扩散与解密结果图像 |
3.3 安全性分析
下面从密钥空间的大小, 灵敏度分析和抗统计攻击分析角度分析该图像加密算法的安全性。
3.3.1 密钥空间分析在64位计算机中, 采用精确到小数点后4位的浮点数, 本文加密算法的密钥空间至少为2120>2100, 满足正常加密需求[19]。
3.3.2 灵敏度分析取复系统(3)的初值为x0=[5,-3,1,-2,0], 生成密钥序列, 而后对Lena图像进行加密流程, 得到加密图像A。之后, 取复系统(3)的初值为一个扰动后的初值x′0=[5, -3, 1.000 1, -2, 0], 生成密钥序列, 用该序列对加密图像A进行解密流程。得到明文图像、加密图像、错解图像如图 10所示。
 |
| 注:a)明文Lean图像; b)加密图像; c)错解图像。 图 10 加密明文图像、加密图像、错解图像 |
可以看出, 用扰动初值生成的序列来解密是不可行的, 即当初值某个分量的微小变化时, 会导致解密失败。这说明了复变形Rikitake系统对密钥的敏感性较强, 即使两个解密密钥仅有微小的差别, 解密结果也会有很大的差别。
3.3.3 抗统计攻击分析为直观的观察加密效果, 首先展示图 11, 加密一次的图像及原图像。而后展示加密一次后图像的直方图, 即图 12, 对比图 13原图像的直方图, 可以看出原图像的直方图(图 13)具有起伏的特征, 利于统计分析; 而从加密一次后的图像的直方图(图 12)可以看出, 标准偏差较大, 像素分布较平均, 对统计性的攻击有很好的抵抗效果。
 |
| 注:a)实施一次加密后的图像; b)原图像。 图 11 加密一次的图像及原图像 |
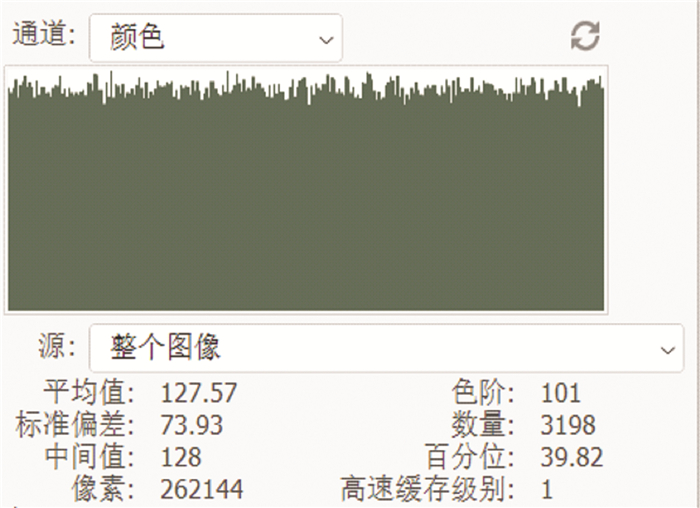 |
| 图 12 加密一次的图像直方图 |
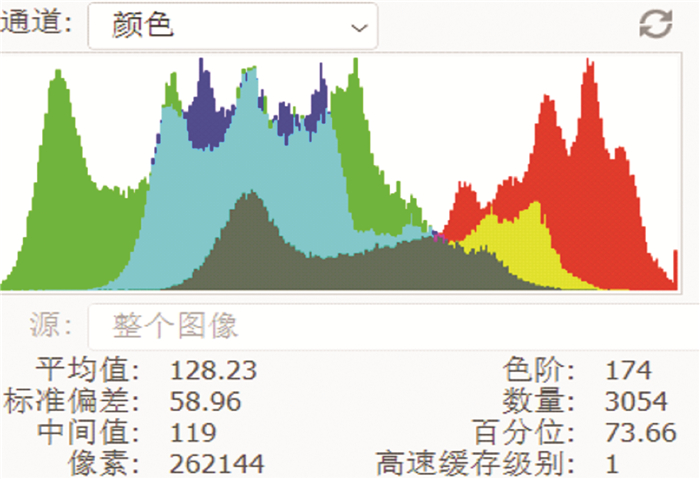 |
| 图 13 原图像直方图 |
图 14显示了加密一次后和原图像的红绿蓝通道直方图, 直观地看出像素被均匀打乱, 图像的直方图[20]均匀分布, 没有明显的统计特性, 很好的隐藏了原图像的统计特征。
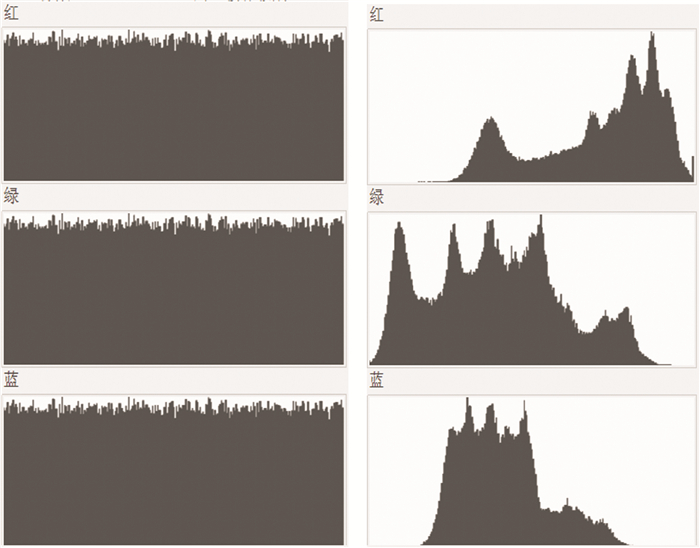 |
| 图 14 加密一次后图像的红绿蓝通道直方图与原图像的红绿蓝通道直方图 |
4 结语
本文构造了一类复混沌系统, 通过耗散性、平衡点的稳定性、初值敏感性、Lyapunov指数和庞加莱截面分析了该系统的混沌特性。本文利用该系统进行了图像加密的研究, 采用置乱加扩散方式进行加密, 通过Matlab仿真分析发现, 加密解密效果良好。
| [1] |
BOLLARD E C. The stability of a homopolar dynamo[J]. Proceedings of the Cambridge Philosophical Society, 1955, 51: 744-760. DOI:10.1017/S0305004100030814 |
| [2] |
RIKITAKE T. Oscillations of a system of disk dynamos[J]. Proceedings of the Cambridge Philosophical Society, 1958, 54: 89-105. DOI:10.1017/S0305004100033223 |
| [3] |
LEBOVITIZ N R. The equilibrium stability of a system of disk dynamos[J]. Proceedings of the Cambridge Philosophical Society, 1960, 56: 154-173. DOI:10.1017/S030500410003440X |
| [4] |
KEISNKE. Chaos in the Rikitake two disk dynamo system[J]. Earth and Planetary Science Letters, 1980, 51(2): 451-456. DOI:10.1016/0012-821X(80)90224-1 |
| [5] |
杨先林. 带摩擦的双盘发电机模型的混沌现象[J]. 广西师范大学学报(自然科学版), 2002, 20(1): 91-93. DOI:10.3969/j.issn.1001-6600.2002.01.017 |
| [6] |
刘晓君, 李险峰, 何万生, 等. 带摩擦的Rikitake双盘发电机模型的混沌与同步[J]. 东北师范大学学报(自然科学版), 2009, 41: 59-63. |
| [7] |
雷腾飞, 陈恒, 王荣, 等. 变形Rikitake双盘耦合发电机系统的动力学分析与控制[J]. 济宁学院学报, 2014, 35(3): 52-56. |
| [8] |
常迎香, 刘晓君, 李险峰. Rikitake发电机模型的混沌与控制[J]. 辽宁师范大学学报(自然科学版), 2006, 29(4): 422-426. |
| [9] |
王诗兵, 王兴元. 超混沌复系统的自适应广义组合复同步及参数辨识[J]. 电子与信息学报, 2016, 38(48): 2062-2067. |
| [10] |
张芳芳, 刘树堂, 余卫勇. 时滞复Lorenz混沌系统特性及其自时滞同步[J]. 物理学报, 2013, 62(22): 220505. DOI:10.7498/aps.62.220505 |
| [11] |
JIANG C M, LIU S T. Generalized combination complex synchronization of new hyperchaotic complex Lü-like systems[J]. Advances in Difference Equations, 2015, 1-17. |
| [12] |
李天择, 郭明, 陈向勇, 等. 基于多切换传输的复变量混沌系统的有限时组合同步控制[J]. 应用数学与力学, 2019, 40: 1299-1308. |
| [13] |
方洁, 姜明浩, 安小宇, 等. 激光复混沌系统构建及其点乘函数投影同步[J]. 复杂系统与复杂性科学, 2021, 18: 30-37. |
| [14] |
LIU H J, ZHANG Z Q, KADIR A, et al. Image encryption using complex hyper chaotic system by injecting impulse into parameters[J]. Applied Mathematics and Computation, 2019, 360: 83-93. DOI:10.1016/j.amc.2019.04.078 |
| [15] |
WANG X Y, HE Y J, WANG M J. Chaos control of a fractional order modified coupled dynamos system[J]. Nonlinear Analysis, 2009, 71(12): 6126-6134. DOI:10.1016/j.na.2009.06.065 |
| [16] |
张识, 王攀, 张瑞浩, 等. 选取任意庞加莱截面的新方法[J]. 物理学报, 2020(4): 32-41. |
| [17] |
李新杰, 胡铁松, 郭旭宁, 等. 0-1测试方法的径流时间序列混沌特性应用[J]. 水科学进展, 2012, 23(6): 861-868. |
| [18] |
张勇. 混沌数字图像加密[M]. 北京: 清华大学出版社, 2016.
|
| [19] |
王宏达. 基于DNA和元胞自动机的新型图像加密算法[J]. 电子科技, 2019, 32(4): 43-47. |
| [20] |
汪乐乐, 李国东. 基于DNA序列的超混沌彩色图像加密算法[J]. 中国科技论文, 2018, 13: 1974-1981. DOI:10.3969/j.issn.2095-2783.2018.17.006 |
 2021, Vol. 35
2021, Vol. 35


