| 海上盘式收油机凸缘圆盘表面油膜特性研究 |
近年来, 海上溢油事故频发, 给海洋生态环境造成了极其恶劣的影响。溢油事故一旦发生, 仅靠海水自身的运动很难清除, 必须用专门的回收设备或处理手段将溢油回收清除[1]。盘式收油机是最常用的溢油回收装备之一, 而转盘反应器是盘式收油机的核心部件, 其表面油膜的形成特性直接影响了盘式收油机的收油效率。因此, 提高转盘反应器的携油量对盘式收油机溢油回收工作至关重要。
转盘反应器作为一种过程强化设备, 具有较快的液膜混合速度和较强的黏性流体吸附能力, 早期主要应用于废水的处理和纤维聚酯的合成[2], 近年来, 其广泛应用于石油回收、光催化和生物化学反应等工业领域[3-5]。针对转盘反应器的表面成膜特性, 国内外诸多学者已展开相关研究。对于标准实心圆盘, 王萌[6]通过正交分析的方法, 认为影响转盘携油能力最显著的因素为圆盘直径, 其次分别是浸没深度、油液黏度、转速等; MS Miah等[7]采用实验研究和数值模拟相结合的方式, 发现膜厚随着转速和黏度的增加而增加, 并提出了膜厚与角位置、半径、转速、黏度和表面张力的关系式。对于其它结构类型圆盘, 王君豪等[8]利用实验和CFD技术研究了高黏性液体在旋转辐条盘上的成膜特性, 发现对于超高黏度液体的成膜, 黏性力和重力比惯性力更加重要, 在重力作用下的膜厚会随着径向位置的减小而增大。Sunil K Saini[9]将一种经过特殊设计的翼型结构被整合到转子中, 以提高其传质性能和液体保持能力, 并发现体积传质系数和液体滞留强烈依赖于转速和淹没水平。可见, 转盘反应器一直以来都是国内外学者研究的热点。当转盘反应器应用于溢油回收时, 其表面成膜特性更是直接影响了盘式收油机的收油效果。
本文以海上盘式收油机的凸缘圆盘为研究对象, 通过分析其在气-油两相流下的表面油膜厚度分布情况, 掌握其表面成膜特性, 获得相关规律, 为后续应用于盘式收油机的转盘结构优化设计奠定了基础。
1 数值模型转盘转动携带油膜的过程, 常采用雷诺时均两方程模型开展数值计算。由Menter[10]提出的SST k-ω模型做为一种混合模型, 其结合了计算自由流的k-ε模型和计算近壁面区域的k-ω模型两者的优点, 应用非常广泛。
湍动能k运输方程:
| $ \frac{\partial(\rho k)}{\partial t}+\frac{\partial\left(\rho k u_i\right)}{\partial x_i}=\tau_{i j} \frac{\partial u_i}{\partial x_j}-\beta^* \rho \omega k+\frac{\partial}{\partial x_j}\left[\left(\mu+\sigma_k \mu_t\right) \frac{\partial k}{\partial x_j}\right] 。$ | (1) |
耗散率ω运输方程:
| $ \frac{\partial(\rho \omega)}{\partial t}+\frac{\partial\left(\rho \omega u_i\right)}{\partial x_i}=\frac{\gamma}{\mu_t} \boldsymbol{\tau}_{i j} \frac{\partial u_i}{\partial x_j}-\beta \rho \omega^2+\frac{\partial}{\partial x_j}\left[\left(\mu+\sigma_k \mu_t\right) \frac{\partial k}{\partial x_j}\right]+2\left(1-F_1\right) \frac{\rho \sigma \omega^2}{\omega} \frac{\partial k}{\partial x_i} \frac{\partial \omega}{\partial x_i}, $ | (2) |
式中, τij为雷诺应力张量; μ为动力黏度; μt为湍流黏度; y为到壁面的距离; F1为混合函数; a1、β*、σk为模型参数的标准值, 由具体的模型而定。
根据圆盘携油过程中气液两相的流动特性, 常采用Hirt等[11]提出的VOF(Volume of Fluid)模型进行数值计算, 其被认为是最适合用来模拟多种非混溶流体的模型之一[12-13]。对于圆盘携油过程, VOF模型的连续性方程、动量方程、流体材料属性计算分别为:
| $ \frac{\partial \alpha_{\mathrm{i}}}{\partial t}+\nabla \cdot\left(\alpha_{\mathrm{i}} \boldsymbol{v}\right)=0 $ | (3) |
| $ \frac{\partial}{\partial t}(\rho \boldsymbol{v})+\nabla \cdot(\rho \boldsymbol{v} \boldsymbol{v})=-\nabla p+\left[\mu\left(\nabla \boldsymbol{v}+\nabla \boldsymbol{v}^T\right)\right]+\rho g+F, $ | (4) |
| $ \rho=\alpha_2 \rho_2+\alpha_1 \rho_1, \mu=\alpha_2 \mu_2+\alpha_1 \mu_1, \alpha_1+\alpha_2=1, $ | (5) |
式中, αi为第i相流体体积分数; v为速度矢量; ρ为密度; μ为动力黏度; p为压强; α1为空气的体积分数; α2为油的体积分数; F为动量源相。
2 计算模型 2.1 网格划分和求解器设置采用SolidWorks绘制两种圆盘模型, 标准实心圆盘直径为200 mm, 厚度为4 mm, 凸缘厚度为5 mm, 宽度为5 mm, 外壁面半径为75 mm, 内壁面半径为70 mm。为方便表示转盘携油的过程, 在转盘的成膜区域, 即转盘与空气接触的部分, 可分为两个区域, 如图 1所示, 0° < θ < 90°为油膜拖出区域, 90° < θ < 180°为油膜拖入区域[14]。根据三维模型, 导入ICEM软件中进行网格划分, 整个计算流域分为流体域和转盘域, 两个流域之间的交界面设置interface面。两种圆盘模型及网格划分如图 2所示。在求解器设置中, 重力沿y轴方向向下, 加速度大小为9.81 m/s2, 圆盘上半部分接触空气, 下半部分浸没于油液之中, 沿z轴方向转动, 圆盘转速为60 r/min, 壁面无滑移。油液的密度设置为800 kg/m3, 动力黏度为0.2 kg/(m·s)。使用PISO算法实现对压力和速度方程的耦合, 通过几何重构方法对气相和油相之间的界面进行重构, 变量差值采用Least Squares Cell Based, 压力差值方式设置为二阶格式, 动量的计算、湍动能及耗散率均采用二阶迎风格式。为使计算不容易发散, 瞬态计算时间步长设置为0.000 1 s[15]。
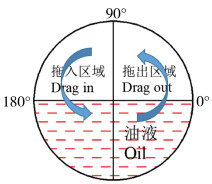 |
| 图 1 区域划分示意图 |
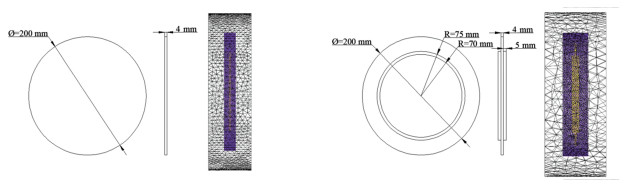 |
| 图 2 两种圆盘模型及网格划分 |
2.2 模型验证及网格无关性分析
为验证模拟方法的可靠性, 设置与邓斌等[16]实验相同的参数条件进行数值模拟。采集相同位置处的膜厚数据进行对比分析, 分析结果如图 3(a)所示。从图中可以看出, 模拟结果和实验结果能够较好的吻合, 采用该模拟方法来分析本文模型是可靠的。网格划分时, 分别划分了数量为617 125、885 376、1 198 360、1 455 931的4套网格, 保证网格质量大部分在0.4以上。设置转速为100 r/min, 介质动力黏度为0.2 kg/(m·s)的油液, 其它条件设置均不变, 以50 mm处的膜厚变化为参考依据, 计算结果如图 3(b)所示, 从图中可以看出, 当网格数大于1 198 360时, 网格数对膜厚变化的影响接近收敛。考虑节约计算时间和资源, 选择方案3作为计算网格, 网格数量为1 198 360。
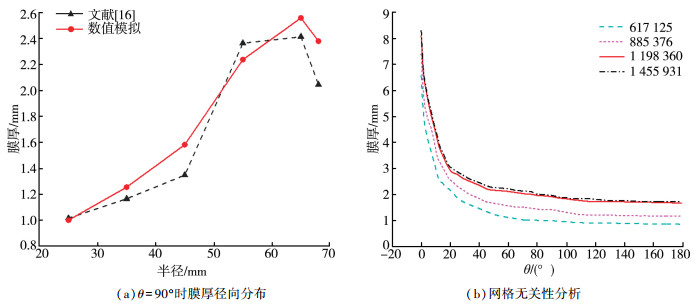 |
| 图 3 模型验证及网格无关性分析 |
3 结果与讨论 3.1 凸缘圆盘与标准实心圆盘膜厚特性对比分析
标准实心圆盘与凸缘圆盘的条件设置和流体物理参数均相同, 分析转盘从刚开始携油到重新转回油液的0°~180°之间的膜厚变化。图 4(a)为凸缘圆盘合速度云图, 从图中可以看出: 在气-油界面的下方出现了许多不规则的圆形物质, 这是因为在圆盘转动过程中发生了气相和油相的传质, 圆盘将部分气体带入到了油液中; 图 4(b)为凸缘圆盘在θ=90°(x=0)时的膜厚分布云图, 由图可以看出: 油膜在凸缘附近发生了堆积。
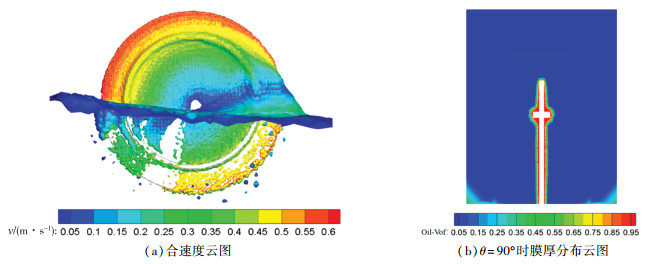 |
| 图 4 仿真云图 |
图 5为标准实心圆盘与凸缘圆盘在θ=90°时径向膜厚分布对比曲线图, 从图中可以看出: 凸缘圆盘的膜厚在整体上要大于标准实心圆盘, 尤其在加装凸缘位置处的膜厚变化最为明显, 产生这种现象的原因是凸缘与圆盘表面交界区域堆积了较多的油液, 膜厚会显著增大, 而凸缘正表面粘附的油液较少, 油膜厚度在凸缘的内外壁边缘处出现了骤降的现象。
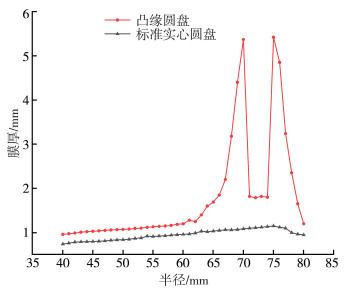 |
| 图 5 θ=90°时径向膜厚分布对比曲线图 |
图 6为凸缘圆盘与标准实心圆盘在r=75 mm和r=70 mm的膜厚随角度变化对比曲线。从图中可以看出, 在相同位置处, 凸缘圆盘比标准实心圆盘起始膜厚大, 在油膜拖出区域的下降幅度较小, 在油膜拖入区域的稳定值更高。图 6(a)与图 6(b)呈现的曲线结果分别是凸缘外壁和凸缘内壁的存在而导致的。凸缘内外壁的存在增大了转盘与油液的接触面积, 且凸缘外壁提供的支撑力能够缓解油液向下流动, 凸缘内壁在一定程度上可以阻挡住半径在70 mm内由于离心作用而被甩出去的油液, 使得凸缘内外壁处的膜厚下降速率相对较小, 最终的稳定值更高。凸缘圆盘在凸缘内外壁处的平均膜厚约是同位置标准实心圆盘的3倍。
 |
| 图 6 凸缘圆盘与标准实心圆盘膜厚随角度变化对比曲线 |
在凸缘位置处, 凸缘圆盘的膜厚要大于标准实心圆盘, 且稳定性好。在其它位置处, 选取半径为60、50和40 mm处的膜厚分布情况进行对比分析。图 7(a)为两种圆盘在不同半径下的膜厚变化对比曲线, 从图中可以看出, 在相同位置处, 凸缘圆盘的膜厚下降幅度小于标准实心圆盘, 最终的稳定值更高。是因为凸缘内壁堆积的油液会受到重力作用而向下流动, 对内壁以下其它位置处的膜厚影响较大。图 7(b)为两种圆盘在不同半径下的平均膜厚变化曲线, 从图中可以看出, 在60 mm处, 凸缘圆盘平均膜厚比标准实心圆盘大21%, 在50 mm处大17%, 在40 mm处大15%。由此可见, 凸缘内壁的油液堆积有利于圆盘携油膜厚的增大, 且越靠近凸缘内壁, 膜厚增大的越多。
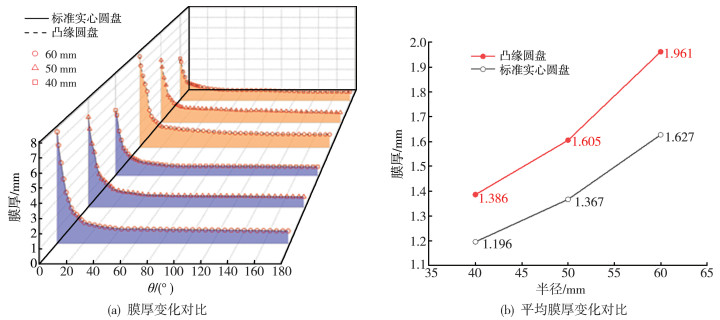 |
| 图 7 两种圆盘在不同半径下的膜厚变化对比曲线 |
3.2 凸缘内外壁附近膜厚特性分析
通过上述分析可知, 凸缘圆盘与标准实心圆盘在凸缘位置处膜厚差异最大, 且油液在凸缘和圆盘表面的交界区域发生了堆积, 应分析凸缘内外壁附近膜厚分布情况。
图 8为凸缘内外壁附近膜厚变化曲线。图 8(a)为半径75~79 mm膜厚变化曲线, 从图中可以看出, 距离凸缘外壁越远, 膜厚越小, 下降速率越快, 且在油膜拖入区域越难以形成一个较为稳定的值。图 8(b)为半径66~70 mm膜厚变化曲线, 与凸缘外壁相比, 内壁附近的油膜在油膜拖出区域下降较快, 在油膜拖入区域形成了相对稳定的膜厚。
 |
| 图 8 凸缘内外壁附近油膜厚度变化曲线 |
图 9为凸缘内外壁附近膜厚的平均值变化曲线。从图中可以看出, 在油膜拖出区域, 外壁附近膜厚平均值较内壁下降慢, 在油膜拖入区域, 内壁附近膜厚变化较为稳定, 其平均值在110°之后大于外壁。原因可以归结为: 在油膜拖出区域, 凸缘外壁提供的支撑力可以缓解外壁堆积油液的流动, 且堆积油液的线速度沿着外壁切线方向向上, 更有利于油膜的附着, 而内壁堆积的油液受到重力的影响较为显著, 膜厚下降速度较快; 在油膜拖入区域, 重力起主要作用, 外壁堆积油液的线速度沿着壁面切线方向向下, 外壁起到的支撑作用不明显, 所以下降速率较快, 不能形成较为稳定的膜厚, 而离心作用使内壁堆积油液流动缓慢, 形成了较为稳定的膜厚。
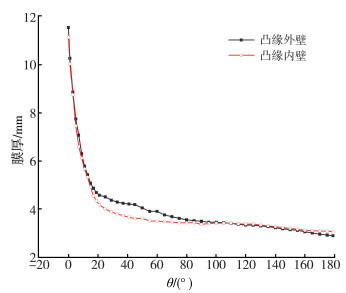 |
| 图 9 凸缘内外壁附近膜厚的平均值变化曲线 |
4 结论
采用数值模拟的方法, 分析了海上盘式收油机的转盘表面油膜形成特性。通过仿真分析发现: 圆盘的转动会把部分气体带入到油液中, 在油相中出现了许多不规则的圆形物质; 凸缘圆盘与普通实心圆盘成膜特点相同, 膜厚在油膜拖出区域下降速度快, 在油膜拖入区域趋于稳定; 凸缘结构有利于圆盘膜厚的增大, 凸缘圆盘在凸缘内外壁处的膜厚增大效果最为显著, 油膜平均厚度约是标准实心圆盘的3倍; 对于其它位置, 距离凸缘越近, 膜厚增大效果越明显; 凸缘内外壁附近发生了油液堆积现象, 在油膜拖出区域, 外壁附近膜厚较内壁下降速度慢, 在油膜拖入区域, 内壁附近膜厚相对稳定, 外壁附近不能形成较为稳定的膜厚。该研究为后续盘式收油机转盘结构的优化设计奠定了一定的理论基础。
| [1] |
FENG Q, AN C J, CHEN Z, et al. Assessing the coastal sensitivity to oil spills from the perspective of ecosystem services: A case study for Canada's pacific coast[J]. Journal of Environmental Management, 2021, 296: 113240. DOI:10.1016/j.jenvman.2021.113240 |
| [2] |
WOO B G, CHOI K Y, SONG K H. Melt polycondensation of bisphenola polycarbonate by a forced gas sweeping process[J]. Industrial & Engineering Chemistry Research, 2001, 40(5): 1312-1319. |
| [3] |
AFANASIEV K, MINCH A, WAGNER B. Thin film dynamics on avertically rotating disk partially immersed in a liquid bath[J]. Applied Mathematical Modelling, 2008, 32(9): 1894-1911. DOI:10.1016/j.apm.2007.06.020 |
| [4] |
ZANGENEH H, ZINATIZADEH A A, NAZARI S, et al. Highly efficient azo dye degradation in a photocatalytic rotating disc reactor with deposited l-histidine-TiO2-CdS[J]. Materials Science in Semiconductor Processing, 2022, 152: 107071. DOI:10.1016/j.mssp.2022.107071 |
| [5] |
CAI Y, LUO Y, SUN B C, et al. A novel plasma-assisted rotating disk reactor: Enhancement of degradation efficiency of rhodamine B[J]. Chemical Engineering Journal, 2019, 377: 119897. DOI:10.1016/j.cej.2018.09.058 |
| [6] |
王萌. 盘式收油机圆盘携油数值模拟研究[D]. 青岛: 中国石油大学(华东), 2018.
|
| [7] |
MIAH M S, AL-ASSAF S, YANG X, et al. Thin film flow on a vertically rotating disc of finite thickness partially immersed in a highly viscous liquid[J]. Chemical Engineering Science, 2016, 143: 226-239. DOI:10.1016/j.ces.2016.01.003 |
| [8] |
WANG J H, FU H, DING H B, et al. Film formation and surface renewal on a rotating spoked disk for polymer devolatilization[J]. Chemical Engineering Research and Design, 2021, 170: 45-53. DOI:10.1016/j.cherd.2021.03.030 |
| [9] |
SAINI S K. Modeling and experimentation for novel aerofoil embedded mesh disk-based partially submerged rotating reactor[J]. Chemical Engineering Journal Advances, 2022, 12: 100382. DOI:10.1016/j.ceja.2022.100382 |
| [10] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [11] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [12] |
GAO H, LUO X, CUI D, et al. A study of film thickness and hydrodynamic entrance length in liquid laminar film flow along a vertical tube[J]. AIChE Journal, 2018, 64(6): 2078-2088. DOI:10.1002/aic.16081 |
| [13] |
XU Y C, LI Y B, LIU Y Z, et al. Liquid jet impaction on the single‐layer stainless steel wire mesh in a rotating packed bed reactor[J]. AIChE Journal, 2019, 65(6): 16597. |
| [14] |
KHESHGI H S, KISTLER S F, SCRIVEN L E. Rising and falling film flows: Viewed from a first-order approximation[J]. Chemical Engineering Science, 1992, 47(3): 683-694. DOI:10.1016/0009-2509(92)80018-8 |
| [15] |
LI Y B, WU X S, LIU Y Z, et al. Three-dimensional large eddy simulation of wave characteristics of liquid film flow in a spinning disk reactor[J]. AIChE Journal, 2020, 66(4): 16894. |
| [16] |
邓斌, 戴干策. 圆盘反应器液膜表面更新数值模拟[J]. 化工学报, 2015, 66(4): 1407-1416. |
 2023, Vol. 37
2023, Vol. 37


