| 基于模糊理论的水下直升机深度跟踪研究 |
在海洋探测过程中, 水下航行器是重要的海洋装备, 主要分为载人水下航行器和无人水下航行器。水下直升机属于无人水下航行器, 不但具有直升直降, 悬停定深航行等功能外, 还可以实现横滚、俯仰、航向等复杂动作[1]。然而水下环境十分恶劣, 不但有着风浪潮汐等水流影响, 而且还有着不规则的暗流涌动的干扰, 因此, 水下直升机对其稳定性的控制提出了更高的要求。
在水下航行器的控制方面, 国内外学者都提出了不同的控制方案。Manzanilla[2]和González-García等[3]采用滑膜控制, 对ROV的深度方向进行控制研究;王子含等[4]、Raju等[5]和Khodayari等[6]采用了模糊PID的控制策略, 对水下航行器进行稳定性控制;赵威等[7]提出一种基于模糊PID的控制方法结合神经网络算法, 对复杂涌流下水下自主航行器横滚抑制进行了研究, 但是其算法计算量较大, 控制能力提高有限;赵朝坤[8]将模糊控制和滑膜控制相结合, 对水下航行器的路径跟踪进行了研究, 但是其算法的实时性还有待提高。Hasan等[9]将一种非线性的自适应模糊PID控制应用在了水下航行器上, 效果显著;D.Karimanzira[10]等将深度学习和模糊控制相结合控制水下航行器, 对水下航行器的航行误差控制在很小的范围之内, 但对其主控芯片的要求较高。Chen等[11]和张家赫[12]对水下航行器在运动中存在的海流干扰等问题, 将遗传算法应用于PID控制, 提高了水下航行器的鲁棒性和稳定性。
基于此, 为了提高水下直升机的鲁棒性, 采用了模糊PID的控制策略, 针对模糊论域带来的控制盲区, 将BP神经网络引入模糊PID控制器之中, 改变其模糊论域, 提高了水下直升机在的控制性能和悬停定深航行的能力。
1 水下直升机的深度运动模型水下直升机的水下数学模型十分复杂, 本文主要研究的是水下直升飞机的垂直面深度跟踪问题, 因此, 简化了水下机器人的数学模型, 仅考虑铅锤平面内的运动方程, 做出了以下假设[13]:
(1) 水下直升机在铅锤平面内运动时, 速度较低, 不会导致其他轴向运动状态的耦合, 各个轴向运动状态直接是相互独立的。
(2) 考虑到水下直升机的对称性, 采用线性模型, 忽略非线性水动力项。
首先建立水下直升机在铅锤面的坐标系, 如图 1所示, 其中E-ζξ为地球坐标系;G-xyz为水下直升机坐标系。
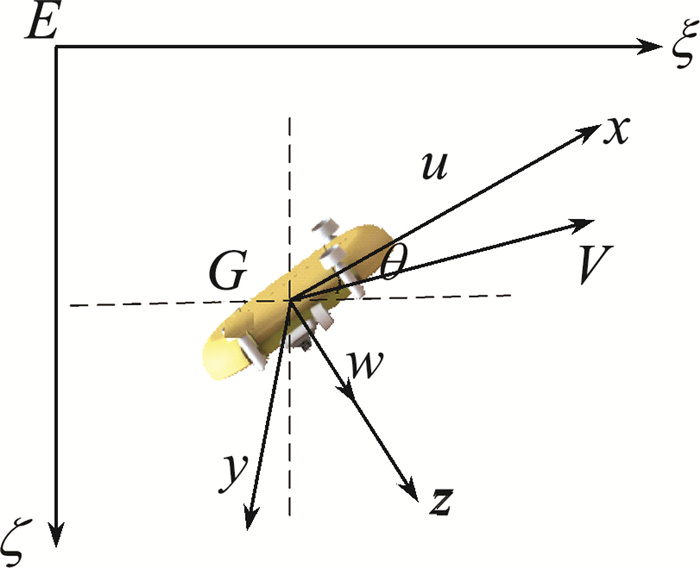 |
| 图 1 水下直升飞机垂直面运动坐标系 |
将水下直升机的重心作为坐标系的原点, 在平衡冲角和舵角的条件下, 水下直升机的定常直线运动线性化数学方程为:
| $ \left\{\begin{array}{l} \left(m-Z_{w^{\prime}}\right) \dot{w}-Z_{q^{\prime}} \dot{q}-\left(m V+Z_q\right) q-Z_w w=T_z \\ \left(I_y-M_{q^{\prime}}\right) \dot{q}-M_{w^{\prime}} \dot{w}-M_q q-M_w w=M_{T_z}, \end{array}\right. $ | (1) |
式中:m为水下直升机质量;Iy为绕y轴的惯性矩;w′为沿Z轴的速度, w=ż;q为纵倾角速度,
| $ G(s)=\frac{z}{\delta_e}=\frac{Z_{\delta_e} V\left(I_y s^2-M_q s+m g h\right)}{C_3 s^4+C_2 s^3+C_1 s^2+C_0 s}, $ | (2) |
式(2)中, C0、C1、C2、C3的表达式为:
| $ \left\{\begin{array}{l} C_0=-m g h Z_w \\ C_1=M_q Z_w+m g h\left(m-Z_w\right)-M_w\left(m V+Z_q\right) \\ C_2=-M_q\left(m-Z_w\right)-I_y Z_{w^{\prime}} \\ C_3=I_y\left(m-Z_{w^{\prime}}\right) \end{array}\right.。$ | (3) |
水下环境复杂多变, 不仅有着风浪潮汐等水流影响, 并且还有着不规则的暗流涌动, 因此水下直升机属于典型的时变非线性系统。在实际测试中, 受到水压水阻和风浪等客观条件的影响, 很难建立具体的数学模型。
传统的模糊控制, 有着可靠性高, 稳定性好等特点, 被广泛应用到各个领域。但是其模糊论域在初始化之后, 将不会再改变。但在水下环境中, 下水最初阶段, 误差相对较大, 待运行一段时间后, 其稳定误差较小。无法改变模糊论域的模糊控制器, 一方面为了将误差范围完全覆盖, 防止出现控制盲区, 需要将模糊论域范围扩大, 另一方面, 为了提高控制精度并防止推理规则过于复杂, 模糊论域范围需要减小[14]。
因此, 提出变模糊论域的方法, 将神经网络引入, 通过当前的误差和误差变化率, 确定其模糊控制器的模糊论域。当前误差较大时, 论域膨胀, 防止出现控制盲区, 且提高系统稳定速度;当前误差较小时, 模糊论域收缩, 提高了控制精度。论域的收缩和膨胀如图 2所示。
 |
| 图 2 论域变化示意图 |
2.2 控制器结构
变论域模糊PID控制器的原理图如图 3所示。
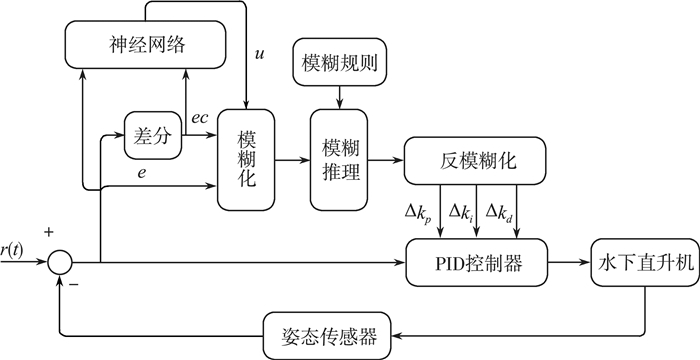 |
| 图 3 变论域模糊PID控制器的原理图 |
系统将误差e和误差变化率ec作为神经网络的输入, 神经网络由先验实验得到的最优模糊论域u, 将最优模糊论域输入到模糊控制器, 模糊控制器也将误差e和误差变化率ec作为输入, 通过模糊化将其转化为模糊向量, 模糊推理机通过模糊规则进行推理, 最终将输出反模糊化, 得到PID控制器的控制参数Δkp、Δki、Δkd。这种实时修正PID控制器参数的方法能够保证在水下复杂的环境之下, 系统同样可以保持很高的鲁棒性。
2.3 神经网络控制器的建立BP神经网络是一种迭代梯度算法, 用于求解前馈神经网络的实际输出于期望输出之间的最小均方误差, 具有非线性的映射关系和柔性的网络结构, 适应于这种没有具体数学模型的系统[15]。本设计采用3层BP神经网络, 其中隐含层神经元数目为3, 根据不同的环境, 改变模糊控制器的模糊论域, 其结构如图 4所示。神经元的输出由加权输入的总和、偏置b和激活函数决定, 将误差e和误差变化率ec作为输入, 则:
| $ \operatorname{net}_k=w_{k 1} e+w_{k 2} e c, $ | (4) |
| $ o_k=F\left(\operatorname{net}_k+b_k\right), $ | (5) |
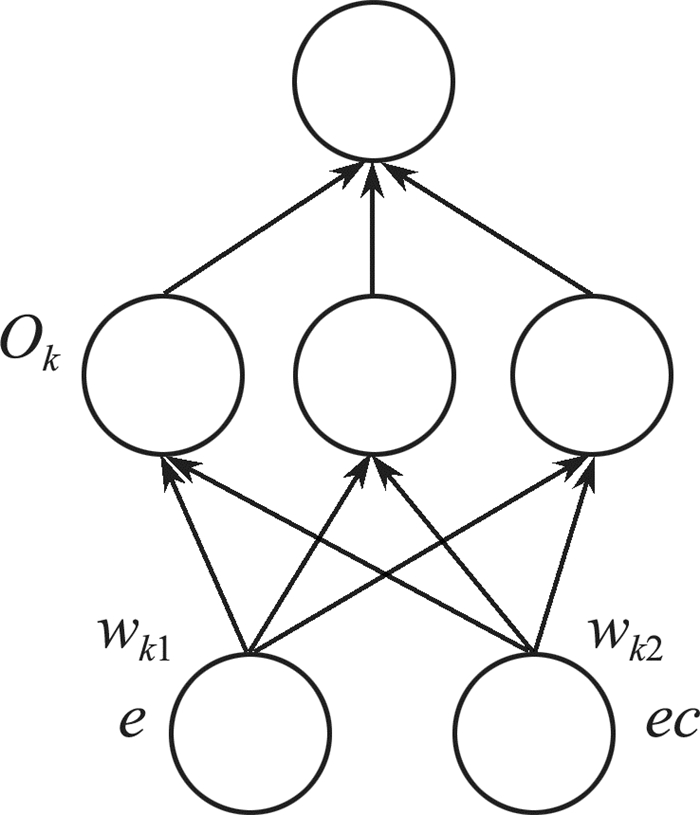 |
| 图 4 神经网络结构图 |
式中:wk1和wk2为误差e和误差变化率ec的权重;netk为第k个神经网络加权和;bk为第k个神经元的偏置;Ok为单元k的输出;F为传递函数, 本文采用Sigmoid函数[16], 即
神经网络需要通过满足工程应用精度的训练样本进行训练, 通过误差的反向传播不断更新权值wk1和wk2, 直至误差在允许范围之内, 其训练过程需要遵循以下原则:
| $ {\mathit{\Delta}} {W^{(l)}}_{j i}(n)=\eta \rho_j^{(l)}(n) u_i^{(l-1)}(n)+\alpha {\mathit{\Delta}} W_{j i}^l(n-1), $ | (6) |
式中:η为学习因子, 决定每次迭代过程中的权值变化量;α为动量因子, 决定权值的变化是否只由梯度决定;ΔW(l)ji(n)为表示时间n连接l-1层中的第i个神经元与l层中的第j个神经元之间的权值变化量;ρj(l)为表示第l层第j个神经元期望输出与实际输出之差;ui(l-1)为表示时刻n第l-1层的第i个神经元的输出。
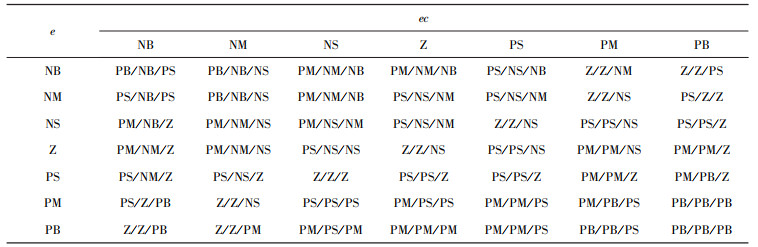
2.4 模糊PID控制器的建立模糊控制器将误差e和误差变化率ec作为输入, PID参数Δkp、Δki、Δkd为输出, 由BP神经网络调节其个参数论域大小, 各参数的模糊子集为NB(负大)、NM(负中)、NS(负小)、Z(零)、PS(正小)、PM(正中)、PB(正大), 隶属函数为高斯函数, 对不同的输入e、ec对应输出的Δkp、Δki、Δkd建立模糊控制规则表[17], 如表 1所示。
| 表 1 模糊控制规则表 |
 |
通过模糊规则处理之后的输出, 还要将输出进行反模糊化, 得到其具体数值Δkp、Δki、Δkd, 本文反模糊化采用的是质心法[18], 其公式为:
| $ x_A=\frac{\sum\limits_{i=1}^m \mu_A\left(x_i\right) x_i}{\sum\limits_{i=1}^m \mu_A\left(x_i\right)}, $ | (7) |
式中:xA为输出值的清晰值;xi为模糊变量元素;μA(xi)为元素xi的隶属度。
在模糊PID控制器中, 首先给定PID控制器参数一个初始值, 然后由模糊控制器不断对其参数进行修正, 即:
| $ k_{p_{t+1}}=k_{p_t}+{\mathit{\Delta}} k_p, $ | (8) |
| $ k_{d_{t+1}}=k_{d_t}+{\mathit{\Delta}} k_d, $ | (9) |
| $ k_{i_{t+1}}=k_{i_t}+{\mathit{\Delta}} k_i, $ | (10) |
式中:kpt、kdt、kit表示PID控制器中t时刻的参数值;kpt+1、kdt+1、kit+1表示PID控制器经过修正后的参数值;Δkp、Δki、Δkd为模糊控制器输出的对PID控制器的修正量。
3 系统仿真及分析选用某款AUV载体作为仿真对象, 将其参数代入动力学模型中, 得到深度控制的传递函数[19]为:
| $ G(s)=\frac{z}{\delta_e}=\frac{0.355\;9 s^2+5.226 s+35.245\;9}{s^4+10.099\;7 s^3+8.387\;9 s^2}。$ | (11) |
由Simulink建立仿真模型, 验证变论域的模糊PID的控制效果, 同时与传统的PID控制效果进行对比。按照经验, 通过扩充临界比例法得到其PID初始参数:kp=280、ki=0.5、kd=30。
试验1, 在1 s的时候加入幅值为10的阶跃信号, 观察并分析两者动态响应曲线, 如图 5所示。
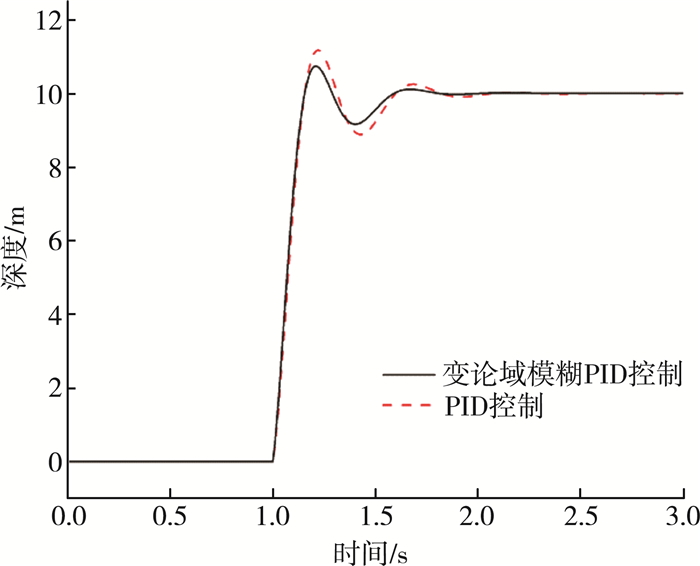 |
| 图 5 阶跃信号下控制效果 |
从图 5可以观察到, 变论域的模糊PID与传统的PID控制效果相比, 峰值时间由0.223 s减少到0.198 s, 速度提升了11.21%, 超调量由14.90%降低到9.80%, 由此可得, 变论域的模糊PID有着上升时间短, 超调量小, 更快达到稳定状态的优点。
试验2在试验1的同样条件下, 加入高斯噪声信号, 测试在有噪声干扰的情况下的稳定性控制能力, 结果如图 6所示。
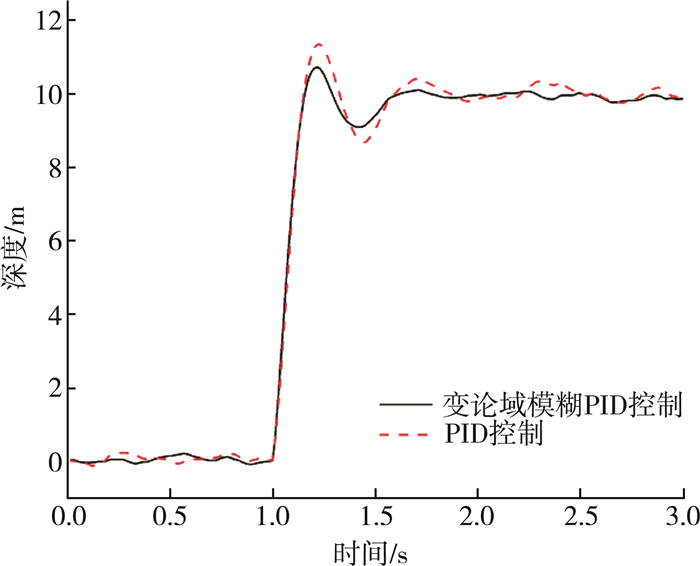 |
| 图 6 存在噪声情况下稳定性效果 |
由结果可知, 在加入噪声干扰后, 变论域的模糊PID的调整时间为0.89 s, 与传统的PID控制的调整时间1.28 s相比, 响应进入稳态值误差范围内的时间减少了30.40%, 变论域的模糊PID控制在保留试验1的优良性能的同时, 有着比传统PID更强的抗干扰能力。
试验3, 测试两种控制器在跟踪时变信号方面的能力, 其他条件和试验1相同, 目标深度以4 m和1 m交替给出。
由图 7可知, 在跟踪时变信号时, 变论域的模糊PID控制器性能同样优于传统PID控制器。
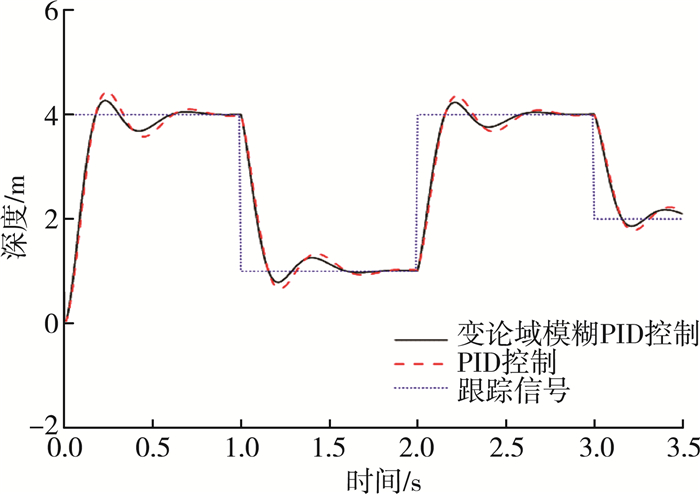 |
| 图 7 跟踪时变信号控制效果 |
4.4 试验验证
使用自研的水下直升机, 采用变论域的模糊PID控制器与传统PID控制器, 目标深度为5 m, 通过深度传感器在10 min内采集到1 000条数据, 如图 8所示。
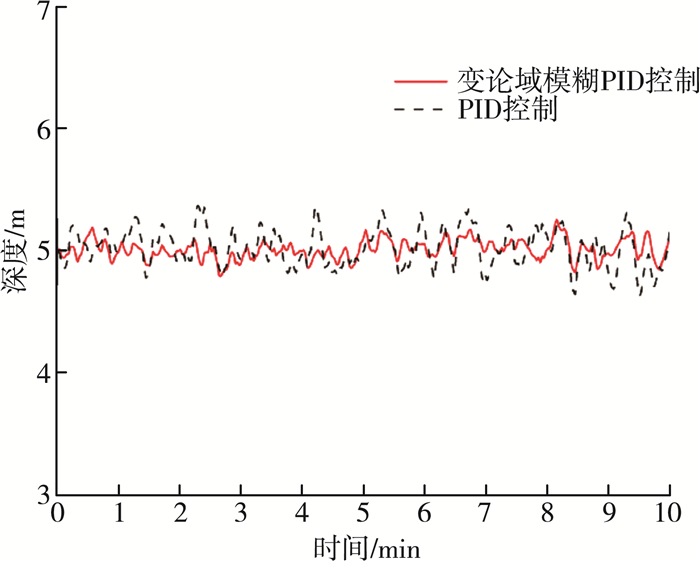 |
| 图 8 深度控制效果对比 |
对深度传感器采集到的数据进行分析, 如表 2所示。
| 表 2 控制误差对比 |
 |
综上, 本文提出的变论域的模糊PID控制器, 相较于传统的PID控制, 能够控制水下直升机更快的达到稳定状态, 且克服噪声和时变信号跟踪的性能同样优秀, 验证了算法的可行性。
5 结论水下直升机具有多自由度, 姿态灵活等优点。首先对水下直升机建立深度的运动学数学模型, 将BP神经网络引入模糊PID控制之中, 能够对模糊论域的范围进行膨胀和收缩。根据不同的环境下, 调节不同的模糊论域, 在避免出现控制盲区的同时, 也能提高控制精确度。最后通过计算机进行仿真分析, 对比了经典的PID控制算法, 结果表明, 该控制策略在稳定性、抗干扰能力和跟随时变信号等方面, 性能有着显著的提升, 证明了该算法的可靠性, 对未知模型的控制策略有着较好的借鉴意义。
| [1] |
冯卓. 圆碟形水下直升机水动力分析与操纵性能研究[D]. 杭州: 浙江大学, 2019.
|
| [2] |
MANZANILLA A, IBARRA E, SALAZAR S, et al. Super-twisting integral sliding mode control for trajectory tracking of an Unmanned Underwater Vehicle[J]. Ocean Engineering, 2021, 234: 109164. DOI:10.1016/j.oceaneng.2021.109164 |
| [3] |
GONZáLEZ-GARCíA J, NARCIZO-NUCI N A, GARCíA-VALDOVINOS L G, et al. Model-free high order sliding mode control with finite-time tracking for unmanned underwater vehicles[J]. Applied Sciences, 2021, 11(4): 1836. DOI:10.3390/app11041836 |
| [4] |
王子含. 基于模糊PID水下航行器运动控制研究[D]. 青岛: 青岛科技大学, 2021.
|
| [5] |
RAJU S S, HARISH P V, NIKHILA G, et al. Design and implementation of fuzzy pid controller for controlling the speed of robotic vehicle system in MATLAB[J]. Available at SSRN 3882549, 2021. |
| [6] |
KHODAYARI M H, BALOCHIAN S. Modeling and control of autonomous underwater vehicle (AUV) in heading and depth attitude via self-adaptive fuzzy PID controller[J]. Journal of Marine Science and Technology, 2015, 20(3): 559-578. DOI:10.1007/s00773-015-0312-7 |
| [7] |
赵威, 王程成. 复杂涌流下水下自主航行器横滚抑制控制仿真[J]. 智能计算机与应用, 2016, 6(3): 11-14. |
| [8] |
赵朝坤. 基于模糊滑模的水下航行器控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [9] |
HASAN M W, ABBAS N H. Disturbance rejection for underwater robotic vehicle based on adaptive fuzzy with nonlinear PID controller[J]. ISA Transactions, 2022. |
| [10] |
KARIMANZIRA D, PFUETZENREUTER T, BAATAR G, et al. Fuzzy logic docking control for underwater vehicles based on deep learning feature selection[C]//IEEE. OCEANS 2021, San Diego-Porto, United States; 2021.
|
| [11] |
CHEN Q, CHEN T, ZHANG Y, et al. Research of GA-based PID for AUV motion control[C]//IEEE. 2009 International Conference on Mechatronics and Automation, Changchun, China; 2009.
|
| [12] |
张家赫. 拖曳式水下航行器定深运动控制研究[D]. 武汉: 武汉理工大学, 2020.
|
| [13] |
杨俭健, 付宗国. 基于滑模控制的ROV深度方向轨迹跟踪研究[J]. 浙江海洋学院学报(自然科学版), 2014, 33(2): 175-179. |
| [14] |
胡锦晖, 胡大斌, 肖剑波. 基于模糊理论的水下航行器运动控制及仿真研究[J]. 舰船科学技术, 2017, 39(23): 59-63. |
| [15] |
NIKITIN V F, KARANDASHEV I M, MALSAGOV E V, et al. Approach to combustion calculation using neural network[J]. Acta Astronautica, 2022, 194: 376-382. DOI:10.1016/j.actaastro.2021.10.034 |
| [16] |
白宇骏, 徐晓苏, 刘国燕. 神经网络辅助卡尔曼滤波技术在组合导航系统中的应用研究[J]. 中国惯性技术学报, 2003(2): 42-45. |
| [17] |
张浩, 任万龙, 华志励, 等. 基于模糊PID控制的主动造波系统研究与应用[J]. 齐鲁工业大学学报, 2021, 35(3): 59-63. |
| [18] |
廉小亲. 模糊控制技术[J]. 电力设备, 2004, 5(1): 73-73. |
| [19] |
马艳彤, 郑荣, 于闯. 过渡目标值的非线性PID对自治水下机器人变深运动的稳定控制[J]. 控制理论与应用, 2018, 35(8): 1120-1125. |
 2022, Vol. 36
2022, Vol. 36

