| 游乐场排队优化系统 |
目前,游乐场是旅游项目中的一大热点,但许多游乐场人流众多,排队时容易发生拥堵现象,降低了游客的满意度。因此,如何优化游乐场排队过程一直是管理人员和游客都非常关注的问题。本文旨在研究开发一个游乐场项目排队优化系统[1],为游客提供多项目的游玩时间推荐表,以方便游客在有限时间内游玩更多项目,同时也能给游乐场带来更多的经济效益,最终改善游乐场服务效率。
1 系统创新“线上线下”同时排队系统:将系统中的一个排队序列分散给线上线下排队的游客,共用同一个资源池进行排队[2]。
个人信息卡:游客在购票入场时,同时发放含有个人信息的游玩卡。个人信息卡在购票处充磁,在出园时回收。实现刷卡入园,刷卡进入(使用)游乐设施。该个人信息卡将作为这个人的唯一标识。
多个项目同时选择、逐项自动排队:游客在APP主界面上可以选择多个项目,而系统只对游客选择的第一个项目进行排队。当游客开始游玩第一个项目时,开始对第二个项目的排队。
团体排队模式可自由增添游客:当游客选择团队排队模式进行排队时,可以在排队页面添加游客,用一个APP给多人同时排队。
游园提示:在该项目开始前,用手机APP排队的游客会收到游园提示,提醒他们按时入场,并且对逾期不到者,系统将取消此游客的该场次排队。
2 基于排队论的数学建模旅游景点、银行、医院、公交站牌[3]等的排队等待是一种大家司空见惯的现象,图 1为排队示意图[4]。
 |
| 图 1 排队示意图 |
顾客随机到达服务点,排队等待服务,服务台根据服务规则按顺序提供服务,服务完成后,顾客离开服务台。对于这类简单的排队系统,涉及等待的队伍长度、顾客排队时间、服务员的数量、服务顺序和规则等问题[5]。实际上,很多排队系统远比上述排队系统复杂。
本研究本质上是一个排队问题,设计思路可用以下数学模型表达。
由于多名游客对应多个项目排队队列,因此多项目排队窗口服务构成了一个等待制的多队列多窗口的M/M/n随机服务排队系统[6]。
参数说明:
λ:游客平均到达率
μ:参数为μ的负指数分布
ρ:服务强度(ρ=λ/μ)
ti:游客到达的时间间隔
ti, m+1:第m+1个游客排队通道系统提示的返回时刻
Ti:接受排队服务的时间
Tw:公园的开放时间
c1(t), c2(t):关于时间的权值函数
Lk:第k个场所游客的平均人数
rk:第k个场所的等候人数比率(rk=Lk, i/Lk)
Lk, i:第k个场所的平均等待人数(Lk, i=λ2/[μk(μk-λk)])
t:该团队在游乐场的平均逗留时间
t2, i-n0:第i-n0位游客花费在排队系统的等待时间
t1, i:第i个游客到达该游乐场的提示返回时刻
X1(t):从普通通道进入游乐场的游客数
X2(t):从排队系统进入游乐场的游客数
X'1(t):从普通通道走出游乐场的游客数
X'2(t):从排队系统走出游乐场的游客数
模型公式如下。
平均排队等待时间:
| $ {\mathit{E}_\mathit{W}} = \mathit{\rho }/(\mathit{\mu } - \mathit{\lambda }) $ |
平均等待时间[7]:
| $ {W_q} = \frac{{{L_q}}}{\mathit{\lambda }} = \frac{\mathit{\rho }}{{\mathit{\mu }(1 - \mathit{\rho })}} = \frac{\mathit{\lambda }}{{\mathit{\mu }(\mathit{\mu } - \mathit{\lambda })}} $ |
平均等待队长:
| $ {E_{qw}} = {\rm{ }}{\mathit{\rho }^2}/(1 - \mathit{\rho }) $ |
T时刻的等待时间分布:
| $ W(x) = \left\{ \begin{array}{l} 1 - \mathit{\rho } * {\rm{ exp}}( - (\mathit{\mu } - \mathit{\lambda })\mathit{x}), (x \ge 0)\\ 0, (x < 0) \end{array} \right. $ |
平均逗留时间[7]:
| $ {d_q} = \frac{L}{\mathit{\lambda }} = \frac{\mathit{\rho }}{{\mathit{\lambda }(1 - \mathit{\rho })}} = \frac{1}{{\mathit{\mu } - \mathit{\lambda }}} $ |
第一个优化目标函数:
| $ Z = {\rm{min}}\left\{ {{c_1}(t){t_{1, i}} + } \right.\left. {{c_2}(t){t_{2, i}}} \right\} $ |
第二个目标函数:
| $ {\rm{min\{ }}{\sum\limits_{i \ne j} {\sum\limits_{j = 1} {\left| {{r_i} - {r_j}} \right|} } ^2}\} $ |
目标约束条件:
| $ {t_{1, i}} \ge \sum\limits_{j = 1}^{i - {n_0}} {{t_j}} + {t_{2, i - {n_0}}} + \bar t + {t_{0, i}} $ |
T时刻可容纳的游客数:
| $ {N_{(t)}} = {\rm{ }}{N_0} - {X_{1(t)}} - {X_{2(t)}} + X{\mathit{'}_{1(t)}} + X{\mathit{'}_{2(t)}} $ |
游客取票后可以自由选择使用APP或者个人信息卡。
1) 如果游客选择APP,首先需要注册并登陆系统。
2) 系统会根据项目的排队时间长短、项目热度以及综合排序等给游客推荐游玩项目表。
3) 游客根据自己的喜好选择项目(最多3个)进行排队,点击确认便可进入系统排队序列。游客将会得到一个该项目的排队号和游玩时间,在该项目开始之前游客不需要站队,可以自由安排这段时间。
4) 在该项目开始前大约15 min,APP将会给游客发送一条信息,提醒游客按时到达,并可用手机扫码入场(如果游客不应在该游玩时间内入场,则不能扫码入场);如果该游客没有按时入场,APP将会自动取消该游客的排队号。
5) 对于团组游客,APP会按照上述同样的方式为游客排队。当遇到该场次剩余的位置小于团组游客人数时,APP会自动判断并询问游客是否愿意分开排队或者等待下一场。
6) 游客如果选择使用个人信息卡,则可以按照普通的排队方式到任意一个项目刷卡排队。该游客刷卡后进入排队序列,得到一个排队号。在此期间,游客必须在该项目排队。
上述排队系统流程如图 2所示。
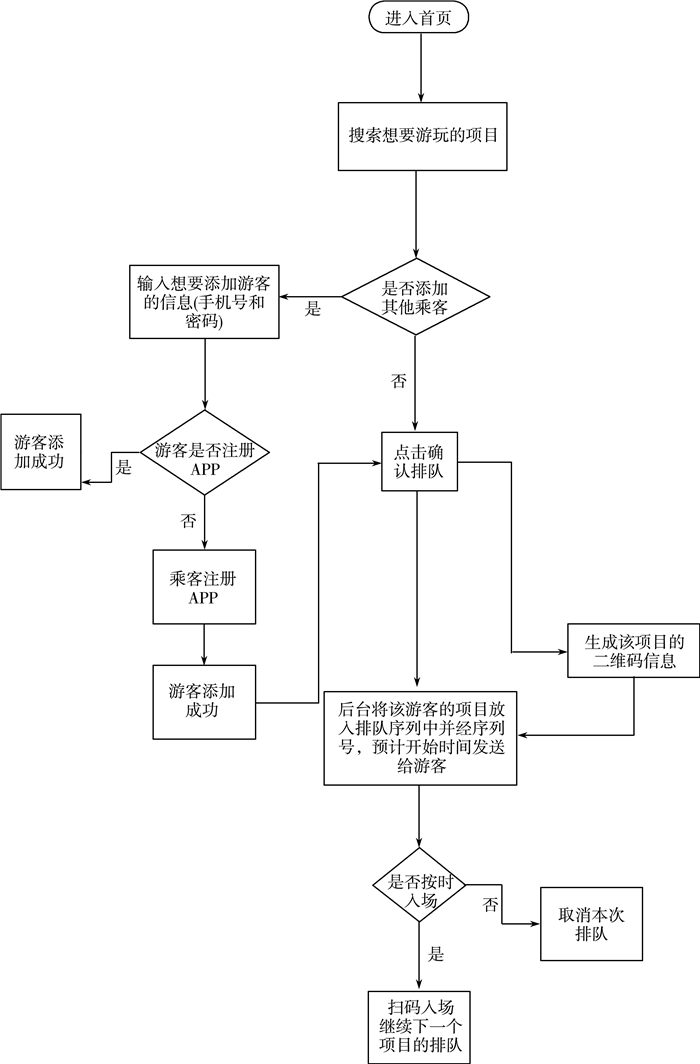 |
| 图 2 排队系统流程图 |
3.2 系统模块分类
系统总体设计分为注册登录模块、排队模块、个人信息模块、地图模块、收发信息模块、检索模块、购票模块,各模块详细功能如图 3所示。
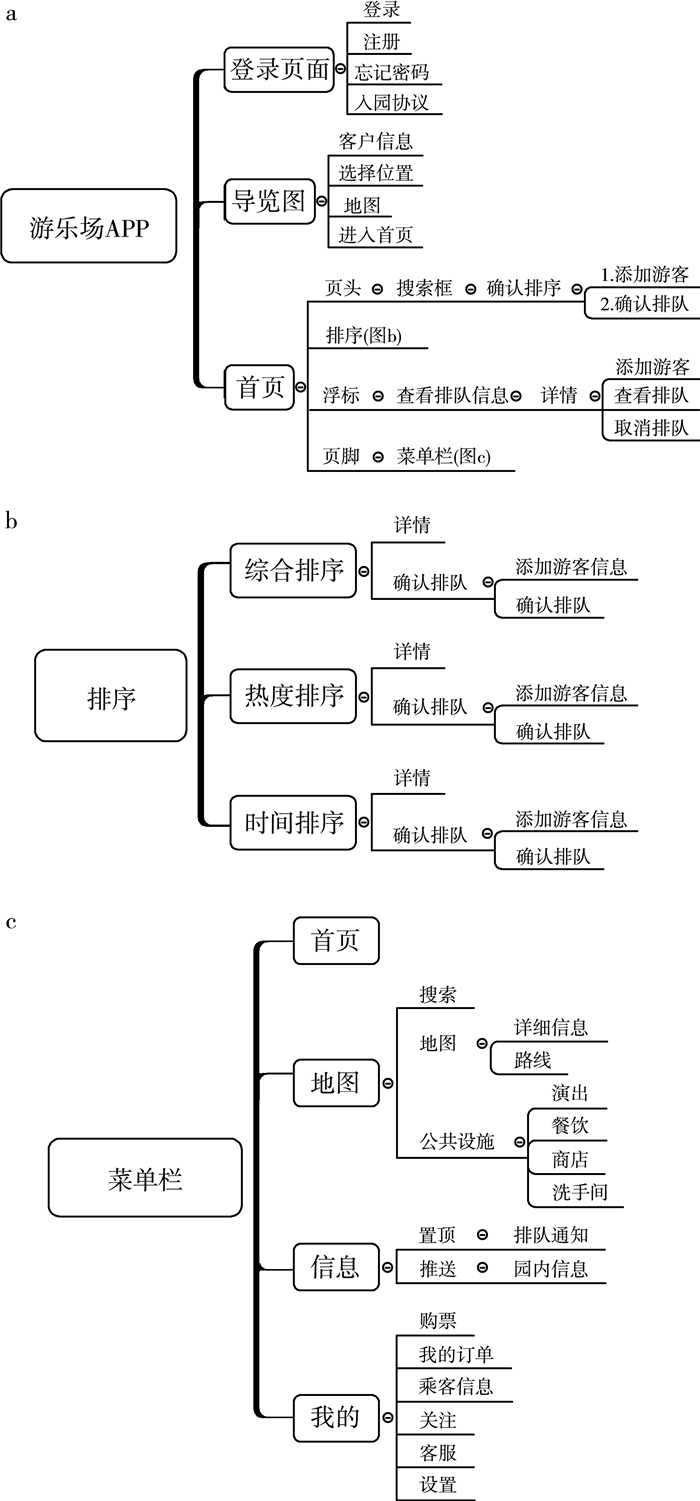 |
| 图 3 模块详细功能图 |
1) 注册登陆模块:用户首先需要注册,需要手机号码(会作为游客身份的唯一标识,以防游客利用同伴手机号进行多次排队)、密码及短信验证码。用户信息将提取并更新到数据库中。注册成功就可以登陆系统。
2) 排队模块:用户登陆APP后可以看到主页面,系统会根据游客所在的游乐场从第三方数据库中查询预先存好的有关该游乐场的所有项目以及项目信息,并以json数据格式反馈;系统会将查询到的数据存储在本地的sqlite数据库中,在用户界面端将这些数据显示出来[8-10]。游客选择想要排队的项目(最多3个)进行排队。选择的第一个项目处于排队序列中,后面的项目处于预排队序列中;当游客进入第一个项目开始游玩时,系统自动将第二个项目置于排队序列中,依此类推。
3) 个人信息模块:包括个人信息管理(手机号码和登录密码)、排队项目管理(选择的排队项目)、好友信息管理(团组游客信息)、退出以及重置密码管理。
4) 搜索模块:系统会提供用户全局搜索的功能,可满足用户对关键词的搜索需求;用户可以搜索项目关键词,系统会在数据库中查询并将结果反馈给用户。
5) 地图模块:系统根据游客所在地进行定位查询游客所在的游乐场,并将该游乐场的地图从第三方数据库中查询出来并显示到用户界面上。
6) 收发信息模块:已登录的游客可收发信息,采用的是调用Bmob第三方服务器实现短信收发的功能。
3.3 系统功能的实现本文设计的排队系统主要功能有:登录注册、游乐场项目排队、个人信息管理。具体功能界面如图 4、图 5所示。
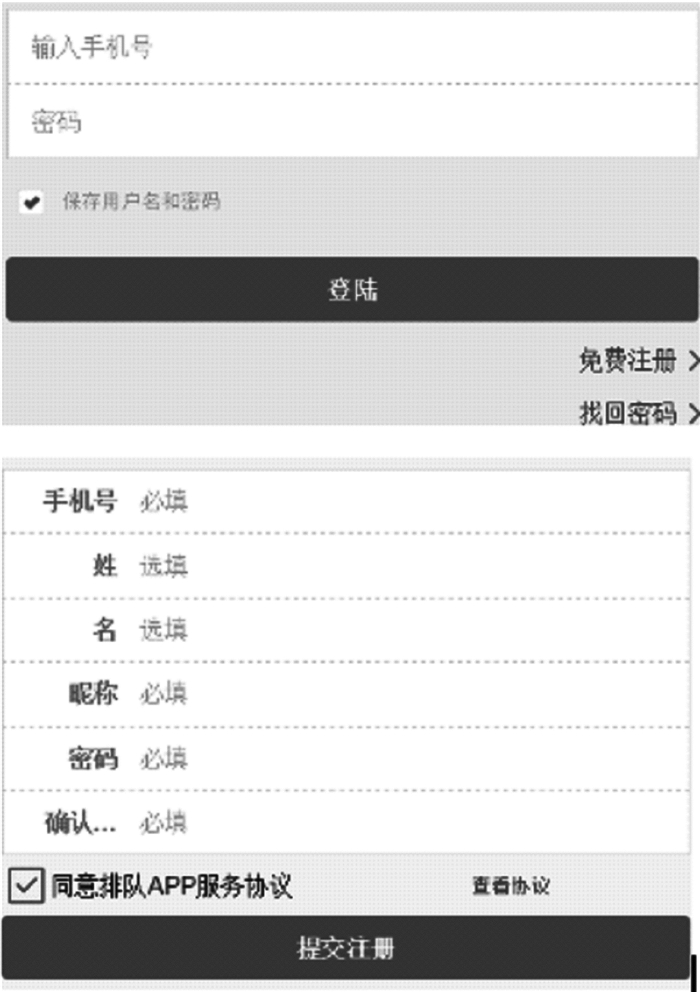 |
| 图 4 注册登录 |
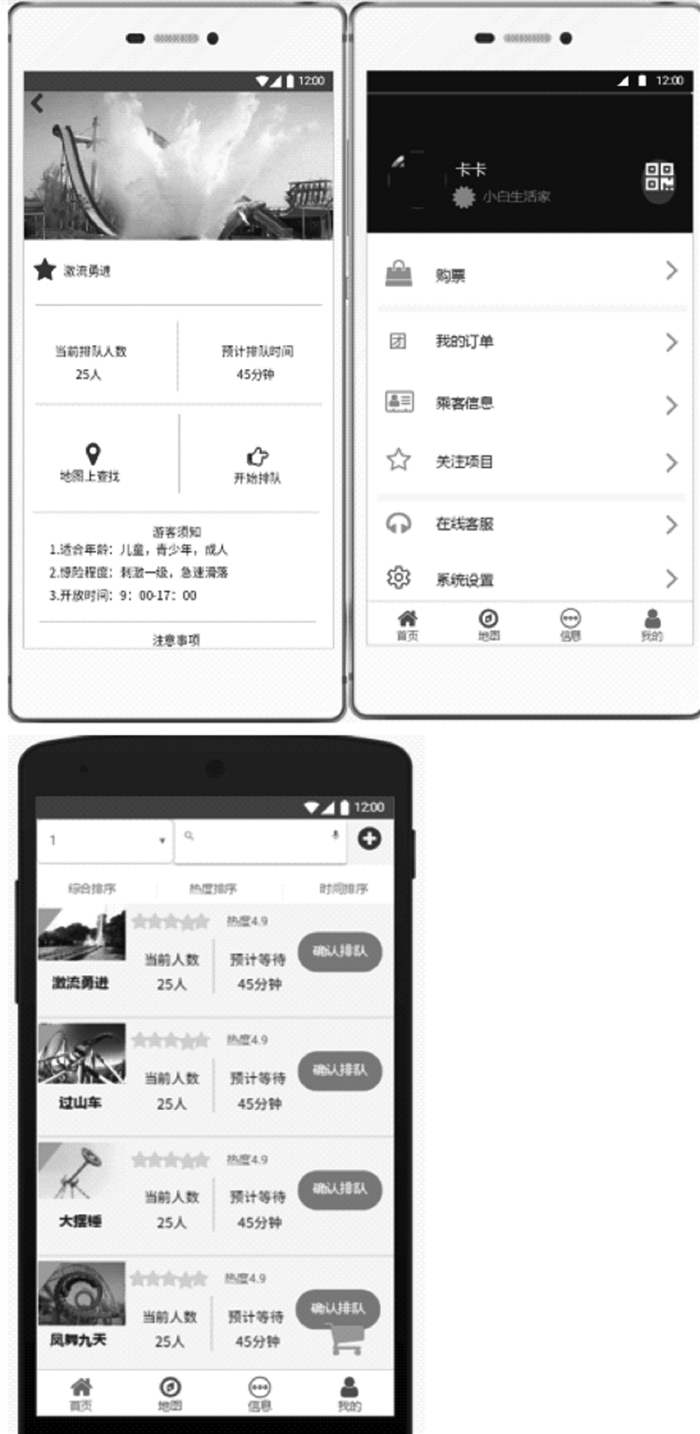 |
| 图 5 项目排队和个人信息管理 |
4 系统测试
本研究只对功能进行测试,分为模块功能测试和系统功能测试。模块测试是对整个系统的各个模块进行模拟用户测试,结果与预期一致。系统功能测试是根据系统的功能分析进行模拟管理员测试,结果与预期一致。
5 结论本文设计并实现了基于排队论的Android游乐场项目排队系统,该系统提供了实时监控和综合统计的功能,可以随时查看排队的人数、发现冷热门项目以及每位游客的实际排队时间,为游乐场的项目管理提供准确的数据。该排队系统的使用,可改善游乐场排队拥堵现象,减少游客等待时间,提高游客满意度和项目管理效率,并可帮助游乐场管理层对引进新设备和淘汰旧设备进行决策,实现收益最大化。
| [1] |
XIAO H M, ZHANG G Z. The queuing theory application in bank service optimization[J]. Logistics Systems and Intelligent Management, 2010, 2(1): 1097-1100. |
| [2] |
李泉林, 马静宇, 李超然, 等. 多类顾客共享排队系统的信息理论[J]. 应用概率统计, 2018(4): 399-415. DOI:10.3969/j.issn.1001-4268.2018.04.005 |
| [3] |
HUI H Q.Urban public transit dispatch based on queuing theory[C].Fifth International Conference on Natural Computation, Tianjin, China, 2009. https://dl.acm.org/citation.cfm?id=1679643
|
| [4] |
杨一帆.运筹排队论在医院门诊排队中的应用[D].济南: 山东大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10422-1019008839.htm
|
| [5] |
严颖, 严凌. 基于排队论的快速路出口匝道反馈控制算法[J]. 物流科技, 2018, 41(10): 73-76. DOI:10.3969/j.issn.1002-3100.2018.10.020 |
| [6] |
王仁志.基于M/M/n排队论的旅游景区内部排队管理研究[D].成都: 电子科技大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10614-1012472759.htm
|
| [7] |
裴明高, 胥如迅, 张强, 等. 基于排队论的铁路售票窗口设置分析与优化[J]. 工业控制计算机, 2016, 29(5): 100-104. DOI:10.3969/j.issn.1001-182X.2016.05.046 |
| [8] |
胡启敏, 薛锦云, 钟林辉. 基于Spring框架的轻量级J2EE架构与应用[J]. 计算机工程与应用, 2008, 44(5): 115-118. DOI:10.3778/j.issn.1002-8331.2008.05.037 |
| [9] |
叶加青. Spring框架技术的应用[J]. 计算机时代, 2009(10): 54-55. DOI:10.3969/j.issn.1006-8228.2009.10.023 |
| [10] |
杜朝. 基于Andriod平台的应用程序开发研究[J]. 信息通信, 2017(2): 285-286. DOI:10.3969/j.issn.1673-1131.2017.02.158 |
 2019, Vol. 33
2019, Vol. 33


