| 基于动力吸振器的整车平顺性研究 |
2. 北京理工大学 宇航学院, 北京 100081
2. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
大型运输车是常见的运载工具, 其平顺性研究一直是研究的热点。荣吉利[1]等基于拉格朗日原理, 建立仪器-车-路耦合的19自由度振动动力学模型, 利用白噪声作为路面激励, 采用粒子群算法对车速、悬置刚度和阻尼优化, 发现速度、仪器悬置的刚度和阻尼, 能够影响仪器振动加速度。上述研究是以被动悬架为研究对象, 与之相对应的是主动悬架, 主动悬架可以更好的改善车辆的平顺性。潘成龙[2]等采用9自由度模型, 设计LQR控制器, 建立主动悬架控制仿真模型, 并采用自适应粒子群算法优化控制器的参数。荣吉利[3]利用线性二次型高斯(LQG)控制理论设计主动悬架控制器。
动力吸振器是由质量、弹簧和阻尼元件组成的单自由度振动系统, 它是一种通过弹性元件把辅助质量连接到振动系统上的减振装置。动力吸振器通过调节自身结构参数及主系统的耦合关系, 将主系统振动能量转移到动力吸振器, 衰减主系统振动。动力吸振器结构简单, 便于维护, 能有效减小系统的振动, 已广泛应用于机械[4-6]、车辆[7-8]和航空航天[9-12]等工程领域。白世鹏[13]等以1/4车辆模型, 研究了不同位置处动力吸振器分析对车辆垂向振动耗散功率及其悬架性能的影响。杜勇[14]设计变质量动力吸振器, 探究其吸振原理。孙吉超[15]以模糊控制原理为基础, 提出了一种变质量动力吸振器控制策略, 并对其控制效果进行研究, 通过上述文献, 我们发现动力吸振器能够抑制系统振动, 其参数和安装位置对振动影响很大。
本文以某大型运输车为背景, 将整车简化为9自由度模型, 基于此模型, 将动力吸振器应用于大型车辆的平顺性分析, 建立含有动力吸振器的整车-路面耦合的13自由度动力学方程, 运用遗传算法对动力吸振器的相关参数进行优化, 并对吸振器安装位置和车辆不同速度进行仿真分析。
1 车-路耦合动力学建模 1.1 整车-路耦合振动方程以4轮胎大型车辆为研究对象, 车辆看作刚体, 建立整车-路面耦合的9自由度模型如图 1所示, 采用4个完全相同的动力吸振器, 分别安装在轮胎上方如图 1a和轮胎下方如图 1b, 在轮胎上方建立动力吸振器-整车-路面的耦合13自由度动力学方程。其中各参数如下: mLi、mRi(i=1, 2)分别为左轮胎和右轮胎的质量; m、mz、mp和m。分别是车身质量, 支架质量, 设备质量和动力吸振器质量; KtLi、KtRi(i=1, 2)分别为左轮胎和右轮胎的刚度; KsLi、KsRi(i=1, 2)分别为左右轮胎对应悬架的刚度; Kp、Kz、K0分别为设备悬置的刚度, 支架的刚度和动力吸振器的刚度; CsLi、CsRi(i=1, 2)分别为左右轮胎对应悬架的阻尼; Cp, Cz, C0分别为设备悬置的阻尼, 支架的阻尼和动力吸振器的阻尼, Zi(i=1, …, 4)为各车轮垂直位移; Zb、Zz、Zp分别为车身位移, 支架和设备位移; ηi(i=1, …, 4)为动力吸振器的位移, wi(i=1, …, 4)为路面激励, a和b分别为前后车轴到质心的距离; L1与L2分别为左右车轮中心到质心的距离; c1与c2分别为设备到车辆横向质心轴与纵向质心轴的距离。
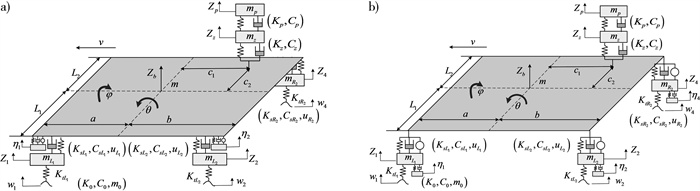 |
| 注: a)动力吸振器位于轮胎上方; b)动力吸振器位于轮胎下方。 图 1 含有动力吸振器的车-路耦合的整车模型 |
当侧倾角φ和俯仰角θ很小时, 悬架端点位移为:
| $ \left\{\begin{array}{l} Z_{5}=Z_{\mathrm{b}}-a \theta+L_{1} \varphi \\ Z_{6}=Z_{\mathrm{b}}+b \theta+L_{1} \varphi \\ Z_{7}=Z_{\mathrm{b}}-a \theta-L_{2} \varphi \\ Z_{8}=Z_{\mathrm{b}}+b \theta-L_{2} \varphi \end{array}\right.。$ | (1) |
含有动力吸振器的整车系统的动能T为:
| $ \begin{aligned} T=& \frac{1}{2} m_{L_{1}} \dot{Z}_{1}^{2}+\frac{1}{2} m_{L_{2}} \dot{Z}_{2}^{2}+\frac{1}{2} m_{R_{1}} \dot{Z}_{3}^{2}+\frac{1}{2} m_{R_{2}} \dot{Z}_{4}^{2}+\frac{1}{2} m \dot{Z}_{b}^{2}+\frac{1}{2} I_{p} \dot{\theta}^{2} \\ &+\frac{1}{2} I_{r} \dot{\varphi}^{2}+\frac{1}{2} m_{z} \dot{Z}_{z}^{2}+\frac{1}{2} m_{p} \dot{Z}_{p}^{2}+\frac{1}{2} m_{0} \dot{\eta}_{1}^{2}+\frac{1}{2} m_{0} \dot{\eta}_{2}^{2}+\frac{1}{2} m_{0} \dot{\eta}_{3}^{2}+\frac{1}{2} m_{0} \dot{\eta}_{4}^{2}, \end{aligned} $ | (2) |
含有动力吸振器的整车系统的势能U为:
| $ \begin{aligned} U=& \frac{1}{2} K_{t L_{1}}\left(Z_{1}-w_{1}\right)^{2}+\frac{1}{2} K_{t L_{2}}\left(Z_{2}-w_{2}\right)^{2}+\frac{1}{2} K_{t R_{1}}\left(Z_{3}-w_{3}\right)^{2}+\frac{1}{2} K_{t R_{2}}\left(Z_{4}-w_{4}\right)^{2} \\ &+\frac{1}{2} K_{s L_{1}}\left(Z_{5}-Z_{1}\right)^{2}+\frac{1}{2} K_{s L_{2}}\left(Z_{6}-Z_{2}\right)^{2}+\frac{1}{2} K_{s R_{1}}\left(Z_{7}-Z_{3}\right)^{2}+\frac{1}{2} K_{s R_{2}}\left(Z_{8}-Z_{4}\right)^{2} \\ &+\frac{1}{2} K_{z}\left(Z_{z}-Z_{b}+c_{1} \theta+c_{2} \varphi\right)^{2}+\frac{1}{2} K_{p}\left(Z_{p}-Z_{z}\right)^{2}+\frac{1}{2} K_{0}\left(Z_{5}-\eta_{1}\right)^{2}+\frac{1}{2} K_{0}\left(Z_{6}-\eta_{2}\right)^{2} \\ &+\frac{1}{2} K_{0}\left(Z_{7}-\eta_{3}\right)^{2}+\frac{1}{2} K_{0}\left(Z_{8}-\eta_{4}\right)^{2} 。\end{aligned} $ | (3) |
含有动力吸振器的整车系统的耗能D为:
| $ \begin{aligned} D=& \frac{1}{2} C_{s L_{1}}\left(\dot{Z}_{5}-\dot{Z}_{1}\right)^{2}+\frac{1}{2} C_{s L_{2}}\left(\dot{Z}_{6}-\dot{Z}_{2}\right)^{2}+\frac{1}{2} C_{s R_{1}}\left(\dot{Z}_{7}-\dot{Z}_{3}\right)^{2}+\frac{1}{2} C_{s R_{2}}\left(\dot{Z}_{8}-\dot{Z}_{4}\right)^{2} \\ &+\frac{1}{2} C_{z}\left(\dot{Z}_{z}-\dot{Z}_{b}+c_{1} \dot{\theta}+c_{2} \dot{\varphi}\right)^{2}+\frac{1}{2} C_{p}\left(\dot{Z}_{p}-\dot{Z}_{z}\right)^{2}+\frac{1}{2} C_{0}\left(\dot{Z}_{5}-\dot{\eta}_{1}\right)^{2}+\frac{1}{2} C_{0}\left(\dot{Z}_{6}-\dot{\eta}_{2}\right)^{2} \\ &+\frac{1}{2} C_{0}\left(\dot{Z}_{7}-\dot{\eta}_{3}\right)^{2}+\frac{1}{2} C_{0}\left(\dot{Z}_{8}-\dot{\eta}_{4}\right)^{2} 。\end{aligned} $ | (4) |
根据非保守系统广义Lagrange方程:
| $ \frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\partial T}{\dot \partial q_{i}}\right)-\frac{\partial T}{\partial q_{i}}+\frac{\partial U}{\partial q_{i}}+\frac{\partial D}{\dot \partial q_{i}}=Q_{i}, $ | (5) |
式中: qi为广义坐标; Qi为所受广义力。
将式(2)~式(4)代入式(5)得到含有动力吸振器的整车振动动力学方程为:
| $ \boldsymbol{M} \boldsymbol {\ddot{Z}}+\boldsymbol {C}_{\mathrm{s}} \boldsymbol {\dot{Z}}+\boldsymbol{K}_{\mathrm{s}} \boldsymbol{Z}=\boldsymbol{K}_{\mathrm{t}} \boldsymbol{W}, $ | (6) |
式中: M、Cs、Ks分别为质量矩阵, 阻尼矩阵和刚度矩阵; Kt为广义激励矩阵; W为激励输入向量, Z为:
| $ \boldsymbol Z=\left[Z_{1}, Z_{2}, Z_{3}, Z_{4}, Z_{\mathrm{b}}, \theta, \varphi, Z_{\mathrm{z}}, Z_{\mathrm{p}}, \eta_{1}, \eta_{2}, \eta_{3}, \eta_{4}\right]^{\mathrm{T}} 。$ | (7) |
通过研究发现, 汽车平顺性和操纵稳定性的影响因素主要有: 车身加速度、设备和支架加速度、悬架动行程及轮胎动位移。因此, 状态向量X和输出向量Y分别为:
| $ \boldsymbol{X}= {\left[Z_{1}, Z_{2}, Z_{3}, Z_{4}, Z_{b}, \theta, \varphi, Z_{z}, Z_{p}, \eta_{1}, \eta_{2}, \eta_{3}, \eta_{4}, \dot{Z}_{1}, \dot{Z}_{2}, \dot{Z}_{3}, \dot{Z}_{4}, \dot{Z}_{b}, \dot{\theta}, \dot{\varphi}, \dot{Z}_{z}, \dot{Z}_{p}, \dot{\eta}_{1}, \dot{\eta}_{2}, \dot{\eta}_{3}, \dot{\eta}_{4}, w_{1}, w_{2}, w_{3},\right.} \\ \left.w_{4}\right]^{\mathrm{T}} 。$ | (8) |
| $ \boldsymbol{Y}= {\left[Z_{1}-w_{1}, Z_{2}-w_{2}, Z_{3}-w_{3}, Z_{4}-w_{4}, Z_{5}-Z_{1}, Z_{6}-Z_{2}, Z_{7}-Z_{3}, Z_{8}-Z_{4}, \ddot{Z}_{b}, \ddot{\theta}, \ddot{\varphi}, \ddot{Z}_{z}, \ddot{Z}_{p}\right]^{\mathrm{T}} } 。$ | (9) |
由式(6), 式(8)和式(9), 得到系统状态方式为:
| $ \begin{aligned} \boldsymbol {\dot{X}} &=\boldsymbol{A} \boldsymbol{X}+\boldsymbol{B} \boldsymbol{U}+\boldsymbol{G} \boldsymbol{W}_{0}, \\ \boldsymbol{Y} &=\boldsymbol{C} \boldsymbol{X}+\boldsymbol{D} \boldsymbol{U} , \end{aligned} $ | (10) |
其中:
| $ \begin{aligned} &\boldsymbol{A}=\left[\begin{array}{ccc} \boldsymbol{0}_{13 \times 13} & \boldsymbol{I}_{13 \times 13} & \mathbf{0}_{13 \times 4} \\ -\boldsymbol{M}^{-1} \boldsymbol{K}_{s} & -\boldsymbol{M}^{-1} \boldsymbol{C}_{s} & \boldsymbol{M}^{-1} \boldsymbol{K}_{\boldsymbol{t}} \\ \mathbf{0}_{4 \times 13} & \mathbf{0}_{4 \times 13} & \boldsymbol{F}_{1} \end{array}\right]_{30 \times 30}, \boldsymbol{B}=\left[\begin{array}{l} \boldsymbol{0}_{13 \times 4} \\ \boldsymbol{M}^{-1} \boldsymbol{E} \\ \boldsymbol{0}_{4 \times 4} \end{array}\right]_{30 \times 4}, \boldsymbol{C}=\left[\begin{array}{ccc} \boldsymbol{I}_{4 \times 4} & \mathbf{0}_{4 \times 22} & -\boldsymbol{I}_{4 \times 4} \\ -\boldsymbol{I}_{4 \times 4} & \boldsymbol{C}_{2} & \boldsymbol{0}_{4 \times 4} \\ -\boldsymbol{M}_{1}^{-1} \boldsymbol{K}_{21} & \boldsymbol{C}_{3} & \boldsymbol{0}_{5 \times 4} \end{array}\right]_{13 \times 30},\\ &\boldsymbol{C}_{2}=\left[\begin{array}{ll} \boldsymbol{C}_{\mathrm{s}_{1}} & \mathbf{0}_{4 \times 19} \end{array}\right]_{4 \times 22}, \boldsymbol{C}_{3}=\left[\begin{array}{ll} -\boldsymbol{M}_{1}^{-1} \boldsymbol{K}_{22}-\boldsymbol{M}_{1}^{-1} \boldsymbol{K}_{23}-\boldsymbol{M}_{1}^{-1} \boldsymbol{C}_{\mathrm{s} 2} & -\boldsymbol{M}_{1}^{-1} \boldsymbol{C}_{23} \end{array}\right]_{5 \times 22} \text {, }\\ &\boldsymbol{C}_{\mathrm{s1}}=\left[\begin{array}{ccc} 1 & -a & L_{1} \\ 1 & b & L_{1} \\ 1 & -a & -L_{2} \\ 1 & b & -L_{2} \end{array}\right], \boldsymbol{C}_{\mathrm{s2}}=\left[\begin{array}{ll} \boldsymbol{C}_{21} & \boldsymbol{C}_{22} \end{array}\right]_{5 \times 9}, \boldsymbol{D}=\left[\begin{array}{l} \boldsymbol{0}_{8 \times 4} \\ \boldsymbol{M}_{1}^{-1} \boldsymbol{E}_{2} \end{array}\right]_{13 \times 4},\\ &\boldsymbol{F}_{1}=-2 \pi f_{0} v \boldsymbol{I}_{4 \times 4}, \boldsymbol{F}_{2}=2 \pi n_{0} \sqrt{G_{q}\left(n_{0}\right) v} \boldsymbol{I}_{4 \times 4},\\ &\boldsymbol{G}=\left[\begin{array}{l} \mathbf{0}_{13 \times 4} \\ \mathbf{0}_{13 \times 4} \\ \boldsymbol{F}_{2} \end{array}\right]_{30 \times 4} \quad \boldsymbol{K}_{2}=\left[\begin{array}{ll} \boldsymbol{K}_{21} & \boldsymbol{K}_{22} \end{array}\right]_{5 \times 9}, \boldsymbol{M}_{1}=diag \left[m, I_{\mathrm{p}}, I_{\mathrm{r}}, m_{\mathrm{z}}, m_{\mathrm{p}}\right]_{\circ} \end{aligned} $ |
左轮路面不平度微分方程为:
| $ w_{i}+2 \pi f_{0} v w_{i}=2 \pi n_{0} \sqrt{G_{q}\left(n_{0}\right) v} W_{0}(t), $ | (11) |
式中: wi为左轮受到不平度随机激励; f0为路面空间下截止频率, 取0.01 m-1; W0(t)为均值0的白噪声随机信号; n0为参考空间频率; v为车速。
由于左、右轮轮迹具有空间相关性, 左右轮路面相关性状态方程[2]为:
| $ w_{i+2}=\left[\boldsymbol{C}_{1}\left(s \boldsymbol{I}-\boldsymbol{A}_{1}\right)^{-1} \boldsymbol{B}_{1}+\boldsymbol{D}_{1}\right] \boldsymbol{w}_{i} , $ | (12) |
其中:
由于性能指标加速度、悬架动行程和轮胎动位移单位及数量级不同, 将13个参数性能指标与无动力吸振器的性能指标相比值, 作为适应度函数, 即:
| $ \begin{aligned} \min f(x)=& \frac{Z_{a 1}(\boldsymbol{x})}{Z_{p 1}}+\frac{Z_{a 2}(x)}{Z_{p 2}}+\frac{Z_{a 3}(\boldsymbol{x})}{Z_{p 3}}+\frac{Z_{a 4}(\boldsymbol{x})}{Z_{p 4}}+\frac{Z_{a 5}(\boldsymbol{x})}{Z_{p 5}}+\frac{Z_{a 6}(\boldsymbol{x})}{Z_{p 6}}+\frac{Z_{a 7}(\boldsymbol{x})}{Z_{p 7}}+\frac{Z_{a 8}(\boldsymbol{x})}{Z_{p 8}}+\frac{\ddot Z_{a b}(\boldsymbol{x})}{\ddot Z_{p b}} \\ &+\frac{\ddot \theta_{a}(\boldsymbol{x})}{\ddot \theta_{p}}+\frac{\ddot{\varphi}_{a}(\boldsymbol{x})}{\ddot{\varphi}_{p}}+\frac{\ddot Z_{a z}(\boldsymbol{x})}{\ddot Z_{p z}}+\frac{\ddot Z_{a p}(\boldsymbol{x})}{\ddot Z_{p p}}, \end{aligned} $ | (13) |
| $ \boldsymbol{x}=\left(q_{1}, q_{2}, q_{3}\right) \text {, } $ | (14) |
| $ \left\{\begin{array}{l} q_{1} \in[0,250] \\ q_{2} \in\left[0,1 \times 10^{6}\right], \\ q_{3} \in\left[0,1 \times 10^{4}\right] \end{array}\right. $ | (15) |
式中:
选取C级路面上进行仿真, 遗传算法参数分别为: 种群规模N=100, 交叉概率n=0.4, 变异概率Pm=0.2, 个体变量数目为3, 迭代次数100, 悬架参数如表 1所示。
| 表 1 悬架参数 |
 |
经过100次迭代, 得到动力吸振器的参数分别为m0=211 kg, K0=9 577 N/m, C0=121 N·s/m。
3.1 动力吸振器不同位置仿真为验证动力吸振器对整车平顺性的影响, 当车速v=20 m/s时, 分别对无动力吸振器、吸振器在轮胎上方、吸振器在轮胎下方三种情况进行仿真。仿真结果如图 2和表 2所示。鉴于性能参数过多, 这里给出了左前轮动位移、车身垂直加速度、支架加速度、设备加速度随时间变化曲线。从图 2可以明显看到, 吸振器在上方时, 振幅变化最小; 其次是吸振器在下方; 然后是无动力吸振器。不难发现, 动力吸振器能够抑制车辆的振动, 提高车辆平顺性。
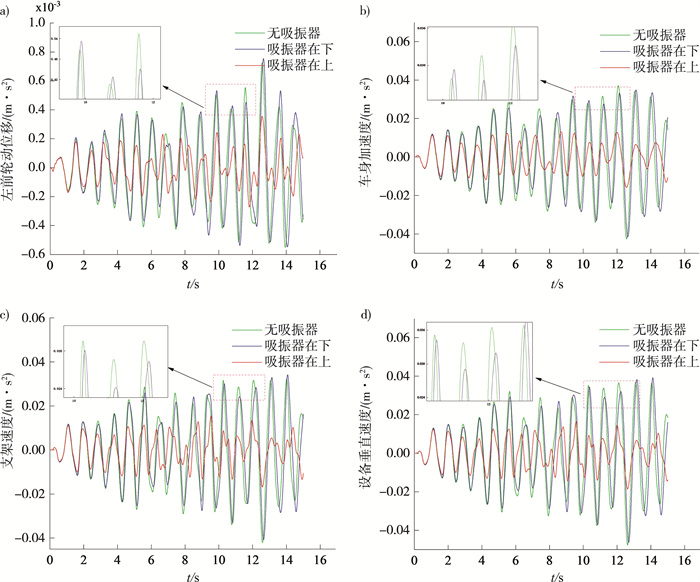 |
| 注: a)左前轮加速度; b)车身加速度; c)支架垂直加速度; d)设备垂直加速度。 图 2 吸振器仿真结果 |
| 表 2 悬架均方根值 |
 |
由表 2可知, 除了侧倾和俯仰加速度外, 其他性能指标动力吸振器在上方比在下方改善50%以上。总体来说, 动力吸振器安装在轮胎上方振动抑制效果更好。
3.2 不同速度下动力吸振器仿真当车速不同时, 动力吸振器对大型车辆振动抑制效果如图 3所示, 其为设备加速度随车速变化曲线。随着车速的增加, 吸振器在上时加速度增长曲线斜率要小于其他两种情况, 并且差距越来越大, 说明动力吸振器在上方时速度越快, 振动抑制效果越好。
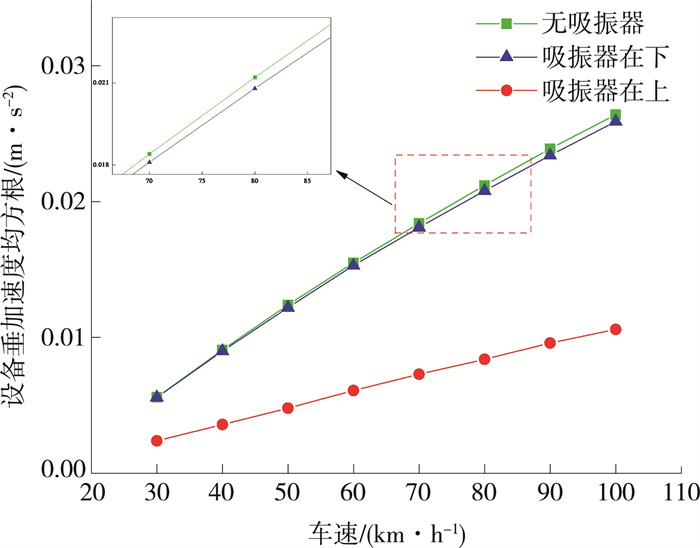 |
| 图 3 不同速度时设备加速度均方根 |
4 结论
针对大型特种设备车辆行驶平顺性问题, 提出了将动力吸振器应用于整车振动控制方法, 建立含有动力吸振器的13自由度的整车-路面耦合动力学方程, 采用遗传算法对动力吸振器相关参数进行优化, 在不同工况下进行数值仿真得到以下结论:
1) 动力吸振器能够抑制车辆振动, 提高车辆行驶平顺性; 2)动力吸振器在上方时振动抑制效果明显好于在下方时; 3)随着速度增加, 动力吸振器振动抑制效率逐渐提升。
| [1] |
荣吉利, 郑育龙, 刘琥, 等. 某大型运输车的时域平顺性仿真分析[J]. 北京理工大学学报, 2017, 37(2): 146-150, 156. |
| [2] |
潘成龙, 荣吉利, 项大林, 等. 9自由度主动悬架平顺性研究[J]. 北京理工大学学报, 2019, 39(10): 1012-1017. |
| [3] |
荣吉利, 邓增琨, 何丽, 等. 整车主动悬架平顺性时域仿真与优化[J]. 北京理工大学学报, 2021, 41(1): 46-52. |
| [4] |
DOUBRAWA F F J, LUERSEN M A, BAVASTRI, C A. Optimal design of viscoelastic vibration absorbers for rotating systems[J]. Journal of Vibration and Control, 2011, 17(5): 699-710. DOI:10.1177/1077546310374335 |
| [5] |
CAMPOS R O, NICOLETTI R. Vibration reduction in vertical washing machine using a rotating dynamic absorber[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2015, 37(1): 339-348. |
| [6] |
杨志荣, 李清云, 戴乐阳, 等. 船用磁流变弹性体动力吸振器的性能研究[J]. 船舶力学, 2018, 22(4): 509-515. DOI:10.3969/j.issn.1007-7294.2018.04.014 |
| [7] |
GONG D, ZHOU J S, SUN W J. On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber[J]. Journal of Vibration and Control, 2013, 19(5): 649-657. DOI:10.1177/1077546312437435 |
| [8] |
HUANG C, ZENG J, LUO G, et al. Numerical and experimental studies on the car body flexible vibration reduction due to the effect of car body-mounted equipment[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail and Rapid Transit, 2016, 232: 103-120. |
| [9] |
HUBBARD S A, FONTENOT R L, MCFARLAND D M, et al. Transonic aeroelastic instability suppression for a swept wing by targeted energy transfer[J]. Journal of Aircraft, 2014, 51(5): 1467-1482. DOI:10.2514/1.C032339 |
| [10] |
HUBBARD S A, MCFARLAND D M, BERGMAN L A, et al. Targeted energy transfer between a swept wing and winglet-housed nonlinear energy sink[J]. AIAA Journal, 2014, 52(12): 2633-2651. DOI:10.2514/1.J052538 |
| [11] |
PAN CHENGLONG, RONG JILI, XU TIANFU, et al. Novel approach for active vibration control of a flexible missile[J]. Defence Technology, 2020(16): 956-967. |
| [12] |
VERSTRAELEN E, HABIB G, KERSCHEN G, et al. Experimental passive flutter suppression using a linear tuned vibration absorber[J]. AIAA Journal, 2017, 55(5): 1707-1722. DOI:10.2514/1.J055397 |
| [13] |
白世鹏, 侯之超. 动力吸振器对车辆垂向振动能量及悬架性能的影响[J]. 振动与冲击, 2020, 39(22): 169-174. |
| [14] |
杜勇. 动力吸振器在汽车振动控制中的应用研究[D]. 合肥: 合肥工业大学, 2015.
|
| [15] |
孙吉超. 基于模糊原理的变质量动力吸振器控制策略研究[D]. 西安: 长安大学, 2020
|
 2022, Vol. 36
2022, Vol. 36


