| 热透镜效应的数值计算 |
2. 齐鲁工业大学 电气工程与自动化学院,济南 250353
2. chool of Electrical Engineering and Automation, Qilu University of Technology, Jinan 250353, China
任何一种物理现象,若其物理量随空间变化或随空间和时间变化,则对这种现象的描述中一定涉及到偏微分方程。对于端面泵浦固体激光器中泵浦介质的热温度梯度,就是典型的三维偏微分方程。由于激光棒的对称性而转化为柱坐标系下的二维偏微分方程。
1988年Innocenzi等人[1]使用有限元方法得到了圆柱状固体激光器在对流边界条件下,连续泵浦和脉冲泵浦的温度分布;1990年Frauchiger等人[2]等人假设热流始终是径向的,激光介质的边缘与散热片相连并以连续的温度进行冷却,得到了稳态的热传导方程;1992年Chen等人[3]采用了基于共振激励原理的数值计算方法,建立了线性热传导方程并给出其求解方法;1997年Pfistner等人[4]假设热效应的边界条件近似于冷却边界条件,也是给出了热传导方程的近似解析解;史彭、李隆、李健、张帅一等人[5-9]采用近似假设,得到了热效应方程的数值解及其解析解。
在经典的数值计算处理方式[10]中,用自变量离散格点上的值来描述因变量,并通过适当的网格离散化,偏微分方程就变成了一大组差分方程,在计算过程中根本无法实施。因此有必要进一步研究二阶偏微分方程更为简单的数值解法,适合更多人群。首先对求解方法及求解步骤进行简要说明,其次对二维热传导方程进行分析求解。
1 求解方法简介 1.1 PDE工具箱PDE工具箱利用有限元法求解偏微分方程,但只能求解形式为二维的偏微分方程,故可以将一维偏微分方程通过增加维数(如增加杆的宽度等)变为二维偏微分方程,三维偏微分方程可以通过减少维数(如减少时间维数)变为二维偏微分方程。如此,偏微分方程可根据其数学特征大致分为三类,即椭圆型方程,抛物型方程和双曲型方程。其形式分别如下:
| $ -\nabla \cdot\left( {c\nabla u} \right) + au = f, $ | (1) |
| $ d\left( {\frac{{\partial u}}{{\partial t}}} \right)-\nabla \cdot\left( {c\nabla u} \right) + au = f, $ | (2) |
| $ d(\frac{{{\partial ^2}u}}{{\partial {t^2}}})-\nabla \cdot\left( {c\nabla u} \right) + au = f, $ | (3) |
式中u为域Ω上的求解变量;d, c, a, f为常数或变量;t为时间变量。
PDE工具箱定义了两类边界条件
| $ \left\{ \begin{array}{l} \;\;\;\;\;\;\;hu = r;\\ \vec n\cdot\left( {c\nabla u} \right) + qu = g; \end{array} \right.\;, $ | (4) |
式中,
从偏微分方程本身入手,由
| $ \nabla \cdot h\left( {r, z} \right) = q\left( {r, z} \right), $ | (5) |
| $ h\left( {r, z} \right) =-k\nabla T\left( {r, z} \right), $ | (6) |
得到
| $ \frac{{dF\left( r \right)}}{{dr}}-\alpha F\left( r \right) = \frac{{-2r{P_{in}}\eta \alpha }}{{\pi \omega _p^2}}exp(\frac{{-2{r^2}}}{{\omega _p^2}}), $ | (7) |
| $ F\left( r \right) = rf\left( r \right), $ | (8) |
| $ \frac{{dT\left( r \right)}}{{dr}}-\alpha T\left( r \right) = f\left( r \right), $ | (9) |
相应的边界条件为
| $ \begin{array}{l} F\left( r \right)|r = 0 = 0{\rm{ }}\;\;\;dF\left( 0 \right) = 0{\rm{ }}\\ T\left( r \right)|r = {r_b} = 300{\rm{ }}\;\;\;dT\left( 0 \right) = 0^\circ \end{array} $ | (10) |
使用Runge-Kutta方法,求解此微分方程组,即得到激光棒内的温度分布。
求解热传导方程的数值解,求解步骤如图 1。
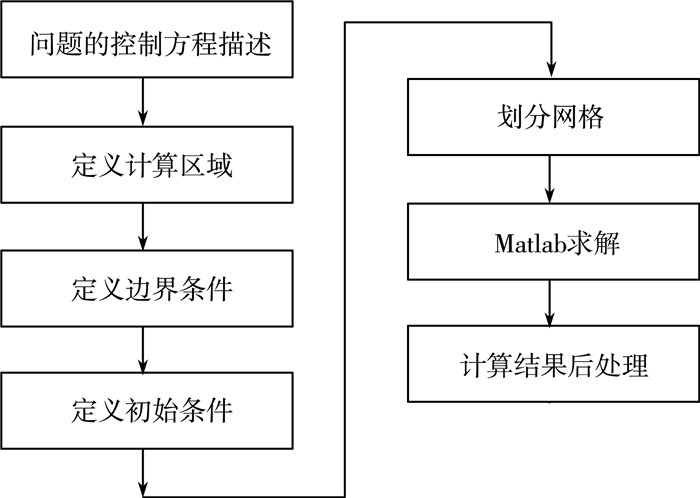 |
| 图 1 求解步骤图 |
2 热传导方程求解 2.1 问题描述
在激光二极管端面泵浦结构的固体激光器的光泵浦过程中,由于激光介质吸收了泵浦辐射而发热,而散热又要求对其表面进行冷却,进而引起激光介质中不均匀的膨胀,导致了严重的热效应[11]。因此,得到热透镜效应的数值解,与实验结果匹配的更好也就成为了降低热透镜效应的关键。一般情况下,激光棒内部产生的热量主要通过热传导方式由周边散失,极少的一部分通过与空气对流散失。在激光棒的冷却过程中常采用制冷器来控制激光棒的周边温度。图 2给出了端面泵浦圆柱状固体激光器Nd:YAG晶体侧面的热模型简图。
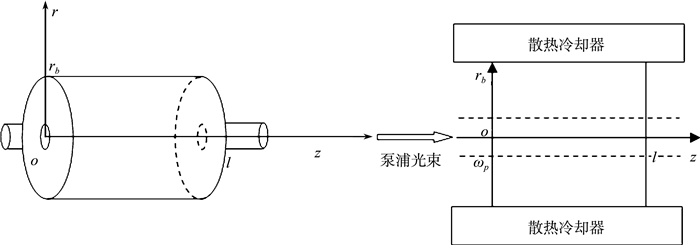 |
| 图 2 泵浦激光晶体侧面热模型简图 |
在热源的作用下,激光棒内的晶体逐渐升温,最后达到稳定。整个过程是关于中心轴对称的,故描述此数物理模型的方程为
| $ \frac{{{d^2}T}}{{d{r^2}}} + \frac{1}{r}\frac{{dT}}{{dr}} + \frac{{{d^2}T}}{{d{z^2}}} + \frac{{q\left( {r, z} \right)}}{k} = 0 。$ | (11) |
激光棒的周边温度主要通过制冷器或者空调机制冷,来控制冷却水和室内温度,假设室温和冷却液的温度为300 K,即T0=Tc=300 K。故激光棒侧面保持温度恒定、端面绝热时的边界条件为
| $ T\left( {0, z} \right) < + \infty, {\left. {\frac{{dT}}{{dr}}} \right|_{r = 0}} = 0, $ | (12) |
| $ {\left. {-k\frac{{\partial T}}{{\partial z}}} \right|_{r = {r_b}}} = 300, $ | (13) |
| $ {\left. {-k\frac{{\partial T}}{{\partial z}}} \right|_{z = 0}} = 0, $ | (14) |
| $ {\left. {k\frac{{\partial T}}{{\partial z}}} \right|_{z = l}} = 0。$ | (15) |
由于端面泵浦固体激光器的输出光强分布较为复杂,故将其近似地描述为高斯光束。假设泵浦光沿平行于z轴的抽运光传播时,入射到z=0平面时,光强Ih(r, 0) 的分布为
| $ {I_h}\left( {r, 0} \right) = {I_{oh}}exp(\frac{{-2{r^2}}}{{{\omega _p}^2}}), $ | (16) |
式中,I0h为入射面轴心处的泵浦光强,ωp为高斯光束束腰半径,r为激光晶体中某点到激光晶体中心轴的距离。
泵浦光束入射到晶体z=0平面时的功率P为
| $ p = \int_0^\infty {{I_{0h}}{e^{-2\frac{{{r^2}}}{{\omega _p^2}}}}2\pi rdr}, $ | (17) |
则有
| $ {I_{0h}} = \frac{p}{{2\pi \int_0^\infty {{I_{0h}}{e^{-2\frac{{{r^2}}}{{\omega _p^2}}}}rdr} }} = \frac{{2p}}{{\pi {\omega _p}^2}} $ | (18) |
在光束传播过程中,光强由于被激光晶体吸收而呈指数形式衰减。当抽运光传播到z=z平面时,光强分布为Ih(r, z)。
| $ {I_h}\left( {r, z} \right) = {I_{oh}}exp(\frac{{-2{r^2}}}{{{\omega _p}^2}})exp\left( {-\alpha z} \right) 。$ | (19) |
故q(r, z)也被近似的描述为高斯分布
| $ q\left( {r, z} \right) = \frac{{2{P_{in}}\eta \alpha }}{{\pi {\omega _p}^2}}exp\{-\frac{{2{r^2}}}{{{\omega _p}^2}}\} exp\left( {-\alpha z} \right)。$ | (20) |
取抽运功率为Pin=10 W,激光棒长度l=0.5 cm,激光棒半径rb=0.2 cm,泵浦光半径ωp=0.03 cm,则在PDE中可得到激光晶体侧面的温度分布区域图 3。
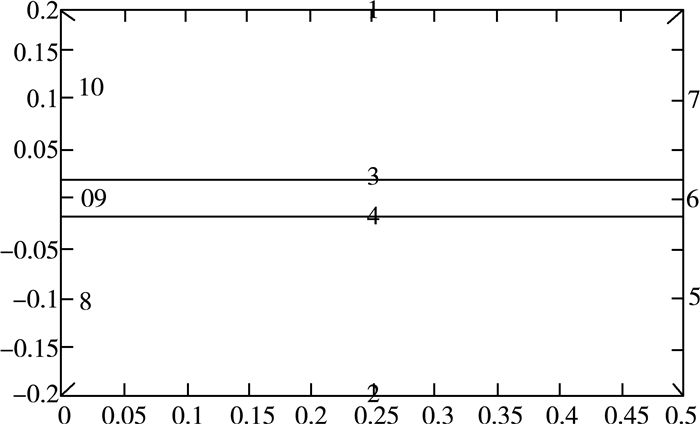 |
| 图 3 激光晶体侧面的温度分布区域 |
根据PDE工具箱显示的边界次序定义边界条件。对于边界1, 2,是第一类边界条件
| $ h = 1, r = 300。$ | (21) |
对于边界3, 4,由于激光棒内部温度的变化率为0,为第二类边界条件
| $ q = 0, g = 0。$ | (22) |
对于边界5-10,是第二类边界条件
| $ q = 0, g = 0。$ | (23) |
确定方程及边界条件,分别使用PDE工具箱和Runge-Kutta方法,得到此热传导方程的温度分布,如图 4。
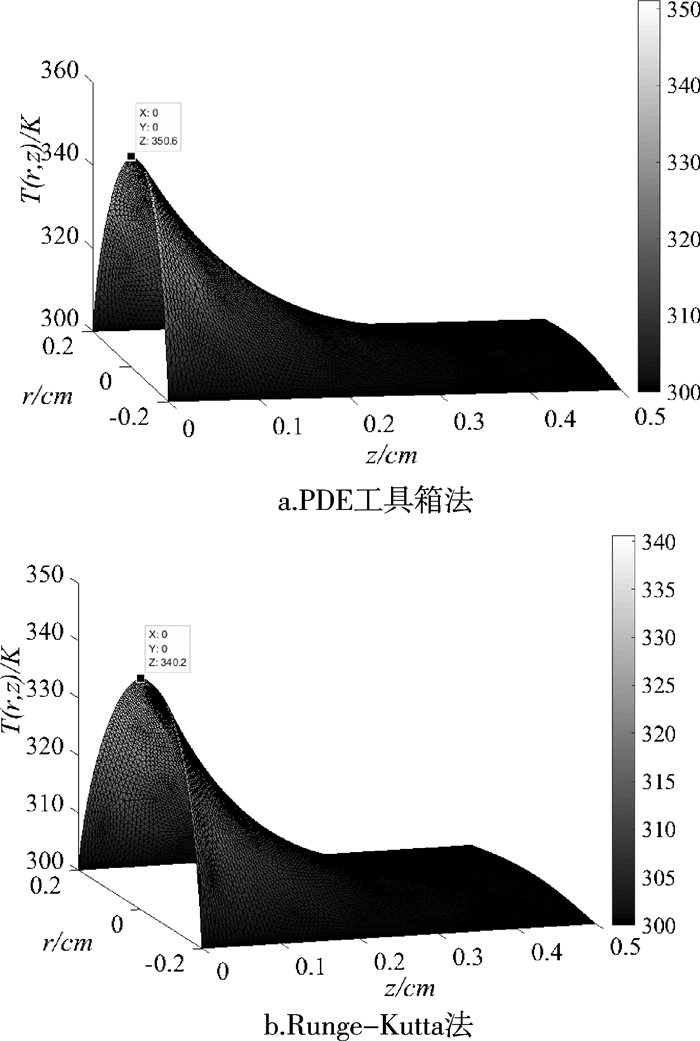 |
| 图 4 激光棒温度分布 |
由分析可知,使用PDE工具箱求得的激光棒轴心处的最高温度为350.6 K,使用Runge-Kutta方法,求得的激光棒轴心处的最高温度为340.2 K,温差为10.4 K。
激光棒内部的温度在向四周扩散的过程中温度逐渐降低,最后慢慢趋于稳定。激光棒的泵浦面的中心温度最高,越往侧面温度越低,沿着z轴温度也越低,最后均趋于平稳,最后r=0.2与z=0.5处的温度基本保持一致。在棒的侧表面由于受到冷却水的强制冷却,温升很小。在棒的右端面由于温度已迅速降到与空气温度差别不大,故温升也很小。晶体的左端面是激光的入射面,所以在向右扩散的过程中,温度是逐渐降低。
虽然抽运光束在介质表面近似为高斯分布,但在稳定状态下,激光棒表面的温度分布已趋近于抛物面分布[12-13]。这是由于激光介质温度分布在到达稳定状态的过程中,介质的边缘受到冷却水的持续冷却,介质内部与介质边缘不断地进行热传导造成的。这为我们研究晶体的热效应提供了良好的依据。
3 结论偏微分方程的数值计算在各门学科中的作用越来越重要,使用PDE工具箱和Runge-Kutta方法求解偏微分方程简单、高效。结果表明,使用这两种方法求解热传导方程,具有步骤简单、可视化程度高的特点,可以较容易的得到热传导方程的温度分布;求解结果准确,能正确的反映实际物理状态,表达物理意义。
| [1] |
INNOCENZI M E, YURA H T, FINCHER C L. Fieids thermal modelingof continuous-wave end-pumped solid-state lasers[J]. IEEE Journal of Applied Physics Letters, 1990, 56(19): 1831-1833. DOI:10.1063/1.103083 |
| [2] |
FRAUCHIGER J, ALBERS P, WEBER H P. Modeling of thermal lensing and higher order ring mode oscillation in end-pumped CW Nd:YAG lasers[J]. IEEE Journal of Quantum Electron, 1992, 28(4): 1046. DOI:10.1109/3.135227 |
| [3] |
CHEN Y F, HUANG T M, KAO CF, et al. Optimization in scaling fiber-coupled laser-diode end-pumped laser to higher power:influence of thermal effect[J]. IEEE Journal of Quantum Electron, 1997, 33(8): 1424-1429. DOI:10.1109/3.605566 |
| [4] |
PFISTNER C, WEBER R, WEBER H P, et al. Thermal beam distortions in end pum ped Nd:YAG, Nd:GSGG, and Nd:YLF Rods[J]. IEEE Journal of Quantum Electron, 1994, 30(7): 1605. DOI:10.1109/3.299492 |
| [5] |
史彭, 李金平, 李隆, 等. 抽运光分布对Nd:YAG微片激光器热效应的影响[J]. 中国激光, 2008, 35(5): 643-646. |
| [6] |
李隆, 史彭, 白晋涛. 单端泵浦激光晶体温度分布的半解析热分析[J]. 西安交通大学学报, 2004, 38(4): 369-372. |
| [7] |
李隆, 甘安生, 齐兵, 等. LD端面抽运变导热系数Nd:YAG晶体热效应[J]. 激光技术, 2012, 36(5): 612-616. |
| [8] |
李健, 孙尧, 李晓敏, 等. Nd:GdYVO4与Nd:YVO4的激广特性比较[J]. 激光器, 2007, 44(2): 11-17. |
| [9] |
张帅一, 刘辉兰, 于果蕾, 等. LD端面泵浦圆柱形Nd:YAG晶体热效应研究[J]. 红外, 2007, 28(3): 1672-1685. |
| [10] |
李有法, 李晓勤. 数值计算方法(第二版)[M]. 北京: 高等教育出版社, 2005.
|
| [11] |
王垚廷. 全固态连续单频473 nm蓝光激光器的理论和实验研究[D]. 太原: 山西大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10108-2010190639.htm
|
| [12] |
李萍. 外热源温度场模拟及其在导热系数测试中应用[D]. 南京: 南京工业大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10291-2007021369.htm
|
| [13] |
乔焱. LD抽运全固态激光晶体热效应的研究[D]. 济南: 山东师范大学, 2012. http://cdmd.cnki.com.cn/article/cdmd-10445-1012339125.htm
|
 2017, Vol. 31
2017, Vol. 31


