| 基于卡方检验和LDOF算法的入侵检测技术研究 |
入侵检测是一种主动的网络安全措施,它不仅可以通过监测网络数据实现对内部攻击、外部攻击和误操作的实时保护,有效地弥补防火墙的不足,而且还能结合其他网络安全产品对网络安全进行全方位的保护,是防火墙重要的和有益的补充。它通过从计算机网络或计算机系统的关键点收集数据并进行分析,从中发现网络或系统中是否有违反安全策略的行为和攻击的迹象[1]。数据挖掘技术在从大量数据中提取特征或规则方面具有很大的优势。因此,可以利用数据挖掘技术对海量的审计记录或网络流量数据进行智能挖掘处理,进而构建检测模型及寻找入侵行为。因此,基于数据挖掘技术的入侵检测系统能自动地从所收集的数据中提取出可用于入侵检测的模式和知识,使用该方法的入侵检测技术不完全依赖于人工分析,具有智能性好、自动化程度高、可扩展性强等优点[2]。
离群点挖掘是一种挖掘较小模式数据的方法,其目的是挖掘大数据集中那些偏离多数数据的异常数据,这些少数的异常数据可能就代表不正常行为。离群点挖掘的一个重要应用领域,就是应用到入侵检测技术当中。对于离群点挖掘来说,判定行为是入侵的方法就是挖掘那些与正常行为不一致的行为[3]。因此可以利用离群点挖掘算法来作为入侵检测系统的核心检测算法来检测异常数据和攻击行为。
但随着大数据时代的到来,不仅数据的规模将会变得越来越大,同时数据的维度和复杂性也会变得高起来,其中冗余特征和一些不相关特征较多,这也会使入侵检测系统中检测算法的运行效率和检测精度受到一定的影响。所以,在大数据时代有必要对检测算法进行一定的优化与改进。
1 研究现状传统的入侵检测系统通常需要通过人工的方式构造检验规则,即由领域专家分析入侵方式后,提取入侵的特征构成规则。人工构造检验规则不仅是一项费时费力的工作,而且将大幅度降低入侵检测系统规则更新的实时性。一旦出现新的入侵,需要领域专家对其进行分析和提取后才能构建相应的新的检验规则。正是在该背景下,数据挖掘等自动化数据分析技术在入侵检测领域中得到了应用[4]。
离群点挖掘是数据挖掘技术的一个分支,其中有几种比较经典的算法。基于统计离群点挖掘,其优点是有坚实的概率论理论支撑,根据概率模型可以揭示离群点的含义等。但也存在着缺点,一是该算法不适合数据未知分布的情况,二是不适合于多维数据集[5]。基于深度的离群点挖掘能很好地处理数据未知分布的情况,但对于高维数据则处理效率比较低[6]。基于聚类的离群点挖掘的优点则是可以同时发现簇和离群点,但是聚类算法的主要目的是为了发现簇,因此对离群点挖掘的效率较低,在离群点很容易影响聚类的过程,从而导致聚类的不准确。基于距离的离群点挖掘能很好地处理高维数据,但是其时间复杂度很高,不能处理稀疏数据,挖掘结果对参数选取很敏感,不能挖掘局部离群点。基于密度的离群点挖掘不仅可以检测到全局离群点,还可以检测到局部离群点,但是仍存在着参数的选择问题和算法的复杂度比较高等问题[7]。
Ke等[8]提出了一种新的离群点挖掘算法——LDOF算法,它不仅能很好地处理高维数据,且能同时检测局部离群点和全局离群点,还能比较好地处理稀疏数据和数据未知分布情况,是目前离群点挖掘算法中比较好的一种。王茜等[9]提出了一种基于频繁模式的离群点挖掘算法,该算法通过计算数据的加权频繁因子来得到相应的离群点,最后将其应用于入侵检测领域,但是该算法复杂度较高。梅孝辉等[10]提出了一种基于聚类剪枝的离群点挖掘算法,首先通过聚类删减数据集,然后进行离群点检测,最后将其应用于入侵检测,但是会有错剪的风险。Abdel-Fattah等[11]提出了一种CPDOD算法,该算法结合了CP-KNN和LDOF两种算法,最后将其用于移动自组网络的入侵检测当中。
在大数据时代,需要检测的数据大多是维数高、样本量大的数据,然而大多数的入侵检测算法在面对高维数据时难有很好的表现。所以研究者们使用一些特征选择的方法去解决这个问题。魏金太等[12]结合了信息增益和随机森林算法来进行入侵检测,使用信息增益进行特征选择,然后将选择出的特征用于随机森林算法的训练。但是信息增益会因为特征的取值不一样而导致结果的不一样,所以该方法具有一定的不稳定性。黄婷[13]提出了一种基于特征选择的集成学习入侵检测模型,将特征集合分为多个特征子集,在多个特征子集上分别执行多个基分类器,最后多个基分类器汇总结果。该方法虽然能很好地检测出异常数据,但是该过程不仅需要划分多个特征子集,还需要训练多个分类器,时间成本消耗太大。刘婷等[14]提出了一种基于主成分分析的入侵检测模型,首先利用PCA对数据进行降维,然后训练核心检测算法模型。虽然也能达到降维的目的,但是通过变换后的数据会丢失掉特征含义,同时特征之间的关系也会被破坏,会使模型的解释性变差。王峰[15]提出了一种基于蚁群算法的入侵检测模型,该方法利用蚁群算法去搜索特征集合的最优解,然后训练入侵检测模型。该方法虽然也取得了不错的检测效果,但是仍然存在着一些缺点。蚁群算法的两个参数α和β如果设置不好的话,其求解过程会非常慢。同时,蚁群算法的计算量非常大,这也会导致求解时间较长。这些都大大影响了入侵检测算法的检测效率。
综上所述,LDOF算法相较于其他离群点挖掘算法有着很大的优越性,能很好地检测出离群点。所以本文将LDOF算法应用到入侵检测领域中去,检测异常数据,同时再对其进行相关的改进优化,使其能更好地处理一些高维数据[16]。
2 LDOF算法介绍2009年澳大利亚国立大学的Ke等人提出了一种新的离群点挖掘算法——LDOF算法[8]。LDOF算法基于密度的离群点挖掘的思想,采用了以距离为度量标准的方法,同时结合了KNN算法和LOF算法的优点。该算法本身定义了一个新的离群因子LDOF(每一个数据对象都有着唯一的LDOF离群因子),按每个数据对象的LDOF离群因子的大小进行排列,以top-n的方式输出n个最大的LDOF离群因子,则该n个离群因子所对应的n个数据对象则被当作离群对象输出。
LDOF算法描述如下:
假设Qp是数据对象P的K个最近邻点的集合(不包含数据对象P)。
定义1 数据对象P的K个最近邻到数据对象P的平均距离。即Qp内所有点到数据对象P的平均距离,记作L1:
| $ {L_1} = \frac{1}{K}\sum\limits_{a \in QP} {dist\left( {a, p} \right)} $ | (1) |
其中a为Qp内任意一数据对象。
定义2 数据对象P的内部距离。即Qp内所有数据对象间的平均距离,记作L2:
| $ {L_2} = \frac{1}{{K\left( {K - 1} \right)}}\sum\limits_{e, r \in {Q_p}, e \ne r} {dist\left( {e, r} \right)} $ | (2) |
其中e和r分别为Qp内任意两个不相同的数据对象。
定义3 数据对象P的LDOF离群因子。可以表示为数据对象P的K个最近邻到数据对象P的平均距离比上数据对象P的内部距离,即L1/L2:
| $ LDOF\left( {\rm{P}} \right) = \frac{{{L_1}}}{{{L_2}}} $ | (3) |
对于一个具体的数据对象来说,其LDOF离群因子的计算过程如图 1所示。
 |
| 图 1 LDOF因子计算过程 |
其中每个数据点之间的连线代表着计算两个数据点之间的距离(比如p1, p2, p3, p4...),所使用的距离计算方式为欧几里得距离,L1和L2计算方式如上所述。最终求得某一个具体数据对象的LDOF因子。
3 LDOF算法改进鉴于LDOF算法的特点,本文将其用于入侵检测领域,能很好地寻找出异常数据。相比其他离群点挖掘算法,LDOF算法既能很好地检测局部离群点也能很好地检测全局离群点,还能比较好地处理一些稀疏数据。但LDOF算法的时间复杂度较高。LDOF算法需要遍历整个数据集去计算每个数据对象的LDOF值。但是,入侵检测数据集中大部分数据都是正常的,不正常数据只占其中的一小部分。所以LDOF算法,需要很长时间去执行大量无效的计算。不仅如此,在面对高维数据时,LDOF算法需要更大的计算成本。
为了减少LDOF算法的计算成本,文献10提出了一种基于剪枝操作的LDOF算法。其中心思想主要是通过剪枝的方法来减少LDOF算法的计算成本。根据聚类算法的特性,将数据集具有相似特征的数据聚拢在一起形成簇,然后删除这些簇并保留剩余数据点为候选集,最后在候选集上执行LDOF算法。
如图 2所示,A、B、C、D四个数据点为异常数据点,在进行聚类时,A数据点很有可能会被“误认为”正常数据而被删减掉。所以,虽然剪枝的方法精简了数据集,提升了LDOF算法的执行速度,但是在剪枝的过程中难免会剪掉一些像A数据点这样的异常数据。而在入侵检测应用场景中,这种操作是不可取的,一旦将某些异常数据剪掉将会对计算机系统带来不可估量的后果。
 |
| 图 2 LDOF算法的聚类过程 |
本文从特征选择的角度去解决这个问题,不通过剪枝操作,而通过特征选择算法来降低入侵检测数据集的维度,从而达到降低计算成本和提高算法精度的目的。
特征选择能够去除一些不相关、冗余、“表达能力差”的特征,从而达到减少特征个数、减少算法运行时间和提高算法的精度等目的。图 3和图 4分别为特征选择前和特征选择后的数据集合,其中的m个特征是从n个特征中通过特征选择算法选出的最具有“表达力”的特征,并且m < n。从数据集的角度来看,通过特征选择,数据集从m列减少到了n列,数据量下降,计算成本也随之降低。从特征的角度来看,特征从n个缩减到了m个,去除了一些冗余的属性,选出的m个特征则是更具有“表达力”的,因而算法的精确度也会随之提高。
 |
| 图 3 特征选择前的数据集合 |
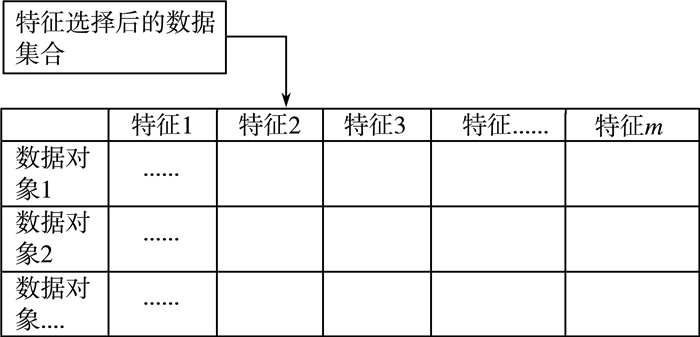 |
| 图 4 特征选择后的数据集合 |
特征选择主要有以下几种方法:
1) 单变量特征选择
单变量特征选择就是对特征集合中每一个特征进行评估,按照一定的规则选取一个小的特征子集,从而达到特征选择的目的。目前有很多种算法可以达到这个目的,例如:信息增益,距离相关系数,主成分分析PCA和卡方检验等。
① 信息增益和信息增益比
信息增益、信息增益比都是基于信息熵的单变量特征选择方法。虽然能比较不错地进行特征选择,但是会因为特征的取值问题导致一定的偏差,所以这种方法也具有一定的局限性。
② 距离相关系数
距离相关系数方法是基于距离的单变量特征选择方法。它通过计算两个数据之间的距离(比如欧几里得距离等)来判断两个对象之间的相关性。该方法只考虑距离,没有考虑两个数据对象之间的其他关系,所以也有着很大的局限性。
③ PCA
PCA方法是对数据进行简单的变换,使其从m维映射到n维,其中m>n。虽然PCA方法也能达到降维目的,但是在降维的过程中会丢失许多重要信息,同样有着很大的局限性。
2) 线性模型和正则化
线性模型本身就能根据自己的函数表达式来对特征进行评价(通常是函数表达式的系数)。例如:线性回归、SVM等都能对特征进行打分评测。
① 线性模型和正则化
这种方法通常利用回归模型的系数来进行特征选择,越是重要的特征在回归模型中相对应的系数就越大,跟类别变量基本不相关的特征其相对应的系数也就非常小。正则化也是相同的原理。
但是,该方法不适合特征个数较多的数据集。
② 决策树和GBDT等算法
该方法的本质是利用信息增益来进行特征选择,其优缺点都与信息增益方法大体相同。
3) 集成学习方法
集成学习方法主要构建多个基分类器,每个基分类器都对应一个不同的特征子集,以此来增加检测算法的准确率。虽然该方法能一定程度上提高算法的准确率,但是其时间复杂度很高,所需的时间成本太大。
相对于其他的特征选择方法来说,卡方检验不像信息增益等方法那样受特征取值的影响很大,同时其复杂性也非常低。所以,本文使用卡方检验来进行特征选择。卡方检验即X2值描述了自变量与因变量之间的相关程度。X2越大,表示实际与期望差距越大,两个变量之独立性越小,也就是越相关;X2越小,表示实际与期望的情况近似,那么独立性越大,相关性越小。所以可以使用X2值来做特征选择等相关的工作。具体公式如下:
| $ {X^2} = \sum {\frac{{{{\left( {A - T} \right)}^2}}}{T}} $ |
其中A为实际频数,T为理论频数,X2为卡方值。
所以本文将LDOF算法拆分为两部分:第一部分为特征选择算法,第二部分为计算LDOF因子。这种做法从纵向的角度删减了数据集,既保证了全体数据对象的完整性,又突出了重要特征,提高了算法的精度;同时也尽可能地避免了剪枝操作所带来的风险,减少了一定的计算成本,加快了LDOF算法的执行效率。入侵检测模型的具体结构如图 5所示。
 |
| 图 5 核心检测模型结构图 |
4 实验验证 4.1 实验环境和条件
本文所采用的数据集为KDD CUP99数据集。该数据集被认为是入侵检测领域中非常重要的一组数据集,常被用于各种比赛和测试入侵检测系统。程序开发工具为IDEA,算法采用Scala实现。
4.2 数据预处理及实验过程数据集里异常攻击数据占据了绝大部分,导致数据集里正常数据与异常数据差距比较大,这与真实的网络环境不同。真实的网络环境中网络攻击并不是很频繁,异常数据只占一小部分。为了使实验更加贴近于实际,所以本文对KDD CUP99数据集进行了一定的调整。本文从KDD CUP99原始数据集中抽取了部分正常数据和少量异常数据,构成了一个新的数据集,使其与真实的网络环境相符合。
为了方便计算数据对象之间的距离,需要将一些符号性质的属性进行数值化。在数据集中共有三种符号性质的属性,分别是service、protocol_type和flag。对于属性protocol_type,取值有三种,分别是TCP、UDP、ICMP,可以令其数值化,让TCP=1、UDP=2、ICMP=3。对于属性service,取值有65种情况,同样可以令其值为1~65。对于属性flag,取值有11种情况,也同样令其值为1~11。完成数值化后,开始进行特征选择(人为确定选取的特征数)。
进行特征选择前的数据集(数据集部分截图)如图 6所示。
 |
| 图 6 特征选择前数据集(部分截图) |
进行特征选择后的数据集(数据集部分截图)如图 7所示。
 |
| 图 7 特征选择后数据集(部分截图) |
对比上面两图可以看出,在完成特征选择后数据量大大减少了。
4.3 数据归一化处理数据归一化是数据预处理阶段常做的工作。一些分类器需要计算样本之间的距离(欧氏距离),例如KNN等。这时,如果一个特征的值域范围非常大,则距离计算就主要取决于这个特征,从而很容易导致分类器的分类精度降低。对于LDOF算法来说,其寻找最近邻的过程主要是根据数据对象间欧氏距离的大小来判断,如果不对数据进行归一化处理的话,很容易会导致算法在寻找最近邻时发生误差,从而导致最终检测结果不准确。
本文使用min-max标准化方法进行归一化处理(特征选择后)。min-max标准化方法是对原始数据进行线性变换,使得结果落到[0, 1]区间。其转换函数如下:
| $ {X^*} = \frac{{X - \min }}{{\max - min}} $ |
其中min为样本数据的最小值,max为样本数据最大值,X为转换前的样本数据,X*为转换后的样本数据。
进行归一化之前的样本数据(数据集部分截图)如图 8所示。
 |
| 图 8 归一化之前样本数据(部分截图) |
进行归一化之后的样本数据(数据集部分截图)如图 9所示。
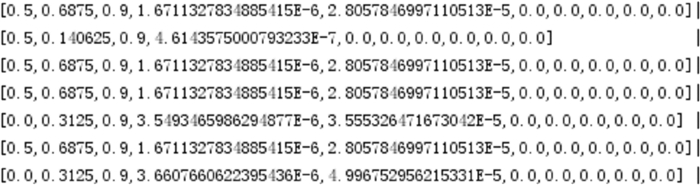 |
| 图 9 归一化之后样本数据(部分截图) |
4.4 实验结果
数据预处理完成后,接下来分别计算每个数据对象的LDOF因子。将经过第一阶段(卡方检验)的数据作为第二阶段(LDOF算法)的输入,来计算它们的LDOF因子。并根据数据对象LDOF因子的大小来判断该数据对象是否为异常数据。
在入侵检测领域中,通常采用检测率(Dr)和误检率(Fdr)这两个检验标准来作为核心检测算法的评价指标。检测率和误检率可以用下列公式表示:
| $ 检测率 = \frac{{被算法检测出的离群点数量}}{{数量数据集中真实的离群点数量}} \times 100\% $ |
| $ 误检率 = \frac{{被误认为离群数据的正常数据}}{{集中正常的数据}} \times 100\% $ |
本文选取误检率作为算法的评价指标值。因为K值代表着数据对象K近邻的个数,所以这里的K值有多种取值,以此来对比特征选择前和特征选择后算法误检率和时间效率的变化。
给定一个具体的n值(n代表着输出数据对象的个数),在得出n个数据对象后(这n个对象被认为是异常数据),看其中有多少正常数据被误判为异常数据,即误检率。测试误检率如表 1和表 2所示。
| 表 1 未进行特征选择前的误检率(LDOF算法) |
 |
| 表 2 进行特征选择后的误检率(卡方检验+LDOF算法) |
 |
特征选择前和特征选择后的运行时间如图 10所示。
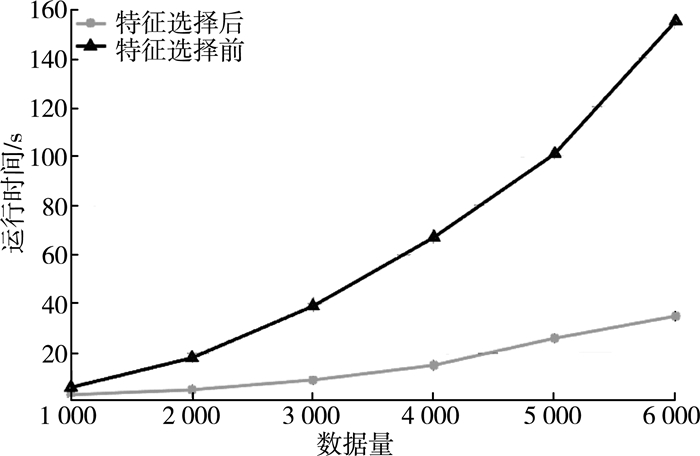 |
| 图 10 特征选择前和特征选择后的运行时间 |
对比上述实验结果可知,在保证相同的K值的情况下,进行特征选择后算法的误检率和运行时间得到了一定的改善。
5 总结本文介绍了离群点挖掘算法——LDOF算法,和入侵检测技术,发现两者相结合可以有效地检测出异常数据。同时为了解决入侵检测领域中数据维度较高等问题,在LDOF算法中加入了卡方检验算法,使其能够很好地处理一些高维数据。实验结果表明,基于卡方检验的LDOF算法既能有效地检测出异常数据,同时还有着较快的检测速度和较低的误检率。
| [1] |
张夏. 基于机器学习算法的网络入侵检测[J]. 现代电子技术, 2018, 41(3): 124-127. |
| [2] |
崔丹丹. 机器学习在网络入侵检测中的应用[J]. 信息与电脑(理论版), 2018(1): 30-32. |
| [3] |
金洪杰. 离群点挖掘技术在入侵检测中的研究[J]. 黑龙江科技信息, 2009(36): 121. DOI:10.3969/j.issn.1673-1328.2009.36.116 |
| [4] |
高周鹏, 熊运余. 基于数据挖掘的网络状态异常检测[J]. 吉林大学学报(理学版), 2017, 55(05): 1269-1273. |
| [5] |
周立军, 张杰, 吕海燕. 基于数据挖掘技术的网络入侵检测技术研究[J]. 现代电子技术, 2016, 39(6): 10-13. |
| [6] |
陈庄, 黄勇, 邹航. 基于离群点挖掘的工业控制系统异常检测[J]. 计算机科学, 2014, 41(5): 178-181, 203. DOI:10.3969/j.issn.1002-137X.2014.05.037 |
| [7] |
尹娜, 张琳. 基于混合式聚类算法的离群点挖掘在异常检测中的应用研究[J]. 计算机科学, 2017, 44(5): 116-119, 140. |
| [8] |
KE Z, HUTTER M, JIN H.A new local distance-based outlier detection approach for scattered real-world data[C]// Pacific-asia Conference on Advances in Knowledge Discovery & Data Mining, 2009. https://www.researchgate.net/publication/24165590_A_New_Local_Distance-Based_Outlier_Detection_Approach_for_Scattered_Real-World_Data?ev=sim_pub
|
| [9] |
王茜, 唐锐. 基于频繁模式的离群点挖掘在入侵检测中的应用[J]. 计算机应用研究, 2013, 30(4): 1208-1211. DOI:10.3969/j.issn.1001-3695.2013.04.067 |
| [10] |
梅孝辉.基于聚类的离群点挖掘在入侵检测中的应用研究[D].重庆: 重庆大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10611-1015969685.htm
|
| [11] |
ABDEL-FATTAH F, DAHALIN Z M, JUSOH S. Dynamic intrusion detection method for mobileAdHocnetworks using CPDOD algorithm[J]. International Journal of Computer Applications, 2010, 12(5): 22-29. |
| [12] |
魏金太, 高穹. 基于信息增益和随机森林分类器的入侵检测系统研究[J]. 中北大学学报(自然科学版), 2018, 39(1): 74-79, 88. DOI:10.3969/j.issn.1673-3193.2018.01.013 |
| [13] |
黄婷.基于特征选择的集成学习在入侵检测中的应用[D].兰州: 兰州大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10730-1017715745.htm
|
| [14] |
刘婷, 刘晓洁, 岳未然. 基于主成分分析法的入侵检测特征选择方法[J]. 网络新媒体技术, 2017, 6(2): 28-32. DOI:10.3969/j.issn.2095-347X.2017.02.006 |
| [15] |
王峰.蚁群算法在网络入侵特征选择上的应用研究[D].长沙: 湖南大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10532-1018023366.htm
|
| [16] |
TSAI C F, HSU Y F, LIN C Y. Intrusion detection by machine learning:A review[J]. Expert Systems with Applications, 2009, 36(10): 11994-12000. DOI:10.1016/j.eswa.2009.05.029 |
 2019, Vol. 33
2019, Vol. 33


