| 基于SVPWM的永磁同步电机调速系统设计 |
随着现科学技术的快速速发展,永磁同步电动机(PMSM)因其具有简单的结构、强大的过载能力、快速的响应速度等优点,已经在伺服领域中占据重要地位。因此对于PMSM的调速系统的要求也变得越来越高[1]。SVPWM算法具有快速准确、效率高、易于实现数字化的优点。因此对基于SVPWM的PMSM调速系统的研究具有重要的意义。
先对SVPWM的知识进行分析总结,然后介绍基于SVPWM的PMSM调速控制系统的实现过程,接着对该PMSM调速系统进行Matlab/Simulink仿真,最后以单片机STM32F103为核心进行实验设计。仿真和实验结果表明了基于SVPWM的永磁同步电机调速控制系统的有效性,在相关电机调速系统的设计中具有重要的指导意义。
1 空间矢量脉宽调制(SVPWM)空间矢量调制就是根据确定位置的有限个空间矢量组合作用来产生满足任意位置和一定幅值范围需要的空间矢量的过程[2]。空间矢量调制有两种情况,分别为电压空间矢量调制和电流空间矢量调制[3]。这次采用电压空调制来控制PMSM的速度。
PMSM电压瞬时值表示为uAN、uBN、uCN,那么任意时刻的电压空间矢量表示如式(1):
| $ {u_{vS}} = {u_S}_\alpha + j{u_{S\beta }} = \frac{2}{3}({u_{AN}} + a{u_{BN}} + {a^2}{u_{CN}}), $ | (1) |
其中单位复矢量
经过变换,用端电压uA、uB、uC表示如下:
| $ {u_{vS}} = \frac{2}{3}({u_A} + a{u_B} + {a^2}{u_C}){\rm{。}} $ | (2) |
用1表示逆变器上桥臂导通时的开关状态,用0表示逆变器下桥臂导通时的开关状态。这样三相逆变器三相导通时有8种开关状态(SA SB SC)模式:(000)(001)(010)(011)(100)(101)(110)(111)[4]。
用Udc来表示直流母线电源电压,则电压空间矢量可表示为:
| $ {u_{vS}}({S_A}{S_B}{S_C}) = \frac{2}{3}{U_{dc}}({S_A} + a{S_B} + {a^{_2}}{S_C}){\rm{。}} $ | (3) |
将整个复平面空间分为6个扇形区域,编号分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ[5]。
1.1 确定电压空间矢量位置为了判断电压空间矢量位于哪一个扇区,引入va、vb、vc[6],
| $ {v_a} = {u_{S\beta }}, $ | (4) |
| $ {v_b} = \frac{1}{2}(\sqrt 3 {u_{S\alpha }} - {u_{S\beta }}), $ | (5) |
| $ {v_c} = \frac{1}{2}( - \sqrt 3 {u_{S\alpha }} - {u_{S\beta }}){\rm{。}} $ | (6) |
如果va>0,那么A=1,否则A=0;如果vb>0,那么B=1,否则B=0;如果vc>0,那么C=1,否则C=0;
再根据A、B、C的值计算扇区编号N的值:
| $ N = 4A + 2B + C{\rm{。}} $ | (7) |
这样我们就可以得到电压空间矢量所在的扇区。
1.2 确定电压空间矢量的作用时间为了得到电压空间矢量的作用时间,引入通用变量X、Y、Z来计算作用时间[7]。
| $ X = \frac{{\sqrt 3 T}}{{{U_{dc}}}}{u_{S\beta }}, $ | (8) |
| $ Y = \frac{{\sqrt 3 T}}{{{U_{dc}}}}{u_{S\beta }} + \frac{{3T}}{{2{U_{dc}}}}{u_{S\alpha }}, $ | (9) |
| $ Z = \frac{{\sqrt 3 T}}{{{U_{dc}}}}{u_{S\beta }} - \frac{{3T}}{{2{U_{dc}}}}{u_{S\alpha }}{\rm{。}} $ | (10) |
t1和t2表示两个工作电压矢量的作用时间的一半,扇区编号与计算时间的关系如表 1所示。
| 表 1 扇区编号与计算时间的关系 |
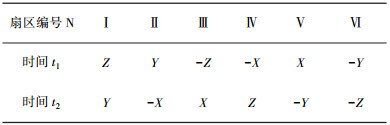 |
如果t1和t2之和大于PWM周期Ts的一半T,表明出现了饱和现象,此时我们需要对t1和t2进行修正,修正后的值为T1和T2,修正方法为:
| $ {T_1} = \frac{{{t_1}T}}{{{t_1} + {t_2}}}, $ | (11) |
| $ {T_2} = \frac{{{t_2}T}}{{{t_1} + {t_2}}}, $ | (12) |
进而可以得到零电压矢量的作用时间为
| $ {T_0} = {T_7} = \frac{{T - {T_1} - {T_2}}}{2}{\rm{。}} $ | (13) |
系统的实现过程SVPWM的核心是要实现对定子电流的分解与控制,而最终操作对象仍然是定子电流(交流量)[8]。由于定子的电压、电流、电动势、磁动势等各物理量都是交流量,当空间以同步转速旋转时,其空间矢量的调节、控制和计算都不是很方便,因此,需要借助于Clarke变换和Park变换,将各个物理量从定子静止ABC坐标系转换到转子dq旋转坐标系[9]。在转子dq旋转坐标系中进行观察,电机的各个空间矢量之间相对静止,各个空间矢量就都变成了直流量,然后按照给定量进行实时控制,最后再经过坐标的逆变换过程,从转子dq旋转坐标系回到定子静止坐标系。直流给定量变换成实际的交流给定量,在三相定子ABC坐标系上对交流量进行控制,使其实际值等于给定值。基于SVPWM的PMSM调速系统原理框如图 1所示:
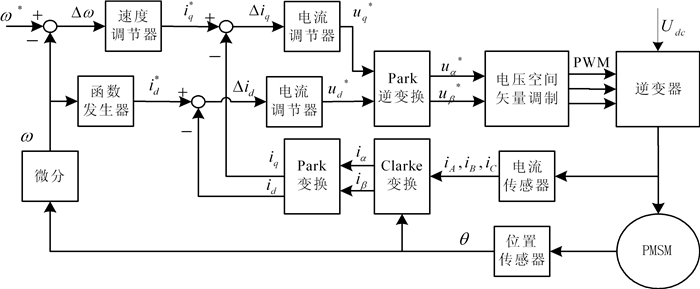 |
| 图 1 基于SVPWM的PMSM调速系统原理框图 |
本PMSM调速控制系统由几大部分构成:PID控制器(调节器)、SVPWM调试、逆变电路、速度反馈、电流反馈、Clarke变换、Park变换等。由图 1可以看出,基于SVPWM的PMSM调速控制系统为双闭环控制系统。外环为速度环,通过位置传感器获得PMSM的转子位置角,经过微分运算得到PMSM的实际转速,与给定转速进行比较得到转速差Δω,再经过速度调节器得到给定转子直轴电流iq*;内环为电流环,通过电流传感器获得实际PMSM的定子三相电流iA、iB、iC,经过Clarke变换得到定子两项电流iα、iβ,再进行Park变换得到转子两项电流iq、id。我们采用直轴为零的PMSM矢量控制,所以给定id*=0,这样给定电流iq*、id*与实际电流iq、id进行比较,得到的电流差Δiq、Δid, 通过电流调节器获得给定电压uq*、ud*,经过Park逆变换得到给定电流uα*、uβ*,再通过电压空间矢量调制得到PWM占空比,最后由逆变器驱动PMSM达到我们设置的转速。
3 仿真利用Simulink模块对基于SVPWM的PMSM调速系统进行仿真,搭建仿真模型,得到仿真结果。
根据基于SVPWM的PMSM调速系统原理框图建立如图 2的仿真模型:
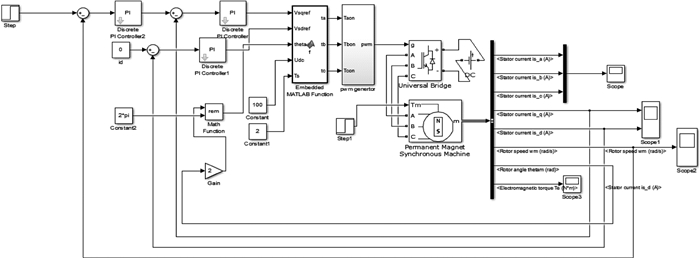 |
| 图 2 PMSM调速系统仿真模型 |
根据占空比T1on、T2on、T3on得到PWM波形的仿真模型如图 3所示,该模型内嵌PMSM调速系统仿真模型中。
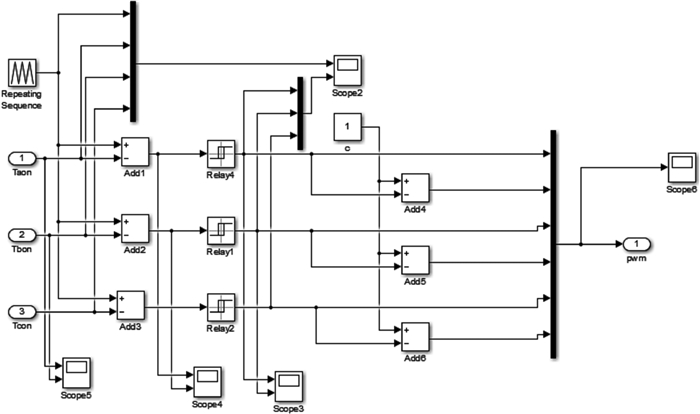 |
| 图 3 PWM波形仿真模型 |
仿真结果:
1) 电机转速角速度波形
由图 4可以看出:在无负载的情况下,电机经过约0.03 s的时间就达到了设定的速度80 rad/s;在t=0.3 s时,给电机加入负载,此时电机速度突然下降,但转速下降的幅度比较小,且经过0.1 s后,速度又回到了设定值80 rad/s;当t=0.6 s时,经过约0.03 s时间,速度提升到了第二个设定值100 rad/s。
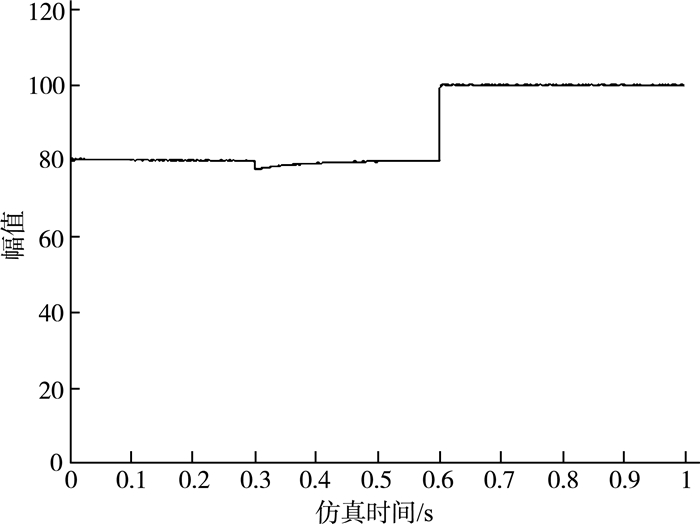 |
| 图 4 电机转速角速度波形 |
2) 电机q轴电流
采用的id=0控制策略,只需分析q轴电流。由图 5可以看出:在t=0 s和t=0.6 s时,此时电机进行加速,q轴电流发生了较大变化;在t=0.3 s时,加入了负载,导致q轴电流增大。
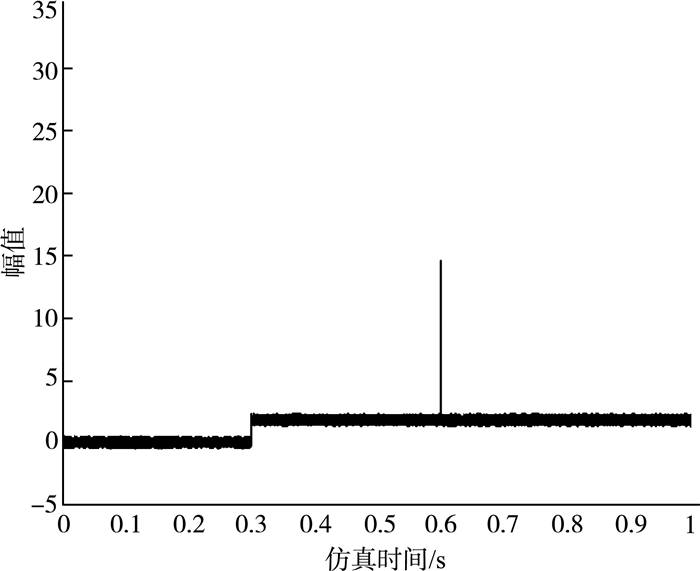 |
| 图 5 电机q轴电流波形图 |
3) 三相电流
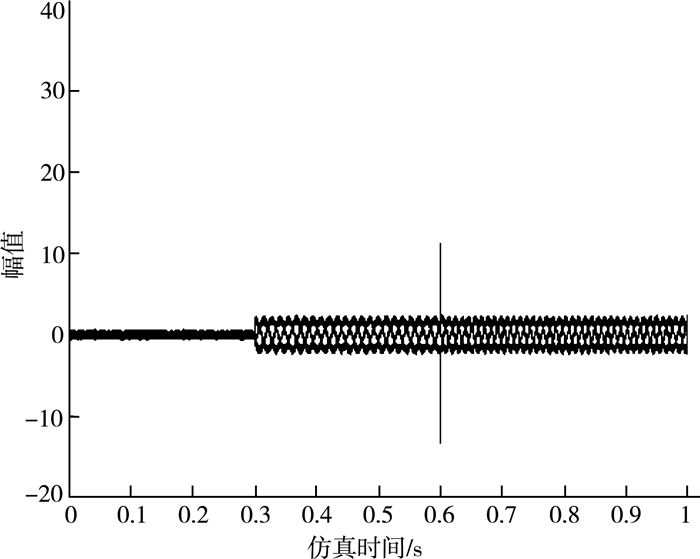 |
| 图 6 电机三相电流波形图 |
由图 6可以看出,三相电流均为正弦波。在t=0.3 s时,给电机加入负载,三相电流在小幅度变化后趋于稳定,且幅值变大;在t=0.6 s时,此时电机速度变大,导致三相电流出现大幅度波动,但随后趋于稳定,且电流周期变小。
通过以上仿真结果,证明了基于SVPWM的PMSM调速系统的可行性,为实体实验的设计做好了理论基础。
4 实验设计及实验结果基于SVPWM的PMSM调速系统的实验设计包括硬件和软件两部分。控制系统硬件主要包括控制电路和驱动电路两部分。控制电路以STM32F103为控制核心,通过上述的SVPWM双闭环控制策略对电机进行控制,采用旋转变压器+AU6803解码获得电机的转速,采用电流传感器获得电机的电流。实验中使用的电机为交流永磁同步电机,其电机参数为:电压范围60 V±30%,最大电流300 A,额定电流80 A,转矩参数0~90 N/m,功率参数额定3.5 kW、峰值10 kW,转速参数额定1 500 RPM、峰值4 000 RPM。所搭建的实验平台如图 7所示:
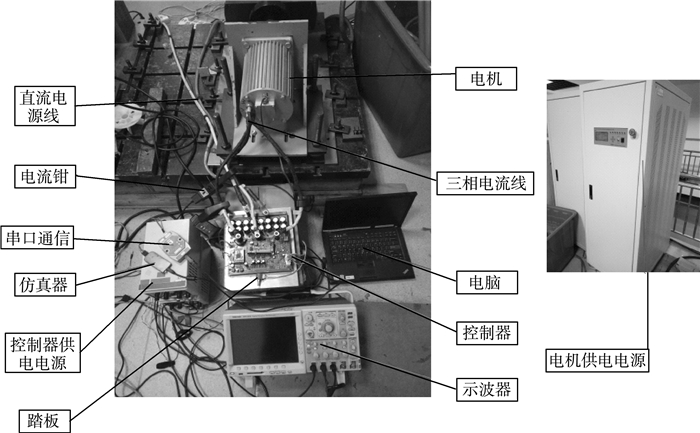 |
| 图 7 实验平台 |
软件部分:用Keil5进行程序设计,包括串口的初始化、AD转换、定时器设置、中断设置、PID控制、Park和Clark变换等。待程序调试通过后,通过仿真器下载到单片机STM32F103中,启动电机供电电源,通过踏板给定电机速度,通过示波器观察三相电流,通过串口通信将实际转速和iq的电流值传输到电脑,用电脑串口软件显示。得到的转速和iq的数据通过MATLAB绘制出相应图像。
实验的过程为:先将电机转速设置为700 rad/min,运行一段时间后,给电机加入负载2 N/m,运行一段时间,再将电机速度增加到1 000 rad/min,运行一段时间后,关闭电源。
结果:
1) 电机转速
图 8中可以看出,基于SVPWM的PMSM调速系统实际转速能够很好地跟随给定转速,当给定转速稳定时,实际转速不会出现较大的超调。
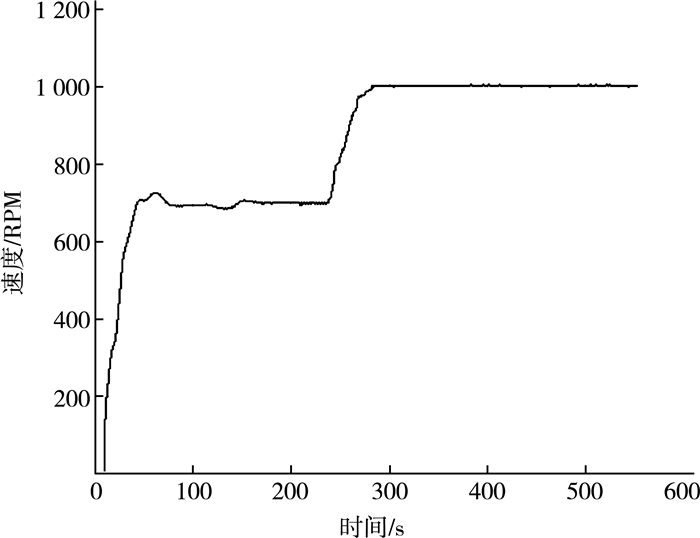 |
| 图 8 电机转速波形图 |
2) iq电流
由图 9可以看出,在电机启动和加速时刻,电流iq存在波动,但很快就趋于稳定。给电机加入负载后,电流iq值增大,这与仿真结果保持一致。
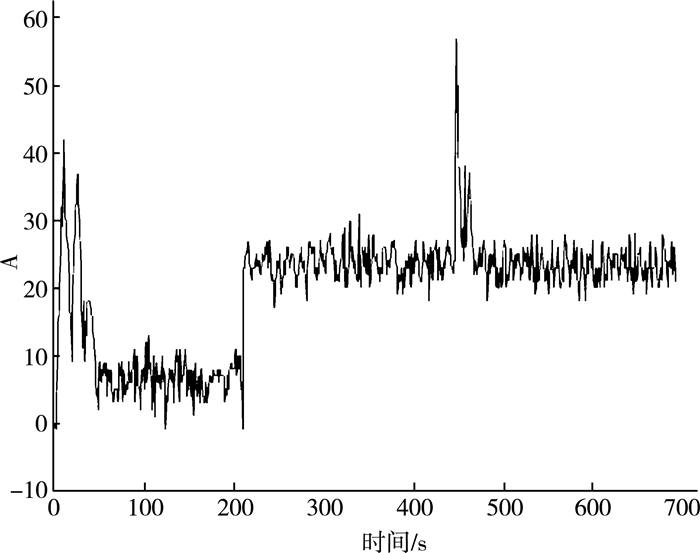 |
| 图 9 iq电流波形图 |
实验结果表明了,基于SVPWM的PMSM调速系统能够快速跟随给定速度,超调小,稳定性强,能够很好地对PMSM进行调速。
5 结论将SVPWM应用到PMSM调速系统之中,通过MATLAB/Simulink进行仿真实验。从仿真结果可以看出,基于SVPWM的PMSM调速系统具有响应速度快、超调小、运行稳定等优点。在仿真的基础上搭建以STM32F103为核心的实验平台,实验结果同样显示了该调速系统的优越性与可行性。仿真和实验都为基于SVPWM的PMSM调速系统提供了依据,同时证明了该系统的有效性。
| [1] |
王晓晨. 基于参数识别技术的永磁同步电机矢量控制研究[D]. 沈阳: 沈阳工业大学, 2015.
|
| [2] |
赵香桂, 王翔, 郭华旺. 基于DSP2812的异步电机VVVF调速系统实现[J]. 变频器世界, 2010(7): 32-34. |
| [3] |
方环. 永磁同步电机伺服控制系统开发平台的设计及研究[D]. 上海: 东华大学, 2014.
|
| [4] |
张练. 基于ASIC的PMSM伺服控制系统设计及实现[J]. 电子科技大学学报, 2009, 38(6): 10-11. |
| [5] |
徐书凯. 中、大功率EMA伺服控制技术与动态性能研究[D]. 南京: 南京航空航天大学, 2010.
|
| [6] |
贾华, 李俊彪, 崔军辉. 基于SVPWM的异步电动机变频调速系统的研究[J]. 自动化与信息工程, 2009(3): 4-6. |
| [7] |
李翠萍, 王新生, 张华强. 基于MATLAB的空间矢量PWM仿真研究[J]. 机床与液压, 2007(7): 220-221. |
| [8] |
童忠华. 基于CAN总线的伺服控制系统的研究[D]. 武汉: 武汉科技大学, 2008.
|
| [9] |
顾军, 陈志辉. 基于DSP的永磁同步电机无传感器矢量控制系统研究[J]. 防爆电机, 2006(1): 37-41. |
 2018, Vol. 32
2018, Vol. 32


