| 液压机摆冲结构计算精度分析及子模型应用 |
2. 齐鲁工业大学(山东省科学院) 机械与汽车工程学院,济南 250000
2. College of Mechanical and Automotive Engineering, Qilu University of Technology(Shangdong Academy of Sciences), Jinan 250000, China
冲孔是液压机锻造工艺中的基本工序, 为提高冲孔效率及精度, 对液压机进行结构改进设计了辅助冲孔结构[1]。摆冲结构在工作时, 其刚度和强度对冲孔精度影响较大, 运用有限元法对摆冲结构进行静力学分析, 较准确地验证该结构的安全性能, 可以有效节约生产成本, 达到安全生产的目的[2]。
摆冲结构主要由原动机部分、传动部分及摆臂部分组成。原动机部分采用摆线液压马达, 输出正、反向转动, 通过齿轮传动实现摆冲结构沿着立柱轴线低速往复摆动。根据液压机的本体结构特点将摆动角度设计成135°。摆冲结构的悬臂部分安装冲头, 摆臂摆出和摆入的极限位置设置限位挡块。外形结构如图 1所示, 在液压机中的位置如图 2所示。冲孔时, 冲头摆至液压机中心处, 使冲头中心与液压机中心重合, 摆冲结构与活动横梁一起下压完成冲孔操作。
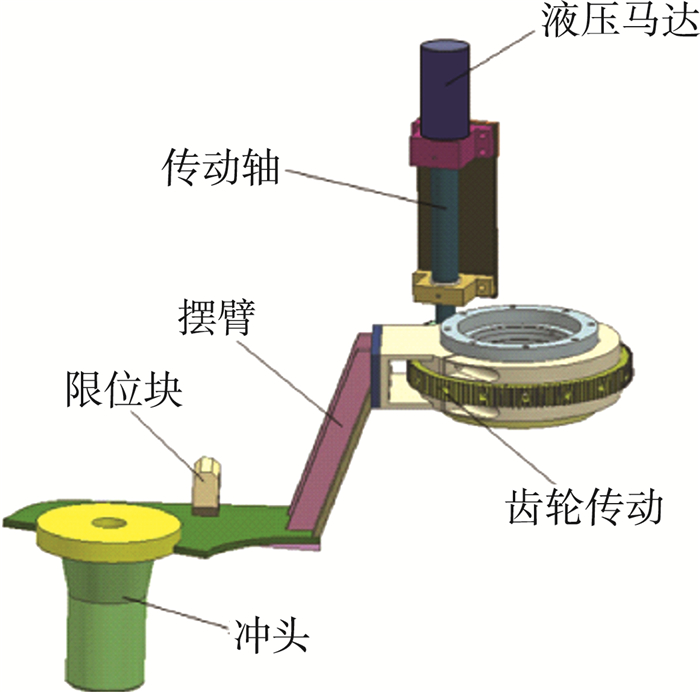 |
| 图 1 摆冲结构外形图 |
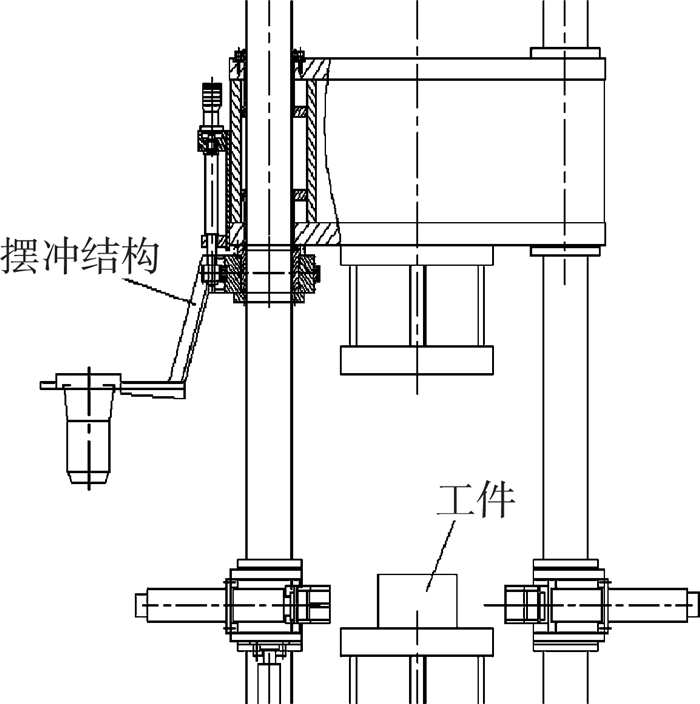 |
| 图 2 摆冲结构在液压机中的位置 |
1 摆冲结构有限元初步分析
在摆冲结构有限元建模之前, 首先对其实际结构进行一定的简化处理。目的是为减小有限元分析成本和规模, 而保证有限元分析的计算精度是简化处理前提条件[3]。
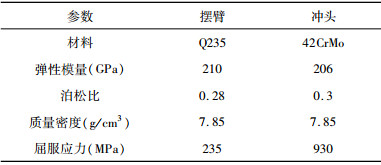
1.1 摆冲结构的计算方案的确定摆冲部分安装可换冲头, 冲头最大直径约为300 mm, 最大重量约为3 356.8 N。摆冲结构及冲头的材料特性如表 1所示。
| 表 1 摆臂和冲头的材料特性 |
 |
采用4节点四面体单元模拟摆冲结构, 由于该摆冲结构旋进工作位冲孔时, 摆臂的上平面与活动横梁接触, 并且随活动横梁一起向下运动, 所以受力主要集中在活动横梁上, 且受力很小, 可忽略不计。因此主要研究摆臂结构在自重作用下, 结构的刚度和强度问题。分析时, 摆臂右端按固定位移边界条件处理。整个摆臂(带冲头)的位移和等效应力云图分别如图 3和图 4所示。冲头的等效应力如图 5所示。
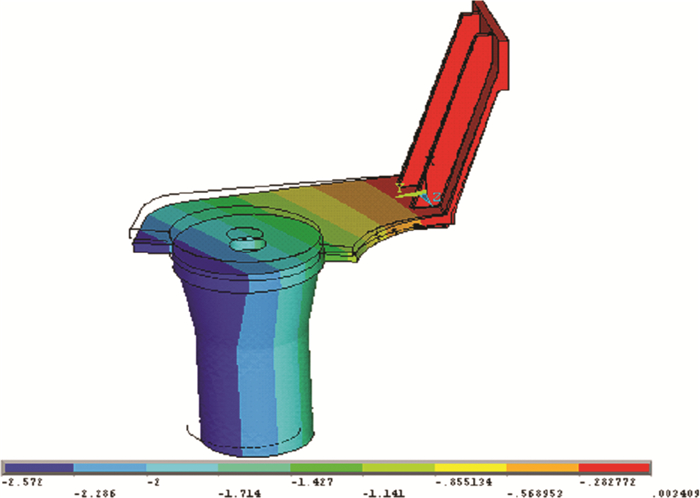 |
| 图 3 摆臂位移云图 |
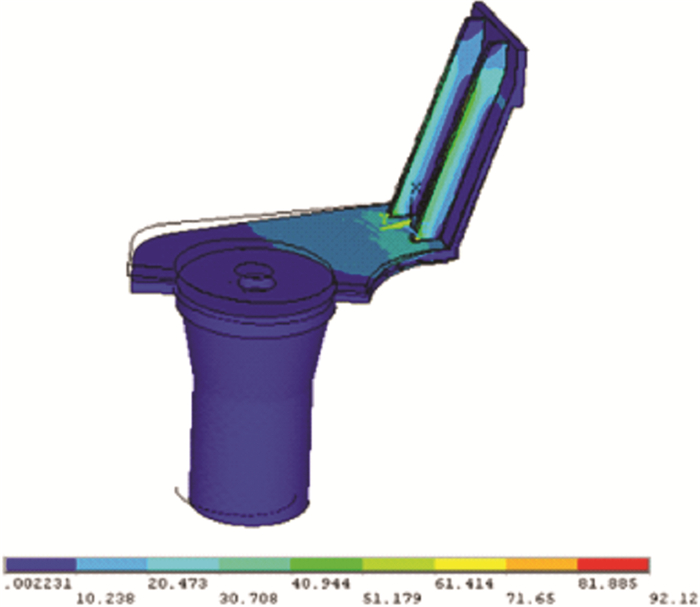 |
| 图 4 摆臂等效应力云图 |
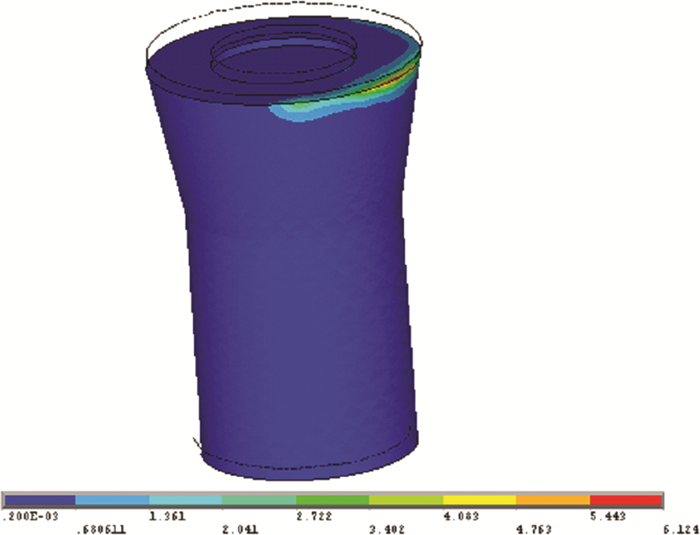 |
| 图 5 冲头的等效应力云图 |
摆臂部分的和位移和等效应力云图分别如图 6和图 7所示。摆臂的最大等效应力为92.12 MPa, 位于两侧肋板、立板和底板三者相接处的地方。摆臂的最大和位移为2.684 mm, 位于摆臂的最前端。
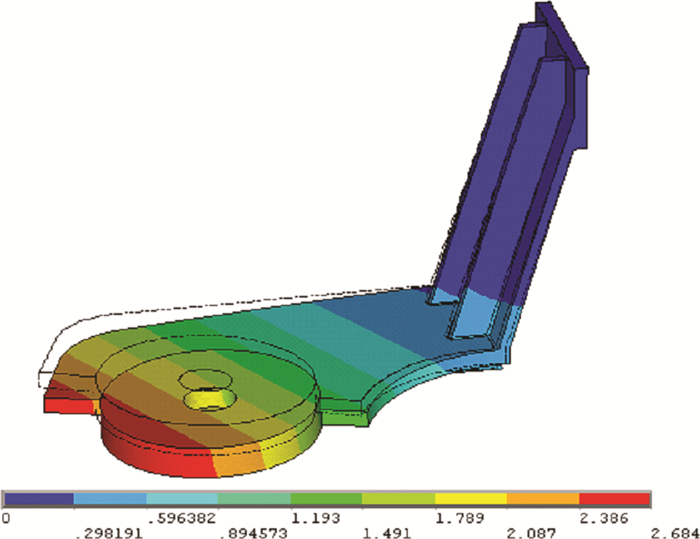 |
| 图 6 摆臂和位移云图 |
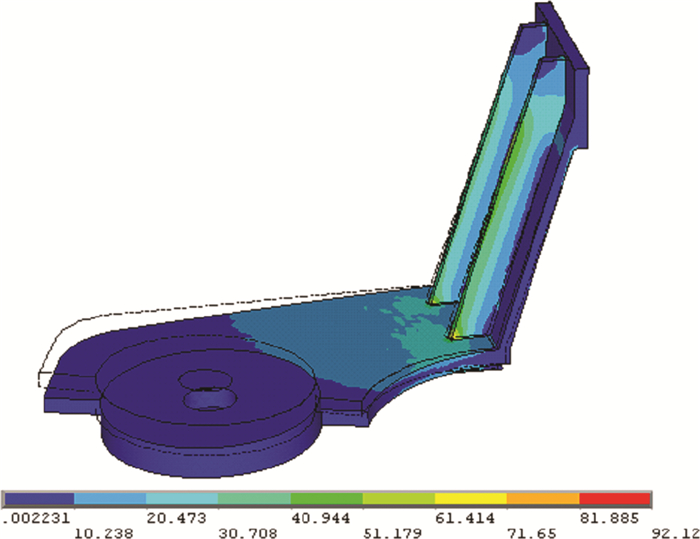 |
| 图 7 摆臂等效应力云图 |
因为冲头刚度比摆臂部分大得多, 而且由图 5可知冲头在自重作用下, 其最大等效应力仅为6.2 MPa, 远远小于其材料的许用应力。若在分析计算时不考虑冲头, 可以极大地减少有限元模型的规模, 降低有限元计算成本, 并能更加精确的分析摆臂部分的位移和应力。为了验证此方法可行, 再次对摆臂进行了分析。此次计算时, 将冲头的最大重量转化为等效的表面力Q=2.94×10-2 MPa施加在摆臂的冲头固定板的上表面处, 在摆臂有限元模型中不再包含冲头, 而其它建模条件不变。其和位移和等效应力计算结果如图 8和图 9所示。
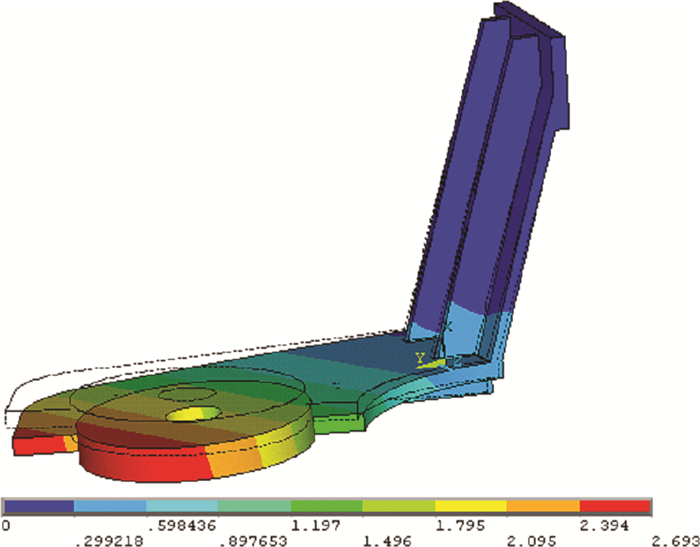 |
| 图 8 无冲头时的和位移 |
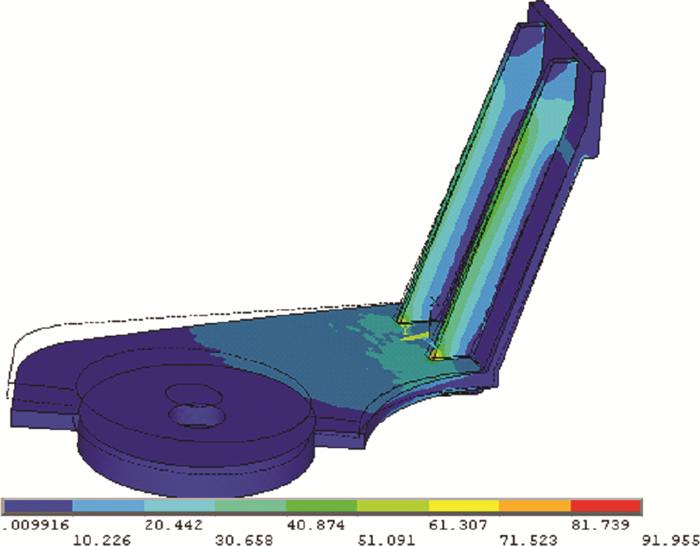 |
| 图 9 无冲头时等效应力云图 |
由计算结果可知, 无冲头摆臂结构的最大和位移为2.693 mm, 最大等效应力为91.955 MPa。位移的相对误差为0.33%, 应力的相对误差为0.92%。由此可见, 两者计算结果几乎相同, 能满足工程精度要求。所以在有限元分析时将冲头的最大重量转化为等效的表面力施加在摆臂的冲头固定板的上表面处, 而不再考虑冲头。
1.2 有限元初步分析选择4节点四面体单元模拟结构, 采用6.2 mm单元边长按均匀化方法对摆臂进行离散化结构。结构整体位移分布如图 10所示, 最大位移2.88 mm, 方向竖直向下, 在摆臂偏离液压机立柱最远的端部。等效应力云图如图 11所示, 等效应力最大为113.764 MPa, 位于两侧肋板、立板和底板三者相接触的地方。通过对摆臂部分的各零件进行有限元等效应力分析可知, 应力最大的是两侧肋板, 其中内侧肋板应力较大, 位置位于肋板与底面连接处。
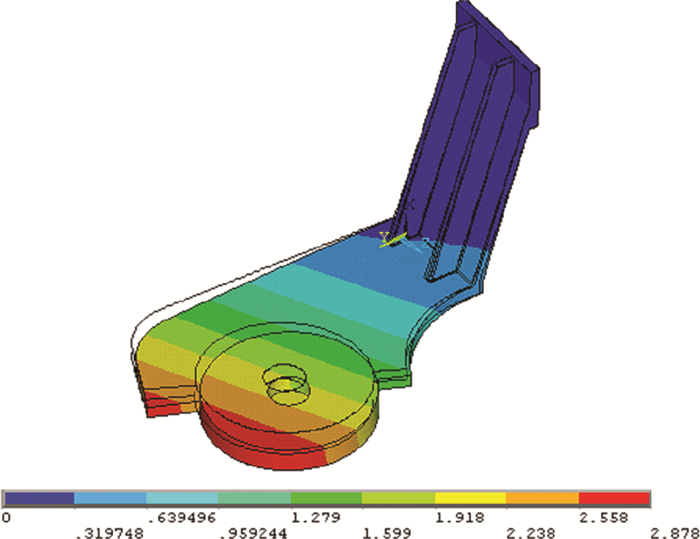 |
| 图 10 摆臂整体位移云图 |
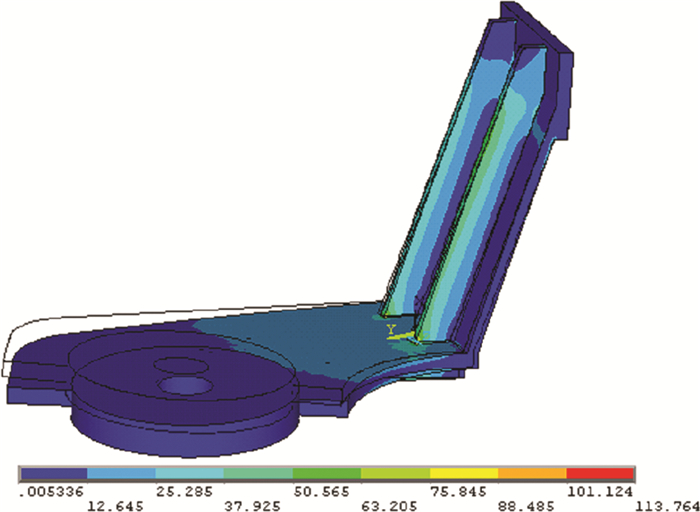 |
| 图 11 摆臂等效应力云图 |
2 计算结果精度分析
为了分析摆臂结构位移和等效应力的计算误差, 分别按单元为10 mm、9 mm、8 mm、7.5 mm、6.5 mm和6.2 mm对摆臂进行离散化并进行了分析计算, 其离散化信息和相应计算结果如表 2所示。
| 表 2 不同参数时摆臂的最大位移和最大等效应力计算结果 |
 |
最大位移变化趋势如图 12所示, 最大等效应力变化趋势如图 13所示。
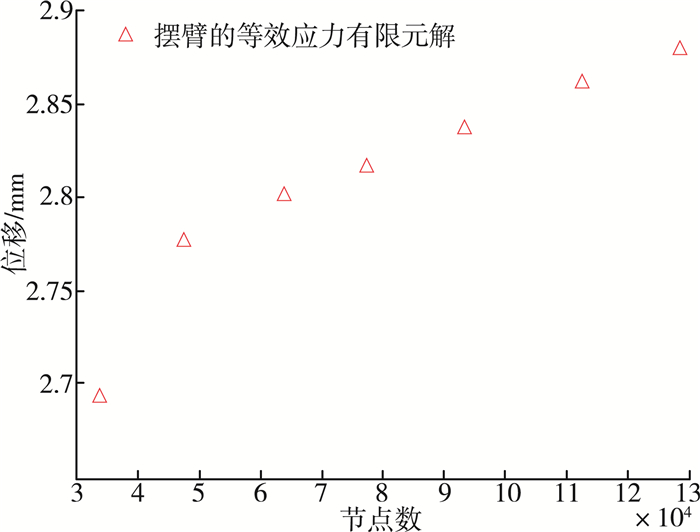 |
| 图 12 位移随节点数变化规律曲线 |
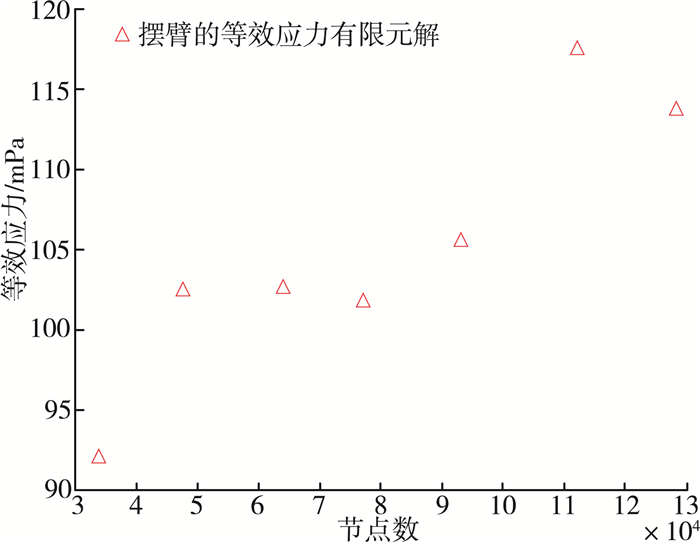 |
| 图 13 等效应力随节点数变化规律曲线 |
从图 12中可以看出, 最大位移随节点数的增加逐渐增大。节点数较少时, 位移变化量较大, 变化量百分比约为2.88%。节点数较多时, 变化量较小, 曲线越趋于水平, 变化量百分比约为0.35%, 这是由于位移法有限元是在单元内假设了位移形态, 即所假设的位移模式对单元的变形进行约束的限制, 这相当于附加了约束。因此, 在给定的载荷下, 位移法有限元分析高估了结构的刚性, 也就是低估了变形量[4]。因而采用完备协调单元得到的位移解是真实解的下限, 并逐渐趋近于真实值。
从图 13中可以看出, 最大等效应力随节点数的增加变化规律不明显。因为应力的求解, 要把位移结果做微分得到应变, 再乘以刚度矩阵得到应力。所以这个微分的过程就导致应力的精度比位移精度要低一些[5]。故采用位移法有限元计算得到应力近似解在精确解上下震荡。可见仅靠分析节点数为128 850时的最大等效应力来判断摆臂的强度是否符合要求是不够准确的。故对摆臂运用高级分析来进行判断, 下面运用子模型技术对摆臂等效应力进行较准确的分析。
3 摆臂子模型有限元分析摆臂结构中侧肋板与底板连接处属于应力集中区域, 对该部分区域划分网格时网格太疏不能得到较准确的结果, 但是对于这些区域之外的部分, 网格密度已经足够。所以对于立板与底板连接的局部区域用子模型技术处理以提高分析的质量[6]。
子模型分析指的是在完成了全局模型分析的基础上把局部位置的网格进行细化, 以用于后期计算, 这样不但节约了时间也使计算的结果更加精确[7]。子模型技术需要在全局较粗网格模型上确定切割边界, 其边界条件是切割边界的计算位移值。该技术主要运用圣维南原理, 即应力分布只对载荷作用的区域产生影响, 此区域会存在应力集中效应[8]。所以在运用子模型技术分析时, 要在远离应力集中区域处确定切割边界以得到更为精确的分析结果。
3.1 建立摆臂子模型首先对网格划分粗的摆臂整体模型进行有限元计算。分析时, 采用10节点四面体单元模拟摆臂结构, 取单元边长16.0 mm对摆臂离散化, 其有限元模型有36 620个单元, 62 153个节点。摆臂整体几何模型和有限元模型分别如图 14和15所示。
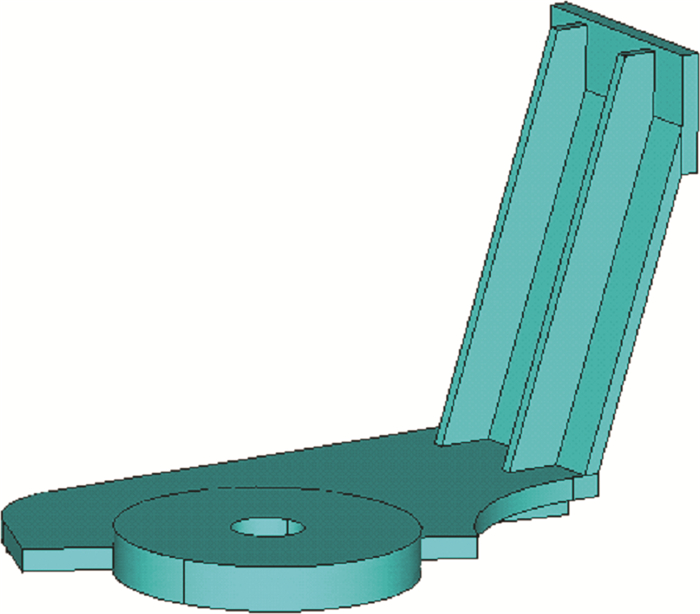 |
| 图 14 摆臂整体几何模型图 |
 |
| 图 15 摆臂整体有限元模型图 |
在前面已分析的全局模型及分析结果的基础上, 从高×宽为605 mm×855 mm的整体模型中切割出一含有应力集中的模型局部(高×宽为180 mm×250 mm), 把它作为一个独立的模型, 单独对它网格细化, 由整体模型计算得到的位移施加在子模型的切割边界处的节点上, 再进行有限元分析计算。这样处理, 不仅使局部的应力计算结果更为准确, 而且计算量也不大。
摆臂子模型的几何模型如图 16所示。采用10节点四面体单元模拟摆臂子模型, 采用非均匀化方法进行网格划分。由于侧肋板应力最大, 故单元边长取4.5 mm, 离散化后, 侧肋板有38 379个节点, 24 877个单元;底板单元边长取9.0 mm, 离散化后, 底板有42 197个单元;底面肋板单元边长取9.0 mm, 底面两块肋板有2 604个单元;因为立板应力最小, 故取立板单元边长取10.0 mm, 立板有105 50个单元。摆臂子模型节点总数为122 091, 单元总数为80 228, 其有限元模型如图 17所示。
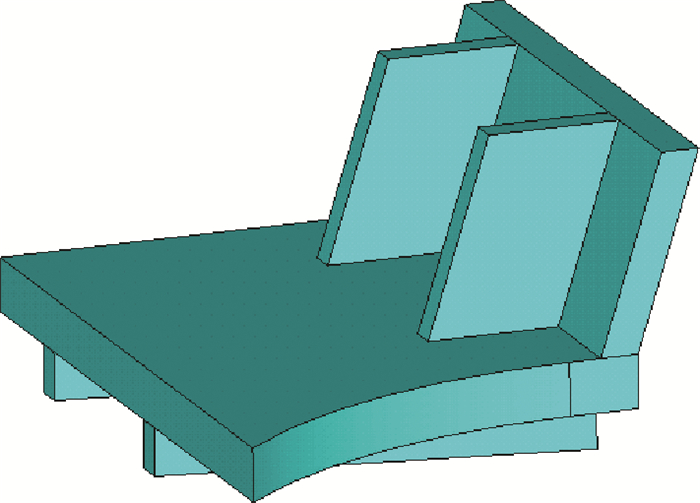 |
| 图 16 摆臂子模型几何模型图 |
 |
| 图 17 摆臂子模型有限元模型 |
3.2 摆臂的子模型有限元分析
摆臂的子模型等效应力云图如图 18所示。从图中可以看出, 最大应力的位置位于肋板与底板的焊接部位, 最大应力为119.247 MPa。较之前进行整体分析得到的113.77 MPa有所提高, 也更加准确。
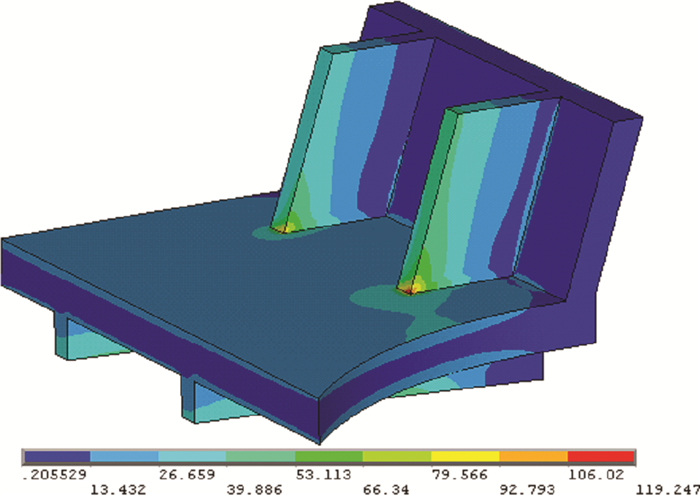 |
| 图 18 摆臂的等效应力云图 |
计算能量百分比误差为10.264, 接近于10, 基本满足工程精度影响要求。
该摆臂的材料全部为Q235A, 各零件之间采用焊接的形式连接。材料的屈服强度σs=235 MPa, 抗拉强度σb=375 MPa, 取许用安全系数S=1.60, 则该结构的许用应力为
| $ {\sigma _s} = \frac{{{\sigma _s}}}{{[s]}} = 146.9\;{\rm{MPa}} > 119.24\;{\rm{MPa}} $ | (1) |
所以摆臂结构满足强度要求。
4 结论1) 通过对有无冲头时摆冲结构的位移和等效应力分析, 确定了较为合理的计算方案。结果表明, 将冲头的最大重量转化为等效的表面力施加在摆臂的冲头固定板的上表面处, 极大地减少了有限元模型的规模, 并能更加精确的分析摆臂部分的位移和应力。
2) 通过对不同参数时摆臂的最大位移和最大等效应力的计算, 分析了计算精度。结果表明, 采用完备协调单元得到的位移解是真实解的下限, 并逐渐趋近于真实值。而用位移法有限元计算得到的应力近似解在精确解上下震荡, 计算结果不准确。
3) 运用子模型技术对摆冲结构进行了较为精确的分析。计算结果表明, 计算能量百分比误差为10.264, 接近于10, 基本满足工程精度影响要求。
| [1] |
樊静.YHC-1000吨门形液压机的三维有限元分析[D].合肥: 合肥工业大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10359-2008143462.htm
|
| [2] |
李刚, 刘培培, 倪承普. 大型锻造液压机工作缸结构设计及有限元分析[J]. 锻压装备与制造技术, 2018, 53(03): 87-90. |
| [3] |
刘叶艳.烟草自动备货补货系统穿梭车的结构分析及优化设计[D].贵州: 贵州大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10657-1016777636.htm
|
| [4] |
黄秀香.基于有限元分析的卡车车架精度控制方法研究[D].青岛: 青岛大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-11065-1018881372.htm
|
| [5] |
卿光辉, 王博鳌. 联合有限元法及其收敛性与精度分析[J]. 中国民航大学学报, 2019, 37(01): 60-64. |
| [6] |
侯澍旻, 邓杨, 李友荣. 子模型技术在精轧机机架强度分析中的应用[J]. 武汉科技大学学报, 2011, 34(03): 178-181. |
| [7] |
崔磊, 毛江鸿, 金伟良, 等. 基于多边界切割插值的改进子模型分析方法[J]. 计算力学学报, 2015, 32(05): 619-626. |
| [8] |
殷正瑞, 李兴成, 刘凯磊, 等. 100 MN液压锻造机预紧组合式机架的有限元分析[J]. 锻压技术, 2019, 44(08): 106-111. |
 2020, Vol. 34
2020, Vol. 34

