| 能源互联网下局域能源微网能量调度算法研究 |
能源互联网的理论与技术正处于快速发展时期, 许多相关工作人员对相关工作展开了研究工作[1]。能源互联网把先进的通信技术和智能能量调度技术结合起来, 将信息能源综合电网、分布式能源等互联起来, 实现能量点对点交换和共享利用[2]。
针对能源互联网中的能量调度问题, 已经提出了多种相关的算法。主要有经典优化方法、基于规划的方法、启发式算法等, 这些算法能够解决电网中许多问题, 但也存在着一定不足[3]。伴随着人工智能的发展, 强化学习(reinforcement learning, RL)的研究也越来越深入, 许多学者开始关注这项技术在电力系统中的应用[4]。在局域微网能量调度策略中, 赵敏等[5]提出了采用非合作博弈研究多微电网交易模式的一般模型及分析方法。将配电网对微电网之间交易的影响以征收服务费用的方式加以考虑, 证明了该博弈存在纳什均衡, 并提出了相应的求解流程。王亚东等[6]利用深度卷积神经网络提取微电网调度时间序列信息特征, 以Q值强化学习机制实现微电网储能调度策略。深度强化学习算法已成功应用于微网定价[7]、能源调度策略[8]中局域微网间能源交易的最优解计算。
局域微网的任务要满足当地客户的用电需求, 但由于客户的独立性, 每个客户都有各自的需求, 这些需求发生在一天当中特定时间段的任意时间。把这些类似的需求归类为日常生活活动需求(daily needs, DN)。局域微网有能力根据当前自己的负载自由调度用户的DN需求。能源交易对于维护微网, 提高其稳定性具有至关重要的作用。同时微网可以通过在微网和广域中央电网之间买卖电力来获取利益。实现利益的最大化是本文的重点, 本文提出的动态定价策略(允许微网根据当前能量供求关系决定售电价格)与DN调度协调工作对实现利益的最大化具有很大的优势。动态定价策略鼓励了微电网进行能量交易, 这无疑加强了各个微网之间的合作, 通过这种合作, 微网能够尽可能的依靠自身的能力来满足本地客户的DN需求, 最大程度上减少对中央电网的依赖。
本文通过研究一种基于深度强化学习的新型局域微网能源调度策略来解决如何应对新型微网能量调度中存在的问题。通过创建两个独立的神经网络(分别用以处理能量调度和能量交易)更好地分析不同应用场景下的定价模型对于微网能量和调度定价策略的作用和影响, 通过对比不同设置下深度Q学习算法在微网能量调度中的表现, 验证了动态定价策略相对于固定定价策略在微网能量调度策略中应用的优越性。
1 局域能源微网调度模型在本节中, 将描述实现能源交易和工作计划的局域微网模型以及提议的算法。如图 1所示, 广域能源互联网下存在着N个相互连接且有着电气交易的局域能源微网[9], 这些局域微网不仅建立了电气连接, 还建立了信息连接[10]。同时这些局域微网都具有本地产生可再生能源的能力, 并且还具有将能量存储在电池单元中的功能。我们将一天分为几个等长的时间段, 在每个时间段, 局域能源微网都具有本地需求、电池中剩余能量、电网发电量和一天剩余日常生活活动需求的信息。取决于以上信息, 局域能源微网在规定的时间段做出相关供应调度决策。接下来对每个局域微网的状态、动作以及奖励进行描述。
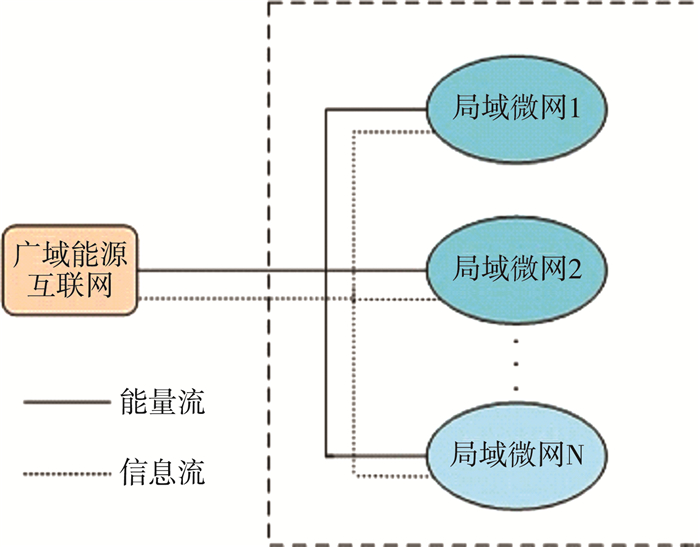 |
| 图 1 相互连接的局域微网模型 |
1.1 状态描述
局域能源微网i在时间t的状态由式(1)给出:
| $ s_{t}=\left(t, \mathrm{DN}_{t}^{i}, c_{t}^{i}, \mathrm{ne}_{t}^{i}, p_{t}^{i}\right), $ | (1) |
其中, t是当下的时刻, DNti表示当前时刻剩余的日常活动需求, cti为本地非日常活动用户的能量需求。DNti并不是立即需要能源完成任务, 而是可以在一定时间范围内完成的任务, 但是要提前预留能够支撑该任务完成的能量。pti表示这是微网向中央电网购买电力的价格, 注意微网以pi—k的价格向中央电网进行销售, 在这里k为一个正整数。净能量neti的定义由式(2)给出:
| $ \mathrm{ne}_{t}^{i}=\mathrm{re}_{t}^{i}+b_{t}^{i}-c_{t}^{i}, $ | (2) |
其中, reti表示微网产生的可再生能源总和, bti为电池值。
1.2 动作描述根据对微网状态的描述, 微网动作需要满足日常生活活动的调配以及做好电量购买/出售的预算。基于上述要求, 局域微网动作由式(3)给出:
| $ a_{t}=\left(a_{\mathrm{DN}}, u_{t}^{i}, a_{p}\right), $ | (3) |
其中, aDN表示局域微网在当前时间段计划完成的日常生活活动需求。uti为局域微网之间或与主电网之间待交易的电量, 其为正值的时候表示该微网在出售电力, 负值的时候表示正向其他微网或者主电网购买电力。另外, 为了确保微网的稳定性, uti受一组约束条件的约束, 在下面的章节我们会详细叙述。ap表示微网选择的售电价格。
接下来每个局域微网根据自己当前的定位, 买方微网根据自身的要求在卖方微网之间选择一个报价最低的微网进行交易。如果在微网相互交易过后, 仍无法满足一些微网的需求, 则可以向中央电网以pi的价格购买需要的能量。相反, 如果买方微网之间的需求已经得到满足, 则卖方微网可以将能量以pi—k的价格卖给主电网。
1.3 奖励每个局域微网的目的是通过电力交易获得足够的利润, 同时满足区域内用户日常需求和非日常需求。基于此要求, 奖励函数由式(4)定义:
| $ \begin{array}{l} R_{t}^{i}=\lambda \times u_{t}^{i} \times p_{t}^{i}-\beta \times\left(\mathrm{unDN}_{t}^{i}+\mathrm{unc}_{t}^{i}\right) \\ \;\;\;\;\;\;\;\;\lambda+\beta=1_{\circ} \end{array} $ | (4) |
上式中, λ与β为一个正常数, 且满足相加和为1, 通过调整λ与β的值可以改变微网销售能源和满足当地消费者需求的权重。这句话的意思是λ的值比较大时, 微网更倾向于向外界出售电力获得利润, 当β的值比较大时, 微网此时便更倾向于满足用户日常和非日常需求。在本文中, 为了更好的模拟现实世界的情景, 将β设定为0.8以便更好的满足区域微网内用户的需求。unDNti和uncti分别是未满足的日常生活需求和未满足的非日常生活需求。
式(4)中, 如果uti为正则表示局域微网正在出售电力获得利润, 相反则表示在购买电力获得负值奖励。另外λ与β为一个正常数, 如果局域微网没有满足用户需求则会获得负值奖励, 用户需求得到满足微网便不会受到惩罚。
1.4 改进的算法为了完成满足能量需求和能量交易的任务, 每个局域微网使用两个代理, 第一个代理叫做DN代理, 负责能量需求调度任务, 由它决定在一天中哪个时间步长调度哪些日常任务, 并将信息提供给第二个代理。第二个代理叫做ET代理, 负责能量交易任务, 它决定购买或者出售的电力单位, 设定交易价格。
局域微网基于DN代理和ET代理执行动作, 两个代理获得共同的奖励或者惩罚。对此只要创建一个MDP(马尔可夫决策)模型, 该模型对两个代理的状态转换、动作选择以及奖励函数进行建模。使用两个独立神经网络结合深度强化学习算法并且让他们共享相同的奖励, 而不是让两个代理使用一个更加庞大的神经网络网络, 这样可以更好的探索动作空间, 减少获得最优策略的迭代次数。用于训练能量调度模型的算法如表 1算法1所示。
| 表 1 |
 |
DN代理和ET代理具有相同的状态空间, DN代理有一个参数叫做DN状态, 对应的ET代理中存在一个DN操作参数, 所以两者具有相似的经验池。在确定DN代理的动作后, 将此作为ET网络的输入, 接下来便知道在具体的时间段留有相关的能量供应日常活动, 进一步指导ET网络是购买还是出售电力。因此两个代理可以通过共享相似的状态空间和奖励进行协作, 同时得到最佳策略。
2 约束条件设定与模拟设置 2.1 约束条件 2.1.1 价格限制本文限制微网进行能源交易的价格范围为[CP-k], 其中CP是中央电网价格, k为正常数。如果微网的报价高于中央电网, 基于前面设置的规则交易不会发生, 因为这样的话微网更愿意直接从中央电网进行购买。同时允许微网可以以报价最低价, 即以CP-k向中央电网出售电力, 这样可以保证微网更愿意出售能源给微网。
其次是能源交易限制为了更加真实的模拟现实情况, 必须要考虑现实世界的物理限制, 例如: 电池的最大容量、每个微网的最大负荷量等。
2.1.2 能量交易限制交易电量的下限, 由式(5)定义:
| $ u_{t}^{i}=\max \left(-M, \mathrm{ne}_{t}^{i}-F\left(A_{t}^{i}\right)-B\right), $ | (5) |
式(5)中, -M表示微网不能购买超过M的电量, 防止产生过载现象, 即-M≤uti。
每次交易完成后, 每个微网电池中剩余的能量量(将微网自身产生的能量、DN需求、非日常需求、交易前电池储存量考虑在内)不能大于最大电池容量B, 最大电池容量B由式(6)更新:
| $ \begin{aligned} &\mathrm{ne}_{t}^{i}-F\left(A_{t}^{i}\right)-u_{t}^{i} \leqslant B, \\ &\mathrm{ne}_{t}^{i}-F\left(A_{t}^{i}\right)-B \leqslant u_{t}^{i}。\end{aligned} $ | (6) |
其中F(Ati)表示完成当前步长所选DN动作所需能量单位, 式(5)中的最大项确保当前DN动作得以实现。
交易电量的上限, 由式(7)定义:
| $ u_{t}^{i} \leqslant \mathrm{ne}_{t}^{i}+c_{t}^{i}-F\left(A_{t}^{i}\right)。$ | (7) |
微网一旦选择了DN动作就必须要满足该动作, 所以微网在能量交易后电池中储存的能量应该大于或等于F(Ati), 满足式(8)的约束条件。
| $ \begin{aligned} &\mathrm{ne}_{t}^{i}+c_{t}^{i}-u_{t}^{i} \geqslant F\left(A_{t}^{i}\right), \\ &\mathrm{ne}_{t}^{i}+c_{t}^{i}-F\left(A_{t}^{i}\right) \geqslant u_{t}^{i}。\end{aligned} $ | (8) |
完成交易之后剩余电量储存在电池中备用。电池状态bti由式(9)更新:
| $ b_{t+1}^{i}=\max \left(0, \mathrm{ne}_{t}^{i}-u_{t}^{i}-F\left(A_{t}^{i}\right)\right)。$ | (9) |
实验中的局域微网使用风能或太阳能可再生资源作为其发电能源。前面提到动态定价模型和固定定价模型。
动态定价模型(DPP): 局域微网自行决定能量交易价格, 并且定价低于中央电网的价格。
固定定价模型(CPP): 局域微网以中央电网的定价进行能源交易。
本文在两种情景设置下对比动态定价模型和固定价格模型, 设置如下:
设置1:设置一个简单的四微网设置, 观察其在固定定价策略和动态定价策略下的奖励曲线, 由此可体现两种策略的优劣性。
设置2:采用更加实用的10微网设置, 在这种设置下, 五个微网产生的能量低于其需求, 另五个微网产生的能量高于前者, 这样做的目的是为了验证调度策略的合理性, 考验电网在匮电状态时能不能合理的的安排日常调度任务。
设置3:在两种定价模型上采用10微网设置, 这样相对于设置2能产生更多的电量用来交易, 由此更能验证动态定价策略的优越性。
在以上基础上, 将局域微网生成的每小时可再生能源数据拟合泊松分布, 并在实验过程中从该分布中采样可再生能源单位。将可再生能源最大发电量限制在10个单位, 并将一天分成四个步长, 每个微网在每个步长进行决策。每个时间步长内, 非日常需求可以是3、4、5、6个单位之一, 在一天开始的时候最多考虑三个日常需求。电池中可以存储的最大能量限制为10个单位, 所以在单个时间段内微网可以购买的最大能量也限制为10个单位。在实验中规定固定的中央电网价格CP=20(每单位电力的价格单位)。在前面提到, 局域微网对中央电网的售价定为cp-k, 在实验中将k的值取为5, 所以动态定价策略的定价区间为[15, 20]个价格单位。局域微网的DN代理和ET代理均使用具有三层前馈神经网络的模型。
DN网络和ET网络均使用三层前馈神经网络, 输入状态和输出动作如上文所述, 使用学习速率为0.000 1、β1=0.9、β2=0.9和ε=10-8的Adam优化器来更新网络权重, 折扣率γ=0.9。
3 结果与分析 3.1 四微网设置结果分析从图 2可以看出, 采用固定定价策略的微网在一开始所获得的利润回报要高于动态定价策略的微网, 但是随着迭代次数的增加, 动态定价策略所具有的优势逐渐显现出来。这是因为采用动态定价策略的微网能源销售价格适中低于固定定价策略的微网, 而微网更倾向于从报价更低的微网进行购买, 所以采取动态定价策略的微网在大多数情况下都能成功的将电力出售, 而采取固定定价策略的微网只能以cp-k的价格(低于动态定价策略出售的价钱)出售给中央电网, 所以利润要低。另外, 相比传统的随机优化探索方法[11], 可以看出提出的基于深度强化学习的新型局域微网能源调度算法有着在能量调度有着明显的优势。
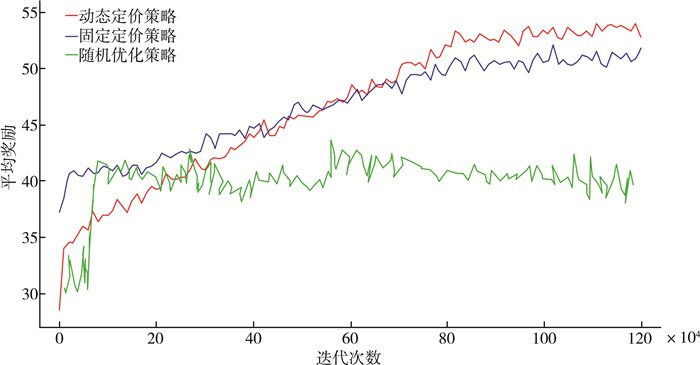 |
| 图 2 四微网设置在三种定价策略下获得的平均利润走势 |
在表 2中, 展示了四微网系统模型在4个时间步长对DN需求的调度状况, 为了能够更好的显示出提出调度策略的合理性, 在系统模型收敛前抽取了12次(对应表 2前12次)迭代结果, 收敛后抽取了8次(对应表 2后8次)迭代结果进行分析, 表 2中D1、D2、D3代表着需要完成的DN需求动作, 表中的空格部分表示在该时间步长没有安排任务执行。通过表 2可以看出看出代理学会了在不同的时间安排DN需求, 这表明本文所提出的微网能量调度模型可以把负载动作从高峰需求转移到其他时间步长执行, 以减轻负载压力。同时通过对比两个微网对三个DN需求任务调度状况, 可以看出两个微网代理在不同的时间步长频繁的选择某个DN动作, 这表明它们DN代理的策略已基本趋于一致。
| 表 2 四微网动态定价策略下不同时间步长的DL调度情况 |
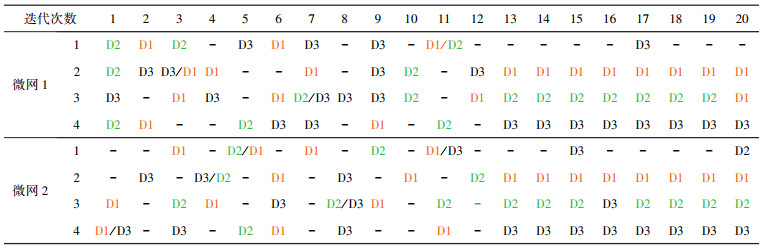 |
图 3中横坐标是指系统模型收敛后的迭代次数, 纵坐标是指模型迭代100次选择价格的平均数。通过图 3可以看出, 在系统模型收敛了后的多次迭代中, 系统选择的价格并不像固定定价策略一直选择售价20, 而是选择了在一个合理的价格区间变化, 曲线的波动体现了系统能根据实时情况选择最合适的价格来获得最大利益, 由此代理学会了合理的安排定价, 也进一步证明了提出的动态定价策略的优越性。
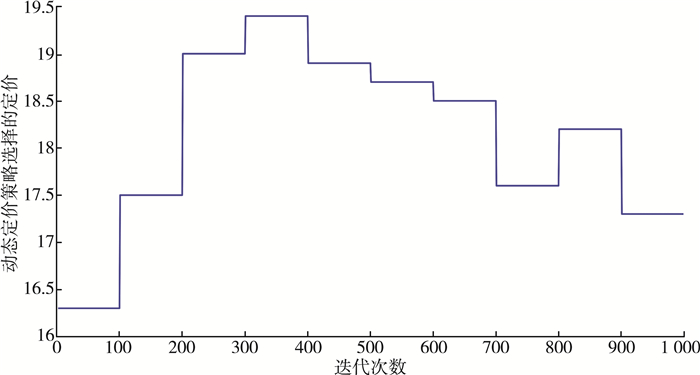 |
| 图 3 四微网动态定价策略采取的定价 |
3.2 十微电网设置结果分析
在图 4中, 整理了设置2下动态定价和恒定定价策略在最近的50 000次迭代(收敛后)中获得的平均回报。五个微网产生的能量低于其需求, 另五个微网产生的能量高于前者, 通过图 4分析发现, 电网并没有受到太多的惩罚, 建议的动态定价模型对于大多数微网(十分之七)的恒定定价模型表现更好, 说明了调度策略的合理性, 电网在面对匮电的状态时仍能够合理的安排调度任务, 由此验证了系统调度模型的合理性。
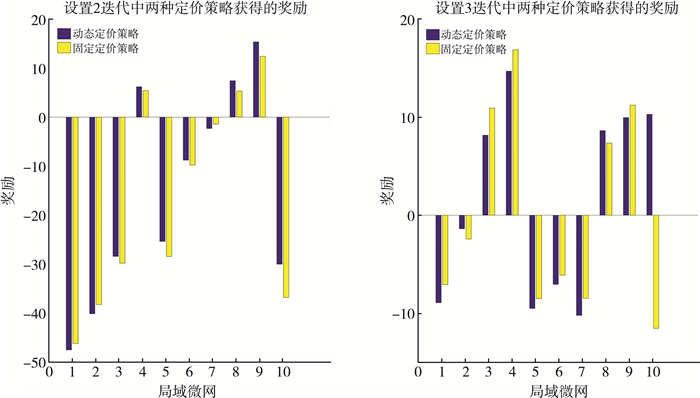 |
| 图 4 设置2和3迭代中两种定价策略获得奖励的差异 |
通过图 4可以观察到, 微网在设置3中比在设置2中获得更好的奖励(设置3中的奖励差异高于设置2)。将其归因于这样一个事实, 即与设置2相比, 大多数微网在设置3中产生的能量更高, 这使它们能够出售更多的能量。此外, 动态定价的效果在它们开始产生更多的权力时就变得更加突出, 正如它们的动态定价奖励和恒定定价奖励之间的差异所注意到的。
从以上三种设置中可以看出, 遵循动态定价策略的代理商通常比固定定价模型表现更好。此外还表明, 除了动态定价外, 微网还学会了智能地调度DN需求, 从而将能耗从峰值需求转移到其他地方。
4 总结本文研究了深度强化学习算法在局域微网能量调度中的应用, 提出了一种可以进行能量交易、工作安排和动态定价的局域微网。为了解决此问题, 为每个微网设计了两个网络模型(DN网络和ET网络), 他们可以同时执行动态定价和需求调度。本文首先通过设置的四电网模型, 经过观察观察其在固定定价策略和动态定价策略下的奖励曲线, 验证了所提出调度策略算法的合理性。为了进一步验证调度策略的调度能力和促进电网之间的交流, 在设置二中采用了十电网案例并模拟了匮电场景, 结果表明电网在面对匮电的状态时仍能够合理的安排调度任务。最后为了更加贴合现实场景, 在设置三中增加了电能产量, 结果表明, 提出的系统模型能够在满足用户需求的同时获得最大的奖励。
| [1] |
慈松, 李宏佳, 陈鑫, 等. 能源互联网重要基础支撑: 分布式储能技术的探索与实践[J]. 中国科学: 信息科学, 2014, 44(6): 762-773. |
| [2] |
CAO J, YANG M. Energy internet-Towards smart grid 2.0[C]//IEEE Computer Society, Fourth International Conference on Networking and Distributed Computing, Hongkong, China, 2013.
|
| [3] |
张自东, 邱才明, 张东霞, 等. 基于深度强化学习的微电网复合储能协调控制方法[J]. 电网技术, 2019, 43(6): 1914-1921. |
| [4] |
刘俊峰, 陈剑龙, 王晓生, 等. 基于深度强化学习的微能源网能量管理与优化策略研究[J]. 电网技术, 2020, 44(10): 3794-3803. |
| [5] |
赵敏, 沈沉, 刘锋, 等. 基于博弈论的多微电网系统交易模式研究[J]. 中国电机工程学报, 2015, 35(4): 848-857. |
| [6] |
王亚东, 崔承刚, 钱申晟, 等. 基于深度强化学习的微电网储能调度策略研究[J]. 可再生能源, 2019, 37(8): 1220-1228. |
| [7] |
WANG H, HUANG T, LIAO X, et al. Reinforce-ment learning in energy trading game among amart microgrids[J]. IEEE Transactions on Industril Electronics, 2016, 63(8): 5109-5119. |
| [8] |
LU R, HONG S H. Incentive-based demand response for smart grid with reinforcement learning and deep neural network[J]. Applied Energy, 2019, 236(15): 937-949. |
| [9] |
周长华. 基于强化学习的微电网电能交易研究[D]. 厦门: 厦门大学, 2017.
|
| [10] |
杨方, 白翠粉, 邱忠涛, 等. 能源互联网路由网络结构与控制机制[J]. 计算机科学与探索, 2018, 12(3): 403-410. |
| [11] |
毛亚哲, 何柏娜, 王德顺, 等. 基于改进深度强化学习的智能微电网群控制优化方法[J]. 智慧电力, 2021, 329(3): 19-25. |
 2022, Vol. 36
2022, Vol. 36


