| 基于信号分析与神经网络的人民币汇率预测模型研究 |
随着国家“一带一路”战略规划推进, 人民币持续升值的趋势下, 外汇风险管理的重要性不言而喻。因此采用科学有效的方法来预测和优化汇率预测模型具有重要意义。
1 人民币汇率行为预测研究现状目前关于人民币汇率行为的描述与预测吸引了众多学者的关注, 主要集中在两个方面, 一是以经典分析方法作出的汇率预测, 比如购买力平价理论、利率平价理论等;二是基于智能算法的汇率预测, 主要的分析方法包括神经网络、粒子群算法、遗传算法、小波分析等多种方法的综合应用[1]。
随着计量经济学在非线性领域、非平衡系统领域的研究进展迅速, 多种新兴的数学手段涌现出来, 技术分析方法逐渐被运用到经济系统的分析中, 而基于宏观经济结构模型的经典分析方法越来越无法解释复杂的非平衡动态变化的现实经济系统。
技术分析法主要是根据汇率的历史时间序列数据, 建立从单变量到多变量的时间序列预测模型来进行预测。技术分析方法从最早采用随机游走的参数化模型, 到后来发展的新的计量经济学和时间序列模型[2-3]。
以本文选用来自中国人民银行每日公布的人民币兑美元汇率价格序列为例, 数据的非线性特征非常明显。美元样本区间选择为2014年1月1日起至2016年7月1日止, 样本数为610个。
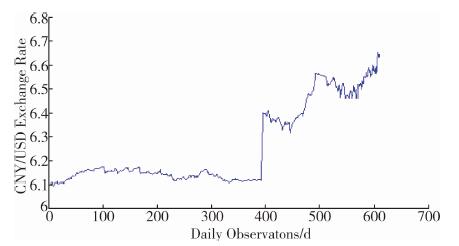 |
| 图 1 近年人民币兑美元汇率价格水平序列图 |
基于汇率行为的复杂性和非线性的特点, 非参数方法和非线性方法应用于预测汇率, 非参数模型方法包括众多智能算法, 如神经网络、粒子群算法、遗传算法、小波分析等方法。
同时采用时频分析方法对汇率价格序列的频谱成分随时间变化的情况进行的研究也逐渐展开。目前应用广泛的时频分析方法如短时傅里叶变换、小波变换等。
但是由于短时傅里叶变换的分辨率会受到窗函数的形状和宽度的影响, 小波变化的分辨率同样也会受到小波函数以及小波基参数的影响, 使用这两种分析方法时都需要根据分析信号的特点进行参数选择。
由Huang等提出的经验模态分解EMD算法, 能够对非线性、非平稳数据进行自适应分析。通过将信号分解为有限的本征模态函数IMF(Intrinsic Mode Function), 实现信号的时频分布表示, 选取有效的IMF分量进行信号的重组即实现了滤波过程[4]。
后续的众多的改进算法中, 集合经验模式分解(Ensemble EMD, EEMD)方法, 通过加入一定幅值的白噪声信号, 并平均分解结果, 得到多个具有物理意义的IMF分量, 对EMD方法的模态分裂的现象进行了抑制, 使此方法得到了广泛的应用。
如利用EEMD来分析时间序列的信号的时频特性, 由此可以对人民币汇率行为进行描述, 并进行噪声信号滤波, 为后续建立非参数模型奠定良好的基础。
2 神经网络模型 2.1 神经网络算法应用简介神经网络是由大量具有简单处理功能的神经元构成的[5-7]。众多的神经元构成了一定的拓扑结构, 不同的拓扑结构决定了信息的传递方式的差异, 对网络的训练过程和结果将产生非常关键的作用[8-10]。
针对具体的问题进行神经网络模型的设计、构建, 要求其中的关键参数能够完成功能和模型复杂程度之间进行折中, 实现模型的经济有效性。
神经网络模型的参数设计主要包括神经网络的层数、神经元数目、网络拓扑结构等参数选择。
而神经网络层数与神经元数目的设计, 主要包括三个关键参数的确定:输入输出神经元数目、隐藏层数和隐藏层神经元数目。
输入输出神经元与输入变量由输出结果的数目来决定, 隐藏层的数目决定了整个网络层数。理论上只有一个隐藏层的神经网络如包含足够多的隐藏神经元, 就能够实现逼近任意连续函数的目标[11-12]。在实际研究中, 包含1-2个隐藏层的神经网络应用较广, 原因是隐藏层数的增加除了引起网络计算时间的增加, 同时也容易产生过拟合问题, 影响网络模型的预测效果。
神经网络拓扑结构是预测模型设计的关键参数, 前向神经网络结构简单, 易于实现, 反馈网络能够实现信号的前向传播和误差的反向传播, 是应用较为广泛的一种拓扑结构, 而且随着计算机计算能力的飞速发展, 充分克服了反馈网络的训练速度缺陷。故本文选择前向反馈神经网络, 学习算法采用神经网络模型进行汇率预测。
运用神经网络技术进行汇率预测, 神经网络可以采用汇率序列的历史数据作为训练样本进行预测研究。
2.2 神经网络模型预测效果评价由于神经网络无法采用常规的计量经济技术中常用的统计学检验指标, 目前的研究大多采用误差等相关指标来判断网络的预测性能[13]。
本文采用均方误差MSE (Mean Square Error)作为神经网络模型预测效果评价指标[14-16]。MSE值能够体现预测数据与实际数据之间差异, 具体表达式如式(1)。
令N预测期数, yt表示变量在t时刻的实际数据,
| $ MSE{\rm{ = }}\frac{1}{N}\sum\limits_{t = 1}^N {({y_t} - {{\hat y}_t})} 2 $ | (1) |
变化方向反映的是模型预测值和实际值的变化趋势的一致程度, 其表达式为:
| $ Gradient = \frac{1}{N}\sum\limits_{t = 1}^N {{b_t}} $ | (2) |
当(yt+1-yt)×(
本文选用来自中国人民银行每日公布的人民币兑美元和人民币兑欧元汇率价格序列观察价格水平变化。美元样本区间选择为2014年1月1日起至2016年7月1日止, 样本数为610。欧元样本区间选择为2014年1月1日起至2016年7月1日止, 样本数为610个。
从图 2中可以看出, 人民币兑美元汇率从2014年年初开始小幅贬值后一直维持稳定状态, 直到2015年8月中旬以来, 开始较大程度贬值, 时间序列曲线从平滑到维持波动上升趋势, 且波动比较剧烈。
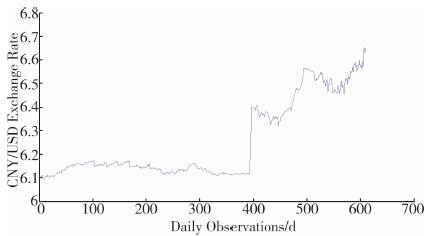 |
| 图 2 人民币兑美元汇率价格水平序列图 |
从图 3中可以看出, 人民币兑欧元汇率从2014年年初开始小幅贬值后, 开始进入升值通道, 随后于2015年3月中旬开始, 小幅贬值, 时间序列曲线维持波动上升趋势。
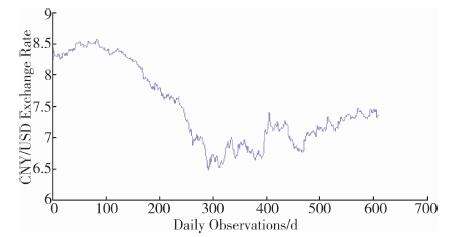 |
| 图 3 人民币兑欧元汇率价格水平序列图 |
从上述图中可以看出, 人民币汇率的时间序列具有的明显的非线性特征。
考虑到人民币汇率系统的上述非线性特性, 本文对人民币兑美元汇率水平价格进行实证研究。
3.2 数据前处理对人民币兑美元汇率时序数据进行初步频谱分析, 结果如下图 4所示。从图 4的汇率价格水平的频谱分布情况来看以中低频成分为主, 幅值较大的成分集中在250 Hz之前, 这说明人民币兑美元汇率价格水平主要是由中低频信号构成, 但是从时序信号来看, 非线性特征又非常明显, 存在一定的噪声干扰。
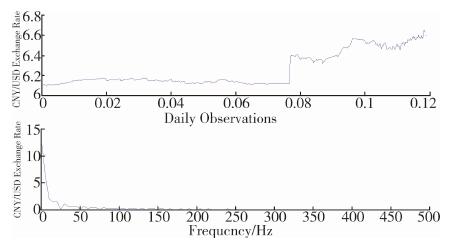 |
| 图 4 人民币兑美元汇率价格水平频谱图 |
利用EEMD方法对汇率数据进行时频特征分析, 并进行信号去噪滤波处理, 将对后续的神经网络模型建立提供较好的数据基础。
对人民币兑美元汇率价格水平序列进行EEMD分解, 参数设置为:加入白噪声信号的均方根值(Nstd)为序列信号的0.1倍, 平均次数设为400, 序列信号的EEMD分解结果见图 5。
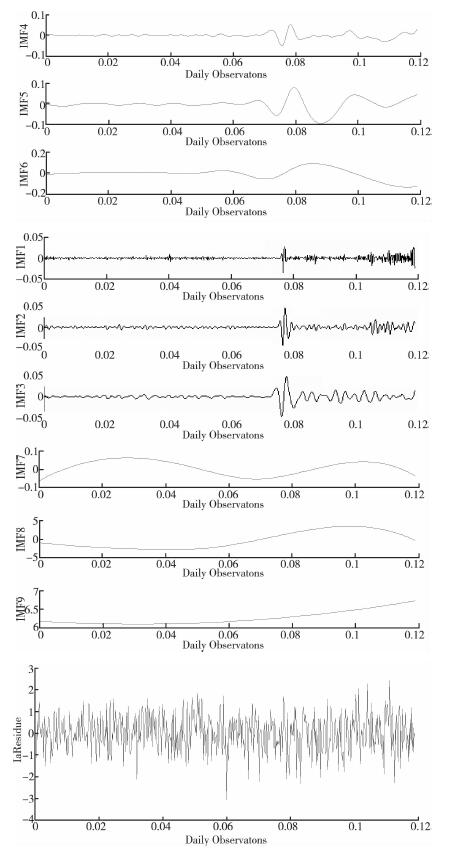 |
| 图 5 人民币兑美元汇率价格水平EEMD分解结果(Nstd=0.1) |
从图 5中可知, 人民币兑美元汇率价格水平序列经EEMD分解后得到9个IMF分量, 经初步分析可知:9个IMF分量由不同频率特征信号组成, IMF1-IMF3是波动明显的高频信号, IMF4-IMF6为中频信号, IMF7-IMF9为明显的低频信号, 且IMF9信号的幅值较大, 结合之前的频谱分析结果, 大致可以了解信号主要成分。
分解得到的IMF分量众多, 各分量特性也不相同, 需要筛选最能代表原信号的IMF分量, 现采用相关系数法进行信号筛选。
各IMF与人民币兑美元汇率价格水平的相关系数结果见表 1, 其中IMF8、IMF9的相关系数最大, IMF5-IMF7的相关系数大于0.1, 其他的IMF与源信号的相关系数范围为0.01~0.05, 均远小于0.1。
| 表 1 各IMF与人民币兑美元汇率价格水平的相关系数 |
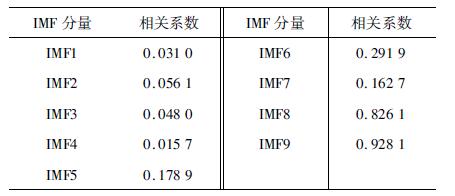 |
综合分析可知, 人民币兑美元汇率价格水平序列中包含有2个与源信号密切相关的分量IMF8、IMF9。现将IMF5-IMF9进行合成, 滤掉不相关的微小分量和噪声, 实现了原始数据的降噪, 构成后续模型建立的基础信号, 重构后的数据如图 6所示。干扰噪声基本得到去除, 去噪后的数据与源数据相比较平滑。
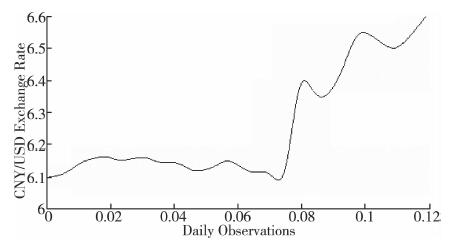 |
| 图 6 人民币兑美元汇率价格水平重构数据 |
3.3 构造训练样本
取人民币兑美元汇率价格水平序列的610个数据的前609个数据, 经前处理后作为网络输入层的输入数据, 记为p。将后2~610共609个数据作为网络输出数据, 记为t。从而构造出神经网络的训练样本。
3.4 建立基于神经网络的预测模型大量实践表明:三层的神经网络由于具有操作性强、计算量小等优点, 是多层式网络训练的主要选用网络结构, 在本论文中将采用三层网络建立模型进行汇率预测。
对于一维时间序列预测问题, 输入层节点数等于所开窗口大小, 本文中输入层节点数即为609, 只需要一个输出层节点。
在三层网络中, 隐藏神经网络个数n2和输入层神经元个数n1之间有近似关系:n2=2*n1+1, 按照本文所列数据, n2的个数很大。为了得到合适的隐藏层节点个数, 试凑法是确定最佳隐藏层节点数的常用方法:用同一样本集进行训练, 先试用较少的隐层节点数进行训练, 后逐渐增加隐藏层节点数, 从训练结果中选出网络误差最小的一组确定为隐藏层节点数。
在采用试凑法时, 也可结合经验公式来确定隐藏层节点数。通过计算粗略估计隐层节点数, 为隐层神经元数目初始值提供大致参考。
在本文的实证研究中采用经验公式
本文采用MATLAB软件进行实证计算, 版本号为R2016a。对人民币兑美元汇率价格水平序列的训练样本进行训练, 得到神经网络模型的训练结果见表 2。
| 表 2 网络训练结果 |
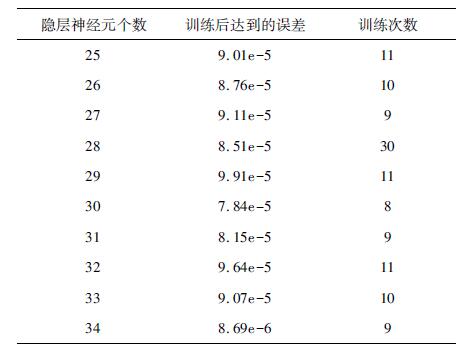 |
从网络误差数据可知:训练误差最小时, 隐层神经元个数为30, f即为30。
3.5 预测过程的具体实现建立一个前向神经网络, 根据前述结果设置网络隐层单元的神经元数为30、输出层节点数1及训练样本p。
新建的BP网络以及网络参数设置如下[17]:net=newff(minmax(p), [n, 1], {'tansig''purelin'}, 'trainlm)
n=30;
当前输入层权值和阈值:
inputWeights=net.IW{1, 1}
inputbias=net.b{1};
当前网络层权值和阈值:
layerWeights=net.LW{2, 1}
layerbias=net.b{2};
设置训练参数, net.trainParam.show=50, 每50步显示一次误差;net.trainParam.lr=0.05, 学习速率为0.05;net.trainParam.mc=0.9, Sigmoid参数0.9;net.trainParam.epochs=10 000, 设置最大训练次数;net.trainParam.goal=le-3, 设定训练期望误差, 取值为0.001;
训练网络[net, tr]=train(net, p, t);
测试网络pTEST=A=sim(net, pTEST);
计算仿真误差E=t-A, MSE=mse(E)。
得到误差趋势如图 7所示。在较少的前20次训练中, 模型在第14次训练时建立的神经网络模型的均方误差MSE达到最小值, 且不再下降, 根据前述预测效果评价指标, 此时网络模型性能最好。
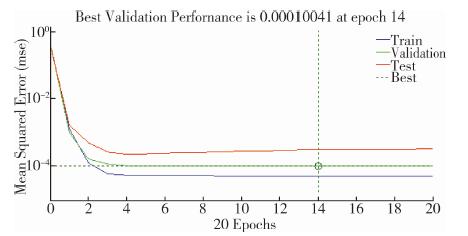 |
| 图 7 人民币兑美元汇率价格水平神经网络预测误差趋势 |
人民币兑美元汇率价格水平神经网络预测模型误差分布如图 8所示, 模型的随机误差基本符合正态分布。
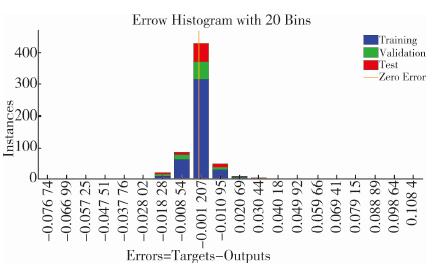 |
| 图 8 人民币兑美元汇率价格水平神经网络预测模型误差分布 |
人民币兑美元汇率价格水平神经网络预测模型训练结果如图 9所示。
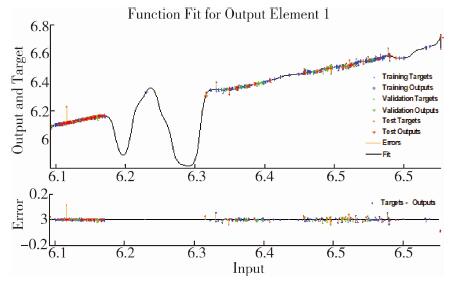 |
| 图 9 人民币兑美元汇率价格水平神经网络预测模型训练结果 |
模型在部分区域与源数据完全贴合, 在整个训练数据范围之内基本完全能够准确反应源数据特点。
通过神经网络模型得到的一步预测值A为6.641 1, 而相对应的2016年7月1日的人民币兑美元汇率中间价为6.649 6, 与预测值相差0.008 5, 误差率仅为0.12%。后续通过调整输入层的网络的阈值和权值, 可达到预测值与实际值的误差进一步缩小的效果。
通过以上的分析计算, 本文建立了基于神经网络的人民币汇率兑美元汇率价格预测模型, 并且取得了较好的预测效果。
4 结论基于汇率行为的复杂非线性特点, 本文根据汇率模型的特点结合了时频信号分析和神经网络模型智能算法的优势, 进行了人民币汇率预测模型实证研究。
本文采用非线性时频分析算法EEMD方法对汇率数据进行了时频特征分析, 并筛选和重构了有效数据, 利用BP神经网络对重构后的数据进行了人民币汇率兑美元汇率价格预测, 模型准确反映了波动变化的趋势, 验证了基于信号分析和智能算法结合方法的有效性。
随着国家“一带一路”战略规划的推进, 以及中美贸易关系越来越复杂, 人民币汇率变化复杂, 本文采用信号分析和神经网络方法相结合, 建立人民币汇率的预测模型这项研究, 为外汇管理规避市场风险, 应对利率、汇率波动带来的影响具有重要的现实意义。
| [1] |
温正. 精通MATLAB智能算法[M]. 北京: 北京出版社, 2015: 14-16.
|
| [2] |
丁晖.基于神经网络模型的人民币汇率预测研究[D].长沙: 湖南大学, 2008: 26-28.
|
| [3] |
熊志斌. ARIMA融合神经网络的人民币汇率预测模型研究[J]. 数量经济技术经济研究, 2011(6): 64-76. |
| [4] |
方兆本, 李勇. 基于HHT-SVR模型的汇率数据去噪与预测[J]. 数理统计与管理, 2015(5): 900-905. |
| [5] |
刘金琨. 智能控制[M]. 北京: 电子工业出版社, 2015: 120-123.
|
| [6] |
张锟, 李红伟, 唐学建, 等. 基于柔性神经网络和转矩分配函数的SRM控制[J]. 微电机, 2015(7): 55-60. |
| [7] |
赵崇文. 人工神经网络综述[J]. 山西电子技术, 2020(3): 94-96. |
| [8] |
徐缘圆. BP神经网络在汇率预测中的应用[J]. 时代金融, 2013(1): 147-148. |
| [9] |
鱼丹. 基于遗传算法的BP神经网络在汇率预测中的应用[J]. 科学技术创新, 2019(3): 100-101. |
| [10] |
谷月霞. 改进的高阶神经网络在汇率市场预测中的应用[J]. 微型机与应用, 2009(20): 71-73. |
| [11] |
谢赤, 欧阳亮. 金融危机背景下的人民币汇率预测[J]. 系统工程理论与实践, 2009(12): 53-64. |
| [12] |
孙柏, 谢赤. 汇率预测的神经网络方法及其比较[J]. 财经科学, 2018(5): 47-53. |
| [13] |
王晓辉, 张卫国, 刘玉芳. 融合ICA的BP网络在人民币汇率预测中的应用[J]. 统工程学报, 2014(3): 344-352. |
| [14] |
廖薇, 冯小兵, 许春冬, 等. 径向基神经网络的汇率预测模型研究[J]. 计算机工程与应用, 2019(24): 210-212. |
| [15] |
周振. 基于径向基神经网络的人民币汇率预测[J]. 电脑开发与应用, 2009(3): 64-66. |
| [16] |
肖强, 钱晓东. 基于RBF神经网络美元兑人民币汇率的预测[J]. 信息技术, 2009(12): 24-26. |
| [17] |
史峰. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011: 28-33.
|
 2020, Vol. 34
2020, Vol. 34

