| 基于连续微分方程对高压油管压力控制的研究 |
在泵-管-嘴燃油系统的实际工作过程中, 燃油首先由高压油泵的柱塞腔进入, 由凸轮驱动柱塞上下运动。柱塞向上运动时, 柱塞腔与高压油管连接的单向阀开启, 燃油由柱塞腔进入高压油管内部; 柱塞向下运动直至下止点时, 低压燃油将充满整个柱塞腔。燃油进入后通过高压油管运动到喷油嘴附近, 由喷油嘴针阀控制燃油的喷出。当针阀升程为0时, 针阀关闭; 针阀升程大于0时, 针阀开启, 燃油向喷孔流动, 通过喷孔喷出, 完成整个喷油周期。燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化, 运用科学方法对压力进行控制能够在一定程度上缩小所喷出燃油量的偏差, 提高发动机的工作效率从而带来更高的经济效益; 同时对高压油管的压力控制能够有效控制喷油量和喷油率, 提高能源利用率, 降低能源消耗。因此, 对发动机高压油管的压力控制问题进行深入研究, 具有一定的应用前景和指导意义。
关于高压油管的压力控制问题, 国内外学者进行了大量的研究。程涛等[1]采用IFR600喷油规律测量仪, 研究了喷孔直径、高压油管尺寸和喷油器针阀开启压力对喷油规律和喷油量的影响; 吴庆林[2]对常见的柴油机燃油系统——高压共轨系统进行MATLAB Simulink仿真, 并在原模型中增加喷油量和轨压补偿模块, 结合遗传算法进一步优化, 得到了良好的控制效果。
1 数据来源与模型假设数据来源于2019年高教社杯数学建模比赛A题, 包括凸轮边缘曲线、针阀运动曲线以及弹性模量与压力关系的相关数据。为便于解决问题, 提出以下几点假设:1)假设不考虑高压油管在高压油泵、喷油嘴两端接口处的流动损失; 2)假设燃油压力的变化是一个瞬间过程; 3)假设在一个喷油周期内燃油的流入和流出都为均匀变化。
2 基于微分方程模型对凸轮角速度的确定 2.1 研究思路由于燃油的物理性质对喷油过程数学模型的精度影响较大, 本文拟采用微分方程进一步得到燃油压力与燃油密度之间的关系, 由于高压油管内的压力难以通过计算得出, 拟通过燃油体积的变化来客观反应压力的变化。对针阀运动曲线数据进行高斯拟合分析, 并结合喷油嘴的工作原理以及高压油泵工作原理如图 1所示, 计算出喷油速率; 建立单位时间内由高压油泵进入高压油管的燃油量与喷油嘴喷出的燃油量相等的微分方程式, 确定高压油管内的压力尽可能稳定在100 MPa左右时凸轮的角速度。
 |
| 图 1 高压油管工作过程示意图 |
2.2 研究方法
等价体积V′:一定量燃油压力为p0时体积为V0, 则在压力为p′时体积为V′;
等价流量Q′:燃油在压力为p0时单位时间喷出量为Q0, 在压力为p′时喷出量为Q′。由于m0=m, 根据以上定义可得:
| $ {\rho _0}{V_0} = \rho 'V' $ | (1) |
| $ {\rho _0}{Q_0} = \rho 'Q' $ | (2) |
喷油流量(速率)Q:单位时间内流过横截面的燃油量, 与截面的面积成正比, 关系式为:
| $ \frac{{{S_{圆环}}}}{{{S_{喷孔}}}} = \frac{{Q\left( t \right)}}{{{Q_{100喷\max }}}} $ | (3) |
式中Q(t)为喷油嘴的喷油速率, 是关于时间t的函数, S喷孔为喷孔的面积, 表达式为:
| $ {S_{喷孔}} = \pi \cdot{ r_{喷孔}}^2 $ | (4) |
环宽Δd:针阀下底面圆周与同一水平面锥形喷嘴截面圆周的距离。针阀上升距离Δh:针阀与初始位置的高度差。由于针阀的运动路径与锥形喷嘴的内边形成直角三角形, 喷油嘴结构见图 2, 则根据正弦定理可以得出Δd与Δh之间的关系式为:
| $ \frac{{\Delta d}}{{\sin \theta }} = \frac{{\Delta h}}{{\sin \left( {{{90}^\circ } - \theta } \right)}} $ | (5) |
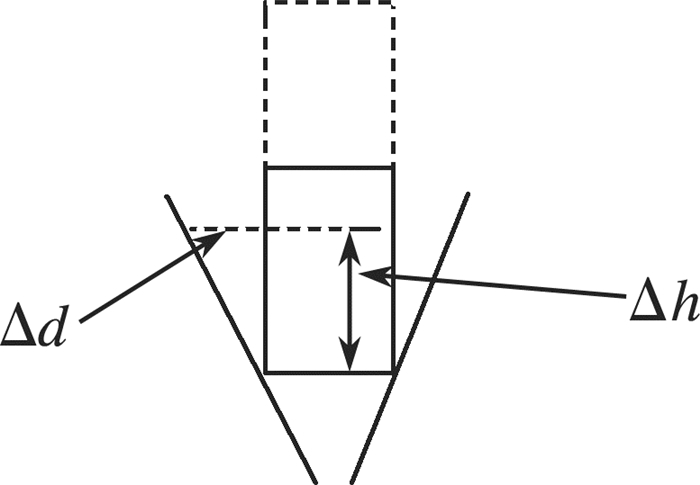 |
| 图 2 喷油嘴结构 |
根据燃油压力、密度、弹性模量三者关系, 推导出燃油的压力p与燃油密度ρ之间的关系式为:
| $ \frac{{d\rho }}{\rho } = \frac{{dp}}{{f\left( p \right)}} $ | (6) |
联立公式(1)(2)(6)可以得到在压力为p′时燃油的体积V′以及在压力为p′时的喷出量Q′。在问题的求解中, 将不同压力下的燃油体积转化为相同压力下的等价体积计算时会更加方便。
2.2.1 确定喷油速率锥形喷嘴的俯视图是一个圆环,如图 3所示, 它的面积表达式为:
| $ {S_{圆环}} = \pi \cdot {\left( {{r_{针阀}} + \Delta d} \right)^2} - \pi \cdot {r_{针阀}}^2 $ | (7) |
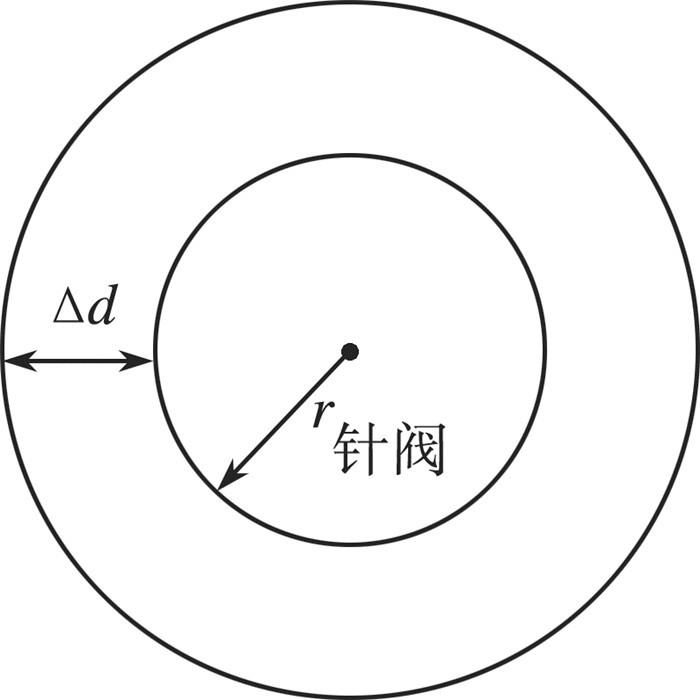 |
| 图 3 锥形喷嘴俯视图 |
联立上式可得出喷油速率Q(t)。喷油速率与喷油时间在喷油嘴的一个工作周期上的积分为α, 它表示喷油嘴在一个工作周期里喷出的100 MPa下的燃油量(mm3), 即Q喷100′。表达式为:
| $ \alpha = \int_0^{{T_1}} Q \left( t \right)dt = {Q_{喷100}}^\prime $ | (8) |
当柱塞腔内充满0.5 MPa低压燃油时燃油的体积为V0.5, 它与极径之间的关系式如下:
| $ {V_{0.5}} = \pi \cdot r_{柱塞腔}^2 \cdot \left( {{r_{极径\max }} - {r_{极径\min }}} \right) + {V_{残余}} $ | (9) |
式中r柱塞腔为柱塞腔内半径(mm), r极径max为极径的最大值(mm), r极径min为极径的最小值(mm)、V残余为残余容积。
V0.5体积的0.5 MPa燃油在100 MPa压力下的等价体积为V″100, 之间的关系为:
| $ {\rho _{0.5}}{V_{0.5}} = {\rho _{100}}{{V''}_{100}} $ | (10) |
其中若V″100≤20mm3, 说明凸轮转动一周不能使柱塞腔内燃油的压力大于高压油管内的压力; 若V″100≥20mm3, 说明凸轮转动一周内可使供油出口A打开。
当V″100≥20mm3时, 凸轮转动一周排出的油量为V″100喷, 其表达式为:
| $ {{V''}_{100喷}} = {{V''}_{100}} - {V_{残余}} $ | (11) |
要使得高压油管内的压力尽量稳定在100 MPa左右, 单位时间内由高压油泵进入高压油管的燃油量与单位时间内喷油嘴喷出的燃油量相等。用等式表达为:
| $ \frac{{{{V''}_{100喷}}}}{{{T_{凸轮}}}} = \frac{{{{Q'}_{喷100}}}}{{{T_1}}} $ | (12) |
式中T凸轮为凸轮转动一周所需要的时间, 它与凸轮的角速度ω(r/ms)的关系为:
| $ \omega \cdot {T_{凸轮}} = 2\pi $ | (13) |
联立式(9)~(13)可得出凸轮的角速度ω。
2.3 结果分析 2.3.1 燃油密度与压力数据拟合利用MATLAB对弹性模量与压力相关数据进行拟合, 得到的方程为E=8.862p+1 379, 拟合优度R2=0.971 4, 拟合精度较高。由方程可知两者存在很强的线性关系, 因此可以将弹性模量E看做压力p的一次函数进行计算。
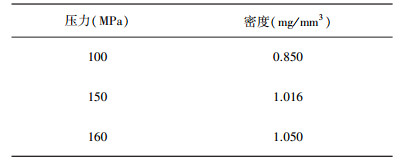
求解微分方程, 得kρ=8.862p+1 379(k为非0正数)。已知当压力为100 MPa时, 燃油的密度为0.850 mg/mm3, 代入方程求解得出参数k=2 664.941, 据此求得100 MPa、150 MPa、160 MPa下燃油的密度见表 1。
| 表 1 燃油密度表 |
 |
2.3.2 高斯函数拟合
利用MATLAB软件对针阀运动曲线中t∈[0, 0.45]的数据进行拟合, 发现针阀的运动距离Δh与时间之间存在着极强的高斯函数关系[3], 如图 4。
 |
| 图 4 针阀运动距离与时间关系拟合图 |
由拟合结果知模型拟合精度达到0.999 9, 拟合效果较好, 因此可以认为针阀上升距离与时间的关系式为:
| $ \Delta h = 2.016 \cdot {e^{ - {{\left( {\frac{{t - 0.455\;1}}{{0.166\;1}}} \right)}^2}}} $ | (14) |
| $ \begin{array}{l} \Delta d = \frac{{\sin {9^\circ }}}{{\sin {{81}^\circ }}} \cdot \Delta h = \frac{{\sin {9^\circ }}}{{\sin {{81}^\circ }}} \cdot 2.016 \cdot \\ {e^{ - {{\left( {\frac{{t - 0.455\;1}}{{0.166\;1}}} \right)}^2}}} \end{array} $ | (15) |
当S圆环=S喷孔=π·0.72时, 针阀上升的高度为1.15 mm, 查阅针阀运动曲线数据, 对应的时间为0.33 s, 可知当针阀打开0.33 s时, 喷油嘴喷油量已经达到最大值20 mm3/ms。
圆环的面积公式与喷油速率Q(t)的表达式分别为:
| $ {S_{圆环}} = \pi \cdot {\left( {1.25 + \frac{{\sin {9^\circ }}}{{\sin {{81}^\circ }}} \cdot 2.016 \cdot {e^{ - {{\left( {\frac{{t - 0.4551}}{{0.1661}}} \right)}^2}}}} \right)^2} - \pi \cdot {1.25^2} $ | (16) |
| $ \begin{array}{l} Q\left( t \right) = \frac{{20 \cdot \left( {1.25 + \frac{{\sin {9^\circ }}}{{\sin {{81}^\circ }}} \cdot 2.016 \cdot {e^{ - {{\left( {\frac{{t - 0.455\;1}}{{0.166\;1}}} \right)}^2}}}} \right) + 20 \cdot {{1.25}^2}}}{{{{0.7}^2}}},\\ t \in \left[ {0,0.33} \right] \end{array} $ | (17) |
利用MATLAB软件对Q(t)求积分, 得到α1=1.13, t∈[0, 0.33];当t∈[0.33, 2.12]时, 喷油量保持最大值, α2=35.8;当t∈[2.12, 2.46]时, α3=α1=1.13;当t∈[2.46, 100]时, α4=0。则一个周期内喷油嘴喷出的100 MPa下的燃油量Q喷100′=α1+α2+α3+α4=38.66 mg。
2.3.4 计算凸轮角速度已知r柱塞腔=2.5 mm, r极径max=7.239 mm, r极径min=2.413 mm, V残余=20 mm3, ρ0.5=0.519 1 mg/mm3, 根据以上数据可求得V0.5=114.76 mm3, V″100=70.08 mm3>20 mm3, 说明凸轮转动一周内可使供油出口A打开[4]。凸轮转动一周排出的油量V″100喷=V″100-V残余=50.08 mm3, 凸轮转动一周所需的时间
当凸轮的角速度为0.048 5 r/ms时, 可以使得高压油管内的压力稳定在100 MPa左右。
3 基于分段函数拟合的控制方案模型 3.1 研究思路为了更有效的控制高压油管的压力, 可以对高压油管进行增加一个喷油嘴和单向减压阀的改进[5], 如图 5, 并相应对供油和喷油策略进行调整。在研究过程中, 本文模拟出一个300 ms的周期, 通过构建这个周期内高压油泵和喷油嘴共同工作引起的高压油管内燃油体积的变化的分段函数进行宏观分析, 得出如何将高压油泵和减压阀相互配合使高压油管内压力趋于稳定。
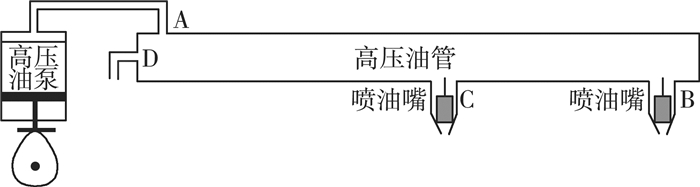 |
| 图 5 具有减压阀和两个喷油嘴时高压油管示意图 |
3.2 研究方法
由于新增一个喷油嘴, 将引起高压油管的喷油量变为原来的2倍, 即Q2=2Q1, 从而应相应地调整高压油泵的供油速率, 即增加凸轮的角速度[6]。根据公式
根据高压油泵与喷油嘴工作周期不同及各自工作的时间不同, 本文模拟出一个300 ms的阶段进行分析。假设随着此阶段开始, 燃油就开始均匀进入高压油管内, 每隔T2进入一次, 在有效工作时间内随着时间的增加, 高压油管内增加的体积呈线性增长(斜率即速率); 两个喷油嘴在每个100 ms的最后2.45 ms同时进行喷油, 即在97.55 ms时开始第一次喷油, 每隔100 ms喷一次, 假设在喷油嘴有效工作的时间内, 高压油管内的燃油迅速均匀减少。当燃油进入高压油管和喷油嘴喷出燃油同时进行时, 由于喷出的速率大于进入的速率, 高压油管内的燃油体积以喷出和进入的速率差值均匀减少; 当处于既无燃油进入, 也无燃油喷出的时间段, 高压油管内的体积保持不变。设斜率k1=57.87/21.31, 斜率k2=77.32/2.45, 斜率k3=k2-k1则在300 ms内高压油管里的体积变化可以用分段函数表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{y_1} = {k_1}x,(0 \le x < 21.31)}\\ {{y_2} = 21.31{k_1},(21.31 \le x < 74.84)}\\ { \cdots \cdots \cdots }\\ {{y_{13}} = 76.84 - {k_2}(x - 297.55),(297.55 \le x < 299.38)}\\ {{y_{14}} = 19.188 - {k_3}(x - 299.38),(299.38 \le x < 300)} \end{array}} \right. $ | (18) |
运用Excel将此分段函数以图像形式表示出来, 通过对图像中高压油管内体积的变化趋势进行分析, 可得出高压油泵和减压阀的控制方案。
3.3 结果分析为了满足增加喷油嘴后的需求量, 所计算出调整后凸轮运动一个周期所需时间为
用EXCEL将高压油管内一个300 ms周期的体积变化分段函数表示, 如图 6实线所示。可以看出, 在整个过程中体积增加量都较大, 无法使高压油管在初始压力状态上下波动, 此时需要高压油泵和减压阀的协同控制影响[7]。若想使高压油管的压力维持在初始状态左右, 则应调节高压油管增加的体积在0上下波动。且高压油管内每一次体积变化量的高点都在喷油嘴喷出燃油之前, 为了降低峰值, 在此使用减压阀降低高压油管内体积的增加量。
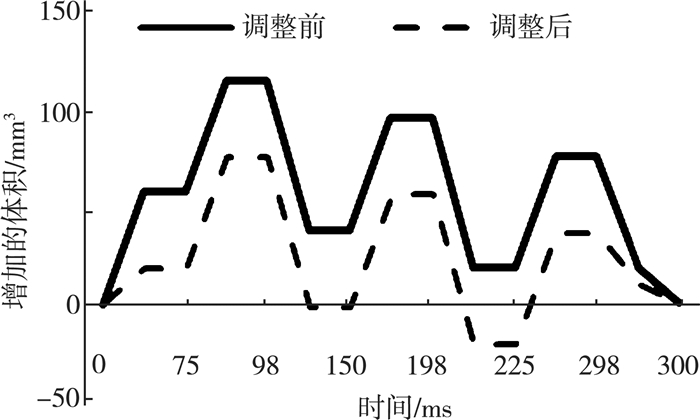 |
| 图 6 调整前后高压油管内体积变化量对比 |
根据题意以及进出高压油管流量的计算公式, 可以计算出单位时间流出减压阀的燃油量
由图 6可知, 调整后高压油管内体积增加量明显减少, 效果较好; 但由于模型假设使问题太过理想化, 该模型存在一定局限性, 故对模型进行了改进。
4 基于连续微分方程控制方案改进模型 4.1 研究思路由于分段函数模型具有一定的局限性, 故选用连续微分方程模型进行改进, 分别求解高压油泵、高压油管、针阀的工作连续方程[8], 得到新的喷油嘴和减压阀控制方案, 并与原方案进行对比评价。
4.2 研究方法 4.2.1 建立高压油泵工作连续方程1) 柱塞腔连续方程
| $ \begin{array}{l} \frac{{{V_{柱塞腔}}}}{E}\frac{{d{p_{柱塞腔}}}}{{dt}} = {S_{柱塞腔}}\frac{{d{H_{柱塞}}}}{{dt}} - \eta \cdot S\\ _A\frac{{{H_{出油阀}}}}{{dt}} - \sum {{Q_{柱塞腔}}} \end{array} $ | (19) |
式中, E为弹性模量, SA是出油阀A的面积, H柱塞是柱塞升程, η为出油阀流量修正系数, ∑Q柱塞腔为单位时间内柱塞腔燃油流出流量、回流量及漏油量总和[9]。
2) 出油阀连续方程
| $ \frac{{{V_{出油阀}}}}{E}\frac{{d{p_{出油阀}}}}{{dt}} = \eta \cdot {S_A}\frac{{{H_{出油阀}}}}{{dt}} - \sum {{Q_{出油阀}}} $ | (20) |
式中, H出油阀为出油阀升程, ∑Q出油阀为单位时间内流入、流出出油阀腔燃油量总和。
3) 油阀运动方程
| $ \begin{array}{l} {m_{出油阀}}\frac{{{d^2}{H_{出油阀}}}}{{d{t^2}}} = {S_A}\left( {{p_{柱塞腔}} - {p_{出油阀}}} \right) - \\ {k_{出油阀}}\left( {{H_{出油阀}} + {H_0}} \right) \end{array} $ | (21) |
式中, m出油阀为出油阀质量, k出油阀为出油阀弹簧刚度, H0为出油阀弹簧预压缩量。
4.2.2 建立高压油管工作连续方程供油管是连接高压油泵及高压油管的通道, 高压油管是高压油泵及喷油器的管路。燃油频繁的从高压油泵供油管流入高压油管, 然后经过喷油器排出, 高压管路的数学模型主要为连续方程:
| $ \begin{array}{l} \frac{{{V_{高压油管}}}}{E}\frac{{d{p_{高压油管}}}}{{dt}} = \sum {{Q_{流入}}{S_{供油管}}} - \\ \sum {{Q_{流出}}{S_{高压油管}}} \end{array} $ | (22) |
式中, Q流入为燃油流入速度, S供油管为供油管横截面积, Q流出为燃油流出速度, S高压油管为高压油管截面积[10]。
4.2.3 建立针阀工作连续方程1) 针阀腔连续方程
| $ \begin{array}{l} \frac{{{V_{针阀腔}}}}{E}\frac{{d{p_{针阀腔}}}}{{dt}} = {Q_{流入}} - \beta \left( {{f_{na}} - {f_{nb}}} \right) \cdot \\ \frac{{d{H_{出油阀}}}}{{dt}} - {Q_{流出}} - {Q_{泄露}} \end{array} $ | (23) |
式中, H出油阀为出油阀升程, β为阻尼修正系数, fna为针阀头部阻尼系数, fnb为针阀后补阻尼系数, Q流入、Q流出、Q泄露分别为单位时间内流入、流出针阀腔燃油量及泄露燃油量。
2) 针阀运动方程
| $ \begin{array}{l} {m_{针阀}}\frac{{{d^2}{H_{针阀}}}}{{d{t^2}}} = {C_{针阀}}\left( {{f_{na}} - {f_{nb}}} \right){p_{针阀腔}} - {k_{针阀}}\\ \cdot \left( {{H_{针阀}} + {H_{针阀0}}} \right) + {f_{压力室}}{p_{压力室}} \end{array} $ | (24) |
式中, m针阀为针阀质量, C针阀为喷嘴偶件流量系数, k针阀为针阀弹簧刚度, H针阀0为针阀弹簧预压缩量, f压力室为压力室阻尼系数。
3) 压力室连续方程
| $ \begin{array}{l} \frac{{{V_{压力室}}}}{E}\frac{{d{p_{压力室}}}}{{dt}} = {Q_{流入压力室}} - {Q_{流出压力室}} - \\ \lambda {C_{针阀}}{f_{压力室}}\frac{{d{H_{出油阀}}}}{{dt}} \end{array} $ | (25) |
式中, λ为针阀偶件流量修正系数, Q流入压力室为单位时间内流入压力室的燃油流量。
4.2.4 计算减压阀排油量| $ {Q_{减压阀}} = CA\sqrt {\frac{{2\left( {{p_{高压油管}} - {p_{低压油路}}} \right)}}{{{\rho _{高压油管}}}}} $ | (26) |
式中p低压油路为外部低压油路的压力, ρ高压油管为高压油管内燃油的密度。
4.3 结果分析喷油嘴数量变为两倍, 而每个喷嘴喷油规律相同, 若要使高压油管内压力稳定在100 MPa左右, 可以将凸轮的转速增加一倍, 即0.048 5 r/ms。运用MATLAB求解连续微分方程, 可以得出高压油管内的压力与时间的关系图如图 7。
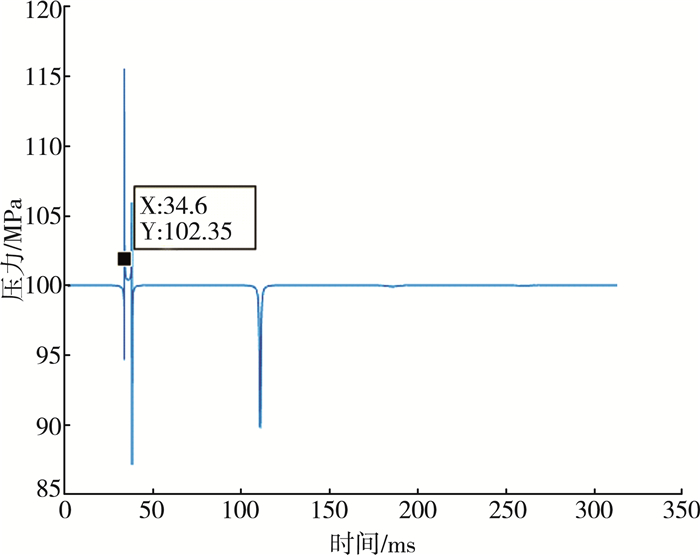 |
| 图 7 压力与时间关系图 |
图 7中压力开始降低的点即打开单向减压阀的时间点, 压力降到100 MPa时, 减压阀关闭。已知两点的横坐标分别为34.6、36.8, 说明在34.6 ms时打开减压阀, 开启时间为2.2 ms可使高压油管内的压力基本稳定在100 MPa。
5 结论本文旨在研究燃油发动机高压油管的压力控制问题, 利用已知参数, 灵活运用微分方程计算压力及等效指标; 运用MATLAB软件对凸轮边缘曲线和针阀运动曲线进行拟合, 并建立微分方程解出能使高压油管内的压力稳定在100 MPa左右时凸轮的角速度; 建立分段函数拟合和连续微分方程模型进一步研究喷油嘴和减压阀的有效控制方案[11], 对两个模型所得喷油策略和减压阀控制方案进行总结, 见表 2。
| 表 2 喷油策略和减压阀控制方案归纳 |
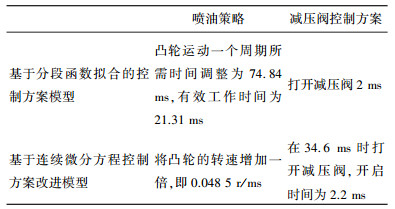 |
两个模型分别从宏观和微观角度对喷油策略和减压阀控制方案进行了研究, 对比两个模型的求解结果, 我们发现两个模型结果较为接近, 且改进模型的模型精度更高, 改进效果明显, 得到了良好的控制效果, 对提高发动机的经济性和环保性有着重要意义。
| [1] |
程涛, 李琦, 朱钰. 柴油机电控组合泵系统喷油特性分析[J]. 集美大学学报(自然科学版), 2015, 20(1): 53-59. DOI:10.3969/j.issn.1007-7405.2015.01.009 |
| [2] |
吴庆林.柴油机高压共轨系统喷油量的控制方法研究[D].重庆: 重庆理工大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-11660-1013154421.htm
|
| [3] |
姜启源, 谢金星, 叶俊. 数学模型(第四版)[M]. 北京: 高等教育出版社, 2011: 15-18.
|
| [4] |
杨逸风.双阀电控燃油系统动态喷射稳定性研究[D].哈尔滨: 哈尔滨工程大学, 2017.
|
| [5] |
蔡梨萍.基于MATLAB的柴油机高压喷油过程的模拟计算[D].武汉: 华中科技大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10487-2006038952.htm
|
| [6] |
王国正.TY3100柴油机燃油喷射系统建模仿真研究[D].武汉: 武汉理工大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10497-1011104629.htm
|
| [7] |
李子竞.基于需求转矩的高压共轨柴油机喷油量的控制策略[D].长春: 吉林大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10183-1016093874.htm
|
| [8] |
李峰.柴油机高压共轨喷射系统的仿真研究[D].大连: 大连理工大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10141-2008034751.htm
|
| [9] |
吕晓辰.高压共轨系统高压管路压力波动特性仿真研究及结构优化[D].北京: 北京交通大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10004-1016116396.htm
|
| [10] |
MIYAURAT., MORIKAWAA., ITOY., 等. 采用新型喷油系统的柴油机开发及应用[J]. 国外内燃机, 2014, 46(2): 31-35. DOI:10.3969/j.issn.2096-4870.2014.02.007 |
| [11] |
居钰生, 金兴才, 缪雪龙, 等. 我国燃油喷射系统行业现状、任务与对策[J]. 现代车用动力, 2007(03): 1-8. DOI:10.3969/j.issn.1671-5446.2007.03.001 |
 2019, Vol. 33
2019, Vol. 33


