2. 中国气象局国家气候中心,北京 100081
近50年来,我国西北地区气候出现由暖干向暖湿转变的特征或信号,新疆在整个西北地区最突出[1-5],同时,新疆极端降水事件呈现增多的趋势[6-8]。IPCC第五次评估报告(AR5) 第一工作组报告指出,在未来变暖的背景下,极端事件将进一步增多,中纬度大部分陆地区域强降水强度可能加大、发生频率可能增加[9-11]。观测事实及最新气候变化情景预估结果均显示,新疆面临的形势较复杂,既要充分利用气候干湿转型带来的机遇,又要谨防极端强降水引发的灾害。因此,有必要充分了解新疆降水极值概率分布特征,以此为相关部门制定政策措施提供科学依据。
1928年Fisher等[12]提出了极值极限分布的三大类型定理,奠定了经典极值理论的基础,在此基础上许多学者对极值理论进行了深入研究。Gumbel [13]在其著作中对这些理论进行了归纳总结,并将极值理论系统地应用到实践中,这进一步促进了极值理论的发展。极值理论早期主要应用于水文、地震、气象等方面,之后进一步拓展到工程、金融、保险等领域[14-15]。在气象领域,极值理论较多地应用到气候变化和极端气候研究方面,且在气候变暖的背景下极端天气气候事件频发,有必要继续加强极端气候事件统计规律的研究[16-18]。
在新疆降水极值研究中,较多地集中在极值的基本事实方面[6-8],而极值概率分布特征研究较少。张廷伟等[19]的结果表明广义极值分布函数能够较好地拟合降水极值的概率分布,但是缺乏对不确定性的深入讨论。江志红等[20]研究指出气候极值推断的不确定性中,最直接因素主要是推断极值的统计理论本身所造成的不确定性。目前国内外普遍采用Log-Pearson 3、Exponential、Log-normal、Gumbel、Wakeby等函数进行降水极值分析,但在各自的分析中往往只采用一种分布函数,导致结果无可比性、随机性或不确定性较大。苏布达等[21]则选用20种分布函数对长江流域极端强降水分布特征进行了统计拟合分析,探索了适应区域极端降水分布规律的一种最优概率分布模型。
新疆地区有特殊的“三山夹两盆”地理特征,降水时空分布极不均匀,同时降水的局地性和极端性非常强,南疆地区年降水量普遍在100 mm以下,日降水量有时超过年降水量,因此在极值函数选择以及重现期极值拟合中必然存在较多的不确定性。为此,本文将采用多种函数(或函数形式)对1961—2014年新疆降水极值进行拟合分析,揭示新疆极端降水时空分布的基本特征,初步探讨拟合的不确定性,为新疆降水重现期极值估算提供一种思路。
1 资料方法选取新疆自治区气候中心提供的1961—2014年新疆地区较完整的98站逐日降水量序列作为分析对象,提取出各站逐年最大日降水量,建立年最大值序列(AM,Annual Maximum)。采用25种极值分布函数及部分函数不同参数形式,共计64种函数① 形式(下文统一简称为函数),分别对各站降水量序列进行拟合分析,利用柯尔莫洛夫-斯米尔诺夫(KS)方法检验,根据检验统计值挑选出各站最优的极值分布函数,共涉及31种函数,在此基础上对新疆地区降水极值拟合分析中的不确定性进行初步讨论。
① 各函数介绍可以参照网址 http://www.mathwave.com/articles/distribution_fitting.html 。
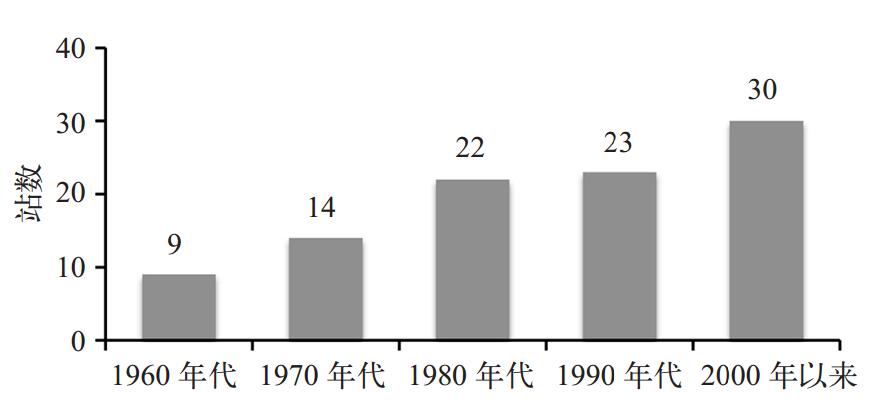
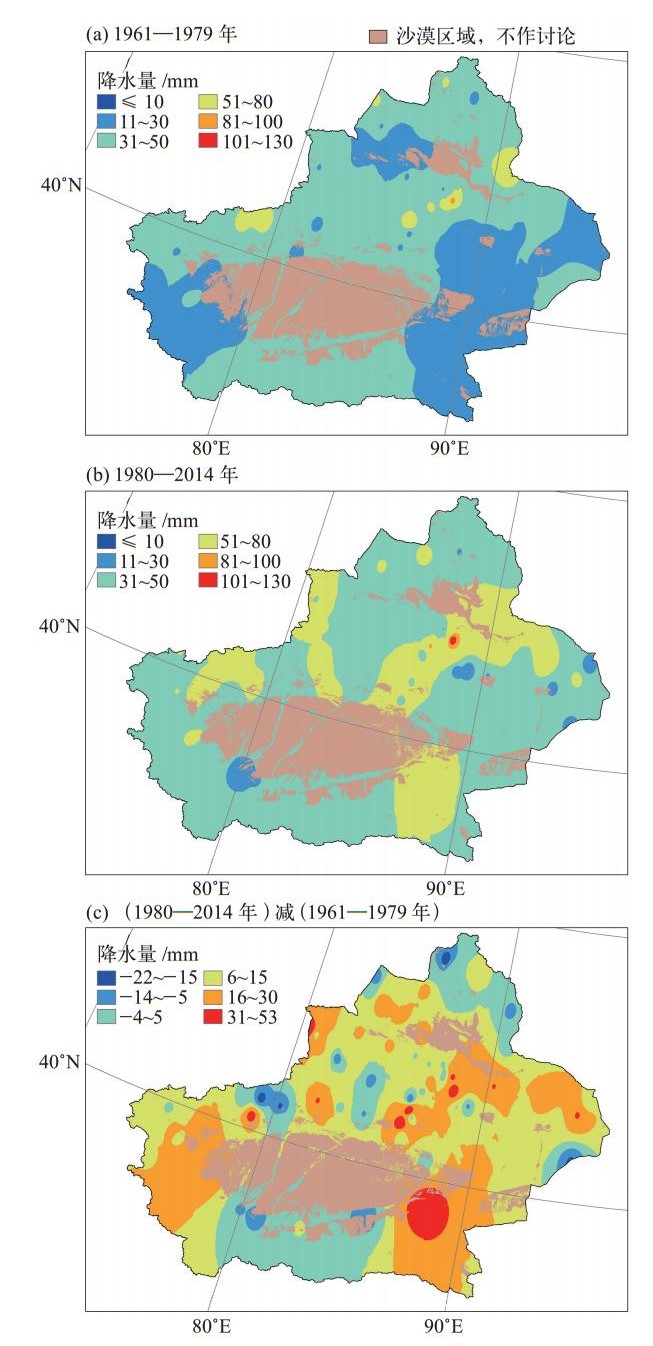
2 结果分析 2.1 降水极值基本特征统计1961—2014年各站日降水极值发现,降水极值主要出现在1980年代及其之后(约占77%),其中进入2000年以来,日降水极值站数达到30站,占总站数的31%左右(图 1)。从日降水极值空间分布上看,1961—1979年,极值突破50 mm的区域较少,较大值以31~50 mm为主,新疆东部、西南部以及西北部部分地区一般在30 mm以下(图 2a);1980—2014年,天山两侧以及新疆东南部地区在51~80 mm之间,局部超过80 mm,其他地区以31~50 mm为主(图 2b);对比可以发现,除南疆中部以及北疆等地区变化不大之外,其余大部分地区日降水极值在1980—2014年出现不同程度增加,新疆东部以及西南部增长幅度在16~30 mm之间,局部在30 mm以上(图 2c)。研究发现,新疆地区自1987年以来降水量持续偏多,21世纪初期比1960年代年降水量增加26%[7],近年来新疆气候由暖干向暖湿转变格局已成事实。在此背景下,更易出现极端强降水事件,由于强降水发生的不确定性显著,因此必然会影响到极值降水的统计拟合。
|
图 1 各年代出现降水极值的站数 Figure 1 Number of stations in different decades with precipitation extremes |
|
图 2 两个时间段日降水极大值空间分布图及其差值图 Figure 2 Distribution of daily precipitation extremes during 1961−1979 (a), 1980−2014 (b) and their difference (c) |
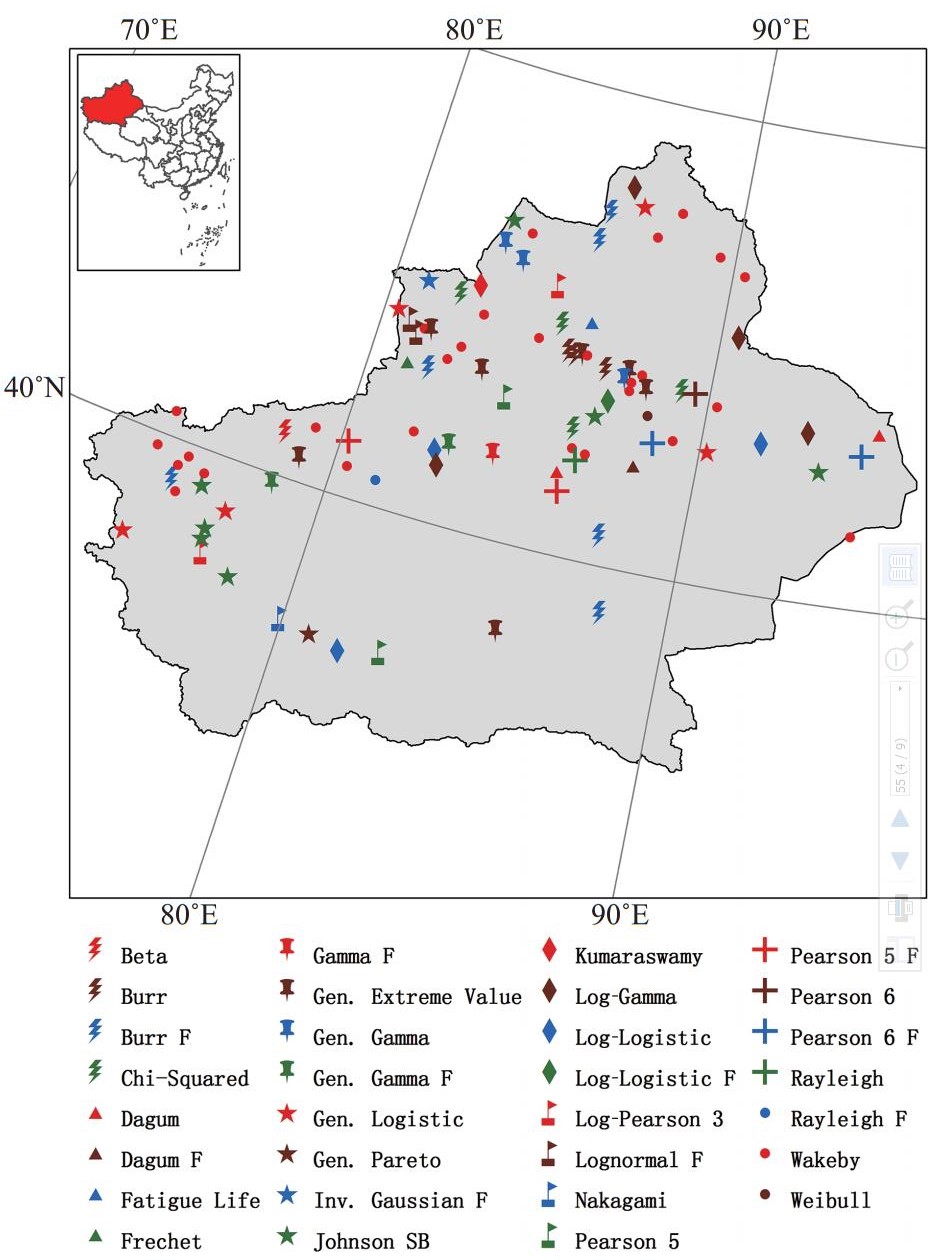
新疆98站降水极值概率分布不尽相同,因此在函数选择上必不可少地存在差异,导致在只选择某一种分布函数进行分析时产生不确定性。本文将考察64种函数对各站降水极值估算的表现,利用KS方法进行检验。根据KS检验统计量,挑选出各站排名第一的函数(即最优函数),结果如图 3所示,各站最优函数不尽相同,共计出现31种,以Wakeby占多数。从表 1可以看出,98站中,Wakeby排名第一的共有29站(其中1站为并列第一),这些站点主要分布在新疆北部和西部(图 3),而其他函数均不足10站。
|
注:函数中无F表示全参数,含F表示参数γ= 0。 图 3 各气象台站最优的降水极值分布函数 Figure 3 The best precipitation extremes distribution function for each station |
|
|
表 1 31种函数检验统计量统计分析 Table 1 Analysis of statistic test measurement for 31 functions |
统计各函数KS检验统计量通过99%信度检验的站数(临界值为0.218),以及有关排名情况,如表 1所示。可以看出大部分函数在90%以上的台站的AM拟合结果满足0.01的假设检验。为了进一步探讨这些函数的整体表现情况,对各函数在98站中的排名进行累加,累加值越低则表示该函数整体越优,从表 1结果可以看出,17个函数累加值在1500以上,12个在1000~1500之间,仅Wakeby和Gen. Extreme Value (GEV)两个函数在1000以下,分别为608和767。统计各函数排名前十的站次,结果表明超过49站的仅6个函数,分别为Burr F、Dagum F、Frechet、GEV、Pearson 5、Wakeby,即使是次多及最多的GEV、Wakeby函数,站次分别为71、78,也只占总站数的72%和80%,表明即使采用GEV或Wakeby函数进行新疆区域分析时,其较好的表现难以覆盖整个新疆。
2.3 极值估算的不确定性重现期极值估算的不确定性主要来源于样本数量及分布、极值分布函数选择等。样本数量偏少,则对于重现期较长的极值估算存在较大误差;样本数值分布离差较大,不利于函数拟合;不同函数在进行拟合分析时,检验统计量可能都通过了较高的信度检验(如表 1所示),而在采用这些函数进行极值估算时,结果也不尽相同,究竟采取何种分布函数结果则依实际状况和气候特点等因素而抉择。
以各站最优函数估算的10年、50年、100年一遇的降水极值为参考,统计31种函数在98个气象台站的估算结果与之差异的平均值,如表 2所示。可以看出,大多函数10年一遇的估算值相对于最优函数的差距较小,基本上在5%以下,其中Wakeby函数最小,为1.2%,GEV函数为2.1%。50年及100年一遇则显示出较大的差异性,最大误差分别可以达到27.6%和40.3% (Pearson 5 F函数);最小误差分别为3.2%和5.9%(Wakeby函数);GEV函数的误差分别为4.3%和6.8%。
|
|
表 2 31种函数估算结果相对于最优函数的平均误差 Table 2 Average error for estimation results of 31 functions relative to Bestfit |
同样以各站最优函数估算结果为基准值,以0.001为间隔(数值表达为1−1/T,T为重现期),采用31个函数估算各站在不同重现期下的极值,计算各函数相对于基准值的误差,对不同重现期下的误差进行平均,结果如图 4(a)所示,可以看出,20年及以下的重现期对应的平均误差在5%左右,之后逐渐增大,在100年重现期时增大至14%。综合可以看出,较短年限的重现期对应的误差相对较小,随着年限增大,数值样本渐少,函数间的误差逐渐增大,由此产生的不确定性也增大。图 4(b),4(c)给出了总体表现较好的Wakeby和GEV函数的误差变化情况,同样出现类似图 4(a)的变化特征,但是对于Wakeby函数,相对于最优函数的误差在不同的重现期大多在5%以下,而GEV函数则在60年及以下的重现期对应的误差在5%以下。

|
图 4 不同重现期下98站平均的相对于最优函数的误差散点图 Figure 4 Scatter diagram between different return period and average error of 98 stations relative to Bestfit |
本文分析时段是1961—2014年,即共有54年的AM序列,因此可以将31种函数及最优函数估算的各站54年一遇降水极值与实测的54年(1961—2014年)极大值进行比较,求算平均误差,以进一步考察极值估算中的不确定性。如表 3可以看出,并不是最优函数或Wakeby函数平均误差最小,而是前文分析中表现一般的Kumaraswamy函数,平均误差为9.9%。最优函数、Wakeby、GEV平均误差分别为13.0%、11.3%、11.4%,排名分别为并列第11、第4、第5,这在一定程度表明采用不同函数时存在的不确定性。
|
|
表 3 各函数估算的54年一遇降水极值相对于1961—2014年实测极值的平均误差 Table 3 Average error of precipitation extremes for 54-year return period estimated by different functions relative to observed extremes during 1961−2014 |
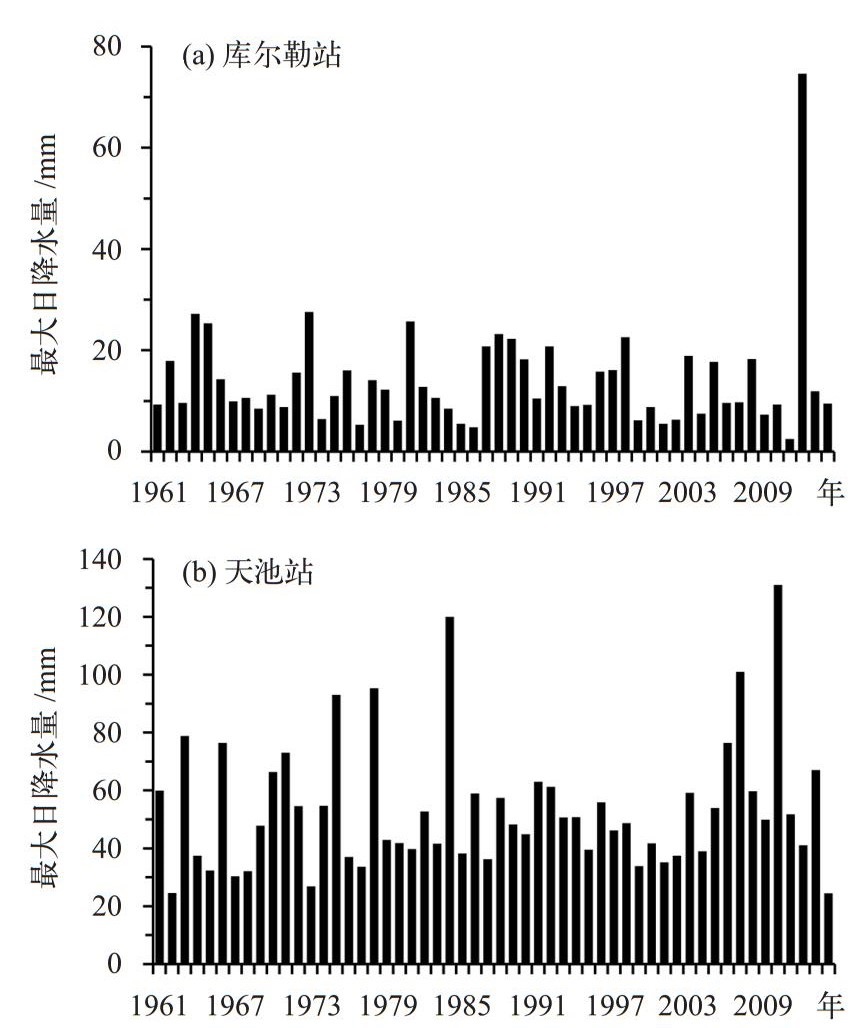
图 5给出了Wakeby函数估算的54年一遇降水极值相对于1961—2014年实测极值的误差分布图,可以看出大多地区误差相对偏小,个别偏大的地区主要是由个别站点引起,特别是南疆东部两个站点。苏布达等[21]指出,这种误差主要是由个别测站降水极值实测记录比该站其余记录高出很多,不足以改变频率曲线的外延趋势所造成。以Wakeby函数拟合误差最大的库尔勒站为例(该站函数排名中Wakeby排第8),其误差达到40.3%。图 6(a)给出了库尔勒站年最大日降水量序列,可以看出54年来,该站的降水极大值为74.6 mm,远大于其他记录。与此同时,其他函数在库尔勒站的拟合误差基本在30%以上,只有Kumaraswamy为18.7%。同时以天池站为例(该站函数排名中Wakeby排第10),该站54年来的降水极大值为131 mm,为98站之最,尽管如此,Wakeby拟合误差却只有5.7%。从图 6(b)可以看出,有多个记录与131 mm接近,故在多个样本支持下,Wakeby能较好地拟合降水极值。可以看出,样本序列数值大小的分布,在一定程度上对函数拟合造成影响,最终使得结果存在不确定性。

|
图 5 Wakeby函数估算的54年一遇降水极值相对于1961—2014年实测的误差分布图 Figure 5 Error distribution of precipitation extremes for 54-year return period estimated by Wakeby relative to observed extremes during 1961−2014 |
|
图 6 1961—2014年库尔勒站(a)和天池站(b)年最大日降水量序列 Figure 6 Maximum daily precipitation of Kuerle (a) and Tianchi (b) station during 1961−2014 |
由于各种不确定性的存在,难以选择一种函数对新疆降水极值进行拟合分析,即便是表现较好的Wakeby或者GEV函数,在部分台站拟合结果也存在一定的不确定性,若采用最优函数,则又显复杂。为了减少不确定性以及简易性,可以考虑采用表现较好的函数进行等权平均分析。结合表 1~3各函数表现情况,共选择5个函数,分别是Wakeby、GEV、Gen. Logistic、Log-Pearson 3和Pearson 6函数。
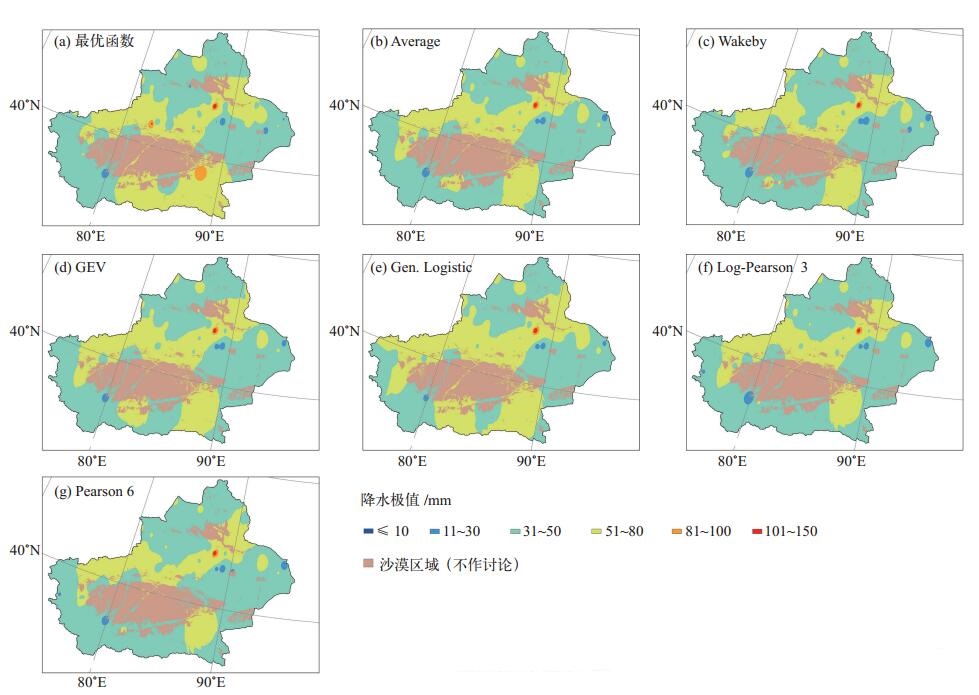
总体上各函数在10年、50年一遇降水极值分布上基本一致(图略),但是在100年一遇上在南疆略显差异,这也印证了2.3节有关结论。如图 7所示,最优函数拟合的100年一遇降水极值在南疆中部至东部一带达51~80 mm,而Log-Pearson 3、Pearson 6和Wakeby函数仅显示出现在南疆东部,GEV、Gen. Logistic函数在南疆中部和东部均有51~80 mm的分布。多函数等权平均结果显示除南疆东部外,中部有一小块51~80 mm区域。从图 3可以看出,南疆中部至东部仅有6个气象台站,其西北部为塔克拉玛干沙漠,因此在空间插值绘图上有一定的不确定性。以Wakeby为例,其检验统计量在这6站的排名累计值为56,排名为第6;排名第1的累计值为38,分别为Burr F及Log-logistic函数。尽管如此,Wakeby、Burr F及Log-logistic函数在南疆6站的100年一遇估算值相对于最优函数估算值的相对误差(取绝对值)平均值分别为9.5%、18.7%和22.1%,可见Burr F及Log-logistic函数在整体上还是比较欠缺。鉴于以上因素,等权平均结果基本能反映出南疆100年一遇的降水极值分布情况。
|
图 7 各函数拟合的新疆100年一遇的降水极值分布图 Figure 7 Precipitation extremes fitted by best functions with probability of 0.01 |
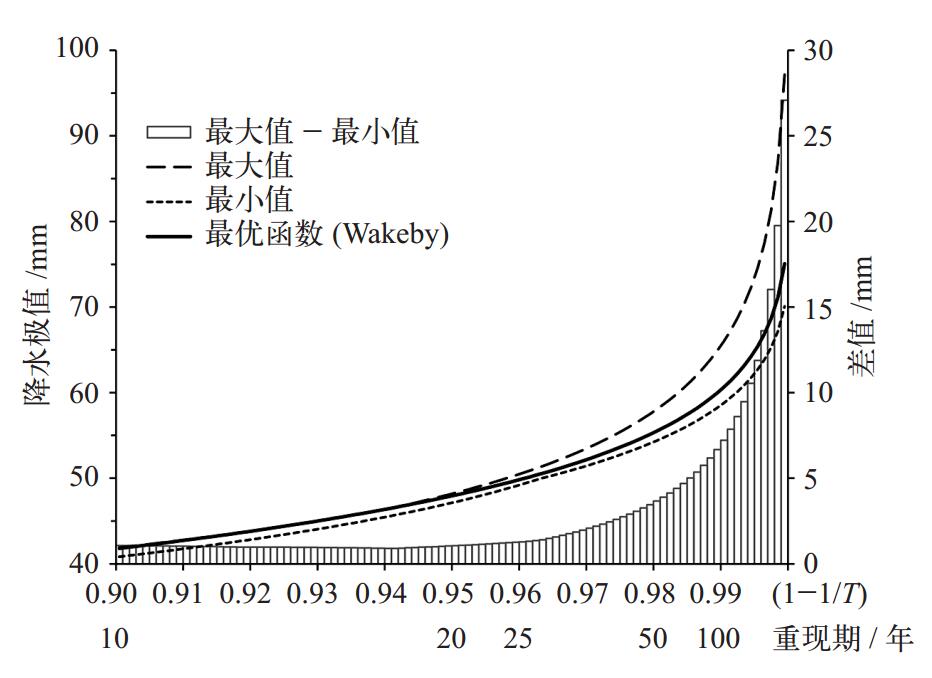
在进行单站分析时,鉴于多种不确定因素的存在,可以给出一张综合分布图,如图 8所示。以乌鲁木齐站为例,挑选出该站排名前10的函数,整理不同重现期内各函数估算的降水极值,分别得出各重现期下最大和最小的估算值,以及两者差值,最终连同最优函数估算值绘制在一张图上,形成具有界限范围的极值综合曲线图。从图 8可以看出,从25年一遇重现期开始,函数估算值间的差异逐渐扩大,至100年一遇时差异达7 mm,基本在可接受范围之内,即日降水量在59~66 mm之间时,其出现的概率均可认为达到100年一遇。
|
图 8 乌鲁木齐站在不同重现期下降水极值综合曲线图 Figure 8 Compositive curve for precipitation extremes with different return periods at Urumqi station |
本文采用多种函数初步探讨了1961—2014年新疆地区日降水极值概率分布拟合中的不确定性,并提出了减少不确定性的方式,得到如下结论。
(1) 随着新疆地区气候由暖干向暖湿转变,98站观测到的降水极值主要出现在20世纪80年代及之后,进入21世纪,站数达到30站,占所研究站数的31%左右。
(2) 各站最优函数选择中,Wakeby函数最多,共29站;各函数降水极值进行拟合排名在前十的站次统计显示,Wakeby、GEV函数分别为78、71站,但也仅占总站数的80%和72%,因此,Wakeby或GEV函数的较好表现难以覆盖整个新疆。
(3) 各函数在较短年限的重现期对应的误差相对较小,随着年限增大,数值样本渐少,函数间的误差逐渐增大,由此产生的不确定性也增大。各站54年一遇降水极值拟合分析表明,并不是最优、Wakeby或GEV函数平均误差最小,而是整体表现一般的Kumaraswamy函数,这凸显出极值拟合时的不确定性。
为了减少来自函数方面的不确定性,在进行新疆区域降水极值分析时,建议采用整体表现较好的GEV、Gen. Logistic、Log-Pearson 3、Pearson 6和Wakeby函数进行合成分析,在进行单站分析时,可以给出一张具有界限范围的降水极值综合曲线图。极值分析中,对于样本的选择主要有两种方法,分别是年最大值序列(AM)以及超门限峰值序列(POT),本文采取的是前者,因此后续工作中将利用POT方法选取样本,采用类似的方法进行分析,进一步探讨新疆降水极值概率分布特征及其不确定性。
| [1] |
施雅风, 沈永平, 胡汝骥. 西北气候由暖干向暖湿转型的信号影响和前景初步探讨[J]. 冰川冻土, 2002, 24(3): 219-226. |
| [2] |
李栋梁, 魏丽, 蔡英, 等. 中国西北现代气候变化事实与未来趋势展望[J]. 冰川冻土, 2003, 25(2): 128-135. |
| [3] |
施雅风, 沈永平, 李栋梁, 等. 中国西北气候由暖干向暖湿型的特征和趋势探讨[J]. 第四纪研究, 2003, 23(2): 152-164. |
| [4] |
胡汝骥, 姜逢清, 王亚俊. 新疆气候由暖干向暖湿转变的信号及其影响[J]. 干旱区地理, 2002, 25(3): 194-200. |
| [5] |
赵兵科, 蔡承侠, 杨莲梅, 等. 新疆夏季变湿的大气环流异常特征[J]. 冰川冻土, 2006, 28(3): 434-442. |
| [6] |
张廷伟, 魏文寿, 姜逢清, 等. 1961—2008年新疆极端降水事件的变化趋势[J]. 山地学报, 2012, 30(4): 417-424. |
| [7] |
Jiang Y A, Chen Y, Zhao Y Z, et al. Analysis on changes of basic climatic elements and extreme events in Xinjiang, China during 1961-2010[J]. Advanced in Climate Change Research, 2013, 4(1). DOI:10.3724/SP.J.1248.2013.020 |
| [8] |
赵丽, 杨青, 韩雪云, 等. 1961—2009年新疆极端强降水事件时空差异特征[J]. 中国沙漠, 2014, 34(2): 550-557. DOI:10.7522/j.issn.1000-694X.2013.00347 |
| [9] |
IPCC. Climate change 2013: the physical science basis[M]. Cambridge: Cambridge University Press, 2013.
|
| [10] |
秦大河, StockerT, 259名作者和TSU(驻伯尔尼和北京). IPCC第五次评估报告第一工作组报告的亮点结论[J]. 气候变化研究进展, 2014, 10(1): 1-6. |
| [11] |
巢清尘, 周波涛, 孙颖, 等. IPCC气候变化自然科学认知的发展[J]. 气候变化研究进展, 2014, 10(1): 7-13. |
| [12] |
Fisher R A, Tippett L H C. Limiting forms of the frequency distribution of the largest or smallest members of a sample[J]. Proc Cambridge Philos Soc, 1928, 24: 180-190. DOI:10.1017/S0305004100015681 |
| [13] |
Gumbel E J. Statistics of extremes[M]. New York: Columbia University Press, 1958.
|
| [14] |
朱国庆, 张维, 张小薇, 等. 极值理论应用研究进展评析[J]. 系统工程学报, 2001, 16(1): 72-77. |
| [15] |
柳会珍. 统计极值理论及其应用研究进展[J]. 统计与决策, 2006, 16: 150-153. DOI:10.3969/j.issn.1002-6487.2006.24.057 |
| [16] |
丁裕国, 申红艳, 江志红, 等. 气候概率分布理论及其应用新进展[J]. 气象科技, 2009, 37(3): 257-262. |
| [17] |
丁裕国, 李佳耘, 江志红, 等. 极值统计理论的进展及其在气候变化研究中的应用[J]. 气候变化研究进展, 2011, 7(4): 248-252. |
| [18] |
Zhou G H, Wan S Q, Feng G L, et al. Effects of regional warming on extreme monthly low temperatures distribution in China[J]. Int J Climatol, 2012, 32: 387-391. DOI:10.1002/joc.v32.3 |
| [19] |
张廷伟, 姜逢清, 魏文寿, 等. 1961—2004年新疆降水极值概率分布特征[J]. 中国沙漠, 2012, 32(2): 503-508. |
| [20] |
江志红, 丁裕国, 马婷婷, 等. 气候极值推断的不确定性及其置信区间初步探讨[J]. 气象学报, 2012, 70(6): 1327-1333. DOI:10.11676/qxxb2012.111 |
| [21] |
苏布达, 姜彤, 董文杰. 长江流域极端强降水分布特征的统计拟合[J]. 气象科学, 2008, 28(6): 625-629. |
2. National Climate Center, China Meteorological Administration, Beijing 100081, China
 2017, Vol. 13
2017, Vol. 13 