2. 岳阳市气象局,岳阳 414000;
3. 无锡市气象局,无锡 214101
20世纪以来,随着全球变暖趋势的进一步加剧,极端气候事件的频繁发生已经严重制约了人类社会、经济的发展和进步,造成巨大的经济损失和人员伤亡[1-2]。极端气温作为一种极端气候事件[3-5],各国气象学家从不同角度做了研究,结果表明,在全球变暖背景下,随着气温的升高[5-6],极端气温事件变化具有明显的区域性[7-8],表现出日夜增温不对称的变化特征,极端气温事件的频率和强度发生了显著的变化[9-11]。因此评估气候变化,尤其是涉及极端气温的变化,成为科学研究的前言课题,在国内外学术界受到了越来越多的重视。
全球模式是进行气候模拟和预估未来气候变化的重要工具[12]。模式对当前气候模拟能力的好坏,直接影响对未来预估的准确性。由于受气候系统的复杂性以及气候模式的不确定性等影响,全球模式对极端气温变化的模拟能力存在一定的不足,因此在对未来气候变化进行预估之前,有必要从多时空尺度定量评估其对当前极端气温变化的模拟能力[13]。由于受东亚季风和青藏高原等大地形因素的影响,中国区域极端气温对全球变暖的响应异常复杂,如何准确地模拟中国地区极端气温的变化特征,一直是中国气象学者关注的问题。很多研究基于IPCC AR4的结果评估了气候模式对中国区域极端气温的模拟能力,如王冀等[14]评估了7个IPCC AR4耦合模式对极端气温的模拟能力,发现模式能够很好地再现极端气温指数的空间分布特征及其线性变化趋势,但不能体现其年际变化特点,且东部地区的模拟效果优于西部地区。Jiang等[15]进一步评估了IPCC AR4模式对极端气温空间结构的模拟能力,发现模式模拟不同极端气温指数偏差的分布相同,但具有明显的区域特点,其中青藏高原及其周围地区的极端气温模拟较差。
世界气候研究计划(WCRP)的第五次耦合模式比较计划(CMIP5)提供了来自全球近30个模式开发机构的气候模式对于当前模拟和未来预估的数据,这些数据可以用来评估不同模式对区域极端气温事件的模拟能力,以及未来变化的预估。相比于前几个阶段的CMIP模式,大部分CMIP5模式在分辨率、参数化方案以及耦合器技术等多方面进行改进,并且很多模式首次考虑到碳氮循环、气溶胶效应以及动态植被过程[16]。众多学者利用这些模式的结果,评估了CMIP5模式对极端气温事件的模拟能力,并指出CMIP5模式对极端气温的模拟能力相比于CMIP3有显著提高[17-21]。针对我国极端气温的评估,姚遥等[22]基于8个CMIP5模式的结果,指出模式对极端气温指数有模拟能力,模拟和观测结果的时间相关通过0.10的显著性检验。Seo等[23]评估了15个CMIP5模式对东亚地区极端气温的模拟能力,挑选了模拟能力最好的5个模式,并且优选模式集合能够显著降低模拟误差。但是以往大部分研究使用的模式较少,无法全面评估CMIP5模式对极端气温的模拟能力,尤其是缺乏对其趋势变化的系统评估。由于极端气温变化趋势与气象灾害发生密切相关,系统评估新一代模式对极端气温的趋势模拟能力尤为重要。因此本文利用30个CMIP5气候模式模拟结果,从气候态的平均场和趋势两个方面,系统评估CMIP5模式对中国区域极端气温的模拟能力,并且基于评估的结果优选出对中国地区极端气温模拟较好的模式以及优选模式的集合方案,为预估中国地区未来极端气温变化提供可靠的科学依据。
1 资料和方法 1.1 观测和模式数据评估极端气温的模拟结果,高分辨率的气温观测资料尤为重要。本文主要使用Chen等[24]根据地面气象台站观测资料制作的中国区域0.5°×0.5°高分辨率的逐日最高气温和最低气温的格点资料,选取时段为1961—2005年,共45年。本文使用的模式资料为参与IPCC AR5中模拟全球气候变化的CMIP5的30个全球气候模式模拟的逐日最高气温与最低气温资料。模式基本信息如表 1所示。评估时段为1961—2005年。
|
|
表 1 CMIP5的30个气候模式的基本信息 Table 1 Basic information of 30 CMIP5 global climate models |
本文使用了常用的5个极端气温指数[15, 25-26],日平均最高气温(TXAV)、日平均最低气温(TNAV)能够直观描述模式模拟极端气温能力的强弱,霜冻日数(FD)能够描述中高纬地区霜冻的长度,热浪指数(HWDI)能反映夏季高温持续的时间,暖夜指数(TNF90)是暖夜所占的比例(表 2)。由此可见,日平均最低气温、霜冻日数和暖夜指数主要反映日最低气温的变化,日平均最高气温、热浪指数则反映日最高气温的变化。由于这些极端气温指数综合考虑了极端气温事件的强度和持续时间,因此能够展现气候不同层面的变化[27-28],同时由于其极端性较弱、噪音低、显著性强等特点,已成为国际上公认的与极端气温事件有关的核心指标。鉴于各模式具有不同的分辨率,首先利用1961—2005年的观测和各模式逐日最高气温、最低气温资料,计算得到每年的极端指数,然后利用双线性插值的方法,将观测和模式资料得到的极端气温指数值统一插值到1°×1°网格点上。
|
|
表 2 极端指数的定义 Table 2 The definition of extreme indexes |
本文使用泰勒图来评估模式对气候平均场以及趋势空间场的模拟能力[29],泰勒图可以提供两个场之间的相关系数、标准差的比及中心化的均方根误差(RMSE),相关系数可以表示模拟结果与观测场之间空间分布的相似程度,RMSE和标准差的比则分别表征模式模拟结果的强度和空间均匀性与观测之间的差异。由于三者之间存在数学三角转换关系,故将其放在同一张图上,从而更加直观地比较出不同模式模拟能力的强弱。
1.4 综合评级指标综合评级指标(MR)分别计算评级指标进而判断评估指标的一致性得到的模式排名[30]。本文使用了泰勒图中的3个评估指标(相关系数、标准差之比、RMSE)。
| $ {{M}_{R}}=\text{1-}\frac{\text{1}}{\text{1}\times n\times m}\sum\limits_{i\text{=1}}^{n}{{{r}_{i}}}。$ | (1) |
式中:m为参与评估的模式个数,m=30;n为用于评估的指标个数,n=3;ri为各模式综合排名,模拟能力最强的模式其ri值为1。MR越接近1,说明模式模拟各指数能力越强。
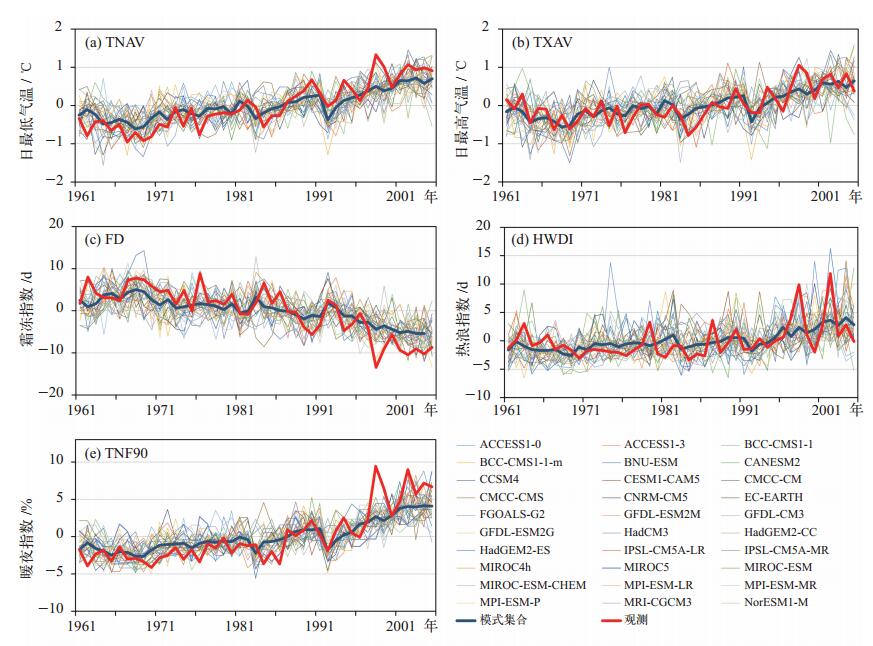
2 模式评估本文计算1961—2005年模式模拟指数和观测指数的距平序列,如图 1所示。从图中可以看出,除了FD呈下降趋势外,其余4个指数都呈上升趋势,而且模式集合能够较好地反映观测的趋势变化,这说明模式集合在模拟中国区域平均极端气温指数具有较好的表现,但各模式之间的差异较大,为了比较不同模式模拟极端指数能力的强弱,下面将从空间(气候平均态)和时间(趋势)两方面分析。
|
图 1 1961—2005年模式模拟指数和观测指数全国平均的距平序列 Figure 1 Time series of national average index anomalies from 1961 to 2005 |
利用泰勒图来评估CMIP5模式对于极端气温指数气候平均场的模拟能力(图 2),泰勒图主要从模式与观测空间相关系数、RMSE以及模式与观测标准差之比3个方面进行评估,其中相关系数越高,模式与观测标准差之比越接近1,且RMSE越小,则模式的模拟能力越好。
|
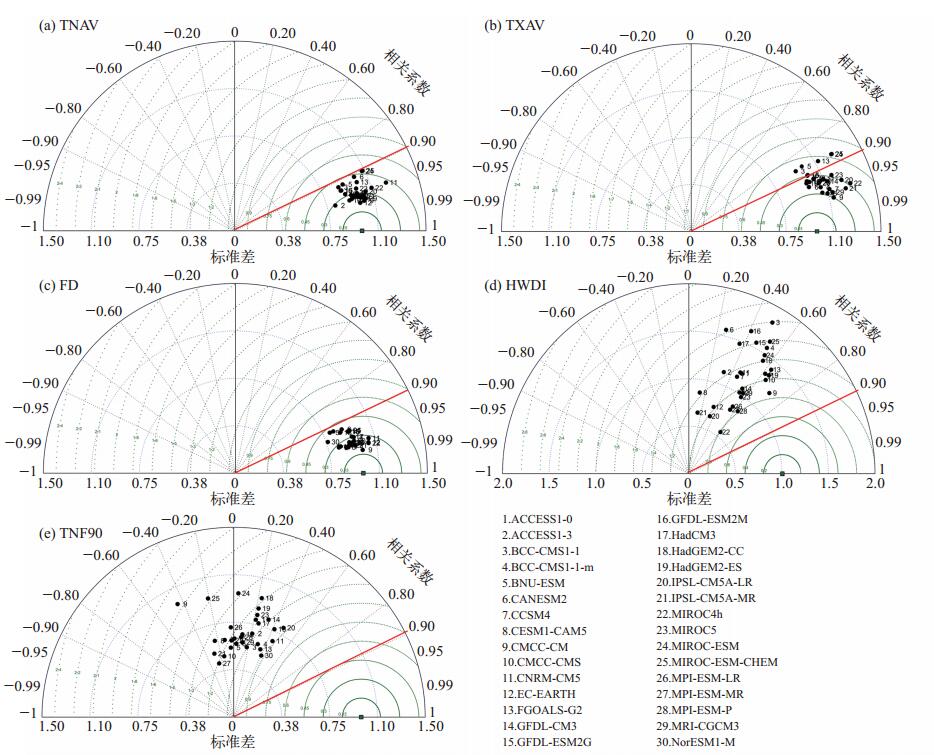
注:红实线表示相关系数达到0.90,黑实线表示标准差的比为1.0,蓝色实线表示RMSE。 图 2 CMIP5模式模拟5个极端气温指数气候平均场分布相对于观测场的泰勒图 Figure 2 Taylor program for the spatial field of TNAV, TXAV, FD, HWDI and TNF90 for climate state in China between CMIP5 models and observation |
总的来说,大部分模式能够较好地模拟出极端指数气候平均场,但对于不同指数,模式的模拟能力存在差异。从图 2中可以看出,模式对TNAV、TXAV和FD的气候平均场模拟能力最好,模式平均场与观测场的相关系数均能超过0.90,大部分模式的RMSE均低于0.50。且不同模式对这3个极端气温指数模拟能力具有较好的一致性,表现为在泰勒图中分布比较集中。另外需要说明的是大部分模式对TXAV空间标准差的模拟大于观测,对FD空间标准差的模拟小于观测,而对TNAV,则是有一半的模式模拟的标准差大于观测。这表明大部分模式对TXAV的空间差异模拟偏强,而对FD的空间差异模拟偏弱。模式对HWDI和TNF90气候平均场的模拟较差。对于HWDI指数,各模式之间的模拟能力差异较大,表现为在泰勒图中分布比较分散。模式模拟其相关系数均低于0.70,有些模式的标准差之比甚至超过了1.5,而且大部分模式的RMSE > 1.0。对于TNF90而言,各模式之间的模拟能力差异较大,所有模式模拟其相关系数均低于0.60,个别模式甚至小于0,大部分模式的RMSE > 1.0。
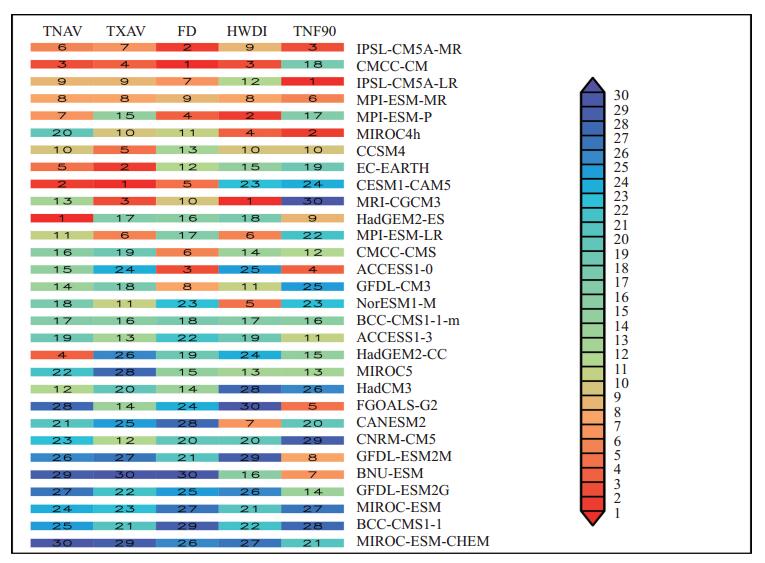
综合各个指数的MR排序结果,图 3给出了30个模式对中国区域极端气温气候平均场模拟能力的综合排名。可以看到模式对TNAV、TXAV、FD和HWDI指数的模拟效果具有较高的一致性,但对TNF90的模拟效果与其余指数存在差别。总的来说模拟性能好的模式,对每个指数都有较好的再现能力。通过基于泰勒图的综合排名可以看到,模拟能力最强的前5个模式分别为:IPSL-CM5A-MR、CMCC-CM、IPSL-CM5A-LR、MPI-ESM-MR和MPI-ESM-P。
|
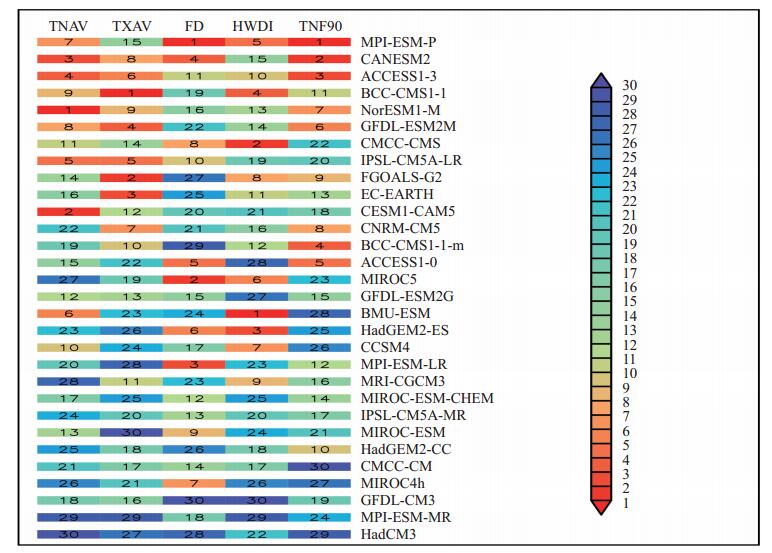
注:色块上的数字表示该模式对各指数模拟能力的排名,颜色越暖表示排名越靠前,颜色越冷排名越靠后,右边各模式名按排名列出。 图 3 基于综合评级指标的模式模拟气候平均场模拟能力综合排名的色块图 Figure 3 The portrait diagram of the models rank based on composite rating indicator for the spatial field of all indices in climate state |
模式能否模拟出极端气温的趋势变化是考察模式模拟能力的一个重要指标。表 3给出观测与模拟中国区域平均各极端气温指数的线性变化趋势。可以看到,所有模式可以模拟出与观测相同的极端气温指数的变化趋势,但大部分模式模拟的趋势强度偏弱。值得一提的是,大多数模式也能很好地模拟出TNAV增加趋势大于TXAV增加趋势,但不同模式模拟趋势的强度存在较大的差异。模式模拟TNAV、TXAV、TNF90、FD和HWDI趋势变化的范围分别为0.10~0.38℃/10a、-0.03~0.36℃/10a、0.75%/10a~1.78%/10a、-2.91~-0.92 d/10a和0.22~2.01 d/10a。对于单个模式而言,BNU-ESM模式对TNAV模拟的趋势最接近观测数据,趋势误差为0.02℃/10a,MPI-ESM-LR对TXAV的趋势模拟与观测最相近,趋势误差为0.01℃/10a。IPSL-CM5A-MR对TNF90的趋势模拟最好,趋势误差为0.32%/10a。对FD趋势模拟最好的模式是CANESM2,趋势误差为0.66 d/10a。MPI-ESM-LR对HWDI的趋势模拟最好,与观测数据的变化趋势完全一致,为0.92 d/10a。
|
|
表 3 模式模拟1961—2005年中国区域平均极端气温指数与观测数据的线性变化趋势 Table 3 The trends of average extreme temperature indices at national scale simulated by models and observation for the period of 1961-2005 |
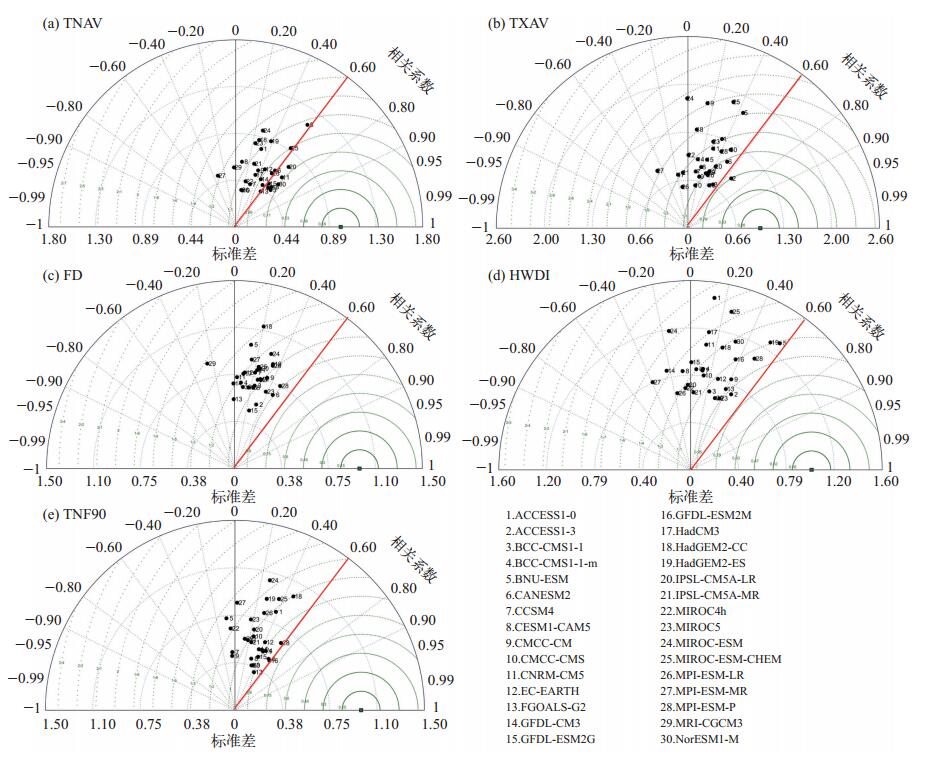
同样利用泰勒图,评估了模式对极端气温指数趋势空间场的模拟能力(图 4)。与气候平均场相比,模式对趋势空间场的模拟能力相对较差。从图 4可以看出,除有1/3的模式模拟TNAV的相关系数超过0.60以外,所有模式对其余指数模拟的相关系数均低于0.60。模式对TNAV和TNF90表现出相对较好的模拟能力,表现为一半的模式模拟趋势空间场的RMSE < 1.0,而对其他3个指数TXAV、FD和HWDI而言,绝大部分模式模拟趋势空间场的RMSE > 1.0。并且模式对于TXAV和HWDI模拟能力差异比较大,表现为在泰勒图中分布比较分散。
|
图 4 同图 2,但为5个极端气温指数趋势空间场的泰勒图 Figure 4 Same as Fig. 2, but Taylor program for spatial pattern of five indices trend |
同样,图 5给出30个模式模拟极端气温指数趋势空间场能力的综合排名。可以看出相比于气候平均场的排序结果,模式对5个极端气温指数模拟能力之间的一致性并不理想,尤其是FD和HWDI,表现出与其他指数较大的差异。但总的来说,排名靠前以及排名靠后的模式模拟各指数具有较好的一致性。模拟能力较优的模式为:MPI-ESM-P、CANESM2、ACCESS1-3、BCC-CSM1-1和NorESM1-M。
3 优选模式的模拟效果根据30个模式对极端气温气候平均场与趋势空间场模拟效果的评估,计算了两者模式排名的相关系数,发现模式排名存在显著的差别。即CMIP5模式对气温平均场模拟较好的模式,对趋势空间场的模拟反而会很差。根据上文模式对气候平均场和趋势空间场的模拟能力,分别将排名前5的模式进行平均称为优选模式集合方案(BMME),所有模式集合称为AMME。以下分别讨论优选模式对气候平均场和趋势空间场的模拟效果,研究时段为1961—2005年。
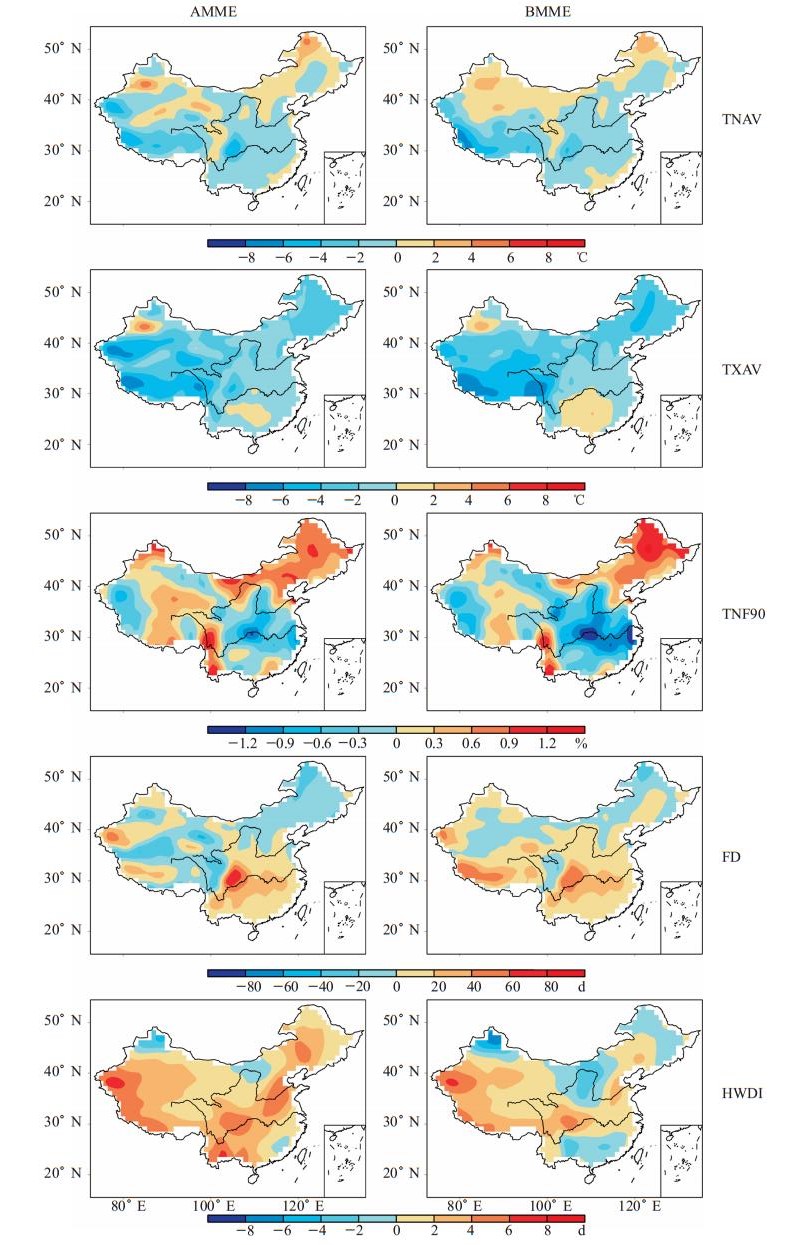
3.1 优选模式对气候平均场的模拟效果图 6给出了两种模式集合方案模拟极端气温指数气候平均场与观测值的偏差分布。对于TNAV,AMME在四川盆地有4℃以上的冷偏差,而BMME能够将四川盆地的冷偏差减少到4℃以下,并且能够缩减偏差大值区。对于TXAV,BMME在新疆地区以及四川盆地有改善效果。对于FD而言,AMME模拟FD偏差大值区主要位于四川盆地,超过了60 d,BMME模拟的偏差显著减小,偏差 < 60 d。对于HWDI,AMME在整个中国区域表现为正偏差,而BMME能够显著减小正偏差,尤其是在我国华北、东北以及西南地区。但是TNF90,BMME相对于AMME的改善并不明显,主要是由于模式基于TNF90的排序与其余指数存在较大差距,优选模式对TNF90的模拟能力并不是很好(图 2)。总的来说,相比于多模式集合,除了TNF90外,优选模式可以更好地模拟出中国区域极端气温分布的空间结构,并且可以有效地缩小偏差大值区、减小偏差值。
|
图 6 1961—2005年AMME和BMME模拟各指数气候平均偏差场(模式场-观测场) Figure 6 The simulation of bias field (model minus observation field in climate state from 1961 to 2005) of five indices for AMME and BMME |
图 7给出了两种模式集合方案模拟极端气温指数趋势空间场与观测值的偏差分布。对于TNAV,AMME在东北和华北有0.4℃/10a以上的负偏差,而BMME能够显著缩小负偏差的范围,减小负偏差值的大小。对于TXAV,AMME在四川地区正偏差 > 0.10℃/10a,在山西到陕西负偏差 > 0.15℃/10a,BMME能够缩小这些地区的偏差。对于TNF90,BMME相对于AMME的改善并不明显。对于FD而言,AMME在东北至华北大部分地区 > 2 d/10a,而BMME能够显著减少偏差范围。对于HWDI而言,相对于AMME,BMME在四川至贵州能够有效减少暖偏差范围,其他地区改善效果不佳。总的来说,BMME模拟趋势空间场能力,相对于AMME有一定程度的改善,但相比于气候平均场的模拟能力,BMME对趋势空间场的模拟有待提高。
4 结论与讨论本文基于中国区域的格点观测资料以及新一代CMIP5中30个全球气候模式模拟的格点资料,通过计算日平均最高气温(TXAV)、日平均最低气温(TNAV)、霜冻日数(FD)、热浪指数(HWDI)和暖夜指数(TNF90),对各模式在中国区域极端气温的时空模拟能力进行了定量、客观的评估。并且在评估的基础上得到了模拟性能较好的模式集合,得到结论如下。
(1) 大部分模式能够较好地模拟出极端指数气候平均场的特征。但对于不同指数,模式的模拟能力存在差异。模式模拟TNAV、TXAV和FD气候平均场的能力较强,大部分模式模拟的气候平均场与观测场的相关系数能够超过0.90,且模式间有较好的一致性。而模式对HWDI和TNF90的模拟能力较弱,模式模拟的空间相关系数低于0.70,且模式间一致性较差。综合模式对极端气温气候平均场的模拟能力,最优的5个模式为:IPSL-CM5A-MR、CMCC-CM、IPSL-CM5A-LR、MPI-ESM-MR和MPI-ESM-P。
(2) 模式模拟的中国区域平均各极端气温指数的线性趋势变化与观测相同,但大部分模式模拟的趋势强度偏弱。相比于气候平均场,模式对趋势空间场的模拟能力相对较差,除有1/3的模式模拟TNAV的相关系数超过0.60外,所有模式模拟其余指数的相关系数均低于0.60。对趋势模拟最好的5个模式为:MPI-ESM-P、CANESM2、ACCESS1-3、BCC-CSM1-1和NorESM1-M。
(3) 模式对极端气温指数的时空模拟能力一致性较差,但基于气候平均场或趋势空间场的优选模式,相比于所有集合模式平均,模拟能力均有一定程度的改善。对于气候平均场,除TNF90外,相比于AMME,BMME可以更好地模拟出中国区域极端气温分布的空间结构,而且可以缩小偏差大值区、减小偏差值。对于TNAV、TXAV和FD,优选模式集合主要改善区域位于我国西北和四川盆地,对于HWDI,在整个东部地区以及西北都有明显的改善;相比于气候平均场的模拟能力,模式对趋势空间场的模拟有待提高。对于TNAV和FD,BMME集合主要改善区域位于我国华北和东北地区,而对于TXAV,BMME能缩小四川和陕西一带的偏差值。对于HWDI,BMME能减少四川至贵州地区偏差范围。
本文系统评估了CMIP5模式对中国极端气温的模拟能力,与以往CMIP5模式对极端气温的评估相比,增加了对趋势空间场的模拟能力。需要指出的是,相比于CMIP3模式,CMIP5模式对极端气温的模拟能力有一定程度的改善,以HWDI为例,CMIP3模式模拟中国区域HWDI气候平均场的相关系数均低于0.60[15],而CMIP5模式中有1/3模式的相关系数超过0.60。另外,本文基于评估的结果分别挑选出了对气候平均场和趋势空间场模拟能力较好的模式集合方案,优选模式能够在一定程度上减少模式的模拟偏差,但优选模式集合的偏差依旧存在,尤其是对趋势空间场的模拟。未来可以通过提高模式本身的动力框架以及物理过程参数化,以及改善与极端气温变化有关的动力过程,来获得对极端气温指数更好的模拟效果。另外,基于模式对中国区域极端气温的模拟性能,可以赋予每个模式不同的权重,依据权重方案可以得到未来中国区域极端气温变化更准确的预估结果[31-32],这将是我们下一步研究的内容。
| [1] |
Orlowsky B, Seneviratne S I. Global changes in extreme events: regional and seasonal dimension[J]. Climatic Change, 2012, 110(3-4): 669-696. DOI:10.1007/s10584-011-0122-9 |
| [2] |
Gao X, Zhao Z, Giorgi F. Changes of extreme events in regional climate simulations over East Asia[J]. Adv Atmos Sci, 2002, 19(5): 927-942. DOI:10.1007/s00376-002-0056-2 |
| [3] |
Sun Y, Zhang X, Zwiers F W, et al. Rapid increase in the risk of extreme summer heat in eastern China[J]. Nature Climate Change, 2014, 4(12): 1082-1085. DOI:10.1038/nclimate2410 |
| [4] |
Zhai P M, Pan X H. Change in extreme temperature and precipitation over northern China during the second half of the 20th century[J]. Acta Geographica Sinica, 2003, 58(S1): 1-10. |
| [5] |
Griffiths G M, Chambers L E, Haylock M R, et al. Change in mean temperature as a predictor of extreme temperature change in the Asia-Pacific region[J]. International Journal of Climatology, 2005, 25(10): 1301-1330. DOI:10.1002/(ISSN)1097-0088 |
| [6] |
Klein Tank A M G, Können G P. Trends in indices of daily temperature and precipitation extremes in Europe, 1946-99[J]. Journal of Climate, 2003, 16(22): 3665-3680. DOI:10.1175/1520-0442(2003)016<3665:TIIODT>2.0.CO;2 |
| [7] |
Vincent L A, Aguilar E, Saindou M, et al. Observed trends in indices of daily and extreme temperature and precipitation for the countries of the western Indian Ocean, 1961-2008[J]. J Geophys Res, 2011, 116(D10). DOI:10.1029/2010JD015303 |
| [8] |
Rusticucci M. Observed and simulated variability of extreme temperature events over South America[J]. Atmospheric Research, 2012, 106(3): 1-17. |
| [9] |
Brown S J, Caesar J, Ferro C A T. Global changes in extreme daily temperature since 1950[J]. J Geophys Res, 2008, 113(D5): 79-88. |
| [10] |
张勇, 曹丽娟, 许吟隆, 等. 未来我国极端气温事件变化情景分析[J]. 应用气象学报, 2008, 19(6): 655-660. DOI:10.11898/1001-7313.20080603 |
| [11] |
杨金虎, 沈永平, 王鹏祥, 等. 中国西北近45 a来极端低温事件及其对区域增暖的响应[J]. 冰川冻土, 2007, 29(4): 536-542. |
| [12] |
IPCC. Climate change 2007: the physical science basis[M]. Cambridge: Cambridge University Press, 2007.
|
| [13] |
Masson D, Knutti R. Spatial-scale dependence of climate model performance in the CMIP3 ensemble[J]. Journal of Climate, 2011, 24(11): 2680-2692. DOI:10.1175/2011JCLI3513.1 |
| [14] |
王冀, 江志红, 丁裕国, 等. 21世纪中国极端气温指数变化情况预估[J]. 资源科学, 2008, 30(7): 1084-1092. |
| [15] |
Jiang Z H, Song J, Li L, et al. Extreme climate events in China: IPCC-AR4 model evaluation and projection[J]. Climatic Change, 2012, 110(1-2): 385-401. DOI:10.1007/s10584-011-0090-0 |
| [16] |
Taylor K E. Summarizing multiple aspects of model performance in a single diagram[J]. J Geophys Res, 2001, 106(D7): 7183-7192. DOI:10.1029/2000JD900719 |
| [17] |
Yao Y, Luo Y, Huang J, et al. Comparison of monthly temperature extremes simulated by CMIP3 and CMIP5 models[J]. Journal of Climate, 2013, 26(19): 7692-7707. DOI:10.1175/JCLI-D-12-00560.1 |
| [18] |
Tolen J, Kodra E A, Ganguly A R. Comparative evaluation of the IPCC AR5 CMIP5 versus the AR4 CMIP3 model ensembles for regional precipitation and their extremes over South America [C]. AGU Fall Meeting Abstracts, 2011
|
| [19] |
Sillmann J, Kharin V V, Zhang X, et al. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. model evaluation in the present climate[J]. J Geophys Res, 2013, 118(4): 1716-1733. |
| [20] |
陈晓晨, 徐影, 许崇海, 等. CMIP5全球气候模式对中国地区降水模拟能力的评估[J]. 气候变化研究进展, 2014, 10(3): 217-225. |
| [21] |
郭彦, 董文杰, 任福民, 等. CMIP5模式对中国年平均气温模拟及其与CMIP3模式的比较[J]. 气候变化研究进展, 2013, 9(3): 181-186. |
| [22] |
姚遥, 罗勇, 黄建斌. 8个CMIP5模式对中国极端气温的模拟和预估[J]. 气候变化研究进展, 2012, 8(4): 250-256. |
| [23] |
Seo Y W, Kim H, Yun K S, et al. Future change of extreme temperature climate indices over East Asia with uncertainties estimation in the CMIP5[J]. Asia-Pacific Journal of Atmospheric Sciences, 2014, 50(1): 609-624. |
| [24] |
Chen D, Ou T, Gong L, et al. Spatial interpolation of daily precipitation in China: 1951-2005[J]. Adv Atmos Sci, 2010, 27(6): 1221-1232. DOI:10.1007/s00376-010-9151-y |
| [25] |
Sillmann J, Kharin V, Zhang V, et al. Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. future climate projections[J]. J Geophys Res, 2013b, 118(6): 2473-2493. |
| [26] |
Ou T, Chen D, Linderholm H W, et al. Evaluation of global climate models in simulating extreme precipitation in China[J]. Tellus A, 2013, 65(5): 1393-1399. |
| [27] |
Firch P, Alexander L V, Della-Marta P, et al. Observed coherent changes in climatic extremes during the second half of the twentieth century[J]. Climate Research, 2002, 19: 193-212. DOI:10.3354/cr019193 |
| [28] |
Alexander L V, Zhang X, Peterson T C, et al. Global observed changes in daily climate extremes of temperature and precipitation[J]. J Geophys Res, 2012, 111(D5): 1042-1063. |
| [29] |
Taylor K E. Summarizing multiple aspects of model performance in a single diagram[J]. J Geophys Res, 2001, 106(D7): 7183-7192. DOI:10.1029/2000JD900719 |
| [30] |
Schuenemann K C, Cassano J J. Changes in synoptic weather patterns and Greenland precipitation in the 20th and 21st centuries: 1. evaluation of late 20th century simulations from IPCC models[J]. J Geophys Res, 2009, 114(D20): 311. |
| [31] |
Santer B D, Taylor K E, Gleckler P J, et al. Incorporating model quality information in climate change detection and attribution studies[J]. Proceedings of the National Academy of Sciences, 2009, 106(35): 14778-14783. DOI:10.1073/pnas.0901736106 |
| [32] |
Knutti R. The end of model democracy[J]. Climatic Change, 2010, 102(3-4): 395-404. DOI:10.1007/s10584-010-9800-2 |
2. Yueyang Meteorological Bureau, Yueyang 414000, China;
3. Weather Bureau in Wuxi, Wuxi 214101, China
 2017, Vol. 13
2017, Vol. 13