随着中国经济步入“新常态”,经济由高速发展转向高质量发展,产能过剩、产业结构亟需转型升级等重大经济问题凸显,加上2020年以来新冠肺炎疫情对全球经济的冲击以及“全球脱钩”趋势的发展,使得传统的三驾马车拉动中国经济增长已不现实。近年,中央反复强调要充分发挥我国超大规模市场和内需动力,加快构建完整的内需体系,逐步形成以国内大循环为主体、国内国际双循环相互促进的新发展格局,这对国内资源优化配置提出了挑战。减少资源错配、提高资源配置效率是目前维持我国经济中高速增长、提高增长质量,实现内外双循环的内生需求和支撑基础(唐志军、苏丽,2019;邓富华、沈和斌,2020)。面对世界百年未有之大变局,处在世界新一轮科技与产业变革同我国发展方式转变历史交汇期的我们不禁思考这一系列问题:工业化作为中国经济发展的主要动力,中国工业行业生产效率如何?存在多大程度的资源配置扭曲?具体到资本、劳动和中间投入三大生产要素来说情况怎样?它们造成了多大程度的工业产出和效率损失?哪一种要素的配置扭曲影响程度更大?影响中国工业总产出和效率损失的根源又在哪里?整个工业体系的资源配置效率是在改进还是恶化?推进双循环促进工业体系健康高效高质量发展的努力方向是什么?
各种经济现象表明,行业内部、行业之间或地区之间的生产情况往往因缺乏整体调控和监督而产生要素配置扭曲。学者们基于不同视角对资源配置扭曲开展了系列研究,研究角度不同、测度方法不同得出的结论也有所不同。鉴于王文、牛泽东(2019)的研究判断——不同行业之间的错配程度大于所有制和不同地区之间的错配。本文秉着抓住主要矛盾与矛盾的主要方面原则,旨在基于中国工业企业微观数据对工业部门中行业间的资源错配进行研究,下面仅对与本文主题相关的主要文献进行简要回顾。
关于TFP与资源配置的关系研究由来已久,Syrquin(1986)通过扩展Solow的内生增长核算框架,将一国TFP增长分解为行业TFP增长与要素配置效应,其研究具有方向性引导作用,但局限于描述性分析。Hsieh and Klenow(2009)将产品价格扭曲和资本价格扭曲引入一般均衡模型,构建出一个垄断竞争宏观模型,成为资源错配与生产率的代表性文献,研究发现若中国的资源配置效率达到美国的水平,则中国TFP将可以提升30%~40%。
随后,国内学者也逐步开始借助“资源错配和总量生产率”框架开展研究。学者们普遍认为资源配置扭曲是影响中国生产率增长的一个重要原因(杨帆、徐长生,2009;龚关、胡关亮,2013;任韬等,2020)。具体到中国工业研究上,姚战琪(2009)通过对1985-2007年中国工业生产率增长和要素再配置效应的比较,认为要素再配置效应是中国工业生产率增长的主要来源,且中国工业要素配置效应改进空间很大。邵挺(2010)使用1999-2007年中国工业企业数据库从金融的视角展开研究,认为通过消除金融错配,中国GDP增长率可提高2%~8%。具体到工业部门内行业间来说,各子行业要素价格的扭曲程度存在较大差异已基本达成共识,但还存在一些争议和不足。首先,在劳动要素与资本要素配置扭曲程度孰高孰低,以及资源在行业间的配置对生产率提升的作用、制造业整体资源配置效率的发展趋势等问题上争议不少,如韩国珍、李国璋(2015)与周新苗、钱欢欢(2017)就劳动和资本配置扭曲的高低,陈永伟、胡伟民(2011)和文东伟(2019)就要素扭曲的发展趋势问题持截然相反的观点。韩国珍、李国璋(2015)使用中国工业1994-2011年两位数行业数据,研究发现中国资本配置扭曲程度总体上高于劳动配置扭曲程度。周新苗、钱欢欢(2017)使用1998-2013年中国工业企业数据库,发现劳动要素配置总体表现的扭曲程度大于资本要素,且资本价格扭曲的变动对制造业总生产效率和产出的贡献呈上升趋势且表现稳定。陈永伟、胡伟民(2011)在Hsieh and Klenow(2009)模型基础上引入中间投入作为生产要素,采用2001-2007年中国工业企业数据库,发现要素价格扭曲导致的资源在行业间的错配使制造业的实际产出降低了15%~20%,且在考察期内扭曲没有得到显著纠正。文东伟(2019)利用1998-2007年中国制造业企业微观数据,研究发现中国大多数制造业行业资本配置不足,劳动配置过度,制造业整体资源错配程度在下降。其次,上述研究都关注到各子行业要素价格的扭曲程度的差异,但基于行业间资源错配的深度分析还是欠缺。最后,关于导致资源错配的摩擦因素,只有张佩(2013)作了相应探讨,研究相对薄弱。张佩(2013)利用1998-2007年中国工业企业数据,发现要素在行业间的错配使工业部门总体全要素生产率降低了18.7%,资本错配造成的效率损失(17%)约为劳动力错配损失(1.6%)的10倍。
与已有研究相比,本文可能的边际贡献有:(1)沿用了陈永伟、胡伟民(2011)的研究框架,将数据样本扩展到2013年,得出相对更为完整客观的结论。研究显示,要素错配使整体产出或TFP降低了7.39%(算术平均值),在某些年份接近9%(如2011年),没有陈永伟、胡伟民(2011)得出的15%-20%和张佩(2013)所得结论18.7%那么高。(2)通过引入中间投入对各子行业要素价格相对扭曲系数进行估算,对各生产要素扭曲影响程度孰高孰低,相对差值为多少有了明确的结论。得出“中间投入扭曲带来的影响>资本扭曲带来的影响>劳动扭曲带来的影响”,资源错配造成的产出缺口平均为8%。其中资本错配造成的效率损失约为劳动错配造成效率损失的2倍,中间投入造成的资源错配效率损失约为劳动错配造成效率损失的4倍。并按六种分类方式对行业间资源错配进行深层剖析。(3)经引入中间投入要素后,本文在行业集中度和中西部企业份额高的行业上和张佩(2013)有着相反的结论。张佩(2013)的研究表明行业集中度越低越倾向于投入过度,国有企业份额越高的行业越可能投入了过多的资本和劳动力,中西部地区的份额越高的行业越倾向于资本投入过度,劳动力的相对扭曲系数没有影响。本文研究认为行业集中度越高的产业要素投入过度现象更为明显,其中资本相对扭曲程度比劳动和中间投入的相对扭曲程度更高。中西部企业份额越高的行业越存在中间投入的配置扭曲,在资本和劳动的配置效率上和东部地区并无显著差异。此外,重资本类型的行业在资本、劳动和中间投入上均存在不同程度的配置扭曲,尤其是在资本和劳动要素上非常明显。
本文其余部分结构为:第二部分,理论模型。在陈永伟、胡伟民(2011)建立的引入中间投入要素的资源配置效率研究框架下,提出了估计资源错配和产出缺口的一系列公式,同时结合Syrquin(1986)的产出变动分解模型,分解出影响产出变动的主要因素。第三部分,为数据处理与样本分析。将目前国内外常用的中国工业企业数据库(1999-2007)延长至2013年。第四部分,实证分析。分析了三种要素价格相对扭曲系数、资源错配程度、效率损失以及产出缺口等。第五部分, 造成行业间资源错配的摩擦因素分析。第六部分,结论与启示。
二、理论模型本文借鉴陈永伟、胡伟民(2011)引入中间投入要素的方式来估计微观企业的资源错配和效率损失,建立一个带有要素价格扭曲的N个行业生产环境,定义竞争均衡与要素价格相对扭曲系数,对中国工业部门行业之间的资源错配程度及其对产出的影响进行实证检验。
(一) 在Hsieh and Klenow(2009)的基础上引入中间投入1.假设条件
(1) 假设工业部门内存在N个子行业,用劳动L和资本K以及中间投入M三种生产要素生产不同的产品。同一子行业内企业的生产函数相同,不同子行业的生产函数不同,每个行业可视为由一个代表性企业进行生产。行业i的代表性企业生产函数为:
| $ Y_{i}=A_{i} \cdot K_{i}^{\alpha_{i}} L_{i}^{\beta_{i}} M_{i}^{\gamma_{i}} $ | (1) |
其中Yi表示产出,Ki、Li、Mi分别表示资本、劳动和中间投入的投入量。参数αi、βi、γi分别表示资本、劳动和中间投入对产出的贡献比例。
(2) 行业中各个企业在产品和要素市场上都是市场价格的接受者,完全竞争条件下要素的价格分别为Pk、Pl和Pm;类似于Hsieh and Klenow(2009),假设企业实际面临的价格是扭曲的,并以从价税的形式体现:行业i中的企业面临的资本、劳动和中间投入的价格分别为(1+τki)Pk、(1+τli)Pl和(1+τmi)Pm,资本、劳动和中间投入的“扭曲税”分别为τki、τli和τmi。
(3) 代表性企业的利润最大化可表示为:
| $ \max \pi_{i}=\left\{P_{i} Y_{i}-\left(1+\tau_{k i}\right) P_{k} K_{i}-\left(1+\tau_{l i}\right) P_{l} L_{i}-\left(1+\tau_{m i}\right) P_{m} M_{i}\right\} $ | (2) |
其中,Pi为行业i的产品价格。为简化起见,假定产品市场价格不存在扭曲。上述(2)式最优解的一阶条件如下:
| $ \frac{\alpha_{i} P_{i} Y_{i}}{K_{i}}=\left(1+\tau_{k i}\right) P_{k}, \quad \frac{\beta_{i} P_{i} Y_{i}}{L_{i}}=\left(1+\tau_{k i}\right) P_{i}, \quad \frac{\gamma_{i} P_{i} Y_{i}}{M_{i}}=\left(1+\tau_{m i}\right) P_{m} $ | (3) |
(4) 资源约束条件为:
| $ \sum\limits_{i} K_{i}=K, \quad \sum\limits_{i} L_{i}=L, \quad \sum\limits_{i} M_{i}=M $ | (4) |
(5) 加总生产函数:整个工业经济的总产量Y由各行业产量决定,且各行业产出的加总函数也采用Cobb-Douglas技术,行业份额为θi,即:
| $ Y=\prod\limits_{i=1}^{I} Y^{\theta_{i}}, \quad \sum\limits_{i=1}^{I} \theta_{i}=1 $ | (5) |
该加总函数规模收益不变,因此根据一阶齐次性可得:
| $ Y=\sum\limits_{i} P_{i} Y_{i} $ | (6) |
如果把Y=Y(Yi)理解为消费者的效用,那么消费者效用最大化问题的一阶条件也得到满足:
| $ \frac{\partial Y}{\partial Y_{i}}=P_{i} $ | (7) |
2. 竞争均衡
在以上假定下,我们定义一个带有扭曲的竞争均衡:假设给定N个行业的生产率水平和扭曲税率(Ai, τki, τli, τmi),以及整个工业体系中资本、劳动和中间投入的要素总量K、L和M,满足以下条件的各行业产出、资本、劳动力、中间投入与产品价格的配置(Yi, Ki, Li, Mi, Pi)构成一个均衡:
(1) 实现利润最大化的一阶条件(3);
(2) 消费者加总函数规模收益不变(6),效用最大化的一阶条件(7);
(3) 资源约束条件(4)。
在包含要素配置扭曲的多行业竞争均衡条件下,可以求解得出i行业的资本投入Ki、劳动投入Li和中间投入Mi的表达式:
| $ K_{i}=\frac{\frac{\alpha_{i} P_{i} Y_{i}}{\left(1+\tau_{k i}\right) P_{k}}}{\sum\limits_{j} \alpha_{j} P_{j} Y_{i} \frac{1}{\left(1+\tau_{k j}\right) P_{k}}} K $ | (8) |
| $ L_{i}=\frac{\frac{\beta_{i} P_{i} Y_{i}}{\left(1+\tau_{l i}\right) P_{i}}}{\sum\limits_{j} \beta_{j} P_{j} Y_{i} \frac{1}{\left(1+\tau_{l j}\right) P_{i}}} L $ | (9) |
| $ M_{i}=\frac{\frac{\gamma_{i} P_{i} Y_{i}}{\left(1+\tau_{m i}\right) P_{m}}}{\sum\limits_{j} \gamma_{j} P_{j} Y_{i} \frac{1}{\left(1+\tau_{m j}\right) P_{m}}} M $ | (10) |
式中下标j表示行业i内的企业j。如果记θi为行业i产值占总产值的比重,α为产出份额加权的资本产出弹性,
| $ K_{i}=\frac{\frac{\theta_{i} \alpha_{i}}{1+\tau_{k i}}}{\sum\limits_{j} \theta_{j} \alpha_{j} \frac{1}{\left(1+\tau_{k j}\right)}} K=\frac{\theta_{i} \alpha_{i}}{\beta_{K}} \tilde{\lambda}_{k i} K $ | (11) |
| $ L_{i}=\frac{\frac{\theta_{i} \beta_{i}}{1+\tau_{l i}}}{\sum\limits_{j} \theta_{j} \beta_{j} \frac{1}{\left(1+\tau_{l j}\right)}} L=\frac{\theta_{i} \beta_{i}}{\beta_{L}} \tilde{\lambda}_{l i} L $ | (12) |
| $ M_{i}=\frac{\frac{\theta_{i} \gamma_{i}}{1+\tau_{m i}}}{\sum\limits_{j} \theta_{j} \gamma_{j} \frac{1}{\left(1+\tau_{m j}\right)}} L=\frac{\theta_{i} \gamma_{i}}{\beta_{M}} \lambda_{m i} M $ | (13) |
为了进一步分析,我们对“扭曲系数”作如下定义:
(1) 行业i的资本绝对扭曲系数为:
| $ \tilde{\lambda}_{k i}=\frac{\lambda_{k i}}{\sum\limits_{j}\left(\frac{\theta_{i} \alpha_{j}}{\alpha}\right) \lambda_{k j}}=\frac{K_{i} / K}{\theta_{i} \alpha_{i} / \alpha} $ | (14) |
(2) 行业i的劳动绝对扭曲系数为:
| $ \tilde{\lambda}_{l i}=\frac{\lambda_{l i}}{\sum\limits_{j}\left(\frac{\theta_{i} \beta_{j}}{\beta}\right) \lambda_{l j}}=\frac{L_{i} / L}{\theta_{i} \beta_{i} / \beta} $ | (15) |
(3) 行业i的中间投入绝对扭曲系数为:
| $ \tilde{\lambda}_{m i}=\frac{\lambda_{m i}}{\sum\limits_{j}\left(\frac{\theta_{i} \gamma_{j}}{\gamma}\right) \lambda_{m j}}=\frac{M_{i} / M}{\theta_{i} \gamma_{i} / \gamma} $ | (16) |
以资本相对扭曲系数为例,分子Ki/K表示行业i实际使用资本占工业总资本的比例,分母θiαi/α可以视作不存在要素错配时所使用的资本理论比例。若
由上可见,绝对扭曲系数与相对扭曲系数在刻画资源扭曲时含义不同,绝对扭曲系数刻画的是行业i面临的要素价格对无扭曲时的加成状况,体现的是资源使用成本绝对值信息。相对扭曲系数反映了经济环境中各种不同类型摩擦对部门间要素配置的影响。决定要素在行业间的配置的重要因素是要素价格相对扭曲程度,在实际中,绝对扭曲系数无法测度,但相对扭曲系数可以被还原出来。式(11)(12)(13)揭示了扭曲税在行业层面上对资本、劳动和中间投入配置的影响,扭曲税通过λ~Ji(J=K, L, M)影响资源在各个行业间的配置。扭曲税率绝对大小并不直接决定配置扭曲的大小,重要的是扭曲在行业间如何分布——i行业要素相对整个工业的扭曲状况影响着资源配置。
(二) 估计产出缺口由(1)(11)(12)(13)式可得,子行业i的代表性企业的产出为:
| $ Y_{i}=A_{i}\left(\frac{\theta_{i} \alpha_{i}}{\alpha} \cdot \tilde{\lambda}_{k i} \cdot K\right)^{\alpha_{i}} \cdot\left(\frac{\theta_{i} \beta_{i}}{\beta} \cdot \tilde{\lambda}_{l i} \cdot L\right)^{\beta_{t}} \cdot\left(\frac{\theta_{i} \gamma_{i}}{\beta} \cdot \tilde{\lambda}_{m i} \cdot M\right)^{\gamma_{t}} $ | (17) |
建立起要素价格的扭曲程度与产出之间的关系。对(17)式两边同时取对数,得:
| $ \begin{aligned} &\ln Y_{i}=\ln A_{i}+\ln \left[\theta_{i} \cdot\left(\frac{\alpha_{i}}{\alpha}\right)^{\alpha_{i}} \cdot\left(\frac{\beta_{i}}{\beta}\right)^{\beta_{i}} \cdot\left(\frac{\gamma_{i}}{\gamma}\right)^{\gamma_{i}}\right] \\ &+\left(\alpha_{i} \cdot \ln \tilde{\lambda}_{k i}+\beta_{i} \cdot \ln \tilde{\lambda}_{l i}++\gamma_{i} \cdot \ln \tilde{\lambda}_{m i}\right)+\left(\alpha_{i} \cdot \ln K+\beta_{i} \cdot \ln L+\gamma_{i} \cdot \ln M\right) \end{aligned} $ | (18) |
可见,子行业i的产出由以下几个方面决定:该行业的TFP水平Ai;子行业内部的要素产出弹性水平αi、βi、γi;生产要素的投入量L、K、M;所面临的要素市场上价格的相对扭曲程度
在式(5)的设定下,我们可以用实际产出和资源有效配置(不存在扭曲)的有效产出之间的比值表示各行业资源相对扭曲系数的函数,即产出缺口:
| $ \left(\frac{Y}{Y_{e}}\right)_{t}=\prod\limits_{i=1}^{N}\left[\frac{A_{i t}\left(\frac{\theta_{i t} \alpha_{i t}}{\alpha} \tilde{\lambda}_{k i t} K_{t}\right)^{\alpha_{i t}}\left(\frac{\theta_{i t} \beta_{i t}}{\beta} \tilde{\lambda}_{ {lit }}\right)^{\beta_{i t}}\left(\frac{\theta_{i t} \gamma_{i t}}{\gamma} \tilde{\lambda}_{\text {mit }}\right)^{\gamma_{i t}}}{A_{i t}\left(\frac{\theta_{i t} \alpha_{i t}}{\alpha_{t}} K_{t}\right)^{\alpha_{i t}}\left(\frac{\theta_{i t} \beta_{i t}}{\beta_{t}} L_{t}\right)^{\beta_{i t}}\left(\frac{\theta_{i t} \gamma_{i t}}{\gamma_{t}} M_{t}\right)^{\gamma_{i t}}}\right]=\prod\limits_{i=1}^{N}\left[\left(\tilde{\lambda}_{k i t}\right)^{\alpha_{i t}}\left(\tilde{\lambda}_{l i t}\right)^{\beta_{i t}}\left(\tilde{\lambda}_{m i t}\right)^{\gamma_{i t}}\right]^{\theta_{i t}} $ | (19) |
将总体产出进行分解,即可直观看出资源错配对总体TFP造成的损失。首先将加总函数取对数:
| $ \ln Y=\sum\limits_{i} \theta_{i} \ln Y_{i} $ | (20) |
代入(1)(11)(12)(13)式可得:
| $ \begin{aligned} \sum\limits_{i} \theta_{i} \ln Y_{i} &=\sum\limits_{i} \theta_{i} \ln A_{i}+\sum\limits_{i} \theta_{i} \alpha_{i} \ln \left(\frac{\theta_{i} \alpha_{i}}{\alpha}\right)+\sum\limits_{i} \theta_{i} \beta_{i} \ln \left(\frac{\theta_{i} \beta_{i}}{\beta}\right)+\sum\limits_{i} \theta_{i} \gamma_{i} \ln \left(\frac{\theta_{i} \gamma_{i}}{\gamma}\right) \\ &+\sum\limits_{i} \theta_{i}\left(\alpha_{i} \ln \tilde{\lambda}_{k i}+\beta_{i} \ln \tilde{\lambda}_{l i}+\gamma_{i} \ln \tilde{\lambda}_{m i}\right)+\alpha \ln K+\beta \ln L+\gamma \ln M \end{aligned} $ | (21) |
将前三项定义为:
| $ A=\sum\limits_{i} \theta_{i} \ln A_{i}+\sum\limits_{i} \theta_{i} \alpha_{i} \ln \left(\frac{\theta_{i} \alpha_{i}}{\alpha}\right)+\sum\limits_{i} \theta_{i} \beta_{i} \ln \left(\frac{\theta_{i} \beta_{i}}{\beta}\right)+\sum\limits_{i} \theta_{i} \gamma_{i} \ln \left(\frac{\theta_{i} \gamma_{i}}{\gamma}\right) $ | (22) |
则A是与资源分配无关的常数。同时,按照TFP的一般概念,定义总体TFP(索洛余项)为:
| $ A T F P=\sum\limits_{i} \theta_{i} \ln Y_{i}-\alpha \ln K-\beta \ln L-\gamma \ln M $ | (23) |
结合(21)可重写为:
| $ A T F P=A+\sum \theta_{i}\left(\alpha_{i} \ln \tilde{\lambda}_{k i}+\beta_{i} \ln \tilde{\lambda}_{l i}+\gamma_{i} \ln \tilde{\lambda}_{m i}\right) $ | (24) |
因此,总体TFP可以分解为两部分:前一项是与资源分配无关的常数A,可以理解为无扭曲状态下的最大TFP;后一项则可定义为行业间扭曲差异造成的资源错配效率损失(AL)。分别为:
| $ A L_{K}=\sum \theta_{i} \alpha_{i} \ln \tilde{\lambda}_{k i} $ | (25) |
| $ A L_{L}=\sum\limits_{i} \theta_{i} \beta_{i} \ln \tilde{\lambda}_{l i} $ | (26) |
| $ A L_{M}=\sum\limits_{i} \theta_{i} \gamma_{i} \ln \tilde{\lambda}_{m i} $ | (27) |
借鉴Syrquin(1986)的产出变动分解模型,假定在观察期内的每一期,整个行业均实现完全竞争均衡。则从t期到t+1期该行业的总产值变动可以定义为:
| $ \varDelta \ln Y_{t}=\ln Y_{t+1}-\ln Y_{t} $ | (28) |
根据多元一阶泰勒式可得:
| $ \varDelta \ln Y_{t} \approx \sum\limits_{i} \frac{\partial \ln Y_{t}}{\partial \ln Y_{i t}} \cdot\left(\ln Y_{i, t+1}-\ln Y_{i t}\right) $ | (29) |
基于
| $ \varDelta \ln Y_{t} \approx \sum\limits_{i} \theta_{i t} \varDelta \ln Y_{i t} $ | (30) |
将投入要素的变化表示为ΔXt=Xt+1-Xt,基于式(21),对产出的变动分解为:
| $ \begin{aligned} \varDelta \ln Y_{i t} &=\varDelta \ln A_{i t}+\ln \left[\left(\frac{\theta_{i, t+1}}{\theta_{i} t}\right) /\left(\frac{\alpha_{t+1}^{\alpha_{i}} \cdot \beta_{t+1}^{\beta_{i}} \cdot \gamma_{t+1}^{\gamma_{i}}}{\alpha_{t}^{\alpha_{i}} \cdot \beta_{t}^{\beta_{i}} \cdot \gamma_{t^{\prime}}^{\gamma_{i}}}\right)\right] \\ &+\left(\alpha_{i} \varDelta \ln \tilde{\lambda}_{k_{i t}}+\beta_{i} \varDelta \ln \tilde{\lambda}_{l_{u}}+\gamma_{i} \varDelta \ln \tilde{\lambda}_{m_{i t}}\right)+\left(\alpha_{i} \varDelta \ln K_{t}+\beta_{i} \varDelta \ln L_{t}+\gamma_{i} \varDelta \ln M_{t}\right) \end{aligned} $ | (31) |
代入式(30),可得:
| $ \begin{aligned} &\varDelta \ln Y_{t}=\underbrace{\sum\limits_{i} \theta_{i t} \varDelta \ln A_{i t}}_{A}+\underbrace{\sum\limits_{i} \theta_{i t} \ln \left[\left(\theta_{i, t+1} / \theta_{i t}\right) /\left(\alpha_{t+1}^{\alpha_{i}} \cdot \beta_{t+1}^{\beta_{i}} \cdot \beta_{t+1}^{\beta_{i}} / \alpha_{t}^{\alpha_{i}} \cdot \beta_{t}^{\beta_{i}} \cdot \gamma_{t}^{\gamma_{i}}\right)\right]}_{B}\\ &+\underbrace{\sum\limits_{i} \theta_{i t}\left(\alpha_{i} \varDelta \ln \tilde{\lambda}_{k_{i t}}+\beta_{i} \varDelta \ln \tilde{\lambda}_{l_{i t}}+\gamma_{i} \varDelta \ln \tilde{\lambda}_{m_{i t}}\right)}_{C}+\underbrace{\sum\limits_{i} \theta_{i t}\left(\alpha_{i} \varDelta \ln K_{t}+\beta_{i} \varDelta \ln L_{t}+\gamma_{i} \varDelta \ln M_{t}\right)}_{D} \end{aligned} $ | (32) |
其中,第A项是各子行业TFP变动的贡献;第B项是产出份额变动带来的贡献,体现资源重配对加总技术的影响;第C项是要素配置扭曲变化对产出的贡献,当C项趋于减少时,资源配置趋向于合理化,经济中的TFP和产出也将得到提升。在柯布道格拉斯加总生产函数的设定下,C项可以理解为产出缺口的变动;第D项是要素投入变动的贡献。
(五) 各行业要素配置相对扭曲变动对产出的影响Aoki(2012)框架在分析要素错配对生产率的影响时,可以识别单个行业、单个要素的配置扭曲对产出的影响程度,这为有关的政策分析提供了考证和支持。在一定的假设下,利用式(11)(12)(13)可以推导出i行业的资本、劳动和中间投入配置扭曲变动对产出变动的影响分别为:
| $ A E_{k i}=\theta_{i} \alpha_{i}\left(1-\frac{1}{\alpha}\right) \varDelta \ln \tilde{\lambda}_{k i} $ | (33) |
| $ A E_{l i}=\theta_{i} \beta_{i}\left(1-\frac{1}{\beta}\right) \varDelta \ln \tilde{\lambda}_{l i} $ | (34) |
| $ A E_{m i}=\theta_{i} \gamma_{i}\left(1-\frac{1}{\gamma}\right) \varDelta \ln \tilde{\lambda}_{m i} $ | (35) |
本文使用1999-2013年中国工业企业数据库,数据库面板构建、行业调整、指标插补、价格平减、派生指标的计算、样本筛选的具体处理过程参见笔者系列论文(李苏苏等,2020)。应付工资总额按照各地居民消费价格指数进行平减。工业包括国民经济行业分类表中BCD三个门类,即采矿业,制造业,电力、热力、燃气及水生产和供应业,共38个两位数代码行业。由于2010年关键指标皆缺失,借鉴王万珺、刘小玄(2018)的思路,对于2010年数据不予使用,将2009年和2011年视为连续年份。文中用到的主要变量有:工业总产值、工业增加值、实际资本存量、固定资产净值、工业中间投入、员工数量。基本变量描述统计如表 1所示。
| 表 1 基本变量的描述统计 |
可以看到,自2008年开始观测值数量呈现出明显下降,主要原因在于2008-2013年工业增加值、固定资产净值年平均余额缺失,本文对仅在这个区间出现的企业样本进行了删除处理。
(二) 企业TFP水平估计为了更贴近规模报酬不变的假定条件,本文采用面板数据约束模型(令αi+βi+γi=1)对38个两位数工业行业的企业TFP进行测度,并分别估计出各个企业的TFP(对数值)。其中企业的产出Yj用工业增加值表示,资本投入Kj用实际固定资产净值表示,劳动投入Lj用工人数来进行表示。得到资本、劳动和中间投入产出弹性系数,如表 2所示。从要素产出弹性的估计结果来看,中间投入系数在0.4~0.7之间,说明了中间投入在生产和效率提升中起着举足轻重的作用,在全要素生产率以及资源配置效率测度中,如果忽略中间投入的影响,会大大低估中间投入的作用和错估资源错配程度,这一结果也进一步说明本文为什么要使用陈永伟、胡伟民(2011)建立的理论框架来分析中国工业行业的资源配置效率。
| 表 2 两位数行业要素产出弹性估计 |
在计算出各企业的生产率之后,以每个企业的工业总产值占各行业总产值的比重为权重,加权得到行业的TFP值,如表 3所示。可以直观看到各行业间以及同一行业不同年份之间TFP值有较大差别。考察期内,多数行业的TFP值从1999年开始递增并在2007年达到阶段性峰值,此后呈持续性低生产率状态,或者在2011年前后呈现先升后降,这意味着2008年全球金融危机爆发以及2012年世界经济周期性衰退对中国工业部门有着显著冲击。特别是从2008年到2009年,行业TFP均呈现出明显的跌幅,甚至多数行业在2008年TFP对数值由正转负。可能因为2008年金融危机使得企业产出锐减,生产要素没有得到充分使用。而为应对金融危机,我国政府采取的投资刺激政策也在一定程度上加剧了市场价格机制失调和资源配置扭曲,挤占了企业TFP的增长空间。只有需求弹性较小的个别行业,如水的生产和供应业(46)受这种外部冲击的影响相对较小。从2007年数据可以看出,我国工业行业中黑色金属矿采选业(08)、非金属矿采选业(10)、农副食品加工工业(13)、废弃资源和废旧材料回收加工工业(43)的TFP值相对最高,说明中国工业部门中传统成熟的产业具有相对生产率优势,而在多数高新技术领域,如专用设备工业(36)、交通运输设备工业(37)、通信设备、计算机及其他电子设备工业(40)等行业生产率对数表现平平,并不突显。说明这些行业的生产率优势并没有得到有效发挥,生产要素的产出效率还有很大提升空间。
| 表 3 两位数行业的TFP值 |
计算出要素产出弹性后,按照(14)(15)(16)式的定义,计算全部两分类行业的资本价格相对扭曲系数、劳动价格相对扭曲系数和中间投入价格相对扭曲系数。附录表 1、表 2、表 3详细报告了1999-2013年期间资本、劳动和中间投入要素分别在各子行业间配置的扭曲程度。可以清晰了解到,不同行业相同生产要素以及同一行业不同生产要素之间的相对扭曲均存在较大程度的差异。
通过计算不同行业三种生产要素的相对价格扭曲系数的均值,总结如表 4所示。可见,煤炭开采和洗选业(06)、黑色金属矿采选业(08)、有色金属矿采选业(09)、燃气生产和供应业(45)、水的生产和供应业(46)这些行业的资本、劳动、中间投入相对价格扭曲系数均值都大于1,说明这些行业的要素使用成本相对过低,资本、劳动和中间投入的使用过度。相反,农副食品加工业(13)、烟草制品业(16)、金属制品业(34)、电气机械及器材工业(39)的资本、劳动和中间投入相对价格扭曲系数均值均小于1,说明这些行业面临过高的要素使用成本,资本、劳动和中间投入的投入和使用过少。
| 表 4 两位数行业的相对要素价格扭曲系数 |
石油和天然气开采业(07)资本扭曲系数均值为0.71,劳动力扭曲系数均值为1.18,中间投入扭曲系数均值为3.68,说明石油和天然气开采业资本使用成本相对过高,导致了资本的投入不足,而劳动和中间投入的成本过低,投入过度。化学原料及化学制品工业(26)资本扭曲系数均值为1.11,劳动力扭曲系数均值为0.93,中间投入扭曲系数均值为0.99,说明化学原料及化学制品工业资本使用成本过低,使得资本投入过多,而劳动和中间投入的成本过高,投入过少。
非金属矿采选业(10)、食品工业(14)、饮料工业(15)、纺织业(17)、木材加工及木、竹、藤、棕、草制品业(20)、造纸及纸制品业(22)、印刷业和记录媒介的复制(23)、橡胶制品业(29)、非金属矿物制品业(31)的资本和劳动力价格扭曲系数均值大于1,中间投入相对扭曲系数均值小于1,说明这些行业的资本和劳动投入过多,中间投入的使用过少。相反,交通运输设备工业(37)、通信设备、计算机及其他电子设备工业(40)、废弃资源和废旧材料回收加工工业(43)的资本和劳动投入过少,中间投入的使用过多。
纺织服装、鞋、帽工业(18)、皮革、毛皮、羽毛(绒)及其制品业(19)、家具工业(21)、文教体育用品工业(24)、医药工业(27)、塑料制品业(30)、通用设备工业(35)、专用设备工业(36)、仪器仪表及文化、办公用机械工业(41)、工艺品及其他工业(42)资本和中间投入扭曲系数小于1,劳动力相对扭曲系数均值大于1,说明这些行业的资本和中间投入使用过少,劳动的使用过多。相反,石油加工、炼焦及核燃料加工业(25)、化学纤维工业(28)、黑色金属冶炼及压延加工业(32)、有色金属冶炼及压延加工业(33)、电力、热力的生产和供应业(44)的资本和中间投入扭曲系数均值大于1,劳动力扭曲系数均值小于1,说明这些行业的资本和中间投入使用过多,劳动的使用过少。
(二) 相对扭曲系数的分组讨论在完成了对两位数行业资本扭曲系数、劳动扭曲系数、中间投入扭曲系数的测度后,进而以每个行业的工业总产值占整个工业总产值的比重为权重,计算出每个组别行业的加权平均相对要素扭曲系数。
1.按照轻、重工业分组
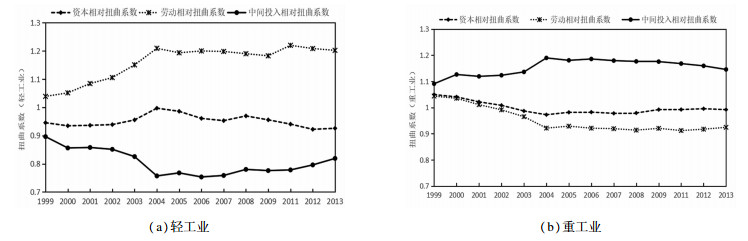
从图 1可以看出,轻重工业的要素价格相对扭曲系数有明显差异。轻工业行业的劳动相对扭曲系数均大于1且在1999-2004年间呈现明显的逐年上升趋势,在2004-2013年间表现平稳,说明中国轻工业部门存在着较为明显的劳动力投入过度问题但已有所控制。资本和中间投入相对扭曲系数均小于1,说明轻工业的资本和中间投入存在投入量偏少问题,尤其是中间投入的使用更低。相应地,重工业部门的资本相对扭曲系数接近1,配置较为合理。劳动扭曲系数介于1和0.9之间,总体表现平稳,说明相对轻工业部门来说,重工业部门对劳动要素配置接近合理。中间投入相对扭曲系数介于1.1~1.2之间,说明重工业部门的中间投入过多。
|
图 1 按照轻重工业分组 注:轻工业行业代码有:13、14、15、16、17、18、19、20、21、22、23、24、27、28、29、30、41、42。重工业行业代码有:25、26、31、32、33、34、35、36、37、39、40、43。 |
2.按照生产技术水平分组
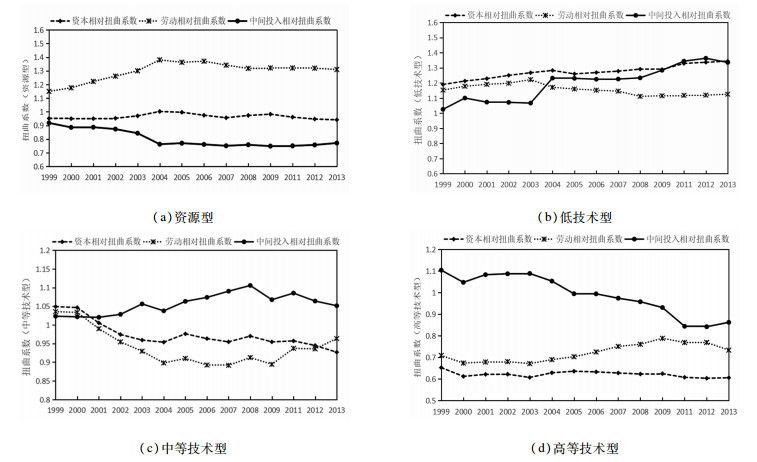
若是将工业行业按照生产技术水平分为4组,从图 2可以看出,三大要素价格扭曲系数在四大行业部门间也存在较大差异。资源型产业劳动投入过多,中间投入的使用相对过少,资本投入相对较为合理;低技术行业各要素的投入量都明显偏高,尤其是中间投入和资本仍旧处于逐年上升状态;中等技术型行业的中间投入使用偏多,2008年开始逐步改善,资本和劳动的投入相对较少;高等技术型行业的生产要素的配置严重偏少,在考察期内一直没有得到有效重视。联系上文不难理解在二位数行业TFP中相应的高新技术产业并没有呈现出期待中的生产率优势的原因了。
|
图 2 按照生产技术水平分组 注:资源型行业代码有:13、14、15、16、20、25、29、31;低技术型行业代码有:17、18、19、21、22、23、24、34、42;中技术型行业代码有:26、28、30、32、33、35、36、37、43。高技术型行业代码有:27、39、40、41。 |
3.按照要素密集度分组
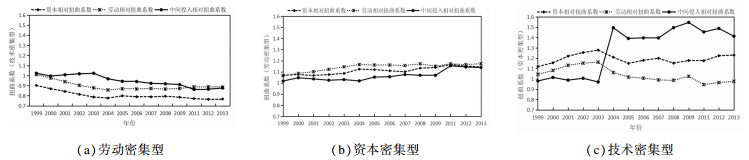
若按照要素密集度分,将行业分为技术密集型、资本密集型、劳动密集型产品产业。如图 3所示,劳动密集型行业所投入的生产要素偏多但尚处于一个可接受范围,对资本密集型行业的投入明显不足,而对于技术密集型行业投入了过量的原材料等中间投入和资本,且长期处于这种状态。
|
图 3 按照行业要素密集度分组 注:技术密集型行业代码有:26、27、28、35、36、37、39、40、41;资本密集型行业代码有:22、23、25、31、32、33、34;劳动密集型行业代码有:13、14、15、16、17、18、19、20、21、24、29、30、42、43。 |
4.按照GVC驱动类型分组
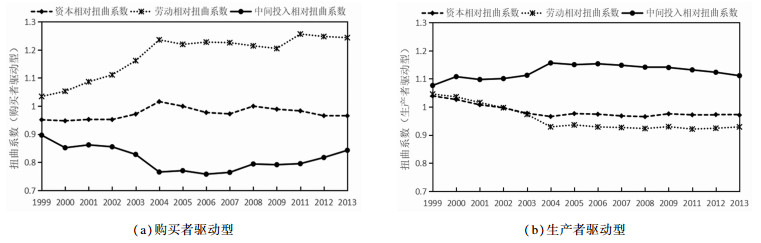
按照GVC驱动类型分组,分成购买者驱动型、生产者驱动型行业。如图 4所示,购买者驱动型行业内部要素的扭曲系数差异巨大,而生产者驱动型行业的差异相对较小。购买者驱动型行业投入了过多的劳动,过少的中间投入,资本要素的投入趋于合理。生产者驱动型行业的中间投入相对过多,资本和劳动要素的投入相对较少,总体状态较为平稳。
|
图 4 按照GVC驱动类型分组 注:购买者驱动型行业代码有:13、14、15、16、17、18、19、20、21、22、23、24、29、30、42;生产者驱动型行业代码有:25、26、27、28、31、32、33、34、35、36、37、39、40、41、43。 |
5.按照生产产品上下游类型分组
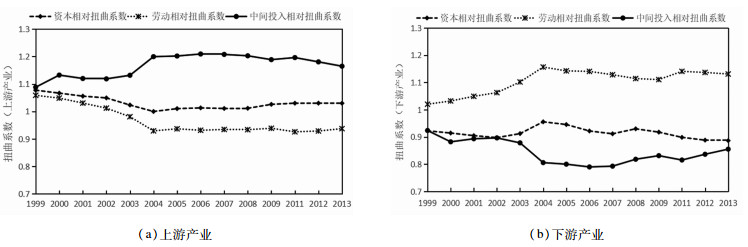
按照所生产产品上下游类型分组。如图 5所示,上游产业的中间投入相对过多,劳动投入相对过少,资本投入较为合理;而下游产业劳动投入过多,资本和中间投入相对过少,尤其可以加大对中间投入的使用。
|
图 5 按照所生产产品上下游产业分组 注:上游产业的行业代码有:25、26、28、29、31、32、33、35、36、37、39、40、41;下游产业的行业代码有:13、14、15、16、17、18、19、20、21、22、23、24、27、30、34、37、42、43。 |
6.按照所生产产品竞争程度分组
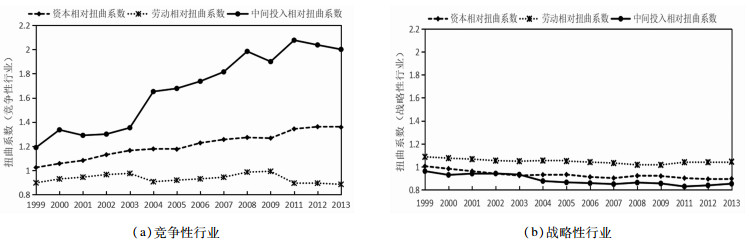
按照所生产产品竞争程度可分为战略性行业和竞争性行业。如图 6所示,两种类型产业的生产要素扭曲程度差异显著。竞争性行业的中间投入和资本投入过多,且呈现出逐年递增状态,劳动投入相对过少且表现平稳。相比而言,战略性行业的劳动投入偏多,中间投入和资本投入偏低,且都保持相对平稳的可接受范围。
|
图 6 按照所生产产品上下游类型分组 注:竞争性行业的行业代码有:13、14、15、17、18、19、20、21、22、23、24、26、28、29、30、31、34、35、36、37、39、40、41、42、43;战略性行业的行业代码有:16、25、27、32、33。 |
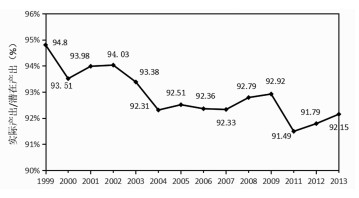
这里在生产函数(1)的设定下根据式(19),估算出各年的产出缺口,即各年实际产出和潜在产出的比例,结果如图 7所示。整体而言,自1999年始,中国工业部门的实际产出和潜在产出的比例总体趋势是下降的,表明考察期内工业部门的产出缺口在持续扩大。从1999年的94.8%下降到2011年的91.49%;2012-2013年逐步上升,2013年达到92.15%。说明虽然中国工业经历了高速发展,但还具有可观的发展潜力。1999-2013年实际产出与有效产出的平均比值为92.90%,平均产出缺口为8%,说明即使不增加投入,也能通过有效消除行业间资本、劳动和中间投入的配置扭曲,使得工业产出提升8%。若按照2011年的水平测算,则可能使产出提高近10%。
|
图 7 历年产出缺口 |
在估算出各行业要素相对扭曲系数以后,我们可以根据(25)(26)(27)式计算行业间资本、劳动力和中间投入要素扭曲差异所造成的产出或效率损失,结果如图 8所示。

|
图 8 资源错配造成的产出损失 |
通过计算可得,要素错配使整体产出或TFP降低了7.39%(算术平均值),在某些年份接近9%(如2011年)。从时间趋势上来看,考察期行业间劳动、资本、中间投入三大要素配置扭曲的变动对工业部门总生产效率和产出的影响均为负数,其中劳动价格扭曲变动对制造业总生产效率和产出的贡献表现较为平稳,中间投入品价格扭曲变动对TFP与产出的影响最大且呈现扩大趋势。2003年前,各要素的配置效应有所恶化但程度较轻,此后劳动和资本的资源配置效应有所改善且各年相差不大,中间投入的配置效应却出现严重恶化,对整体产出或TFP造成的损失高达6.4%,成为导致产出与效率损失的主要原因,这也反应出前期学者只研究劳动和资本配置扭曲对TFP和产出的影响存在局限性,中间投入的有效配置成为工业产出和TFP损失不可忽视的因素。
对比图 7估计的历年产出缺口可见,中间投入错配造成的效率损失和产出缺口的走势和形态高度一致,再次说明了中间投入配置扭曲在总体经济效率损失中的重要负面影响。中美贸易摩擦以来,为应对外部需求冲击和逆全球化对中国经济正常运行的影响,中央提出了双循环的发展战略,而如何加快和建立国内国外的双循环体系,学者们提出了诸多有价值的政策建议,而本文的研究为加快和建立国内循环体系提供了学理支持。图 7和图 8清晰表明,考虑到中间投入错配是国内商品、货物以及要素的主要错配体现,尽快纠正中间投入的价格扭曲,进而优化中间投入在行业之间的配置效率,不仅可以提高总量生产率水平,而且可以在不动用更多资源和更多宏观政策的情况下弥补产出缺口,进而实现经济总量的稳步提升和快速增长。
(五) 分解产出变动接下来,根据(32)式考察纠正扭曲对制造业产出和TFP变动的影响。将产出在1999-2013年的变动分解为行业生产率变动贡献(A)、产出份额变动贡献(B)、配置扭曲变动贡献(C)和要素投入变动贡献(D)。将结果整理如表 5所示。
| 表 5 产出变动与分解结果 |
通过分解可见,结论与我国工业部门的发展现实相符合。(1)在拉动中国工业高速发展的决定因素中,要素投入增长的作用(D)依旧是非常大的,对产出的平均贡献率达到10.8%。表明我国工业部门粗放型增长模式尚未得到根本改变。(2)工业总体生产效率水平的表现并不平稳,各年间差异很大,增长主要依靠各子行业TFP的演进,有赖于行业内部各企业的技术进步和创新。份额效应(B)和扭曲改变效应(C)的作用微乎其微。(3)观察期内各年间的要素投入变动贡献差异明显,从均值上来看,资本和劳动的贡献率相当,中间品投入的贡献率最大。
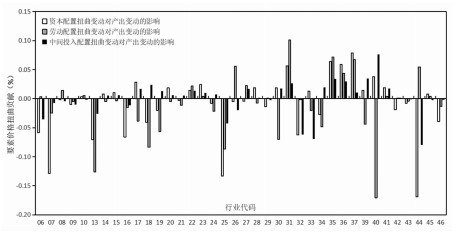
(六) 各行业要素价格扭曲变动对产出的影响按照(33)(34)(35)计算各个行业的要素价格变动对TFP和产出变动的贡献。限于篇幅,我们只列出了各行业1999-2013年要素价格扭曲变动的平均贡献,结果呈现在图 9中。总体而言,不同行业的不同要素价格扭曲的产出贡献差异很大,并且确实在很多行业存在大量的要素价格扭曲问题,严重影响了行业的资源配置效率和产出水平,即使是正面影响,很多行业看起来还是“微乎其微”,说明加大行业要素资源配置效率的空间巨大。具体而言,可以发现,石油和天然气开采业(07)、农副食品加工业(13)、石油加工、炼焦及核燃料加工业(25)这三个行业中,三种要素的价格扭曲和资源错配均对效率和产出造成了严重的负面影响。而非金属矿物制品业(31)、通用设备工业(35)、专用设备工业(36)这三个行业中,三种要素均得到优化配置,对总量生产率和经济产出产生了正面作用。
|
图 9 各行业要素价格扭曲变动的贡献 |
与此同时,在造纸及纸制品业(22)、印刷业和记录媒介的复制(23)、非金属矿物制品业(31)、通用设备工业(35)、专用设备工业(36)、交通运输设备工业(37)、仪器仪表及文化、办公用机械工业(41)、燃气生产和供应业(45)行业,通过纠正要素价格扭曲,对产出的贡献已经产生了较大的正面影响。而在石油和天然气开采业(07)、有色金属矿采选业(09)、农副食品加工业(13)、烟草制品业(16)、纺织服装、鞋、帽工业(18)、皮革、毛皮、羽毛(绒)及其制品业(19)、石油加工、炼焦及核燃料加工业(25)、黑色金属冶炼及压延加工业(32)、有色金属冶炼及压延加工业(33)、金属制品业(34)、电力、热力的生产和供应业(44)等行业要素价格扭曲的加剧对工业产出的贡献产生了严重的负面影响。
五、造成行业间资源错配的摩擦因素分析借鉴张佩(2013)的研究,我们将行业间相对扭曲系数与行业特征变量相联系,探究导致资源错配的摩擦因素。考察的行业特征变量包括:(1)行业集中度CR10,由于销售产值存在大量的缺漏值,本文采用行业中前十家企业工业总产值之和占行业的比重来衡量该行业竞争程度;(2)国有企业比重SOES,为国有企业总产值占行业总产值的比重,用以衡量该行业国有化程度;(3)资本份额α,为“1-劳动份额(劳动回报占增加值的比重)”,衡量行业的资本密集度;(4)中西部企业比重MWS,为中西部企业增加值总额占全国的比重。对行业和年份进行双向固定,建立回归模型:
| $ \ln \tilde{\lambda}_{J i t}=\beta \ln X_{i t}+\mu_{i}+\theta_{t}+\varepsilon_{i t} $ | (36) |
其中,β为待估系数,Xit为解释变量向量,μi为固定效应,εit为随机误差项,θt为时间哑变量。本文对被解释变量和解释变量均取对数,采用双对数模型。得到表 6回归结果。
| 表 6 造成行业间资源错配的摩擦因素回归分析 |
如表 6所见,得到的结果与张佩的研究结论有所差异但更贴近中国工业部门与工业企业发展的状态。(1)三个模型中,行业集中度(lnCR10)的系数均显著为正,这说明行业集中度越高的产业,投入的要素过度现象更为明显,资源配置扭曲程度更高,存在大量的资源浪费,比较而言,行业间的资本相对扭曲程度比劳动和中间投入的相对扭曲程度更高。工业领域行业集中度高的产业通常具有较大程度的垄断属性,其中以与国家基础设施、国防军工等领域相关行业较多,得到国家的政策和资金支持相对较大,因此更可能出现资本的相对扭曲。(2)国有企业比重(lnSOES)资本和中间投入扭曲系数显著为正,劳动相对价格扭曲系数为负但系数很小且并不显著,说明国有企业份额越高的行业可能投入过多的资本和中间投入。可能因为国有企业通常可以更容易地获得成本较低的信贷,在原材料等中间投入的配给上也没有其他性质的企业“精打细算”。(3)资本份额(lnα)的系数均显著为负,说明重资本类型的行业在资本、劳动和中间投入上均存在不同程度的配置扭曲,尤其是在资本和劳动要素上非常明显。(4)中西部企业份额(lnMWS)的系数只有在中间投入相对价格扭曲系数上显著为负,存在中间投入的配置扭曲,在资本和劳动的配置效率上和东部地区并无显著差异。
六、结论与启示本文以1999-2013年中国工业企业数据库为研究样本,重点测算了中国制造业行业间的资源错配的程度及其发展趋势,分析了资源错配对产出和TFP的影响,并对造成行业间资源错配的摩擦因素进行分析。发现不同行业同一生产要素以及同一行业不同生产要素之间的相对扭曲均存在较大差异。在时间趋势上,考察期内行业间的劳动、资本、中间投入对产出的扭曲变动效应均为负数,中间投入扭曲带来的影响>资本扭曲带来的影响>劳动扭曲带来的影响。因此,需高度重视中间投入所带来的资源扭曲问题。资源错配造成了中国工业部门实际产出占潜在产出的比例逐年下降,产出缺口高达10%。资本错配造成的效率损失是劳动错配损失的2倍,中间投入造成的资源错配效率损失是劳动错配损失的4倍。要素投入增长依旧是中国工业发展的决定因素,各行业TFP的提升主要动力源于各个行业总体TFP的增长,份额效应和扭曲改变效应微乎其微。针对行业间的资源错配,需加快产业结构调整,在部门间实现要素的自发流动,从低效率行业流向高效率行业,实现对落后产能的淘汰、传统产业的改造升级,以及高科技新兴产业的布局来实现整体工业资源配置效率的提高。
本文研究有两个重要启示:(1)纠正要素价格扭曲仍然是优化资源配置效率的根本前提。研究表明,要素价格的扭曲是造成行业之间资源配置效率损失以及经济产出缺口的根本原因,因此,可以在不加大投入的情况下,通过深化要素价格改革来避免经济增速的持续下滑和提升经济效率水平,而且这个改革举措是成本较低但效果较大的措施。(2)优化行业之间的资源配置效率,尤其是中间投入的资源配置效率,是构建国内国际双循环相互促进的新发展格局的重要举措。改革开放后,我国利用劳动力低成本优势,积极参与国际分工与国际经济大循环,市场和资源“两头在外、大进大出”,通过产业不断升级提高在全球价值链中的位置,逐步成长为“世界工厂”。但目前在外部环境发生深刻复杂变化,世界经济持续低迷、全球市场萎缩、保护主义上升的背景下,从被动参与国际经济大循环转向主动推动国内国际双循环,加快形成以国内大循环为主体、国内国际双循环相互促进的新发展格局,是在一个更加不稳定不确定的世界中谋求我国发展的大战略,是适应内外环境变化的重大战略调整。而提升不同行业之间的要素配置效率,尤其是考虑到中间投入在国内大循环中的重要性,加快中间投入要素配置效率就是构建以国内大循环为主体,畅通国内大循环,推动形成国内国际双循环,为我国经济发展增添新动力的应然之举。
附录、分行业的资本、劳动以及中间投入价格的相对扭曲系数| 表 7 两位数行业的资本要素价格相对扭曲系数 |
| 表 8 两位数行业的劳动要素价格相对扭曲系数 |
| 表 9 两位数行业的中间投入要素价格相对扭曲系数 |
| [] |
陈永伟、胡伟民, 2011, “价格扭曲, 要素错配和效率损失: 理论和应用”, 《经济学(季刊)》, 第 4 期, 第 1401-1422 页。 |
| [] |
邓富华、沈和斌, 2020, “进口贸易自由化对制造业资源错配的影响——基于中国加入WTO的自然实验”, 《国际经贸探索》, 第 6 期, 第 73-88 页。 |
| [] |
龚关、胡关亮, 2013, “中国制造业资源配置效率与全要素生产率”, 《经济研究》, 第 4 期, 第 4-15 页。 |
| [] |
韩国珍、李国璋, 2015, “要素错配与中国工业增长”, 《经济问题》, 第 1 期, 第 69-76 页。 |
| [] |
李苏苏、叶祥松、张少华, 2020, “中国制造业企业全要素生产率测度研究”, 《学术研究》, 第 3 期, 第 105-113 页。 |
| [] |
姚战琪, 2009, “生产率增长与要素再配置效应: 中国的经验研究”, 《经济研究》, 第 11 期, 第 130-143 页。 |
| [] |
邵挺, 2010, “金融错配”, 《所有制结构与资本回报率: 来自1999~2007年我国工业企业的研究", 《金融研究》, 第 9 期, 第 47-63 页。 |
| [] |
唐志军、苏丽, 2019, “资源错配与我国经济发展研究述评”, 《湖北经济学院学报》, 第 2 期, 第 16-28 页。 |
| [] |
王文、牛泽东, 2019, “资源错配对中国工业全要素生产率的多维影响研究”, 《数量经济技术经济研究》, 第 3 期, 第 20-37 页。 |
| [] |
文东伟, 2019, “资源错配, 全要素生产率与中国制造业的增长潜力”, 《经济学(季刊)》, 第 2 期, 第 617-638 页。 |
| [] |
任韬、孙潇筱、褚晓琳, 2020, “重点行业资本配置扭曲对中国全要素生产率的影响”, 《经济与管理研究》, 第 1 期, 第 63-77 页。 |
| [] |
杨帆、徐长生, 2009, “ 中国工业行业市场扭曲程度的测定”, 《中国工业经济》, 第 9 期, 第 56-66 页。 |
| [] |
张佩, 2013, “中国工业部门的行业间资源错配研究”, 《投资研究》, 第 6 期, 第 15-27 页。 |
| [] |
周新苗、钱欢欢, 2017, “资源错配与效率损失: 基于制造业行业层面的研究”, 《中国软科学》, 第 1 期, 第 183-192 页。 |
| [] |
Ao ki, S ., 2012, "A Simple Accounting Framework for the Effect of Resource Misallocation on Aggregate Productivity". Journal of the Japanese and International Economies, 26(4), 473–494.
DOI:10.1016/j.jjie.2012.08.001 |
| [] |
Hsieh C.T., Klenow. P.J., 2009, "Misallocation and Manufacturing TFP in China and India". Quarterly Journal of Economics, 124(4).
|
| [] |
Hsieh C.T., Song Z., 2015, "Grasp the Large". Let Go of the Small: The Transformation of the State Sector in China", Brookings Papers on Economic Activity, 295–366.
|
| [] |
Syrquin M., 1986, "Productivity Growth and Factor Reallocation in Industrialization and Growth: A Comparative Study", Oxford: Oxford University Press: 229-262.
|




