以新古典经济学为核心的现代经济学以“经济人”假设为基础,以追求自身利益最大化为目标,以利己作为个人行为选择的内在依据(杜书伟、郑大喜,2009;章平、黄傲霜,2018)。然而,随着行为经济学的发展,经济学家发现人的行为部分偏离自利假设,有一定程度的利他倾向。这点在医疗领域更明显,因为利他性是医生职业规范和医学专业精神的重要组成部分之一(Jones, 2002)。医疗服务市场具有两个显著的特征,即医患的信息不对称性和医疗服务与健康结果的不确定性。这使得患者不能在接受医疗服务之前判定服务的质量,对医生具有较高的依赖性。另一方面,医疗资源有限,而目前的支付机制设计难以实现医生利益和患者利益同时达到最优,这使得医生不可避免地要在医院利润和患者利益之间权衡。医生决策过程中医患双方的委托代理关系及由此产生的道德损害问题使管理者难以设计有效的最优契约治理医生的行为(Choné and Ma, 2011; McGuire, 2000)。但是,利他性作为一种内在动机即便在没有外部干预的情况下依然可以内在激励医生提供高质量的医疗服务(Leonard and Masatu, 2010; Barigozzi and Burani, 2016; Lagarde and Blaauw, 2017)。所以,医疗服务过程中人们希望医生能够更多地关注患者健康福利,充分地体现其利他性。
将患者健康效益纳入医生效用函数是医生利他性分析的基本范式。自从Arrow (1963)强调了医疗服务市场中医生仁慈动机的重要性,利他性医生的假设在医生行为分析中广泛应用(Chalkley and Malcomson, 1998; Choné and Ma, 2011; Ellis and McGuire, 1986, 1990; Jack, 2005)。Ellis and McGuire (1986)在医生效用函数中加入了患者健康效益,医生对患者健康效益的关注可认为具有利他性,可通过患者健康效益对医院利润的边际替代率表示,即医生为了增加一单位患者健康效益愿意牺牲多少单位个人收益。在此理论模型的基础上,学者探讨了利他性对支付方式选择的重要意义(Chalkley and Malcomson, 1998; Allard et al., 2011; Liu and Ma, 2013)。但相关的实证较少,主要是因为医生决策的复杂性及利用现场数据量化医生和患者收益的困难性(Galizzi et al., 2015)。
显示偏好理论和实验经济学的发展为医生利他性测量提供了理论和方法学的支持。显示性偏好原理认为决策者的选择暴露或显示了其偏好,所以独裁者博弈中独裁者偏离纯自利纳什均衡的分配可显示其利他偏好。Andreoni and Miller (2002)通过一组独裁者实验发现参与人的行为基本符合广义显示偏好原理,说明包含了利他偏好的效用函数是连续、单调的凸函数,经济学模型可用来研究利他偏好并予以量化(陈叶烽等,2011)。Brosig-Koch et al. (2017)基于Ellis and McGuire (1986)的模型,通过模拟医疗决策情景下独裁者博弈的实验室实验测量了医生的利他性。Li (2018) and Li et al. (2017)通过修正的独裁者博弈实验,利用不变替代弹性效用函数估计了医生的利他性。以上研究假设医生始终选择效用最大化决策,效用函数为确定性形式。但是,医生的选择可能具有随机性和不一致性,引入随机效用模型的分析产生了另外一种利他性测量的方式。在随机效用模型中,决策者并不总是选择效用最高的选项。Godager and Wiesen (2013)利用Hennig-Schmidt et al. (2011)的实验数据,通过随机效用模型估计了医生的利他性。也有不少学者通过基于随机效用模型的离散选择实验测量医生的经济动机(e.g., Lagarde et al., 2013; Scott et al., 2013; Honda et al., 2019),但它们并未涉及医生在自身利益和患者健康效益间的权衡,无法实现其对患者健康效益偏好的测量。
因此,现有研究中对医疗决策情景下医生利他性测量形成了两种分析范式。一是基于效用最大化模型的医生效用函数计算利他性(Brosig-Koch et al., 2017; Li, 2018; Li et al., 2017),二是基于随机效用模型(Godager and Wiesen, 2013)估算医生利他性。但两类研究分别测量未见交叉,测量结果是否具有相关性和可比性尚未知晓。本研究欲基于显示偏好原理并采用模拟医疗决策情景下的独裁者博弈实验,通过医生效用函数和随机效用模型分别测量医生的利他性,进一步探究两种方法下测量的利他性是否具有相关性及不同方法可能存在的问题。研究发现,纳入研究的医学生受试者利他性总体处于较高水平,对患者健康效益的重视程度大于自身利益。但不同个体利他性存在异质性,少数个体始终选择患者健康效益最优决策。利他性越高的个体对患者健康效益的重视程度相对自身利益更大。
本文主要存在以下贡献:首先,本文医生利他性测量所依托的支付方式在以往研究按项目付费(fee-for-service, FFS)和按人头付费(capitation, CAP; Hennig-Schmidt et al., 2011; Brosig-Koch et al., 2016, 2017)的基础上结合目前医疗决策情景设计按疾病诊断相关分组付费(diagnosis related groups, DRGs)和优化设计的按项目付费,丰富了不同支付方式下医生利他性研究。其次,本文同时利用医生效用函数和随机效用模型测量医生的利他性,进一步检验了两种方法的可行性。最后,本文将两种方法的测量结果进行对比研究,检验两种方法的测量结果是否具有一致性,为后续研究对于测量方法的选择提供依据。
二、文献综述 (一) 医生利他性测量的意义利他性在经济学中通常被定义为对纯粹自利行为的偏离,以自己的代价造福他人的行为;在卫生经济学领域,利他性被嵌入到医患关系中,被定义为在医生的效用函数中除了对自身利益的考虑外,对患者健康效益的重视(Galizzi et al., 2015; 韩优莉、张悦,2020)。
医生利他性的测量对于支付方式的选择具有重要意义。学者在对医生支付机制的规范研究中,通常基于不同的利他性假设前提下分析支付方式的效果。在利他性未知的前提下的规范研究提出最优的支付方式决定于利他性的水平。Jack (2005)研究指出在非对称信息下医生的行为是不可契约化的,需要设计激励机制使医生揭示他们的利他类型,此时非线性的支付方案是最优的。Choné and Ma (2011)构建了信息不对称下的医生代理模型,其中患者对健康效益的评估以及医生对患者健康效益和自身利润的权重对于支付方是未知的,均衡机制取决于医生的利他水平。Liu and Ma (2013)研究表明对于医生的支付应考虑医生的利他水平的差异。在利他性已知或固定的假设前提下,不同利他程度医生的最优支付方式不同。Ellis and McGuire (1986)研究指出如果医生是患者完美的代理人,完全的预付制就是最优的;Chalkley and Malcomson (1998)研究表明对于利他性医生,预付制将导致最优的降低成本的努力、积极的提升服务质量的倾向但次优的服务质量;Eggleston (2005)研究显示对于利他性较高的医生应该按人头支付而不需要考虑疾病的严重程度;Barham and Milliken (2015)研究指出利他的医生主要治疗脆弱患者应该按项目付费,而非利他的医生治疗健康病人应该采取按人头付费。因此,如何测量利他性成为医生激励机制选择和优化的重要前提。
(二) 医生利他性测量的理论与方法利他性被认为是私人信息,显示性偏好理论为利他性的测量提供了理论基础。显示性偏好原理(Samuelson, 1938)建立在追求效用最大化、理性选择、偏好稳定基础上,认为消费者根据偏好所选择的商品或商品组合必然是效用最大化的,“效用最大化”正是通过消费者的选择行为“显示”出来的(叶航,2003;周小亮、笪贤流,2009)。基于显示性偏好原理,经济学领域对利他性的测量可通过行为和实验经济学的方法,通过其决策行为显示其利他性偏好,常用方法有独裁者博弈和最后通牒博弈等。但如果效用无法计量就难以说明消费者的选择是由偏好或效用最大化所决定,基数效用理论假设效用可计量,消费者的选择以效用最大化为目标,效用可以进行大小比较与加总求和。以此为基础的医生效用函数可以量化医生的利他性。但是,有学者认为决策行为具有随机性和不一致性,当重复面对两个相同选项时,被试在各种情况下可能并不总是选择相同选项(Davidson and Marschak, 1959; Luce, 1959; Tversky, 1969; Camerer, 1989; Hey and Orme, 1994; Agranov and Ortoleva, 2017)。因此,有学者提出在传统的效用函数基础上添加一个随机成分(e.g., Thurstone, 1927; Marschak, 1960; McFadden, 1974, 2001)。这就构成了现有研究中的两种利他性测量的研究范式。
1. 基于医生效用函数计算的利他参数
Ellis and McGuire (1986)构建的医生效用函数将患者健康效益纳入其中,即医生效用由医生提供医疗服务带来的收益和医生决策给患者带来的健康效益构成。根据满足医生效用最大化的效用函数的一阶条件
2. 基于随机效用模型估算的医生利他参数
随机效用模型中医生的效用函数加入随机成分, 包含两部分,即固定效用和随机效用。固定效用可通过观测要素来解释,随机部分表示未被观测到的效用和观测误差(个体偏好的差异)产生的影响(聂冲、贾生华,2005)。假定随机项εni服从独立同分布极值(independent and identically distributed extreme value, ⅡD),可用计量经济学模型(Logit模型或Probit模型)估计观测要素的系数,进一步通过可观测要素xm的估计系数比值计算边际替代率。在医生效用函数中计算患者健康效益与医生利润的边际替代率,可实现利他性的测量。Godager and Wiesen (2013)利用Hennig-Schmidt et al. (2011)以德国医学生为被试的实验数据,通过随机效用模型(混合logit、多项式logit模型)对医生的利他性进行估计。计算患者健康效益与医生利润的边际替代率,即利他参数,结果显示医学生中44%对患者健康效益的权重更大,29%对患者健康效益和个人利润权重相等,26%对个人利润的权重更大。
不同利他性测量方法的研究对于医生利他性估计显示具有一致性。Godager and Wiesen (2013)、Brosig-Koch et al. (2017)研究均显示医生利他性存在异质性,“一刀切”的支付方式无法实现最佳医疗服务量。可以看出对医生支付方式的设计依赖于医生利他性的状况,揭示和测量医生的利他性是优化支付机制设计的前提和关键。但是,上述研究是在不同的实验情景和实验对象下做出的,不能够进行直接的比较。本研究基于同一医疗决策情景下的实验设计,分别用两种方法对医生利他性进行测量,以比较两种测量方法的一致性和差异性。
三、实验设计基于Ellis and McGuire (1986)的模型及Hennig-Schmidt et al. (2011)、Brosig-Koch et al.(2016, 2017) 的实验设计,我们设计了按项目付费(FFS)和按疾病诊断相关分组付费(DRGs)及其不同比例混合支付下医生决策行为的受控实验室实验,实验局设置见表 1。实验模拟医生医疗决策情景,采取被试内设计,每名被试仅参与一个实验局。实验任务为医学生担当医生在单一按项目付费(FFS)或按疾病诊断相关分组付费(DRGs)及其相应混合支付下根据电脑屏幕显示的患者类型、服务量、诊疗费用、成本、个人利润、患者健康效益为虚拟患者选择要提供的医疗服务项目数量q。医生的决策同时决定了自身利润π(q)和患者健康效益B(q),两者均以实验代币的形式表示,实验结束后按10:1的比例转换成人民币分别支付给受试者和捐赠给慈善机构(中国红十字会)。具体来说,医生需要为3种疾病(A、B、C)和3种严重程度轻、中、重(1、2、3)组合的9种患者(A1……C3)从0-10范围内选择一个整数代表其所要为每个患者提供的医疗服务项目数量。实验共进行5轮,每轮中患者的数量和类型保持不变,患者顺序预先设定为A1、B1、C1、A2、B2、C2、A3、B3、C3。实验中假设患者为医保全覆盖且被动接受医生所提供的医疗服务项目数量。
| 表 1 实验局设置 |
按项目付费(FFS)下设定每单位服务量的补偿价格为p,医生提供的服务量q越多,获得的利润(π(q)=pq-c(q))越多。考虑到有三种疾病类型(A、B、C)的患者,设定了三种补偿价格(pA、pB、pC)。即同种疾病类型的患者每单位服务量补偿价格相同,不受疾病严重程度影响。医生最大利润水平π(q^)以患者最佳健康效益B(q*)为参照,同时满足在q=10处取得最大值。
按疾病诊断相关分组付费(DRGs)设计为多病组的按人头付费,针对每个不同类型的患者设定固定的支付额(lump-sum, L)。因为3种疾病类型和3种严重程度类型组合产生了9种患者类型(A1……C3),所以设定了9种不同的固定支付额。每种患者类型的固定支付额与按项目付费下医生为该患者提供患者最佳健康效益服务量(q*)时所获收益一致。医生提供的服务量越少,获得的利润(π(q)=L-c(q))越多。具体设计如下:
(一) 患者健康效益患者健康效益B(q)采取对称设计,为服务量q的凹函数,表示同等程度的服务不足和过度医疗对患者健康效益的损失一样。即:
| $ B(q)=B_{0}+\theta q\left(q \leq q^{*}\right), B(q)=B_{1}-\theta q\left(q \geq q^{*}\right), B_{1}=B_{0}+2 \theta q^{*} $ |
B0为初始健康状态,疾病严重程度越轻该值越大,9种患者A1、A2、A3、B1、B2、B3、C1、C2、C3分别为4、2、0、7、5、3、8、4、0。θ为患者健康边际效益,仅受疾病类型影响,A、B、C分别为1、1、2。q*为患者健康效益取得最大值时对应的服务量,仅受疾病严重程度轻、中、重(1、2、3)的影响,对应q*分别为3、5、7。患者健康效益的最大值B(q*)仅受疾病类型的影响,A、B、C分别为7、10、14。具体设计如表 2所示。
| 表 2 患者健康效益的设计 |
在FFS下医生每提供一单位服务量获得一定补偿p,医生收益R(q)=pq,利润π(q)=R(q)-c(q)。c(q)为每单位服务的成本,设计为凸函数0.1·q2 (Choné and Ma, 2011; Ma, 1994)。为了体现不同疾病(A、B、C)在FFS下的补偿差异,我们设计了三种补偿pA、pB、pC。设计原则为保证医生利润π(q)在q^=10处取得最大值π(q^),医生最大利润π(q^)与患者最佳健康效益B(q*)接近。基于此,我们设定pA=1.91、pB=2、pC=2.1,对应医生最大利润分别为9.1、10、11。具体设计见表 3。
| 表 3 医生支付的设计 |
在DRGs下考虑到不同患者疾病类型和严重程度的差异,医生针对每种患者收到一个固定支付L,即R(q)=L。医生利润π(q)=L-c(q)=L-0.1·q2,在q=0处取得最大值L。L的设定考虑与FFS相关联,即以FFS下患者健康效益最佳时对应服务量q*的医生收益(R(q)=pq*)为参照。9种患者A1、A2、A3、B1、B2、B3、C1、C2、C3的L依次为1.91×3、1.91×5、1.91×7、2×3、2×5、2×7、2.1×3、2.1×5、2.1×7。具体设计见表 3。
(三) 实验实现实验程序通过z-Tree (Fischbacher, 2007) 编写。于2020年10月在首都医科大学通过海报招募医学生被试,并将其随机分配到各个实验组,每组30人,5组共150人。1-3组为DRGs,4-5组为FFS。每组包含单一和混合两部分,每部分实验进行5轮。每名被试分别参加单一和混合两部分。具体步骤:首先,将到达实验室的受试者随机分配到某一电脑前就坐。然后,实验员为每名受试者分发实验材料,并介绍实验的目的和预设的实验情景。受试者阅读实验材料并签署知情同意书。实验过程中受试者不允许相互交流,如有问题可举手示意,实验员会单独为其解答。为了测试受试者是否理解实验任务,他们必须回答一组控制问题,并完成先导实验。只有所有受试者都正确回答了问题并通过了先导实验,正式实验才能开始。正式实验中需要受试者根据电脑屏幕显示的0-10项服务量分别对应的医生利润、患者健康效益等信息为预设的9名患者选择要提供的医疗服务项目数。实验重复5轮。决策任务完成后,受试者填写一份个人信息问卷。顺利完成实验后每名受试者获得30元参与实验的费用,外加决策产生的个人利润(按10 ∶ 1折算)。患者健康效益按同样比例折算后捐赠给中国红十字会。为了确保捐赠的真实性,我们随机抽取一名受试者进行监督。最后,将捐赠成功的结果对参与实验的受试者进行公示,监督者额外获得50元。
本研究中每场实验持续时间平均90分钟。受试者平均获得实验报酬108元,累计捐赠患者健康效益3420元。
四、模型与估计 (一) 基于医生效用函数的利他参数估计医生效用函数为:
| $ U(q)=(1-\alpha) \cdot \pi(q)+\alpha \cdot B(q) $ |
π(q)、B(q)含义和表达式与医生利润和患者健康效益设计中一致。α为利他参数,可利用医生效用最大化的效用函数的一阶条件来计算。
在FFS下,
当q≤q*时,U′=(1-α)(p-0.2q)+αθ,α=(0.2q-p)/(0.2q-p+θ)
当q≥q*时,U′=(1-α)(p-0.2q)-αθ,α=(0.2q-p)/(0.2q-p-θ)
在DRGs下,
当q≤q*时,U′=(1-α)(-0.2q)+αθ,α=(0.2q)/(0.2q+θ)
当q≥q*时,U′=(1-α)(-0.2q)-αθ,α=(0.2q)/(0.2q-θ)
针对每个患者的具体量化见表 4。为了使医生的利他性可比,采用Brosig-Koch et al. (2017)的利他性量化方法将α标化,即分别除以同组最大值αopt,即医生选择患者健康效益最佳服务量q*对应的α,使α取值在[0, 1]。考虑到医生决策的有效性,只有做出30(45·2/3) 个及以上帕累托效率决策的受试者才被计算利他参数。帕累托效率决策范围根据不同疾病严重程度轻、中、重,在FFS下定义为[3, 10]、[5, 10]、[7, 10],在DRGs下定义为[0, 3]、[0, 5]、[0, 7]。个体水平的利他性为所做帕累托效率决策标化利他参数均值。
| 表 4 未标化的利他参数 |
本研究中应用的随机效用模型为混合logit模型(Hole, 2007)。混合logit模型具有高度灵活性,允许违反无关替代方案独立性假设(independence of irrelevant alternatives, ⅡA),广泛的包含了任何形式的混合分布(既包含离散分布,也包括连续分布),因而它可以近似于任何随机效用模型。此外,该模型还可实现对系数标准差的估计,进而判定对可观测要素的个体偏好差异。利用计算支付意愿(willingness to pay, WTP)的命令(Hole, 2007)可实现患者健康效益与医生利润边际替代率的计算。进一步利用固定效应条件logit模型来识别个体水平上对患者健康效益的偏好异质性,即假设医生对自身利润的偏好固定,通过个体编号ID与患者健康效益B(q)的交互项来识别未被观测到的个体水平偏好异质性与患者健康效益B(q)的交互作用。
具体估计中可将医生N针对每个患者的服务量选择视为一个选项集K∈[1, 9],服务量取值[0, 10]可理解为11个替代方案J∈[0, 10],每个方案包含医生利润π(q)和患者健康效益B(q)两个属性。基于这一思路,我们构建随机效用模型的医生效用函数:
| $ U_{n j k}=\beta_{n}^{\prime} x_{n j k}+\varepsilon_{n j k} $ |
n=1, 2, 3, ..., N, j=1, 2, 3, ..., J, k=1, 2, 3, ..., K, 即医生n为患者k选择了替代方案j时的效用。xnjk可理解为医生利润π(q)和患者健康效益B(q)的向量,系数向量βn为两者的边际效用(δn-医生利润,γn-患者健康效益),两者的比值γn/θn为边际替代率。
根据边际替代率与1的比较,可判断利他性程度,大于1表示更加重视患者健康效益,等于1表示同等程度重视个人利润与患者健康效益,小于1表示更加重视个人利润。具体估计原理为通过假设随机扰动项εnjk服从ⅡD,系数β遵循密度函数f(β|θ),θ表示总体参数分布。在一个概率框架下个体n选择为患者k选择i时的条件概率为:
| $ L_{n i k}\left(\beta_{n}\right)=\frac{\exp \left(\beta^{\prime}{ }_{n} x_{n i k}\right)}{\sum _{j=1}^{J} \exp \left(\beta_{n}^{\prime} x_{n j k}\right)} $ |
K个患者的条件联合密度为:
| $ S_{n}\left(\beta_{n}\right)=\prod\limits_{k=1}^{K} L_{n i(n, k) k}\left(\beta_{n}\right) $ |
通过对β积分,可得到非条件概率密度:
| $ P_{n}(\theta)=\int S_{n}(\beta) f(\beta \mid \theta) d \beta $ |
假设β服务正态分布,可通过极大模拟似然估计方法对其进行估计。用M表示随机抽样次数,βm表示来自f(β|θ)的第m次随机抽样的参数,则模拟似然函数为:
| $ S L L_{M L}(\theta)=\sum\limits_{n=1}^{N} \ln \left[\frac{1}{M} \sum\limits_{m=1}^{M} S_{n}\left(\beta^{m}\right)\right] $ |
在固定效应条件logit模型中只允许不同个体对患者健康效益的偏好存在异质性(δn固定),γn=uωn,u为(1×N)个体n的哑变量,n=1表示个体n的观测值,n=0表示其他N-1个个体的观测值。系数向量ωn被分配到交互项向量中,可使我们观测到不同个体对患者健康效益的偏好异质性。
五、结果150名医学生被试中三年级及以上本科生85人,研究生65人,女生106人,平均年龄22岁。人口学统计学特征卡方检验和方差分析结果显示受教育水平、性别、年龄在5组间的分布无差异(p≥ 0.111)。为了与Godager and Wiesen (2013)、Brosig-Koch et al. (2017)的研究进行比较,本研究主要利用150名受试者单一支付下的实验数据进行测量。
(一) 医生的服务提供行为医生提供的服务量在前三组单一DRGs下的组间比较显示不存在差异(p=0.293, Kruskal-Wallis H检验),在单一FFS(4-5组)下也不存在差异(p=0.879, Mann-Whitney U检验)。这意味着单一DRGs下和单一FFS下医生提供的服务量可以汇总进行支付方式的组间比较。汇总后的结果显示,在单一DRGs下医生提供的服务量均值为3.71 (s.d. 0.90),在单一FFS下为5.82 (s.d. 0.88),表明医生在DRGs下提供的服务量比在FFS下少36%(p < 0.001, two-sided Mann-Whitney U检验)。进一步将医生提供的服务量与患者健康效益最佳服务量进行比较,我们发现在DRGs下的服务量偏离(q-q*)为-1.29 (s.d. 0.90),在FFS下为0.82 (s.d. 0.82)。这说明在DRGs下医生存在服务不足,在FFS下存在过度供给,且前者的程度大于后者(p < 0.001, two-sided Mann-Whitney U检验)。(见表 5)
| 表 5 医疗服务数量 |
根据符合帕累托效率决策的定义范围,共有143名受试者做出了30个及以上帕累托效率决策,纳入本部分研究。利他性测量结果显示总体的利他参数均值为0.82 (s.d. 0.15)。个体水平的利他参数累计频率分布图(图 1)显示不同个体间的利他性存在异质性,其中96%的医生利他性大于0.5,50%的医生利他性大于0.85,33%的医生利他性大于0.9。约8%的受试者5轮决策始终选择患者健康效益最大化时对应的服务量,利他性为1。1名受试者在DRGs下的5轮45个决策中40个选择了个人利润最大化服务量0,利他性最小为0.028。
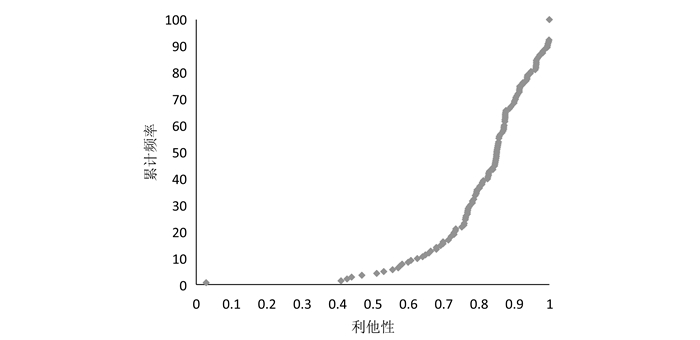
|
图 1 利他性累计频率分布图 |
本部分研究首先对每名医学生5轮决策通过Kruskal-Wallis H检验进行组间分布差异检验,结果显示除编号为2、7、14、97、123的受试者决策结果组间分布有差异(p < 0.05), 其余无差异。针对无差异的受试者从5轮决策中随机抽取一轮,5名有差异的受试者进一步做组间的两两比较,排除与其他轮大多都有差异的一轮后从剩余轮次中随机抽取一轮或根据决策结果观察其决策较为稳定后从剩余轮次中随机抽取一轮决策。
来自混合logit模型的估计结果(表 6)显示,医生利润和患者健康效益的估计系数有统计学显著性(p < 0.001)且符号为正,表明两者都会对医生的决策产生正向影响。但患者健康效益的系数大于医生利润,说明医生决策时对患者健康效益的偏好更大。估计系数的标准差具有统计学显著性(p < 0.001),表示医生对个人利润和患者健康效益的偏好具有异质性。进一步计算患者健康效益与医生利润的边际替代率为1.078>1,说明总体上医生决策时给予了患者健康效益相对个人利润更大的权重。
| 表 6 利他性混合logit模型回归分析 |
进一步通过混合logit模型对个体水平的个人利润和患者健康效益系数进行估计,计算单个受试者的边际替代率。结果显示边际替代率最小为0.037,最大为6.027(该值为绝对值,因为医生利润估计系数为负)。61名受试者的边际替代率大于1,对患者健康效益重视程度大于个人利润。另有11名受试者5轮决策始终选择了患者健康效益最大化服务量,2名受试者随机抽取的一轮决策也是如此,意味着这13名受试者的个人利润估计系数趋向于0,混合logit模型无法对其进行估计,也无法计算边际替代率。但理论上他们的边际替代率趋向于一个相比其他受试者的较大值。所以,相当于有74名受试者(49.3%)的边际替代率大于1。排除了这13名受试者的边际替代率累计频率分布图(图 2)显示44.5%的受试者大于1。
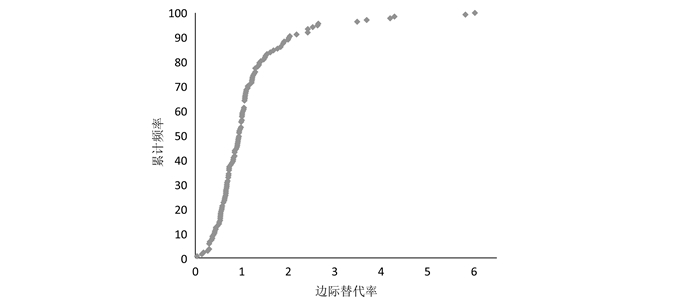
|
图 2 边际替代率累计频率分布图 |
进一步通过固定效应条件logit模型研究医生决策过程中对患者健康效益的偏好在不同个体之间是否存在异质性(表 7)。结果显示在固定了对医生利润的偏好后,个体编号与患者健康效益的交互项有21名受试者不存在统计学显著性(p>0.10),表示他们对患者健康效益的偏好不存在异质性,其中包含了上述13名倾向于最大化患者健康效益的受试者及利他性较低的受试者。即追求个人利润最大化的受试者较少关注患者健康效益,而追求患者健康效益最大化的受试者只关注患者健康效益,他们代表了两个极端群体。交互项系数的大小可以反映个体对患者健康效益的偏好程度,上述13名边际替代率未能计算的受试者交互项系数明显大于其他人,可以理解为对其边际替代率的一种替代解释。而交互项系数较小的受试者与边际替代率和利他性较低的受试者相对应,可以理解为对两者的补充解释。
| 表 7 患者健康效益固定效应条件logit回归分析 |
第一种方法中医生效用函数为标准化形式,利用满足医生效用最大化时效用函数的一阶条件对利他参数α进行计算,可实现针对每个患者的计算。但α有效值的计算仅限于在帕累托效率决策范围内,范围外可能为负或其他异常情况不能纳入分析。理论上对α的比较应该按照其未标化的真实值,但这样会导致针对不同患者以及不同支付方式下的最利患者行为无法以统一标准进行界定。标化后的α∈[0, 1]为相对水平,可实现在统一边界进行比较。虽然能量化个体水平的α,但无法实现个体水平上偏好异质性的判断。随机效用模型下医生并不一定总是做出效用最大化的选择,而是带有一定的随机性。医生效用函数为非标准化形式,且加入随机成分。医生的选择反映顺序偏好,按照定性选择进行处理。通过拟合随机效用模型对边际替代率进行估计,估计结果可用于判断偏好异质性和界定利他水平。但个体在完全利他选择下的估计无法实现,且边际替代率没有确切的取值范围,可能出现极值。
两种方法都可以估计医生个体水平上的利他性参数,因此,本研究进一步将基于医生效用函数计算的医生个体水平的利他性参数与随机效用模型估算的利他性参数(边际替代率)进行相关分析。结果显示两者存在显著正相关,Spearman秩相关系数为0.715 (p < 0.001)。散点图(图 3)更能直观地显示它们的相关性。
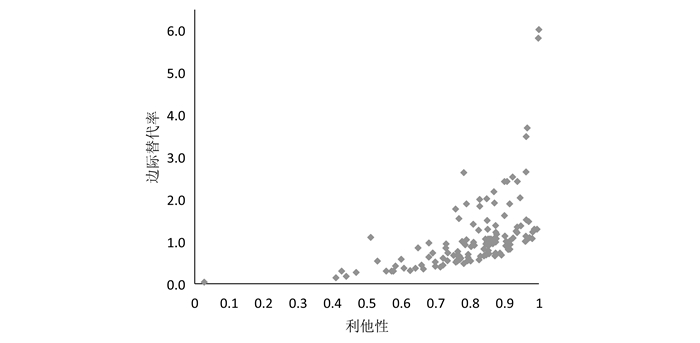
|
图 3 利他性与边际替代率 |
临床实习经历是影响医生医疗服务提供行为的重要因素之一。本研究进一步将两种方法的比较分析聚焦于实习经历的差异。因本研究调查的实习时间以月为单位,所以定义实习时间大于1个月为具有实习经历。经统计,本研究招募的受试者中87人有临床实习经历(三年级及以上本科生29人、研究生58人),63人无临床实习经历(三年级及以上本科生56人、研究生7人)。基于个体水平的利他参数α和边际替代率,通过非参数Kolmogorov-Smirnov检验对两组进行比较分析,结果显示虽然具有实习经历的医学生的利他参数和边际替代率均值(0.826 [s.d. 0.14],1.317 [s.d. 1.12])略高于无实习经历的医学生(0.820 [s.d. 0.16],0.911 [s.d. 0.47]),但差异无统计学显著性(p>0.05)。提示两种测量方法的估计结果在不同组的比较分析中具有一致性。
六、总结与讨论我们的研究基于医生效用函数计算的医生利他性(0.82)高于Brosig-Koch et al. (2017)研究中的0.75,主要是因为他们的研究使用单一和混合支付下的利他参数均值来计算个体水平利他性,但是他们并未比较单一与混合支付下医生利他性的差异。考虑到支付方式的变化可能对利他参数产生影响,这点在本研究中两种单一支付方式下的利他性测量结果存在差异得到初步验证(Mann-Whitney U检验,p < 0.001)。所以,本研究首先应用的是单一支付方式下的实验数据进行利他性测量,也方便与基于随机效用模型估算的利他性(边际替代率)比较。Li (2018)的研究中估算的α值0.72实际为医生利润的估计系数,并非患者健康效益的估计系数,不能直接和Brosig-Koch et al. (2017)研究中的0.75比较。按照他们研究中定义对患者健康效益的估计系数为1-α,利他性应该为0.28远低于0.75和本研究的0.82。这可能与他们所使用的非医疗决策情景独裁者博弈及估计方法有关。
基于随机效用混合logit模型估计的边际替代率1.078低于Godager and Wiesen (2013)研究中的1.84(该值并未直接报道,系该研究中表 2混合logit模型中患者健康效益与医生利润估计系数比值)。主要是因为他们的研究中针对疾病类型为1的患者或Hennig-Schmidt et al. (2011)研究中A类型患者(因为Godager and Wiesen (2013)使用Hennig-Schmidt et al. (2011)的实验数据),在FFS支付下医生利润最大化服务量(q^=4)与患者健康效益最大化服务量(q*=5)接近,导致医生在个人利润与患者健康效益之间权衡减少,因为针对其他患者医生利润最大化服务量q^=10。这从设计的角度与本研究中FFS下医生个人利润最大化服务量均为q^=10存在差异,而他们的这一设计会导致边际替代率与本研究相比的潜在增加。另外,Godager and Wiesen (2013)研究中疾病类型为1的患者医生利润最大化服务量(q^=4)和医生利润最大值π(q^)=8.4与Hennig-Schmidt et al. (2011)研究中A类型患者医生利润最大化服务量(q^=5)和医生利润最大值π(q^)=8不一致,理论上基于同一研究的参数应该完全一致。如果严格按照Hennig-Schmidt et al. (2011)的设计,边际替代率应该还会有变化(可能增加)。但是,本研究中边际替代率大于1的受试者占比49%略高于Godager and Wiesen (2013)研究中44%。另外,本研究中两种单一支付方式下边际替代率组间比较不存在差异(Mann-Whitney U检验,p=0.898),这与Godager and Wiesen (2013)研究一致(p>0.25)。说明边际替代率可能受到支付方式变化的影响相比利他性较小。
本研究招募的受试者均为医学生,他们都完成了医学基础知识的学习并接受了医学职业教育,实习经历对利他性的影响并不显著。同类研究中Wang et al.(2019, 2020) 针对中国医学生、医生和德国医学生的比较发现,三者的利他偏好没有显著差异。Brosig-Koch et al.(2013a, 2013b, 2020) 的研究发现德国医学生和非医学生的决策、德国医学生和医生的服务提供和相对质量没有显著差异。Hennig-Schmidt et al. (2014)基于德国受试者的研究显示非医学生与医学生相比,更少关心患者健康效益,更不愿意牺牲个人利润。Brosig-Koch et al.(2015, 2017) 基于德国受试者的研究发现医学生的利他参数(0.75)显著高于非医学生(0.60)。Brosig-Koch et al. (2016)的研究表明德国医学生、非医学生、医生对FFS、CAP的响应方式一致,但响应强度(过度供给和服务不足的程度)最大为非医学生,其次为医学生,最小为医生。这些研究显示医生和医学生利他性高于非医学生较为一致,而医生与医学生之间的差异尚没有一致结论。本研究的受试者仅限于医学生,仅分析不同实习经历之间的差异,并不能明确分离医学生与非医学生、医生的差异,这是本研究的局限之一。
本研究除测量了基于两种方法的医生利他性,更重要的是揭示了两种方法测量结果的相关性。目前呈现的结果表明基于医生效用函数计算的利他参数α与随机效用模型估计的边际替代率显著正相关,可以互相印证。但是边际替代率的估计容易受限于模型对个人利润与患者健康效益的估计系数,全部为患者最优决策可能导致医生利润估计系数趋向于0,最终无法实现边际替代率的计算。优势为能较好地区分个体利他性程度。基于医生效用函数的利他性测量不存在无法计算的情况,但是限定在帕累托效率决策范围内,帕累托效率决策范围外的受试者无法计算利他参数,另外不足之处是利他性程度没有界定标准。两种分析各有其优缺点,都可以选择使用。基于不同的分析目的可有所侧重,如果期望针对患者特征分析医生利他性的差异可选择基于医生效用函数计算的利他参数;如果想分析医生个体水平上对于个人利润和患者健康效益偏好的替代程度及其个体间的差异可选择随机效用模型估计的边际替代率,两种方法具有一定的互补性。
| [] |
陈叶烽、叶航、汪丁丁, 2012, “超越经济人的社会偏好理论: 一个基于实验经济学的综述”, 《南开经济研究》, 第 1 期, 第 63-100 页。 |
| [] |
杜书伟、郑大喜, 2009, “医患关系中医务人员行为的利他主义经济学分析”, 《医学与社会》, 第 22 期, 第 40-42 页。 |
| [] |
韩优莉、张悦, 2020, “医疗服务提供者利他性: 内涵、测量及对供方激励政策的启示”, 《中国卫生政策研究》, 第 11 期, 第 1-8 页。DOI:10.3969/j.issn.1674-2982.2020.11.001 |
| [] |
聂冲、贾生华, 2005, “离散选择模型的基本原理及其发展演进评介”, 《数量经济技术经济研究》, 第 11 期, 第 151-159 页。DOI:10.3969/j.issn.1000-3894.2005.11.016 |
| [] |
叶航, 2003, “西方经济学效用范式的逻辑缺陷”, 《经济学家》, 第 1 期, 第 93-97 页。DOI:10.3969/j.issn.1003-5656.2003.01.014 |
| [] |
章平、黄傲霜, 2018, “引入异质性社会偏好的利他行为决策及激励机制比较”, 《复杂系统与复杂性科学》, 第 15 期, 第 19-26 页。 |
| [] |
周小亮、笪贤流, 2009, “效用、偏好与制度关系的理论探讨——反思消费者选择理论偏好稳定之假设”, 《学术月刊》, 第 1 期, 第 75-85 页。 |
| [] |
Andreoni J., Miller J., 2002, "Giving According to GARP: An Experimental Test of the Consistency of Preferences for Altruism". Econometrica, 70(2), 737–753.
DOI:10.1111/1468-0262.00302 |
| [] |
Agranov M., Ortoleva P., 2017, "Stochastic Choice and Preferences forRandomization". Journal of Political Economy, 125(1), 40–68.
DOI:10.1086/689774 |
| [] |
Allard M., Jelovac I., Léger P.T., 2011, "Treatment and Referral Decisions Under Different Physician Payment Mechanisms". Journal of Health Economics, 30(5), 880–893.
DOI:10.1016/j.jhealeco.2011.05.016 |
| [] |
Arrow K.J., 1963, "Uncertainty and the Welfare Economics of Medical Care". American Economic Review, 53(5), 941–969.
|
| [] |
Barham V., Milliken O., 2015, "Payment Mechanisms and the Composition of Physician Practices: Balancing Cost-Containment Access". and Quality of Care", Health Economics, 24(7), 895–906.
|
| [] |
Barigozzi F., Burani N., 2016, "Competition and Screening with Motivated Health Professionals". Journal of Health Economics, 50, 358–371.
DOI:10.1016/j.jhealeco.2016.06.003 |
| [] |
Brosig-Koch J., Henning-Schmidt H., Kairies-Schwarz N., Kokot J., Wiesen D., 2020, "Physician Performance Pay: Experimental Evidence". HERO Working Paper Series, 3.
|
| [] |
Brosig-Koch J., Hennig-Schmidt H., Kairies-Schwarz N., Wiesen D., 2017, "The Effects of Introducing Mixed Payment Systems for Physicians: Experimental Evidence". Health Economics, 26(2), 243–262.
DOI:10.1002/hec.3292 |
| [] |
Brosig-Koch J., Hennig-Schmidt H., Kairies-Schwarz N., Wiesen D., 2016, "Using Artefactual Field and Lab Experiments to Investigate How Fee-for-Service and Capitation Affect Medical Service Provision". Journal of Economic Behavior & Organization, 131(Part B), 17–23.
|
| [] |
Brosig-Koch, J., Hennig-Schmidt, H., Kairies-Schwarz, N., Wiesen, D., 2015, "The Effects of Introducing Mixed Payment Systems for Physicians-Experimental Evidence", Working Paper, Ruhr Economic Papers, No. 543.
|
| [] |
Brosig-Koch, J., Hennig-Schmidt, H., Kairies-Schwarz, N., Wiesen, D., 2013a, "How to Improve Patient Care? An Analysis of Capitation, Fee-for-service, and Mixed Payment Schemes for Physicians", Working Paper, Ruhr Economic Papers, No. 412.
|
| [] |
Brosig-Koch, J., Henning-Schmidt, H., Kairies-Schwarz, N., Wiesen, D., 2013b, "How Effective are Pay-for-performance Incentives for Physicians? A Iaboratory Experiment", Working Paper, Ruhr Economic Papers, No. 413.
|
| [] |
Camerer C.F., 1989, "Does the Basketball MarketBelieve in the 'Hot Hand'". American Economic Review, 79, 1257–1261.
|
| [] |
Chalkley M., Malcomson J.M., 1998, "Contracting for Health Services When Patient Demand Does Not Reflect Quality". Journal of Health Economics, 17(1), 1–19.
DOI:10.1016/S0167-6296(97)00019-2 |
| [] |
Choné P., Ma C.T.A., 2011, "Optimal Health Care Contract Under Physician Agency". Annals of Economics and Statistics, 101/102, 229–256.
|
| [] |
Davidson, D. and Marschak, J., 1959, "Experimental Tests of Stochastic Decision Theory", In: C. W. Churchman (ed. ), Measurement Definitions and Theories, New York, NY: John Wiley & Sons, pp. 233-269.
|
| [] |
Eggleston K., 2005, "Multitasking and Mixed Systems for Provider Payment". Journal of Health Economics, 24(1), 211–223.
DOI:10.1016/j.jhealeco.2004.09.001 |
| [] |
Ellis R.P., McGuire T.G., 1986, "Provider Behavior Under Prospective Reimbursement: Cost Sharing and Supply". Journal of Health Economics, 5(2), 129–151.
DOI:10.1016/0167-6296(86)90002-0 |
| [] |
Ellis R.P., McGuire T.G., 1990, "Optimal Payment Systems for Health Services". Journal of Health Economics, 9(4), 375–396.
DOI:10.1016/0167-6296(90)90001-J |
| [] |
Fischbacher U., 2007, "z-Tree: Zurich Toolbox for Ready-Made Economic Experiments". Experimental Economics, 10, 171–178.
DOI:10.1007/s10683-006-9159-4 |
| [] |
Galizzi, M.M., Tammi, T., Godager, G., Linnosmaa, I. and Wiesen, D., 2015, "Provider Altruism in Health Economics", Discussion paper 4. Helsinki, Finland.
|
| [] |
Godager G., Wiesen D., 2013, "Profit or Patients' Health Benefit? Exploring the Heterogeneity in Physician Altruism". Journal of Health Economics, 32(6), 1105–1116.
DOI:10.1016/j.jhealeco.2013.08.008 |
| [] |
Hennig-Schmidt H., Wiesen D., 2014, "Other-regarding Behavior and Motivation in Health Care Provision: An Experiment with Medical and Non-medical Students". Social Science & Medicine, 108, 156–165.
|
| [] |
Hennig-Schmidt H., Selten R., Wiesen D., 2011, "How Payment Systems Affect Physicians' Provision Behaviour—An Experimental Investigation". Journal of Health Economics, 30(4), 637–646.
DOI:10.1016/j.jhealeco.2011.05.001 |
| [] |
Hey J.D., Orme C., 1994, "Investigating Generalizations of Expected Utility Theory Using Experimental Data". Econometrica, 62(6), 1291–1326.
DOI:10.2307/2951750 |
| [] |
Hole A.R., 2007, "Fitting Mixed Logit Models Using Maximum Simulated Likelihood". The Stata Journal, 7(3), 388–401.
DOI:10.1177/1536867X0700700306 |
| [] |
Honda A., Krucien N., Ryan M., Diouf I.S.N., Salla M., Nagai M., Fujita N., 2019, "For More Than Money: Willingness of Health Professionals to Stay in Remote Senegal". Human Resources for Health, 17(1), 28.
DOI:10.1186/s12960-019-0363-7 |
| [] |
Jack W., 2005, "Purchasing Health Care Services From Providers with Unknown Altruism". Journal of Health Economics, 24(1), 73–93.
DOI:10.1016/j.jhealeco.2004.06.001 |
| [] |
Jones R., 2002, "Declining Altruism in Medicine". BMJ, 324(7338), 624–625.
DOI:10.1136/bmj.324.7338.624 |
| [] |
Lagarde M., Pagaiya N., Tangcharoensathian V., Blaauw D., 2013, "One Size Does Not Fit All: Investigating Doctors' Stated Preference Heterogeneity for Job Incentives to Inform Policy in Thailand". Health Economics, 22(12), 1452–1469.
DOI:10.1002/hec.2897 |
| [] |
Lagarde M., Blaauw D., 2017, "Physicians' Responses to Financial and Social Incentives: A Medically Framed Real Effort Experiment". Social Science & Medicine, 179, 147–159.
|
| [] |
Leonard K.L., Masatu M.C., 2010, "Professionalism and the Know-Do Gap: Exploring Intrinsic Motivation among Health Workers in Tanzania". Health Economics, 19(12), 1461–1477.
DOI:10.1002/hec.1564 |
| [] |
Li J., 2018, "Plastic Surgery or Primary Care? Altruistic Preferences and Expected Specialty Choice of U.S. Medical Students". Journal of Health Economics, 62, 45–59.
DOI:10.1016/j.jhealeco.2018.09.005 |
| [] |
Li J., Dow W.H., Kariv S., 2017, "Social Preferences of Future Physicians". Proceedings of the National Academy of Sciences of the United States of America, 114(48), E10291–E10300.
DOI:10.1073/pnas.1705451114 |
| [] |
Liu T., Ma C.T.A., 2013, "Health Insurance TreatmentPlan. and Delegation to Altruistic Physician". Journal of Economic Behavior & Organization, 85, 79–96.
|
| [] |
Luce, R.D., 1959, "Individual Choice Behavior: A Theoretical Analysis", Wiley, New York.
|
| [] |
Ma C.T.A., 1994, "Health Care Payment Systems: Cost and QualityIncentives". Journal of Economics & Management Strategy, 3(1), 93–112.
|
| [] |
Marschak, J., 1960, Binary Choice Constraints on Random Utility Indicators. In Arrow, K. J., editor, Stanford Symposium on Mathematical Methods in the Social Sciences, pages 312-329. Stanford University Press, Stanford, CA.
|
| [] |
McFadden, D., 1974, "Conditional Logit Analysis of Qualitative Choice Behavior", In: Frontiers in Econometrics, ed. by P. E. Zarembka, Academic Press, New York, 105-142.
|
| [] |
McFadden D., 2001, "Economic Choices". American Economic Review, 91(3), 351–378.
DOI:10.1257/aer.91.3.351 |
| [] |
McGuire, T.G., 2000, "Physician Agency", In: Culyer, A.J., Newhouse, J.P. (Eds. ), Handbook of Health Economics, North-Holland Elsevier, Amsterdam.
|
| [] |
Samuelson P.A., 1938, "A Note on the Pure Theory of Consumer's Behaviour". Economica, 5, 61–71.
DOI:10.2307/2548836 |
| [] |
Scott A., Witt J., Humphreys J., Joyce C., Kalb G., Jeon S.H., McGrail M., 2013, "Getting Doctors Into the Bush: General Practitioners' Preferences for Rural Location". Social Science & Medicine, 96, 33–44.
|
| [] |
Thurstone L., 1927, "A Law of Comparative Judgement". Psychological Review, 34, 273–286.
DOI:10.1037/h0070288 |
| [] |
Tversky A., 1969, "Intransitivity of Preferences". Psychological Review, 76, 31–48.
DOI:10.1037/h0026750 |
| [] |
Wang J., Iversen T., Hennig-schmidt H., Godager G., 2019, "Are Patient-regarding Preferences Stable? Evidence from a Laboratory Experiment with Physicians and Medical Students from Different Countries". HERO Working Paper Series, 1.
|
| [] |
Wang J., Iversen T., Hennig-Schmidt H., Godager G., 2020, "Are Patient-regarding Preferences Stable? Evidence from a Laboratory Experiment with Physicians and Medical Students from Different Countries". European Economic Review, 125, 103411.
DOI:10.1016/j.euroecorev.2020.103411 |




