2014年中央经济工作会议首次提出我国经济步入“新常态”的战略判断,虽然近年来保持目标经济增速的压力持续加大,但中国经济规模与发展质量仍在不断实现突破。一是经济体量平稳增长,2020年名义GDP达到14.73万亿美元,占美国GDP的比重超过70%;二是经济增长质量不断提高,2020年第三产业增加值占GDP比重升至54.5%,战略性新兴产业增速持续快于规模以上工业平均增速2个百分点以上,经济发展的创新驱动特征凸显。但与此同时,必须对当前世界经济诸多潜在风险的累积保持高度警惕,中美贸易摩擦可能是其中深刻影响中国对外贸易环境与长期经济增长潜力的重要变量。
2017年8月,美国贸易代表办公室宣布对中国发起“301调查”,成为中美贸易摩擦的导火索,此后双方围绕加征进口关税展开多轮交锋。2018年6月15日,美国公布对总额约500亿美元中国信息通讯、机械等行业出口品25%税率的关税清单,次日中国宣布对美国大豆等价值500亿美元进口品征收25%关税。2019年5月10日,美国将原征收10%关税的1000亿美元进口品税率提高至25%,作为回应,中国于6月1日起将600亿美元进口品关税从5-10%提高至10-25%。关税成为此次贸易摩擦中双方的主要工具,但中国从未主动升级关税,始终遵循理性克制、反制及时、兼顾打击面与针对性的基本原则。2021年以来,美国新政府尚未取消任何一项针对中国的贸易制裁措施,因此贸易摩擦的风险和不确定性或将长期存在。
近年来,国内学者围绕贸易摩擦的经济影响与应对政策开展了大量研究。崔琨、施建淮(2020)发现无论对中间品还是最终品征收关税,都会导致显著的福利恶化与消费下降,单边关税是一种短视的贸易政策,对本国而言,钉住中间品通胀的货币政策比钉住CPI更为有效。肖祖沔等(2020)利用两国DSGE模型的研究发现关税摩擦在中长期会造成贸易条件持续恶化,引起本国出口与产出下降,但适度提高贸易开放水平能够使本国在贸易摩擦中形成相对竞争优势,这与黄鹏等(2018)的研究结论比较接近,即在贸易摩擦背景下更加需要深化对外开放、推动我国与世界经济紧密融合,搞经贸“脱钩”对中美两国而言都是一种弊大于利的“双输”选择。邓力平等(2018)则从关税税目设置角度剖析了贸易摩擦的应对策略,研究认为针对不同行业贸易特点设置差异化税目能够在一定程度上缓和与贸易伙伴国的紧张关系。刘维林等(2020)使用HS6双边贸易数据测算了关税摩擦对两国就业的影响,发现中国制造业就业受影响最大,美国则是三次产业的就业损失基本相当。
此外,还有一些学者从股市与金融风险、制造业发展质量等维度探讨了贸易摩擦的广泛溢出效应。朱民、徐钟祥(2021)使用事件分析法的研究显示,贸易摩擦会导致农林牧渔业上市公司产生显著的负异常收益率但持续时间较短,长期中多数行业收益率波动很小,说明贸易摩擦不会显著提高股市系统性风险。方意等(2019)考察了贸易摩擦对三类金融市场的风险溢出效应,发现债券市场受影响程度最大,外汇市场次之,股票市场所受影响确实最小。孙文浩、张杰(2020)的实证研究还发现,中美贸易战与技术封锁对于侧重引进创新的制造企业产生了显著负面冲击,但有利于处于自主创新起步阶段的制造企业集聚人才,因此贸易摩擦对中国经济发展既是一种紧迫的外部压力,也是一次推动制造业技术自强与高质量增长的重要契机。
从上述研究来看,国内研究虽从不同视角对贸易摩擦的经济影响进行了诸多探讨,但从经济收益与福利视角分析,中国是否应在贸易摩擦中作出反制?应在多大程度上进行关税反制?关税反制是否需与货币政策搭配实施?鲜有文献就这些问题给出回答。本文通过构建新凯恩斯主义两国DSGE模型,将进口品从价关税与关税反制特征纳入理论模型,使用数值模拟与福利分析等方法详细探讨了在中美贸易摩擦中进行关税反制的必要性。研究还发现,关税反制存在明显的福利转移效应,在提升中国经济产出与社会福利的同时,也会导致美国经济萎缩与福利水平恶化,容易引起美国的关税报复。而货币政策在应对关税冲击方面同样非常有效,但缺点也比较突出:即对挑起贸易摩擦的美国也会产生显著的正向溢出作用。本研究的主要结论对于我国在应对贸易摩擦过程中优化关税反制措施与货币政策组合具有一定借鉴意义。
剩余部分的结构安排如下:第二节介绍理论模型的构建过程,第三节利用中美宏观经济数据进行参数校准与估计,第四节实证分析不同关税反制强度与货币政策组合下美国关税冲击的国际传导与福利效应,最后总结主要结论与政策启示。
二、两国模型框架为构建一个较为准确的反映中美经济重要特征的两国模型,本文参考并融合了近年来新凯恩斯主义DSGE相关研究的重要成果,如工资和价格粘性、异质性劳动与外汇风险溢价等。同时,我们还放松了以往研究中对贸易开放度的对称约束以体现两国经济规模的显著差距,并通过持有外国资产组合的调整成本来反映资本管制所造成的资本不完全流动。最后,考虑到美元仍是当今国际贸易体系中最重要的结算媒介与计价货币,因此我们假设模型中双边贸易均以美元定价。
(一) 家庭部门消费与投资决策世界经济由均匀分布于[0, 1]区间的人口组成,其中本国人口分布于[0, n],外国人口位于(n, 1],假设消费者同时也是相应中间品生产者,因此参数n体现了本国在世界经济产出中所占比重。以本国变量加星号上标代表相应外国变量,如Ut*即外国消费者的终生贴现效用。将本国代表性家庭的效用贴现函数设为下式:
| $ U_{t}=E_{0} \sum\limits_{s=0}^{\infty} \beta^{s} D_{c, t+s}\left[\frac{\left(C_{t+s}^{j}-b C_{t+s-1}\right)^{1-\sigma^{-1}}}{1-\sigma^{-1}}-\frac{\left(N_{t+s}^{j}\right)^{1+\eta}}{1+\eta}\right] $ | (1) |
其中,跨期替代弹性因子σ>0且σ≠1,η为Frisch逆劳动供给弹性,β代表跨期效用贴现系数,b∈[0, 1]体现了实际消费习惯对消费者效用的影响。Dc, t表示服从AR(1)过程的跨期消费偏好外生冲击。代表性家庭的收入来源于持有国内外单期债券的净收益、为中间品生产提供劳动的工资所得、进行固定资产投资的租金收益以及作为垄断竞争中间品生产企业最终所有者的超额利润,将这些收入用于消费、再投资和支付税收。家庭预算约束为:
| $ P_{t}\left(C_{t}^{j}+I_{t}^{j}+T_{t}\right)+\frac{B_{t}^{j}}{R_{t}}+\frac{S_{t} B_{h, t}^{j *}}{R_{t}^{*} e^{u i p_{t}}} \leq B_{t-1}^{j}+S_{t} B_{h, t-1}^{j *}+W_{t}^{j} N_{t}^{j}+R_{t}^{K} K_{t-1}^{j}+\varPi_{t}^{j}-\frac{\varphi^{f} S_{t}}{2}\left(B_{h, t}^{j *}-\bar{B}_{h}^{*}\right)^{2} $ | (2) |
Rt-1与Rt* -1分别表示两国单期债券发行价格,Wt和RtK为名义工资率及资本名义收益率,Tt代表实际政府税收(Lump-sum Tax),St为直接标价法的本币名义汇率,Πt代表中间品生产企业利润。(2)式右侧最后一项为家庭调整国外资产组合的成本,当资产组合维持稳态不变时,资产调整成本为零。参数φf衡量了资本管制强度:资本管制越严格,国际资本流动性越低,调整国外资产组合的难度与成本越高。
假设外国家庭不能买卖本国债券①,其预算约束除不包括持有本币债券的净收入及资产组合调整成本外,与(2)式相同。家庭积累生产资本并出租给中间品生产企业,生产资本的动态积累路径如(3)式所示:
① 这是一个能够有效简化模型复杂度的技术性设定,不会对本研究的主要结论产生影响。
| $ K_{t}^{j}=(1-\delta) K_{t-1}^{j}+V_{t} I_{t}^{j} $ | (3) |
此处引入了一个反映投资技术波动的内生变量Vt,假设其服从AR(1)形式。本国代表性家庭的最优化问题即在预算方程(2)与资本积累方程(3)约束下最大化贴现效用,分别对实际消费、债券持有量、实际投资与资本存量求导,可解得如下一阶条件:
| $ \beta R_{t} P_{t} D_{c, t}^{-1}\left(C_{t}-b C_{t-1}\right)^{\sigma^{-1}}=E_{t}\left[P_{t+1} D_{c, t+1}^{-1}\left(C_{t+1}-b C_{t}\right)^{\sigma^{-1}}\right] $ | (4) |
| $V_{t}^{-1}=\beta E_{t}\left\{\frac{D_{c, t+1}\left(C_{t}-b C_{t-1}\right)^{\sigma^{-1}}}{D_{c, t}\left(C_{t+1}-b C_{t}\right)^{\sigma^{-1}}}\left[(1-\delta) V_{t+1}^{-1}+\frac{R_{t+1}^{K}}{P_{t+1}}\right]\right\} $ | (5) |
将本国消费者j提供给中间品生产企业h的劳动时间记为Ntj(h),个人提供给不同中间品厂商的劳动是同质的,但生产一单位中间品的劳动投入则由不完全替代的异质性劳动加总而成,定义劳动替代弹性系数为εw:
| $ N_{t}(h)=\left[\left(\frac{1}{n}\right)^{\frac{1}{\varepsilon_{w}}} \int{ }_{0}^{n} N_{t}^{j}(h)^{\frac{\varepsilon_{w}-1}{\varepsilon_{w}}} d j\right]^{\frac{\varepsilon_{w}}{\varepsilon_{w}-1}} $ | (6) |
因此,决定个人工作时间的劳动需求曲线为工资差异与总劳动时间的函数:
| $ N_{t}^{j}=\left(\frac{W_{t}^{j}}{W_{t}}\right)^{-\varepsilon_{w}} N_{t}, W_{t}=\left[\frac{1}{n} \int_{0}^{n}\left(W_{t}^{j}\right)^{1-\varepsilon_{w}} d j\right]^{\frac{1}{1-\varepsilon_{w}}} $ | (7) |
现实经济运行中由于存在劳动合同、最低工资制度、工会势力等因素约束,雇主与劳动者都不可能随时调整工资水平,因此工资调整的粘性客观存在。参考在DSGE模型中广泛应用的Calvo(1983)交错定价模型来表述工资粘性,假设每期有1-θw比例的工资能够调整到最优水平Wtopt,由于我国工资增长率与CPI存在较强相关性,因而将剩余θw比例的工资设为按部分钉住上期通胀率的方式进行调整:
| $ E_{t} \sum\limits_{k=0}^{\infty}\left(\beta \theta_{w}\right)^{k} \frac{D_{c, t+k} N_{t+k \mid t}}{\left(C_{t+k}-b C_{t+k-1}\right)^{\sigma^{-1}}}\left[\frac{W_{t}^{o p t}}{P_{t+k}}\left(\frac{P_{t+k-1}}{P_{t-1}}\right)^{\lambda_{w}}-\frac{\varepsilon_{w}}{\varepsilon_{w}-1} N_{t+k \mid t}^{\eta}\left(C_{t+k}-b C_{t+k-1}\right)^{\sigma^{-1}}\right]=0 $ | (8) |
结合按照物价指数调整的工资与根据效用最大化目标确定的最优工资率,得到本国总工资水平的决定方程:
| $ W_{t}=\left\{\left(1-\theta_{w}\right)\left(W_{t}^{o p t}\right)^{1-\varepsilon_{w}}+\theta_{w}\left[W_{t-1} \varPi_{t-1}^{\lambda_{w}}\right]^{1-\varepsilon_{w}}\right\}^{\frac{1}{1-\varepsilon_{w}}} $ | (9) |
假设中间产品可进行跨国贸易,最终产品生产者分别从国内外中间品厂商购买α比例的本国中间品YH, t和1-α比例的外国中间品YF, t,以生产Yt单位的最终产品:
| $ Y_{t}=\left[(1-\alpha)^{\frac{1}{\theta}} Y_{H, t}^{\frac{\theta-1}{\theta}}+\alpha^{\frac{1}{\theta}} Y_{F, t}^{\frac{\theta-1}{\theta}}\right]^{\frac{\theta}{\theta-1}} $ | (10) |
θ表示合成中间品价格替代弹性,α代表最终产品篮子中的进口比重,即本国贸易开放度。由于两国经济规模不对称,因此外国贸易开放度α*≠α,二者满足α*=nα/(1-n)。YH, t与YF, t对初级中间产品的CES加权形式与(10)式一致:
| $ Y_{H, t}=\left[\left(\frac{1}{n}\right)^{\frac{1}{\varepsilon_{p}}} \int_{0}^{n} Y_{H, t}(h)^{\frac{\varepsilon_{p}-1}{\varepsilon_{p}}} d h\right]^{\frac{\varepsilon_{p}}{\varepsilon_{p^{-1}}}}, Y_{F, t}=\left[\left(\frac{1}{1-n}\right)^{\frac{1}{\varepsilon_{p}}}\int_n^1 {} Y_{F, t}(f)^{\frac{\varepsilon_{p}-1}{\varepsilon_{p}}} d f\right]^{\frac{\varepsilon_{p}}{\varepsilon_{p}-1}} $ | (11) |
本国对进口品加征关税将会通过进口品价格直接反映到最终产品价格上,现实中的关税措施一般只针对部分特定产品,为简化分析,我们假设关税平均加征于所有进口品,从价关税税率为τt。最终产品价格即CPI可以表示为:
| $ P_{t}=\left\{(1-\alpha) P_{H, t}^{1-\theta}+\alpha\left[\left(1+\tau_{t}\right) P_{F, t}\right]^{1-\theta}\right\}^{\frac{1}{1-\theta}} e^{\mu_{t}} $ | (12) |
在(12)式还引入了一个最终品价格加成率外生冲击μt来体现现实经济中消费价格相对生产价格的频繁波动。根据(10)至(12)式的约束条件,可以推导出对本国与外国合成中间产品的需求曲线:
| $Y_{H, t}=[1-\alpha(1-n)]\left(\frac{P_{H, t}}{P_{t} e^{-\mu_{t}}}\right)^{-\theta} Y_{t}, Y_{F, t}=\alpha(1-n)\left(\frac{\left(1+\tau_{t}\right) P_{F, t}}{P_{t} e^{-\mu_{t}}}\right)^{-\theta} Y_{t} $ | (13) |
参考以往文献的做法,假设两国模型中代表性家庭同时也是相应的中间品生产者,两国虽发生国际贸易,但并不引起中间品生产技术扩散,各国中间品生产成本的降低依赖于其自身R&D投入与技术进步。因此,中间品生产函数可设为如下包含劳动附加型技术进步的Cobb-Douglas形式:
| $ Y_{H, t}(h)+Y_{H, t}^{*}(h)=\left[K_{t-1}(h)\right]^{\varphi}\left[A_{t} N_{t}(h)\right]^{1-\varphi} $ | (14) |
假设生产技术冲击是AR(1)平稳过程,即不存在长期持续进步或衰退情形。φ表示实际产出的资本份额,在(14)式约束下解成本最小化问题,得到如下中间品实际边际生产成本函数:
| $ M C_{t}(h)=\frac{\left(R_{t}^{K} / P_{t}\right)^{\varphi}\left(W_{t} / P_{t}\right)^{1-\varphi}}{A_{t}{ }^{1-\varphi} \varphi^{\varphi}(1-\varphi)^{1-\varphi}} $ | (15) |
从(15)式右边可以注意到,实际生产成本与中间品类别无关,因此所有差异性中间品生产者在同样的边际成本约束下决定实际产量。且产出水平的差异不会影响资本与劳动时间的相对投入,最优资本—劳动投入比满足:
| $ \frac{N_{t}(h)}{K_{t-1}(h)}=\frac{N_{t}}{K_{t-1}}=\frac{(1-\varphi)}{\varphi} \frac{R_{t}^{K}}{W_{t}} $ | (16) |
与工资粘性类似,参考Calvo(1983)引入价格粘性。与以往许多研究不同的是,考虑到美元仍然是国际贸易中的主要定价与结算货币,因此本文假设中美两国出口品均以美元定价,即本国出口企业采取依市定价(Pricing to Market)形式,外国出口品则服从依成本定价的传统假设,这也有助于增强模型对实际数据偏离一价定律和购买力平价等现象的刻画能力。假设每期有1-θp比例的本国中间产品可以调整到当前供求关系决定的最优价格水平,剩余部分保持上期确定的价格不变。因此,厂商面临的最优化问题是在(15)式成本约束下最大化如下折现名义利润:
| $ \mathop {Max}\limits_{{{\tilde P}_{H, t}}(h), {{\tilde P}_{H, t}}(h)} \quad {E_t}\sum\limits_{k = 0}^\infty {{{\left({\beta {\theta _p}} \right)}^k}} {\varLambda _{t, t + k}}\left[ {\begin{array}{*{20}{l}} {\left({{{\tilde P}_{H, t}}(h) - {P_{t + k}}M{C_{t + k}}} \right){Y_{H, t + k\mid t}}(h) + \cdots }\\ {\left({{S_{t + k}}\tilde P_{H, t}^*(h) - {P_{t + k}}M{C_{t + k}}} \right)Y_{H, t + k\mid t}^*(h)} \end{array}} \right] $ |
Λt, t+k表示随机贴现因子(SDF),对
| $ \frac{\tilde{P}_{H, t}(h)}{P_{H, t}}=\frac{\varepsilon_{p}}{\varepsilon_{p}-1} \frac{{{E_t}\sum\limits_{k = 0}^\infty {{{\left( {\beta {\theta _p}} \right)}^k}} {\varLambda _{t,t + k}}M{C_{t + k}}{P_{t + k}}{{\left( {{P_{H,t}}/{P_{H,t + k}}} \right)}^{ - {\varepsilon _p}}}{Y_{H,t + k}}}}{{{E_t}\sum\limits_{k = 0}^\infty {{{\left( {\beta {\theta _p}} \right)}^k}} {\varLambda _{t,t + k}}{P_{H,t + k}}{{\left( {{P_{H,t}}/{P_{H,t + k}}} \right)}^{1 - {\varepsilon _p}}}{Y_{H,t + k}}}} $ | (17) |
本国出口品的国外价格
| $ \frac{\tilde{P}_{F, t}^{*}(f)}{P_{F, t}^{*}}=\frac{{{\varepsilon _p}}}{{{\varepsilon _p} - 1}}\frac{{{E_t}\sum\limits_{k = 0}^\infty {{{\left( {\beta \theta _p^*} \right)}^k}} \varLambda _{t,t + k}^*MC_{t + k}^*P_{t + k}^*{{\left( {P_{F,t}^*/P_{F,t + k}^*} \right)}^{ - {\varepsilon _p}}}\left( {{Y_{F,t + k}} + Y_{F,t + k}^*} \right)}}{{{E_t}\sum\limits_{k = 0}^\infty {{{\left( {\beta \theta _p^*} \right)}^k}} \varLambda _{t,t + k}^*P_{F,t + k}^*{{\left( {P_{F,t}^*/P_{F,t + k}^*} \right)}^{1 - {\varepsilon _p}}}\left( {{Y_{F,t + k}} + Y_{F,t + k}^*} \right)}} $ | (18) |
我们将两国对进口品互相加征关税作为贸易摩擦的直接表现形式,虽然贸易摩擦还包括非关税壁垒等众多措施,但中美贸易摩擦双方均以加征和提高关税作为主要手段,且从宏观经济层面看,非关税壁垒也可以折算为等价关税(Engler and Tervala, 2018)。根据最终产品与中间品部门的模型设定,当两国分别对进口品施加τt与τt*的从价关税时,关税收入可以表示为:
| $ T R_{t}=\tau_{t} P_{F, t} Y_{F, t} e^{\mu_{t}} / P_{t}, T R_{t}^{*}=\tau_{t}^{*} P_{H, t}^{*} Y_{H, t}^{*} e^{\mu_{t}^{*}} / P_{t}^{*} $ | (19) |
贸易摩擦中的相互加征关税行为可以近似看作一个轮流“出价”并最终达成妥协的过程,本文借助纳什议价博弈模型对此加以刻画。假设双方均可接受的总关税上限为τmax①,即双方加征关税之和不得超过τmax,否则可能由于关税过高导致贸易量锐减或贸易中断;且双方的关税分配均应在0至τmax之间,否则至少一方不能接受,从而导致谈判破裂。满足以上两个条件的关税组合Sτ={(τt, τt*) | 0≤τt≤τmax, 0≤τt*≤τmax, τt+τt*≤τmax}称为该议价博弈的可行分配集,我们以ζ∈(0, 1)表示中国在贸易摩擦中的相对议价能力(Relative Nash Bargaining Power),并构建“纳什积”τtζτt* 1-ζ作为目标函数②,解Sτ约束下的目标函数最大化问题,可以得到如下一阶条件:
② 以“纳什积”作为目标函数,所得到的利益分配组合兼顾公平与效率,是双边议价博弈模型的一种重要解法。
| $ \tau_{t}=\frac{\zeta}{1-\zeta} \tau_{t}^{*}+\varepsilon_{\tau, t} $ | (20) |
① τmax最终不会纳入DSGE模型的一阶条件中,因此我们不需要具体讨论其赋值问题。
ζ取值越趋近1,意味着中国的谈判势力越强,在双边贸易摩擦中的反击越坚决、对美国的关税反制力度越大,上式中还纳入了一个服从正态分布的外生冲击ετ, t,以体现除对美国进行关税反制之外,中国对进口中间品主动征收关税的政策动机。假设美国加征进口关税的决策服从以下AR(1)外生冲击过程:
| $ \log \left(\frac{1+\tau_{t}^{*}}{1+\tau^{*}}\right)=\rho_{\tau}^{*} \log \left(\frac{1+\tau_{t-1}^{*}}{1+\tau^{*}}\right)+\varepsilon_{\tau, t}^{*} $ | (21) |
假设政府部门执行平衡预算的财政政策,每期支出全部来自家庭税收及进口关税收入②,且政府支出服从AR(1)外生冲击过程:
| $ G_{t}=T_{t}+T R_{t} $ | (22) |
② Engler and Tervala(2018)等假设政府部门将进口关税全部作为对家庭部门的转移支付,与本文做法有一定差异,但对于考察除财政政策外的其他宏观经济政策效果而言不会造成影响。
由于最终产品不能进行国际贸易,因此本国全部最终品产出与关税收入均用于代表性家庭消费、固定资产投资以及政府支付。市场均衡条件为:
| $ Y_{t}+T R_{t}=C_{t}+I_{t}+G_{t} $ | (23) |
将以上市场出清条件代入本国家庭预算约束,考虑到经济处于稳态路径时国内债券市场均衡,可以得到决定本国消费者持有外国债券(名义经常项目)增长路径的动态方程:
| $ \frac{S_{t} B_{h, t}^{*}}{R_{t}^{*} e^{u i p_{t}}}-S_{t} B_{h, t-1}^{*}=P_{H, t} Y_{H, t}+S_{t} P_{H, t}^{*} Y_{H, t}^{*}-P_{t} Y_{t}-\frac{\varphi_{t}^{f} S_{t}}{2}\left(B_{h, t}^{*}-\bar{B}_{h}^{*}\right)^{2} $ | (24) |
为提高货币政策独立性、并缓和与主要贸易伙伴国的贸易摩擦,近年来我国致力于推进汇率形成机制改革。1994年1月取消双重汇率制度,实现官方汇率与市场汇率并轨;2005年7月进一步由钉住美元的联动汇率制转变为参考一篮子货币定价的管理浮动汇率制;2008年9月受金融危机影响,作为紧急的应对措施、人民币汇率暂时返回钉住美元制;2010年6月至今,我国重启汇改进程、继续提高人民币汇率弹性,并多次扩大汇率的管理浮动区间。可以看到,人民币汇率体制改革是一个持续而复杂的过程,因此难以在统一的DSGE框架内体现出其所有的阶段性特征、对外汇市场的模型化处理需要有所侧重。在有管理的浮动汇率体系内,央行围绕其政策目标对外汇市场进行干预正是当前人民币汇率的关键制度性特征,而这将不可避免地影响市场参与者的汇率波动预期,我们通过引入一个外汇中间商部门对此进行模型化描述。
假设本国消费者除持有本国债券、还可以通过外汇中间商参与外币债券交易,外汇市场存在大量债券中间商,整个市场是完全竞争的。在预算方程(2)约束下对本国持有外国债券Bh, t*求偏导,解贴现效用最大化问题可以得到以下无抛补利率平价条件(UIP方程):
| $ \frac{R_{t}}{R_{t}^{*} e^{u i p_{t}}}+\varphi^{f} R_{t}\left(B_{h, t}^{*}-\bar{B}_{h}^{*}\right)=E_{t}^{f x}\left(\frac{S_{t+1}}{S_{t}}\right) $ | (25) |
由(25)式可以看到,外汇中间商的投资决策不但决定于两国的利率差,还受到他们对汇率波动预期以及调整国外资产组合成本的影响。根据汇率预测规则的差异,假设外汇市场存在两种债券代理商,一种是与传统国际经济学文献的设定一致、掌握完全有效市场信息的理性预期者,其汇率波动预期为
① 借助噪声交易理论刻画管理浮动体系内汇率波动特征的合理性在于:虽然央行可能在汇率波动幅度较大时才加以干预、但市场参与者并不能确知政策干预的临界点;即使汇率波动幅度很小,也总有“警惕”的参与者认为央行会干预外汇市场以使汇率回调。
| $E_{t}^{n}\left(\hat{s}_{t+1}-\hat{s}_{t}\right)=-\varphi_{n}\left(\hat{s}_{t}-\hat{s}_{t}^{T}\right), \hat{s}_{t}^{T}=\sum\limits_{k=1}^{m t} \frac{q_{n}^{m t-k}}{K} \hat{s}_{t-k}, K=\sum\limits_{k=1}^{m t} q_{n}^{k-1} $ | (26) |
其中,
| $ E_{t}^{f x}\left(\hat{s}_{t+1}-\hat{s}_{t}\right)=g_{n} E_{t}^{n}\left(\hat{s}_{t+1}-\hat{s}_{t}\right)+\left(1-g_{n}\right) E_{t}\left(\hat{s}_{t+1}-\hat{s}_{t}\right) $ | (27) |
对于货币政策,由于通货膨胀具有较强惯性,我们以上年第四季度CPI作为通胀预期的代理变量,对名义利率进行简单回归分析发现二者呈显著正向关系,这说明我国货币政策调控具有较强的前瞻性动机。因此,借鉴Clarida et al.(2000)及国内学者王冰冰(2020)、李成等(2010)对中国最优利率规则的研究,将其设为如下前瞻性泰勒规则:
| $ \frac{R_{t}}{\bar{R}}=\left(\frac{R_{t-1}}{\bar{R}}\right)^{\varphi_{R}}\left[\left(\frac{E_{t} \varPi_{t+1}}{\bar{\varPi}}\right)^{\varphi_{\pi}}\left(\frac{G D P_{t}}{\overline{G D P}}\right)^{\varphi_{y}}\left(\frac{1+\tau_{t}^{*}}{1+\tau^{*}}\right)^{-\varphi_{\tau}}\right]^{1-\varphi_{R}} e^{m_{t}} $ | (28) |
| $ m_{t}=\rho_{m} m_{t-1}+\varepsilon_{m, t} $ | (29) |
在围绕初始稳态对模型进行线性化转换的基础上,我们使用贝叶斯法进行参数估计:通过将线性化DSGE模型表示为状态空间形式,并结合卡尔曼滤波进行递归估计以得到参数的后验分布密度;然后,使用Metropolis-Hastings算法对后验分布进行2万次抽样,以计算各参数的后验均值、中位数及置信区间等统计量。贝叶斯方法的优势在于可以将观测数据的一阶矩等信息融入先验分布设定,一定程度上避免了MLE方法估计包含大量参数的DSGE模型时面临的弱识别问题。
(一) 样本选择与混频数据处理根据理论部分的定义,将中国作为模型中的本国、美国作为外国。模型共包括跨期消费偏好、生产技术波动等15个外生冲击,因此我们选取15个观测变量作为参数估计的数据样本,分别是两国的人均实际产出、实际消费与投资、实际工资率、CPI和名义利率、GDP平减指数及人民币兑美元汇率。由于中国的GDP平减指数只能从《中国统计年鉴》得到年度数据,因此本文将中国实际GDP与GDP平减指数以年度数据作为观测变量、其他指标均以季度频率数据作为观测变量,所组成混频数据样本的时间跨度为1996Q1-2019Q4共96个季度。
美国的季度实际产出、实际私人消费、实际私人固定资产投资、GDP平减指数数据来自经济分析局(BEA)数据库,16岁以上劳动力实际周薪(工资)、CPI与16岁以上就业人口数据来自劳工统计局(BLS)网站,将实际产出等总量数据除以人口得到人均实际产出等数据,分别使用美联储公布的3个月期国债二级市场利率与美元兑人民币汇率作为名义利率及汇率的代理变量。
对于相应的中国数据,以名义GDP除以GDP平减指数得到年度实际产出。以城镇单位平均劳动报酬、社会消费品零售总额除以CPI作为实际工资与实际消费的替代指标,将银行间7天同业拆借加权平均利率作为名义利率代理变量,将私人固定资产投资(包括投资来源中的国内贷款、实际使用外资、自筹资金与其他资金等四部分)除以投资价格指数作为实际投资的观测变量。数据来自于中宏数据库和中经网统计数据库,然后,将实际产出等除以城镇单位就业人员数得到对应人均指标①
① 之所以将总量数据除以就业人口得到人均指标,一是契合理论模型的定义,二是就业人口间接反映了生产技术波动,有利于识别劳动附加型技术进步。。
将中国人均实际产出、投资、消费及工资与CPI进行IRIS-X12调整以剔除季节趋势①。最后,对观测变量进行HP滤波处理以剔除趋势性部分。理论模型所包含的15个外生冲击对应于15组观测变量,满足进行贝叶斯估计的识别条件。
① 美国经济分析局与劳工统计局公布的数据均已去除季节趋势,不需再进行季节调整。
(二) 参数校准与贝叶斯估计为减少待估参数,本文对部分参数进行校准以改善整体估计效果。这类参数有一些是稳态结构参数,能够结合模型稳态与数据样本矩信息进行直接赋值(如效用折现因子β与外国产品偏好α),另一些则是由于观测样本包含的有效信息很少、识别性比较差(如劳动及中间品替代弹性εw、εp)。
参考陈利锋(2017)等大量基于DSGE模型的研究做法,将β校准为0.98。参考徐宁等(2020)将年度资本折旧率设为10%,对应季度资本折旧率δ=0.025。将资本产出弹性φ设定为0.34,略小于王云清(2014)所构建能源价格冲击模型中的取值0.36。借鉴Rabanal and Tuesta(2010)将劳动与中间品替代弹性分别设为εw=6和εp=11,将政府支出占产出比重校准为0.2,与王云清(2014)及Rabanal and Tuesta(2010)对美国与欧盟的研究一致。借鉴Schmitt-Grohé and Uribe(2003)将反映资本管制强度的国外资产组合调整成本φf校准为0.01。对与噪声交易相关的两个参数qn和mt,参考Cavaglia et al.(1993)的研究均取为2。2019年,中国GDP总量约占美国的68.5%,我们据此将本国占两国总产出比重n校准为0.4。按照理论模型定义,应以两国贸易规模占各自GDP比重对贸易开放度进行校准,根据2009—2019年双边服务与货物贸易数据计算的平均贸易开放度为9.78%,考虑到两国间还存在密切的直接投资往来以及大量贸易经由香港等地转口的事实,因此平均贸易开放度的估计值偏低,我们参考杨子荣等(2018)将贸易开放度设定为25%。
其他结构参数与深度参数通过贝叶斯估计得到。根据各个参数的经济意义,对取值位于[0, 1]区间的参数使用BETA分布,对取值范围大于零的深度参数使用GAMMA分布,对无约束参数使用正态分布。对于服从AR(1)过程的投资技术波动等11个外生冲击,其自回归系数先验分布统一设为BETA(0.75, 0.075),标准差统一设为INV_GAMMA(0.1, 0.2)。利率平价条件等其他4个冲击为白噪声过程,其标准差先验分布统一设为INV_GAMMA(0.025, 0.1)。主要深度参数的先验分布及估计结果见表 1。
| 表 1 模型参数先验设定与估计结果 |
从表 1可以看到,对两国跨期替代弹性系数的贝叶斯估计结果非常接近1,说明我们在理论模型中虽然将代表性家庭的效用函数设为CRRA(常相对风险规避系数)的一般化形式,但实际上将其设为对数效用函数也不会显著影响研究结论。其他深度参数在两国间的估计结果差异很大,如中国实际消费惯性较高,后验均值约为57%,但相对而言美国家庭消费的“攀比效应”更强,其估计值约73%。中国的工资与价格调整粘性更大,劳动力市场大约每4个季度能够完成一次工资调整,而美国每季度有53.5%的劳动合同能够重新确立均衡工资;同时,美国劳动力市场的工资指数化水平更高,每期未获得劳动合同调整机会的工人,其工资也可依照上期通胀率28.5%的幅度进行调整。
此外,关税反制系数的后验均值为0.6827,表明针对美国发起的贸易摩擦,中国的反制力度较强:美国对中国出口品平均关税税率每提高1%,中国将相应提高进口关税约2.15%。从其他参数估计结果看,外汇市场中噪声交易者占比16.03%,说明人民币兑美元汇率波动存在较强的后向预期,完全理性预期假设下的传统汇率理论显然忽视了这一现实特征,会显著低估外生冲击对世界经济的持续性影响。
四、美国进口关税冲击的国际传导与福利效应自2018年6月美国宣布对中国产品加征进口关税以来,贸易摩擦伴随美国多次升级关税措施而不断升温,表 2梳理了中美先后五次互征关税的规模与涉税商品类别等信息,从中可以发现双方加征关税的主要特点。一是政策博弈特征明显,在美国宣布前两轮进口关税措施后,中国均按规模与税率大致相当的原则进行对等反制,但由于双方出口规模存在较大差距,在此后的几轮关税清单中,中国加征关税的进口品价值与税率明显低于美国。二是涉税进口品的覆盖范围不断扩大,美国最初对华加征关税主要是针对《中国制造2025》中的新能源、新材料等高技术产业,中国的反制集中于农产品与初级工业品等低技术行业;随着贸易关系不断恶化,美国逐渐将纺织服装等轻工业品和低端制造业纳入关税清单,而中国也开始将反制范围扩大到部分高技术制造业与IT通讯产品。
| 表 2 中美互加关税重要时间节点与内容 |
从表 2看,2019年中国的反制力度似乎有所减弱,但考虑到美国纳入关税豁免清单的产品也更多,因此截至2021年1月,中国对美国出口品的平均关税率为20.7%,高于美国对中国出口品19.3%的实际税率(Bown,2021)。那么,目前的关税反制强度是否合理?与不进行反制的情形相比,美国关税冲击对中国宏观经济的传导是否存在显著差异?关税反制是否应与货币政策搭配实施?
基于两国模型的参数估计结果,我们拟借助数值方法对上述问题进行分步讨论。首先,区分中国是否对美国进口关税作出反制两种情形,使用脉冲响应函数(IRF)分析和比较关税冲击对两国经济运行的短期影响。其次,在中国征收报复性进口关税的前提下,利用数值模拟考察不同的关税反制强度是否显著影响关税冲击的传导路径。最后,借鉴Ganelli and Tervala(2015)等的研究,考察不同货币政策响应与反制强度下美国关税冲击的长期与动态福利效应。
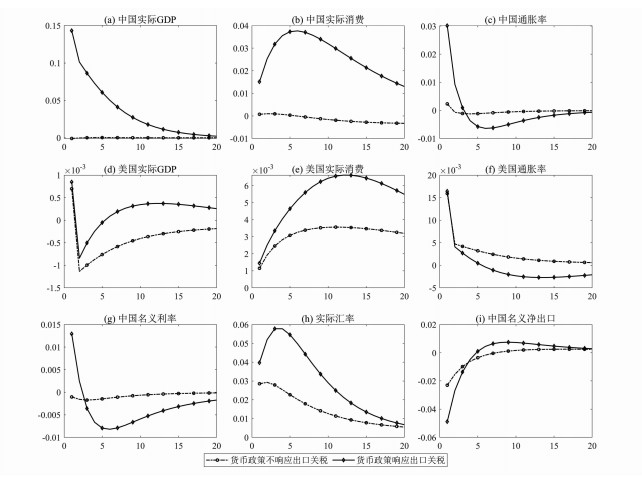
(一) 中国不加反制时美国关税冲击的国际传导假设美国将进口关税暂时性提高10%,且中国不对美国加征关税行为作出反制、但可以选择将出口品关税纳入货币政策调控框架,通过调整短期利率应对美国进口关税冲击。两国主要经济变量对美国关税冲击的脉冲响应曲线见图 1。
|
图 1 美国关税冲击对两国经济的短期传导(无关税反制) |
当中国货币政策调整不对美国进口关税做出响应时,如图 1h所示,关税冲击导致中国贸易条件恶化与实际汇率立即贬值(肖祖沔等,2020),但出口价格下降不足以完全抵消美方加征关税的影响,实际出口显著萎缩。产出下滑的压力迫使央行在美国加征关税后较长时期内保持稍低于初始稳态的名义利率以刺激经济复苏(图 1g中的虚线近乎水平)。受央行降息的影响,实际GDP在冲击初期短暂下降后迅速反弹,此后维持略高于初始稳态的水平、但幅度很小(见图 1a)。另外,从图 1c中的虚线可以看出,关税冲击造成的人民币贬值还使采取成本定价模式的美国出口商显著提高其出口价格,成为推动中国消费品价格上涨的重要外源性因素。图 1i还显示中国在美国加征进口关税后出现约2%的贸易逆差,此后关税税率逐渐下降,逆差也逐步回落至稳态。净出口降幅之所以明显低于关税税率,主要是执行依市定价策略的中国出口企业愿意牺牲价格以维护市场份额;可以预见,若中国出口商也采取成本定价方式,那么关税冲击造成的净出口下滑将更严重。
对美国而言,加征进口关税虽使一部分对中国进口品的消费需求转移至国内产品,但是美国出口品价格的大幅提高却使更多中国消费与投资需求转移至国内产品,因此进口关税对美国实际产出的刺激作用非常有限,并且从冲击后第2期开始其实际GDP长期低于稳态。若考虑到2019年以来美国加征关税的相当一部分进口品为低技术品,这些产品即使减少从中国进口,也会转移到其他发展中国家,难以转化为对美国产品需求的增长,因此关税冲击对美国产出的消极影响可能比本文所估计的大得多。不过,由于美元实际汇率升值导致其购买力增强,加之贸易条件改善以及经常项目持续顺差产生的财富效应,因此图 1e显示美国实际消费会持续增加,约10个季度后才缓慢回归模型稳态。由此推测,加征进口关税可能显著地提高了美国消费者的福利水平(消费者在付出更少劳动的同时,享受到更多的实际消费)。
那么,若中国将出口品关税纳入货币政策调控框架,是否能够对冲美国进口关税冲击的不利影响呢?从图 1的各IRF曲线看,货币政策在应对关税冲击方面确实比较有效。在此种扩展货币政策规则下,美国关税冲击导致的人民币实际汇率贬值与贸易条件恶化幅度更大(图 1h),一价定律约束下的美国出口品厂商倾向于更大幅度地提高出口价格,因此如图 1c所示,人民币贬值几乎等比例地由进口品价格渠道传导至国内,致使中国在关税冲击初期面临更大的输入型通胀压力。从而如图 1g所体现的,虽然将出口关税纳入货币政策框架,但中国在关税冲击初期反而需要约1.25%的加息以应对CPI上涨。随着通胀率迅速回落,为应对美国进口关税冲击,名义利率转而下调并长期低于稳态。央行降息降低了消费者储蓄意愿与资本品价格,使实际产出显著扩张,与人民币贬值等因素叠加还促使出口迅速反弹,图 1i中贸易逆差在约5个季度后由负转正。
中国将出口关税纳入货币调控规则还有利于改善关税冲击对美国经济的传导效果。扩张性货币政策在促进中国产出增长的同时,也相对增加了对美国出口品的需求,因此图 1d中美国实际产出在冲击后恢复更为迅速。相较于中国货币政策不响应关税冲击的情形,图 1e中的实际消费增长幅度也更大。
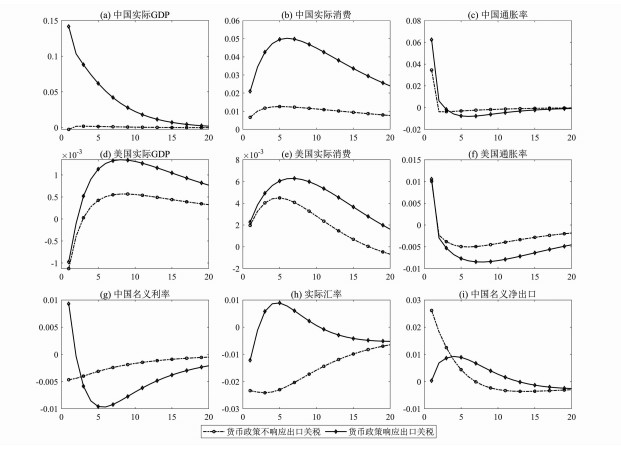
(二) 中国加征反制关税时美国进口关税的冲击扩散图 2绘制了当中国进行关税反制时,两国经济对美国关税冲击的脉冲响应曲线。与图 1货币政策不对关税做出响应且不进行反制的情形相比,对美国产品征收报复性关税能够有效遏制贸易条件恶化。由于关税反制力度ζ>0.5,即中国所征进口品关税税率高于美国(过度反制),使人民币汇率如图 2h所示在冲击后明显升值,因此中国实际消费有较明显增长。相互加征关税显著抬升了进口品价格,造成通货膨胀在冲击初期有所上升。出口萎缩造成的实际GDP下降也比较明显,如图 2g央行将小幅降息加以应对。美国出口商由于采取成本定价模式规避汇率风险、并承担比本国企业更高的关税成本,其出口价格上涨与规模下降幅度更大①,因此图 2i中美国出现一定时期的贸易逆差。在贸易摩擦初期,中国主要对美国农产品及初级工业品加征关税,2019年下半年才将高技术制造业产品纳入关税清单。如果考虑到高技术产品的替代弹性较低、进口关税的贸易转移效应也更小,那么2020年美国对华出口的下滑幅度应该比2019年小。事实也的确如此,根据海关统计,若以2018年为基期,2020年美国对华出口下降约13.02%,明显小于2019年20.76%的降幅。
① 由此可见,不论是否考虑关税反制,对中美贸易均以美元定价的理论假设都能够较好地解释为何2019年中国对美出口仅下滑12.5%,明显小于美国对华出口20.9%的同比降幅。
|
图 2 中美经济对美国进口关税冲击的脉冲响应(关税反制) |
关税反制也显著影响到关税冲击对美国经济的传导,与中国不实施关税反制相比,在冲击初期美国产出明显下降、通胀率上升,此后随关税冲击逐渐转弱以及美联储降息,实际产出恢复并长期略高于稳态。受较强的消费惯性所影响,美国家庭消费的调整比较滞后,实际消费在关税冲击初期略有增加,主要是由于贸易品定价模式差异使中国出口品价格优势更加突出,美国家庭收入虽略有减少,但可以将消费篮子更多分配于中国产品,实际购买力并未显著降低,这也是使图 2i中国净出口在冲击初期增长近3%的重要原因。
当中国既对美国进口关税进行反制、又使货币政策调控部分钉住出口关税税率时,与图 1a仅调整货币政策而不进行关税反制相比,实际产出的IRF曲线非常接近,说明产出扩张主要得益于将出口品关税纳入货币调控框架,关税反制对促进产出增长有一定作用但非常有限。扩张性货币政策配合严厉的关税反制措施使中国出口具有明显价格优势,美国出口下滑幅度比中国更大,因此图 2i中的中国净出口在冲击后多数时期内都处于顺差状态,同时人民币实际汇率贬值幅度更小、持续时间更短,这种财富效应使得图 2b中实际消费比不加关税反制的情形增长更显著。美国经济也从中国货币调控框架的转型中获益,图 2中的美国实际消费与实际GDP均比中国货币政策不响应出口关税的情形涨幅更大。
对比图 1和图 2我们发现,面对美国挑起贸易摩擦、肆意提高进口关税,坚决予以反制能够使中国实现产出与消费小幅扩张,并有助于抑制人民币汇率贬值、保持经常项目收支盈余。如果进一步配合部分钉住出口关税的货币政策规则,总体来看,对于促进产出与消费增长、保持汇率稳定与贸易平衡都更有利。对于美国经济,中国实施报复性关税的短期影响具有不确定性(产出出现下滑,但实际消费有所增长),但长期来看是不利的:美国消费迅速下降,并面临一定的通货紧缩压力。相对而言,美国更乐见中国采取扩张性货币应对政策,对美国产出与消费具有较显著的正向溢出效应。
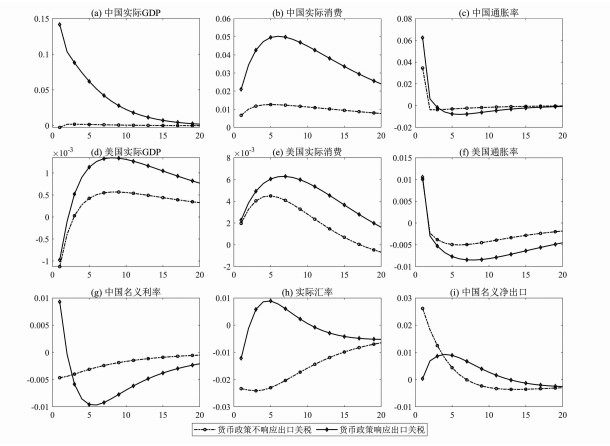
(三) 敏感性分析:反制力度差异对关税冲击国际扩散的影响图 1与图 2的对比分析显示,关税反制能够有效对冲美国加征进口关税的负面影响,更符合本国利益,那么反制强度是否存在最优水平呢?为此,我们将关税反制系数ζ依次取0(不加反制)、0.5(对等反制)与0.75(过度反制),其他参数沿用表 1的估计结果,考察关税反制对美国进口关税冲击传导效果的影响,见图 3。
|
图 3 关税反制强度对美国关税冲击扩散路径的影响 |
在不同关税反制强度设定下,中国实际GDP的IRF曲线基本重合,完全验证了图 1与图 2的分析结论,即产出扩张主要取决于货币当局是否将出口品关税纳入利率规则,提高关税反制强度对实际产出扩张有一定促进作用、但差异很小。关税反制力度越强,美国企业承担的关税成本相对越高,其出口品价格与出口规模下降越明显,中国出口下降幅度比美国企业小得多。因此如图 3i所示,随着关税反制力度增强,在冲击前期的贸易逆差逐渐收窄、甚至出现2%的盈余。同时,实际汇率贬值幅度也随关税反制增强而减小,如采取过度反制措施,实际汇率在冲击初期还会升值近4%。实际汇率升值与出口盈余带来的财富积累使中国实际消费随关税反制的加强而显著增长。
伴随中国关税反制力度的增强,美国实际产出与国内通胀在关税冲击初期都有所下降,美联储需要大幅降息刺激产出与通胀回升,与中国的利率差扩大也是造成美元贬值的一个重要因素。从较长时期看,中国加强关税反制对美国产出增长有一定积极影响,同时使实际消费的波动性增强,关税冲击初期的消费增幅虽然更大,但8个季度后实际消费持续下降的速度也更快。
(四) 关税反制与货币调控政策组合的福利效应分析通过前述分析可以发现,仅从促进经济增长的角度看,加强关税反制并将出口关税纳入货币调控框架对中国而言是最为有利的。但经济发展的最终目的是促进消费并提升社会福利,为从福利视角对美国关税冲击的贸易与货币应对政策组合进行量化评价,本文拟借鉴Schmitt-Grohé and Uribe(2007)以及Ganelli and Tervala(2015)等做法,借助对代表性家庭效用函数的有效变形,得到用以测度宏观经济政策福利效应的近似指标①。
① 相较于Woodford(2002)等其他方法,本文的福利测度指标有两点优势,一是既可用以考察短期福利动态,也可用于计算长期福利效应;二是其他福利测算方法需要计算部分内生变量方差,这要求模型在进行数值模拟分析时保持非线性形式(或者至少展开至二阶近似),本文的福利计算方法无此要求,对线性化模型仍适用。
在保持就业水平不变的前提下,我们将某一经济政策或外生冲击所产生的第t期福利损失(或收益)表示为代表性家庭愿意减少(或需要增加)当前有效消费(即Ct-bCt-1)的百分比,并将这一比值记为λt。由于表 1的参数估计结果显示σ近似等于1,为简化模型推导,我们将家庭效用函数直接写为对数形式。将未发生关税冲击的情形作为基准模型,此情形下第t期家庭效用函数可表示为:
| $ U_{t}^{B M}=\log \left(C_{t}^{B M}-b C_{t-1}^{B M}\right)-\frac{\left(N_{t}^{B M}\right)^{1+\eta}}{1+\eta} $ | (30) |
面临关税冲击时,代表性家庭效用函数可记为:
| $ U_{t}^{T R}=\log \left[\left(1+\lambda_{t}\right)\left(C_{t}^{B M}-b C_{t-1}^{B M}\right)\right]-\frac{\left(N_{t}^{B M}\right)^{1+\eta}}{1+\eta} $ | (31) |
对(31)式可以继续变形得到关于短期福利损失λt的表达式:
| $ \lambda_{t}=100\left[\exp \left(U_{t}^{T R}-U_{t}^{B M}\right)-1\right] $ | (32) |
上述模型分析中所指的效用为发生关税冲击时的t期效用水平,因此UtTR=Ut。基准模型所对应的未发生关税冲击时的家庭效用应保持稳态水平不变,与时期t无关:UtBM=U0。利用效用函数的一阶泰勒展开式可以得到:
| $ d U_{t}=U_{t}-U_{0}=\frac{\hat{c}_{t}-\hat{b c}_{t-1}}{1-b}-\bar{N}^{1+\eta} \hat{n}_{t} $ | (33) |
将(33)式代入(32)式即可得到利用对数线性化模型变量计算短期福利损失的表达式:
| $ \lambda_{t}=100\left[exp \left(\frac{\hat{c}_{t}-\hat{b c}_{t-1}}{1-b}-\bar{N}^{1+\eta} \hat{n}_{t}\right)-1\right] $ | (34) |
Reitzand Slopek(2005)研究发现加征关税一般在短期内增加进口国福利,但是长期福利效应可能逆转。也就是说,加征进口关税或是一种短视行为,因而对关税冲击长期福利效应的测度同样重要。计算长期福利效应时,我们需要关注家庭终生贴现效用与福利效应净现值(Discounted Present Value)。未来各期效用的净现值可表示为:
| $ U_{D P V}^{B M}=E_{t} \sum\limits_{s=t}^{\infty} \beta^{s-t}\left[log \left(C_{s}^{B M}-b C_{s-1}^{B M}\right)-\frac{\left(N_{s}^{B M}\right)^{1+\eta}}{1+\eta}\right] $ |
将关税冲击的长期福利效应记为λDPV,利用与短期福利效应类似的推导思路可以得到:
| $ U_{D P V}^{T R}=\frac{1}{1-\beta} log \left(1+\lambda_{D P V}\right)+U_{D P V}^{B M} $ | (35) |
同样将长期福利变化表示为占稳态有效消费的百分比,利用(35)式解λDPV得:
| $\lambda_{D P V}=100\left\{exp \left[(1-\beta)\left(U_{D P V}^{T R}-U_{D P V}^{B M}\right)\right]-1\right\} $ | (36) |
最后利用与(34)式同样的推导步骤可将(36)式进一步变形得到:
| $ {\lambda _{DPV}} = 100\left\{ {exp \left[ {(1 - \beta )\sum\limits_{s = t}^\infty {{\beta ^{s - t}}} \left( {\frac{{{{\hat c}_s} - \hat b{c_{s - 1}}}}{{1 - b}} - {{\bar N}^{1 + \eta }}{{\hat n}_s}} \right)} \right] - 1} \right\} $ | (37) |
对世界经济而言,关税冲击的总福利损失可以表示为两国相对经济规模对长期福利效应的加权求和:
| $ \lambda_{D P V}^{\text {world }}=n \lambda_{D P V}+(1-n) \lambda_{D P V}^{*} $ | (38) |
根据上述福利测度方法,本文计算了四种关税政策与货币政策组合下美国关税冲击的短期福利效应,见图 4。其中ζ=0代表中国不对美国加征进口关税进行反制,φτ=0表示央行不将出口品关税纳入利率调控规则。福利损失(或收益)数值单位为1%。
|
图 4 不同政策组合下美国关税冲击对中国福利的动态影响 |
在中国应对关税冲击的所有政策选项中,既不进行关税反制也不将出口品关税税率纳入货币政策规则所产生的福利收益最小,社会福利仅在关税冲击的前4个季度略高于稳态,此后所有时期的福利水平都低于稳态并不断恶化。其次,货币政策不对出口品关税做出响应、但对进口品加征报复性关税的福利收益明显增加,在关税冲击后20个季度内社会福利平均高于初始稳态约1%。不进行关税反制但将出口关税纳入利率规则,会进一步提升福利水平。货币政策对出口关税做出响应、并搭配征收报复性进口品关税的政策组合,能够实现最大化本国福利。对四种政策组合下关税冲击的短期福利效应排序与图 1、图 2的脉冲响应分析结论是一致的。
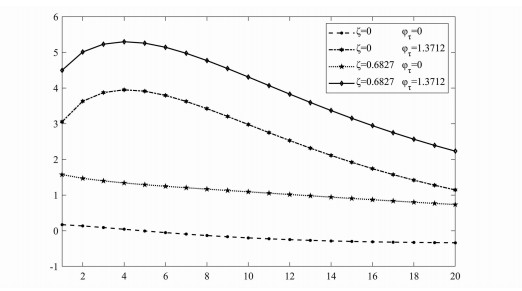
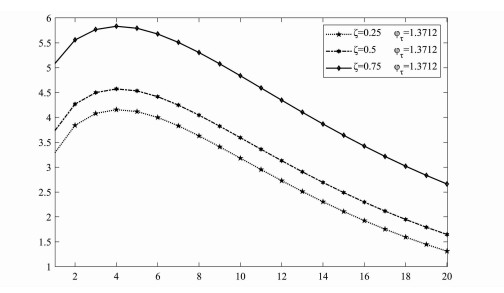
在货币政策对出口关税做出响应的前提下,图 5进一步汇报了不同关税反制强度对应的短期福利收益。图 3的分析显示,中国实际GDP的IRF曲线基本重合,这意味着在不同关税反制力度设定下,就业率对关税冲击的脉冲响应幅度也基本相同,福利效应差异取决于不同反制强度下的消费波动。因此,图 5不同关税反制强度的福利效应排序与图 3b实际消费的增长幅度完全相对应,对美国进口关税的反制越强,越有利于促进本国福利增长。
|
图 5 不同关税反制强度下美国关税冲击的福利效应 |
我们还根据(37)式与(38)式计算了不同政策组合下关税冲击对中美两国的长期福利效应和总福利变化。若不考虑其他因素、仅以长期福利变化作为政策选择依据,从表 5中可以得出以下结论。一是如果中国针对美国加征进口关税不采取任何应对策略,会造成社会福利的显著下降(长期中,每一时期的家庭有效消费相比稳态均减少0.17%)。二是不论是否对美国加征关税进行反制,中国都倾向于使货币政策对出口品关税做出积极响应。三是在货币政策对出口品关税做出响应的基础上,中美利益冲突非常明显:从美国角度看,中国不对其加征进口关税进行报复更符合自身利益,是所有政策组合中对美国最有利的选项;但于中国而言,对美国肆意加征关税做出严厉反制更符合福利最大化目标,此时以实际消费衡量的美国社会福利仅增长约0.03%,说明在此政策选项下,美国挑起对华贸易摩擦几乎是徒劳,不会显著改善其福利状况。最后,假设中国基于其他政策考量,坚持货币政策“中立”,仅对美国进口关税采取针锋相对的反制策略,则可造成美国长期福利下降(美国家庭每期的实际消费相比稳态减少0.06%),这也是唯一使美国社会福利恶化的政策选项。
| 表 3 美国进口关税冲击对中美社会福利的长期影响 |
通过构建一个包含贸易品美元定价约束、外汇噪声交易与关税反制等特征的两国DSGE模型,在结合宏观经济数据进行参数贝叶斯估计的基础上,本文实证分析了美国肆意加征进口关税、挑起对华贸易摩擦背景下,中国的关税反制策略与货币政策协调等问题。
针对美国进口关税冲击的数值模拟结果表明,当中国对美国提高进口关税不加反制时,若货币政策同样不对出口品关税做出响应,关税冲击会导致中国贸易条件恶化与实际汇率贬值,使中国经济产出、消费与净出口都有所下滑,但降幅较小;若将出口品关税纳入货币政策调控框架,能够显著促进本国产出与消费增长,但在关税冲击初期会产生较大的输入型通胀压力,并且实际汇率贬值幅度与净出口波动性显著增强。当中国对美国加征进口关税进行反制时,即使货币政策规则不作调整,也能够较有效地对冲关税冲击的不利影响,产出与消费增长明显,并有助于在抑制人民币汇率贬值的同时,实现经常项目收支小幅顺差;如进一步将出口品关税纳入货币调控规则,对于促进实际产出与消费增长、保持汇率稳定和经常项目温和扩张都更为有利。无论中国是否进行关税反制,实施部分钉住出口品关税的扩张性货币政策都相对有利于提高美国产出与消费,产生明显的正向溢出效应。
此外,对美国进口关税冲击的长期与短期福利分析都表明,关税反制力度与中国社会福利水平的提升呈正相关。通过对两国长期福利效应的对比分析,本文得出三点结论:一是如果关税与货币政策不做任何调整,那么美国关税冲击将导致中国长期福利显著恶化;二是随着关税反制强度的提高,与中国长期福利提升相应的是美国福利水平不断下降,即产生了显著的福利转移效应,因此比较容易引发美国的关税报复;三是无论关税反制强度如何,将出口品关税纳入货币政策调整框架,都能显著地提升中美两国福利水平与整体福利。
上述研究结论具有鲜明的政策含义。面对美国不顾各方激烈反对、执意挑起对华贸易争端,不论是为削弱关税冲击对宏观经济的不利影响,抑或保持汇率稳定与社会福利增长,中国都应进行坚决有力的关税反制。在应对中美贸易摩擦过程中,货币政策调整具有很强的灵活性:如果政策调整的首要目标是促进经济增长,那么可以将出口品关税纳入利率规则,与关税反制措施搭配,能够显著带动产出与消费扩张、实现长期福利水平提升,但也会对美国产生明显的正向溢出作用;若经济政策的优先目标在于促使美方停止贸易摩擦,则应保持货币政策中性、仅采取针锋相对的关税反击策略,既可有效应对美国加征关税对本国经济的不利影响,又可提升长期福利水平,并使美国经济承受关税反制的负面冲击与社会福利恶化,实现“以战促和”的目的。最后,探讨如何在两国DSGE模型中纳入中美产业与贸易结构差异,从而更准确地分析不同反制策略下关税冲击的国际传导,应是下一步研究的重要改进方向。
| [] |
陈利锋, 2017, “劳动力流动模式、宏观经济波动与社会福利——基于包含正规就业与非正规就业的NK-DSGE模型”, 《经济与管理评论》, 第 4 期, 第 18-28 页。 |
| [] |
崔琨、施建淮, 2020, “关税冲击下的中间品贸易、通货膨胀目标规则与福利分析”, 《世界经济》, 第 10 期, 第 169-192 页。 |
| [] |
邓力平、樊政荣、王智烜, 2018, “关税税目比较研究与新形势下我国对策建议”, 《经济与管理评论》, 第 5 期, 第 107-113 页。 |
| [] |
方意、文佳、荆中博, 2019, “中美贸易摩擦对中国金融市场的溢出效应研究”, 《财贸经济》, 第 6 期, 第 55-69 页。DOI:10.3969/j.issn.1002-8102.2019.06.004 |
| [] |
黄鹏、汪建新、孟雪, 2018, “经济全球化再平衡与中美贸易摩擦”, 《中国工业经济》, 第 10 期, 第 156-174 页。 |
| [] |
李成、王彬、马文涛, 2010, “资产价格、汇率波动与最优利率规则”, 《经济研究》, 第 3 期, 第 91-103 页。 |
| [] |
刘维林、程倩、王敏, 2020, “全球价值链视角下中美贸易摩擦的就业影响测算”, 《中国人口科学》, 第 2 期, 第 15-29 页。 |
| [] |
孙文浩、张杰, 2020, “中美贸易战何以影响制造业高质量发展”, 《科学学研究》, 第 9 期, 第 1559-1569 页。DOI:10.3969/j.issn.1003-2053.2020.09.004 |
| [] |
王冰冰, 2020, “利率市场化及其传导效率的时变效应——基于DSGE和SV-TVP-VAR模型的分析”, 《南方经济》, 第 12 期, 第 74-89 页。 |
| [] |
王云清, 2014, “能源价格冲击与中国的宏观经济: 理论模型、数值分析及政策模拟”, 《经济学动态》, 第 2 期, 第 44-57 页。 |
| [] |
肖祖沔、彭红枫、向丽锦, 2020, “贸易摩擦、宏观经济波动与经济开放程度的选择”, 《金融研究》, 第 10 期, 第 74-91 页。 |
| [] |
徐宁、丁一兵、张男, 2020, “利率管制、LPR与完全市场化下的货币政策传导机制: 理论对比与实证检验”, 《南方经济》, 第 5 期, 第 34-48 页。 |
| [] |
杨子荣、徐奇渊、王书朦, 2018, “中美大国货币政策双向溢出效应比较研究——基于两国DSGE模型”, 《国际金融研究》, 第 11 期, 第 14-24 页。 |
| [] |
朱民、徐钟祥, 2021, “中美贸易摩擦对中国股票市场的影响”, 《国际金融研究》, 第 4 期, 第 3-12 页。 |
| [] |
Bown C. P., 2021, "The US-China Trade War and Phase One Agreement". Journal of Policy Modeling, 43(4), 805–843.
DOI:10.1016/j.jpolmod.2021.02.009 |
| [] |
Calvo G. A., 1983, "Staggered Prices in a Utility-maximizing Framework". Journal of Monetary Economics, 12(3), 383–398.
DOI:10.1016/0304-3932(83)90060-0 |
| [] |
Cavaglia S., et al., 1993, "Further Evidence on Exchange Rate Expectations". Journal of International Money and Finance, 12(1), 78–98.
DOI:10.1016/0261-5606(93)90011-Y |
| [] |
Clarida R., et al., 2000, "Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory". Quarterly Journal of Economics, 115(1), 147–180.
DOI:10.1162/003355300554692 |
| [] |
Engler P., Tervala J., 2018, "Welfare Effects of TTIP in a DSGE Model". Economic Modelling, 70, 230–238.
DOI:10.1016/j.econmod.2017.11.007 |
| [] |
Ganelli G., Tervala J., 2015, "Value of WTO Trade Agreements in a New Keynesian Model". Journal of Macroeconomics, 45, 347–362.
DOI:10.1016/j.jmacro.2015.06.001 |
| [] |
Rabanal P., Tuesta V., 2010, "Euro-dollar Real Exchange Rate Dynamics in an Estimated Two-country Model: An Assessment". Journal of Economic Dynamics and Control, 34(4), 780–797.
DOI:10.1016/j.jedc.2009.11.003 |
| [] |
Reitz S., Slopek U. D., 2005, "Macroeconomic Effects of Tariffs: Insights from a New Open Economy Macroeconomics Model". Swiss Journal of Economics and Statistics (SJES), 141(Ⅱ), 285–311.
|
| [] |
Schmitt-Grohé S., Uribe M., 2003, "Closing Small Open Economy Models". Journal of International Economics, 61(1), 163–185.
DOI:10.1016/S0022-1996(02)00056-9 |
| [] |
Schmitt-Grohé S., Uribe M., 2007, "Optimal Simple and Implementable Monetary and Fiscal Rules". Journal of Monetary Economics, 54(6), 1702–1725.
DOI:10.1016/j.jmoneco.2006.07.002 |
| [] |
Woodford M., 2002, "Inflation Stabilization and Welfare". Contributions to Macroeconomics, 2(1), 1009.
|




