创新是一个经济体实现长期持续增长的源泉(Romer,1990;Grossman and Helpman, 1991;Aghion and Howitt, 1992)。然而,经济学家普遍认为,改革开放以来中国经济近40年的高速增长主要来自“汗水而非灵感”,即经济增长主要依靠劳动力、资本和资源等要素投入而非技术进步和效率改善。随着劳动力和土地成本攀升、资本回报率下滑、生态环境压力日益加大等诸多问题涌现,原有的增长和发展方式已然不可持续。近年来,中国经济增长模式进入转型期,不再过度追求增长的速度,而是更加关注增长的质量。提高增长的质量,本质上是要提高技术进步对增长的贡献,将增长动力由要素、投资驱动向创新驱动转换。
作为创新资源及要素的主要集聚地,在国家政策引领下,2008年起,各地纷纷开展创新型城市建设。实践表明,创新为中国城市注入了增长的新动能,总体上提升了城市经济发展的质量和效益。然而,不少城市仍面临较为严峻的资源与环境挑战,而脱离了可持续意义上的增长过程不可能是真正的高质量发展。创新与城市绿色发展之间的失衡不禁让我们产生疑问:创新是否必然促进绿色发展?不同城市的创新活动对绿色发展的影响效应有何差异?
回答这些问题首先要明确绿色发展的内涵。绿色发展来源于可持续发展,可将其视为实现可持续发展目标的一项中短期战略或工具(OECD,2011)。这说明,绿色发展绝不简单等同于环境保护,其关注的是如何在保持增长的同时改善资源效率、提升环境绩效并由此增进社会福祉。从这个内涵出发,生态效率无疑是一个评价绿色发展的有力工具,因为其综合考虑了经济、资源与环境的协调发展,为衡量绿色发展提供了一个更具综合性的视角(黄建欢,2016)。然而,尽管创新是改善生态效率的核心动力,但创新却不天然具有“绿色”属性。与此相对,现有研究在探讨创新对绿色发展的影响时也形成了两种代表性观点。一种观点认为,创新特别是绿色创新能够对绿色发展产生积极影响。Ghisetti and Quatraro(2017)考察了绿色技术创新对意大利不同区域多个生产部门环境绩效的影响,研究表明绿色创新能有效提升区域生产部门的环境生产力。罗能生、余燕团(2018)分析了城市创新空间溢出的高位压力和低位吸力对绿色发展的影响机制,并基于实证检验得出邻近城市创新的高位压力对本城市生态效率提升具有显著促进作用。Zhang et al.(2018)运用空间自回归模型检验了技术创新对城市生态效率的影响。结论表明,技术创新显著促进了城市绿色发展且这种效应在东部及高行政级别城市更为明显。持相反观点的学者认为创新也可能阻碍绿色发展,Saunders(2008)、邵帅等(2013)研究指出,依赖技术创新提高资源效率进而降低资源消费的政策思路可能需要重新审视,因为技术创新可能产生资源回弹效应,从而使生产中资源消耗增加、污染排放加剧。同时,尽管有些创新产品在应用时可能是绿色的,但其生产过程却带来大量的资源消耗和持续的环境威胁(Chang et al., 2014)。
可见,关于创新对绿色发展的影响并未形成一致结论。在一定程度上,只有当创新行为符合可持续性准则,能充分协调经济、生态、社会等多个目标时,才能对绿色发展产生积极影响(张江雪等,2018)。在实践中,创新对生态效率的影响还有两方面问题需要考虑:一是不同区域及城市的发展水平、科技政策、环境政策、产业政策等存在较大差异,这些差异将导致创新对绿色发展的影响存在异质性,分析这个问题有利于不同城市在发展战略上采取差异化的对策。二是随着区域间生产要素流动愈加自由和频繁,城市间的空间关联性也逐渐增强,不可忽视由空间关联而产生的空间溢出问题。外溢是创新的一个重要特征,且创新的外溢效应不单发生在微观的企业、科研院所等层面,也很可能发生在区域之间(白俊红、蒋伏心,2015)。不仅如此,生态效率或绿色生产率也可能存在空间相关性(陈阳、唐晓华,2019)。这意味着,在一定区域范围内,一个城市的创新行为、生态效率都可能对其它城市产生溢出。近年来,空间计量技术在创新和绿色发展研究领域已有所应用,但多数研究只揭示了创新或生态效率某一方面的空间依赖特征,尚未深入考察创新空间溢出对生态效率的影响效应(Moreno et al., 2005;余泳泽、刘大勇,2013;赵增耀等,2015;黄建欢、许和连,2016)。那么,创新空间溢出对生态效率的影响如何?回答这个问题对于破除地区垄断和政策壁垒、加强区域协同创新以更好地推进绿色发展具有重要作用。
目前,学术领域仍缺乏创新及其空间溢出影响城市绿色发展的经验研究成果。同时,由于城市创新能力及绿色发展水平差异显著,研究创新对绿色发展的影响还需基于城市异质性进行深入考察。本文的边际创新主要体现在,在理论层面探讨了创新对生态效率的影响机制,并将空间计量模型运用于影响机制检验中。同时,相比于以往研究只检验区域生态效率、创新某一方面的空间溢出效应,本文不仅考察了生态效率的空间溢出效应,同时还检验了创新空间溢出对生态效率的影响效应,即通过创新溢出,将城市创新行为与空间关联城市的绿色发展水平联系起来,弥补了以往研究只从静态层面考察创新对本城市绿色发展的影响或单纯考虑创新本身空间溢出效应的不足。进一步地,本文还通过对不同距离阈值上的创新空间溢出效应进行估计,测算了创新空间溢出的距离边界,检验了创新空间溢出驱动城市绿色发展的最佳地理距离区间,从而为增强区域创新合作以提升区域整体绿色发展水平提供了可供参考的量化依据。
二、理论机制本文主要关注技术创新对生态效率、绿色发展的影响。从理论上讲,作为一种知识技术密集型活动,城市创新行为会对绿色发展起到显著促进作用。从生产端来看,创新具有增长效应、资源与环境效应和结构优化效应,三大效应将对生态效率产生正向作用,进而促进城市绿色发展。首先,实现可持续的经济增长是绿色发展的主要目标之一。内生经济增长理论认为技术进步、研究开发、知识积累、人力资本等是克服要素报酬递减、维持经济持续增长关键。事实上,内生增长模型所讨论的技术、研发、知识、思想等增长“发动机”在广泛意义上可归为创新。而Aghion and Howitt(1998)等学者进一步将熊彼特创新理论引入内生增长模型,并基于“创造性毁灭”的思想定义了创新的过程和结果,从动态和竞争视角揭示了创新是经济持续增长的源泉。在实践中,创新本质上是追求利润最大化的厂商对新知识、新技术进行有意识投资的结果。厂商为获得垄断利润不断增加研发支出,这增加了知识存量、推动了技术创新,技术创新又进一步推动了新产品和新方法的实现,进而促进了经济增长(严成樑、龚六堂,2009)。因此,从微观企业创新到宏观技术进步,创新能够为城市经济增长注入持久的动能,也成为城市生态效率改善的重要条件。
其次,在资源与环境效应层面,一方面,资源化技术、再利用技术、节能技术、新材料技术、智能控制等先进技术的诞生,无疑为高效利用资源提供了解决方案。技术创新降低了资源在生产、传导过程中的耗损量,或通过研发出其他可替代材料,促进了资源集约与循环利用。另一方面,技术创新通过改进治污设施提升了污染控制与治理水平,还通过作用于生产系统形成前端预防,对于清洁生产、遏制污染排放、提升环境复原力具有重要作用(王鹏、谢丽文,2014)。随着城市创新能力的提升及绿色发展理念的增强,将使技术创新朝着绿色技术创新的方向演进。绿色技术创新关注全面的经济和生态利益,追求生态平衡、经济增长和社会发展等多个目标之间的协调发展(关成华、韩晶,2018)。绿色技术创新不仅限于产品生产过程,而是产品的研发、生产、销售乃至产品本身的废弃物全生命周期的绿色化创新,尽最大可能预防和降低经济活动对生态环境带来的危害。
第三,在结构优化效应层面,绿色发展目标的实现需要一个高级化的产业结构,尽管决定和影响产业结构演进与变革的因素表现在很多方面,但在根本上,技术创新是推动和实现产业结构变革的主要动力。在绿色发展进程中,技术创新将冲破各种“瓶颈”制约,实现资源优化配置和产业结构质的变革,淘汰低端落后产业、改造和提升传统产业、催生新兴绿色产业,推动产业结构逐步实现高级化和绿色化。以智能制造、新能源、新材料、信息技术等为代表的新兴绿色产业具有低消耗、低排放、高产出的特点,能够在不增加资源消耗和环境污染负担的前提下实现产业升级和产能增加,是城市现代产业体系的重要支撑,能极大改善城市经济发展与资源环境之间的协调性。
然而,尽管创新是改善生态效率和驱动绿色发展的根本动力,但创新也可能对绿色发展具有负面作用。作为一种投资活动,如果企业未能将资源及环境成本纳入其创新决策,那么在追求利润最大化的过程中,一旦经济与生态效益发生冲突,企业可能会不牺强化对资源及环境的消耗和掠夺,从而造成高消耗、高排放。从企业到地方政府,如果一个城市的创新目标是以追求经济增长为导向而不将生态环境纳入其目标体系,那么城市的创新行为就可能无法实现经济、生态环境等多目标之间的有效协调。基于此,不同城市的创新基础、能力、目标、决策等将在很大程度上决定创新对绿色发展的影响大小和方向。同时,由于创新具有较高的机会成本,风险与收益并存,很多时候创新的投资回报难以预料,在技术开发、成果转化应用阶段都存在较大的不确定性及风险。当创新收益小于成本时,不仅会将降低增长的集约度还会滞缓技术创新的进程。此外,创新带来的资源效率的提升会促进整个社会经济的快速增长,而提高资源效率所节约的能源、资源,可能通过替代效应、收入效应和产出效应等产生新的资源需求而被部分甚至完全抵消。
综合以上分析,尽管在实践中,创新活动有可能对生态效率产生某些负面影响,但其正向效应应远大于其负面影响。作为实现可持续发展目标的重要战略或工具,绿色发展强调的是经济、环境与社会系统的共生性、整体性和协调性。创新不仅能够创造新的经济增长点、释放经济增长潜能,还能为破除资源环境瓶颈约束找到有效途径,增强了经济体绿色发展的内生动力,也提升了经济和环境双赢所带来的社会福祉。基于此,提出以下研究假设:
假设1:创新是促进城市绿色发展的根本途径,将对城市生态效率改善产生积极影响。
假设2:生态效率是考虑各种投入和产出时的综合效率,而创新具有的增长效应、资源与环境效应、结构优化效应能够成为促进城市生态效率改善的重要途径。
在现实经济中,城市的一系列经济社会活动并不是封闭的,城市之间将通过物质资源、生产要素等的流动而产生空间上的相互联结,即城市之间具有空间关联效应。从区域角度来看,创新活动具有很强的空间外溢性,不少学者考察了一定区域范围内创新的空间分布特征和溢出机制、溢出的增长效应、溢出边界等问题,这些研究揭示了一个城市的创新溢出能对空间关联城市的创新行为产生显著影响。而如前所述,创新可以通过三大正向传导机制影响城市绿色发展,那么创新的空间溢出也很可能影响空间关联城市的生态效率。当前,中国城市发展已逐渐形成以城市群为标志的高级空间组织形式,城市之间联系紧密、互动频繁,通过竞争、合作、模仿等方式,新知识、新发明、新技术等各类创新成果得到溢出,不仅有利于提升区域整体的创新绩效,还将对空间关联城市的经济增长、资源利用及环境保护产生影响。基于此,提出以下研究假设:
假设3:创新的空间溢出会对空间关联城市的生态效率产生影响。
三、空间计量模型、变量与数据 (一) 空间面板模型多数文献采用空间计量模型对空间关联和溢出效应进行研究。一般而言,空间计量模型主要包括空间杜宾模型(SDM)、空间自回归模型(SAR)和空间误差模型(SEM)等形式(Anselin,1988),其中,SDM是更为一般化的空间计量模型,本文首先设置如下的空间杜宾模型:
| $ ef{f_{it}} = \rho Wef{f_{it}} + {X_{it}}\beta + W{X_{it}}\delta + {\kappa _i} + {v_t} + {\mu _{it}} $ | (1) |
式(1)中,i代表城市,t代表年份,被解释变量eff代表生态效率;W为空间权重矩阵,Weff表示被解释变量的空间滞后项,P为空间自相关回归系数;X为核心解释变量城市创新行为(inv)及其它控制变量集合;WX为解释变量及控制变量的空间滞后项,δ为各变量对应的系数;ki和vt分别表示个体和时间固定效应,μ为随机误差项。当δ=0时,SDM退化为SAR;当δ+ρβ=0时,SDM退化为SEM。
构建空间权重矩阵W是空间计量分析的关键,地理距离权重矩阵是现有研究广泛采用的矩阵形式,该矩阵假定空间效应的强度取决于地理距离,空间单元之间的距离越近则空间效应越强。依据地理距离标准,构建反距离空间权重矩阵Wijd,其元素满足:对角元素为0,非对角元素为城市之间距离平方的倒数。虽然空间溢出效应具有距离属性,但地理特征并不是产生空间效应的唯一因素,城市间的空间联系还受到经济发展水平等各类因素的影响。为此构建经济空间权重矩阵Wije,其元素满足:对角元素为0,非对角元素为城市间实际GDP之差绝对值的倒数。此外,为了综合考虑地理因素和经济因素,基于引力模型,本文还构建了经济地理空间权重矩阵Wijde,其元素满足:对角元素为0,非对角元素为城市间实际GDP乘积与距离平方之比。本文研究将综合采用Wijd、Wije、Wijde3种空间权重矩阵进行分析。
(二) 变量与数据鉴于数据的完整性、连续性以及行政区划调整,本文最终选取了中国260个地级及以上城市作为研究样本,研究周期为2007-2016年。数据来自各期《中国城市统计年鉴》《中国省市经济发展年鉴》以及各省、区、市历年统计年鉴和统计公报。城市间的距离数据根据国家基础地理信息系统网站提供的1:400万电子地图,利用Geoda软件测量得到欧式直线距离。城市专利数据来自国家知识产权局的专利信息中心。
1. 被解释变量
城市生态效率(eff):在区域层面,生态效率是全面考虑劳动力、资本、能源等各种投入和各种产出尤其是环境非期望产出时的投入产出效率。本文采用Tone and Tsutsui(2010)提出的EBM模型(Epsilon-Based Measure)对中国城市生态效率进行测算,该模型的最大优势在于其能够实现径向比例与非径向松弛的兼容。包含非期望产出的、基于非导向的EBM模型线性规划构建如下:
| $ \begin{array}{l} {\tau ^*} = \min \frac{{\theta - {\varepsilon _x}\sum\limits_{i = 1}^m {\frac{{w_i^ - s_i^ - }}{{{x_{io}}}}} }}{{\eta + {\varepsilon _y}\left({\sum\limits_{r = 1}^s {\frac{{w_r^{ + g}s_r^{ + g}}}{{{y_{ro}}}}} + \sum\limits_{k = 1}^q {\frac{{w_k^{ - b}s_k^{ - b}}}{{{b_{ko}}}}} } \right)}}\\ s.t.\;\;\;\sum\limits_{j = 1}^n {{x_{ij}}{\lambda _j} + s_i^ - = \theta {x_{io}}}, i = 1, \ldots, m\\ \;\;\;\;\;\sum\limits_{j = 1}^n {{y_{rj}}{\lambda _j} + s_r^{ + g} = \eta {y_{ro}}}, r = 1, \ldots, s\\ \;\;\;\;\;\sum\limits_{j = 1}^n {{b_{kj}}{\lambda _j} + s_k^{ - b} = \eta {b_{ko}}}, k = 1, \ldots, q\\ \;\;\;\;\;\;\;\;\;\;{\lambda _j} \ge 0;s_i^ -, s_r^{ + g}, s_k^{ - b} \ge 0 \end{array} $ | (2) |
式(2)中,τ*代表生态效率,如果τ*=1,说明决策单元(DMU)是技术有效的;m、s、q分别表示投入、期望产出及非期望产出的数量;xio、yro、bko分别表示第o个决策单元的第i种投入、第r种期望产出及第k种非期望产出;wi-、wr+g、wk-b分别表示各项投入及产出指标的相对重要程度,即权重;si-、sr+g、sk-b分别为投入松弛、期望产出松弛以及非期望产出松弛;λ为DMU的线性组合系数;εx、εy是EBM模型中的重要参数,满足条件0≤εx≤1、0≤εy≤1,反映了效率测度中非径向部分的重要程度。根据Tone and Tsutsui(2010)的方法,本文基于数据本身客观设置参数,并借鉴Cheng and Qian(2011)提出的调整后的Pearson相关系数构建关联指数矩阵,通过计算关联指数矩阵中的最大特征根和其对应的特征向量得到参数εx、εy及各项投入产出指标的权重。在测度生态效率时,需要选择合适的投入及产出指标。本文的期望产出为各城市2007年不变价的地区生产总值;考虑到工业污染排放是城市非期望产出的主要来源,选择各城市工业废水排放量、工业二氧化硫排放量、工业烟粉尘排放量3种非期望产出。投入要素为劳动、资本及自然资源,其中,劳动投入采用各城市从业人员期末人数;资源投入的理想指标为各城市的能源消费量,但鉴于城市一次能源消费数据的缺失,采用全社会用电量作为资源投入(Zhang et al., 2018;韩晶等,2019);资本投入为采用永续盘存法估算的资本存量:
| $ {K_{i, t}} = \left({1 - {\delta _{i, t}}} \right){K_{i, t - 1}}\left({{I_{i, t}}/{P_{i, t}}} \right) $ | (3) |
其中,Ki, t表示i城市t期的资本存量;Ii, t为当年价社会固定资产投资,并根据各地区固定资产投资价格指数对新增固定资产投资进行平减;Pi, t为价格指数,δi, t为折旧率,本文将资本折旧率统一设定为5%。基期资本存量采用“稳态方法”进行估算确定:
| $ {K_{i, 0}} = {I_{i, 1}}/\left({{g_{i, 1}} + {\delta _{i, 1}}} \right) $ | (4) |
其中,Ki, 0表示i城市的基期资本存量,Ii, 1表示i城市第1期的社会固定资产投资,gi, 1表示i城市第1期的总产出增长率。在此基础上,采用EBM模型测算得到各年份各城市的生态效率。
2. 核心解释变量
城市创新行为(inv):既有研究主要采用3类指标来度量创新:其一是使用投入端创新相关指标,如R & D支出、R & D人员等;其二是使用产出端创新相关指标,如专利数量、新产品销售收入等;其三是使用测算类指标,如全要素生产率、创新效率等。其中,以专利度量创新更具优势(Bettencourt,2007)。首先,相比投入端指标、创新效率等,专利能更加直接体现创新主体的创新能力;其次,专利数据公开客观、更新及时,能够较为准确地反映技术变化趋势;第三,在一国范围内,各地专利申请、审查、授权的制度法规基本一致,且专利包含了关于发明类别、发明者等方面的信息,有便于直接比较不同区域创新能力差异。结合中国城市创新实践,为更加全面反映城市创新行为及能力,本文综合考虑了投入端创新及产出端创新的相关指标,通过构建综合指数对各城市的创新行为进行度量。在投入端创新方面,鉴于城市R & D相关数据可获得性差,采用各城市科学研究和技术服务业从业人员数量来度量创新;在产出端创新方面,采用寇宗来、刘学悦(2017)测度的各城市发明专利价值来度量创新。最后,通过熵权法将上述2个指标合成为城市创新综合指数。
3. 其余控制变量
(1) 环境规制强度(enr):运用熵权法将二氧化硫去除率、生活污水处理率和固体废弃物综合利用率3个指标合成为环境规制综合指数以反映各城市的环境规制强度。(2)教育水平(edu):采用每万人高等学校在校人数来衡量各城市的教育水平。(3)对外开放(for):采用当年实际使用外商直接投资(FDI)占GDP的比重来衡量各城市的对外开放水平,并按照当年人民币对美元的平均汇率进行折算。(4)产业集聚(inc):采用第二产业总产值计算区位熵来衡量城市产业集聚。如式(5),其中,eir表示i城市r产业的产值,r为各城市第二产业总产值。(5)产业结构(ind):通过测度产业结构高级化水平来衡量产业结构升级。将三次产业中每个产业部门产值占GDP的比重作为空间向量中的一个分量,从而构成一组3维向量X0=(x1, 0, x2, 0, x3, 0),然后分别计算向量X0与产业结构由低到高排列的基向量的夹角θ1、θ2、θ3,如式(6),则产业结构高级化可由式(7)计算得出。(6)人口密度(dpo):采用各城市单位土地面积人口数来衡量。
| $ ic = \frac{{{e_{ir}}}}{{\sum\limits_i {{e_{ir}}} }}/\frac{{\sum\limits_r {{e_{ir}}} }}{{\sum\limits_i {\sum\limits_r {{e_{ir}}} } }} $ | (5) |
| $ {\theta _j} = \mathit{arcos}\left({\frac{{\sum\limits_{i = 1}^3 {\left({{x_{i, j}}*{x_{i, 0}}} \right)} }}{{\sum\limits_{i = 1}^3 {{{\left({{x^2}_{i, j}} \right)}^{\frac{1}{2}}}} *\sum\limits_{i = 1}^3 {{{\left({{x^2}_{i, 0}} \right)}^{\frac{1}{2}}}} }}} \right){\rm{j = 1, 2, 3}} $ | (6) |
| $ \mathit{ind = }\sum\limits_{k = 1}^3 {\sum\limits_{j = 1}^k {{\theta _j}} = 3} {\theta _1} + 2{\theta _2} + {\theta _3} $ | (7) |
以上各变量的描述性统计如表 1所示。
| 表 1 变量描述性统计 |
按照Anselin(1998)的建议,采用极大似然法(MLE)对空间面板模型进行估计。在对模型进行估计之前,需对变量的空间相关性及模型的选择进行检验。经Moran's I检验,在三种不同空间权重矩阵下,各年度eff、inv的Moran's I指数值均大于0.1,且均在1%条件下统计显著,表明城市生态效率及创新行为均存在较强的正空间相关性,故构建空间计量模型是必要的。在模型选择方面,经LM检验,LM-lag、LM-err均拒绝了不存在空间滞后及空间误差的原假设,故需进一步估计SDM并利用LR、Wald统计量检验原假设H0:δ=0及H0:δ+ρβ=0以判断SDM是否可以简化为SAR或SEM。结果表明,LR-sar、LR-sem、Wald-sar、Wald-sem统计量均在1%水平下拒绝了原假设,表明空间面板的最佳形式应是更广义的SDM。由于无法事先判断模型变量之间存在何种空间相关关系,故将SDM、SAR、SEM在3种空间权重矩下的估计结果均报告在表 2中,但选择SDM的估计结果进行分析与讨论,SAR、SEM的估计结果作为对比分析使用。
| 表 2 空间面板基本回归结果 |
从基本回归结果来看,对于空间效应的考察显示,在各种不同空间权重矩阵下,SDM、SAR、SEM的空间自回归系数ρ或空间误差系数λ均通过了1%的显著性检验,论证了中国城市生态效率具有显著的空间依赖性,即空间关联城市的绿色发展对本城市的绿色发展能产生显著的空间溢出效应。在核心解释变量方面,创新对生态效率的影响高度正向显著,在3种空间权重矩阵下创新带来的城市生态效率边际改善分别为0.070 3、0.054 3、0.057 2,如在经济地理空间权重矩阵下,城市创新综合指数每提升1个单位,生态效率提升5.72%。这说明,总体而言,创新提升了中国城市的绿色发展水平,论证了研究假设1。此外,空间滞后项Winv的系数在3种空间权重矩阵下均为正向显著,说明一个城市的创新活动不仅能改善本城市的生态效率,还对改善空间关联城市的生态效率起到了积极作用,初步论证了研究假设3。因此,推进绿色发展的关键是创新及其背后的相关驱动力,经济增长带来的资源环境问题并不需要通过否定增长本身来解决,而恰恰应该依靠创新和增长本身来解决。
在控制变量方面,环境规制对改善城市生态效率起到了显著正向影响,同时,环境规制空间滞后项系数不显著,说明环境规制对绿色发展的影响更多地体现为地区内溢出而非空间溢出;教育水平在一定程度上促进了城市绿色发展,但教育水平的空间溢出项系数却显著为负,这说明城市间教育资源的不均衡可能不利于区域整体绿色发展水平的提升;对外开放估计系数在经济权重矩阵及经济地理权重矩阵下正向显著,且空间溢出效应明显,说明FDI不仅改善了当地生态效率,且通过溢出效应对其它城市的绿色发展起到了积极影响;产业集聚系数、空间滞后项系数均为负但不显著;产业结构系数正向显著,产业结构的升级过程,也是城市主导产业由技术含量低、附加值低、依靠要素驱动的产业逐步向技术含量高、附加值高、依靠创新驱动的产业转变的过程,而这一过程正是践行绿色发展的题中之义。同时,产业结构的空间溢出系数不显著或为负,反映出产业结构升级尚未形成区域协调发展的局面;人口密度系数及其空间滞后项系数均不显著,一定程度上说明人口密度并非是决定城市生态效率的主要因素。
在基本回归结果基础上,为验证研究假设2,我们进一步对城市创新行为产生的增长效应、资源与环境效应、结构优化效应进行检验。我们以三大效应为被解释变量,以inv为核心解释变量。对于增长效应的衡量,采用各城市人均GDP的对数值来衡量创新带来的增长效应(eco);对于资源与环境效应的衡量,选择各城市能源利用强度、废水排放及二氧化硫排放三个具体资源消耗与污染排放指标,鉴于数据的可得性,能源利用强度采用单位GDP用电量表示(ene),两个污染排放指标均取对数值(wat、so);对于结构优化效应的衡量,采用前文构造的产业结构高级化指标(ind)。同时,鉴于基本回归中3种空间权重矩阵下的估计结果差异较小,而经济地理空间权重矩阵更具综合性,故回归采用SDM并基于经济地理空间权重矩阵进行估计,结果如表 3。
| 表 3 创新的三大效应检验 |
回归(1)给出了增长效应的回归结果,可以看出,inv显著为正,说明创新显著促进了城市经济增长,而经济增长能够通过增加正产出改善生态效率。在资源与环境效应的检验中,回归(2)-(4)显示,资源效应的估计系数不显著,但环境效应估计系数显著,且创新显著降低了城市废水和二氧化硫排放。显然,污染排放作为负产出对生态效率有负向影响,而创新则有助于通过减少污染排放从而改善生态效率。回归(5)显示创新促进了城市产业结构的高级化,而产业结构的高级化过程也是生产技术水平不断提高、资源配置更加合理以及生产更加集约、高效、清洁的过程,这有助于生态效率的总体改善。基于此,以上结果基本验证了研究假设2的成立。
(二) 城市异质性检验基本回归结果表明,创新总体上改善了城市生态效率,但这种积极影响恐不能一概而论。为了进一步检验由城市异质性而产生的创新驱动效应差异,表 4、表 5报告了依据不同标准划分的城市异质性检验结果,回归均采用SDM并基于经济地理空间权重矩阵进行估计。
| 表 4 基于区域及城市群的分组检验 |
| 表 5 基于环境政策、资源禀赋、创新能力及市场化水平的分组检验 |
表 4的估计结果显示,除关中平原城市群外,生态效率的空间溢出系数ρ在其它分组检验中均正向显著。整体而言,经济越发达且联系越紧密、要素流动性越大、创新对生态效率驱动效应越强的地区,生态效率的空间外溢效应也越强。例如,东部地区的ρ值显著大于中西部、东北部和全国值,而长三角、珠三角、海西城市群的ρ值显著大于其它城市群、东部值和全国值。在创新的绿色发展效应方面,区域分组检验表明,创新估计系数在东部正向显著,而在西部负向显著,在中部及东北部不显著。受益于区位及经济先发优势,东部的创新环境良好、创新资源和要素富集,是区域创新的领跑者。东部的创新指数均值为3.926,高于全国平均水平的3.846,也高于东北部、西部和中部的3.817、3.814、3.798。同时,东部的生态效率均值为0.747,同样领先于其他地区,说明东部创新与绿色发展的融合较好,创新能够对区域生态效率产生积极影响。相较于东部,其他地区的创新活动尚未对绿色发展起到显著促进作用。特别是西部,创新甚至对生态效率起到了抑制作用。事实上,近年来西部在节能减排、污染治理等绿色发展实践中取得了许多有益成果,但总体而言仍面临经济、资源与环境之间的失衡问题。城市群分组检验表明,长三角、珠三角、京津冀及海西城市群的创新活动显著改善了生态效率,但珠三角的创新驱动效应最强,其次是海西和长三角,而京津冀的创新能力尽管最为突出,其创新指数均值为4.137,在所有城市群中最高,但创新对生态效率的改善作用却最弱。原因可能在于,一方面,京津冀城市群内部发展极不平衡,创新贡献主要来自北京。另一方面,京津冀面临着环境改善及生态修复的艰巨任务,但创新能力的分化使得创新对区域整体生态效率改善作用受限。与上述4个城市群相比,长江中游、成渝、北部湾、哈长城市群的创新活动均未显著改善生态效率,而中原和关中平原城市群的创新系数甚至显著为负。总体而言,尽管这些城市群在区域经济发展中起着核心作用,但不论是创新投入还是产出能力和沿海领先城市群相比仍存在较大差距,尚未构建创新驱动绿色发展的内在动力机制。
表 5结果显示,创新影响系数在环保重点城市、两控区城市、非资源型城市显著为正,而在非重点城市、非两控区、资源型城市显著为负或不显著。环保重点城市、两控区城市涵盖了直辖市、省会城市、计划单列市以及其它经济发展水平较高的城市,这些城市往往在区域、城市群发展中处于主导或领先地位。正是因为如此,这些城市受到了更强的环境政策约束,而政策约束不仅能有效控制城市污染排放,同时还有利于激发城市创新动力,从而倒逼城市经济绿色转型。相较而言,非重点城市、非两控区城市由于受到的环境监管及约束较少,其创新活动可能并非是绿色导向的,从而不利于城市绿色发展。与产业发展多元化、具有较强创新活力的非资源型城市相比,资源型城市具有经济重型化、主导产业单一且集聚程度高、资源环境负荷大等特征,这类城市创新能力较薄弱,且容易陷入“资源诅咒”陷阱,因而创新难以促进城市生态效率改善。基于城市创新能力和市场化水平的分组检验表明,高创新力城市、高市场化城市的创新活动对绿色发展的驱动作用十分显著。事实上,这两类城市主要集聚在东部沿海,这一结论与创新的绿色发展效应在东部、珠三角、长三角、京津冀、海西显著为正的结论可以相互印证。此外,低创新力城市的创新对绿色发展具有正向促进作用,但这类城市的创新活动很可能带来的是边际经济产出的增加而非真正意义上的资源、环境与经济整体效率的提升。低市场化城市经济开放度较差,要素流动障碍、市场分割问题较为突出,城市经济发展缺乏活力,难以激发各类主体的创新动力和潜力以促进生态效率改善。
(三) 稳健性讨论鉴于空间面板回归可能存在的内生性问题,在基本回归、城市异质性检验中我们都采用了极大似然法(MLE)进行估计。为了进一步检验实证结果的稳健性,我们采用SDM动态空间面板GMM估计对基本回归结果进行再检验。事实上,MLE估计、GMM估计都可以在一定程度上控制模型的内生性问题,但核心解释变量可能存在的内生性问题仍值得关注,即创新与生态效率之间可能存在反向因果关系。为此,在构建创新影响城市生态效率的空间面板模型之前,我们已经排除了在现有研究样本和数据条件下两者之间可能存在的反向因果问题,限于篇幅,内生性检验结果未列出。从表 6的检验结果来看,在动态空间面板GMM估计中,尽管生态效率的空间自回归系数有所上升,但创新的系数符号与MLE的估计结果保持一致,只有数值大小和显著性程度有少许差异,同时其它控制变量估计系数的方向和大小与MLE的估计结果也差异较小,因此,MLE和GMM的估计结果再次论证了本文模型构建的合理性以及实证结论的可靠性。此外,考虑到指标选择可能对估计结果造成一定影响,本文对创新的指标进行替换,分别采用各城市公共财政支出中的科学技术支出、各城市发明专利数量2个指标衡量投入端创新和产出端创新,并基于MLE对SDM进行再估计。在创新指标替换的检验中,尽管因指标选择不同,在3种不同空间权重矩阵之下的创新系数大小、显著性与基本回归结果略有差异,但创新系数的方向以及控制变量的估计系数与基本回归保持高度相似。在分别检验了投入端创新和产出端创新对生态效率的影响后,我们发现,在各个空间权重矩阵下,产出端创新的估计系数均大于投入端创新的估计系数,而创新综合指数的估计系数最大,说明产出端创新的绿色发展效应强于投入端创新,而创新综合能力的提升则能带来更强的绿色发展效应。
| 表 6 稳健性检验 |
大量研究都论证了中国区域创新存在显著的空间溢出效应,但创新空间溢出能否对生态效率产生影响仍未得到足够关注。由于SDM同时包含了解释变量与被解释变量的空间滞后项,LeSage and Pace(2009)运用偏微分方法将总边际效应分解为直接效应和间接效应,该方法能更好地捕捉和解释SDM中解释变量的边际效应。本文将运用他们的方法重点考察创新对生态效率的空间溢出效应,从而对前文研究结论进行拓展和完善。为此,将式(1)的SDM重新改写成如下形式:
| $ ef{f_{it}} = {\left({I - \rho W} \right)^{ - 1}}\alpha {\iota _N} + {\left({I - \rho W} \right)^{ - 1}}\left({{X_{it}}\beta + W{X_{it}}\delta } \right) + {\left({I - \rho W} \right)^{ - 1}}\xi $ | (8) |
其中,I代表单位矩阵,ιN代表N×1的单位向量,ζ包含了扰动项、空间和时间固定效应。那么,求effit关于第1至第N个城市的第k个解释变量Xk的一阶偏导,可得N×N维矩阵表示的边际效应:
| $ \partial eff/\partial {X_k} = {\left({I - \rho W} \right)^{ - 1}}\left({{\beta _k}I + W{\delta _k}} \right) $ | (9) |
其中,βk、δk分别代表第k个解释变量的系数估计值。对于式(9)所对应的N×N维矩阵,LeSage and Pace(2009)将直接效应界定为主对角元素的均值,反映了一个地区特定解释变量变化对本地区被解释变量的平均影响;将间接效应界定为非主对角元素的均值,反映了一个地区特定解释变量变化对其它地区被解释变量的平均影响;将总效应界定为矩阵中所有元素的均值,在数值上等于直接效应与间接效应的和。具体地,对于从城市1至城市N的解释变量inv,被解释变量eff的期望值的偏导数矩阵可写为:
| $ \begin{array}{l} \left[ {\frac{{\partial E\left({eff} \right)}}{{\partial in{v_1}}} \cdots \frac{{\partial E\left({eff} \right)}}{{\partial in{v_N}}}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial E\left({ef{f_1}} \right)}}{{\partial in{v_1}}}}& \cdots &{\frac{{\partial E\left({ef{f_1}} \right)}}{{\partial in{v_N}}}}\\ \vdots & \ddots & \vdots \\ {\frac{{\partial E\left({ef{f_N}} \right)}}{{\partial in{v_1}}}}& \cdots &{\frac{{\partial E\left({ef{f_N}} \right)}}{{\partial in{v_N}}}} \end{array}} \right]\\ = {\left({I - \rho W} \right)^{ - 1}}\left[ {\begin{array}{*{20}{c}} \beta &{{w_{12}}\delta }& \cdots &{{w_{1N}}\delta }\\ {{w_{21}}\delta }&{\beta \beta }& \cdots &{{w_{2N}}\delta }\\ \vdots & \vdots & \ddots & \vdots \\ {{w_{N1}}\delta }&{{w_{N2}}\delta }& \cdots &\beta \end{array}} \right] \end{array} $ | (10) |
在此基础上,我们对SDM基本回归以及稳健性检验中各个创新指标的边际效应进行分解,分别考察创新综合指数、投入端创新、产出端创新的空间溢出对中国城市生态效率的影响,结果见表 7。此外,为进一步检验创新空间溢出的普遍存在性,我们参考邵朝对、苏丹妮(2017)等学者的做法,对不同距离阈值上的创新溢出效应进行估计。为此,设置如下以指数衰减函数为元素的空间权重矩阵:
| $ {W_{ij}}\left(D \right) = \left\{ \begin{array}{l} \exp \left({ - {d_{ij}}/\omega } \right)\;, \;\;\;\;{d_{ij}} \ge D\\ 0\;, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{d_{ij}} < D \end{array} \right. $ | (11) |
| 表 7 创新溢出对生态效率的影响检验 |
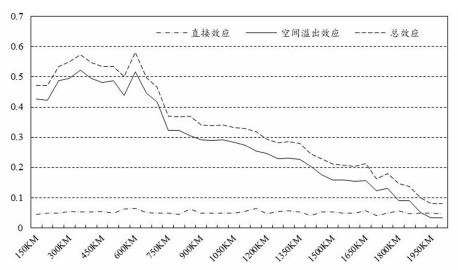
其中,D为距离阈值。如此,我们不仅可以验证空间衰减的地理学规律,且能识别出创新空间溢出影响生态效率的距离边界。ω为外生参数,本文将ω设置为150。在此基础上,将式(11)代入式(1)中进行回归,并根据上述方法,从150公里开始,每隔50公里考察不同距离阈值下的创新溢出效应。表 7列出了6个主要距离阈值的详细结果,而图 1则报告了每一个距离阈值下的溢出系数变化。当距离阈值达到1650公里时,空间溢出系数就已不再显著且易受异常值影响而出现较多噪声,故本文只报告1800公里之内的结果。
|
图 1 创新空间溢出效应的距离边界检验 |
表 7的估计结果显示,创新对生态效率的直接影响效应与点估计的结果接近,进一步验证了创新能够显著改善城市生态效率、促进城市绿色发展。不仅如此,inv的空间溢出系数也基本上是显著的,这说明创新对城市生态效率具有显著的空间溢出效应,这使得加总后的总效应系数显著大于点估计的结果。因此,如未考虑创新空间溢出的影响将会低估创新的绿色发展效应。该结论说明,城市创新行为对提升本城市的生态效率是有效的,且随着创新资源和要素的流动、创新成果的扩散,某城市的创新将辐射至周边乃至距离更远的城市,从而提升关联城市的绿色发展水平。
在基于距离阈值的创新溢出检验中,创新的空间溢出系数从150公里至1600公里都至少通过了10%的显著性检验,这说明创新具有显著空间溢出效应的结论是可信的。检验结果显示,创新总效应的变化趋势与空间溢出变化趋势基本保持一致,而创新直接效应则较为稳定,未产生明显波动。在空间溢出方面,350公里是创新空间溢出系数的峰值,系数达0.522;700公里以内的空间溢出系数均在0.4之上,从700公里至1400公里,创新的空间溢出效应衰退趋势明显,系数在0.2至0.4之间;而从1650公里开始,空间溢出系数不再显著,最终接近于0。因此,350公里和700公里可视为创新对绿色发展空间溢出效应的2个距离边界,350公里以内为创新的密集溢出区,而700公里以内为创新的较密集溢出区。
六、主要结论与启示本文研究发现:中国城市生态效率具有显著的空间依赖性,经济越发达且联系越紧密、要素流动越自由、创新对生态效率驱动效应越强的地区,生态效率的空间外溢效应也往往越强;城市创新行为具有增长效应、资源与环境效应、结构优化效应,这是改善生态效率的重要途径,同时,产出端创新对生态效率的驱动效应强于投入端创新,而创新综合能力提升带来的绿色发展效应则最为突出。尽管如此,创新对绿色发展的影响具有显著的城市异质性。事实上,创新显著改善城市生态效率的主要贡献来自东部发达地区的创新行为,而在中西部和东北部等地区,粗放式增长的惯性以及与东部创新能力的巨大差距,使得创新不仅无法有效改善生态效率甚至可能对生态效率起到一定的阻碍;创新对城市生态效率的空间溢出效应显著存在,但创新的空间溢出随距离变化呈现衰退趋势,350公里以内是创新空间溢出改善城市生态效率的最佳地理距离区间。
上述研究结论蕴含了如下的政策启示:其一,除了重视投入端创新激励外,政府应更加重视利用产出端激励政策来鼓励技术创新。为此,应进一步加强对发明专利的保护和支持力度,如加大专利资助、简化行政审批流程、加快专利成果推广及应用等,以充分发挥发明专利在建设创新型城市和经济绿色转型中的驱动作用。其二,为创新外溢创造良好条件,不断扩大创新的外溢半径。基于创新外溢驱动生态效率改进的最佳地理区间,着力促进城市群内部的创新合作,以提升城市群总体生态效率为目标,促进城市间形成新型的产业分工、技术合作与污染防治联防联控,推动技术创新与绿色发展的深度融合。同时,建立以中心城市引领城市群发展、城市群带动区域发展的新模式,推动区域板块融合互动。围绕黄河流域、长江经济带的绿色发展实践,以边界城市为依托,形成跨城市群、跨区域的绿色创新协作机制及上中下游城市的创新要素流动机制。其三,注重引导创新的方向,提升绿色创新的供给能力。一方面,政府应进一步激发各类主体的绿色创新供给能力,以可持续发展为导向对创新成果及其价值进行评估,并基于绿色发展理念在专利新颖性、实用性和创造性标准的基础上增加“绿色性”审查标准。另一方面,政府应加强财政金融政策的绿色导向,对企业的绿色创新项目给予更多的财税支持,建立并完善多元化和竞争性的绿色创新投融资体系,加快绿色创新成果的转化和应用。其四,根据区域及城市发展实际,采取差异化的创新驱动绿色发展策略。例如,对于珠三角、长三角等创新驱动绿色发展效应显著的区域来说,应进一步加快绿色智能制造技术、现代能源技术等关键技术的研发和应用,实现产业链、创新链与价值链的深度融合,打造成为智能化、绿色化、高端化、服务化的现代产业发展新高地。对于京津冀等内部发展不平衡且资源环境约束较强的区域来说,应加速推进创新空间外溢以提升区域整体的创新能力,通过加强各城市在污染控制与治理、节能减排、环境材料领域的联合技术攻关,促进区域、城市经济协调发展与绿色转型。对于中西部等创新能力和绿色发展水平相对较低,或是创新与绿色发展融合度不佳的地区来说,应以区域核心城市为引领,增进地方政府间的创新合作,同时有针对性地引进东部地区的先进创新成果,在生态修复、资源循环利用、污染防控等技术领域取得新突破。
| [] |
白俊红、蒋伏心, 2015, “协同创新, 空间关联与区域创新绩效”, 《经济研究》, 第 7 期, 第 174-187 页。 |
| [] |
陈阳、唐晓华, 2019, “制造业集聚和城市规模对城市绿色全要素生产率的协同效应研究”, 《南方经济》, 第 3 期, 第 71-89 页。 |
| [] |
关成华、韩晶, 2018, 《绿色发展经济学》, 北京: 北京大学出版社。 |
| [] |
韩晶、孙雅雯、陈超凡, 等, 2019, “产业升级推动了中国城市绿色增长吗?”, 《北京师范大学学报:社会科学版》, 第 3 期, 第 139-151 页。 |
| [] |
黄建欢, 2016, 《区域异质性, 生态效率与绿色发展》, 北京: 中国社会科学出版社。 |
| [] |
黄建欢、许和连, 2016, “中国区域生态效率的时空演变和提升机制”, 《湖南大学学报(社会科学版)》, 第 1 期, 第 60-70 页。DOI:10.3969/j.issn.1008-1763.2016.01.008 |
| [] |
寇宗来、刘学悦, 2017, 《中国城市和产业创新力报告2017》, 上海: 复旦大学产业发展研究中心。 |
| [] |
罗能生、余燕团, 2018, “创新对中国城市生态效率的影响研究——基于空间溢出分解的视角”, 《环境经济研究》, 第 2 期, 第 34-51 页。 |
| [] |
邵朝对、苏丹妮, 2017, “全球价值链生产率效应的空间溢出”, 《中国工业经济》, 第 4 期, 第 94-114 页。 |
| [] |
邵帅、杨莉莉、黄涛, 2013, “能源回弹效应的理论模型与中国经验”, 《经济研究》, 第 2 期, 第 96-109 页。 |
| [] |
王鹏、谢丽文, 2014, “污染治理投资, 企业技术创新与污染治理效率”, 《中国人口·资源与环境》, 第 9 期, 第 51-58 页。DOI:10.3969/j.issn.1002-2104.2014.09.008 |
| [] |
严成樑、龚六堂, 2009, “熊彼特增长理论:一个文献综述”, 《经济学(季刊)》, 第 3 期, 第 1163-1196 页。 |
| [] |
余泳泽、刘大勇, 2013, “我国区域创新效率的空间外溢效应与价值链外溢效应——创新价值链视角下的多维空间面板模型研究”, 《管理世界》, 第 7 期, 第 6-20 页。 |
| [] |
张江雪、张力小、李丁, 2018, “绿色技术创新:制度障碍与政策体系”, 《中国行政管理》, 第 2 期, 第 153-155 页。 |
| [] |
赵增耀、章小波、沈能, 2015, “区域协同创新效率的多维溢出效应”, 《中国工业经济》, 第 1 期, 第 32-44 页。 |
| [] |
Aghion P., Howitt P., 1992, "A Model of Growth through Creative Destruction". Econometrica, 60(2), 323–351.
DOI:10.2307/2951599 |
| [] |
Aghion P., Howitt P., Brant-Collett, M., 1998, Endogenous Growth Theory, Boston: MIT press.
|
| [] |
Anselin, L., 1998, Spatial Econometrics: Methods and Model, Dordrecht: Kluwer Academic Publishers.
|
| [] |
Bettencourt L. M. A., Lobo J., Strumsky D., 2007, "Invention in the City:Increasing Returns to Patenting as a Scaling Function of Metropolitan Size". Research Policy, 36(1), 107–120.
DOI:10.1016/j.respol.2006.09.026 |
| [] |
Chang Y., Huang R., Ries R. J., et al., 2014, "Shale-to-Well Energy Use and Air Pollutant Emissions of Shale Gas Production in China". Applied Energy, 125, 147–157.
DOI:10.1016/j.apenergy.2014.03.039 |
| [] |
Cheng G., Qian Z., 2011, "An Epsilon-based Measure of Efficiency in DEA-An alternative Method for the Affinity Index", MPRA Paper, No.41680.
|
| [] |
Ghisetti C., Quatraro F., 2017, "Green Technologies and Environmental Productivity:A Cross-Sectoral Analysis of Direct and Indirect Effects in Italian Regions". Ecological Economics, 132, 1–13.
DOI:10.1016/j.ecolecon.2016.10.003 |
| [] |
Grossman G. M., Helpman E., 1991, "Quality Ladders in the Theory of Growth". The Review of Eonomic Studies, 58(1), 43–61.
DOI:10.2307/2298044 |
| [] |
LeSage, J., and Pace, R. K., 2009, Introduction to Spatial Econometrics, Florida: CRC Press, Taylor and Francis Group.
|
| [] |
Moreno R., Paci R., Usai S., 2005, "Spatial Spillovers and Innovation Activity in European Regions". Environment and Planning A, 37(10), 1793–1812.
DOI:10.1068/a37341 |
| [] |
Organization for Economic Co-operation and Development (OECD), 2011, Towards Green Growth: Monitoring Progress, Paris: OECD press.
|
| [] |
Romer P. M., 1990, "Endogenous Technological Change". Journal of Political Economy, 98(5), S71–S102.
DOI:10.1086/261725 |
| [] |
Saunders H D., 2008, "Fuel Conserving (and using) Production Functions". Energy Economics, 30(5), 2184–2235.
DOI:10.1016/j.eneco.2007.11.006 |
| [] |
Tone K., Tsutsui M., 2010, "An Epsilon-Based Measure of Efficiency in DEA-a Third Pole of Technical Efficiency". European Journal of Operational Research, 207(3), 1554–1563.
DOI:10.1016/j.ejor.2010.07.014 |
| [] |
Zhang J., Chang Y., Zhang L., et al., 2018, "Do Technological Innovations Promote Urban Green Development?-A Spatial Econometric Analysis of 105 Cities in China". Journal of Cleaner Production, 182, 395–403.
DOI:10.1016/j.jclepro.2018.02.067 |




