基础设施作为经济发展的车轮,在我国过去依靠投资驱动的高速经济增长中扮演着非常重要的角色,其人工智能、大数据中心等新基建领域将在经济转向高质量发展过程中继续发挥重要带动作用。改革开放以来,尤其是从1998年实施扩张性财政政策开始,我国政府都将加速基础设施建设作为重大举措,先后推动实施西部大开发、中部崛起、振兴东北老工业基地、“一带一路”建设、京津冀协同发展、长江经济带发展、粤港澳大湾区建设等重大国家战略,从而带动基础设施存量急剧攀升。然而,近年来随着中国经济转向高质量发展阶段,不仅整体投资尤其是基础设施领域投资的增速放缓,而且经济下行压力加大、区域发展不平衡等突出问题越发显现,“质量变革”、“效率变革”等已成为政策高频词汇。事实上,实现经济高质量增长不仅要保证投资规模,更要注重投资效率,提高资本回报率(赵善梅、吴士炜,2018)。在此背景下,我们关心的是,中国基础设施资本回报率处于何种水平,其时间动态变化趋势如何?在不同类型设施和不同地区之间是否存在差异?产生差异的原因何在?以上问题的回答对于回应不断上升的基础设施投资率是否合理,具有重要的现实意义。
关于资本回报率的估计,大致可归纳为侧重于微观和宏观两个层面。由于基础数据限制,本文主要从宏观层面估算基础设施资本回报率。目前,估算宏观资本回报率的主流方法有两种,即Hall-Jorgenson租金公式法(Bai et al.,2006;白重恩、张琼,2014)和生产函数法(胡李鹏等,2016;陈英楠、吉晓萌,2018)。两种方法的本质均是指资本的边际产出(Lucas,1990),只是在对资本份额αt的处理上存在差异,前者主要通过公式“资本份额=1-劳动者报酬/收入法GDP”获取,而后者则用估计出的资本产出弹性值近似代替资本份额(郭鹏飞、曹跃群,2020)。对于整个经济体而言,就算资本投入存在行业溢出效应,产出作为统一数据也可将其内部化,不存在低估或高估问题。但是对于基础设施而言,由于其作为公共品,对于非基础设施部门可能产生较强的行业和空间溢出效应,故基础设施涉及的相关行业增加值总和难以有效反映其实际产出。鉴于此,本文拟采用生产函数法,将资本投入拆分为基础设施资本投入和非基础设施资本投入,同时考虑空间影响,由此计量得到基础设施资本产出弹性值以近似代替其资本份额。国际上,采用此方法的典型研究如Moreno and Lopez-Bazo(2007)、Shi and Huang(2014);在国内,胡李鹏等(2016)尝试性地推导出基础设施资本回报率测算公式。郭鹏飞、曹跃群(2020)测算并分析了中国经济基础设施资本回报率。
采用生产函数法估计资本回报率对于资本存量和产出弹性值的估计非常敏感。首先,关于物质资本的测算,Goldsmith(1951)、Jorgenson(1963)和OECD(2009)等在理论和操作层面做出了突出贡献。与国际实践相比,国内存在混淆使用财富性资本存量总额(K)、财富性资本存量净额(KN)与生产性资本存量(KP)等问题。现有研究在估计资本投入效率时,更多地使用的是从衡量价值财富出发的K和KN。然而,KP在测算时由于综合考虑了资产的效率损失情况,从而使其更能反映资本在役龄阶段的实际生产能力和服务效率,用于投入产出分析(魏辉、王春云,2016;杨玉玲、郭鹏飞,2017)。具体在基础设施领域,金戈(2012,2016)和胡李鹏等(2016)进行了探索性研究,但是两者估算的基础设施存量都是财富性质的,并且前者由于忽略了2003年国民经济行业范围的调整,从而使估算数据在可比性方面存在挑战。其次,由于中国基础设施资本存量估算已属起步较晚,故鲜有研究其资本产出弹性,目前仅有金戈(2016)采用增长核算法进行初步研究,实证结果为0.2263。此外,考虑到样本期间我国经济先后经历工业化初期、中期和后期三个不同阶段(廖茂林等,2018),导致基础设施资本的产出弹性值可能随其数量和价格的逐期变化而变化(章上峰,2011)。因此,估计基础设施资本的时变产出弹性值,将更有利于精确地估算其资本回报率。
关于资本回报率影响因素的研究源于“卢卡斯悖论”。由于基础设施资本回报率的估算已属较少,故鲜有研究分析其影响因素。鉴于基础设施资本回报率可能受到整个经济体的传导影响,故此主要从整体上梳理资本回报率的影响因素。部分学者(Gordon,1999;黄先海等,2012;杨校美、谭人友,2017)认为资本深化对资本回报率(或劳动生产率)产生重要影响,并且长期内两者的关系较为复杂。Robertson(1999)研究发现产业结构是影响资本回报率的重要因素。樊潇彦(2004)发现国家资本占比中等的行业资本收益率明显低于国资占比高或低的行业;邵挺(2010)认为国有企业的资本收益率相比其他所有制类型企业要低,Song et al.(2011)也持相同的观点。胡凯、吴清(2012)研究发现政府干预和非税负担对资本回报率产生抑制作用。白重恩、张琼(2014)研究发现投资率和政府干预对资本回报率产生显著负向影响,而第二产业比重和第三产业比重则对资本回报率产生正向影响。赵善梅、吴士炜(2018)发现资本深化、投资结构、政府干预、开放水平等因素及其空间滞后项对资本回报率产生了显著影响。
综上所述,本文围绕以下三点展开进一步探索:一是不同于以往研究在估算基础设施资本存量时多采用永续盘存法(PIM)的传统途径,而本文借鉴《Measuring Capital OECD Manual(2009)》,采用PIM的非传统途径,不仅估算出基础设施的财富性存量K和KN,更为难得的是获取了生产性存量KP,后者的获取对于将基础设施存量纳入生产函数,估计其产出弹性值具有更为重要的意义。二是聚焦基础设施及其所属不同类型设施的资本回报率估算,并进一步分析其行业和地区差异。三是在要素贡献分解基础上,围绕基础设施本身和整个经济体的技术效率和要素结构效率三个维度,实证检验影响基础设施资本回报率的相关因素。
二、资本存量与资本回报率的估算框架 (一) 资本存量的估算方法资本存量有K、KN和KP等概念。其中,K是指目前正在服役的所有资本品在某一年份的购置价值总和;KN是以市场价格估计的资产价值,等于K减去固定资本消耗累计额;KP能反映资本品的生产能力,在生产分析中能够恰当地测量资本服务流量,表示标准效率单位下的资本数量。三者既存在共同点,都是以固定资产投资的时间序列为起点进行计算,存在相同的退役函数和资产使用年限;又具有较大差异,KP严格区别于K或KN(见表 1)。K和KN作为价值指标,分别通过退役模式和平均役龄价格函数加总可比固定资产投资获得,用于收入和财富测度,可推导出资本品的时变折旧率,是资产负债表的重要组成部分。KP则作为物量指标,通过平均役龄效率函数加总可比固定资产投资获得,用于资本生产能力与效率测度,可推导出按资产类型划分的资本服务,是衡量经济增长的基础。总之,K、KN和KP三者之间,既存在本质区别又内在紧密联系,本文将基于PIM的非传统途径,估算出基础设施KN推导其时变折旧率,估算基础设施KP计量其产出弹性。
| 表 1 KN(K)与KP的主要区别 |
根据对固定资本折旧的处理方式不同,OECD(2009)将PIM归纳为传统和非传统两种途径。相对传统途径,非传统途径的估算更为系统科学(杨玉玲、郭鹏飞,2017),不仅基于资产价值公式,将资本存量及其服务效率纳入统一框架中,保证存量和流量数据估算的假设一致,可同时估算K、KN、KP等;而且不是孤立地分析折旧率,是与资产效率相结合,计算时变折旧率。因此,下文将按照PIM的非传统途径估计基础设施的全套资本存量并进一步倒推其时变折旧率。首先,估算资本存量总额:
| $ {K_t} = {K_{t - 1}} + {I_t} - {R_t} = \sum\limits_{\tau = 0}^T {{S_\tau }{I_{t - \tau }}} $ | (1) |
其中,Kt和Kt-1分别为第t和t-1年的资本存量总额,It为第t年的可比价投资额。Rt为第t年的资产重置需求,Sτ为购置的资本品到τ时的残值率,两者由退役模式决定。相比其他退役模式,我们选择国际核算中采用较多的钟型退役模式,其对数正态频率分布形式为:
| $ \begin{array}{l} {f_r} = \frac{1}{{\sqrt {2\pi } \times \sigma }} \times \frac{1}{\tau } \times \exp \left( { - \frac{{{{\left( {\mathit{ln\tau - }\mu } \right)}^2}}}{{2{\sigma ^2}}}} \right), \\ \sigma = \sqrt {\ln \left( {1 + 1} \right)/{{\left( {m/s} \right)}^2})} , \mu = \ln m - 0.5{\sigma ^2} \end{array} $ | (2) |
其中,fτ为资本品在役龄为τ时的退出比例,σ和μ分别为对数正态频率分布的标准差和均值,m和s分别为正态分布的标准差和均值。参考曹跃群等(2012)的研究,我们取s=m/4。据此,可得相应的存活函数Sτ=1-∫0tfτ。
其次,分别考虑资本品的价值和效率变化,估算KN和KP。考虑到资本品随着役龄的增加,由于物理上有形和新技术出现的无形磨损,其相对效率会下降,本文通过平均役龄效率函数加总可比固定资产投资获得标准效率单位下的KP:
| $ KP = \sum\limits_{\tau = 0}^{T - 1} {{d_\tau } \times {S_\tau } \times {{\rm{I}}_{t - \tau }}} = \sum\limits_{\tau = 0}^{T - 1} {{\varphi _\tau } \times {{\rm{I}}_{t - \tau }}} $ | (3) |
其中,dτ为“年龄—效率”函数;φτ平均役龄效率函数,由退役模式和“年龄—效率”函数共同决定。参考杨玉玲、郭鹏飞(2017)的研究,并与国际测算接轨,本文选择双曲线下降模式的“年龄—效率”函数,即:
| $ {d_t} = {d_0}\left( {T - t} \right)/\left( {T - \beta t} \right) $ | (4) |
其中,d0=1表示初始年份资本品的相对效率;β为斜率参数,与各类资本品的使用年限相关,取值越高表明该类资本品的相对效率损失越慢。
同时,考虑到资本品随着役龄的增加,由于运作方式的改变和时间变化产生的贬值,其价格也会下降,本文通过平均役龄价格函数加总可比固定资产投资,可获得资本存量净额:
| $ KN = \sum\limits_{\tau = 0}^{T - 1} {{p_\tau } \times {S_\tau } \times {{\rm{I}}_{t - \tau }}} = \sum\limits_{\tau = 0}^{T - 1} {{\psi _\tau } \times {{\rm{I}}_{t - \tau }}} $ | (5) |
其中,pτ为“年龄—价格”函数;ψτ为平均役龄价格函数,由退役模式和“年龄—价格”函数共同决定。根据《资本测算手册(2004)》第7页的资产定价公式,假定资本服务价格C恒定不变,则可通过公式(6)连接起资本品的相对价值与相对效率。
| $ {P_t} = \sum\limits_{\tau = 1}^T {\frac{{{d_t} \times {C_{t + \tau }}}}{{{{\left( {1 + \xi } \right)}^\tau }}}} $ | (6) |
其中,ξ为贴现率,一般取5%。基于此,“年龄—价格”函数为pt = Pt / P1。
最后,根据PIM公式和式(1),反推出各类资本品的时变折旧率δt:
| $ {\delta _t} = 1 - \left( {K{N_t} - K{N_{t - 1}}} \right)/{\mathit{I}_t} $ | (7) |
本文采用C-D生产函数法,估算基础设施资本回报率。一般而言,C-D生产函数有常数模型、非参数模型、变系数模型等多种形式。章上峰(2011)指出时变弹性生产函数具有更好的统计性质,建议在相关研究中加以运用。我们采纳这一建议①,具体形式如下:
① 经检验,在1%显著性水平下拒接不变系数的原假设,应采用变系数生产函数。由于变系数模型容易忽视变量在不同时点(地区)之间的共性特征并损失自由度,再结合本文的主要目的在于计算基础设施产出弹性值,故采用“部分变系数模型”,即变基础设施资本产出弹性系数和不变其他参数的变系数模型。
| $ {Y_{it}} = AL_{it}^{\alpha L}K_{it}^{\beta K}G_{it}^{\beta G} $ | (8) |
其中,Yit、Lit、Kit和Git分别表示第i省t期的实际产出、劳动力投入、非基础设施资本投入和基础设施资本投入。α和β分别表示劳动力和各类资本的产出弹性。
由于影响经济增长的因素是非常复杂的,经济增长的实现是多维要素协同作用的结果,基础设施投入是实现经济增长的必要前提,而不是充分条件(张学良,2012),故在估计基础设施的产出弹性时,需要考虑人力资本积累、城市化和贸易依存度等新经济增长与新经济地理因素的影响。由此,根据式(8)可构建本文的基准计量模型
| $ \begin{array}{l} \ln {Y_{it}} = \theta + {\alpha _L}\ln {L_{it}} + {\beta _K}\ln {K_{it}} + {\beta _{G1}}\ln {G_{i1}} + \\ \sum\nolimits_{t = 2}^{24} {{\beta _{Gt}}\ln {G_{it}}*{\rm{year}}} + \sum\nolimits_{j = 1}^6 {{\psi _j}contro{l_{i, j, t}} + {u_i} + {\gamma _t} + {\varepsilon _{it}}} \end{array} $ | (9) |
其中,lnGit*year为基础设施投入与年份的交互项,用以反映基础设施资本产出弹性的时间变化趋势;controlj为影响总产出的其他各类因素所组成的控制变量向量;uit+γt+εit为复合误差项,同时考虑个体ui和时间γt两种效应。
根据已有研究可知,基础设施具有空间外部性,在估计基础设施资本的产出弹性时,需考虑其空间影响(张学良,2012)。在经过Moran's I检验之后,进一步通过Lratio检验和Wald检验发现,空间面板杜宾模型(SDM)更为合适。基准模型可改写为:
| $ \begin{array}{l} \ln {Y_{it}} = {\theta _o} + {\alpha _L}\ln {L_{it}} + {\beta _K}\ln {K_{it}} + {\beta _{G1}}\ln {G_{i1}} + \\ \sum\nolimits_{t = 2}^{24} {{\beta _{Gt}}\ln {G_{it}}*{\rm{year}}} + \sum\nolimits_{j = 1}^6 {{\psi _j}contro{l_{i, j, t}}} \\ + \rho W\ln {Y_{it}} + W\alpha _L^W\ln {L_{it}} + W\beta _K^W\ln {K_{it}} + W\beta _{G1}^W\ln {G_{i1}} + \\ \sum\nolimits_{t = 2}^{24} {W\beta _{Gt}^W\ln {G_{it}}*{\rm{year}}} + \sum\nolimits_{j = 1}^6 {\psi _j^Wcontro{l_{i, j, t}} + {u_i} + {\gamma _t} + {\varepsilon _{it}}} \end{array} $ | (10) |
其中,W为反映区域之间特定空间联系的空间权重矩阵。根据研究需要,本文主要构建反映地理连接联系的0—1二进制空间权重矩阵Wbin和反映经济社会联系的空间权重矩阵Wdev。其中, Wbin按照以下规则赋予权重元素值:若两个区域在地理位置上相邻为1,否则为0;Wdev则根据公式wij=(GDPj/Dij2)/∑j(GDPj/Dij2)计算权重元素值,以反映经济发展和地理距离对邻近区域的综合影响,GDPj表示地区i在全样本时期人均GDP的均值。
根据估计的基础设施时变产出弹性,计算其资本回报率。具体公式为:
| $ R_t^G = \frac{{\partial {Y_t}}}{{\partial {G_t}}} = \frac{{\partial \ln {Y_t}}}{{\partial \ln {G_t}}} \times \frac{{{Y_t}}}{{{G_t}}} = {\beta _{G, t}}\frac{{{Y_t}}}{{{G_t}}} $ | (11) |
扣除基础设施资本折旧后,可得其净资本回报率为:
| $ r_t^G = R_t^G - \delta _t^G = {\beta _{G, t}}\frac{{{Y_t}}}{{{G_t}}} - \delta _t^G $ | (12) |
若进一步考虑宏观税负的影响,基础设施的资本净回报率可改写为:
| $ r_t^G = {\beta _{G, t}}\left( {1 - {\tau _t}} \right)\frac{{{Y_t}}}{{{G_t}}} - \delta _t^G $ | (13) |
其中,τt为宏观税率,有大、中、小三个口径的指标(郭庆旺、吕冰洋,2010)。综合比较后,选择中口径指标量化宏观税负,即(地方)财政收入占GDP比例。
(三) 资产分类、指标选取及数据处理1. 资产分类与口径调整
(1) 统计范围调整。根据《为发展提供基础设施》(World Bank,1994)和金戈(2016)的研究,本文将基础设施分为经济基础设施和社会基础设施。进一步结合1993年和2002年国民经济行业分类标准,将未调整前的基础设施统计范围界定为2002年以前的八个行业和2003年以后的九个行业。据测算,行业大类城镇固定资产投资在所属行业门类中的比例较为稳定,故以2003-2008年各行业大类城镇固定资产投资所占比例的均值作为替代,对全国和各地区1993-2002间基础设施相关行业大类拆分合并。基础设施统计范围的行业大类级调整见表 2。综上,经济基础设施的统计范围包括四个行业门类、十八个行业大类,社会基础设施则包括五个行业门类、十八个行业大类。需要说明的是,2011年国民经济行业的统计范围也发生略微调整,但是对基础设施所属行业影响较小,仅将“公共管理和社会组织”中的“社会保障业”调回到“卫生、社会保障和社会福利业”。
| 表 2 中国基础设施行业分类(1993-2016年) |
(2) 统计口径调整。参考金戈(2016)的研究,本文以“全社会”作为固定资产投资的统计口径,并通过固定资产投资交付使用率将全社会固定资产投资调整为全社会新增固定资产投资。由于本文对基础设施进行了统计范围调整,故在缺失数据处理上与金戈不同。首先,需要处理2003年而不是1996年以前缺失的基础设施所属不同行业的固定资产投资数据。其次,根据所有制的分类,将基础设施所属行业中的基本建设、更新改造和城镇集体经济的新增固定资产投资加总,作为其数据缺失年份的全社会新增固定资产投资。最后,在全社会新增固定资产中扣除基础设施新增固定资产投资,作为非基础设施新增固定资产投资。
2. 关键指标构建
(1) 资产使用寿命。《中华人民共和国企业所得税法实施条例(2008)》公布了固定资产的最低折旧年限,房屋、建筑物为20年,生产设备为10年。黄勇峰等(2002)认为中国建筑和设备的寿命分别为40年、16年。曹跃群等(2012)假定“其他资产”的使用年限为20年。由于政府存在采用不同的加速折旧体系以鼓励投资的倾向,故其公布的折旧年限与资产实际使用寿命相比口径偏小,且所公布的是最低年限,故本文假定建筑、设备和其他费用的使用年限分别为40年、16年和20年。然后,采用《中国固定资产投资统计年鉴》提供的城镇分行业、分资产类型数据,分别计算2003-2016年建筑、设备和其他费用三类投资在各行业中的构成比例,进而通过加权平均,推算出基础设施、经济基础设施和社会基础设施的使用寿命分别为33年、32年和35年。
(2) 基期资本存量估算。鉴于官方统计年鉴提供的全国分行业基本建设、更新改造和城镇集体投资数据在1985年以前并不完整,故将全国的基年定为1985年。在确定分省基年时,由于对处理1993以前分省基础设施统计范围的调整存在较大挑战,故将其定为1993年。在估算基期资本存量时,我们采用Young(2003)的增长率法计算,即K0=I0/(g+δ)。其中,g为固定资产投资的平均增长率,δ为资产的平均折旧率,借鉴张军等(2004)的研究,将两者之和定为10.0%。
(3) 固定资产投资价格指数。统计资料中公布的投资额是以当年价格计算的名义值,需将其缩减为不变价格的实际值才具可比性。由于缺乏分行业固定资产投资价格指数,我们采用全国和分省的固定资产投资价格指数予以替代。对于全国1985-1990年的缺失数据,借鉴张军等(2004)的做法,利用以当年价格衡量的全国固定资本形成总额和以不变价格衡量的固定资本形成指数推算得之。
(4) 当年投资序列与缺失数据处理。所有未缺失年份全国和各地区的固定资产投资总额、新增固定资产总额、分行业固定资产投资额、分行业新增固定资产额数据,均来源于《中国统计年鉴》。缺失数据包括全国1985-1992年城镇集体经济的分行业新增固定资产额、各地区1985-2002年城镇集体经济的分行业新增固定资产投资、各地区2003-2016年全社会分行业新增固定资产投资。对此,需要估计缺失年份的固定资产交付使用率,再乘以相应的固定资产投资额,进而获得相应年份的新增固定资产投资。在具体估计缺失年份的分行业交付使用率时,对于全国1985-1992年城镇集体经济,假定其为1993-2002年间的平均值。对于各地区1985-2002年城镇集体经济,采用相应年份的基本建设分行业交付使用率替代。对于各地区2003-2016年的处理,全社会固定资产分行业交付使用率i, t=城镇固定资产分行业交付使用率i, t×(全社会固定资产总交付使用率i, t÷城镇固定资产总交付使用率i, t)。
(5) 产出、劳动力投入和控制变量。全国和各地区的总产出采用生产总值(GDP)衡量,按照GDP平减指数折算为1993年不变价。全国和各地区的当年劳动投入以每年年初和年末就业人口的平均值衡量。在借鉴相关研究的基础上,本文主要选取以下控制变量:①人力资本积累(hum)。人力资本作为新经济增长理论中的重要变量,对经济发展的作用为越来越多的学者所重视,采用《2018中国人力资本报告》中的各省份人均劳动力人力资本存量数据来衡量。②国有经济比重(soe)。国有经济作为我国现代经济体系中的重要组成部分,以国有经济固定资产投资在全社会固定资产投资中的占比来衡量。③产业结构(is)。产业结构升级对于提高劳动生产率具有重要作用,采用第三产业增加值占地区生产总值比重来衡量。④城市化水平(urb)。城市化一直被认为和工业化一样,是中国经济发展的重要引擎,采用非农业人口占总人口的比重来衡量。⑤贸易依存度指标(tdd),以各地区按当年汇率中间价折换成人民币形式的进出口贸易总额占当年名义GDP的比重来量化。⑥制度因素(md)。地方政府依然对生产要素具有较强的宏观调控作用,财税等相关配套政策对经济发展的影响仍不容忽视。在此,采用各省政府消费支出占该地区GDP的比重,作为衡量政府职能不恰当和市场机制配置资源不充分的代理指标。以上数据均来源于历年《中国统计年鉴》、《中国固定资产投资统计年鉴》和《各地区统计年鉴》等。
(三) 基础设施的资本存量与资本回报率估算结果及分析 一. 基础设施的资本存量估算结果与分析1. 估算结果
基于上述估算框架和相关指标数据,本文估计了全国和省际基础设施及其所属不同行业的K、KN和KP。限于篇幅,表 3仅汇报了全国四个代表性年份数据。从中容易发现,基础设施K>KP>KN,这一变化趋势与杨玉玲、郭鹏飞(2017)关于第三产业K、KN和KP间的差异分析基本一致。鉴于基础设施K和KN仅考虑该资本品由于老化等产生的价值损失,基础设施KP综合考虑了该类资本品随着役龄增加导致的退役和生产力损失情况,能更准确地用以测算基础设施资本回报率。因此,除有特殊说明,本文均以基础设施KP作为其资本投入的度量指标。进一步分析发现,全国基础设施资本存量由1985年的1.08万亿元快速攀升至2016年的42.21万亿元,年均增长12.6%。在基础设施结构方面,经济基础设施的资本存量一直远高于社会基础设施,且差距逐渐拉大,占比由70.8%增至77.7%。这一方面说明社会基础设施建设相对滞后,亟需加强社会公共服务体系建设;另一方面根据要素边际报酬递减规律,暗含着社会基础设施的资本回报率可能高于经济基础设施,当然这还需要进一步验证。
| 表 3 全国基础设施及其所属不同行业的K、KN和KP |
2. 可信度检验
本文将通过“自比”和“他比”两种方式,检验基础设施资本存量估算的可信度,说明固定资产投资统计范围和口径调整的必要性。首先,在保证其他诸如估算方法和关键指标等相同时,仅调整基础设施的统计口径(全社会固定资产投资、新增固定资产投资两类)或者统计范围(是否进行行业大类级调整),分别获得两套测算数据,并分别绘制成图 1和图 2。从图 1容易发现,采用全社会固定资产投资口径,将比采用新增固定资产投资口径,平均高估47个百分点,并且这种高估效应随着基础设施投资力度的加大而被放大。事实上,在实际生产过程中,固定资产投资不可避免地存在浪费现象。因此,需要通过固定资产交付使用率将其调整为全社会新增固定资产投资,以更好体现全社会固定资本的新增价值。另外,如果不进行行业大类级统计范围调整,采用金戈(2016)确定的基础设施范围,所得到的估算结果与调整后的进行比较(如图 2所示),可发现两套数据虽然在2003之后差距逐渐缩小且在样本期末基本达到一致,但是在此之前将平均低估基础设施、经济基础设施和社会基础设施存量8.26、10.43和2.16个百分点,平均高估非基础设施存量接近12个百分点。
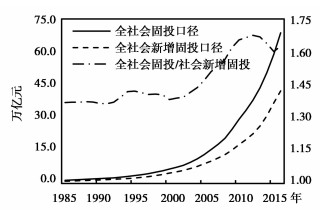
|
图 1 统计口径调整与否的差异 |
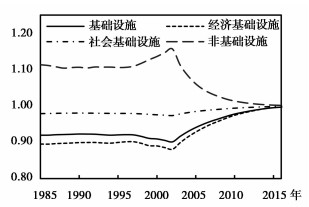
|
图 2 统计范围调整与否的差异 |
其次,采用文献比较法,将本文的估算结果与金戈(2016)和田友春(2016)公布的数据进行比较。由于田友春公布的是分行业资本存量,故根据基础设施所属行业划分标准将其结果加总得到经济基础设施和社会基础设施存量。由于金和田采用的是PIM传统途径的估算方法,所得结果为资本存量净额。因此,本文在同一口径与相同价格的对比原则下,采用资本存量净额结果分别与之对比(见图 3和图 4)。总体来看,本文的估算结果与金和田的数据在变动趋势和数值上较为一致,但是也略有差异。究其原因,主要有以下三点:一是在于估算方法。相比PIM传统途径默认选取同时退役模式,本文基于非传统途径估算框架,采用了更符合实际的钟型退役模式,估算方法的不同造成结果存在一定差异。二是在于统计范围。本文对2003年之前的投资数据进行了行业大类级调整,将社会服务门类中涉及的基础设施行业数据,拆分合并至经济和社会基础设施部门。由此所致,在前期,我们估算的经济和社会基础设施存量均高于金和田的结果,而非基础设施存量低于金的结果。三是在于折旧率。本文根据公式(7)可倒推出经济基础设施、社会基础设施和非基础设施的时变折旧率序列(限于篇幅,未列出),进一步计算出三者在样本期间的平均折旧率分别为6.1%、5.3%和6.2%,低于金戈估算的9.2%、8.5%和9.7%,由此导致本文的基础设施资本存量估算结果在后期相对较高。需要说明的是,本文估计得到的经济基础设施平均折旧率与Munnell and Cook(1990)估算的美国公共资本折旧率6.1%非常接近,同时与胡李鹏等(2016)假定的经济基础设施折旧率6.9%也相差不大。
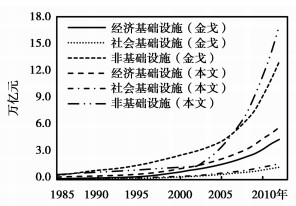
|
图 3 本文与金戈(2016,1988=1)比较 |
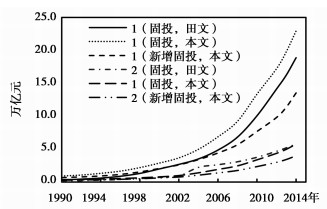
|
图 4 本文与田友春(2016,1990=1)比较 |
1. 资本产出弹性估算
在不考虑基础设施投入的空间影响时,参考金戈(2016)和郭鹏飞、曹跃群(2020)的研究,并经过系列检验后,我们采用面板修正标准误方法(PCSE)估计模型(9),回归结果汇报于表 4①第[1]列。进一步考虑基础设施资本投入的异质性,将其拆分为经济基础设施资本投入(Ge)和社会基础设施资本投入(Gs),再次采用PCSE估计模型(9),回归结果汇报于该表第[2]-[3]列。根据第[1]-[3]列的结果可知,基础设施资本的产出弹性值在样本期间呈现倒“U”型变化趋势,在2012年左右到达顶峰,并且各期均值为0.225,与金戈(2016)估计其不变产出弹性值0.226非常接近,一定程度上表明本文的估计结果是可靠的。同时,发现经济基础设施的产出弹性值平均为0.143,比社会基础设施高0.057。需要说明的是,历年基础设施的产出弹性值,是由基准年份和基础设施与年度交互项的估计结果相加所得。
① 限于篇幅,未列出基础设施与年度交互项的估计结果。同时,0—1权重矩阵下估计的结果与经济社会权重矩阵下估计的结果较为一致,在此也未列出,如有需要可向作者索取。
| 表 4 基础设施与区域经济增长的基本计量结果 |
进一步考虑基础设施投入的空间影响,由于模型中包括了解释变量和被解释变量的空间滞后项,为降低估计时可能产生的内生偏差,本文参考Lee and Yu(2010)的研究,采用极大似然法(MLE)估计模型(10)。表 4第[4]-[6]列分别报告了基础设施资本投入、经济基础设施资本投入和社会基础设施资本投入的回归结果。我们发现此时基础设施资本的产出弹性值平均为0.156,比不考虑空间影响时平均低0.069,这表明在实证基础设施对区域经济增长的作用时,需要考虑其空间影响,不然将会高估基础设施的产出弹性值。与此同时,在考虑解释变量的空间影响后,经济基础设施资本和社会基础设施资本的产出弹性值也有所降低,分别为0.121、0.080。此外,基础设施虽然在基准年份的空间溢出效应不显著,但是在2002年之后显著为正,经济基础设施在样本期间内一直保持正向溢出效应,而社会基础设施则保持负向溢出效应。
2. 全国和地区基础设施资本回报率
基于已测算的基础设施资本存量、产出弹性值和时变经济折旧率等数据,本文根据式(10)-(13)估算了全国和各地区基础设施资本回报率,全国层面(限于篇幅,未列出省级层面)计算结果汇报于表 5和图 5。由图 5可知,基础设施资本回报率的变化趋势在样本期间呈现倒“U”型,并且在三种模型中保持稳健,即在1993-1998年间波动上升,1999-2003年间快速下降,2004-2008年间保持平稳,之后又迅速下滑。具体来看,基准模型的基础设施资本回报率从1993年的0.207上升到1999年的0.273,接着下降至2004年的0.196,一直保持平稳到2008年,之后快速下降至2016年的0.089。与之相比,进一步考虑固定资产折旧后,基础设施资本回报率在数值上大约平均低4~7个百分点;再进一步剔除宏观税负影响,我们发现计算结果将平均低7~10个百分点。
| 表 5 全国基础设施及其所属类型的历年资本回报率 |
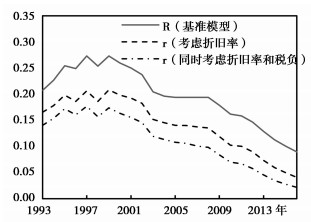
|
图 5 三种模型下基础设施资本回报率 |
进一步考虑基础设施的异质性,分别测算出经济和社会基础设施的资本回报率(同时考虑折旧率和宏观税负),计算结果见图 6。容易发现,经济基础设施的资本回报率在数值和变动趋势上均与基础设施整体非常一致,已低至2016年的0.012。社会基础设施的资本回报率虽然在变动趋势上与整体基础设施和经济基础设施基本一致,但是在数值上比经济基础设施平均高19个百分点,暗含着其具有更大的投资潜力和更好的投资收益。更重要的是,样本期间内两类基础设施的资本回报率与整体基础设施一样均出现两次下降,即在1999-2003年和2009-2016年间。不过,在前一阶段下降之后触底并保持了平稳,而后者却一直处于下降态势。我们感兴趣的是,为什么两次金融危机之后,基础设施的资本回报率均会下降,如何使当前的下降态势触底,甚至反弹。
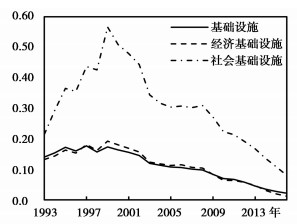
|
图 6 经济和社会基础设施资本回报率 |
分地区来看,我们仅给出了基础设施的资本回报率(同时考虑折旧率和宏观税负),见图 7。容易发现,各地区基础设施资本回报率的变动趋势与全国基本一致,即先上升后下降,接着保持平稳,之后再次下降。其中,东部地区的基础设施资本回报率在进入21世纪之后始终处于最高位置,由1993年的0.346波动降至2016年的0.192,累计降幅0.154。中部地区的基础设施资本回报率在早期高于东部地区,目前处于东部地区和西部地区之间,样本期间累计降幅0.259。西部地区的基础设施资本回报率则一直处于最低位置,可能的原因在于实施西部大开发战略之后,虽然越来越多的基础设施投资被投向西部地区,但是人口的流动方向却是从西部地区转移到东部地区(胡李鹏等,2016),导致该地区现有基础设施的利用效率并不高。
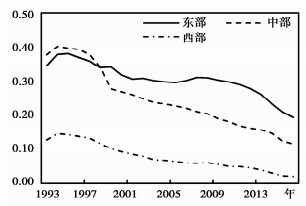
|
图 7 各地区基础设施资本回报率 |
具体到省份,本文估算了历年省际基础设施的平均资本回报率(同时考虑折旧率和宏观税负),见图 10。容易发现,基础设施省际平均资本回报率的变动趋势也与全国基本一致,有两个明显加快的下降阶段。不同的是,在第一个阶段,省际平均曲线提前两年下降,在第二个阶段,省际平均曲线的下降更为平缓。可能的解释是,由于部分省份数据的变动与整体存在较大差异,导致加快(或拖慢)了平均变化趋势。例如,北京和上海的基础设施回报率呈现明显的“U”型,显著异于整体趋势,特别是在2008年之后仍处于较快的上升态势。
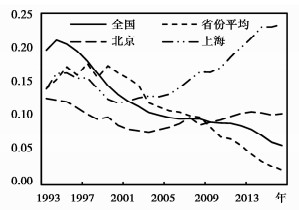
|
图 8 基础设施省份平均资本回报率 |
模型(13)表明基础设施的产出弹性值、资本产出比、宏观税负和折旧率是其资本回报率变动的重要组成部分。为判断何种要素更为重要,本文参考白重恩、张琼(2014)的研究,将模型(13)进行全微分,进而得到样本期间基础设施资本回报率变动△rtG的近似表达式:
| $ \begin{array}{l} \Delta r_t^G = \left( {1 - {\tau _t}} \right)\frac{{{Y_t}}}{{KP_t^G}}\Delta {\beta _{G, t}} + {\beta _{G, t}}\left( {1 - {\tau _t}} \right)\Delta \left( {\frac{{{Y_t}}}{{KP_t^G}}} \right)\\ + {\beta _{G, t}}\frac{{{Y_t}}}{{KP_t^G}}\Delta \left( {1 - {\tau _t}} \right) - \Delta \delta _t^G \end{array} $ | (14) |
其中,△βG, t、Δ(Yt/KPtG)、Δ(1-τt)和△δtG分别表示基础设施的产出弹性值、资本产出比的倒数、宏观税负和折旧率的变化值。因此,各要素的贡献度分别为同期该要素的变化值与资本回报率的变化值之比。例如,资本产出比的贡献度C(Yt/KPtG)=Δ(Yt/KPtG)/△rtG×100%。
表 6汇报了1994-2016年各要素对基础设施资本回报率变动的近似影响情况。在绝大部分年份,各要素汇总之和都非常接近100.0%,因此表达式(14)具有很高的准确度。在样本期间,基础设施的产出弹性值、资本产出比的倒数、宏观税负和折旧率的平均解释比例分别为27.8%、61.4%、15.3%和-6.1%。同时,我们发现基础设施资本回报率与这四个要素的相关系数依次为0.165、0.894、0.896和0.140。综上,本文认为影响中国基础设施资本回报率的核心因素为资本产出比(一定程度上刻画了资本生产效率),其他要素的贡献相对较小。这一结论成为下文识别并检验基础设施资本回报率影响因素的逻辑起点。
| 表 6 全国基础设施资本回报率的贡献分解 |
基于上述贡献度分解的结论,我们认为影响基础设施生产效率的变化因素主要有以下三类:一是基础设施本身的投入效率类因素,主要表现为要素边际报酬递减规律,即随着基础设施资本的积累,每一单位的新投入带来的边际效益逐渐下降。在此类因素中,我们主要选择基础设施投资率(nir)和基础设施资本深化程度(icd)进行实证分析。其中,nir采用基础设施新增投资与GDP的比值来衡量;icd运用基础设施资本存量与劳动力数量之比来刻画。二是整个经济体的技术效率类因素,主要表现为经济运行的“润滑剂”,可对各生产要素整体生产力产生影响。根据本文测算,样本期间基础设施资本存量在整个经济体的资本存量中占比平均高达41.8%,因此基础设施生产效率应该会受到整个经济体的传导影响。在此类因素中,我们选取贸易依存度(tdd)和人力资本积累(hum)进行实证分析,两者与模型(9)中相关控制变量的界定一致。三是整个经济体的要素配置类因素,主要变现为当要素配置结构发生变化,即要素从生产力低的部门流向生产力高的部门时,单位要素的总生产力将有所提高。我们选取政府规模(gz)、国有经济比重(soe)、城镇化率(urb)、第二产业占比(sec)和第三产业占比(thi)进行实证分析。其中,gz定义为地方政府财政支出占地区生产总值的比重,soe和urb与模型(9)中相关控制变量的界定一致,sec和thi分别定义为第二产业增加值和第三产业增加值占地区生产总值的比重。基于此,构建了如下基础设施资本回报率影响因素的计量模型:
| $ \begin{array}{l} r_{it}^G = {\theta _o} + {\alpha _1}ni{r_{it}} + {\alpha _2}nir_{it}^2 + {\alpha _3}ic{d_{it}} + {\beta _1}td{d_{i, t - 1}} + {\beta _2}hu{m_{i, t - 1}} + \\ {\varphi _1}g{z_{i, t - 1}} + {\varphi _2}so{e_{i, t - 1}} + {\varphi _3}ur{b_{i, t - 1}} + {\varphi _4}{\sec _{i, t - 1}} + {\varphi _5}th{i_{i, t - 1}} + {\gamma _t} + {\varepsilon _{it}} \end{array} $ | (15) |
其中,γt表示控制了时间效应。考虑可能存在的内生性,将整个经济体的技术效率类和要素配置类影响因素均采用其滞后一期数据。
由于模型(15)的随机扰动项同样存在较为严重的组间异方差、组内自相关和截面相关问题,故采用PCSE方法进行回归,估计结果汇报于表 7。其中,结果[7]报告了三类因素对rG的整体影响,结果[8]进一步报告了控制时间效应后的估计结果。根据前文可知,rG的变动趋势存在阶段性差异,即在1993-1998年处于波动上升态势,1999年之后快速下降,2004-2008年保持了短期平稳之后,接着又快速下降。同时,我们也发现基础设施资本回报率在不同区域也存在较大差异。鉴于此,本文一方面将样本分为1993-1998年、1999-2008年和2009-2016年三个阶段,另一方面将其划分为东部、中部和西部三个区域,分别考察三类因素对rG的时空异质性影响。
表 7的计量结果显示,无论是在时间还是空间上,基础设施投资率(nir)对rG都呈现出显著的“U”型关系。进一步将样本观测值的均值和中位数与“U”型曲线顶点所在位置进行比较发现,前者位于后者的左侧,这表明在样本期间nir对rG主要产生负向作用。由此可知,持续处于高水平的nir并没有产生同样高的rG。究其原因,相比消费品,资本品的单位能耗强度下降更慢且始终处于更高水平(白重恩、张琼,2014);同时当基础设施的投资率持续处于较高水平时,难以筛选更高质量的投资项目,从而不利于提升其资本回报率。基础设施资本深化程度(icd)对其资本回报率的影响存在显著的负向关系,符合新古典经济学的资本边际收益递减规律,例外的是在中西部地区这种关系并不显著。可能的解释是,中西部地区的基础设施总体水平仍然偏低,进而使其资本深化程度的提高较为有限。
| 表 7 基础设施资本回报率影响因素的回归结果 |
在第二类因素中,贸易依存度(tdd)整体上对rG存在统计不显著的正向影响。可能的解释在于,对外开放的提升不仅有利于学习和引进先进经济体的技术,对基础设施资本回报率产生正向作用,而且也可能通过加剧市场竞争对基础设施资本回报率产生负向冲击,这两方面作用是相互抵消的(张勋、徐建国,2016)。进入21世纪后,随着中国对外开放水平提高,其对基础设施资本回报率的正向作用逐渐强于负向作用,值得注意的是这种“正强负弱”的格局虽然在2009年之后依然保持,但是存在被打破的风险。与东中部地区相比,西部地区的技术水平离前沿面更远,在相同的开放水平下,技术进步速度更快,对资本回报率的正向作用更为明显。人力资本积累(hum)整体上对rG存在显著的正向影响,但是这种正向影响随着时间的推移正在不断减弱,并且在中西部地区出现不显著甚至显著负向的情形。这一方面说明通过教育和培训提升人力资本积累,可为提高整个经济体的知识储备为技术进步提供基础条件,从而提高rG。另一方面,具有较高人力资本的地区倾向于产生更快的技术进步,进而更为显著地提升该地区的rG,然而中国中西部地区的人力资本仍相对匮乏。
在第三类因素中,政府规模(gz)、国有经济比重(soe)对rG存在显著的稳健负向影响。这与直观相符,即政府规模越大意味着其对市场的干预能力越强,而这种干预通常被认为不利于包括基础设施在内的各类要素的优化配置。城镇化率(urb)整体上对rG存在显著的负向影响,但是随着发展阶段的不断深入,这种负向关系逐渐减弱甚至转为了正向影响。究其原因在于,存在一正一负两种作用,即随着该指标的持续扩大,一方面城市资本积累在不断增加的过程中边际效应递减,另一方面从事第一产业的人口流向生产率和技术进步要求更高的第二和第三产业,整个经济体的资源配置效率得以提升,进而传导提高了rG。第二产业比重(sec)和第三产业比重(thi)整体上对rG分别存在显著正向和不显著的影响,这表明相比第三产业,第二产业对基础设施投入的利用效率更高,能显著提升rG。与之形成印证的是,欧阳艳艳、张光南(2016)发现基础设施行业供给对制造业具有显著的产出促进作用,高翔等(2015)认为从高速公路连接中受益的仅是可贸易服务业。同时,由于基础设施行业大多属于第三产业,随着第三产业比重增加,基础设施积累也相应扩大,这制约了rG提升。
五、主要结论和政策含义在基础设施投资规模不断升高的现实背景下,本文采用永续盘存法非传统途径和生产函数法,谨慎测算出全国和省际基础设施及其所属不同类型设施的资本存量与资本回报率,并从时间和区域角度考察其动态变化,进一步基于“从整体到局部”的逻辑思路,分解并识别检验了基础设施资本回报率变化的影响因素。研究发现:(1)与基础设施资本存量总额和净额相比,基础设施生产性资本存量综合考虑了资产退役和效率损失情况,更能反映实际服务于生产过程的资本投入规模,其在样本区间急剧攀升,年均增长12.6%。其中,经济基础设施资本存量一直远高于社会基础设施,并且两者差距呈现扩大态势。(2)基础设施资本回报率的变动趋势在样本期间内呈现倒“U”型,且在不同基础设施类型和区域间保持稳健,即在1993-1998年波动上升,1999-2003年快速下降,2004-2008年保持平稳,之后又迅速下滑。其中,社会基础设施的资本回报率整体上高于经济基础设施,东部地区的基础设施资本回报率高于中部地区,西部地区则长期处于低位运行。(3)基础设施资本产出比不断上升是其资本回报率持续下降的核心因素。基于此,从影响基础设施本身和整个经济体的生产效率出发,实证分析出基础设施投资率与其资本回报率存在稳健的“U”型关系,基础设施资本深化程度、国有经济比重和城镇化水平对基础设施资本回报率产生负向影响,人力资本积累和第二产业比重则对基础设施资本回报率产生正向作用。分阶段来看,基础设施资本深化程度和城镇化水平的负向作用以及人力资本积累的提升作用均在减弱,贸易依存度的影响在统计上由不显著变为显著正向。
上述结论所蕴含的政策启示是,在中国经济由高速增长阶段转向高质量发展阶段中,必然要求从战略高度重新审视基础设施投资的行业和区域配置问题,从片面强调投资规模转向全面把握投资规模与投资效率相协调的目标上来,持续增强基础设施对促进城乡和区域协调发展、改善民生等的支撑作用。第一,由于我国社会基础设施和东、中部地区基础设施的资本回报率相对较高,故在制定基础设施投资策略时,应适当向社会基础设施领域倾斜,并且注重提升东中部地区的基础设施质量,加强西部地区现有基础设施资本存量的使用效率。第二,持续加大人力资本投入,提升人力资本质量和水平,有效缓解因基础设施投资率和资本深化程度不断提升而导致的基础设施资本边际报酬递减问题。尤其是中、西部地区人力资本水平较低,更应“筑巢引凤”和本地培育并举。第三,考虑到贸易依存度近十几年来对基础设施资本回报率产生显著正向影响,因此应继续扩大对外开放水平,提高外资利用质量。东、中部地区要加大技术密集型高附加值产品出口规模;西部地区则应充分抓住“一带一路”建设、中新(重庆)互联互通项目、成渝地区双城经济圈建设等区域合作倡议带来的新一轮发展机遇,发挥资源和劳动力比较优势,积极承接产业转移。第四,鉴于国有经济比重对基础设施资本回报率产生负向影响,同时在基础设施补短板的过程中依然存在较大资金缺口,因此应鼓励各级地方政府依法合规采用政府和社会资本合作(PPP)等方式,吸引民间社会资本投入到基础设施短板领域,提高其项目实施和利用效率。
| [] |
白重恩、张琼, 2014, “中国的资本回报率及其影响因素分析”, 《世界经济》, 第 10 期, 第 3-30 页。 |
| [] |
曹跃群、秦增强、齐倩, 2012, “中国资本服务估算”, 《统计研究》, 第 12 期, 第 45-52 页。DOI:10.3969/j.issn.1002-4565.2012.12.008 |
| [] |
陈英楠、吉晓萌, 2018, “中国城市住宅资本存量及资本回报率的估算”, 《统计研究》, 第 10 期, 第 3-14 页。 |
| [] |
樊潇彦, 2004, “中国工业资本收益率的测算与地区, 行业结构分析”, 《世界经济》, 第 5 期, 第 48-57 页。DOI:10.3969/j.issn.1007-0947.2004.05.011 |
| [] |
郭庆旺、吕冰洋, 2010, “国税收负担的综合分析”, 《财经问题研究》, 第 12 期, 第 3-10 页。DOI:10.3969/j.issn.1000-176X.2010.12.001 |
| [] |
高翔、龙小宁、杨广亮, 2015, “交通基础设施与服务业发展——来自县级高速公路和第二次经济普查企业数据的证据”, 《管理世界》, 第 8 期, 第 81-96 页。 |
| [] |
郭鹏飞、曹跃群, 2020, “中国经济基础设施资本回报率:测算, 分解及影响因素”, 《当代财经》, 第 10 期, 第 3-17 页。 |
| [] |
黄勇峰、任若恩、刘晓生, 2002, “中国制造业资本存量永续盘存法估计”, 《经济学(季刊)》, 第 1 期, 第 377-396 页。 |
| [] |
胡凯、吴清, 2012, “制度环境与地区资本回报率”, 《经济科学》, 第 8 期, 第 66-79 页。 |
| [] |
黄先海、杨君、肖明月, 2012, “资本深化, 技术进步与资本回报率:基于美国的经验分析”, 《世界经济》, 第 9 期, 第 3-20 页。 |
| [] |
胡李鹏、樊纲、徐建国, 2016, “中国基础设施存量的再测算”, 《经济研究》, 第 8 期, 第 172-186 页。 |
| [] |
金戈, 2016, “中国基础设施与非基础设施资本存量及其产出弹性估算”, 《经济研究》, 第 5 期, 第 41-56 页。 |
| [] |
廖茂林、许召元、胡翠、喻崇武, 2018, “基础设施投资是否还能促进经济增长?——基于1994-2016年省际面板数据的实证检验”, 《管理世界》, 第 5 期, 第 63-73 页。DOI:10.3969/j.issn.1002-5502.2018.05.005 |
| [] |
欧阳艳艳、张光南, 2016, “基础设施供给与效率对'中国制造'的影响研究”, 《管理世界》, 第 8 期, 第 97-109 页。 |
| [] |
邵挺, 2010, “金融错配, 所有制结构与资本回报率:来自1999~2007年我国工业企业的研究”, 《金融研究》, 第 9 期, 第 51-68 页。 |
| [] |
田友春, 2016, “中国分行业资本存量估算:1990~2014年”, 《数量经济技术经济研究》, 第 6 期, 第 3-21+76 页。 |
| [] |
魏辉、王春云, 2016, “准确理解资本存量与资本服务测度”, 《经济统计学(季刊)》, 第 2 期, 第 194-209 页。 |
| [] |
辛清泉、林斌、杨德明, 2007, “中国资本投资回报率的估算和影响因素分析——1999-2004年上市公司的经验”, 《经济学(季刊)》, 第 4 期, 第 1143-1164 页。 |
| [] |
杨校美、谭人友, 2017, “资本深化对中国制造业劳动生产率的影响:市场选择与政府行为”, 《南方经济》, 第 7 期, 第 51-69 页。 DOI:10.3969/j.issn.1000-6249.2017.07.004 |
| [] |
杨玉玲、郭鹏飞, 2017, “省际第三产业资本存量:框架, 检验及动态轨迹”, 《数量经济技术经济研究》, 第 10 期, 第 78-93 页。 |
| [] |
张军、吴桂英、张吉鹏, 2004, “中国省际物质资本存量估算:1952-2000”, 《经济研究》, 第 10 期, 第 35-44 页。 |
| [] |
章上峰, 2011, “时变弹性生产函数生产率分解公式及其政策含义”, 《数量经济技术经济研究》, 第 7 期, 第 106-121 页。 |
| [] |
张学良, 2012, “中国交通基础设施促进了区域经济增长吗——兼论交通基础设施的空间溢出效应”, 《中国社会科学》, 第 3 期, 第 60-77+206 页。 |
| [] |
张勋、徐建国, 2016, “中国资本回报率的驱动因素”, 《经济学(季刊)》, 第 3 期, 第 1081-1112 页。 |
| [] |
赵善梅、吴士炜, 2018, “基于空间经济学视角下的我国资本回报率影响因素及其提升路径研究”, 《管理世界》, 第 2 期, 第 68-79 页。DOI:10.3969/j.issn.1002-5502.2018.02.007 |
| [] |
Bai C., Hsieh C., Qian Y., 2006, "the Return to Capital in China". Brookings Papers on Economic Activity, 2, 61–88.
|
| [] |
Goldsmith R. W., 1951, "A Perpetual Inventory of National Wealth". in Conference on Research in Income and Wealth, 5–73.
|
| [] |
Jorgenson D. W., 1963, "Capital Theory and Investment Behavior". American Economic Review, 53(2), 247–259.
|
| [] |
Lucas R. E., 1990, "Why doesn't Capital Flow from Rich to Poor Countries?". American Economic Review, 80, 92–96.
|
| [] |
Lee L. F., Yu J., 2010, "A Spatial Dynamic Panel Data Model with Both Time and Individual Fixed Effects". Econometric Theory, 26(2), 564–597.
DOI:10.1017/S0266466609100099 |
| [] |
Munnell A. H., L. M. Coo, 1990, "How does Public Infrastructure Affect Regional Performance?". New England Economic Review, sep, 11–33.
|
| [] |
Moreno R.and Lopez-Bazo E., 2007, "Returns to Local and Transport Infrastructure Under Regional Spillovers". International Regional Science Review, 30(1), 47–71.
DOI:10.1177/0160017606296728 |
| [] |
OECD, 2009, "Measuring Capital OECD Manual 2009", Paris: OECD Publishing.
|
| [] |
R.J. Gordon, 1999, "US Economic Growth since 1870:One Big wave?". American Economic Review, 89(2), 123–128.
DOI:10.1257/aer.89.2.123 |
| [] |
Robertson P., 1999, "Economic Growth and the Return to Capital in Developing Economies". Oxford Economic Papers, 51(4), 577–594.
DOI:10.1093/oep/51.4.577 |
| [] |
Song Z., Storesletten K.and Zilibotti F., 2011, "Growing Like China". American Economic Review, 101(1), 196–233.
DOI:10.1257/aer.101.1.196 |
| [] |
Shi H., Huang S. Q., 2014, "How Much Infrastructure Is Too Much? A New Approach and Evidence from China". World Development, 56(4), 272–286.
|
| [] |
World Bank, 1994, "Infrastructure for Development", Oxford: Oxford University Press.
|
| [] |
Young A., 2003, "Gold into Base Metals:Productivity Growth in the People' Republic of China during the Reform Period". Journal of Political Economy, 111(6), 1220–1261.
DOI:10.1086/378532 |




