2020年全球新冠肺炎疫情让世界经济陷入深度衰退。在全球产业链中,中国被赋予“世界工厂”的角色,从供给端来看,我国作为全球产业链的上游供给方,随着中国疫情复工复产稳步推进,供给能力从“骤然暂停”至“逐步修复”,供给端的恢复面对的是后续全球疫情发酵下的需求疲软,我国出口商品中主要是以家庭消费类产品为主,该类产品需求弹性较大,随着全球主要疫情国家的需求下降,贸易企业将受到持续负面影响,我国经济与全球经济的关系正逐渐由“中国供给复苏”到“全球需求疲软”转变。从需求端来看,中国是石油、铁矿石和大豆等大宗商品以及集成电路等电子零部件的最大进口国,在全球资源品链条当中属于主要原材料进口方,全球疫情爆发以来对能源产品的需求大幅下降,进而导致国际大宗商品价格持续走低。随着国内疫情的好转,中国作为国际大宗商品主要进口国,需求能力得到极大提升,将会缓释全球疫情对国际资源品的冲击,虽然国际资源品供应链价格下降使国内进口端成本下行,这对于我国家庭部门消费具有显著刺激作用,但是中国大宗商品对外依存度较高,大宗商品国际定价权缺失,极易受国际价格波动及汇率波动影响,随着全球疫情演进其对我国经济的影响还存在较大不确定性。
面对全球疫情冲击,各发达经济体相继推出内低利率货币政策,缓解企业融资约束,降低因总需求疲软企业潜在的资产负债风险,然而单纯的放松货币政策只能缓解本国经济暂时性衰退,利率政策在发挥刺激产出的作用同时又要防止疫情结束后的需求拉动型通货膨胀,利率政策如何做到“保增长”与“防通胀”的兼顾?众所周知,我国货币政策的最终目标为“保持货币币值的稳定,并以此促进经济增长”,但在开放经济条件下货币政策要保持人民币币值的稳定最终表现为两个方面:一是对内保持通货膨胀的稳定;二是对外保持人民币汇率波动处于合理区间。长期以来我国双顺差的贸易格局带来巨额的外汇储备,为稳定人民币汇率提供了政策工具,但我国以往冲销式外汇干预在稳汇率的同时,难以保证稳定的基础货币供给,人民币往往陷入“外升内贬”的不利局面,造成出口贸易冲击、外汇资产缩水、热钱流入等一系列问题。因此,汇率政策应“稳汇率”还是“稳货币”?从现实情况来看,目前我国央行实行“双政策双工具”的货币政策体系,采用利率和汇率并重的货币政策框架,同时利用利率和汇率两种工具以实现人民币币值内外均衡稳定的目标,在后疫情时代,应采取怎样的政策组合才有助于实现经济回到长期均衡路径,是保增长还是防通胀、稳汇率还是稳货币,这些是后疫情时代我国央行面临的新问题。
二、文献综述与理论分析 (一) 文献综述国内外较多文献探讨了货币政策中利率政策与汇率政策的“双政策”协调机制。Benes et al.(2012)将外汇冲销干预作为与泰勒规则同时操作的央行工具,以考虑外汇干预政策对资产负债表的影响,发现外汇干预可以帮助经济免受国际金融不利环境的冲击。金中夏、洪浩(2015)运用两国开放经济体动态随机一般均衡(DSGE)模型,分析并解释我国均衡利率和均衡汇率形成机制及其主要变动原因,他们认为利率和汇率失衡后的动态最优调整路径取决于利率和汇率相对于各自均衡状态的失衡程度,应先调整失衡程度较重者,后调整失衡程度较轻者。伍戈、刘琨(2015)对中国“多目标、多工具”的货币政策框架以及规则体系进行了系统分析和实证检验。在外部持续失衡的环境下,分别基于内部和外部均衡的货币政策反应函数能较充分地刻画转型中国的特征。陈师等(2015)发现汇率渠道会放大货币政策的宏观效应,对实际汇率做出反应优于不做反应或对名义汇率做出反应;在利率规则下,增加政策工具变化的持续性、放松对汇率变化的干预会增进社会福利。胡小文(2019)基于我国的汇率管理事实,构建不完全冲销下的外汇储备稳定汇率、利率调控通胀的“双目标双工具”DSGE货币政策框架,研究发现,面对国际贸易条件恶化,双目标双工具的固定汇率制度因阻止汇率变化反而引发较大的产出和通胀波动。
构建我国开放经济DSGE模型需要体现我国实体经济的特征事实。首先,对于资本项目并非完全开放的国家而言,忽略汇率波动性本身会导致较高的成本,发展中国家进行外汇干预是较优的选择。Ostry et al.(2012)认为央行对汇率波动进行干预会提高福利,因此对新兴市场经济体而言,为应对金融稳定与危机,在政策工具方面除了使用传统的利率工具应对通胀外,还可运用对冲干预工具来管理汇率,稳定汇率与实现通胀并不矛盾。国际收支的现实特征表现为“双顺差”,积累了巨额外汇储备,为外汇干预的实施提供了政策工具,但也引起了国内通胀压力。朱孟楠、曹春玉(2018)发现通过外汇干预实施管理浮动汇率安排可根据逆经济风向行事原则权衡调整汇率浮动区间,比单纯使用利率规则实施管理浮动汇率更为有效。彭红枫等(2018)发现在现行有管理浮动汇率制度下,一味降低外汇市场干预力度或者放松资本管制会降低经济福利水平,资本账户管制和有管理的浮动汇率制度是当前作为应对短期国际资本冲击的有效工具。
其次,就是我国的“世界工厂”特征,即作为全球产业链的上游供给方进口初级产品,出口最终产品,这也是全球新冠疫情冲击的渠道。因此本文参考(Gertler et al., 2007;Chang et al., 2015)的研究,模型将外国投资作为本国生产企业的中间投入引入本国经济体系更好地契合中国经济特征。最后一个特征事实就是我国存在金融摩擦(梅冬州、龚六堂,2011;康立、龚六堂,2014),尤其是对我国中小企业而言面临较强的信贷约束,由于信息不对称导致融资成本较高,在金融加速器机制下会放大全球新冠疫情冲击强度。Blanchard et al.(2013)认为新兴市场经济体由于金融市场的不完善,往往存在相比发达国家存在更大金融摩擦,贸易顺差积累的外汇储备可以使得央行将外汇干预作为一种政策工具,其中政策利率用于稳通胀,外汇干预则用于稳汇率。
(二) 理论分析在选择最优货币政策应对全球新冠疫情冲击之前,需要对全球新冠疫情对我国实体经济影响的演进机制进行理论分析与刻画,全球新冠疫情会对世界经济造成的冲击表现为供给面断裂而引发总需求萎缩进而产生恶性循环,全球新冠疫情会从供给侧和需求侧共同影响宏观经济(Mckibbin and Fernando, 2020;刘瑶、陈珊珊,2020;杨子晖等,2020),尤其是对于我国贸易部门企业的冲击影响更大,通过贸易渠道进一步全面降低国内家庭消费和企业投资,新冠疫情所带来的冲击包括总量冲击(GDP、投资、消费、进出口)、要素冲击(劳动力、资本等要素)和结构冲击(不同行业异质性影响)等(胡滨等,2020),全球新冠疫情冲击机制主要分为两个渠道,分别是国际贸易渠道和资产负债表渠道。国际贸易渠道具体表现为全球新冠疫情蔓延,世界各国贸易封锁带来的需求骤降,从我国外贸企业供给层面来讲,全球新冠疫情严重影响国内贸易企业的正常生产经营,国外订单减少出口下降,进一步影响企业利润,尤其对于我国外向型中小企业在资本市场上比大企业面临着更严重的融资约束,更加依赖于贸易信贷融资,而在利率和汇率大幅波动的情况下,会影响到贸易企业的贸易信贷融资成本,进而放大国际贸易渠道这一影响机制。资产负债表渠道具体表现为全球主要发达经济体量化宽松政策的溢出效应,在投资者情绪、预期和不完全信息等因素影响下,会逐步衍生为国际金融市场投资者的羊群效应与国际投融资的金融加速器效应,其对金融市场的冲击造成利率和汇率的大幅波动,引起全球资产价格波动,具体表现为国际大宗商品价格大幅波动,若企业未在金融市场进行套期保值等金融工具对冲风险,将对于企业成本造成较大冲击,进而导致贸易企业资产负债表的恶化。例如全球疫情爆发以来世界各国采取的旅行和货物限制,导致对燃料、煤炭和其他能源产品的需求下降,国际大宗商品价格持续走低,联合国发布的数据报告显示,受到新冠疫情影响,2020年第一季度全球贸易额下降3%,大宗商品价格创纪录的下跌了20%①。
① 联合国:新冠疫情引发全球贸易下滑3%大宗商品价格下跌20%第二季度将加剧,网址:https://www.sohu.com/a/394980616_120124605
无论是国际贸易渠道还是资产负债表渠道,全球新冠疫情冲击对于我国实体经济的影响都与央行制定的货币政策息息相关,本文在已有研究基础上将央行利率政策与汇率政策同时纳入包含金融加速器的开放经济模型,将全球新冠疫情冲击(供给端和需求端影响路径)引入开放经济DSGE模型,研究全球疫情对我国宏观经济的影响以及央行政策偏好在减缓疫情冲击方面的作用。进一步从家庭动态福利角度探讨面对全球新冠疫情蔓延形势下,外国需求不足与外国投资实际价格骤降冲击下的央行最优货币政策选择。本文的边际贡献包括:一是目前国内外相关文献(郭栋,2020;汤铎铎等,2020;周梅芳等,2020)主要聚焦国内疫情爆发初期我国实体经济所受到的影响,而全球疫情爆发以来我国经济受到的外部冲击目前仍然处于经验分析阶段,我们利用DSGE模型模拟了在面对外国需求和外国投资实际价格供给冲击下,利率和汇率政策传导机制在我国的实施效果。二是针对全球新冠疫情蔓延对我国贸易部门产生的冲击,参考(康立、龚六堂,2014)将中间品厂商分为非贸易中间品厂商和贸易中间品厂商,针对性的探讨了外国需求负向冲击对我国贸易部门的影响;三是由于国外疫情冲击会对贸易部门就业产生冲击,因此我们在家庭部门融入异质性劳动供给,利用二阶泰勒展开式构建家庭福利函数,参考彭红枫等(2018)做法本文通过度量家庭福利水平变化研究“双政策双目标”政策偏好的社会效用。
本文剩余部分结构安排如下:第二部分构建了包括外汇干预、“世界工厂”、“双政策双目标”金融加速器等特征的一般均衡动态模型;第三部分对央行不同利率政策和汇率政策偏好下的脉冲响应进行分析,以探讨在外国需求冲击和外国投资实际价格冲击下经济变量的波动;第四部分通过对家庭效用利用二阶泰勒展开进行福利分析;最后给出了结论与政策建议。
三、模型构建模型构建参考Chang et al.(2015)做法将外国投资中间品引入本国经济体系,其次设定银行与贸易和非贸易部门之间存在金融摩擦,央行为保持汇率稳定同时权衡外汇储备变动与基础货币供给的变动对汇率的影响。
(一) 最终品厂商假设经济系统中存在一个代表性最终品厂商,对于非贸易中间品厂商,使用斯蒂格利茨生产函数生产最终品Yt,表示如下:
| $ {Y_t} = {\left( {\int_0^1 {{Y_{D,t}}} {{(j)}^{\frac{{{\varepsilon _p} - 1}}{{{\varepsilon _p}}}}}dj} \right)^{\frac{{{\varepsilon _p}}}{{{\varepsilon _p} - 1}}}} $ | (1) |
其中εp表示不同非贸易中间品之间的替代弹性,1<εp<+∞表示中间品厂商具有一定垄断能力,由最终品厂商利润最大化利润一阶条件可得非贸易品YD, t(j)的需求函数为:
| $ {Y_{D,t}}(j) = {\left( {\frac{{{P_t}(j)}}{{{P_t}}}} \right)^{ - {\varepsilon _p}}}{Y_t} $ | (2) |
上式表示非贸易中间品YD, t(j)的需求依赖于相对价格和价格需求弹性εp,非贸易中间品YD, t(j)的需求随其价格Pt(j)上升而下降,进而可得价格总水平指数决定方程为:
| $ P_{t}=\left(\int_{0}^{1}\left(P_{t}(j)\right)^{1-\varepsilon_{p}} d j\right)^{\frac{1}{1-\varepsilon_{p}}} $ | (3) |
假设经济中存在代表性家庭,在贸易部门与非贸易部门之间家庭劳动具有异质性,i∈(0, 1)均匀连续分布,每个家庭通过劳动获得收入,效用函数设定为:
| $ \mathop {\max }\limits_{\left( {{C_t},{L_t},{M_{t + 1}}} \right)} {E_0}\sum\limits_{t = 0}^\infty {{\beta ^t}} \left( {\ln \left( {{C_t} - b{C_{t - 1}}} \right) - {\psi _L}\frac{{{{\left[ {{\gamma ^{1/\eta }}{L_{D,t}}^{(\eta - 1)/\eta } + {{(1 - \gamma )}^{1/\eta }}{L_{F,t}}^{(\eta - 1)/\eta }} \right]}^{\eta /(\eta - 1)}}}}{\eta } + {\psi _M}\ln \frac{{{M_t}}}{{{P_t}}}} \right) $ | (4) |
代表性家庭预算约束可表示为:
| $ {{\rm{C}}_t} + \frac{{{B_{H,t}}}}{{{\omega _t}{P_t}}}\left( {1 + {\Theta _{B,t}}} \right) + \frac{{{M_t}}}{{{P_t}}} \le {w_{D,t}}{L_{D,t}} + {w_{F,t}}{L_{F,t}} + \frac{{\prod\nolimits_t {} + {\varXi _{D,t}} + {\varXi _{M,t}}}}{{{P_t}}} +\\ \frac{{{R_{H,t - 1}}{B_{H,t - 1}} + {e_t}{R_{Hf,t - 1}}{B_{Hf,t - 1}}}}{{{P_t}}} + \frac{{{M_{t - 1}}}}{{{P_t}}} $ | (5) |
其中β为家庭贴现因子,Ct为家庭消费,LD, t为家庭对非贸易部门提供的劳动供给,LF, t为家庭对贸易部门提供的劳动供给,γ反映了家庭在两个部门劳动中负效用的异质性,本文设定劳动供给为贸易厂商与非贸易厂商劳动供给的复合,其中参数γ∈[0, 1]表示劳动供给偏好,因此(1-γ)越大表示经济开放程度越高,当γ=1时表示该国劳动供给完全满足本国需求,当γ=0时表示该国劳动供给完全满足外国需求,参数η>0表示非贸易厂商与贸易厂商劳动供给之间的替代弹性。
这里设定本国家庭同时持有本国债券和外币债券,用
最优消费一阶条件为:
| $ {\lambda _t} = \frac{1}{{{C_t} - b{C_{t - 1}}}} - \beta {E_t}\frac{b}{{{C_{t + 1}} - b{C_t}}} $ | (6) |
非贸易和贸易部门最优劳动一阶条件分别为:
| $ \frac{{{\gamma ^{1/\eta }}}}{\eta }{\left[ {{\gamma ^{1/\eta }}{L_{D,t}}^{(\eta - 1)/\eta } + {{(1 - \gamma )}^{1/\eta }}{L_{F,t}}^{(\eta - 1)/\eta }} \right]^{\frac{1}{{\eta - 1}}}}L_{D,t}^{ - \frac{1}{\eta }}{\psi _L} = {\lambda _t}{w_{D,t}} $ | (7) |
| $ \frac{{{{(1 - \gamma )}^{1/\eta }}}}{\eta }{\left[ {{\gamma ^{1/\eta }}{L_{D,t}}^{(\eta - 1)/\eta } + {{(1 - \gamma )}^{1/\eta }}{L_{F,t}}^{(\eta - 1)/\eta }} \right]^{\frac{1}{{\eta - 1}}}}L_{F,t}^{ - \frac{1}{\eta }}{\psi _L} = {\lambda _t}{w_{F,t}} $ | (8) |
两式相除可得两部门最优劳动工资比:
| $ \frac{w_{F, t}}{w_{D, t}}=\left(\frac{1-\gamma}{\gamma} \frac{L_{D, t}}{L_{F, t}}\right)^{1 / \eta} $ | (9) |
货币需求函数Mt一阶条件表示如下:
| $ {E_t}\beta \frac{{{\lambda _{t + 1}}}}{{{\lambda _t}{\pi _{t + 1}}}} + \frac{{{\psi _M}}}{{{\lambda _t}{m_t}}} = 1 $ | (10) |
其中λt为拉格朗日乘子,mt=Mt/Pt为实际货币需求,Et表示基于t期信息的期望算子。
本国债券BH, t一阶条件表示如下:
| $ {E_t}\beta \frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}\frac{{{R_{H,t}}}}{{{\pi _{t + 1}}}} = 1 + {\Theta _{B,t}} + {\Omega _B}\left( {1 - {\omega _t}} \right)\left( {{\omega _t} - \bar \omega } \right) $ | (11) |
外国债券BHf, t一阶条件表示如下:
| $ {E_t}\beta \frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}\frac{{{e_{t + 1}}}}{{{e_t}}}\frac{{{R_{Hf,t}}}}{{{\pi _{t + 1}}}} = 1 + {\Theta _{B,t}} - {\Omega _B}\left( {{\omega _t} - \bar \omega } \right){\omega _t} $ | (12) |
两式相减得到:
| $ {E_t}\frac{\beta }{{{\pi _{t + 1}}}}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}\left( {{R_{H,t}} - {R_{Hf,t}}\frac{{{e_{t + 1}}}}{{{e_t}}}} \right) = {\Omega _B}(\omega - \bar \omega ) $ | (13) |
其中πt=Pt/Pt-1,上式表示带有资本管制的非抛补利率平价,当家庭配置更多外国债券时,有ω < ω,此时调整成本会越高,则有
将中间品厂商分为贸易厂商和非贸易厂商,并且均按照柯布道格拉斯生产函数进行生产。
1.贸易部门
贸易厂商生产函数为:
| $ E{X_t} = {A_t}K_{F,t - 1}^{{\alpha _F}}FL_{F,t}^{1 - {\alpha _F}} $ | (14) |
贸易中间品厂商资本累积函数为:
| $ {K_{F,t}} = \left[ {1 - \frac{{{\Omega _F}}}{2}{{\left( {\frac{{{I_{F,t}}}}{{{I_{F,t - 1}}}} - 1} \right)}^2}} \right]{I_{F,t}} + (1 - \delta ){K_{F,t - 1}} $ | (15) |
贸易厂商的预算约束为:
| $ {D_{F,t}} = {R_{F,t - 1}}{D_{F,t - 1}} - E{X_t} + {w_{F,t}}{L_{F,t}} + {r_{F,t}}{k_{F,t}} + {\Omega _{F,t}} $ | (16) |
其中DF, t表示贸易厂商债务余额,ΩF, t表示贸易厂商净利润,RF, t-1表示债务利息率。
最优资本劳动比为:
| $ \frac{{{K_{F,t}}}}{{{L_{F,t}}}} = \frac{{{\alpha _F}}}{{1 - {\alpha _F}}}\frac{{{w_{F,t}}}}{{{r_{F,t}}}} $ | (17) |
贸易厂商边际成本满足:
| $ m{c_{F,t}} = {\alpha _F}^{ - {\alpha _F}}{\left( {1 - {\alpha _F}} \right)^{{\alpha _F} - 1}}A_t^{ - 1}w_{F,t}^{1 - {\alpha _F}}r_{F,t}^{{\alpha _F}} $ | (18) |
2.非贸易部门
非贸易厂商生产函数为:
| $ {Y_{D,t}} = {A_t}K_{D,t - 1}^{{\alpha _D}}L_{D,t}^{1 - {\alpha _D}} $ | (19) |
同样设定贸易中间品厂商资本累积函数为:
| $ {K_{D,t}} = \left[ {1 - \frac{{{\Omega _D}}}{2}{{\left( {\frac{{{I_{D,t}}}}{{{I_{D,t - 1}}}} - 1} \right)}^2}} \right]{I_{D,t}} + (1 - \delta ){K_{D,t - 1}} $ | (20) |
参考Chang et al.(2015)的做法,本文假设非贸易厂商投资ID, t是国内投资IDd, t和国外投资IDf, t的组合函数:
| $ {I_{D,t}} = I_{Dd,t}^\rho I_{Df,t}^{1 - \rho } $ | (21) |
其中ρ表示国内投资权重,设国内投资价格成本为PId, t国外投资价格成本为PIf, t,由成本最小化问题可表示为:
| $ \frac{{{I_{Dd,t}}}}{{{I_{Df,t}}}} = \frac{\rho }{{1 - \rho }}\frac{{{e_t}{P_{If,t}}}}{{{P_{Id,t}}}} $ | (22) |
由于投资价格波动会导致最终品价格产生同向波动,因此这里假设实际汇率
| $ {{I_{Dd,t}} = \left[ {{\rho ^{1 - \rho }}{{(1 - \rho )}^{\rho - 1}}q_t^{1 - \rho }} \right]{I_{D,t}}} $ | (23) |
| $ {{I_{Df,t}} = \left[ {{\rho ^{ - \rho }}{{(1 - \rho )}^\rho }q_t^{ - \rho }} \right]{I_{D,t}}} $ | (24) |
由此国内和国外投资相对于复合中间品的实际价格为:
| $ {{Q_{Dd,t}} = {\rho ^{1 - \rho }}{{(1 - \rho )}^{\rho - 1}}q_t^{1 - \rho }} $ | (25) |
| $ {{Q_{Df,t}} = {\rho ^{ - \rho }}{{(1 - \rho )}^\rho }q_t^{ - \rho }} $ | (26) |
其中QDd作为国内异质性非贸易中间品生产商资本成本进入生产函数,QDf作为外生冲击变量。
将第i个非贸易中间品生产商表示为:
| $ {Y_{D,t}}(i) = {A_{D,t}}K_{D,t - 1}^{{\alpha _D}}(i)L_{D,t}^{1 - {\alpha _D}}(i) $ | (27) |
其成本最小化问题为:
| $ \min {Q_{Dd,t}}{K_{D,t}}(i) + {w_t}{L_{D,t}}(i)\quad {\rm{ }}s.{\rm{ }}t.\quad {Y_{D,t}}(i) = {A_{D,t}}K_{D,t - 1}^{{\alpha _D}}(i)L_{D,t}^{1 - {\alpha _D}}(i) $ | (28) |
由资本与劳动一阶条件可得:
| $ \frac{K_{D, t}(i)}{L_{D, t}(i)}=\frac{\alpha_{D}}{1-\alpha_{D}} \frac{w_{D, t}}{Q_{t}} $ | (29) |
由资本或者劳动一阶条件可得边际成本为:
| $ m{c_t} = {\alpha _D}^{ - {\alpha _D}}{\left( {1 - {\alpha _D}} \right)^{{\alpha _D} - 1}}A_t^{ - 1}w_t^{1 - {\alpha _D}}Q_t^{{\alpha _D}} $ | (30) |
参考Rotemberg(1982)的二次项价格调整成本函数,设定产品价格有黏性,设定具体形式为:
| $ {\Theta _{\pi ,t}} = \frac{{{\Omega _\pi }}}{2}{\left( {\frac{{{P_t}(j)}}{{\bar \pi {P_{t - 1}}(j)}} - 1} \right)^2}\left( {{C_t} - b{C_{t - 1}}} \right) $ | (31) |
其中Ωπ为非贸易中间品厂商调整成本参数。
价格最优化问题为
| $ \mathop {\max }\limits_{{P_t}(j)} {E_t}\sum\limits_{t = 0}^\infty {{\beta ^t}} \frac{{{C_t} - b{C_{t - 1}}}}{{{C_{t + k}} - b{C_{t + k - 1}}}}\left( {\left( {\frac{{{P_{t + k}}(j)}}{{{P_{t + k}}}} - m{c_{t + k}}} \right){Y_{D,t + k}}(j) - {\Theta _{\pi ,t + k}}} \right) $ | (32) |
中间品厂商j的选择P(j)独立于j,所有中间品厂商选择相同的最优调整价格,有Pt(j)=Pt,因此由一阶条件可得最优价格方程为:
| $ m{c_t} = \frac{{{\varepsilon _p} - 1}}{{{\varepsilon _p}}} + \frac{{{\Omega _\pi }}}{{{\varepsilon _p}}}\frac{{{C_t} - b{C_{t - 1}}}}{{{Y_{D,t}}}}\left[ {\left( {\frac{{{\pi _t}}}{{\bar \pi }} - 1} \right)\frac{{{\pi _t}}}{{\bar \pi }} - \beta {E_t}\left( {\frac{{{\pi _{t + 1}}}}{{\bar \pi }} - 1} \right)\frac{{{\pi _{t + 1}}}}{{\bar \pi }}} \right] $ | (33) |
本文假设银行部门分为信贷业务与中间业务,信贷业务主要负责为本国贸易部门和非贸易部门提供信贷,中间业务主要负责承销本国央行发行的本币债券,同时为本国家庭提供外币债券交易。
1.信贷业务
银行同时为贸易厂商和非贸易厂商提供信贷业务,这里假定银行部门与贸易、非贸易部门存在信息不对称和融资约束,当银行调整两类信贷结构时,会增加厂商的外部融资溢价增大金融摩擦程度进而提高调整成本,即存在金融加速器效应,同时调整成本与两类信贷规模成正比,并且假设银行对于贸易厂商提供外币信贷,因此银行部门信贷业务调整成本设定如下式:
| $ {\Theta _{L,t}} = \frac{{{\Omega _L}}}{2}{\left( {{\kappa _t} - \bar \kappa } \right)^2}\left( {{D_{D,t}} + {e_t}{D_{F,t}}} \right) $ | (34) |
其中用ΩL表示银行信贷业务运营成本系数,
| $ \max \sum\limits_{t = 0}^\infty {\frac{{{\varXi _{D,t}}}}{{{{\left( {D{R_t}} \right)}^t}}}} $ | (35) |
| $ {\rm{ }}s.{\rm{ }}t.\;\;{S_{H,t}} = D{R_{t - 1}}{S_{H,t - 1}} + \left( {D{R_{t - 1}} - {R_{LD,t - 1}}} \right){D_{D,t - 1}} + \left( {D{R_{t - 1}} - {R_{LF,t - 1}}} \right){D_{F,t - 1}} + {\Theta _{L,t}} + {\varXi _{D,t}} $ | (36) |
其中SH, t为家庭储蓄,表示来自家庭的银行债务余额,DRt为银行存款利率,DLD, t、DLF, t分别表示非贸易厂商和贸易中间品厂商的债务余额,即银行贷款。假定银行每期债务余额(SH, t-DRt-1SH, t-1)等于零,以满足非蓬齐博弈条件,分别求解非贸易厂商和贸易厂商债务一阶条件可得:
| $ {{R_{LD,t}} = D{R_t} + \left[ {\frac{{{\Omega _L}}}{2}{{\left( {{\kappa _t} - \bar \kappa } \right)}^2} + {\Omega _L}\left( {{\kappa _t} - \bar \kappa } \right)\left( {1 - {\kappa _t}} \right)} \right]D{R_t}} $ | (37) |
| $ {{R_{LF,t}} = D{R_t} + \left[ {\frac{{{\Omega _L}}}{2}{{\left( {{\kappa _t} - \bar \kappa } \right)}^2} - {\Omega _L}\left( {{\kappa _t} - \bar \kappa } \right){\kappa _t}} \right]D{R_t}} $ | (38) |
本文假设我国存在金融体系非有效,因此式(36)(37)加号右侧表示银行部门与两个实体部门之间的利差,以衡量银行部门国内信贷业务的金融摩擦程度,这里存款利率等于央行无风险利率,即DRt=Rt。
2.中间业务
参考Uribe and Yue(2006)、Kitano(2011)以及彭红枫等(2018),设定本国银行由于金融体系不完善,设定为非有效状态,中间业务同样存在运营成本, 设定如下式:
| $ {\Theta _{M,t}} = \frac{{{\Omega _M}}}{2}{\left( {{\omega _t} - \bar \omega } \right)^2}\left( {{B_{H,t}} + {e_t}{B_{Hf,t}}} \right) $ | (39) |
其中ΩM表示银行中间业务运营成本系数,中间业务运营成本同样取决于银行本外币债券结构变动和家庭持有本外币债券规模。银行中间业务最大化问题为:
| $ \max \sum\limits_{t = 0}^\infty {\frac{{{\Xi _{M,t}}}}{{{{\left( {{R_t}} \right)}^t}}}} $ | (40) |
从流动性的角度考虑,国家债券因期限长而缺乏流动性,金融债券和企业债券的流动性要强于国家债券,我国国券利率高于金融债券利率,因此设定商业银行中间业务面临预算约束为:
| $ {S_{H,t}} = D{R_{t - 1}}{S_{H,t - 1}} + \left( {{R_{H,t - 1}} - {R_{t - 1}}} \right){B_{H,t - 1}} + \left( {{R_{Hf,t - 1}} - {R_{F,t - 1}}} \right){e_{t - 1}}{B_{Hf,t - 1}} + {\Theta _{M,t}} + {\varXi _{M,t}} $ | (41) |
求解银行中间业务关于BH, t和BHf, t一阶条件可得:
| $ {{R_t} = {R_{H,t}} + \left[ {\frac{{{\Omega _M}}}{2}{{\left( {{\omega _t} - \bar \omega } \right)}^2} + {\Omega _M}\left( {{\omega _t} - \bar \omega } \right)\left( {1 - {\omega _t}} \right)} \right]{R_t}} $ | (42) |
| $ {{R_{F,t}} = {R_{Hf,t}} + \left[ {\frac{{{\Omega _M}}}{2}{{\left( {{\omega _t} - \bar \omega } \right)}^2} - {\Omega _M}\left( {{\omega _t} - \bar \omega } \right){\omega _t}} \right]{R_t}} $ | (43) |
式(42)右侧表示本国央行发行债券利率与本国家庭持有本币债券利率之差,式(43)右侧表示外国央行发行债券利率与本国家庭持有外币债券利率之差,两者共同体现了在开放经济条件下银行部门中间业务的金融摩擦程度。
(五) 政府部门央行当期储备资产变动受到家庭当期本币债券余额增长和实际货币余额变动的约束:
| $ {e_t}\left( {{B_{Gf,t}} - {R_{F,t}}{B_{G,t - 1}}} \right) \le \left( {{B_{H,t}} - {R_{H,t}}{B_{H,t - 1}}} \right) + \left( {{m_t} - {m_{t - 1}}} \right) $ | (44) |
在封闭经济条件下当经济体中仅包含价格扭曲时,央行在防通胀和保增长之间会存在“神奇的巧合”,当一种目标实现时另一种目标也会实现,但是当经济包含更多扭曲和摩擦时,央行就会存在权衡取舍,尤其是在开放经济条件下,汇率不会立即对利率波动做出反应的原因在于我国资本账户管制下资本流动成本较高,央行的“双政策双工具”,首先体现在我国目前正在由数量型向价格型转变的利率政策,按照泰勒规则设定如下式:
| $ {R_t} = \left( {1 - {\rho _R}} \right)\bar R + {\rho _R}{R_{t - 1}} + \left( {1 - {\rho _R}} \right)\left[ {{\varphi _\pi }\left( {{\pi _t} - \bar \pi } \right) + {\varphi _Y}\left( {{Y_t} - \bar Y} \right)} \right] $ | (45) |
其中,ρR为利率平滑系数,R、π与Y分别表示稳态时利率、通胀与产出。
对于汇率政策规则而言,设定央行的汇率政策由两个目标推动,一是央行利用外汇储备实施非冲销式外汇干预,使得对汇率波动进行逆风干预;二是央行实施冲销式外汇干预,通过外汇冲销手段来对冲因外汇占款增加而被动发行的基础货币,维持基础货币供给稳定,以往我国央行多实行的是冲销式干预。然而,通过利用外汇储备的公开市场操作来进行逆风外汇干预,可以同时兼顾基础货币供给的弹性,以维持汇率波动与基础货币供应、外汇储备波动之间的平衡。2002年我国加入WTO后出口和外商直接投资增长迅速,央行资产负债表科目下的外汇占款大幅增长,成为央行投放基础货币的主要形式。由于外汇占款不受央行直接调控,为了有效控制货币供给总量,央行利用公开市场操作等政策工具进行基础货币发行量及流动性管控,具体表现为“逆风式”的汇率政策,参考Chutasripanich et al.(2015)设定如下等式以体现我国央行有管理的浮动汇率制度:
| $ {{{\left( {{B_{Gf,t}}/{{\bar B}_{Gf}}} \right)}^{{\theta _{Gf}}}} = {e_t}/{e_{t - 1}}} $ | (46) |
| $ {{{\left( {{M_t}/\bar M} \right)}^{{\theta _M}}} = {e_t}/{e_{t - 1}}} $ | (47) |
这里θM表示汇率波动的货币供给弹性,θGf表示汇率波动的外汇储备弹性,由购买力平价可知,当汇率高于目标汇率水平往往伴随着货币供给增加造成本币贬值,因此θM>0,此时央行在公开市场售出美元债券兑换本币,外汇储备减少以降低本币供给,所以θGf < 0。当θGf→0时表示央行对外汇市场干预程度较高,更侧重“稳汇率”的汇率政策。当θGf→-∞时表示央行对外汇市场干预程度较低,并且若同时θM→+∞表示央行更加侧重“稳货币”的汇率政策。
本文“双政策双目标”的特点是将汇率政策规则作为一个独立的工具,当汇率波动幅度较大或者基础货币供给波动偏离较高时,央行会采取逆风式外汇干预政策。结合式(46)(47)并参考Neumann and Manfred(1984), Bene et al.(2012)的汇率政策模型,建立如下央行汇率政策规则:
| $ {e_t} = \left( {1 - {\rho _e}} \right)\bar e + {\rho _e}{e_{t - 1}} + \left( {1 - {\rho _e}} \right)\left[ {{\theta _M}\left( {{M_t} - \bar M} \right) + {\theta _{Gf}}\left( {{B_{Gf,t}} - {{\bar B}_{Gf}}} \right)} \right] $ | (48) |
由支出法总产出可表示为:
| $ {Y_t} = {C_t} + {I_{D,t}} + {I_{F,t}} + N{X_t} $ | (49) |
根据收入法等于支出法,总产出可表示为:
| $ {Y_t} = {W_{D,t}}{L_{D,t}} + {W_{F,t}}{L_{F,t}} - {\Theta _{B,t}}\left( {{B_{H,t}} + {e_t}{B_{Hf,t}}} \right) - {\Theta _{L,t}} - {\Theta _{M,t}} $ | (50) |
设定本国净出口为:
| $ N{X_t} = E{X_t} - {q_t}{I_{Df,t}} $ | (51) |
本国经常账户余额为净出口与外币债券利息之和:
| $ C{A_t} - C{A_{t - 1}} = N{X_t} + {e_t}\left[ {{B_{Hf,t - 1}}\left( {{R_{Hf,t - 1}} - 1} \right) + {B_{Cf,t - 1}}\left( {{R_F} - 1} \right)} \right] $ | (52) |
我们假设国外进口需求与本国出口实际价格成反比,与国外总需求成正比,因此设定出口满足下式:
| $ E{X_t} = {\left( {\frac{{{P_{d,t}}}}{{{e_t}{P_{f,t}}}}} \right)^{ - \theta }}F{D_t} $ | (53) |
其中Pd, t为国内最终品价格,Pf, t为国外最终品价格,设
本文假设涉及外国变量均为外生变量,均服从如下外生平稳过程:
| $ \left( {\begin{array}{*{20}{l}} {\ln F{D_t}}\\ {\ln {Q_{Df,t}}}\\ {\ln {R_{Hf,t}}}\\ {\ln {R_{F,t}}} \end{array}} \right) = \left( {\begin{array}{*{20}{l}} {1 - {\rho _{FD}}{\rho _{FD}}1}\\ {1 - {\rho _{{Q_{Df}}}}{\rho _{{Q_{Df}}}}1}\\ {1 - {\rho _{Hf}}{\rho _{Hf}}1}\\ {1 - {\rho _F}{\rho _F}1} \end{array}} \right)\left( {\begin{array}{*{20}{l}} {\ln \overline {FD} }&{\ln {{\bar Q}_{Df}}}&{\ln {{\bar {\rm{R}}}_{Hf}}}&{\ln {{\bar {\rm{R}}}_F}}\\ {\ln F{D_{t - 1}}}&{\ln {Q_{Df,t - 1}}}&{\ln {{\rm{R}}_{Hf,t - 1}}}&{\ln {{\rm{R}}_{F,t - 1}}}\\ {{\varepsilon _{FD}}}&{{\varepsilon _{{Q_f}}}}&{{\varepsilon _{Hf}}}&{{\varepsilon _F}} \end{array}} \right) $ | (54①) |
① 全球新冠疫情发生以来,多国央行降低利率以刺激经济,对于外国债券利率和外国央行基准利率的外生冲击,限于篇幅我们将在后续研究中继续探讨。
四、脉冲响应与政策分析 (一) 参数校准我国2007-2019年国债3个月到期年化收益率均值为2.83%,本文将贴现因子(β)校准为0.993,参考王彬(2015)将消费习惯参数(b)校准为0.5,参考Chari et al.(2000)将家庭效用函数中货币余额权重参数(ψM)校准为0.06,根据稳态计算劳动权重参数(ψL)为3.46,参考康立、龚六堂(2014)劳动工资弹性的倒数(η)校准为1.5,参考Chang et al.(2015)将家庭投资组合调整成本参数(ΩB)校准为0.6。参考Kitano(2011)将银行中间业务和信贷业务运营成本参数分别校准为0.001和0.01,价格调整成本校准为Ωπ=31.76②。参考孙俊、于津平(2014)的研究,将中间产品替代弹性参数(εP)校准为11,代表中间品厂商的成本加成率为10%,资本折旧率校准为0.025,代表年折旧率为10%,自中国加入世贸组织以来,我国出口贸易依存度均值约为0.25,因此本文将(γ)校准为0.75,根据Cook & Devereux(2006)对亚洲国家的研究,贸易部门和非贸易部门的资本份额分别校准为0.7和0.3。参考彭红枫等(2018)将异质性中间品厂商本国投资权重(ρ)校准为0.74;参考Gertler et al.(2007)和张勇(2015)将出口需求汇率弹性(θ)校准为1。
② 参考Chang(2015)的方法校准参数(ΩB)。在Calvo(1983)价格合同中,当β=0.993时,菲利普斯曲线斜率为(1-βαP)(1-αP)/αP,假设价格不能调整的周期为一年,则有1/(1-αP)=4,αP=0.75,因此菲利普斯曲线斜率为0.085,由于本文方程(32)对数线性化后菲利普斯曲线斜率为κP=(Ωπ/εp)(1-b)C/YD, t=0.085,由于我国2002-2018年消费占GDP均值为53%,εp=11、b=0.5则有Ωπ=31.18。
对于外国需求冲击参数(ρFD)的校准,我们基于中国2002年第1季度-2020年第2季度出口数据,首先进行季节调节然后通过HP滤波得到波动趋势后进行一阶自回归,外国需求冲击参数最终近似为0.81。对于外国投资实际价格冲击(ρQDf)的校准,我们基于2006年6月-2020年3月国际大宗商品价格指数月度数据,通过HP滤波得到波动趋势后进行一阶自回归,外国投资实际价格冲击参数最终近似为0.95。对于国外央行利率冲击参数(ρF)的校准,基于2002-2019年美国联邦基金利率季度数据进行一阶自回归,冲击参数近似为0.98。对于国外债券利率冲击参数(ρHf),基于2002-2019年美国三月期国债收益率均值进行回归校准,冲击参数近似为0.98,所有外部冲击随机项标准差设定为0.01。参考王曦等(2017)将货币政策泰勒规则中利率持续性参数(ρR)、通货膨胀缺口(φπ)和产出缺口(φY)分别校准为0.32、1.46和0.3。汇率政策规则中汇率持续性参数(ρe)根据人民币汇率一阶自回归近似为0.51,汇率波动对货币供给弹性(θm)和外汇储备变化弹性(θGf)的校准,我们采用2002-2019年我国外汇储备、美元兑人民币汇率和广义货币供应量(M2)月度数据测算,将货币供给弹性近似为0.05,外汇储备变化弹性近似为-0.11,数据来自万得数据库。
| 表 1 基准模型主要参数校准 |
1.利率政策目标
图 1展示了不同利率政策外国需求负向冲击下的脉冲响应,在基准模型中可以看到外国需求的负向冲击使得我国出口降低,对经常账户产出大约10期的负向冲击,由于出口直接影响央行资产负债表中的外汇占款,出口贸易放缓导致央行外汇占款进一步萎缩,外汇储备进而下降,同样大约在10期回归稳态与经常账户在时间上保持一致,当出口额下降时,央行与企业通过换汇使央行外汇占款降低,从而导致国内流动性对国内流动性产生影响,国内货币供应量相应下降。如图 1所示外汇储备来源的降低同时降低了货币余额,在外国需求的负向冲击下净出口降低,本来会降低外汇市场美元供给造成人民币贬值进而造成人民币名义汇率的上升,但是在“逆风干预”的汇率政策规则下,可以看到名义汇率的反应为小幅升值后再进入贬值区间,可以看到逆风干预的汇率政策会降低人民币汇率波动,名义汇率、外汇储备和货币余额都表现出了较为平稳的驼峰状走势。在家庭效用函数作用下,货币余额效用的降低,会使得家庭增加消费进而产生需求拉动型的通货膨胀,同样在家庭最优货币需求函数中货币余额的降低会使得通货膨胀上升,可以看到面对外国需求负向冲击,经济状态为维持大约40期的“滞胀”,其短期影响表现为通货膨胀会降低家庭消费需求,进而导致经济产量下降,降低企业劳动供给需求导致失业率上升,高失业率最终导致国民收入下降。整个经济呈现衰退的趋势。
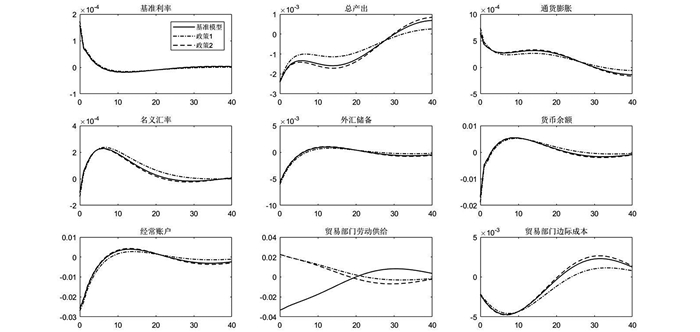
|
图 1 不同利率政策目标下外国需求负向冲击脉冲响应 注:政策1表示产出缺口系数由基准模型0.3上升至0.35,政策2表示通胀缺口系数由基准模型1.46上升至1.51。纵轴表示百分比,横轴为季度时间,下同。 |
在通货膨胀上升总产出下降的情况下,央行泰勒规则利率政策使得基准模型利率上升,表明在外国需求冲击下央行表现出“防通胀”的政策偏好,同时在资本账户管制的作用下,非抛补利率平价发生扭曲,使得利率的波动也显著降低,在第10期回归稳态。最后可以看到外国需求负向冲击使得贸易部门劳动供给下降,劳动供给的下降使得贸易部门边际成本降低。对比基准模型,政策1表示较大的产出缺口系数,表示央行以“保增长”为主的利率政策转变,政策2表示较大的通胀缺口系数,表示央行以“防通胀”为主的利率政策转变,将两种利率政策与基准模型对比,可以看出“保增长”的政策1偏好,降低了外国需求冲击对产出的负向冲击,但对于通货膨胀的冲击略微升高,不论是政策1还是政策2均有利于贸易部门就业率的提高,并且“保增长”的政策对于外贸部门的刺激效果更好。因此,央行“保增长”的政策1偏好要优于政策2和基准模型,能够缓释外国需求对经济波动冲击。
图 2显示了外国投资实际价格成本负向冲击,与外国需求冲击不同,外国投资实际价格成本是一种供给冲击,从模型结构来看外国投资实际价格下降,能够降低国内非贸易部门的成本,增加对于非贸易部门劳动供给的需求拉动就业,可以看出其对总产出产生正向冲击,不难猜测与外国需求冲击相反,外国投资负向冲击使得国内贸易部门成本降低,使得最终消费品价格下跌引起通货膨胀的下降,总体而言,由全球疫情冲击造成的外国投资实际价格下降,会刺激国内消费需求,中国作为国际大宗商品净进口国会对我国经济产生正面影响,有利于我国经济恢复。另一方面,相比较外国需求冲击,外国供给冲击对于名义汇率、外汇储备和货币余额的冲击更强,回到稳态的时间更加持久,大约在40期回到稳态,对于总产出和通胀的影响也大于外国需求冲击,在外国投资实际价格成本供给负向冲击下,进口企业需要的外汇减少,造成外汇储备和货币余额的升高,名义汇率和货币余额的同向变动,在基准模型中央行表现出“稳货币”的汇率政策偏好,由式(24)外国投资实际价格成本与实际汇率的关系可知,外国投资实际价格成本负向冲击会使得实际汇率出现较大幅度的升高进而导致名义汇率升高,这在新冠疫情蔓延至全球以来国际大宗商品价格和人民币汇率走势得到了验证(如图 3)。对比基准模型,可以发现政策1在降低外国投资实际价格成本负向冲击的作用仍然优于政策2,在对总产出正向冲击程度相同的情况下,政策1引起的各经济变量变动更小。
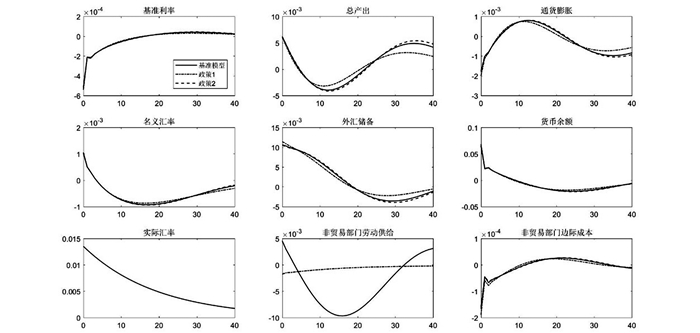
|
图 2 不同利率政策目标下外国投资实际价格成本负向冲击脉冲响应 注:政策1表示产出缺口系数由基准模型0.3上升至0.35,政策2表示通胀缺口系数由基准模型1.46上升至1.51。 |
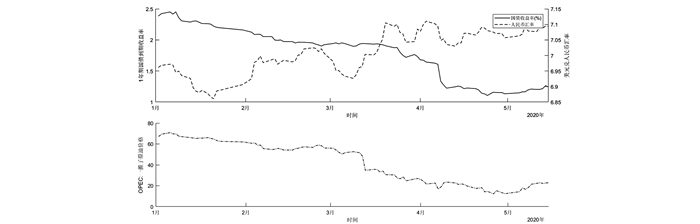
|
图 3 全球新冠疫情冲击下原油价格、我国国债和人民币汇率走势 注:数据来源于Wind数据库。 |
2.汇率政策目标
图 4显示了不同汇率政策目标下外国需求负向冲击脉冲响应。与利率政策相比,汇率政策的调整对于基准利率与名义汇率的影响更大,政策3表示“稳汇率”的央行汇率政策偏好,政策4表示“稳货币”的央行汇率政策偏好,可以明显看到政策3下名义汇率的波动要显著低于基准模型与政策4,对货币余额的负向冲击也较小。同时相比于政策4和基准模型,政策3会降低外国需求对基础利率的正向冲击,这是由于外汇储备弹性降低,使得央行表现出“稳汇率”的政策偏好,同时在非抛补利率平价扭曲的情况下,造成国内资本外流面临更高的成本,减少了短期资本外流,降低了国内资金压力,从而降低了对利率的冲击,因此政策3对于利率的正向冲击要低于政策4和基准模型,进而降低了对于总产出的负向冲击和对通货膨胀的正向冲击,从对经济波动的影响考虑,政策3优于政策4和基准模型。
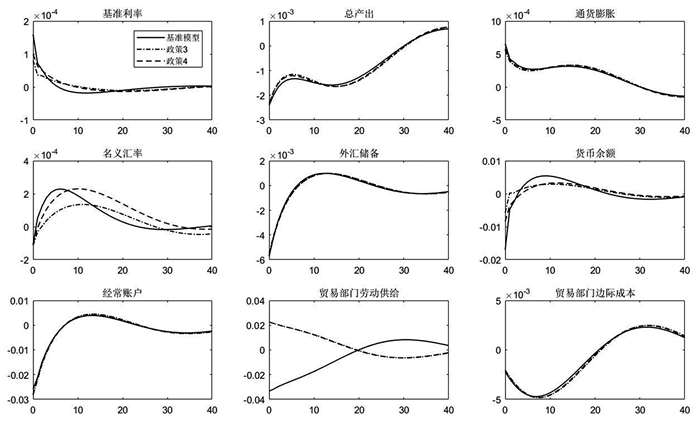
|
图 4 汇率政策目标下外国需求负向冲击脉冲响应 注:政策3表示外汇储备弹性系数由基准模型-0.11的提高至-0.01,政策4表示货币供给弹性系数由基准模型0.05提高至0.1。 |
从图 5可以看出,在外国投资实际价格成本负向冲击下,不同于利率政策、汇率政策目标的差异对于名义利率的影响较为显著,“稳汇率”的政策3大幅降低了外国投资对名义汇率的波动程度,对比基准模型,政策3对于基准利率的冲击更小,对于产出和通货膨胀的影响能够达到基准模型的程度,这对于央行而言是有利的,降低了刺激经济的成本同样能够达到预期的效果。可以看到,相比于利率政策1和2,汇率政策3和4与基准模型在面对外国投资实际价格负向成本冲击差异明显,原因仍然在于非抛补利率平价扭曲,降低了资本外流,导致国内资金流动性充足,进而缓解了利率政策压力,而“稳汇率”的政策3显然优于“稳货币”的政策4,其对基准利率、外汇储备甚至是货币余额的冲击更小。
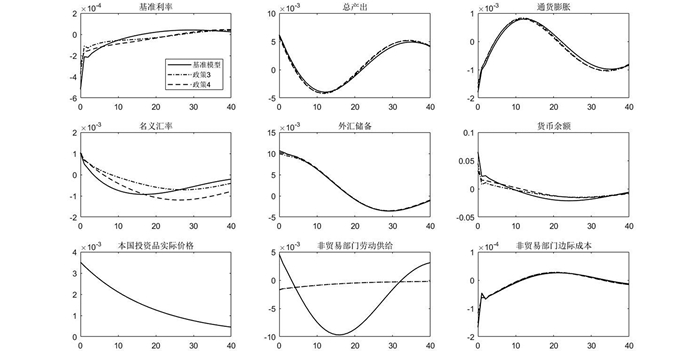
|
图 5 汇率政策目标下外国投资实际价格成本负向冲击脉冲响应 注:政策3表示外汇储备弹性系数由基准模型-0.11的提高至-0.01,政策4表示货币供给弹性系数由基准模型0.05提高至0.1。 |
本部分通过设定不同总产出缺口系数和通货膨胀缺口系数,来模拟不同利率政策偏好下带来的家庭动态福利变化,以及设定不同外汇储备弹性和货币供给弹性,来模拟不同汇率政策偏好下带来的家庭动态福利变化,以研究央行的最优货币政策组合。
首先我们参考Gal¡(2015)利用泰勒二阶展开,以即期效用与稳态效用的偏离度量家庭福利损失,可表示为:
| $ \begin{array}{l} {U_t} - \bar U \approx {U_c}\bar C\left( {\frac{{{C_t} - \bar C}}{{\bar C}}} \right) + \frac{1}{2}{U_{cc}}{{\bar C}^2}{\left( {\frac{{{C_t} - \bar C}}{{\bar C}}} \right)^2} + {U_L}\bar L\left( {\frac{{{L_t} - \bar L}}{{\bar L}}} \right) + \frac{1}{2}{U_{LL}}{{\bar L}^2}{\left( {\frac{{{L_t} - \bar L}}{{\bar L}}} \right)^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + {U_m}\bar m\left( {\frac{{{m_{t + 1}} - \bar m}}{{\bar m}}} \right) + \frac{1}{2}{U_{mm}}{{\bar m}^2}{\left( {\frac{{{m_t} - \bar m}}{{\bar m}}} \right)^2} \end{array} $ | (56) |
这里设
| $ {U_t} - \bar U \approx {U_c}\bar C\left[ {{{\hat C}_t} + \frac{1}{2}\left( {1 + \frac{{{U_{cc}}}}{{{U_c}}}\bar C} \right)\hat C_t^2} \right] + {U_L}\bar L\left[ {{{\hat L}_t} + \frac{1}{2}\left( {1 + \frac{{{U_{LL}}}}{{{U_L}}}\bar L} \right)\hat L_t^2} \right] + \\ {U_m}\bar m\left[ {{{\hat m}_t} + \frac{1}{2}\left( {1 + \frac{{{U_{mm}}}}{{{U_m}}}\bar m} \right)\hat m_t^2} \right] $ | (57) |
对无穷期终生效用加总并取期望,可得家庭福利水平相对稳态时的变化,如下式:
| $ {{\rm{E}}_0}\sum\limits_{t = 0}^\infty {{\beta ^t}} \left( {{U_t} - \bar U} \right) \approx \frac{1}{{1 - \beta }}\left\{ {\begin{array}{*{20}{l}} {{U_c}\bar C \times \frac{1}{2}\left( {1 + \frac{{{U_{cc}}}}{{{U_c}}}\bar C} \right){\mathop{\rm Var}\nolimits} \left( {{{\hat C}_t}} \right) + {U_L}\bar L \times \frac{1}{2}\left( {1 + \frac{{{U_{LL}}}}{{{U_L}}}\bar L} \right)Var\left( {{{\hat L}_t}} \right)}\\ { + {U_m}\bar m \times \frac{1}{2}\left( {1 + \frac{{{U_{mm}}}}{{{U_m}}}\bar m} \right)Var\left( {{{\hat m}_t}} \right)} \end{array}} \right\} $ | (58) |
图 6显示了泰勒规则下货币政策组合选择,对应于图 1和图 2中的脉冲响应分析,可以明显看到政策1路径要优于政策2,在利率政策变动区间,提高产出缺口系数并降低通胀缺口系数的“保增长”政策1路径会经历福利增益,而提高通胀缺口系数并降低产出缺口系数的“防通胀”政策2会经历福利损失,从模型角度分析其原因在于“防通胀”的政策2,抑制了本币贬值,进一步削弱出口竞争力,造成贸易部门产出的降低,使得家庭消费的降低超过劳动供给的减少,引起家庭总体福利水平下降,适宜的通胀水平有助于家庭福利的提高,因此从利率政策福利角度分析,“保增长”的政策1的社会效用大于“防通胀”的政策2。
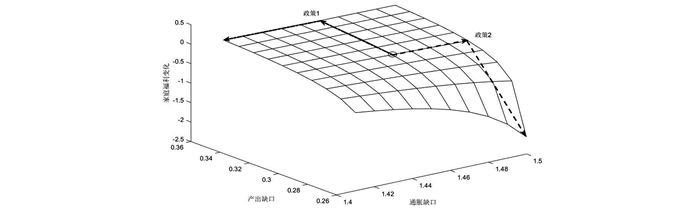
|
图 6 不同货币政策偏好下家庭福利变化 注:o点表示稳态时家庭福利变化值, X轴和Y轴分别对应产出缺口与通胀缺口系数。 |
政策3表示稳汇率政策,表现为加强对于外汇市场的干预,使得人民币汇率稳定后,再逐步适度扩大人民币汇率浮动区间,逐步调整由外汇储备变动引起的基础货币供给变动,制定以稳定货币供给为偏好的政策,政策4表示首先实现“稳货币”的汇率政策,具体表现为首先央行不断减少外汇市场干预,适度扩大人民币汇率浮动区间,再考虑外汇储备变动对于基础货币供给变动的影响,从图 7可以看出“稳汇率”的政策3能够达到福利最高水平,而“稳货币”的政策4对于家庭福利影响较小,“稳汇率”的政策3之所以能够使得家庭福利水平达到较高的水平,在于外汇储备弹性的提高,使得汇率波动大幅降低,从而降低了汇率政策规则中货币余额与汇率的联动性,基础货币供给的增加使得家庭持有更多的货币余额,以此来提高家庭福利水平。
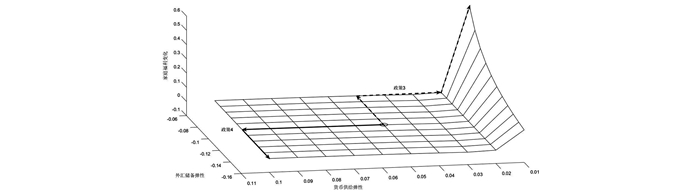
|
图 7 不同汇率政策偏好下家庭福利变化 注:o点表示稳态时家庭福利变化值,X轴和Y轴分别对应外汇储备弹性与货币供给弹性。 |
在全球疫情冲击蔓延下,未来我国将面临外国需求与供给降低的双重冲击,本文通过构造包含非贸易部门和贸易部门的开放经济DSGE模型,探讨了在两种冲击下我国主要经济变量的波动,同时利用二阶泰勒近似方法对家庭效用进行福利度量,对利率与汇率政策偏好引起的家庭福利变化进行对比分析。研究发现:“保增长”的利率政策和“稳汇率”的汇率政策,能够更好的缓释新冠疫情带来的外部冲击,在“保增长”的利率政策下家庭福利水平高于“防通胀”的利率政策,而在“稳汇率”的汇率政策下家庭福利水平高于“稳货币”的汇率政策。在外国需求和供给双重冲击下,我国央行“双政策双目标”的最优选择是制定以“保增长”为主的利率政策和以“稳汇率”为主的汇率政策。
基于上述结论,本文提出以下政策建议:
第一,在新冠疫情冲击下外国需求下降,央行以外汇占款增量增加的基础货币供给将逐渐减少,“稳汇率”的政策应降低对外汇储备的依赖,逐步扩大人民币汇率双向浮动区间,通过多种传统汇率政策调节工具增强央行调控主动性,不断通过鼓励“藏汇于民”、加强外汇市场预期管理等非常规政策工具协调管理货币供给流动性。第二,增强货币政策有效性与独立性。通过将货币发行机制由“以人民币汇率为锚”的被动型调控转向“以债券利率为锚”的主动型调控转变,逐步由数量型转变到价格型货币政策,切实降低实体经济融资成本,以增强金融服务实体经济的能力。货币政策要更加灵活适度,针对受疫情严重影响的部门制定差异化信贷支持政策,对于支持小微企业复工复产的民营银行制定差异化的存款准备金率等特殊支持政策,通过“精准发力”实现“保增长”效力。
| [] |
陈师、郑欢、郭丽丽, 2015, “中国货币政策规则、最优单一规则与宏观效应”, 《统计研究》, 第 1 期, 第 41-51 页。DOI:10.3969/j.issn.1002-4565.2015.01.007 |
| [] |
胡滨、范云朋、郑联盛, 2020, “'新冠疫情'、经济冲击与政府干预”, 《数量经济技术经济研究》, 第 9 期, 第 42-61 页。 |
| [] |
胡小文, 2019, “国际经济冲击与我国汇率制度选择:基于双目标双工具政策理论的研究”, 《南开经济研究》, 第 6 期, 第 37-63 页。 |
| [] |
金中夏、洪浩, 2015, “国际货币环境下利率政策与汇率政策的协调”, 《经济研究》, 第 5 期, 第 35-47 页。 |
| [] |
刘瑶、陈珊珊, 2020, “新冠疫情对全球供应链的影响及中国应对——基于供给侧中断与需求侧疲软双重叠加的视角”, 《国际贸易》, 第 6 期, 第 53-62 页。 |
| [] |
郭栋, 2020, “灾难风险经济冲击效应与货币政策机制选择研究——基于DSGE模型的新冠肺炎疫情经济模拟”, 《国际金融研究》, 第 8 期, 第 24-34 页。 |
| [] |
康立、龚六堂, 2014, “金融摩擦、银行净资产与国际经济危机传导——基于多部门DSGE模型分析”, 《经济研究》, 第 5 期, 第 147-159 页。 |
| [] |
梅冬州、龚六堂, 2011, “新兴市场经济国家的汇率制度选择”, 《经济研究》, 第 11 期, 第 73-88 页。 |
| [] |
彭红枫、肖祖沔、祝小全, 2018, “汇率市场化与资本账户开放的路径选择”, 《世界经济》, 第 8 期, 第 26-50 页。 |
| [] |
汤铎铎、刘学良、倪红福、杨耀武、黄群慧、张晓晶, 2020, “全球经济大变局、中国潜在增长率与后疫情时期高质量发展”, 《经济研究》, 第 8 期, 第 4-23 页。 |
| [] |
王彬, 2015, “人民币汇率均衡、失衡与贸易顺差调整”, 《经济学(季刊)》, 第 4 期, 第 1277-1302 页。 |
| [] |
王曦、汪玲、彭玉磊、宋晓飞, 2017, “中国货币政策规则的比较分析——基于DSGE模型的三规则视角”, 《经济研究》, 第 9 期, 第 24-38 页。 |
| [] |
伍戈、刘琨, 2015, “探寻中国货币政策的规则体系:多目标与多工具”, 《国际金融研究》, 第 1 期, 第 15-24 页。 |
| [] |
杨子晖、陈雨恬、张平淼, 2020, “重大突发公共事件下的宏观经济冲击、金融风险传导与治理应对”, 《管理世界》, 第 5 期, 第 13-35+7 页。 |
| [] |
张勇, 2015, “热钱流入、外汇冲销与汇率干预——基于资本管制和央行资产负债表的DSGE分析”, 《经济研究》, 第 7 期, 第 116-130 页。 |
| [] |
周梅芳、刘宇、张金珠、崔琦, 2020, “新冠肺炎疫情的宏观经济效应及其应对政策有效性研究”, 《数量经济技术经济研究》, 第 8 期, 第 24-41 页。 |
| [] |
朱孟楠、曹春玉, 2018, “加息周期、汇率安排与储备需求”, 《金融研究》, 第 1 期, 第 1-17 页。 |
| [] |
Benes, Jaromir, et al, 2012, "Modeling Sterilized Interventions and Balance Sheet Effects of Monetary Policy", IMF Working Paper 13/11.
|
| [] |
Calvo G. A, 1983, "Staggered Prices in a Utility-maximizing Framework". Journal of monetary Economics, 12(3), 383–398.
|
| [] |
Chari V. V., Kehoe P. J., Mcgrattan E. R, 2000, "Sticky Price Models of the Business Cycle:Can the Contract Multiplier Solve the Persistence Problem?". Econometrica, 68(5), 1151–1179.
|
| [] |
Chang C, Liu Z., Spiegel M. M, 2015, "Capital Controls and Optimal Chinese Monetary Policy". Journal of Monetary Economics, 74, 1–15.
|
| [] |
Chutasripanich, Nuttathum and James Yetman, 2015, "Foreign Exchange Intervention: Strategies and Effectiveness", BIS Working Papers, No 499.
|
| [] |
Cook, David, Michael B. Devereux, 2006, "External Currency Pricing and the East Asian Crisis". Journal of International Economics, 69(1), 37–63.
|
| [] |
Gal'ı, Jordi, 2015, "Monetary Policy, Inflation, and the Business Cycle: An Introduction to the New Keynesian Framework and Its Applications", Princeton University Press.
|
| [] |
Gertler, Mark, Simon Gilchrist, Fabio M. Natalucci, 2007, "External Constraints on Monetary Policy and the Financial Accelerator". Journal of Money, Credit and Banking, 39(2-3), 295–330.
|
| [] |
Kitano S, 2011, "Capital Controls and Welfare". Journal of Macroeconomics, 33(4), 700–710.
|
| [] |
McKibbin, Warwick J.and Roshen Fernando, 2020, "The Global Macroeconomic Impacts of COVID-19: Seven scenario", Australian National University, Centre for Applied Macroeconomic Analysis Working Paper19/2020.
|
| [] |
Neumann, Manfred JM, 1984, "Intervention in the Mark/dollar Market:the Authorities' Reaction Function". Journal of International Money and Finance, 3(2), 223–239.
|
| [] |
Olivier Blanchard, Giovanni DellAriccia and Paolo Mauro, 2013, "Rethinking Macro Policy II: Getting Granular", IMF Staff Discussion Note, April 15.
|
| [] |
Ghosh, Atish R., Jonathan D.Ostry, Marcos Chamon, 2016, "Two Targets, Two Instruments:Monetary and Exchange Rate Policies in Emerging Market Economies". Journal of International Money and Finance, 60, 172–196.
|
| [] |
Rotemberg, Juilo. J., 1982, "Sticky Prices in the United States". Journal of Political Economy, 90(6), 1187–1211.
|
| [] |
Uribe M., Yue V. Z., 2006, "Country Spreads and Emerging Countries:Who Drives Whom?". Journal of International Economics, 69(1), 6–36.
|



