政策利率调控是现代化经济体系中最为重要的宏观调控手段之一,如果传导渠道不畅,传导过程中存在摩擦,其向最终目标的传导效率必然下降。在诸多影响政策利率传导效率的因素中,利率市场化程度至关重要,并且随着金融深化程度的加深其重要性愈发凸显。一方面,基准利率、公开市场操作利率、中期借贷便利(MLF)利率等政策利率是中央银行重要的政策工具。另一方面,我国货币政策中介目标由数量型向价格型转型并且现阶段价格型指标更加重要已经成为研究领域的共识(刘达禹等,2016;潘长春、李晓,2018;徐忠,2018),同业拆借利率、回购利率等货币市场利率则是主要的价格型指标。鉴于此,为提升政策利率传导效率和调控的有效性进而更好发挥金融支持实体经济发展的功能,我国政府部门高度重视利率市场化。党的十九大报告指出,“健全货币政策和宏观审慎政策双支柱调控框架,深化利率和汇率市场化改革”,十九届四中全会进一步强调,“建设现代中央银行制度,完善基础货币投放机制,健全基准利率和市场化利率体系”。从实践层面来看,自1996年放开同业拆借市场以来,我国利率市场化遵循“先外币、后本币,先贷款、后存款,先长期大额,后短期小额”的总体思路不断推进,现阶段已经完全放开存贷款浮动上下限管制,并且完善了贷款市场报价利率(LPR)形成机制,名义上已经完成了利率市场化。但是,实际上的利率形成机制仍然没有完全市场化,窗口指导、自律机制等对存贷款利率的隐形管制仍然存在,银行自主定价能力和权利均有待提升,货币和债券市场利率向信贷市场的传导仍然不畅,利率双轨制仍未完全解决(刘金全、石睿柯,2017;李俊江、黄潇雨,2019)。与此同时,LPR改革进一步导致了存款利率和贷款利率形成机制的不一致,存款利率仍然锚定基准利率,贷款利率锚定MLF,二者的联动性进一步下降,导致近期关于调整存款基准利率的讨论日益增多,但中国人民银行在统计数据新闻发布会等场景多次表示“存款基准利率是我国利率体系压舱石,要长期保留”,上述矛盾归根结底是不完全利率市场化的问题。那么,在我国不完全市场化的利率体系下,政策利率的传导效率如何?随着利率市场化水平的提升,其传导效率是否得到了提升?上述问题对于推进我国利率市场化改革以及理解政策利率调控效果具有理论重要性。本文将综合运用新凯恩斯动态随机一般均衡模型(DSGE)和包含随机波动的时变参数向量自回归模型(SV-TVP-VAR)进行理论模拟和实证研究,我国渐进式的利率市场化改革实践为本文的研究提供了可能,同时本文的研究也可以为未来的利率市场化改革提供理论参考和经验证据。
针对政策利率传导问题,现有文献进行了大量卓有成效的探讨,主要包括其目标体系、传导渠道、传导效率。其中,目标体系应当包括操作目标、中介目标和最终目标,操作目标是传导的第一个环节,并无太大争议。中介目标在不同国家以及不同金融发展阶段不尽相同,主要包括价格型和数量型,早期的研究可以追溯至Poole(1970),文章对宏观经济的冲击进行分类,认为数量型中介目标适用于来自商品市场的冲击,价格型中介目标适用于来自货币市场的冲击。从现阶段的发展来看,金融市场发达的国家往往采用价格型中介目标,随着我国金融市场的深化和快速发展,由数量型调控模式转向价格型并推进利率市场化是大的趋势(孙国峰,2019),这一点也已经基本成为共识。最终目标方面,传统的理论强调对产出和价格的调控,经典的泰勒规则指出了利率对产出缺口和通货膨胀率进行反应,此后的研究对其进行了拓展,认为政策利率还应当钉住汇率(邓创、石柱鲜,2011)、资产价格(徐宁等,2017)甚至是金融稳定(刘金全、毕振豫,2019;周德才等,2019)。
传导渠道方面,现有研究成果较为丰富并且仍在不断拓展。传统的传导渠道主要包括货币渠道和信用渠道,一个强调金融机构的负债端,另一个强调金融机构的资产端(盛松成、吴培新,2008)。总体来看,现有研究对传导渠道的拓展并没有跳出货币和信用渠道的范畴,可以看作是对这两个渠道的延续和细化,大体包括银行信贷渠道(Salachas et al., 2017;Ippolito et al., 2018)、资产价格渠道(Rahal,2016;Fausch and Sigonius, 2018)、汇率渠道(Dybowski et al., 2018;Kim and Lim, 2018)、影子利率渠道(Galariotis et al., 2018;Hajek and Horvath, 2018;马理、尤阳,2019)以及银行风险承担渠道(Borio and Zhu, 2008;张强、张宝,2011)。任泽平等(2019)总结了信贷、利率、资产价格、汇率、预期等五大传导渠道,分析了不同的货币宽松周期从宽货币到宽信用的传导效率。
根据上述传导渠道,现有研究重点关注了在不同渠道的传导效率,并分析了影响货币渠道以及信用渠道传导效率的因素。在国际上,银行信贷传导渠道的重要性已经被证实(Bernanke and Blinder, 1988;Kishan and Opiela, 2006),在国内以银行间接融资为主的情况下银行信贷传导渠道的重要性更加突显(李涛、刘明宇,2012),因此信贷传导渠道是否通畅直接影响传导效率。其中,大量研究指出银行业结构可以影响信贷渠道的传导效率,比如Kashyap and Stein(1997)指出,银行业的集中程度可以影响传导效率,Adams and Amel(2005)以及Olivero et al.(2011)进一步通过实证研究得出银行业集中程度较高的国家政策利率传导效率往往较低。此外,银行业准入壁垒以及竞争程度也会影响传导效率,准入壁垒越高,竞争程度越大,传导效率越低(Sellon,2002;Amidu and Wolfe, 2013)。国内研究方面,董华平、干杏娣(2015)基于银行业结构的古诺模型分析了银行贷款渠道传导效率,认为在我国竞争性的银行业结构有利于改善银行贷款渠道的传导效率。此外,随着利率市场化不断推进,利率传导渠道更加重要,有少数研究开始关注影响利率传导渠道效率的相关因素。比如,钱雪松等(2015)研究指出,我国的融资存在所有制歧视,导致利率传导效率出现所有制分化,国有企业享有资金获取的优势,而宽松的政策并不能降低民营企业融资成本,为进一步提高我国利率传导效率,需要继续深化利率市场化改革。
综合来看,现有研究虽然指出了需要通过利率市场化提升利率传导效率,但仍然未能从实证层面回答随着利率市场化水平的提升其传导效率的时变效应问题。区别于现有文献,本文的贡献主要是综合理论模拟和实证研究为利率传导效率和利率市场化分析提供了一个新的思路。文章余下的章节安排如下:第二部分构建DSGE模拟我国政策利率在理想情况下传导的基准效应,第三部分构建SV-TVP-VAR模型实证研究实际情况下利率市场化进程中传导效率的时变效应,第四部分进一步讨论利率市场化和利率传导效率问题,最后进行结论性评述。
二、我国政策利率传导基准效应的理论模拟为模拟我国政策利率传导的基准效应,本文构建了一个包含粘性价格、粘性工资设定的新凯恩斯DSGE模型。模型基本结构如下:典型家庭根据效用最大化原则决定自身消费、储蓄、持有的货币以及劳动供给;生产环节包括最终产品生产厂商和中间产品供给厂商,中间产品供给厂商面临不完全竞争环境,并租用资本和雇佣劳动力进行生产,最终产品生产厂商使用中间产品输出最终产品;中央银行通过公开市场操作影响名义利率进行调控。需要说明的是,本文在参数设定部分参考我国国情和现有国内文献的设定,保证模型基础框架更加贴近我国经济运行的实际情况,但同时文章假定传导过程不存在阻塞,利率完全市场化,上述两方面的设定保证了模型可以模拟得出我国政策利率传导的基准效应,为后续传导效率的计算奠定基础。
(一) 新凯恩斯DSGE模型构建1.家庭部门
假定经济体中存在无限存活的代表性家庭j。家庭通过消费cjt、实际货币持有mjt/pt、劳动供给ljt决策实现如下终身效用函数的最大化:
| $ \max \mathrm{E}_{0} \sum\limits_{t=0}^{\infty} \beta^{t} d_{t}\left[\log \left(c_{j t}-h c_{j t-1}\right)+v \log \left(\frac{m_{j t}}{p_{t}}\right)-\varphi_{t} \psi \frac{l_{j t}^{1+\gamma}}{1+\gamma}\right] $ |
其中,β、h、γ、dt、φt分别代表效用贴现因子、消费惯性系数、Frisch劳动供给弹性的倒数、偏好冲击、劳动供给冲击,pt代表价格水平。dt和φt分别遵循如下的AR(1)动态过程:
| $ \begin{aligned} \log d_{t} &=\rho_{d} \log d_{t-1}+\sigma_{d} \varepsilon_{d, t}, \varepsilon_{d, t} \sim N(0, 1) \\ \log \varphi_{t} &=\rho_{\varphi} \log \varphi_{t-1}+\sigma_{\varphi} \varepsilon_{\varphi, t}, \varepsilon_{\varphi, t} \sim N(0, 1) \end{aligned} $ |
家庭面临的预算约束如下:
| $ \begin{array}{c} c_{j t}+x_{j t}+\frac{m_{j t}}{p_{t}}+\frac{b_{j t+1}}{p_{t}}+\int q_{j t+1, t} a_{j t+1} d \omega_{j, t+1, t} \\ =\omega_{j t} l_{j t}+\left(r_{t} u_{j t}-\mu_{t}^{-1} a\left[u_{j t}\right]\right) k_{j t-1}+\frac{m_{j t-1}}{p_{t}}+R_{t-1} \frac{b_{j t}}{p_{t}}+a_{j t}+T_{t}+F_{t} \end{array} $ |
其中,xjt表示投资支出,bjt表示政府债券持有量,Rt表示政府债券名义收益率,ajt+1表示家庭一单位工资收入中用来投资有价证券的数量,qjt+1, t表示有价证券价格,ωjt代表实际工资,rt表示实际资本回报率,ujt表示资本使用强度,
资本存量kjt的动态演进过程如下:
| $ k_{j t}=(1-\delta) k_{j t-1}+\mu_{t}\left(1-S\left[\frac{x_{j t}}{x_{j t-1}}\right]\right) x_{j t} $ |
δ表示折旧率,S[·]表示调整成本函数,在平衡增长路径上的调整成本为0,即S[Λx]=0。投资冲击遵循如下的动态过程:
| $ \mu_{t}=\mu_{t-1} \exp \left(\Lambda_{\mu}+z_{\mu, t}\right), z_{\mu, t}=\sigma_{\mu} \varepsilon_{\mu, t}, \varepsilon_{\mu, t} \sim N(0, 1) $ |
假定每个家庭提供差异化劳动,总量劳动需求可以表示如下:
| $l_{t}^{d}=\left(\int_{0}^{1} l_{j t}^{\eta-1} d j\right)^{\frac{\eta}{\eta-1}} $ |
η表示不同劳动之间的替代弹性,家庭工资决策遵循Calvo工资粘性设定(Calvo,1983),即在每期只有1-θω比例的家庭可以决定其工资,其他家庭根据前期的通货膨胀率被动调整工资,调整的通胀滞后权重为χω∈[0, 1],劳动力市场中介的最大化问题可以表示如下:
| $ \max\limits_{l_{j t}} \omega_{t} l_{t}^{d}-\int_{0}^{1} \omega_{j t} l_{j t} d j $ |
在上述设定下,家庭通过选择cjt、bjt、ujt、kjt、xjt、ωjt、ljt、ajt+1最大化效用函数,令λjt和Qjt分别表示预算约束和资本演化方程的拉格朗日乘子,πt表示通货膨胀率,并以
| $ \begin{array}{l} d_{t}\left(c_{t}-h c_{t-1}\right)^{-1}-h \beta \mathrm{E}_{t} d_{t+1}\left(c_{t+1}-h c_{t}\right)^{-1}=\lambda_{t} \end{array} $ | (1) |
| $ \beta \mathrm{E}_{t}\left(\lambda_{t+1} \frac{R_{t}}{\pi_{t+1}}\right)=\lambda_{t} $ | (2) |
| $r_{t}=\mu_{t}^{-1} a'\left[u_{t}\right] $ | (3) |
| $ q_{t}=\beta \mathrm{E}_{t}\left(\frac{\lambda_{t+1}}{\lambda_{t}}\left((1-\delta) q_{t+1}+r_{t+1} u_{t+1}-\mu_{t+1}^{-1} a\left[u_{t+1}\right]\right)\right) $ | (4) |
| $ q_{t} \mu_{t}\left(1-S\left[\frac{x_{t}}{x_{t-1}}\right]-S^{\prime}\left[\frac{x_{t}}{x_{t-1}}\right] \frac{x_{t}}{x_{t-1}}\right)+\beta \mathrm{E}_{t} q_{t+1} \mu_{i+1} \frac{\lambda_{t+1}}{\lambda_{t}} S^{\prime}\left[\frac{x_{t+1}}{x_{t}}\right]\left(\frac{x_{t+1}}{x_{t}}\right)^{2}=1 $ | (5) |
| $ f_{t}=\frac{\eta-1}{\eta}\left(\omega_{t}^{*}\right)^{1-\eta} \lambda_{t} \omega_{t}^{\eta} l_{t}^{d}+\beta \theta_{\omega} \mathrm{E}_{t}\left(\frac{\pi_{t}^{\gamma \omega}}{\pi_{t+1}}\right)^{1-\eta}\left(\frac{\omega_{t+1}^{*}}{\omega_{t}^{*}}\right)^{\eta-1} f_{t+1} $ | (6) |
| $ f_{t}=\psi d_{t} \varphi_{t}\left(\pi_{t}^{* \omega}\right)^{-\eta(1+\gamma)}\left(l_{t}^{d}\right)^{1+\gamma}+\beta \theta_{\omega} \mathrm{E}_{t}\left(\frac{\pi_{t}^{\chi \omega}}{\pi_{t+1}}\right)^{-\eta(1+\gamma)}\left(\frac{\omega_{t+1}^{*}}{\omega_{t}^{*}}\right)^{\eta(1+\gamma)} f_{t+1} $ | (7) |
式(1)-(5)分别表示家庭决策最优化的消费一阶条件、欧拉方程、资本利用率一阶条件、资本一阶条件、投资一阶条件,式(6)和式(7)表示工资决定方程。
2.最终产品生产厂商
假定最终产品生产厂商使用中间产品生产一种最终产品,生产函数设定为如下CES形式:
| $ y_{t}^{d}=\left(\int_{0}^{1} y_{i t}^{\frac{\varepsilon-1}{\varepsilon}} d i\right)^{\frac{\varepsilon}{\varepsilon^{-1}}} $ |
ε表示不同中间产品的替代弹性,最终产品生产厂商的最大化问题可以表示为:
| $ \max\limits_{y_{j t}} p_{t} y_{t}^{d}-\int_{0}^{1} p_{j t} y_{j t} d i $ |
3.中间产品生产厂商
假定存在多个中间产品生产厂商,每个厂商面临的生产函数如下:
| $ y_{i t}=A_{t} k_{i t-1}^{\alpha}\left(l_{i t}^{d}\right)^{1-\alpha}-\phi z_{t} $ |
kit-1表示企业租赁的资本,litd表示企业从劳动中介市场雇佣的劳动,At表示生产技术水平,ϕ表示企业固定生产成本参数,
| $ A_{t}=A_{t-1} \exp \left(\Lambda_{A}+z_{A, t}\right), z_{A, t}=\sigma_{A} \varepsilon_{A, t}, \varepsilon_{A, t} \sim N(0, 1) $ |
中间产品生产厂商的最优化问题包括两个方面,即工资和资本回报率既定情况下的成本最小化和通过价格调整的利润折现值最大化。以mc表示厂商的边际成本,企业价格决策同样遵循Calvo价格粘性设定,在每期只有1-θp比例的企业可以决定其价格,其他企业根据前期的通货膨胀率被动调整价格,调整的通胀滞后权重为χ。两个最优化问题分别表示为:
| $ \begin{array}{l} \min\limits_{l_{d}^{d}, k_{i t-1}} \omega_{t} l_{i t}^{d}+r_{t} k_{i t-1} \\ \max\limits_{p_{i t}} \mathrm{E}_{t} \sum\limits_{\tau=0}^{\infty}\left(\beta \theta_{p}\right)^{\tau} \frac{\lambda_{t+\tau}}{\lambda_{t}}\left(\left(\prod\limits_{s=1}^{\tau} \pi_{t+s-1}^{\chi} \frac{p_{i t}}{p_{t+\tau}}-m c_{t+\tau}\right) y_{i t+\tau}\right) \end{array} $ |
求解可得如下均衡方程:
| $ g_{t}^{1}=\lambda_{t} m c_{t} y_{t}^{d}+\beta \theta_{p} \mathrm{E}_{t}\left(\frac{\pi_{t}^{\chi}}{\pi_{t+1}}\right)^{-\varepsilon} g_{t+1}^{1} $ | (8) |
| $ g_{t}^{2}=\lambda_{t} \pi_{t}^{*} y_{t}^{d}+\beta \theta_{p} \mathrm{E}_{t}\left(\frac{\pi_{t}^{\chi}}{\pi_{t+1}}\right)^{1-\varepsilon}\left(\frac{\pi_{t}^{*}}{\pi_{t+1}^{*}}\right) g_{t+1}^{2} $ | (9) |
| $\varepsilon g_{t}^{1}=(\varepsilon-1) g_{t}^{2} $ | (10) |
| $ \frac{u_{t} k_{t-1}}{l_{t}^{d}}=\frac{\alpha}{1-\alpha} \frac{\omega_{t}}{r_{t}} $ | (11) |
| $ m c_{t}=\left(\frac{1}{1-\alpha}\right)^{1-\alpha}\left(\frac{1}{\alpha}\right)^{\alpha} \frac{\omega_{t}^{1-\alpha} r_{t}^{\alpha}}{A_{t}} $ | (12) |
| $1=\theta_{\omega}\left(\frac{\pi_{t-1}^{\chi_{\omega}}}{\pi_{t}}\right)^{1-\eta}\left(\frac{\omega_{t-1}}{\omega_{t}}\right)^{1-\eta}+\left(1-\theta_{\omega}\right)\left(\pi_{t}^{* \omega}\right)^{1-\eta} $ | (13) |
| $ 1=\theta_{p}\left(\frac{\pi_{t-1}^{\chi}}{\pi_{t}}\right)^{1-\varepsilon}+\left(1-\theta_{p}\right)\left(\pi_{t}^{*}\right)^{1-\varepsilon} $ | (14) |
式(8)-(10)为企业定价方程,式(11)和式(12)为最优要素投入方程,式(13)和式(14)分别代表工资和价格演进方程。
4.中央银行
中央银行通过公开市场操作影响名义利率Rt,遵循经典的泰勒规则(Taylor rule)进行宏观调控:
| $ \frac{R_{t}}{R}=\left(\frac{R_{t-1}}{R}\right)^{\gamma_{R}}\left(\left(\frac{\pi_{t}}{\pi}\right)^{\gamma_{\pi}}\left(\frac{\frac{y_{t}^{d}}{y_{t-1}^{d}}}{\Lambda_{y^{d}}}\right)^{\gamma_{y}}\right)^{1-\gamma_{R}} \exp \left(m_{t}\right) $ | (15) |
其中,R代表稳态名义利率,Λyd代表稳态经济增长率,π代表目标通货膨胀率,γR、γπ、γy分别代表利率平滑系数、通胀反应系数、产出反应系数,mt代表政策利率冲击,并且
5.市场出清和冲击设定
市场出清条件为:
| $ y_{t}^{d}=\frac{A_{t}\left(u_{t} k_{t-1}\right)^{\alpha}\left(l_{t}^{d}\right)^{1-\alpha}-\varphi z_{t}}{v_{t}^{p}} $ | (16) |
| $ y_{t}^{d}=c_{t}+x_{t}+\mu_{t}^{-1} a\left[u_{t}\right] k_{t-1} $ | (17) |
| $ l_{t}=v_{t}^{\omega} l_{t}^{d} $ | (18) |
| $ v_{t}^{p}=\theta_{p}\left(\frac{\pi_{t-1}^{\chi}}{\pi_{t}}\right)^{-\varepsilon} v_{t-1}^{p}+\left(1-\theta_{p}\right) \pi_{t}^{*-\varepsilon} $ | (19) |
| $ v_{t}^{\omega}=\theta_{\omega}\left(\frac{\omega_{t-1}}{\omega_{t}} \frac{\pi_{t-1}^{\chi_{\omega}}}{\pi_{t}}\right)^{-\eta} v_{t-1}^{\omega}+\left(1-\theta_{\omega}\right) \pi_{t}^{*-\eta} $ | (20) |
| $ k_{t}-(1-\delta) k_{t-1}-\mu_{t}\left(1-S\left[\frac{x_{t}}{x_{t-1}}\right]\right) x_{t}=0 $ | (21) |
其中,式(16)和式(17)为宏观经济市场出清条件,式(18)-(20)分别代表劳动、价格、工资条件,式(21)为加总的资本演进方程。式(1)-(21)以及偏好冲击、劳动供给冲击、投资冲击、生产技术冲击、政策利率冲击共同构成了模型的方程系统。
(二) 模型参数设定本文模型参数设定的主要思路是参考国内的经典文献,使其更加符合中国经济发展的实际情况,其中对于常规的确定性参数,我们直接对其稳态值进行校准,对于不确定性参数和动态参数我们使用贝叶斯方法进行估计,先验分布的设定也主要是参考国内的现有经典文献。表 1给出了确定性参数的校准结果和参考文献,所有参数均是DSGE模型常用的参数,并且在长期的研究过程中针对中国实际情况的参数取值已经比较固定,因此我们直接赋值。表 2设定了不确定性和动态参数的先验分布,包括Beta、Gamma、Normal、Inv.Gamma等常用分布。其中不确定性参数的分布设定主要参考仝冰(2017)的研究,动态参数包括各类冲击的一阶自回归系数和标准差,根据王国静、田国强(2014)的思路,将处于0和1之间的一阶自回归系数设定为Beta(0.5, 0.2)分布, 将标准差设定为Inv.Gamma(0.01, 2)分布。
| 表 1 确定性参数的校准结果 |
| 表 2 不确定性和动态参数的先验分布设定 |
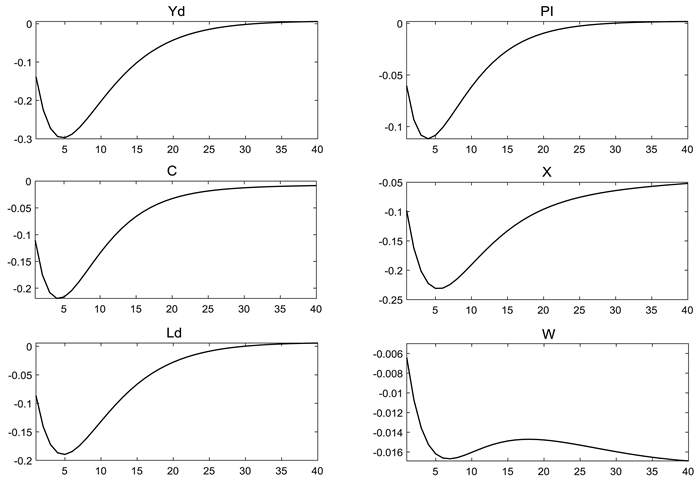
参数设定完成后,本文根据参数校准和贝叶斯估计的结果,运用脉冲响应函数模拟政策利率调控对实际产出(Yd)、通货膨胀率(PI)、消费(C)、投资(X)、劳动力需求(Ld)、工资水平(W)等重要宏观经济变量影响的基准效应。根据近期国家统计局对宏观经济数据的解读,评价中国经济发展水平既要看经济增长,同时也要看通货膨胀率,居民收入和消费以及劳动力市场情况,因此本文选择的变量具有代表性。
图 1展示了政策利率传导的基准效应结果。当政策利率发生一标准差大小的冲击后,所有的宏观经济变量均产生了负向的响应,表明我国政策利率的逆周期调控效果良好,在理想的情况下政策利率可以传导至产出、价格、消费、投资等变量以及影响劳动力市场和工资水平,同时理想的政策利率传导没有时滞效应。从持续期来看,政策利率冲击对产出、价格、消费、投资、劳动力需求等变量的调控效果在中长期趋于收敛,但对工资的影响并没有表现出收敛趋势。脉冲响应的数值可以衡量政策利率传导的基准效应大小,本文将在实证研究部分将其与实证得出的传导效果进行对比,进而计算出传导效率并分析时变特征。
|
图 1 政策利率传导的基准效应 |
本文参考Nakajima et al.(2011)的研究,将随机波动(SV)和时变参数(TVP)设定引入政策利率传导效率框架构建SV-TVP-VAR模型,实证分析我国政策利率实际传导效应的时变特征,并结合上文得出的基准效应计算政策利率传导效率的时变特征。上文模拟了政策利率对产出、通货膨胀率、消费、投资、劳动需求、工资等六大变量的影响,但鉴于我国劳动市场和工资缺乏代表性、高质量的时间序列数据,因此我们在实证部分选择考察政策利率对其他四个变量的影响。模型包含利率(I)、实际产出(Yd)、通货膨胀率(PI)、消费(C)、投资(X)五个时间序列变量。利率变量用以衡量政策利率,参考多数文献的做法,本文使用市场化程度较高并且代表性较强的银行间同业拆借加权平均利率数据。实际产出使用工业增加值同比增速衡量,通货膨胀率使用CPI同比增速衡量,消费使用社会消费品零售总额同比增速衡量,投资使用固定资产投资同比增速衡量。数据频率为月度数据,样本区间为1996年1月至2019年10月。利率数据来自中国人民银行网站,其他宏观经济数据来自国家统计局网站。
SV-TVP-VAR模型首先需要从典型SVAR模型开始,然后引入随机波动和时变参数的设定,一个基准的SVAR模型可以如下:
| $ A y_{t}=F_{1} y_{t-1}+\cdots+F_{s} y_{t-s}+\mu_{t}, t=s+1, \cdots, n, $ | (22) |
其中,yt是包含上述五个变量的时间序列向量,A为联立参数矩阵,F1……FS为系数矩阵,扰动项μt为三个变量各自结构性冲击构成的向量,μt~N(0, ΣΣ)。
| $\Sigma=\left[\begin{array}{cccc} \sigma_{1} & 0 & \cdots & 0 \\ 0 & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \sigma_{k} \end{array}\right] A=\left[\begin{array}{cccc} 1 & 0 & \cdots & 0 \\ a_{21} & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ a_{k 1} & \cdots & a_{k, k-1} & 1 \end{array}\right] $ |
式(22)可以简化为:
| $ y_{t}=B_{1} y_{t-1}+\cdots+B_{s} y_{t-s}+A^{-1} \Sigma \varepsilon_{t}, \varepsilon_{t} \sim N\left(0, I_{k}\right) $ |
其中,
| $ y_{t}=X_{t} \beta+A^{-1} \Sigma \varepsilon_{t}, $ | (23) |
式(23)代表了SVAR模型的简化式,在此基础上将时变参数设定和随机波动引入模型,得到如下SV-TVP-VAR模型:
| $ y_{t}=X_{t} \beta_{t}+A_{t}^{-1} \Sigma_{i} \varepsilon_{t}, t=s+1, \cdots, n, $ | (24) |
其中,所有系数、参数和协方差矩阵均具有了时变性。进一步处理At中的元素:
| $ a_{t}=\left(a_{21}, a_{31}, a_{32}, a_{41}, \cdots, a_{k, k-1}\right), \text { 令 } h_{t}=\left(h_{1 t}, \cdots, h_{k t}\right), $ |
其中,
| $\begin{aligned} \beta_{t+1} &=\beta_{t}+\mu_{\beta t} \\ a_{t+1} &=a_{t}+\mu_{a t} \\ h_{t+1} &=h_{t}+\mu_{h t} \end{aligned}, \left(\begin{array}{c} \varepsilon_{t} \\ \mu_{\beta t} \\ \mu_{a t} \\ \mu_{h t} \end{array}\right) \sim N\left(0, \left(\begin{array}{cccc} I & O & O & O \\ O & \Sigma_{\beta} & O & O \\ O & O & \Sigma_{a} & O \\ O & O & O & \Sigma_{h} \end{array}\right)\right), t=s+1, \cdots, n, $ |
其中,
至此,SV-TVP-VAR模型构建完成,由于需要估计的参数较多并且所有参数均具有了时变性,无法使用传统的OLS和极大似然估计方法,需要在贝叶斯框架下运用马尔科夫蒙特卡洛模拟(MCMC)进行估计。首先设定先验值,然后运用MCMC模拟完成模型估计,令β、a和h服从先验正态分布,
参与计算之前,使用X12方法对五个变量进行了季节调整,根据VAR模型滞后期判别准则,本文选择2阶滞后。经过1000次的退火灼烧预模拟之后,本文通过10000次模拟得到最终的估计结果,将其列于表 3。其中,CD统计量和无效因子是衡量模型估计效果的主要指标,CD统计量用以衡量MCMC模拟的收敛效果,无效因子用以衡量样本的自相关性。两个统计量由Geweke(1991)提出,CD统计量计算公式如下:
| $ C D=\left(\bar{x}_{0}-\bar{x}_{1}\right) / \sqrt{\hat{\sigma}_{0}^{2} / n_{0}+\hat{\sigma}_{1}^{2} / n_{1}}, \bar{x}_{j}=\frac{1}{n_{j}} \sum\limits_{i=m_{j}}^{m_{j}+n_{j}-1} x^{(i)} $ |
| 表 3 SV-TVP-VAR模型的参数估计结果 |
其中,
| $ 1+2 \sum\nolimits_{s=1}^{B_{m}} \rho_{s} $ |
从本文的估计结果来看,CD统计量均较小,低于5%显著性水平的临界值,表明MCMC模拟的收敛性良好,无效因子均低于100,在10000次模拟的情况下至少可以得到100个不相关样本,表明样本自相关性较低。
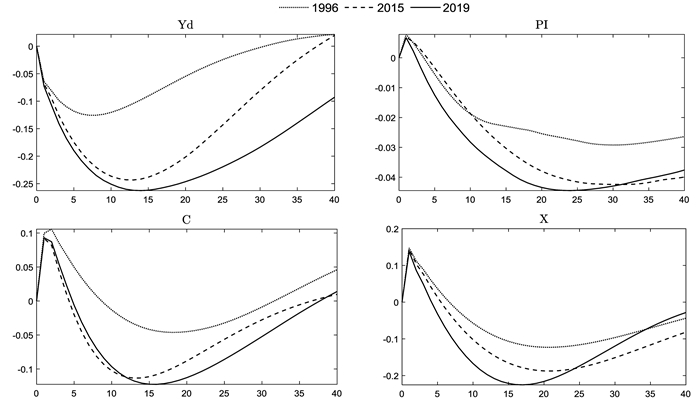
(三) 政策利率传导效率的时变特征分析为方便分析随着利率市场化推进我国政策利率传导效果的变化,本文选择了三个利率市场化的代表性时点进行分析,分别为1996年、2015年和2019年。从我国利率市场化的历史进程来看,主要包括货币市场利率的市场化、信贷市场利率市场化(浮动上下限管制放开)、基准利率和利率传导市场化三个阶段。1993年党中央、国务院提出利率市场化改革的目标和任务之后,1996年我国首次放开银行间同业拆借市场,标志着货币市场利率市场化正式开启,因此1996年可以代表利率市场化水平相对较低的时期。伴随着货币市场利率的改革,信贷市场利率改革同步推进,其核心是逐步放开对存贷款利率浮动的限制,2015年我国将存款利率上限先后调整至基准利率的1.3倍和1.5倍,最终完全放开限制,标志着名义上利率市场化的完成,因此2015年可以代表利率市场化水平较高的时期。为进一步推进利率市场化,中国人民银行于2019年完善了贷款市场报价利率(LPR)的形成机制,将其锚定MLF利率并作为银行贷款利率制定的基准,标志着基准利率和利率传导市场化改革向前迈进一步,因此2019年代表了利率市场化水平更高的发展阶段。本文分别计算了政策利率冲击对实际产出、通货膨胀率、消费、投资在三个代表性时点影响的时变脉冲响应函数(见图 2)。可以看出,一标准差大小的正向利率冲击引致产出、通货膨胀率、消费、投资的下降,表明我国政策利率对四个宏观经济变量均产生了良好的逆周期调控效果,这一结果与DSGE模型的模拟结果相一致,但也存在一定的差异,即政策利率对通货膨胀率、消费和投资的调控存在一定的时滞效应。
|
图 2 政策利率实际传导的时变效应 |
从时变特征来看,政策利率对四个变量的调控效果在1996年利率市场化程度较低的阶段最弱,2015年明显提升,2019年进一步提升,表明随着利率市场化的推进,我国政策利率调控的效果不断增强。1996年同业拆借市场放开后,宏观经济变量开始对市场化利率产生反应,政策利率调控具有一定效果,但仍然以信贷和货币数量的管制为主,数量型主导特征明显,因此利率调控效果较弱。1996-2015年经历20年的利率市场化改革后,我国货币市场已经完全市场化,信贷市场利率浮动也完全放开,中国人民银行对数量型指标有所淡化,对价格型指标的关注明显提升,利率调整对宏观经济的影响效果明显增强。2019年进一步完善贷款市场利率形成机制后,中国人民银行打破隐性贷款下限,引导贷款利率稳步下行,政策利率向市场利率的传导更加市场化,政策利率的调控效果进一步增强。
根据政策利率实际传导效应以及DSGE模型估计的基准效应,本文进一步计算了政策利率的传导效率,其基本思路是将实际传导效果的最大值与基准效应的最大值相比,如果等于1表明传导效率达到了合意水平,小于1表明存在效率损失。事实上在实际的经济运行过程中,利率传导受多种复杂因素的影响,很难确定准确的基准传导效果,甚至计算实际的传导效果也存在争议。因此,本文使用DSGE和SV-TVP-VAR模型在这一方面进行了尝试,得出的传导效率具体数值可能不完全与现实相符,但也是一次有益的探索。表 4的结果显示,我国政策利率实际的传导效率均低于1,即存在效率损失,随着利率市场化水平的提升,政策利率对四个变量的传导效率均不断提升。比如,1996年政策利率对实际产出、通货膨胀率、消费、投资等传导效率分别为43%、27%、18%、52%,2019年分别上升至86%、36%、54%、95%。由此我们可以推断,造成政策利率调控效率损失的原因之一是利率市场化程度较低,“利率双轨制”造成的结构性扭曲和金融摩擦降低了利率传导效率。同时还可以看出,政策利率对投资的传导效率最高,其原因可能是投资对利率最为敏感,利率变动对投资的作用效果最为直接,而投资变动又可以影响实际产出,因此政策利率对实际产出的传导效率也较高。传导时滞方面,基准效应没有时滞,但无论哪一个时期,政策利率对通货膨胀率、消费、投资的传导均存在时滞。
| 表 4 政策利率传导效率的时变效应 |
本文的研究结果显示,随着我国利率市场化的推进,政策利率的传导效率不断提升,对产出、价格、消费、投资等主要宏观经济变量的影响更加明显,但是与合意的传导效果相比仍然存在一定差距。我们将进一步对上述研究结果进行延申和拓展,从理论层面进一步提炼总结,讨论影响我国政策利率传导效率的可能因素以及利率市场化未来的改革方向。
政策利率有效传导存在两个大的前提,一是包括银行、非银金融机构、企业、居民等所有的市场主体对利率变化敏感,利率变动可以直接影响其决策,进而中央银行的政策意图可以很好地传导至微观主体;二是存在顺畅的利率传导链条,中央银行政策利率可以影响货币市场和债券市场短期利率,短期利率通过利率期限结构传导至中长期利率,货币市场和债券市场利率又可以传导至信贷市场利率影响居民储蓄和实体经济融资成本,形成跨市场跨期限的理想传导链条。
从第一个方面来看,现阶段我国不同市场主体对利率的敏感程度不同,存在明显的分层现象,政策利率调控效果在总量上可以影响流动性,但是在结构上却存在流动性分层现象。首先,银行和非银金融机构对利率的敏感程度较高,但是在流动性获取方面也存在结构性差异,大型国有银行和股份制银行对利率的敏感度低于中小银行,流动性相对充足,中小银行流动性相对不足,风险溢价提升,局部信用风险时有发生。其次,企业主体对市场利率的敏感程度低于金融机构,主要原因是利率形成机构尚未完全市场化,同时也存在结构性问题,国有企业主体存在隐性担保和软预算约束,资金获取能力较强,对利率变动不敏感,中小微企业对利率变动敏感,但获取资金能力较弱,融资成本显著高于国有企业。最后,居民主体由于缺乏良好的资产保值增值渠道,对银行储蓄的偏好较高,存在储蓄刚性需求,对利率变化的敏感程度也较低。上述问题导致政策利率传导效果存在结构性差异,难以实现理想的调控目标。
从第二个方面来看,中央银行政策利率向下的传导链条也存在阻塞。中央银行公开市场操作和再贷款等政策利率可以顺畅传导至货币市场和债券市场短期利率,但是货币市场和债券市场利率无法有效向信贷市场传导,信贷市场利率仍然锚定存贷款基准利率,即便完善了LPR形成机制,其利率水平仍然与基准利率高度接近,形成机制仍然不是完全的市场化,同时短期利率向中长期利率的传导机制也不够完善。上述现状就是在我国长期存在的“利率双轨制”,导致政策利率传导分层,市场轨的政策利率传导仅仅停留在短期货币和债券市场,与实体经济运行高度相关的信贷市场利率基本不受市场利率的影响,计划轨的存贷款基准利率的存在是银行体系不参考市场利率定价的主要原因(孙国峰、栾稀,2019),计划轨利率可以直接调控信贷市场进而影响实体经济运行。
进一步来看,利率传导链条的一个关键环节是货币和债券市场利率对存款利率的传导,理想的情况下商业银行的存款负债和同业负债弹性较大,对利率变动的敏感性较高,因此在无套利条件下政策利率可以传导至存款利率。当前我国居民缺乏良好的资产保值增值渠道,对银行储蓄的偏好较高,存在储蓄刚性需求,因此银行的存款负债具有稳定性,而同业负债具有不稳定性,因此银行自身(存款偏好)和监管部门导向(同业负债监管等)方面均强调存款的重要性,无论市场利率如果变化,对存款负债的要求均较高,因此存款对利率变化不敏感,存款利率具有刚性导致传导受阻。利率传导链条的另一个关键环节是存款利率向贷款利率的传导,这一环节主要依赖商业银行的内部资金转移定价(FTP)体系,银行综合考虑负债和各类成本、战略布局等因素确定FTP曲线,操作层面基层业务员根据考核激励机制、市场竞争情况等与客户商定最终的贷款利率。现阶段,受多方面因素的影响,我国商业银行的内部资金定价体系难以实现科学决策,在操作层面基层管理等因素也可能导致贷款定价的偏离。
解决第一个方面的问题需要金融市场改革和国企改革等多部门的协调配合。应突破单一的金融改革思路,加大财税体制改革和国有企业改革力度。要打破地方政府和国有企业部门的预算软约束,弱化信贷方面隐性担保的体制优势,使得所有市场主体真正对利率变动敏感,货币政策可以更加顺畅地传导至实体经济。其中,地方政府方面,应理顺地方政府财权事权的匹配机制,优化税收分配机制,减轻发展型政府面临的财政约束,弱化投资冲动,降低对资金的刚性需求。国有企业方面,应着力破除“政企不分”的弊病,保持竞争中性,使得国有企业真正作为市场主体参与竞争,提升对利率变动的敏感性。
解决第二个方面的问题则更多依靠利率市场化改革理顺利率传导链条,其总体方向应当是逐步取消利率双轨制和存贷款基准利率,实现利率并轨。市场化的利率形成机制完成后,整体的利率体系应当唯一锚定市场基准利率,中央银行通过政策利率影响市场基准利率,货币市场、债券市场、信贷市场联动传导,短期利率向中长期利率有序传导,最终作用于宏观经济进而实现政策调控目标。在微观层面,一方面,应完善多层次资本市场构建,健全金融体系制度和监管机制,向公众普及金融知识,增加居民资产保值增值的渠道,尤其是无风险或者低风险的稳定投资渠道,在长期引导公众改变银行存款是主要理财渠道的预期,同时在监管方面适当弱化对同业负债等指标的刚性约束。另一方面,应提升商业银行的内部资金定价能力和管理能力,加快完善或者构建FTP体系,提升FTP的科学性和及时性,同时加强管理,完善对基层单位的绩效考核制度,提升基层业务员的业务能力。
五、结论性评述本文研究所要解决的理论问题是随着利率市场化的推进我国政策利率传导效率发生了何种变化,现实问题是如何通过改革提升利率市场化水平和传导效率,为此首先构建新凯恩斯DSGE模型从理论上模拟了我国政策利率传导的基准效应,然后构建SV-TVP-VAR模型实证研究利率市场化进程中政策利率传导的时变效应,最后根据基准效应和实证结果分析了政策利率传导效率的时变效应。研究结果显示,我国政策利率对产出、通货膨胀率、消费、投资均产生了良好的逆周期调控效果,随着利率市场化的推进,我国政策利率调控的效果不断增强,传导效率不断提升。进一步来看,利率市场化程度较低造成政策利率传导效率的损失,但并不是唯一的原因,市场主体对利率敏感程度以及利率传导链条的顺畅程度均可以影响政策利率传导效率,后者与利率市场化相关,前者可能更多与经济体制相关。具体而言,所有制差异和利率双轨制可能是现阶段制约政策利率传导效率提升的两大问题。所有制差异导致不同微观主体对利率的敏感程度不同,政策利率传导存在结构性扭曲,利率双轨制则进一步阻塞了政策利率传导渠道。本文的研究结论具有明显的政策含义,即应当以破解利率双轨制为抓手推进利率市场化,并在微观层面推进资本市场建设和商业银行改革等,同时通过国有企业改革打破预算软约束,促进政策利率传导效率提升。
| [] |
卞志村, 2006, “泰勒规则的实证问题及在中国的检验”, 《金融研究》, 第 8 期, 第 56-69 页。 |
| [] |
陈利锋、范红忠, 2014, “房价波动, 货币政策与中国社会福利损失”, 《中国管理科学》, 第 5 期, 第 42-50 页。 |
| [] |
邓创、石柱鲜, 2011, “泰勒规则与我国货币政策反应函数——基于潜在产出, 自然利率与均衡汇率的研究”, 《当代财经》, 第 1 期, 第 64-73 页。 |
| [] |
董华平、干杏娣, 2015, “我国货币政策银行贷款渠道传导效率研究——基于银行业结构的古诺模型”, 《金融研究》, 第 10 期, 第 48-63 页。 |
| [] |
刘金全、毕振豫, 2019, “基于金融稳定目标的规则型货币政策研究”, 《南方经济》, 第 3 期, 第 1-16 页。 |
| [] |
刘达禹、赵婷婷、刘金全, 2016, “我国价格型与数量型货币政策工具有效性的实时对比及其政策残余信息估计”, 《经济学动态》, 第 10 期, 第 63-75 页。 |
| [] |
刘金全、石睿柯, 2017, “利率双轨制与货币政策传导效率:理论阐释和实证检验”, 《经济学家》, 第 12 期, 第 66-74 页。 |
| [] |
李涛、刘明宇, 2012, “资本充足率, 银行信贷与货币政策传导——基于中国25家银行面板数据的分析”, 《国际金融研究》, 第 11 期, 第 14-22 页。 |
| [] |
李俊江、黄潇雨, 2018, “外部经济冲击的实际产出效应和通货膨胀效应检验——基于开放经济新凯恩斯DSGE模型的分析”, 《中南大学学报(社会科学版)》, 第 6 期, 第 118-128 页。 |
| [] |
李俊江、黄潇雨, 2019, “中国货币政策中介目标的量价选择——现实困境与混频数据模型预测效果分析”, 《西安交通大学学报(社会科学版)》, 第 1 期, 第 9-17 页。 |
| [] |
刘晓星、姚登宝, 2016, “金融脱媒, 资产价格与经济波动:基于DNK-DSGE模型分析”, 《世界经济》, 第 6 期, 第 29-53 页。 |
| [] |
马理、尤阳, 2019, “货币政策传导路径阻滞与对策建议——基于欧洲央行影子利率的数据检验”, 《国际金融研究》, 第 6 期, 第 14-25 页。 |
| [] |
潘长春、李晓, 2018, “M2指标失效与货币政策转型——基于货币创造渠道结构分解的视角”, 《经济学家》, 第 2 期, 第 28-35 页。 |
| [] |
钱雪松、杜立、马文涛, 2015, “中国货币政策利率传导有效性研究:中介效应和体制内外差异”, 《管理世界》, 第 11 期, 第 11-28 页。 |
| [] |
任泽平、方思元、杨薛融, 2019, “宽货币到宽信用的传导效率”, 《中国金融》, 第 7 期, 第 26-28 页。 |
| [] |
孙国峰, 2019, “货币政策回顾与展望”, 《中国金融》, 第 2 期, 第 41-43 页。 |
| [] |
孙国峰、栾稀, 2019, “利率双轨制与银行贷款利率定价——基于垄断竞争的贷款市场的分析”, 《财贸经济》, 第 11 期, 第 81-97 页。 |
| [] |
盛松成、吴培新, 2008, “中国货币政策的二元传导机制——'两中介目标, 两调控对象'模式研究”, 《经济研究》, 第 10 期, 第 37-51 页。 |
| [] |
仝冰, 2017, “混频数据, 投资冲击与中国宏观经济波动”, 《经济研究》, 第 6 期, 第 60-76 页。 |
| [] |
王立勇、张良贵、刘文革, 2012, “不同粘性条件下金融加速器效应的经验研究”, 《经济研究》, 第 10 期, 第 69-81 页。 |
| [] |
王国静、田国强, 2014, “金融冲击和中国经济波动”, 《经济研究》, 第 3 期, 第 20-34 页。 |
| [] |
徐宁、刘金全、于洋, 2017, “理解我国名义利率传导机制有效性的时变特征——基于DSGE模型的理论分析与TVP-VAR模型的实证检验”, 《南方经济》, 第 7 期, 第 70-84 页。 |
| [] |
徐忠, 2018, “经济高质量发展阶段的中国货币调控方式转型”, 《金融研究》, 第 4 期, 第 1-19 页。 |
| [] |
周德才、纪应心、李晓璇, 2019, “金融稳定是否应纳入中国货币政策目标——基于混频IS-Phillips模型的实证分析”, 《南方经济》, 第 6 期, 第 10-28 页。 |
| [] |
张强、张宝, 2011, “货币政策传导的风险承担渠道研究进展”, 《经济学动态》, 第 10 期, 第 103-107 页。 |
| [] |
Adams R M, Amel D F., 2005, "The Effects of Local Banking Market Structure on the Bank-Lending Channel of Monetary Policy", FEDS Working Papers, NO.10.
|
| [] |
Amidu M, Wolfe S., 2013, "The Effect of Banking Market Structure on the Lending Channel: Evidence from Emerging Markets". Review of Financial Economics, 22(4), 146–157.
|
| [] |
Borio C, Zhu H.Capital, 2008, "Regulation, Risk-Taking and Monetary Policy: A Missing Link in the Transmission Mechanism", BIS Working Paper No. 268.
|
| [] |
Bernanke B S, Blinder A S., 1988, "Credit Money And Aggregate Demand". The American Economic Review, 78(2), 435.
|
| [] |
Calvo G A., 1983, "Staggered Prices in a Utility-Maximizing Framework". Journal of monetary Economics, 12(3), 383–398.
|
| [] |
Dybowski T P, Hanisch M, Kempa B., 2018, "The Role of the Exchange Rate in Canadian Monetary Policy: Evidence from a Tvp-Bvar Model". Empirical Economics, 55(2), 471–494.
|
| [] |
Fausch J, Sigonius M., 2018, "The Impact of ECB Monetary Policy Surprises on the German Stock Market". Journal of Macroeconomics, 55, 46–63.
|
| [] |
Galariotis E, Makrichoriti P, Spyrou S., 2018, "The Impact of Conventional and Unconventional Monetary Policy on Expectations And Sentiment". Journal of Banking & Finance, 86, 1–20.
|
| [] |
Geweke J., 1991, "Evaluating the Accuracy of Sampling-Based Approaches to the Calculation of Posterior Moments", Federal Reserve Bank of Minneapolis, Research Department.
|
| [] |
Hajek J, Horvath R., 2018, "International Spillovers of (un) Conventional Monetary Policy: The Effect of the ECB and the US Fed On Non-Euro EU Countries". Economic Systems, 42(1), 91–105.
|
| [] |
Ippolito F, Ozdagli A K, Perez-Orive A., 2018, "The Transmission of Monetary Policy Through Bank Lending: The Floating Rate Channel". Journal of Monetary Economics, 95, 49–71.
|
| [] |
Kim S, Lim K, 2018, "Effects of Monetary Policy Shocks on Exchange Rate in Small Open Economies". Journal of Macroeconomics, 56, 324–339.
|
| [] |
Kishan R P, Opiela T P., 2006, "Bank Capital and Loan Asymmetry in the Transmission of Monetary Policy". Journal of Banking&Finance, 30(1), 259–285.
|
| [] |
Kashyap A K, Stein J C., 1997, "The Role of Banks in Monetary Policy: A Survey with Implications for the European Monetary Union". Economic Perspectives-Federal Reserve Bank of Chicago, 21(9), 2–18.
|
| [] |
Nakajima J, Kasuya M, Watanabe T., 2011, "Bayesian Analysis of Time-Varying Parameter Vector Autoregressive Model for the Japanese Economy and Monetary Policy". Journal of the Japanese and International Economies, 25(3).
|
| [] |
Olivero M P, Li Y, Jeon B N., 2011, "Consolidation in Banking and the Lending Channel of Monetary transmission: Evidence from Asia and Latin America". Journal of International Money and Finance, 30(6), 1034–1054.
|
| [] |
Poole W., 1970, "Optimal Choice of Monetary Policy Instruments in a Simple Stochastic Macro Model". The Quarterly Journal of Economics, 84(2), 197–216.
|
| [] |
Rahal C., 2016, "Housing Markets and Unconventional Monetary Policy". Journal of Housing Economics, 32, 67–80.
|
| [] |
Salachas E N, Laopodis N T, Kouretas G P., 2017, "The Bank-Lending Channel and Monetary Policy During Pre-And Post-2007 Crisis". Journal of International Financial Markets Institutions and Money, 47, 176–187.
|
| [] |
Sellon G H., 2002, "The Changing US Financial System: Some Implications for the Monetary Transmission Mechanism". Economic Review-Federal Reserve Bank of Kansas City, 87(1), 5–36.
|



