为应对2008年全球金融危机,中国实施了“四万亿”经济刺激计划,尽管推动了中国经济率先复苏,却也带来了地方政府债务规模的快速增长。据Wind数据库统计,地方政府债券余额与银监会口径的城投债余额在2009年末均为0.2万亿元,2018年末已分别高达18万亿元和8万亿元。地方政府债务规模的快速膨胀,加剧了对地方政府债务违约风险的担忧。考虑到政府财政调整能力受限的现实,政府债务违约风险分析应综合考虑政府债务负担和政府债务限度(李丹等,2017)。对地方政府而言,各省在经济发展特征和财政收支结构等方面存在差异,政府债务承受能力不同,因而政府债务限度的存在性与取值均应有所区别。是否存在以及如何确定合理的地方政府债务限度,如何评估以及如何通过制度设计降低地方政府债务违约风险,皆是中央政府和地方政府需要共同面对和解决的问题。
基于财政反应的政府债务可持续性分析为政府债务违约风险评估提供了新思路。其核心思想在于,政府可以通过主动调整基础盈余率影响政府债务率的动态变化路径,债务率超过某一特定临界值后不可控的状态称为债务不可持续状态,以债务不可持续状态发生的概率度量政府债务违约风险。早期的政府债务可持续性研究基于跨期预算平衡展开,McCallum(1984)从理论上证明,在动态有效经济中,跨期预算约束条件能够保证政府债务可持续;而Hamilton and Flavin(1986)、Wilcox(1986)以及Trehan and Walsh(1991)针对政府债务路径是否满足跨期预算约束条件,给出了实证检验的方法。自Bohn(1998)以来,政府债务可持续性分析开始围绕财政反应和政府债务率是否可控进行。Bohn(1998)放松了财政变量间存在协整关系的要求,并证明只要基础盈余率始终对政府债务率积极反应,政府债务就是可持续的;文中基础盈余率对政府债务率的线性反应机制是财政反应函数的雏形。Ghosh et al.(2013)选用三次函数刻画财政反应函数的非线性特征,以发达经济体为样本进行实证研究发现,通过主动调整基础盈余率,政府可以确保债务率稳定在一定水平上;然而基础盈余调整的作用有限,使得政府债务率超过某一特定临界值后将难以控制,最终导致政府不得不选择违约;该债务率临界值称为债务上限或债务率警戒水平,当前债务率水平与债务上限的距离称为债务空间。国内学者基于财政反应机制展开政府债务可持续性评估的研究相对较少。唐文进等(2014)和李丹等(2017)测算了中国政府债务上限,并先后将居民储蓄和财政后备引入财政反应函数,作为政府基础盈余调整的储备渠道。陈宝东、邓晓兰(2018)测算了各省地方政府债务上限,发现大部分省份政府债务可持续。杜彤伟(2019)构建了有效财政空间指标,以度量地方政府债务可持续性,并实证检验了转移支付对地方政府债务可持续性的影响。
在基于财政反应的政府债务可持续性分析框架下,债务空间是债务可持续性的量化体现,债务不可持续状态发生的概率则可以很好反映政府债务违约风险。然而需要注意的是,由于中国地方政府的财政反应特征与发达经济体存在显著差异,进行中国地方政府债务可持续性评估时,应充分考虑基础盈余主动调整的有效性,并相应完善债务不可持续状态的定义和度量方法。具体而言,本文定义基础盈余主动调整的有效性为,政府主动调整所能达到的最高基础盈余足以偿付政府债务利息的性质。一方面,基础盈余主动调整有效,是债务上限存在的前提条件;另一方面,基础盈余主动调整无效,将同财政疲劳一样,导致政府债务率处于不可控状态。由于发达经济体的经济增速和财政反应均已稳定,现有政府债务可持续性分析框架默认了基础盈余主动调整的有效性条件成立。但是对经济增速和财政反应尚未稳定的中国地方政府而言,存在基础盈余主动调整无效的可能。相应地,政府债务空间应以条件期望的形式度量;政府债务不可持续状态,即政府债务率不可控状态,应综合考虑两种情况,一是基础盈余主动调整无效导致的政府债务率不可控状态,二是在基础盈余主动调整有效时财政疲劳导致的政府债务率不可控状态。
本文研究的主要创新如下:第一,考虑到中国地方政府与发达经济体的财政反应特征存在差异,本文在债务可持续性分析框架中,首次引入基础盈余主动调整的有效性条件作为分析前提,进而完善了债务不可持续性的定义内涵和度量方法,最终建立了地方政府债务违约风险评估模型。第二,在探究财政制度对地方政府债务违约风险的影响时,现有文献往往直接以违约风险指标对财政制度变量进行线性回归,对作用机制刻画得不够直观准确;本文则是在债务可持续性分析框架下,以基础盈余主动调整为中介,探究财政制度对地方政府债务违约风险的影响,既能直观反映作用机制,更能刻画作用机制的非线性。
本文其余部分的结构安排如下:第二部分结合中国地方政府的财政反应特征,构建地方政府债务违约风险评估模型;第三部分展开地方政府债务违约风险评估,并进行风险度量指标的可靠性检验;第四部分探寻可能降低地方政府债务违约风险的财政制度;第五部分为结论和相关政策建议。
二、地方政府债务违约风险评估模型构建在借鉴Ghosh et al.(2013)的债务可持续性分析框架的基础上,本文结合中国地方政府财政反应特征,引入基础盈余主动调整的有效性条件,进而完善债务不可持续状态定义内涵和度量方法,最终构建中国地方政府债务违约风险评估模型。
(一) 基本设定假设我国地方政府预算约束方程为:
| $ {d_{i, t + 1}} - {d_{i, t}} = \left({{r_{i, t + 1}} - {g_{i, t + 1}}} \right){d_{i, t}} - {s_{i, t + 1}} $ | (1) |
其中di, t为第i省第t年末地方政府债务率,ri, t+1为第i省第t+1年地方政府债务利率,gi, t+1为第i省第t+1年GDP增长率,si, t+1为第i省第t+1年基础盈余率。
假设我国地方政府财政反应函数的一般形式如下:
| $ {s_{i, t + 1}} = f\left({{d_{i, t}}} \right) + \beta {X_{i, t}} + {\mu _i} + {\varepsilon _{i, t + 1}} $ | (2) |
其中f(·)是连续有界的三次函数,X包含除前一年地方政府债务率之外所有影响基础盈余率的因素,ε为服从独立同正态分布的基础盈余率外生冲击,有ε~N(0, σ2)。
三次函数形式反映了财政反应的非线性特征。当债务率较低时,基础盈余率对政府债务率的反应较微弱;随着地方政府债务率不断上升,地方政府会开始主动增加基础盈余率,以保证地方政府债务率处于合理区间,表现为财政反应的主动调整阶段;然而地方政府财政调整的能力是有限的,当地方政府债务率高于临界值dm时,基础盈余率的变化率f′(di, t)始终低于经GDP增长率调整的政府债务利率(ri, t+1-gi, t+1),地方政府进入财政疲劳阶段。
假设基础盈余率外生冲击服从正态分布的主要依据如下:央地间财政转移支付之中,税收返还和一般性转移支付均按照事前给定的计算公式进行分配,资金数额基本可预期;相比之下,专项转移支付的项目类型和金额在不同年份间差异较大,项目申报和审批的不确定性高,地方政府当年所能获得的专项转移支付数额通常难以预期。因此,对于地方政府而言,基础盈余的收入端冲击主要来源于专项转移支付。计算各省各年专项收入占GDP比重并绘制直方图,可见专项转移支付占比的分布接近正态分布①。不考虑地震灾后重建支出和疫情防控支出等极端冲击,基础盈余的支出端冲击与收入端冲击总体而言具有对称性,因而假设基础盈余率外生冲击服从正态分布具有合理性。此外,在正态分布假设下,基础盈余率外生冲击将以99%的置信水平落在三个标准差区间内;实证检验可知,基础盈余率外生冲击的标准差通常只有几个百分点,足以保证基础盈余率小于100%的约束成立。
① 为节省篇幅,专项转移支付占比的分布图未在文中展示,感兴趣的读者可向作者索取。
(二) 基础盈余主动调整的有效性条件本文定义基础盈余主动调整的有效性为,地方政府主动调整所能达到的最高基础盈余足以偿付债务利息的性质。基础盈余主动调整无效时,财政反应函数的主动调整段与财政疲劳段均处于利息偿付函数之下,财政疲劳段与利息偿付函数不存在交点。
由预算约束方程可知,若一省基础盈余的主动调整长期无效,无论基础盈余率是否对地方政府债务率积极调整以及调整速率如何,地方政府债务率将始终处于不可控状态。除非财政反应函数中的结构性变量改善,即财政反应函数垂直向上移动,以满足基础盈余主动调整的有效性条件,地方政府债务率才有可能实现可控。
在经济增速不稳定的背景下,由于财政支出模式的调整滞后于经济增速的变化,中国地方政府可能存在基础盈余主动调整无效的情况。地方政府会在高速经济增长阶段实施扩张性财政政策,财政反应函数位置低;一旦经济增速冲击较大,即利息偿付函数逆时针旋转,而支出模式还未及时调整时,地方政府便容易临时处于基础盈余主动调整无效的状态。相比之下,Ghosh et al.(2013)在模型中默认了基础盈余主动调整的有效性,可能是因为发达经济体的财政反应已经适应稳定在低位的经济增速,基础盈余主动调整无效的情况较为罕见。
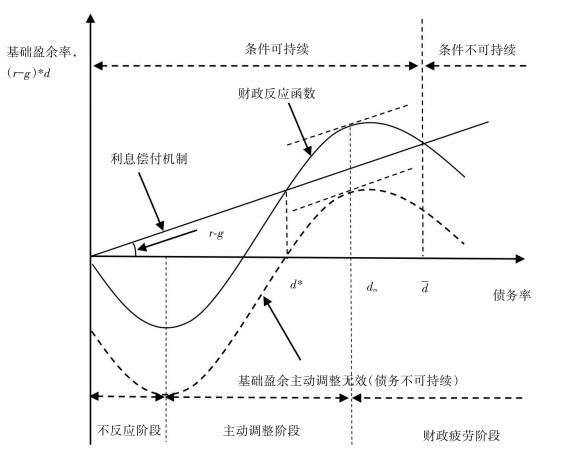
|
图 1 含主动调整有效性条件的政府债务可持续性分析框架 |
1.基础盈余主动调整无效的情况
记第i省第t+1年经济增长率在第t年末的期望为Et(gi, t+1),财政反应函数的主动调整段或财政疲劳段与利息偿付函数相切时,临界政府债务率
| $ f\prime \left({\bar d_{tangent}^{i, t + 1}} \right) = {r_{i, t + 1}} - {E_t}\left({{g_{i, t + 1}}} \right) $ | (3) |
| $ \varepsilon _{min}^{i, t + 1} = \left({{r_{i, t + 1}} - {E_t}\left({{g_{i, t + 1}}} \right)} \right)*\bar d_{tangent}^{i, t + 1} - f\left({\bar d_{tangent}^{i, t + 1}} \right) - \beta {X_{i, t}} - {\mu _i} $ | (4) |
第i省第t+1年基础盈余主动调整无效等价于:
| $ f\left({\bar d_{tangent}^{i, t + 1}} \right) + \beta {X_{i, t}} + {\mu _i} + {\varepsilon _{i, t + 1}} < \left({{r_{i, t + 1}} - {E_t}\left({{g_{i, t + 1}}} \right)} \right)*\bar d_{tangent}^{i, t + 1} $ | (5) |
即εi, t+1 < εmini, t+1。因而第i省第t+1年基础盈余主动调整无效的概率为:
| $ P_{IE}^{i, t + 1} = \Phi \left({\varepsilon _{min}^{i, t + 1}/\sigma } \right) $ | (6) |
其中Φ(·)为标准正态分布累积分布函数。
2.基础盈余主动调整有效的情况
当基础盈余主动调整的有效性条件满足时,财政反应函数的财政疲劳段与利息偿付函数的交点d为债务上限,政府债务率在高于债务上限后将会发散;主动调整段与利息偿付函数的交点d*为稳态点,政府债务率在未超过债务上限时,最终会收敛到稳态点d*。
| $ \begin{array}{l} f\left({{{\bar d}_{i, t + 1}}} \right) + \beta {X_{i, t}} + {\mu _i} + {\varepsilon _{i, t + 1}} = \left({{r_{i, t + 1}} - {E_t}\left({{g_{i, t + 1}}} \right)} \right){\bar d_{i, t + 1}}\\ f\left( {d_{i,t + 1}^*} \right) + \beta {X_{i,t}} + {\mu _i} + {\varepsilon _{i,t + 1}} = \left( {{r_{i,t + 1}} - {E_t}\left( {{g_{i,t + 1}}} \right)} \right)d_{i,t + 1}^*\\ {{\bar d}_{i,t + 1}} > d_{i,t + 1}^*,f'\left( {{{\bar d}_{i,t + 1}}} \right) < 0,f'\left( {d_{i,t + 1}^*} \right) > 0 \end{array} $ | (7) |
在含主动调整有效性条件的政府债务可持续性分析框架下,本文重新定义政府债务不可持续状态为政府债务率不可控的状态,其中既包括基础盈余主动调整无效导致的政府债务率不可控状态,也包括当基础盈余主动调整有效时,财政疲劳导致的政府债务率不可控状态。相比之下,Ghosh et al.(2013)定义的债务不可持续状态,仅考虑了财政疲劳导致的政府债务率不可控状态,本文则是根据中国地方财政反应的特征,完善了政府债务不可持续状态的定义内涵以及相应的度量方式。
本文重新定义债务上限为,在基础盈余主动调整有效的条件下,财政反应函数的财政疲劳段与利息偿付函数的交点,记为:
第i省第t+1年政府债务空间的条件期望为:
| $ debt\;space_{cond}^{i, t + 1} = E\left({\overline d \left({{\varepsilon _{i, t + 1}};{r_{i, t + 1}}, {E_t}\left({{g_{i, t + 1}}} \right)} \right)|{\varepsilon _{i, t + 1}} \ge \varepsilon _{min}^{i, t + 1}} \right) - {d_{i,t}} $ | (8) |
第i省第t+1年政府债务处于可持续状态的条件概率为:
| $ P_{sustainable, cond}^{i, t + 1} = {\rm{Pr}}\left({{d_{i, t}} < \overline d \left({{\varepsilon _{i, t + 1}};{r_{i, t + 1}}, {E_t}\left({{g_{i, t + 1}}} \right)} \right)|{\varepsilon _{i, t + 1}} \ge \varepsilon _{min}^{i, t + 1}} \right) $ | (9) |
第i省第t+1年政府债务处于可持续状态的概率为:
| $ P_{sustainable}^{i, t + 1} = P_{sustainable, cond}^{i, t + 1}*\left({1 - P_{IE}^{i, t + 1}} \right) $ | (10) |
当政府债务率不可控时,政府将不得不选择违约,因而政府债务不可持续状态发生的概率可以很好反映政府债务违约风险,有:
| $ P_{default}^{i, t + 1} = 1 - P_{sustainable}^{i, t + 1} = \left({1 - P_{sustainable, cond}^{i, t + 1}} \right)*\left({{\rm{ }}1 - P_{IE}^{i, t + 1}} \right) + P_{IE}^{i, t + 1} $ | (11) |
基于上述模型,对我国30个省级行政区(未包括西藏自治区)的政府债务违约风险进行评估。首先,估计地方政府财政反应函数;其次,结合地方政府债务利息率和期望经济增长率,评估地方政府债务违约风险;最后,检验地方政府债务违约风险度量指标的可靠性。
(一) 地方政府财政反应函数估计地方政府财政反应函数的估计中,使用变量为:(1)基础盈余率si, t,等于(财政收入-财政支出-利息支出)/GDP,其中财政收入为地方一般公共预算收入,财政支出为地方一般公共预算支出,利息支出为地方政府债券利息和地方政府融资平台债券利息之和。(2)地方政府债务率di, t,等于年末地方政府债务存量/ GDP,其中地方政府债务存量为地方政府债券余额和地方政府融资平台债券余额之和。(3)产出缺口gapi, t,等于对数GDP减去其HP滤波,HP滤波计算过程中的参数取值为6.25。(4)GDP竞速项compi, t,等于各省GDP增长率减去同组GDP增长率平均值,差值反映了该省的GDP竞速强度。省份分组的思想如下:首先,将各年各省按GDP增长率从高到低排序,序号依次为1-30,得到各省的排序向量;其次,计算不同省份排序向量元素之差的平方和,以度量不同省份GDP增长率排序的距离;最后,将GDP增长率排名接近的省份分在同一小组①。样本区间选取2008至2019年,数据来源为Wind数据库。
① 分组结果为(北京,河北,上海,浙江,广东),(天津,重庆),(山西,内蒙古,辽宁,吉林,黑龙江),(江苏,山东,河南,宁夏),(安徽,福建,江西,湖北,湖南,青海),(广西,海南),(四川,陕西),(贵州,云南),(甘肃,新疆)。
考虑到本省经济增长率和地区间经济增长竞争均可能影响未来基础盈余主动调整的动力和能力,控制变量分别取产出缺口滞后项gapi, t-1和GDP竞速滞后项compi, t-1、compi, t-2。考虑到基础盈余率的自相关性,财政反应函数中加入了基础盈余率滞后项si, t-1。财政反应函数形式为:
| $ \begin{array}{l} {s_{i, t}} = \alpha {s_{i, t - 1}} + {\beta _0} + {\beta _1}*{d_{i, t - 1}} + {\beta _2}*d_{i, t - 1}^2 + {\beta _3}*d_{i, t - 1}^3 + {\beta _{gap}}*ga{p_{i, t - 1}} + {\beta _{comp, 1}}*com{p_{i, t - 1}}\\ \;\;\; + {\beta _{comp, 2}}*com{p_{i, t - 2}} + {\varepsilon _{i, t}}, 其中, i = 1, 2, \ldots 30;t = 2010,\ldots, 2019 \end{array} $ |
采用系统GMM方法估计模型参数,估计结果如表 1所示。财政反应函数中,前一年末地方政府债务率平方项的系数显著为正,表明地方政府会主动增加基础财政盈余率以应对债务率的上升;立方项的系数显著为负,表明地方政府主动调整基础盈余率的能力有限,存在显著的财政疲劳现象。
| 表 1 地方政府财政反应函数估计(2010-2019)——基于系统GMM方法 |
前一年产出缺口系数显著为负,表明地方政府的财政政策存在顺周期性。具体而言,地方政府控制债务率的动力会随着经济增长率的提高而减弱,而随着经济增长率的下降而增强,表现为高速经济增长期的扩张型财政政策和低速经济增长期的紧缩型财政政策。原因在于,给定财政反应函数下,经济增长率越高,债务空间便越充裕,地方政府控制债务率的积极性则越发不足;反之,经济增长率下降会导致债务空间收缩,地方政府若预期经济增速将会持续放缓的话,则需要积极调整财政,以维持债务空间尽量充裕。
前一年GDP竞速指标系数显著为正,前两年GDP竞速指标系数显著为负,说明地区间竞争推动的经济高速增长,短期内有助于地方政府基础盈余的主动调整,但长期内反而会削弱地方政府的调整能力。原因在于,地方政府往往依靠“信贷—投资”驱动模式获得短期高速经济增长,但因为形成大量低效投资、扭曲资源配置,长期来看难以为继。低效投资往往项目工程量大、投资周期长,既会持续拖累资本效率,也会因为长期占据信贷资源而阻碍潜在低资本产出比项目的实施,均不利于长期经济增长。
(二) 2010-2019年中国地方政府债务违约风险评估估计出财政反应函数之后,结合各省下一年的地方政府债务利息率ri, t+1和期望经济增长率Et(gi, t+1),评估下一年地方政府债务违约风险。以发行总额为权重,对未到期地方政府债券和地方政府融资平台债券的票面利率进行加权平均,算得下一年平均债务利息率;下一年期望经济增长率假设等于当年的经济增长率。
债务违约风险评估分为两步。首先,计算财政反应函数与利息偿付函数相切对应的临界债务率
1.基础盈余主动调整无效的概率的计算
记回归(6)的残差平方和为SSR,观测数为N,可得基础财政盈余外生冲击的估计值
| $ \begin{array}{l} \frac{1}{{1 - \hat \alpha }}\left({{{\hat \beta }_1} + 2{{\hat \beta }_2}*\overline d _{tangent}^{i, t + 1} + 3{{\hat \beta }_3}*{{\left({\overline d _{tangent}^{i, t + 1}} \right)}^2}} \right){\rm{ = }}{r_{i, t + 1}} - {E_t}\left({{g_{i, t + 1}}} \right)\\ \varepsilon _{min}^{i, t + 1}{\rm{ = }}\left({1 - \hat \alpha } \right)*\left({{r_{i, t + 1}} - {E_t}\left({{g_{i, t + 1}}} \right)} \right)*\overline d _{tangent}^{i, t + 1} - {h_{i,t}}\left({\overline d _{tangent}^{i, t + 1}} \right) \end{array} $ |
可得第i省第t+1年基础盈余主动调整无效的概率
| 表 2 各省各年基础盈余主动调整无效的概率(单位:%) |
2.条件可持续概率与条件期望债务空间的计算
采用蒙特卡洛模拟,可计算在基础盈余主动调整有效的条件下,第i省第t+1年的条件可持续概率与条件期望债务空间。具体步骤如下:
(1) 产生10000个服从
K=0, N=0。
(2) 对于j=1, 2, …, 10000,
若
若
(3) 条件债务上限
条件可持续概率
条件债务空间
给定基础盈余主动调整有效的条件下,大部分省份尚无可能跨入财政疲劳引起的债务不可持续状态,仅有天津、吉林、贵州、云南和青海等五省于2017-2019年间条件可持续概率小于100%,如表 3所示。2019年,天津和青海的条件可持续概率均不足20%,贵州更是接近于0。考察各省各年的条件期望债务空间,如表 4所示。纵向比较可知,2012年后,各省的条件期望债务空间逐年缩减;自2017年起,陆续有省份出现条件期望债务空间不足20%的情况;自2018年起,先后有省份进入财政疲劳引起的债务不可持续状态。横向比较可知,在2019年,天津、贵州和青海已处于财政疲劳引起的债务不可持续状态;内蒙古、辽宁、吉林、重庆、云南和宁夏等六省的条件期望债务空间不足20%,需要防范债务不可持续的风险;其余省份的条件期望债务空间仍然较为充裕。
| 表 3 各省各年债务条件可持续概率不为100%的情况(单位:%) |
| 表 4 各省各年条件期望债务空间 |
通过前文的计算,可得到地方政府债务违约风险的直接度量指标和间接度量指标,即地方政府债务不可持续概率Pdefaulti, t+1和地方政府条件期望债务空间debtspacecondi, t+1。假设地方政府债务信用价差反映了市场对地方政府债务违约风险的认知,地方政府债务违约风险越高,信用价差也越高,则可通过检验两个指标对下一年地方政府债务信用价差的解释力,来检验其作为地方政府债务违约风险度量指标的可靠性。可靠性检验使用的变量包括:(1)地方政府债务信用价差spreadi, t+1。具体计算方式为,选取1年期上海银行间同业拆放利率(SHIBOR)作为无风险利率,对每一只新发行的地方政府债券或地方政府融资平台债券,以票面利率减去发行当日的SHIBOR,得到该只债券的信用价差;以新发行债券额为权重,计算各省各年新发行债券的加权平均信用价差,作为各省各年地方政府债务信用价差。(2)储蓄率savei, t,等于居民存款/GDP。(3)通货膨胀率inflationi, t+1,等于各省居民消费价格指数(CPI)的年增长率。地方政府债务信用价差和通货膨胀率的样本区间为2010至2019年,储蓄率的样本区间为2009至2018年,数据来源为Wind数据库。
以下一年地方政府债务信用价差spreadi, t+1分别对两个债务违约风险度量指标回归,控制变量选取储蓄率savei, t和下一年通货膨胀率inflationi, t+1;作为对比,以信用价差对年末债务率di, t进行回归,检验年末债务率能否反映下一年地方政府债务违约风险。模型选用误差项为AR(1)过程的固定效应模型。
由表 5可知,年末估计的地方政府债务不可持续概率指标与下一年地方政府债务信用价差呈显著正相关,表明债务不可持续概率可较好地反映地方政府债务违约风险;年末估计的地方政府条件期望债务空间指标与下一年地方政府债务信用价差呈微弱的负相关,体现了条件期望债务空间越充裕,市场认知的地方政府债务违约风险越低,但因为条件期望债务空间指标并不直接度量政府债务违约风险,其显著性弱于债务不可持续概率指标。相比之下,由于未考虑债务上限的变化,年末债务率并不能反映地方政府债务违约风险。
| 表 5 地方政府债务违约风险度量指标可靠性检验 |
为探寻可能降低中国地方政府债务违约风险的财政制度,以基础盈余主动调整为中介,将地方政府财政透明度与专项转移支付占比纳入地方政府债务可持续性分析。地方政府财政透明度transparency的数据来源于上海财经大学发布的《中国财政透明度报告》,满分标准化为1;专项转移支付占比transfer等于专项收入/GDP,数据来源为Wind数据库;样本区间均为2009至2018年。由于财政信息的公开存在滞后性,且当年专项转移支付资金存在高度不确定性和下拨时滞,地方政府财政反应函数中仅纳入前一年地方政府财政透明度与专项转移支付占比,及其与前一年政府债务率的交叉项,估计结果如表 6所示。为更直观地展示财政制度对地方政府债务违约风险的影响,以2017年贵州省为例,前一年财政透明度和专项转移支付占比取值对政府债务可持续性的综合影响如图 2和图 3所示。
| 表 6 地方政府财政反应函数估计——虑前一年财政透明度与专项转移支付占比 |
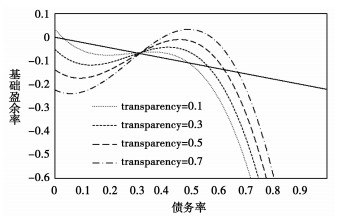
|
图 2 前一年财政透明度对地方政府债务可持续性的影响——以2017年贵州为例 |
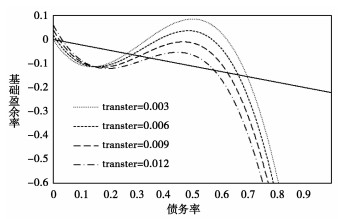
|
图 3 前一年专项转移支付占比对地方政府债务可持续性的影响——以2017年贵州为例 |
财政信息的透明化,对地方政府基础盈余主动调整的约束作用同时体现在收支两端。一方面,非税收入的立项与征管均集中于地方政府,有效监督机制的建立将制约地方政府通过增加非税收入来提高基础盈余,体现为前一年地方政府财政透明度的系数为负;另一方面,财政透明度的提高会增加地方政府的违规举债成本、强化中央对地方政府“不予救助”的承诺,有效抑制地方政府的举债冲动、规范政府支出,提升地方政府对债务率的反应强度,体现为前一年地方政府财政透明度与政府债务率交叉项的系数为正。
专项转移支付占比对地方政府基础盈余主动调整的影响,存在目标与现实的偏离。一方面,专项转移支付能够缓解地方财政压力,提高地方政府主动调整基础盈余率的能力,体现为前一年专项转移支付占比的系数为正;另一方面,专项转移支付占比的提高可能会引发“公共池”和“预算软约束”等道德风险问题,致使地方政府控制债务率的动力不足,过度扩张支出,带来基础盈余的恶化,体现为前一年专项转移支付占比与政府债务率交叉项的系数为负。
综合而言,财政透明度的提高可有效降低地方政府债务违约风险。随着地方政府财政越来越透明,规范政府支出对基础盈余的改善作用要高于非税收入减少的不利影响,具体表现为:一是促使政府从更低的债务率开始主动调整基础盈余;二是提高基础盈余对债务率的反应强度;三是提高政府主动调整所能达到的最高基础盈余率,降低基础盈余主动调整无效的概率;四是减缓财政疲劳现象的发生,提高债务上限,降低财政疲劳引起的债务不可持续的条件概率。
相比之下,专项转移支付占比的综合作用机制则完全相反。随着前一年专项转移支付占比的提高,地方政府债务违约风险将会逐步上升。道德风险诱发的地方政府支出过度扩张,不仅违背了缓解财政压力的初衷,反而带来了基础盈余的进一步恶化。尽管地方政府开始主动调整基础盈余对应的债务率无显著变化,基础盈余反应强度的降低和主动调整能力的下降,导致基础盈余调整无效的概率显著提高,以及债务空间的条件期望急剧缩减。
五、主要结论和政策建议在充分考虑中国地方政府财政反应特征的基础上,本文在政府债务可持续性分析框架中,首次识别基础盈余主动调整的有效性条件作为分析前提,完善了地方政府债务不可持续性的定义内涵,进一步建立了地方政府债务违约风险评估模型。凭借该模型,本文展开中国地方政府债务违约风险评估,并将财政透明度和专项转移支付占比纳入政府债务可持续性分析框架,以探寻可能降低地方政府债务违约风险的财政制度。
本文主要结论有四点:首先,在经济增速不稳定的背景下,施行顺周期财政政策的中国地方政府容易落入基础盈余主动调整无效的境况。地方政府主动控制债务率的积极性会随着经济增长率的提高而减弱,表现为高经济增速下的扩张性财政政策;经济增长遭受负向冲击而财政政策未能及时调整时,地方政府基础盈余主动调整无效的概率会显著上升。地区间的经济增长竞争会放大这一机制的影响。因而,在进行中国地方政府债务可持续性分析时,有必要考虑基础盈余主动调整的有效性。其次,将基础盈余主动调整的有效性条件纳入政府债务可持续性分析框架后,相应构造的债务不可持续概率和条件期望债务空间指标,均能较好反映下一年地方政府债务违约风险;相比之下,由于没有考虑债务上限的变化,单纯的年末债务率指标对下一年地方政府债务违约风险无解释力。再者,在2019年,天津、贵州和青海等地的条件期望债务空间为负,可视为已跨入财政疲劳引起的债务不可持续状态;内蒙古、辽宁、吉林、重庆、云南和宁夏等省份的条件期望债务空间不足20%,需防范债务不可持续风险;其余省份的条件期望债务空间虽呈现逐年缩减趋势,但仍相对充裕。最后,通过考察债务可持续性的改善渠道又进一步发现,财政透明度的提高能有效降低地方政府债务违约风险,专项转移支付占比的提高则会显著增加地方政府债务违约风险。地方政府财政信息的透明化,尽管不利于地方政府通过增加非税收入提高基础盈余,却更能有效抑制地方政府的举债冲动、规范政府支出,促使政府从更低的债务率开始主动调整基础盈余,提高基础盈余对债务率的反应强度和主动调整能力,减缓财政疲劳现象的发生。相比之下,专项转移支付占比的提高,尽管能够缓解部分的财政压力,但是道德风险诱发的地方政府支出过度扩张,更会带来基础盈余反应强度的降低和主动调整能力的下降,导致基础盈余调整无效的概率显著提高、条件期望债务空间急剧缩减。
本文对应的政策建议有两点:第一,为更好评估地方政府债务违约风险,中央和地方应充分考虑地方政府基础盈余主动调整无效的可能性,更多关注债务不可持续概率和条件期望债务空间,而非仅关注债务率。第二,为有效降低地方政府债务违约风险,地方政府自身需要摒弃速度情结、优化资源配置,以高质量经济增长提升地方政府主动调整基础盈余的能力;改变财政政策的顺周期性,在高经济增长阶段提升主动控制债务率的动力;提高财政透明度,增加外界对地方政府规范支出的约束力。中央应谨慎考虑对地方专项转移支付的额度与范围,取消不必要的专项转移支付项目,规范专项转移支付资金的分配,以防止道德风险诱发地方政府债务可持续性恶化。
| [] |
陈宝东、邓晓兰, 2018, “中国地方债务扩张对地方财政可持续性的影响分析”, 《经济学家》, 第 10 期, 第 47-55 页。 |
| [] |
杜彤伟、张屹山、杨成荣, 2019, “财政纵向失衡、转移支付与地方财政可持续性”, 《财贸经济》, 第 11 期, 第 5-19 页。 |
| [] |
李丹、庞晓波、方红生, 2017, “财政空间与中国政府债务可持续性”, 《金融研究》, 第 10 期, 第 1-17 页。 |
| [] |
唐文进、苏帆、彭元文, 2014, “财政疲劳、储备渠道与中国政府债务上限的测算”, 《财经研究》, 第 10 期, 第 18-31 页。 |
| [] |
Bohn H., 1998, "The Behavior of US Public Debt and Deficits". The Quarterly Journal of Economics, 113(3), 949–963.
DOI:10.1162/003355398555793 |
| [] |
Ghosh A., Kim J., Mendoza E., et al., 2013, "Fiscal Fatigue, Fiscal Space and Debt Sustainability in Advanced Economies". The Economic Journal, 123(566), F4–F30.
DOI:10.1111/ecoj.12010 |
| [] |
Hamilton J.D., Flavin M., 1986, "On the Limitations of Government Borrowing:A Framework for Empirical Testing". American Economic Review, 76(4), 808–819.
|
| [] |
McCallum B. T., 1984, "Are Bond-Financed Deficits Inflationary? A Ricardian Analysis". Journal of Political Economy, 92(1), 123–135.
DOI:10.1086/261211 |
| [] |
Trehan B., Walsh C.E., 1991, "Testing Intertemporal Budget Constraints:Theory and Applications to US Federal Budget and Current Account Deficits". Journal of Money, Credit and Banking, 23(2), 206–223.
DOI:10.2307/1992777 |
| [] |
Wilcox D. W., 1989, "The Sustainability of Government Deficits:Implications of the Present-Value Borrowing Constraint". Journal of Money, Credit and Banking, 21(3), 291–306.
DOI:10.2307/1992415 |



