自1995年双休日制度正式实行以来,我国的假日制度又经历了1999年的《全国年节及纪念日放假办法》(俗称五一、十一及春节三个“黄金周”制度)和2007年的《国务院关于修改〈全国年节及纪念日放假办法〉的决定》(取消“五一黄金周”,增加清明、端午、中秋三个中国传统节日),至此形成了52个双休日和11天法定节假日共计115天的节假日制度安排。按照《国民旅游休闲纲要(2013-2020年),国办发[2013]10号》的要求,到2020年,职工带薪休假制度基本得到落实之后,我国居民超过1/3的时间都在“纯休闲”中度过。当然,居民闲暇时间和假日数量增多,主要得益于技术进步和劳动生产率的提高。那么,随着假日数量和结构安排的变化,其对经济效率将产生何种影响以及由此引发的假日政策有效性问题就成为国内外休闲经济学者研究的重点内容。
具体来看,国内外学者对假日政策与经济效率关系的争论主要集中在以下三个方面:一是认为假日政策有效论。公共节假日的增加可以刺激消费,并通过乘数效应产生更大规模的需求,进而进一步促进经济增长(Ford,1926;Knack and Keefer, 1997;廖凯等,2009;Fodranova et al., 2015;Bloom et al., 2012等);二是认为假日政策无效论。具有代表性观点的是清华大学假日改革课题组(2009),他们对中国“黄金周”经济效应的长期追踪发现:从“黄金周”设置前后的对比来看,旅游收入整年的增长率没有任何明显变化。金融资本市场的数据也表明,假日政策会在短期内带来一定的正面效应,但从长期来看,“黄金周”制度带来的负面效应更加明显(张信东等,2008);三是条件决定论。假日政策是否有效应取决于该国的经济发展阶段(魏翔等,2014;Wei et al., 2016)、公共节假日的数量(Barrera and Garrido, 2018)和休闲活动内容(李仲广,2005;Bloom et al., 2018); 四是休闲内容决定论。休闲时间增加不会直接促进经济增长,它与经济效率或经济收益的兼容要看休闲的内容、方式和结构,能促进个人获取学习效率提升和放松身体、心灵等全面发展的休闲活动都具有促进经济效率提高的生产属性(李仲广,2005;魏翔、虞义华,2011;谢雅萍等,2018)。
从国内外学者对假日政策与经济效率有效性问题的研究可以看出,假日数量、休闲活动内容和经济发展阶段等内容条件是影响假日政策有效性的关键因素。然而,除了上述因素之外,工作日-休息日的制度性安排也进入到休闲经济学者的研究视野。因为连续太长的工作时间或太久的休闲时间都不利于经济增长(Eden,2016),即,假日结构同样是影响假日政策有效性的重要变量。本文对1995年-2015年136个国家的假日结构离散指数与劳动生产率①的关系作出散点图如下:
① 假日结构离散指数是假日结构集中程度的刻画指标,劳动生产率用时人均GDP来表示,具体解释见本文第四部分。
从图 1的散点图可知,假日结构设置与该国的劳动生产率之间非线性关系明显,且呈现出“倒U型”曲线,即太分散或是太集中的假日结构都不利于个体劳动生产率的提高。Pencavel(2015)指出相较于对工人工作时长的调整,假日结构改变对经济产出的影响更大。进一步的,Eden(2016)对一周“5+2”工作-休息模式的研究表明,在“疲劳效应”和“学习效应”的共同作用下,每工作两天或三天休息一天的模式更有助于福利改进:一方面,当连续工作时间过长时,个体容易产生“疲劳效应”,从而降低劳动生产率(Dixon and Freebairn, 2010;Pencavel,2015);另一方面,连续工作给个体带来的“干中学”效应又可以促进个体效率提升,这也是兼职员工效率要低于全职员工的原因所在(Hirsch,2005;Garnero and Rycx, 2017)。当个体连续休假时间太长时,需要时间去重新熟悉休假之前的工作和任务,因而人力资本会贬值,这也是失业人员劳动生产率降低的原因所在(Mincer and Ofek, 1982;Pavoni,2009)。Lee and Lim(2014)在对工作时长和生产效率之间的非线性关系进行解释时也认为,随着工作时长的增加,在“学习效应”的作用下会增加个体工作效率和技能,同时也会导致其“疲劳效应”加剧,最优工作时长的确定要根据最初的工作效率和行业特征而定。
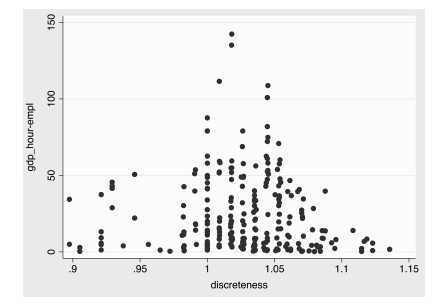
|
图 1 1995-2015年国家假日集中度与劳动生产率关系图 |
可见,假日结构与工作效率的非线性关系也是影响假日政策有效性的关键变量。但让人遗憾的是,到目前为止,现有的大部分研究尚没有给予假日结构问题以足够重视。虽然清华大学假日制度改革课题组(2009)也认为应该将“集中度假”的休假制度改为“分散度假”,但他们的结论仅是建立在“集中度假”带来的交通拥堵、旅游资源过度利用和旅游服务质量下降等负面影响的基础上而得,并没有进行理论上的系统分析和论证。虽然已有学者就“学习效应”和“疲劳效应”对个体绩效的作用机制进行研究和论证(Lee and Lim, 2014;Eden,2016;Garnero and Rycx, 2017),但他们关注的焦点问题是工作时长、假日总时间和周工作—休息模式,忽略了假日结构设置对经济绩效的影响,也较为缺乏经验数据的有效验证。为了弥补国内外学者的研究不足,本文尝试将“疲劳效应”和“学习效应”纳入新古典经济的分析框架,在此基础上运用136个国家、跨度20年的面板数据对假日结构设置和劳动生产率的关系进行验证,为研究假日政策的有效性提供新的研究视角和证据支持。
二、理论模型分析 (一) 理论模型考虑到分析国际面板数据的特征和前人文献中的经验做法,本文以Mankiw et al.(1992)构建的含有人力资本的Solow模型为分析基础,其生产函数的基本模型为:
| $ {Y_{it}} = K_{it}^\alpha H_{it}^\beta (AL)_{it}^{1 - \alpha - \beta }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < \alpha < 1,0 < \beta < 1,0 < \alpha + \beta < 1 $ | (1) |
其中,Y为总产出,K为物质资本,H为人力资本,A为全要素生产率TFP,L为劳动力,i为国家,t为时间。为了分析简便,我们假定全要素生产率TFP、储蓄率和人口增长率外生给定。全要素生产率A的增长率为g,劳动力增长为n,储蓄率为s,物质资本折旧率为δ。当然,有效劳动力(AL)的增长率为n+g。
对于一个在短期内技术水平、人力资本、物质资本和经济制度等保持不变的微观个体来说,假日结构对工作效率影响体现在两个方面:一是通过连续工作带来技能和知识积累所引致的“学习效应”(Learning Effect)(实际上,这类似Arrow所说的“干中学”效应),这有助于个体工作效率的提升;二是随着工作时间延长所导致个体精力贬值带来的“疲劳效应”(Fatigue Effect),其会降低个体的工作效率(Eden,2016)。除了“学习效应”和“疲劳效应”,Lee and Lim(2014)认为个体为准备日常工作而付出的总时间为“固定成本效应”(Fixed Cost Effect),固定成本效应随着工作时间的增加而递减。考虑到本文关注的重点是假日结构与工作绩效,因而文章并未将“固定成本效应”考虑在内。
在以往的研究当中,当个体的受教育水平、工作经验、健康状况等条件确定时,其劳动效率通常被假定为固定不变。当然,这是一种理想状况或模型假设。本研究尝试放松这一假设条件,认为个体的日常工作效率受“学习效应”和“疲劳效益”的共同影响,会随着工作时间和休息时间的不同而改变。借鉴Eden(2016)的做法,文章对人力资本质量H进一步具体设定为:
| $ {H_{realit}} = (1 - \zeta (t))(M_{it}^{{\omega _1}}/F_{it}^{{\omega _2}}){H_{it}} $ | (2) |
其中,ζ(t)为工作日或休息日标值,当天为工作日时,ζ(t)=0;当天为休息日时,ζ(t)=1,这也意味着方程(2)Hit为无效劳动力供给。ω1和ω2分别为“学习效应”和“疲劳效应”对人力资本质量的影响参数,0<ω1 < 1,0 < ω2 < 1。Hit为理想的人力资本质量。马红旗、王韧(2014)指出受教育程度所表征的人力资本仅是个体所能达到的潜在人力资本,真实人力资本质量还取决于个体实践中所处的制度环境、个人意志、经济载体等主客观因素。方程(2)所表达的意思为:相同教育程度个体的人力资本是异质的,生产实践中的真实人力资本质量会随着个体“学习效应”和“疲劳效应”的变化而不同。为了便于处理,工作日增加的“学习效应”和休息日得到缓解的“疲劳效应”,文章将其贬值衰减速度按照标准化单位1处理。
因此,考虑“学习效应”和“疲劳效应”对人力资本影响的C-D生产函数表达式为:
| $ \begin{array}{*{20}{l}} {{Y_{it}} = K_{it}^\alpha \left[ {(1 - \zeta (t))(M_{it}^{{\omega _1}}/F_{it}^{{\omega _2}})H} \right]_{it}^\beta (AL)_u^{1 - \alpha - \beta }}\\ {0 < \alpha < 1,0 < \beta < 1,0 < \alpha + \beta < 1} \end{array} $ | (3) |
为了便于衡量劳动生产率,令y=Y/AL,k=K/AL,h=H/AL,则hreal=h*(1-ζ(t))Mitω1/Fitω2。当k ˙ (t)=0, h ˙ (t)=0时,k和h的稳态值如下(具体算法见Mankiw et al.(1992),本文不再赘述):
| $ {k^*} = {\left( {\frac{{s_k^{1 - \beta }s_h^\beta }}{{n + g + \delta }}} \right)^{\frac{1}{{(1 - \alpha - \beta )}}}} $ | (4) |
| $ {h^*} = {\left( {\frac{{s_k^\alpha s_h^{1 - \alpha }}}{{n + g + \delta }}} \right)^{\frac{1}{{(1 - \alpha - \beta )}}}} $ | (5) |
那么,
| $ {h_{real}} = {h^*}(1 - \zeta (t))(\frac{{M_{it}^{{\omega _1}}}}{{F_{it}^{{\omega _2}}}}) = {\left( {\frac{{s_k^\alpha s_h^{1 - \alpha }}}{{n + g + \delta }}} \right)^{\frac{1}{{(1 - \alpha - \beta )}}}}*(1 - \zeta (t))(M)_{it}^{{\omega _1}}/F_{ii}^{{\omega _2}}) $ | (6) |
方程(3)两边同除AL可得:
| $ \frac{{{Y_{it}}}}{{A{L_{it}}}} = {k^\alpha }{(h*(1 - \zeta (t))(M_{it}^{{\omega _1}}/F_{it}^{{\omega _2}}))^\beta } $ | (7) |
方程(7)两边取对数可得,
| $ ln{\kern 1pt} {\kern 1pt} {Y_{it}} - ln{\kern 1pt} {\kern 1pt} {A_{it}} = \alpha ln{\kern 1pt} k + \beta lnh + \beta ln (1 - \zeta (t))(M_{ii}^{{\omega _1}}/F_{il}^{{\omega _2}}) $ | (8) |
将方程(4)和(5)带入方程(8),可得
| $ ln{\kern 1pt} {\kern 1pt} {Y_{it}} = ln{\kern 1pt} {\kern 1pt} {A_0} + gt + \frac{\alpha }{{1 - \alpha - \beta }} ln{\kern 1pt} {\kern 1pt} \frac{{s_k^{1 - \beta }s_h^\beta }}{{n + g + \delta }} + \frac{\beta }{{1 - \alpha - \beta }} ln{\kern 1pt} {\kern 1pt} \frac{{s_k^\alpha s_h^{1 - \alpha }}}{{n + g + \delta }} + \beta ln{\kern 1pt} {\kern 1pt} (1 - \zeta (t))(M_{it}^{{\omega _i}}/F_{it}^{{\omega _2}}) $ | (9) |
我们仅考虑工作日时个体的工作绩效,此时ζ(t) =0,对方程(9)进行整理可得:
| $ \begin{array}{l} ln{\kern 1pt} {\kern 1pt} \left( {\frac{{{Y_{it}}}}{{{L_{it}}}}} \right) = ln{\kern 1pt} {\kern 1pt} A{(0)_i} + gt - \frac{{\alpha + \beta }}{{1 - \alpha - \beta }} ln{\kern 1pt} {\kern 1pt} (n + g + \delta ) + + \frac{\alpha }{{1 - \alpha - \beta }} ln{\kern 1pt} {\kern 1pt} ({s_k})\\ + \frac{\beta }{{1 - \alpha - \beta }} ln{\kern 1pt} {\kern 1pt} ({s_h}) + \beta ({\omega _1} ln{\kern 1pt} {\kern 1pt} {M_{it}} - {\omega _2} ln{\kern 1pt} {\kern 1pt} {F_{it}}) \end{array} $ | (10) |
为了控制经济制度、气候等国家因素不同而对因变量造成的影响,设定μi为国家固定效应;为了控制世界性的宏观经济波动(例如2008年金融危机等)对所有国家经济产出的影响,设定时间虚拟效应η t;∈it为模型的误差项。则,假日结构设置与劳动生产率的模型最终设定为:
| $ \begin{array}{*{20}{l}} {ln{\kern 1pt} {\kern 1pt} \left( {\frac{{{Y_{it}}}}{{{L_{it}}}}} \right) = ln{\kern 1pt} {\kern 1pt} A{{(0)}_i} + gt - \frac{{\alpha + \beta }}{{1 - \alpha - \beta }} ln{\kern 1pt} {\kern 1pt} (n + g + \delta ) + \frac{\alpha }{{1 - \alpha - \beta }} ln{\kern 1pt} {\kern 1pt} ({s_k})}\\ { + \frac{\beta }{{1 - \alpha - \beta }} ln{\kern 1pt} {\kern 1pt} ({s_h}) + \beta ({\omega _1} ln{\kern 1pt} {M_{it}} - {\omega _2} ln{\kern 1pt} {\kern 1pt} {F_{it}}) + {\mu _i} + {\eta _t} + {\epsilon_{it}}} \end{array} $ | (11) |
假说1:假日结构与劳动生产率之间是非线性关系,假日集中度太分散或太集中都不利于个体劳动生产率的提高,存在最优的假日集中度以实现劳动生产率最高。
假日结构对劳动生产率的影响机制通过β(ω1 ln Mit-ω2 ln Fit)来实现,也就是说,假日结构设置通过影响“疲劳效应”和“学习效应”的综合效应来作用于经济绩效。随着连续工作或休息时间的增加,“学习效应”的贬值速度δm和“疲劳效应”的积累速度δf呈加速特证,因而其作用机制是非线性的。当假日结构太集中时,“学习效应”得到不断加强,但“疲劳效应”也相应得到积累;当假日结构太分散时,“疲劳效应”可以得到有效缓解,但“学习效应”却被频繁的休假切换而中断。因此,假日结构设置所导致的集中度肯定存在一个最优解促使“疲劳效应”和“学习效应”的综合效应最大。
假说2:假日结构通过影响个体日常工作中的“学习效应”和“疲劳效应”进而作用于个体的劳动生产率。
由方程(2)“学习效应”和“疲劳效应”对个体工作绩效的影响可知,个体所处的工作-休息模式,即假日结构设置决定的连续工作或连续休息范式会影响个体真实人力资本表现,最终通过方程(11)直接影响劳动生产率。当“学习效应”大于“疲劳效应”时,Mitω1/Fitω2>1,亦即,(ω1 ln Mit-ω2 ln Fit)>0,此时的节日结构设置有利于劳动生产率的提高;反之,则会阻碍个体的劳动生产率提升。
假说3:假日结构设置需与一国的经济发展阶段相适应,在不同的经济发展阶段,“学习效应”和“疲劳效应”对生产率的相对重要程度不同。
国家所处的经济发展阶段不同,个体对休闲偏好表现出较大差异。处于工业化进程中的个体会主动性的放弃休闲时间、更加偏向工作,后工业化社会的个体则表现出对休闲的更大偏好(魏翔,2018)。这就意味着,当一国处于劳动密集型经济时期,“学习效应”对人力资本的弹性ω1就相对更加重要,这就更加适合较为集中的假日结构设置;而当一国进入服务经济或知识经济时代,个体更加偏好休闲时,“疲劳效应”对人力资本的弹性ω2就会相对重要,那么,假日结构的分散设置就更有利于个体绩效体现。
三、研究设计 (一) 样本数据来源本文所选取的样本以世界发展报告(World Development Report 2016)所涵盖的国家或地区为统计基础,并结合OECD成员国名录,共计136个样本国家。所选取的时间范围为1995年、2000年、2005年、2010年和2015年五年的跨期面板数据,缺失年份的数据通常用前一年或后一年的有效数据来替代。基于数据的完整性和可得性要求,本研究最终选取52个国家、跨期5个阶段的244组实际样本。为保持统计数据口径的一致性,本文使用的数据来源于《世界银行》(The Word Bank),劳动力年均工作时长数据来源于世界大型企业联合会(The Conference Board),假日数量和假日结构来自于当年各国公共政策相关部门官方网站。
(二) 变量的选取因变量为时人均GDP(yit,美元/小时/人)。Yit为各国当年消除通货膨胀的实际GDP,用Lit表示当年各国总劳动人口,WKit表示劳动力的年均劳动时长。被解释变量时人均GDP用
核心解释变量休假离散指数(Xit)。休假离散指数(Xit)是为了刻画一个地区当年假日结构的集中程度,它的构建思路是:当每年节假日总天数不变时,连续休假的时间越长,该国假日结构的集中程度就越高;反之,当连续休假的时间较短时,则该国假日结构的设置就愈分散。因此,休假离散指数由假日得分和假日天数两部分构成:
| $ {x_{it}} = \frac{{{S_{it}}}}{{{N_{it}}}} = \frac{{\sum\limits_{n = 1}^{365} {{M_{itn}}} }}{{{N_{it}}}} $ | (12) |
其中,Sit反映了i国在t年人们“连续休假”的集中程度总得分,Nit为第i国t年度的假日总数(含周休日),则休假离散指数的数值含义为:i国t年度每个休息日的集中平均分值。Mitn表示在第i国t年度中每天的休假得分,
控制变量的选取如下:经济规模(kit)。为了反映各国物质资本和自然资源禀赋,同时也为了控制各国劳动力的努力程度和不可见的技术水平,本文沿用Barro(1998)的做法:选取各国当年实际GDP水平对数为经济规模的代理变量,取对数是为了降低GDP的量级规模;人力资本(hit)。关于人力资本存量的核算方法有很多,有成本法、收入法和教育指标法,鉴于数据的可得性和国际数据的可比性原则,本文采用杜伟等(2014)的做法,用各国当年的人均受教育年限来表征人均资本存量hit。Barro(1998)的研究显示,在控制住出生率时,女性受小学初等教育水平对经济增长没有显著作用;相比之下,25岁以上人口受教育程度比15岁以上人口受教育程度更具解释力。因而,本文选取25岁以上男性受高等教育的平均年限作为人力资本的代理变量。因调查样本中大部分国家男性受高等教育的平均年限小于1,参考杜兴强、彭妙薇(2017)的处理办法,对受高等教育的平均年限加1后取对数;出生率(brit)。新古典经济增长理论的假设是,更高的出生率将导致更多的资源用来抚养孩子而不是用于商品生产(Becker and Barro, 1988),因此,出生率越高,劳动生产率和经济增长率会越低。由于出生率通常会随着人均收入的增加而下降(Behrman, 1990),因此本文选取各国前一期的出生率做工具变量以克服内生性。
失业率(uerit)。失业率是影响劳动力变化水平的三大影响因素之一(马忠东等,2010),根据奥肯定律关于失业率与经济增长的反向变动关系可知,失业率可以反映该国某时间段内的经济发展态势,同时也可以在侧面反映该国劳动力参与情况,因此本文也选取失业率作为检验影响劳动生产率的控制变量。除此之外,参照Barro(1998)的做法,文章还选取通货膨胀率(iit)、政府消费(geit)和贸易条件(trit)作为跨国经济增长实证分析的控制变量。表 1为2015年各国因变量、解释变量和控制变量相关情况的详细描述。
| 表 1 2015年各国家截面数据的描述性统计 |
本文的分析样本为连续多年的跨国面板数据,为了消除因国别不同而存在的个体固定效应,本研究采用个体固定效应模型对方程进行评估,其基本模型为:
| $ {y_{it}} = {x_{it}}\beta + {z_i}\theta + {u_i} + {\varepsilon _{it}} $ | (13) |
其中,xit为解释变量,zi为不随时间而变的个体特征,ui+εit为复合扰动项。综上所述,为了检验假日结构对劳动生产率是否存在影响效应,本研究建立的计量模型如下:
| $ {y_{it}} = {\alpha _0} + \beta {\kern 1pt} {x_{it}} + \gamma {\kern 1pt} {C_{it}} + + {u_i} + {\varepsilon _{it}} $ | (14) |
其中,yit为因变量劳动生产率时人均GDP,α0为常数截距项,xit为核心解释变量休假离散指数,Cit表示物质资本、人力资本、出生率、政府消费支出(教育和国防支出除外)、贸易条件、通货膨胀和失业率等控制变量;设定μi为国家的固定效应;∈it为模型的误差项。
四、实证分析 (一) 固定效应分析基于跨国面板数据的个体特征差异,我们选取面板固定效应分析作为本研究的主回归分析方程。从表 2的结果可知,加入核心解释变量假日离散指数平方项xit2后,模型(2)的拟合结果更为优化。结合图 1假日离散指数与时人均GDP的“倒U型”散点图可得,劳动生产率时人均GDP yit与假日离散指数xit的非线性关系明显,即,随着假日集中度的增加,劳动生产率呈现先增加、后减少的趋势,促使劳动生产率最优的休假模式存在唯一解。
| 表 2 假日结构对劳动生产率的双向固定效应影响结果分析 |
具体来看,表 2模型(1)和(2)的固定效应回归结果符合我们的理论预期。首先,重点考察休假离散指数对劳动生产率的作用。数据显示,核心解释变量假日离散指数xit对劳动生产率的作用系数显著为正,而假日离散指数的平方项xit2对劳动生产率的作用系数则显著为负:即,在一国总休假天数不变的情况下,假日结构太集中或太分散都不利于劳动生产率的提高,这与我们对休假离散指数与劳动生产率的预期理论高度一致。这一结果表明,在“疲劳效应”和“学习效应”的共同作用下:当假日结构较为集中时(集中工作、集中休息的假日模式),工作日中的“疲劳效应”对个体的消极作用大于“学习效应”带来的绩效提高,休息日中“学习效应”的持续衰退程度大于“疲劳效应”缓解工作压力的积极效率,从而不利于工作时的效率恢复,出现“假日综合效应”;当假日结构较为分散时(工作日和休息日交替较为频繁的假日模式),工作日中的“学习效应”因持续中断而对个体的消极作用大于“疲劳效应”带来精力缓解程度的绩效提高。因此,假日结构的设置应该在一定程度上“中和”集中和分散特性,适宜的假日离散指数更有助于工作效率提高。Eden(2016)对一周“5+2”的工作模式进行研究也印证了本文的结论:发现每工作3天或2天休息一天的模式比现有“5+2”的制度更有助于个体劳动生产率的提高。基于模型(2)“倒U型”的曲线参数,我们可计算出劳动生产率最优的假日离散指数。由估计方程yit=1359.325xit-693.21xit2,对xit一阶可导等于0,可得xit≈0.98。即,最优的假日离散指数约为0.98。对比来看,我国2015年假日离散指数为1.12,这表明现阶段我国假日结构设置较为集中,在一定程度上抑制了经济绩效的提升。
其次,考察控制变量对劳动生产率的作用情况。人力资本hit对劳动生产率的作用显著为正①,意味着人力资本已经成为促进各国经济发展的主要驱动因素,这再一次验证了Lucas(1988)和Romer(1986)的人力资本内生增长理论。与Barro(1988)的研究结果一致,扣除教育和国防开支的政府公共支出对劳动生产率的负面作用显著,说明庞大的政府开支并不利于经济增长。其背后的原因在于,政府性支出作为非生产性投入,比例越高意味着税收越高,而较高的税负不利于生产。在其他控制变量方面,与前人的研究较为相似,出生率、物质资本、失业率和贸易条件对劳动生产率的作用再一次得到验证。
① 本研究还分别计算了男女劳动力在不同教育水平下人力资本对劳动生产率的影响效果:一方面,数据表明男女受中等和高等教育的平均年限均积极作用于劳动生产率:25岁以上男性受中等和高等教育的平均年限(thcit25f)对劳动生产率的作用系数为37.72,25岁以上女性受中等和高等教育的平均年限(thcit25f)对劳动生产率的作用系数更是高达46.31。这一结果表明一国劳动力受中等和高等教育的总体水平是决定该国劳动生产率的首要影响因素,男女受中等和高等教育平均年限每增加1年,时人均GDP分别增加37.72、43.31美元,另一方面,男女受小学初等教育的平均年限对劳动生产率均表现出显著的抑制作用。结果显示,男女受小学初等教育平均年限每增加1年,时人均GDP分别下降29.42和33.43美元。这一结果不仅验证了Behrman(1990)关于女性受小学初等教育水平对经济增长没有显著作用的结论,还表明男性受小学初等教育的平均年限也无益于经济增长。
(二) 内生性讨论本研究采用的个体固定效应评估模型能消除因个体效应造成的遗漏变量问题,可以在一定程度上较好的缓解内生性问题。然而,经济影响因素与最终产出常常会出现互为因果的依存关系,即本研究中的核心解释变量假日离散指数不但影响劳动生产率,而劳动生产率的变化也会在一定程度上影响该国的假日政策和假日结构。控制变量中的政府消费支出和人口出生率等因素已被前人证明存在很强的内生性问题(Barro,1998)。因此,本研究参考李涛、张文韬(2015)和胡浩等(2018)的处理方法,采用提前一期变量值为方程备用的工具变量,即,保持因变量劳动生产率为当期数据,而核心解释变量假日离散指数和控制变量用前一期的数据,然后使用面板工具变量法进一步减弱方程估计的内生性问题,具体结果见表 3模型(3)和(4)。
| 表 3 内生性检验:面板工具变量法 |
从面板工具变量法评估的结果可知,核心解释变量假日离散指数xit和其平方项xit2通过了显著性检验,且影响系数的符号并未改变。其他控制变量对因变量的影响结果与Barro(1998)的研究也较为一致,这在一定程度上增加了本研究的稳定性和可信性。
(三) 稳健性检验由上文分析可知,连续工作带来的技能增加和知识积累可以给个体带来积极的“学习效应”,而工作时间延长所导致个体精力贬值带来的“疲劳效应”也会随之增加。因此,个体的日常工作效率受“学习效应”和“疲劳效应”的共同影响:当“学习效应”大于“疲劳效应”时,连续工作有利于劳动生产率的提高;反之,则会阻碍个体的劳动生产率。为了验证“学习效应”和“疲劳效应”对个体工作效率影响结论的稳健性,本部分利用实地调研的微观数据对论文结论进行进一步检验。为此,本文采用现场研究(Field Research)方法对80名企业员工的日常工作时间、工作间的闲暇时间和工作绩效等微观数据进行观察和记录。具体做法如下:首先,选取一家企业同一部门的80名员工作为研究对象;其次,招聘18名在校大学生作为科研志愿者,对其进行正规的时间日志表使用说明培训;第三,对研究对象的工作时间、工作间的闲暇时间和工作绩效进行观察和记录。其中,现场配备2名指导老师进行协助,每名志愿者负责4-5名员工,每10分钟记录一次,连续记录9天。
本文用连续工作时间来表征员工的“学习效应”,用员工在工作间的闲暇时间(包括休息、喝水、聊天等)来代理“疲劳效应”的缓解程度,当天员工的综合工作绩效作为其劳动生产率的代理变量。为了衡量“学习效应”和“疲劳效应”对个体工作效率的综合影响,本研究根据员工在工作中的“疲劳效应”缓解程度(即工作间闲暇时间),将其划分为“低学习、低疲劳效应型”、“高学习、高疲劳效应型”和“学习、疲劳效应相间型”:以工作间闲暇时间的1/3位数和2/3位数为划分标准,当工作间闲暇时间大于2/3位数时,定义为“低学习、低疲劳效应型”;当工作间闲暇时间小于1/3位数时,定义为“高学习、高疲劳效应型”;中间的1/3为“学习、疲劳效应相间型”。然后,基于“疲劳效应”缓解程度的类型对员工当天工作绩效进行方差分析,具体结果见表 4。
| 表 4 “学习效应”和“疲劳效应”对经济效率综合影响的方差分析 |
由表 4的分析结果可知,在“学习效应”和“疲劳效应”的共同影响下,个体的工作绩效在“学习、疲劳效应相间型”时最大,其数值为0.12;而连续工作时间较长时的“高学习、高疲劳效应”和工作间闲暇时间较多时的“低学习、低疲劳效应型”个体的工作绩效都显著较低,假日结构与劳动生产率的“倒U型”非线性关系得到微观数据的进一步支持。
(四) 机制检验由前文的理论分析和实证检验可知,假日离散指数与劳动生产率之间存在显著的“倒U型”关系。假日结构设置不同,导致假日离散指数的集中程度出现较大差异,进而通过影响个体工作时的“学习效应”和“疲劳效应”最终作用于劳动生产率。为了检验假日结构带来的“学习效应”和“疲劳效应”对劳动生产率的作用机制,本部分从人力资本和经济结构的调节效应两个维度分别进行验证。
1.人力资本的调节效应
人均受教育程度代理的人力资本变量只是潜在的人力资本水平,真实人力资本质量取决于“学习效应”和“疲劳效应”的综合作用。工作日中“学习效应”和“疲劳效应”对个体的综合作用为正时,有利于潜在的人力资本水平发挥,从而提高劳动生产率;“学习效应”和“疲劳效应”对个体的综合作用为负时,则不利于劳动生产率的提升。即,假日结构配置通过“人力资本”通道而最终作用于劳动生产率。
为了检验假日结构配置对劳动生产率的作用机制,本研究构造假日离散指数和人力资本的交互项xit*hit。由表 5评估模型(5)和(6)的结果可知,交互项xit*hit的作用系数在1%的水平上显著为正。这表明,随着人均受教育程度的提高,假日离散指数越大,其对个体劳动生产率的抑制作用越显著。为了验证结论的稳定性,模型(7)和(8)分别评估了因变量为人均GDPyit*时的计量模型,结果显示,交互项xit*hit对因变量的影响系数依然显著为正,本文结果较为稳健可信。
| 表 5 人力资本的调节效应分析 |
2.经济结构的调节效应
假日结构设置促进个体劳动生产率提高的“机会窗口”会随着经济发展阶段的变化而出现不同:处于劳动密集型经济的国家更为适合较为集中的假日结构设置,而进入服务经济阶段以后,较为分散的假日结构设置就更有利于个体工作绩效提升。这是因为劳动密集型产业主要依靠个人工作经验和员工身体素质,连续工作“学习效应”的增加能最大程度抵消“疲劳效应”带来的损失,所以较为集中的休假模式就是最优的假日安排;但是,如果产业的增长方式主要依靠人力资本和创新能力,连续工作的“疲劳效应”对个体工作绩效的负面影响就更为明显,则适当的降低假日离散指数,通过灵活的假日制度安排更有利于提升国家的经济效率(Eden,2016)。
为了检验经济结构对作用机制的调节效应,本部分构造假日离散指数和经济结构的交互项xit*esit。其中,经济结构(Economic Structure,简称esit)由当年该国第三产业与第二产业比值来表征。为了降低假日离散指数xit与交互项xit*esit的共线性影响,我们对交互项取对数值处理。由表 6的评估结果可知,假日离散指数和经济结构交互项xit*esit对因变量的作用系数在5%的水平上显著为正。这表明,假日离散指数对劳动生产率的作用机制受该国经济结构的调节作用明显,即,随着经济结构的不断优化,较为分散的假日结构更有利于劳动生产率的提高。
| 表 6 经济结构的调节效应分析 |
本文的敏感性检验需要重点关注分样本的稳健性分析,以检测模型结果在不同样本中的实现情况。对于跨国数据来讲,发达国家和发展中国家在经济发展阶段、资源利用效率、劳动生产率和居民生活水平等方面存在显著差异。除此之外,国民所处的经济发展阶段不同,休闲时间的收入效应、代替效应和对经济的互补效应会有较大不同,其对休闲时间的偏好也存在较大差异(魏翔,2018)。因此,对样本按照是否为OECD国家进行分类来检测休假离散指数对各国劳动生产率的影响差异性和敏感性,两类样本国家模型的参数估计结果如表 7所示。
| 表 7 发达国家和发展中国家假日离散度对劳动生产率的面板数据分析 |
对比发达国家和发展中国家的模型评估结果显示,OECD国家的休假离散度对劳动生产率的“倒U型”非线性关系进一步得到验证,模型整体拟合情况较好,且通过5%水平上的显著检验;发展中国家(非OECD)样本的评估系数虽然也呈现出先上升、后下降的趋势,但评估结果并未通过显著性检验。这表明对发达经济体而言,休假结构越是集中,其对劳动生产率的反向作用愈加明显。这是因为发达国家已经进入后工业化的服务经济时代,劳动生产率和初始物质禀赋较高,个体对休闲时间更为偏爱,因此“疲劳效应”对其人力资本质量的影响更大,而“学习效应”则相对处于次要位置;在发展中国家,其经济发展正处于“补短板”的劳动密集型经济时期,对于连续工作带来的“疲劳效应”来讲,“学习效应”带来的技能提升更有助于个体工作效率提高。实际上,经过对模型的测算,OECD国家的最佳假日离散指数为0.96,略小于全样本的最优值0.98,这一结果表明,经济发展水平越高,其假日结构的设置越分散,越有利于个体绩效的体现。值得注意得是,无论是OECD国家代表的发达经济体,还是非OECD的发展中国家,假日离散指数和人力资本的交互项xit*hit都通过了显著性检验。
五、拓展性讨论由上文分析可知,假日结构设置的太过集中或分散都不利于个体劳动生产率的提高,而且假日结构的有效性还与国家所处的发展水平和经济结构有关。实际上,除了经济因素以外,假日结构设置与国家的文化传统和居民的消费习惯等深层次原因也密切相关。从文化传统上来看,以欧美为代表的西方国家居民普遍具有休假意识:在带薪休假和度假权利神圣不可侵犯传统的影响下,每年7-9月份①是欧美居民的家庭“休假季节”,这也是很多海外客户在7-9月份回复工作邮件较慢的原因所在。在儒家文化的影响下,我们习惯上推崇“勤劳致富”,因此文化上的休假基因并不深厚。从消费习惯上来看,欧美国家居民多为轮休式或灵活性的度假模式,具体的度假时间可以根据家庭需要而自主选择;而我国则多为全国性的集中式休假,在法定节假日前后会主动性的选择“拼假”和“凑假”。
① 每个国家的休假时间略有不同,但大都集中在7、8、9这三个月份,例如波兰集中在7月初至7月底;比利时在7月中旬至8月初;挪威和德国是在7、8、9三个月轮休;西班牙是7月7日至8月4日;葡萄牙是7月14日至7月27日;法国是7月最后一周至8月,几乎全部放假。
当然,导致国家间休假模式差异的影响因素还有制度上的差别。从表面上看,我国居民较为偏好“黄金周”或“拼假”、“凑假”的度假模式,而背后深层次的原因在于:1、我国居民的日常生活较为忙碌,缺乏休闲时间。据《中国劳动力动态调查:2017年报告》的数据显示,2016年我国居民的周劳动时长超过44.75小时,即年均劳动时长超过2300小时。相比之下,美国人2016年的年均劳动时长为1766小时,而德国人的这一数据仅为1367小时。因此,在缺乏日常休闲时间的现实中,我国居民对长假期意愿表现的更为强烈;2、带薪休假制度并未得到全面落实。我国居民热衷于集中休假的另一个原因是带薪休假制度在企业层面上落实不够,居民缺乏长时间的休假机会。除去春节这个特殊的假期之外,居民真正的休假时间只有“十一黄金周”一个。所以,改善我国居民休假习惯的前提在于满足居民的休假需求,重点在于落实带薪休假制度。
此外,假日结构与经济效率的非线性关系也表明,假日结构设置可以成为一个很好的政策工具:当连续工作时间过长,“学习效应”积累的效率提高不足以抵消“疲劳效应”带来的人力资本损失时,可以通过休息日来缓解;当连续休假时间过长时,“疲劳效应”带来的精力缓解不足以弥补“学习效应”对效率的减少时,可以通过缩短假期长度来解决。通过灵活的假日结构设置方式,可以促使经济效率水平一直在高位运行。Eden(2016)通过将“5+2”的工作制度改变为每工作2天或3天休息1天的“2+1”+“3+1”的工作-休息模式已经验证了这一观点。Aguiar et al.(2013)对美国居民从2003到2010年近十年的时间配置分析也表明,当经济处于大萧条时期,可以通过减少市场工作时间、增加闲暇时间的方式刺激居民产生新的消费需求,进而通过扩大内需规模和拉动消费升级来促进经济内生增长。因此,实施多个公共短假期和灵活带薪长假期相结合的假日结构模式,不仅可以避免旅游资源过度集中消费,还可以提高国家和个人的经济效率、促使个人的生活品质得到较大提升。
六、结论与建议 (一) 结论首先,假日结构设置模式对劳动生产率存在非线性关系,随着假日离散指数的增长,劳动生产率呈现先上升、后下降的“倒U型”曲线。假日结构设置太过集中或分散都不利于劳动生产率的提高。第二,在“学习效应”和“疲劳效应”共同作用下,假日离散指数存在最优解,即当xit=0.98时,个体的劳动生产率最高。当连续工作时间/休息时间太长时,“学习效应”带来的促进作用无法抵消“疲劳效应”带来的负面作用;当工作和休闲时间交替频繁时,“疲劳效应”带来精力恢复也不足以中和“学习效益”衰退带来的消极作用。因而,劳动生产率提高的机会窗口取决于合理的节日结构设置和适中的假日离散指数。第三,假日结构对劳动生产率的非线性影响关系是通过人力资本和经济结构的中介效应来完成。假日结构设置通过调节不同的“学习效应”和“疲劳效应”比例来实现真实人力资本水平,进而影响经济绩效。第四,假日结构设置需与一国的经济发展阶段相适应,在不同的经济发展阶段,“学习效应”和“疲劳效应”对生产率的相对重要程度不同。对于经济发达国家,相对较为分散的假日结构更有利于劳动生产率的提高。本文的研究结论为国务院办公厅《完善促进消费体制机制实施方案(2018—2020年),国办发〔2018〕93号》中“落实带薪休假制度,鼓励错峰休假和弹性作息”提供了有力注脚。
(二) 政策建议首先,适时推动假日结构改革。目前,我国的年节假日(带周休日)总数已达到115天。从总量上来看,节假日总量已经处于发达国家水平。然而,从结构上来看,假日结构的离散指数还需调整。因为从经济效率的角度来说,较高的假日离散指数的确不利于个体工作绩效的提高。Eden(2016)和本文的研究结果已经表明,受到“疲劳效应”和“学习效应”的综合影响,较长的连续工作和休息天数均不利于个体工作效率。因此,“集中式休假”模式不利于经济效率提高,“分散式休假”的自主模式才是最优的假日政策。在现有假日政策的基础上,我国应适时推动“集中休假”制度向“分散休假”制度转变,进一步考虑把重阳节和元宵节这两个重要的历史文化节日纳入到法定假日范畴:这样不但可以消除集中休假带来的交通拥堵、旅游服务质量下降、价格攀升、旅游资源过度消费和员工“假日综合症”等种种弊端,还可以增加2个传统文化节日,推动我国假日结构向分散化、扁平化转变。值得注意的是,推动假日制度改革的前提和时机是全面落实《国民旅游休闲纲要(2013-2020)》中的带薪休假制度,即充分满足国民的长假需求是假日制度改革的基础。
其次,推行弹性工作制。弹性工作制以其灵活性、便利性和兼顾工作效率的特点,在发达国家积累了成熟的工作体系和运行经验。相较于固定工时制来说,弹性工作制是更为个性化和人性化的工时制度,个体可以根据自身实时“疲劳效应”和“学习效应”的综合指数自主调整工作模式,以达到个体最优的劳动效率。基于行业特点,弹性工作制可以在金融业、旅游业和文化咨询等知识密集型服务业先行先试。当然,弹性工作制的实施和推广关键在于国家提供相应的制度保证和理念推广。同时,弹性工作制也为在不缩短工时的前提下,增加居民日常休闲时间提供了可借鉴的蓝本。因为弹性工作制有利于减少通勤时间,增加居民日常休闲时间。随着城市化的日益推进,居民日常通勤时间不断增加。可以尝试在每周40小时工时不变的情况下,实现“错峰”上下班,减少交通拥堵带来的效率无效。
最后,制定差别化的假日政策。假日结构的最佳设置与一国的经济发展程度密切相关,应当根据国家的具体情况因地制宜,制定差别化的假日制度。一方面,对于发达国家,假日改革适宜较为分散的设置模式,而对于发展中国家而言,适当集中的假日结构更为有效;另一方面,在区域间、城乡间收入差距扩大的同一国家内部而言,应当给地方更大的调整权限,在全国假日结构的框架下,结合地方节日特色,制定更加地方化、差别化的假日政策。
| [] |
杜伟、杨志江、夏国平, 2014, “人力资本推动经济增长的作用机制研究”, 《中国软科学》, 第 8 期, 第 173-183 页。DOI:10.3969/j.issn.1002-9753.2014.08.018 |
| [] |
杜兴强、彭妙薇, 2017, “高铁开通会促进企业高级人才的流动吗?”, 《经济管理》, 第 12 期, 第 89-107 页。 |
| [] |
李涛、张文韬, 2015, “人格特征与股票投资”, 《经济研究》, 第 6 期, 第 103-116 页。 |
| [] |
李仲广, 2005, “休闲、效率及两者的相容——兼与唐任伍等《效率的追求与休闲的异化》商榷”, 《改革》, 第 8 期, 第 116-118 页。 |
| [] |
胡浩、王海燕、张沛莹, 2018, “社会互动与家庭创业行为”, 《财经研究》, 第 12 期, 第 31-43 页。 |
| [] |
廖凯、徐虹、杨威, 2009, “黄金周休假制度对我国旅游业发展影响的实证研究”, 《旅游学刊》, 第 10 期, 第 12-18 页。DOI:10.3969/j.issn.1002-5006.2009.10.007 |
| [] |
马红旗、王韧, 2014, “对人力资本形成理论的新认识”, 《经济学家》, 第 2 期, 第 33-41 页。 |
| [] |
马忠东、吕智浩、叶孔嘉, 2010, “劳动参与率与劳动力增长:1982-2050年”, 《中国人口科学》, 第 1 期, 第 11-27 页。 |
| [] |
清华大学假日制度改革课题组, 蔡继明, "中国假日制度改革的政治经济学分析", 《学习与探索》, 第5期, 第30-39页。 |
| [] |
魏翔、李伟、陈琪, 2014, “中国假日政策有效性问题研究——基于非正常收益率视角”, 《当代经济研究》, 第 7 期, 第 44-50 页。DOI:10.3969/j.issn.1005-2674.2014.07.009 |
| [] |
魏翔、虞义华, 2011, “闲暇效应对经济产出和技术效率的影响”, 《中国工业经济》, 第 1 期, 第 130-139 页。 |
| [] |
谢雅萍、沈淑宾、陈睿君, "越休闲越激情?-休闲参与与知识型员工工作激情的影响机制研究", 《经济管理》, 第7期, 第128-145页。 |
| [] |
张信东、宋鹏、秦旭艳, 2008, “旅游经济增长点分析-基于'黄金周'效应的实证”, 《旅游学刊》, 第 10 期, 第 16-22 页。DOI:10.3969/j.issn.1002-5006.2008.10.008 |
| [] |
张震, 2016, “1950年代以来中国人口寿命不均等的变化历程”, 《人口研究》, 第 1 期, 第 8-21 页。 |
| [] |
Aguiar M, Hurst E, Karabarbounis L, 2013, "Time Use During the Great Recession". American Economic Review, 103(5), 1664–1696.
DOI:10.1257/aer.103.5.1664 |
| [] |
Anderson J. R. and Schooler. L, 2000, "Adaptive Memory", Oxford Handbook of Memory, Oxford, UK: Oxford University Press.
|
| [] |
Barrera F, Garrido N, 2018, "Public Holidays, Tourism, and Economic Growth". Tourism Economics, 24(4), 473–485.
DOI:10.1177/1354816617749340 |
| [] |
Barro R J. 1998, "Determinants of Economic Growth: A Cross-Country Empirical Study", The MIT Press, edition 1, volume 1, number 0262522543.
|
| [] |
Barro R J, 1990, "Government Spending in a Simple Endogenous Growth Model". Journal of Political Economy, 98(5), 103–126.
DOI:10.1086/261726 |
| [] |
Becker G S, Barro R J, 1988, "A Reformulation of the Economic Theory of Fertility". Quarterly Journal of Economics, 103(1), 1–25.
|
| [] |
Berhman, J. R, 1990, "Women's Schooling and Nonmarket Productivity: A Survey and a Reappraisal", Unpubished, University of Pennsylvania.
|
| [] |
Bloom J D, Rantanen J, Tement S, et al., 2018, "Longitudinal Leisure Activity Profiles and Their Associations with Recovery Experiences and Job Performance". Leisure Sciences, 4(3), 151–173.
|
| [] |
Bloom J, Geurts S A, Kompier M A, 2012, "Effects of Short Vacations, Vacation Activities and Experiences on Employee Health and Well-Being". Stress & Health, 28(4), 305–318.
|
| [] |
Dixon R, Freebairn J, 2010, "Models of Labour Services and Estimates of Australian Productivity". Australian Economic Review, 42(2), 131–142.
|
| [] |
Eden M, 2016, "The Week", Policy Research Working Paper 7598.
|
| [] |
Fodranova I, Kubiková V, Michalková A, 2015, "Measuring Societal Value of Tourism:A New Approach". Tourism:An International Interdisciplinary Journal, 63(4), 423–434.
|
| [] |
Ford H, 1926, "Leisure and Economic Growth", An interview with World's Work Magazine.
|
| [] |
Garnero A, Kampelmann S, Rycx F, 2017, "Part-Time Work, Wages and Productivity:Evidence from Belgian Matched Panel Data". Iza Discussion Papers, 67(3), 926–954.
|
| [] |
Knack S, Keefer P, 1997, "Does Social Capital Have an Economic Payoff? A Cross-Country Investigation". Quarterly Journal of Economics, 112(4), 1251–1288.
DOI:10.1162/003355300555475 |
| [] |
Lee D, Lim H, 2014, "Nonlinearity in Nexus between Working Hours and Productivity", Social Science Electronic Publishing, BOK Working Paper No. 24.
|
| [] |
Lucass R. E. Jr, 1988, "On the Mechanics of Economic Development". Journal of Monetary Economics, 22(1), 3–42.
DOI:10.1016/0304-3932(88)90168-7 |
| [] |
Mankiw N G, Weil R D N, 1992, "A Contribution to the Empirics of Economic Growth". The Quarterly Journal of Economics, 107(2), 407–437.
|
| [] |
Mincer J, Ofek H, 1982, "Interrupted Work Careers:Depreciation and Restoration of Human Capital". Journal of Human Resources, 17(1), 3–24.
DOI:10.2307/145520 |
| [] |
Pavoni N, 2009, "Optimal Unemployment Insurance, with Human Capital Depreciation, and Duration Dependence". International Economic Review, 50(2), 323–362.
DOI:10.1111/j.1468-2354.2009.00532.x |
| [] |
Pencavel J, 2015, "The Productivity of Working Hours". Economic Journal, 125(589), 2052–2076.
DOI:10.1111/ecoj.12166 |
| [] |
Romer P M, 1986, "Increasing Returns and Long-Run Growth". Journal of Political Economy, 94(5), 1002–1037.
DOI:10.1086/261420 |
| [] |
Wei X, Qu H, Ma E, 2016, "How does Leisure Time Affect Production Efficiency? Evidence from China, Japan, and the US". Social Indicators Research, 127(1), 101–122.
DOI:10.1007/s11205-015-0962-1 |




