信用债市场是我国债券市场的重要组成部分, 也是全球第二大信用债市场, 规模快速增长, 投资者结构也在不断壮大;信用债不仅是我国商业银行、保险公司等机构投资者资产配置的重要品种, 且随着“债券通”的开启, 也吸引了更多国际投资者的参与;信用债市场的快速发展, 有效地解决了企业融资需求, 大力地支持了实体经济发展, 也推动了多层次资本市场建设;但随着国内金融去杠杆等供给侧结构性改革的推进, 刚性兑付被打破, 近年来信用债违约风险有逐渐上升的趋势。截至2019年5月30日, 自2014年公开市场首只债券(11超日债)发生违约至今, 我国信用债市场已有123个主体发行的416只债券发生了违约(仅计银行间、交易所交易的债券), 涉及违约的债券本金规模达2166亿元(数据来源:Wind数据库);尤其是2018年, 信用债违约空前爆发, 仅一年便有176只债券发生违约, 涉及规模和新增主体均达历史新高。作为重要的资产配置组成, 信用债的价格波动预测是投资者十分关心的问题。信用债的信用利差是市场对发行主体违约风险的补偿, 是市场违约风险预期的表现。信用债的定价依赖于有效的违约风险度量, 因此针对我国信用债市场的违约风险量化模型研究十分必要, 也具有重要意义。
然而, 国际市场已有成熟的信用债风险度量模型应用于我国信用债市场具有一定的缺陷。首先, 模型应用的计算依据不充分。Feldhütter and Schaefer (2018)总结, 大部分的信用风险结构化模型都是根据建模对象的信用评级与到期时间, 通过对应的穆迪平均历史违约概率(Moody Realized Default Rate)计算其违约概率(如KMV模型)。而我国的信用评级修正延迟, 且缺少历史违约数据库, 采用类似的方法进行计算会产生较大的误差。除了依据信用评级, 国际市场中CDS(信用违约互换)产品为投资者提供保护, 且有效地对企业的破产风险进行了定价, 为信用债违约预警提供有效依据;而我国在2010年底中国银行间市场交易商协会引导设立了的信用风险缓释凭证(CRMW), 总体表现为市场发行动力不足, 标的少且重复率较高, 因此也较难成为市场对违约风险量化的依据。企业公开财报和二级市场交易行情仍旧是我国信用风险建模的重要数据来源。
其次, 模型所需的基本假设与我国不匹配, 在计算信用债条件违约概率(即市场违约风险预期)及信用利差预测中会产生较大的误差。经典的结构化违约风险理论模型均是基于完全信息和同质信念假设, 假设投资者具有完整的信息集, 并可通过信息准确判断违约(Hong and Stein, 2007)。同质信念的假设虽然便于量化模型的构建, 但忽略了市场中具有不同预期的投资者之间的交易对资产价格影响, 会造成结果的偏差。异质信念(Heterogeneous Beliefs)也称为意见分歧, 是指投资者对未来资产价格的预期存在不同意见(张维, 2006)。异质信念的存在会促使投资者之间的交易, 乐观的投资者买入, 悲观的投资者卖出或观望, 通过市场均衡形成价格。因此, 异质信念的强度与变化会影响市场投资者的违约风险预期, 进而影响价格的走势与波动, 也因此被认为是市场价格偏离同质预期假设下理论价格的影响因素。由于市场的不成熟性, 我国市场中的投资者异质信念是客观存在且不容忽视的, 表现为两点:第一, 企业信用债偿付无硬约束, 企业没有偿债意愿不代表没有偿债能力。基于传统的公司金融理论, 企业的破产清算是指企业价值低于短期负债, 或企业不足以偿付到期债券本息时, 企业宣告或债权人申请债务人破产;而企业破产与信用债违约的条件是显著不同的, 企业自主宣告违约, 违约触发通常缘由现金流状况甚至其他关联条款, 并不严格依赖于企业的资产负债结构, 因此, 投资者不具有完整信息, 无法根据公开信息中的企业资产与企业负债的关系准确判断信用债的违约。第二, 涌现的信息披露问题使得我国投资者客观上无法判断违约。近年来, 以康得新、康美药业、绿大地、雅百特、万福生科、金亚科技为代表的上市公司财务造假案, 体现了我国资本市场的系统性诚信危机(黄世忠, 2019)。陈秀梅(2012)、王芳(2013)等学者都指出我国债券市场信息披露扭曲较为严重。近年甚至出现披露中仍有150亿货币资金的企业宣告10亿超短融信用债违约①, 及毫无预兆地宣告减计300亿货币资金的事件②。除此之外, 我国违约追偿机制也尚未成熟, 对违约处置过程中的不同主体尚无比较有效的约束机制。因此发行人违约成本较低, 还款意愿不明确, 导致投资者无法对债券的实际价值和违约后果做预测, 且不断出现企业信息披露扭曲、业绩“爆雷”形成市场恐慌, 投资者信念异质水平波动大。因此, 对我国信用债违约风险的量化中, 对投资者做同质信念的简化假设会使得计算出现巨大误差。基于以上事实, 我们在建模中引入投资者异质信念强度变化的因素, 也是本文的一个创新点。
① 18康得新SCP001、SCP002是由康得新复合材料集团股份有限公司于2018年发行的, 期限为0.7397年的固定利率AA+债, 实际发行总额分别为10亿和5亿, 发行利率分别为5.5%和5.83%, 到期一次性还本付息。该债券发行时, 康得新还是市值700亿的白马股, 债券亦被市场认可, 2018年三季度年报显示公司货币资金储备仍高达150.14亿元, 另有银行理财17.34亿元。然而至SCP001到期日2019年1月15日公司发布公告称“不能按期足额偿付本息”, 发生实质性违约。
② 康美药业2019年4月29日公告称, 因会计处理错误, 货币资金多计29, 944, 309, 821.45元。2019年8月16日, 证监会发布会指出, 康美药业2016-2018年期间, 康美药业涉嫌通过仿造、变造增值税发票等方式虚增营业收入, 定性此事件为“有预谋有组织的系统造假”。
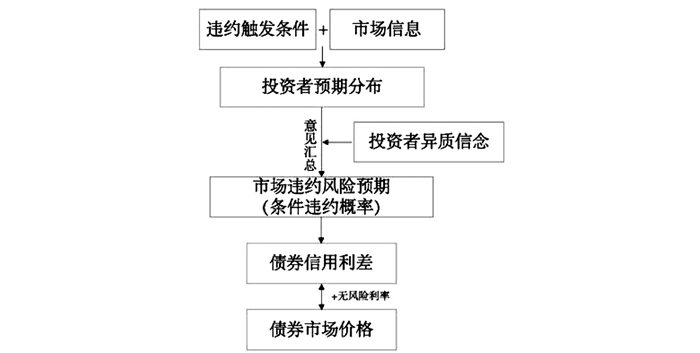
本文的主要贡献在于, 在Giesecke(2006)的理论模型的基础上, 基于我国信用债市场的上述特点, 提出了一个考虑投资者异质信念的信用债违约风险量化的理论模型(后简写为“HB模型”, Heterogeneous Belief Model), 并针对我国市场给出投资者异质信念度量和模型应用的方法。图 1总结了该模型构造思路。该模型结合了结构化模型和强度模型两大类模型的优点, 利用经典结构化模型的思想构建具有经济含义的条件违约概率, 也结合了强度模型的方法考虑违约的不可预测性与动态性, 研究了投资者异质信念强度对条件违约概率, 信用利差的影响, 给出了条件违约概率和信用利差的一般解析表达式。本文给出了利用市场公开数据计算模型结果的方法, 并利用国内信用债市场发生的违约案例对本文模型进行了实证检验, 通过与Black-Cox模型、Giesecke(2006)模型进行了比较, 本文提出的HB模型出现违约预警信号较好, 且预测精度较优, 表现出了良好的应用价值。
|
图 1 考虑投资者异质信念的信用债模型构建思路示意图 |
信用风险度量两大类理论模型中, 结构化模型最为经典的就是Merton模型(Merton, 1974)和Black-Cox模型(Black and Cox, 1976)。Merton模型假设企业的负债为一个无分红的债券, 企业的资产价值是一个关于企业负债的看涨期权, 当债券到期时企业的资产价值低于企业负债时即发生违约。穆迪公司简化Merton(1974)开发了KMV模型, 为市场广泛应用。杨世伟、李锦成(2015)针对中国市场, 应用KMV模型对公司债、企业债及私募债进行研究, 得出公司债违约风险最大的结论, 也指出因我国违约数据库缺乏, 在实践中难以直接应用于量化和预警。张永东(2019)基于财务数据构建的分类模型也只是达到识别效果, 而不能计算信用利差用于交易指导。Black-Cox模型考虑时间段内发生违约概率, 利用首达时间计算预测概率, 与现实更为贴近, 后续的理论研究多是在Black-Cox基础上做出扩展(Geske, 1977;Geske and Johnson, 1984;Anderson and Sundaresan, 1996;Leland, 1994;Leland and Toft, 1996)。结构化模型较大的缺陷在于对违约概率的低估, 它们均假设违约是一个可预测的事件, 这里的可预测是一个数学的概念, 是指由特定的、可以观测的事件(如资产价值低于负债价值)所触发的;而实际上, 违约不一定完全由定义的事件触发。Giesecke(2004)指出, 经典结构化模型的天生缺陷在于其应用于短期到期的债券时, 计算所得信用利差接近于零, 会出现短期的垃圾债券风险与国库券风险甚至相近的严重误差。吴建华等(2017)在Black-Cox模型基础上引入信息披露扭曲的假设, 但实证结果中, 已经触发违约的11超日债仍旧只得出了15.764%的违约概率。已有基于结构化模型的实证与衍生都难以避免地低估违约概率。
信用风险模型的另一大类—强度模型突破了结构化模型中“可预测”的局限但较难实证应用。Duffie and Singleton (1999), Jarrow and Turnbull (1995)最早提出了强度模型(Intensity Model), 又叫做简约模型(Reduced Model), 模型假设企业的违约是意外地发生, 即每个企业在每一个时间点都有违约强度或条件违约概率。从测度论的角度来说, 如果已知条件违约概率的过程, 那么债券的价格就可以通过将违约风险补偿考虑入折现利率, 得到相应风险中性测度下的期望(Collin-Dufresne et al., 2004)。强度模型中的假设贴近实际, 但条件违约概率较难有对应的经济含义, 难以通过实际数据进行计算得到, 因此多为理论研究。Çetin et al.(2004)、Guo et al.(2009)分别从投资者信息不完整、信息披露延迟的角度对强度模型中条件违约概率过程的性质进行了建模, 讨论了估计违约强度过程的方法, 因其仍需要对市场信息的滤波做较强的假设, 难以对应提出实证的方法。Duffie and Lando(2001)、Giesecke(2006)结合两类模型提供了重要研究思路:保留了首达时间计算概率的方法, 且假设投资者并不能完全观测企业的价值或违约的条件, 这为本文讨论投资者异质信念下的信用风险量化模型提供了重要基础。
除了将两类模型的优势结合, 我们还引入了行为金融中的重要概念——投资者异质信念。投资者异质信念也称为投资者意见分歧(David, 2008)。在针对债权类产品的理论研究中, Yan and Xiong (2010)在将投资者中的异质信念简化为两组意见不同的投资者, 通过市场出清条件推导债券价格, 并指出异质信念可以解释在同质预期债券定价模型中出现的“过度波动”之谜, 且会极大的影响信用风险的溢价在时间维度上的变化。Chiarella et al.(2015)也通过对欧洲主权CDS市场的实证研究指出, 假设投资者对国家基本面的异质信念可以更好地解释CDS息差的变动, 尤其在全球经济危机之后, 异质信念加剧了CDS息差(CDS spread)及其波动的增大。Boswijk and Hommes(2007)总结, 异质信念的形成主要来自于两个方面:市场中的信息不对称和投资者判断决策的差异。对应于我国市场, 异质信念因素更不可忽视:由于信息披露滞后、信息来源不完整和信息披露扭曲, 投资者所掌握的信息集与债券发行人的信息集之间具有差异;而对于市场的公开信息, 资本市场的系统性诚信危机下(黄世忠, 2018), 投资者对信息披露的信息不同, 判断决策的差异也在拉大。Gao et al.(2019)通过实证研究也指出, 风险警示的发布增加了市场中买卖价差和价格的波动, 说明投资者异质信念程度因此增加, 进而推动了企业债券价格下行, 信用利差增大。从建模的角度, 异质信念表现为投资者对于相同持有期下资产收益率的条件期望、方差—协方差矩阵或其变动方式的估计不同(David, 2008)。因此在对我国当前债券市场信用风险量化建模中, 我们将Giesecke(2006)中关于企业违约阈值预期的均匀分布假设拓展到一般的Beta分布, 通过Beta分布的方差刻画投资者异质信念的强度, 进而得到信用债条件违约概率和信用利差的一般解析式, 并在此基础上进行数值分析和实证案例检验。
三、模型构建 (一) 模型基本假设首先给出债券市场上不确定性经济环境的数学刻画, 用概率空间(Ω, F, P)来表示不确定性的宏观经济环境和微观市场主体可能拥有的所有的信息的概率空间, 其中F为由Ω子集生成的事件域, 表示在时刻债券发行人财务状况、公司资产价值、市场信息、投资者预期等集合, 例如企业资产和负债, 企业利润表和现金流量表等, 企业的资产价值以及投资者对债券是否违约的分歧等, 也包括债券发行后企业披露的信息, 以及所有与企业经营管理有关的重大事件, 例如管理层的变化等事件, P表示投资者能够获取这些信息的客观概率测度。以下都在这样的概率空间中研究债券条件违约概率及信用利差。
1.对于公司价值的基本假定
对于投资者而言, 投资者不可能知道每个时刻的公司价值, 通常我们假设公司的价值服从几何布朗运动, 与结构化模型(Black and Scholes, 1974)的假设一致:
| $ \frac{{d{X_t}}}{{{X_t}}} = rdt + \sigma d{W_t},{X_0} > 0 $ | (1) |
Xt表示t时刻公司的价值, X0表示公司初始价值, r表示公司价值的预期增长率, σ是公司价值预期增长的波动率, Wt为标准布朗运动, 具有唯一解:
| $ {X_t} = {X_0}{e^{{V_t}}} $ | (2) |
其中Vt=mt+σWt是一个带漂移的布朗运动, 其漂移项为
2.对公司债务及违约的基本设定
本文假设投资者具有异质信念, 即对企业违约阈值的分布具有不同的预期;另外假设在时刻0, 企业发行有限期的贴现债券, 到期日为T。债券违约时间仅由公司的管理层决策, 在债权到期之前的任意时间点都可能发生违约。假设d为投资者预期企业违约时的资产价值, 即投资者预期当Xt<d时, 公司的管理层选择违约, 在投资者异质信念的假设下, d不为常数, 假设D=log(d/X0), 从而D也不为常数。参照Black-Cox(1976), 我们使用首达时间的方法, 用随机变量τ来描述债券的违约时间:
| $ \tau = inf\left\{ {t > 0:{V_t} \le D} \right\} $ | (3) |
而且我们在此定义一个违约的示性变量:Nt=1{τ≤t}, 即当τ≤t, 取值1, 否则取值0。则该企业直到时刻t之前的历史违约状态对应的信息滤波为
| $ {{\rm{g}}_t} = {F_t} \vee \sigma \left( {{N_s}:s \le t} \right) \in F $ | (4) |
这里gt为投资者对公司资产价值、债券价格、违约时间、异质信念的总信息滤波。因此, 我们可以通过违约过程F(t)=Nt的条件期望得到条件违约概率, 即:
| $ IE\left[ {F\left( t \right)|{{\rm{g}}_t}} \right] = IE\left[ {{N_t}|{{\rm{g}}_t}} \right] = P\left[ {\tau \le t|{{\rm{g}}_t}} \right] $ | (5) |
在上述假设下, 假设投资者可以观测到完整且连续的企业资产价值过程, 在到期日前的任意时间点, 在资产价值第一次低于违约阈值时, 企业即为违约, 即当企业资产价值过程的最低值Mt=mins≤tVs低于违约阈值D时会发生违约, 在Black-Cox(1976)模型中, 违约概率可以通过一个首达时间的概率计算。
| $ {P_{Black - Cox}}\left[ {\tau \le T|{{\rm{g}}_{\rm{t}}}} \right] = \mathit{\Phi }\left( {\frac{{{\rm{D}} - {{\rm{M}}_{\rm{t}}} - {\rm{m}}\left( {{\rm{T}} - {\rm{t}}} \right)}}{{\sigma \sqrt {{\rm{T}} - {\rm{t}}} }}} \right) + \mathit{exp}\left( {\frac{{2{\rm{m}}}}{{{\sigma ^2}}}} \right)\Phi \left( {\frac{{{\rm{D}} - {{\rm{M}}_{\rm{t}}} + {\rm{m}}\left( {{\rm{T}} - {\rm{t}}} \right)}}{{\sigma \sqrt {{\rm{T}} - {\rm{t}}} }}} \right) $ | (6) |
其中Φ(·)表示标准正态分布累积函数。
(二) 投资者异质信念下的条件违约概率在上述假设下, 本文先根据结构化模型Black-Cox思想, 当企业资产价值过程的最低值Mt=mins≤tVs低于违约阈值D时会发生违约, 而在投资者具有异质信念的假设下, 不同投资者对于企业违约阈值的分布具有不同的预期, D不为常数, 参照Giesecke(2006)的假设, 假设D是一个不可观察的连续随机变量, 服从先验概率分布G(·)。
再结合强度模型思想, 考虑了在测度gt下的企业条件生存概率Lt=1-F(t)=P[τ>t|gt], 则Lt过程是一个测度gt下的上鞅, 生存的预期随时间增加而降低, 且条件生存概率具有动态性。在D服从先验概率分布G(·)假设下, 有:
| $ {L_t} = P\left[ {D < {M_t}|{{\rm{g}}_t}} \right] = G\left( {{M_t}} \right) $ | (7) |
因此我们可得(限于篇幅, 具体证明可向作者索取):
| $ P\left[ {\tau \le T|{{\rm{g}}_t}} \right] = 1 - {\rm{IE}}\left[ {\frac{{G\left( {{M_T}} \right)}}{{G\left( {{M_t}} \right)}}|{{\rm{g}}_t}} \right],t < \tau ,\tau \le T $ | (8) |
定义首达时间τx=inf{t>0:Vt≤x}, 则其是一个反式高斯过程P(τx≤t)=P(mins≤tVt≤x), 因此, 我们有τx的分布函数和分布密度(参见Karatzas and Shreve, 1998):
| $ \Psi \left( {t,x} \right) = P\left[ {{V_t} < x} \right] = P\left[ {\mathop {\min }\limits_{s \le t} \left( {ms + \sigma {W_s}} \right) \le x} \right] = \Phi \left( {\frac{{x - mt}}{{\sigma \sqrt t }}} \right) + \exp \left( {\frac{{2mx}}{{{\sigma ^2}}}} \right)\Phi \left( {\frac{{x + mt}}{{\sigma \sqrt t }}} \right) $ | (9) |
| $ \psi (t,x) = \frac{d}{{dx}}\Psi (t,x) = \frac{{\Phi \left( {\frac{{x - mt}}{{\sigma \sqrt t }}} \right)}}{{\sqrt t }} + \frac{{2m}}{{{\sigma ^2}}}\exp \left( {\frac{{2mx}}{{{\sigma ^2}}}} \right)\Phi \left( {\frac{{x + mt}}{{\sigma \sqrt t }}} \right) + \exp \left( {\frac{{2mx}}{{{\sigma ^2}}}} \right)\frac{{\Phi \left( {\frac{{x + mt}}{{\sigma \sqrt t }}} \right)}}{{\sigma \sqrt t }} $ | (10) |
Ψ(t, x), ψ(t, x)分别表示τx的分布函数和分布密度, 其中Φ(·)表示标准正态分布累积函数。我们用κ表示违约时企业资产价值可能值的上限, 代入我们得条件违约概率:
| $ P\left[ {\tau \le T|{{\rm{g}}_t}} \right] = 1 - \frac{1}{{G\left( {{M_t}} \right)}}\int_{ - \infty }^{{M_t} \wedge \frac{\kappa }{{{x_0}}}} G (y)\psi \left( {T - t,y - {M_t}} \right)dy $ | (11) |
在真实的金融市场中, 投资者无法在违约发生之前直接观察到企业管理层对于违约的决策, 而违约成本低、市场信息披露扭曲、市场评级有效性较弱等我国信用债市场一系列的问题导致市场对企业还债意愿的判断模糊。投资者异质信念最终体现在不同投资者对于企业发生违约的资产阈值预期不同, 异质信念的强度与企业资产状况、当下投资者对企业的信心相关。Giesecke(2006)假设市场中的投资者预期违约时的企业资产价值d=X0eD为[0, X0]上的均匀分布, 则先验分布GGiesecke(x)=ex, x < 0。然而, 均匀分布并不适合对于市场的描述, 因为在实际情况中, 接近均匀分布两侧极值的数字几乎不可能取到, 不会有投资者预期企业价值为零时才宣告违约, 且预期违约阈值为[0, X0]中各个值的投资者不可能数量相同, 企业当下的财务状况与投资者信息会影响投资者对于债券违约的预期。
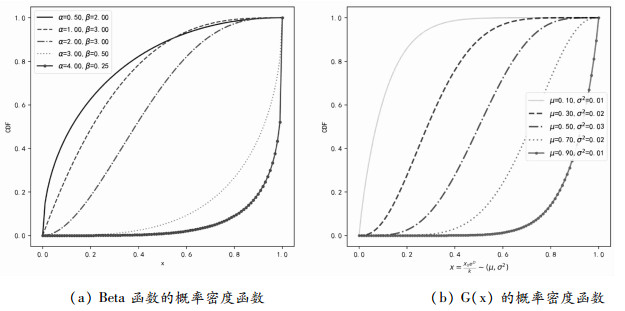
本文通过假设违约阈值服从Beta(α, β)分布来引入投资者异质信念的影响, 可以看成是Giesecke(2006)模型的拓展, 因为均匀分布其实可以看成特殊的Beta分布。Beta(α, β)分布是由其均值和方差决定其概率分布的形状, 可以很好地描述投资者不同情况下不同形状的预期概率分布(见图 2), 当方差越大, 即投资者对于违约阈值异质信念的强度越大时, 预期违约概率随违约阈值增长的变化也越大。
|
图 2 Beta函数可较好刻画投资者不同的预期偏好变化 |
与上文一致, 我们用κ表示触发违约时所有可能企业资产价值的最大值。在真实情况下, 违约时的企业资产价值可能为[0, κ]中的任意值。为了更真实的刻画企业违约与企业的资产及负债规模均相关, 我们将Beta分布扩展到κ规模中, 记为Betaκ分布, 其中κ是与企业资产及负债规模相关的参数。假设违约阈值d服从Betaκ(α, β), 即
| $ G\left( x \right) = \frac{{{X_0}}}{{B\left( {\alpha ,\beta } \right)\kappa }}\int_{ - \infty }^x {{{\left( {\frac{{{X_0}{e^u}}}{\kappa }} \right)}^{\alpha - 1}}} {\left( {1 - \frac{{{X_0}{e^u}}}{\kappa }} \right)^{\beta - 1}}{e^u}du $ | (12) |
这里,
| $ \alpha = \frac{{\mu _{Beta}^2\left( {1 - {\mu _{Beta}}} \right)}}{{\sigma _{Beta}^2}} - {\mu _{Beta}},\beta = \frac{{{{\left( {1 - {\mu _{\sigma Beta}}} \right)}^2}}}{{\sigma _{Beta}^2}} - \left( {1 - {\mu _{Beta}}} \right) $ |
参考Giesecke (2004)的思路, κ设定为负债总额除以过去六个月最高的资产负债率。κ∈(0, X0]即违约阈值的上限, 且κ与企业的资产负债率相关, 当企业的资产负债率是六个月以来最高时, κ即为企业的资产总值。
Betaκ分布的均值μBetaκ是投资者的预期, 即市场投资者对于管理层违约时资产价值的平均判断, 当企业资产价值Xt<μBetaκ时, 50%的投资者认为企业管理层会选择违约;Betaκ分布的方差σBetaκ2是投资者对于违约阈值意见分歧的表现, 表现的是投资者的异质信念。如果建模对象是企业发生破产的概率, μBetaκ应设为企业的短期负债(到期期限一年以内的负债数额)。而信用债违约对于企业来说是一个更为主观的过程, 企业管理者的偿付意愿不一定完全依赖于资产负债结构, 因此, 在此我们假设μBetaκ为企业的短期负债加上50%的非流动负债(μBetaκ=SD+0.5*TD), 且对Betaκ的方差σBetaκ2构建如下:
| $ \sigma _{Beta\kappa }^2 = \left( {\left( {\kappa - {\mu _{Beat\kappa }}} \right) * {\mu _{Beat\kappa }} + \sigma _{2w}^2 * {\kappa ^2}} \right) * \frac{1}{{10}} $ | (13) |
σBetaκ2第一项是与企业资产价值状况相关的参数(κ-μBetaκ)*(μBetaκ/10), 企业的短期负债相较于违约上限越远, 投资者对于违约的分歧越大, 异质信念越强。相对来说, 我国的股票市场交易活跃, 企业信息在股票市场中反映强烈, 除了企业的财务数据以外, 股票市场的价格可作为预测债券违约的重要信息来源。上市公司在二级市场的股价波动体现了投资者对于企业未来预期的不确定性, 我们使用股票日收益率最近两周的年化波动率σ2w2作为投资者信心的代理变量, 当股价波动越剧烈时, 投资者对于企业价值的分歧越大, 异质信念越强。
| $ \begin{array}{l} P\left[ {\tau \le T|{{\rm{g}}_t}} \right] = 1 - {\rm{IE}}\left[ {\frac{{G\left( {{M_T}} \right)}}{{G\left( {{M_t}} \right)}}|{{\rm{g}}_t}} \right]\\ = 1 - \frac{{{X_0}}}{{B\left( {\alpha ,\beta } \right)\kappa G\left( {{M_t}} \right)}}\int_{ - \infty }^{{M_t} \wedge \mathit{log}\left( {\frac{\kappa }{{{X_0}}}} \right)} {{{\left( {\frac{{{X_0}{e^u}}}{\kappa }} \right)}^{\alpha - 1}}} {\left( {1 - \frac{{{X_0}{e^u}}}{\kappa }} \right)^{\beta - 1}}{e^u}\Psi \left( {T - t,u - {M_t}} \right)du \end{array} $ | (14) |
此外还考虑到, 债券违约后通常也不会毫无剩余价值。通过不良资产处置、展期等渠道, 2014年首例11超日债违约事件以来, 债券违约的整体回收率平均为30.37%, 其中国企债券为55.13%, 民企债券为24.18%。假设当公司债券违约时, 尚能收回比例R的面值, 可得有剩余价值的债券条件违约概率(HB模型)(限于篇幅, 推导过程可向作者索取):
| $ P\left[ {\tau \le T|{{\rm{g}}_t}} \right] = 1 - IE\left[ {{{\left( {\frac{{G\left( {{M_T}} \right)}}{{G\left( {{M_t}} \right)}}} \right)}^{\left( {1 - R} \right)}}|{\mathit{g}_t}} \right],t < \tau ,\tau \le T $ | (15) |
假设债券信用利差为CS(t, T), CS(t, T)是指t时刻, 一只T时刻到期的公司零息债券的内部收益率与T时刻到期的无风险债券的利率之差。信用利差是市场对于公司违约风险的利率补偿。不失一般性, 假设T时刻到期的债券在t时刻的理论价格为B(t, T), f(T-t)为期限为(T-t)的市场无风险利率, 根据资产定价的风险中性公式和信用利差的定义:
| $ \begin{array}{l} B\left( {t,T} \right) = {e^{ - f(T - t)(T - t)}}IE\left[ {{1_{\left\{ {\tau > T} \right\}}}} \right] + R{e^{ - f(T - t)(T - t)}}IE\left[ {{1_{\left\{ {\tau \le T} \right\}}}} \right]\\ = {e^{ - f(T - t)(T - t)}}\left( {1 + \left( {R - 1} \right)P\left[ {\tau \le T|{{\rm{g}}_t}} \right]} \right) = {e^{ - \left( {f\left( {T - t} \right) + CS\left( {t,T} \right)} \right)\left( {T - t} \right)}} \end{array} $ |
对该式子两边取对数, 整理后可得t时刻的具有违约剩余价值的债券的理论信用利差CS(t, T), 即:
| $ CS\left( {t,T} \right) = - \frac{1}{{T - t}}\mathit{log}\left( {1 + \left( {R - 1} \right)P\left[ {\tau \le T|{{\rm{g}}_t}} \right]} \right) $ | (16) |
特别的, 当t∈[0, T], R=0时, 由、可得信用利差CS(t, T):
| $ CS\left( {t,T} \right) = - \frac{1}{{T - t}}\mathit{log}\left( {\frac{1}{{G\left( {{M_t}} \right)}}\int_{ - \infty }^{{M_t} \wedge \frac{\kappa }{{{x_0}}}} G (y)\psi \left( {T - t,y - {M_t}} \right)dy} \right),t < \tau ,\tau \le T $ | (17) |
为了进行比较, 我们对模型进行数值分析。假设企业初始资产价值X0=100, 当前t时刻企业资产价值为Xt=70, 即t时刻的企业的资产价值过程为Vt=log(Xt/X0)=-0.1549, 到期时间T=1, 短期负债SD=30, 长期负债TD=40, 违约剩余价值R=30%, 违约阈值上限κ=90, 股票两周年化波动率σ2w2=0.25, Betaκ分布的方差σBetaκ2由(13)可得。为了研究异质信念强度变化的影响, 我们对异质信念强度做ξ倍扩展代入数值模拟中, ξ倍的投资者异质信念强度即指σBetaκ2(ξ)=ξσBetaκ2。
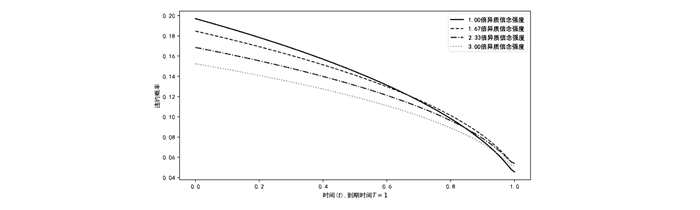
图 3给出了不同异质信念强度下违约概率随距离到期日变化的情况。越接近到期日, 相同资产水平情况下, 可能发生违约的条件概率越低。在距离到期日较远, 模型估计违约概率较大时, 异质信念强度越高, 模型估计违约概率越低。
|
图 3 信用债(T=1)违约概率在不同异质信念强度下随距离到期日变化的情况 |
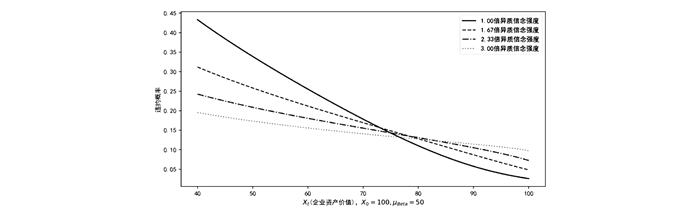
在图 4中, 我们研究了研究不同异质信念强度下违约概率和企业资产价值变化的影响关系, 假设当前时刻t=0.2。通过(13)可以直接地看出, 投资者的意见分歧一部分来自于企业的资产价值距离违约阈值的距离, 距离越远, 违约的不确定性越高, 异质信念强度越大;另一部分来自于投资者对于企业未来收益的不确定性(在我们的数值分析模拟中, 我们将此部分简化为常数代入)。可以看出, 在企业资产价值较低, 即违约可能性较高时, 投资者预期同质性越高, 即异质信念越弱时, 模型估计违约概率越高;而当企业资产价值较大, 违约可能性较低时, 异质信念的减弱反而降低模型估计违约概率。因此, 在信用债偿付预期良好时, 异质信念可能导致违约概率的高估, 而在信用债违约的可能性较大时, 市场中投资者异质信念强度越高, 越有可能低估信用债的违约概率, 一旦违约事件发生, 易造成更大的市场冲击。
|
图 4 信用债(T=1)违约概率在不同异质信念强度下随企业资产价值变化的情况 |
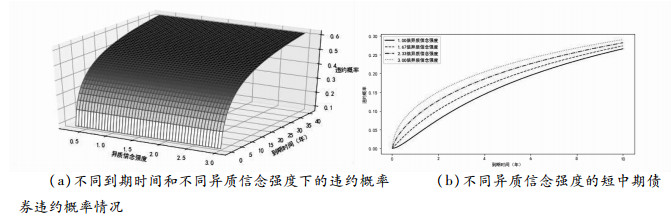
在图 5中, 我们研究了异质信念强度和违约概率期限结构的关系, 考虑预测时间点t=0时, 不同期限的信用债的模型估计违约概率, 其余参数假设与图 3一致, 考虑不同到期时间T的信用债。图 5(a)中我们可以看到, 随着信用债到期时间的增加, 对应违约概率增大, 且通过图 5(b)可以发现, 在期限结构上, 投资者异质信念越强, 预期违约概率越高;期限越长, 异质信念的影响越弱。这可以解释, 在中长期债券市场上, 信用利差差别较小的现象:对于中长期债券来说, 投资者的意见分歧大小对违约概率影响在长期限的作用下被稀释, 违约的不确定更多来自于信用债的时间效应。
|
图 5 异质信念强度与违约概率的期限结构关系 |
如所示, 信用利差与信用债违约概率估计值是一一对应的关系, 在图 6中, 我们应用了与图 4相同的数值假设, 可以得到与图 4相同的结论:企业资产价值较低, 违约可能性较高时, 投资者预期同质性越高, 即异质信念越弱时, 模型估计信用利差越高。
|
图 6 信用债(T=1)信用利差在不同异质信念强度下随企业资产价值变化的情况 |
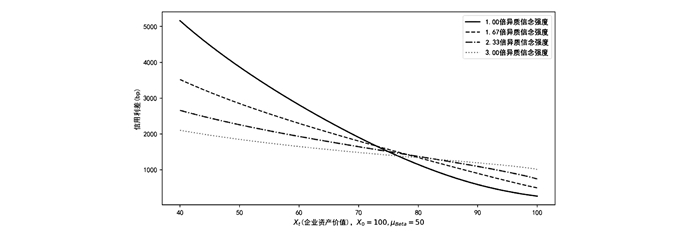
在图 7中, 我们考虑t=0时刻, 不同期限的信用债, 异质信念强度对信用利差期限结构的影响。其他的参数设置与图 3一致, 即X0=100, SD=30, TD=40, R=30%, κ=90, σ2w2=0.25。与图 5的结论一致, 在异质信念的影响下, 3年期以内的信用债会受到投资者异质信念的影响, 而对10年期以上的长期债券影响较小。

|
图 7 异质信念强度对信用利差期限结构的影响 |
图 7也同时说明我们模型的有效性。可以看出, 对于投资者异质信念强度极低的情形里, 短期信用利差趋近于0, 而对于存在异质信念的情况下, 得到了非零的短期信用利差, 且随着异质信念强度的增大而增加, 这可以很好地对应真实债券市场中短期信用利差的非零现象。投资者异质信念增加, 因此增加了违约的不确定性, 从而投资者需要从信用利差中得到对应的风险补偿。
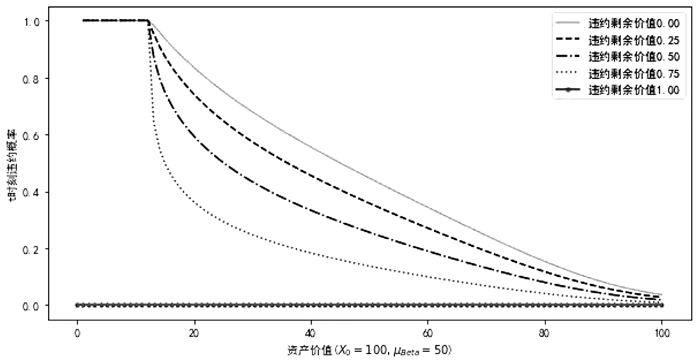
(三) 债券剩余价值(“刚性兑付”预期)对违约概率影响的数值分析债券违约剩余价值依赖于企业可变现资产的结构及违约追偿规则。投资者预期的债券违约剩余价值约接近于1, 投资者的“刚性兑付”预期越大。我们研究了投资者异质信念下, 投资者预期的债券违约的余价值对债券违约的条件概率的影响。除了违约剩余价值R会在数值分析中取不同的值, 其他的参数设置与图 3均一致。根据图 8可以看出, 债券违约后的剩余价值会显著的影响债券违约概率。在模拟的极端情况下, 模型也具有有效性:当债券违约的剩余价值为1时, 即如果债券违约也会得到全额兑付的情况下, 无论企业的资产增长还是下降, 企业违约与否是没有区别的, 所以模型估计的违约概率都为0。而在相同资产水平下, 随着剩余价值增加, “刚性兑付”预期的增强, 条件违约概率减少;在越接近企业初始资产水平时, 违约剩余价值的影响越弱。这与我们真实的债券市场观测也一致, 违约剩余价值高的债券通常为国企或政府支持的债券, 违约与否更有赖于企业对当地的贡献, 政府从中协调、隐性担保, 使得投资者对应“刚性兑付”预期高(狄灵瑜、步丹璐, 2019), 条件违约概率也相对较低;企业资产价值下降较小时, 违约概率较低, 违约剩余价值的差异也就并不会对违约估计概率造成很大影响。
|
图 8 违约概率与债券违约剩余价值之间的关系 |
根据以上的数值分析可以看出, 从期限结构上来看, 投资者异质信念对于短中期信用债的影响最为显著, 异质信念越高, 预期违约概率与信用利差越大。对于单只信用债而言, 在违约可能性较低的情况下, 投资者异质信念会造成违约概率的高估;而在违约事件发生可能性高的情况下, 投资者的异质信念低估违约概率。这说明, 对于短中期信用债而言, 投资者对于企业信息披露的准确、及时性要求更为迫切, 如果企业无法及时、真实地披露营运状态和兑付意愿, 会造成二级市场上的迅速抛售。而在违约阈值附近时, 企业的信息模糊造成的投资者异质信念增高, 可能会造成违约概率的低估, 如果真正发生信用违约事件时, 债券价格发生断崖式下降, 对市场的冲击巨大。此外, 投资者预期的违约债券剩余价值越高, 模型估计违约概率越低, 当投资者具有“刚性兑付”预期时, 投资者甚至对企业资产价值的变化不敏感, 价格波动反映在市场中也较小。通过模型的数值分析, 说明了模型的有效性, 并从投资者异质信念的角度解释了短中期债券信用利差的非零现象, 以及信用债市场违约事件造成的价格断崖式下降的现象。
五、实证分析与结果为了验证模型的有效性, 我们以两起违约事件来进行检验, 并与Black-Cox(1976) (见(26))、Giesecke(2006)的理论模型结果与我们的模型(HB模型)进行比较。其中, Giesecke(2006)对投资者违约阈值预期做均匀分布的假设, Black-Cox直接假设投资者违约阈值为固定值
检验违约事件包括一只公司债“11超日债”和一只短融债券“17永泰能源CP005”, 回测所用的模型参数估计见表 1①。选择公司债“11超日债”是因为该债券是中国债券市场的首例债券违约事件, 且最终债券发行人上海超日太阳能科技股份有限公司发生破产重组, 是一例典型的公司破产导致的信用违约事件, 2014年被因此称为“债券违约元年”。而选择短融债券违约事件的原因有二:一, 短融债券标的为上市公司, 股权价值的数据更新频率为日;二, 大部分上市公司的债券含有增信的条款;大部分企业债都为城投债, 或具有回售、赎回条款, 债券价格无法直接反映信用利差, 而超短融时间较短, 不具有外部增信或其他附加条款, 可以近似认为信用风险补偿是利差的唯一原因。
| 表 1 模型参数估计 |
① 本文数据来源于Wind数据库和Bloomberg, 使用Python3.7.1计算, 代码可向作者索取。
| 表 2 信用违约事件基本信息 |
(四) 模型计算步骤
(1) 企业价值Xt与企业价值的波动σtX的计算
在模型的应用中, 企业价值和企业价值的波动是重要的输入参数。每日的企业价值无法观测, 因此我们可以利用企业的负债和股权价值的波动来反推企业的资产价值与波动。我们可以把企业的股权价值(St)看成企业的一个关于企业资产价值的欧式看涨期权, 其执行价为Kt(企业的短期负债(小于一年)), 到期时间为一年(T=1)。
| $ {S_t} = {X_t}N\left( {{d_1}} \right) - {K_t}{e^{ - rT}}N\left( {{d_2}} \right) $ | (18) |
其中,
| $ {S_t}\sigma _t^S = \frac{{\partial S}}{{\partial X}}{X_t}\sigma _t^X = N\left( {{d_1}} \right){X_t}\sigma _t^X $ | (19) |
股权价值St对应股票市值除以流通股比例, σtS为过去100周的股价波动率, 联立(18)(19), 即可得Xt和σtX。
(2) 债券价格超额利差与隐含违约概率
为了与模型所得的信用利差进行比较, 我们从市场价格倒推债券的超额利差。市场中的简化做法是计算债券的到期收益率后, 减去期限相同的无风险收益率(T-Spread)。但对于我们的样本期, 市场的无风险收益率变化较大, 而这种方法忽视了债券面值和付息结构的特征对收益率曲线的影响, 会造成较大的误差。考虑市场的无风险收益率的期限结构, 我们认为Z-Spread(Zero-Volatility Spread)可以较好的体现债券价格的超额利差, 定义CS*(t, T)为到期日为T, 面值为100, 年化利率为c的债券在t时刻的超额利差(考虑到我国的国债和大部分企业债都为单利, 下面也只考虑单利的情况), f(t)表示是t时刻到期的无风险利率, B(t, T)表示T时刻到期债券在t时刻的价格:
| $ \begin{array}{l} B\left( {t,T} \right) = c * (t - [t]) * \rho + \frac{{c * \rho }}{{\left( {1 + f(1 + t - [t]) + C{S^*}(t,T)} \right)}} + \\ \cdots + \frac{{(c + 100) * \rho }}{{\left( {1 + f(1 + t - [t]) + C{S^*}(t,T)} \right)\left( {1 + f(2 + t - [t]) + C{S^*}(t,T)} \right) \cdots \left( {1 + f(t) + C{S^*}(t,T)} \right)}} \end{array} $ | (20) |
| $ \rho = \frac{1}{{1 + \left( {f(t - [t]) + C{S^*}(t,T)} \right) * (t - [t])}} $ |
在计算得到超额利差后, 根据式(16)即可得考虑违约剩余价值的债券价格市场隐含条件违约概率:
| $ {P_{imp}}\left[ {\tau \le T|{{\rm{g}}_t}} \right] = \frac{{{e^{ - CS*}}(t,T)(T - t) - 1}}{{R - 1}} $ |
(五)模型应用——以11超日债和17永泰能源CP005为例
“11超日债”是由上海超日太阳能科技股份有限公司2011年发行的公司债券, 发行期限5年, 利率为固定利率的3+2结构。其历史价格变动见图 4。“11超日债”的利息偿付期为每年的3月7日, 第二期2014年3月7日应偿付8, 980万元利息, 实际仅兑付400万元, 构成实质性违约, 且于同年4月8日申请破产重组。该债券违约事件为国内首例公司债违约, 因此, 2014年也被称为债市违约元年。“17永泰债CP005”是由永泰能源股份有限公司2017年发行的短融债券, 发行期为1年, 固定利率。在2018年7月4日交易日后, “17永泰债CP004”宣告到期本息兑付违约, 同时永泰能源和永泰集团在银行间市场的14支存续债券触发交叉违约条款。短融债中“17永泰债CP005”(2017年8月28日到期)后在2017年7月31日摘牌, “17永泰债CP005”存续时间较长, 因此本文选取“17永泰债CP005”进行运算。
本文的模型计算利用了超日股份(002506.SZ)从2012年3月7日到2014年3月4日的日交易行情数据, 其相关财务数据来自于2012年3月至2013年12月的披露财务报表;永泰能源(600157.SH)2017年7月5日至2018年7月31日的交易日行情数据, 相关财务数据来自于2017年6月至2018年6月的季度报, 数据均来源于Wind数据库。
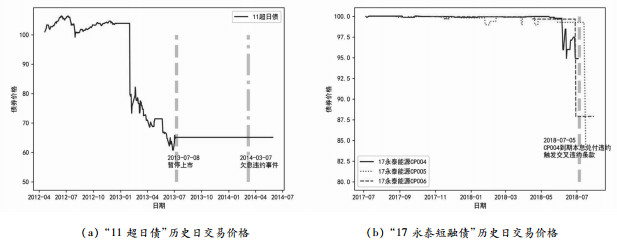
|
图 9 “11超日债”与“17永泰短融债”历史日交易价格 |
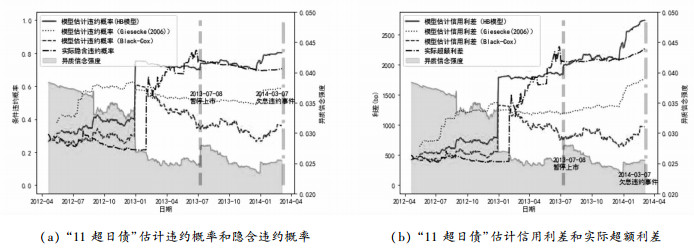
“11超日债”的估计结果见图 10。实线为HB模型的估计结果, 为了比较预测能力, 我们给出了Giesecke(2006)模型、Black-Cox模型结果及利用市场数据计算的隐含违约概率与超额利差(见图中虚线部分), 投资者异质信念强度用阴影部分表示。随着企业财务状况的恶化, 投资者对违约的预期更为集中, 投资者异质信念呈现下降趋势。可以直观的看到, 市场中投资者异质信念的突变被HB模型捕捉到, 让HB模型比实际市场数据提前一个月出现了违约概率的突增(2012年12月28日从39.67%到12月31日的75.18%), 欠息违约事件发生时, HB模型计算的条件违约概率为80.17%, Black-Cox模型虽然也体现了突增的预警, 但大部分时间都较市场更低估违约概率, 甚至在预警出现后出现违约概率下降的趋势。因为超日债2013年7月8日起暂停上市, 因此市场价格超额利差与隐含违约概率仅体现出期限结构的变化, 并没有体现实际的信用风险, 与模型的估计结果方向不一致, 其他的时间HB模型的估计结果都与真实的市场表现更为符合。Giesecke(2006)模型中对违约阈值预期的均匀分布假设与市场相差较大, 因此估计结果误差较大且无预警能力。
|
图 10 “11超日债”的模型计算结果和实际数据 |
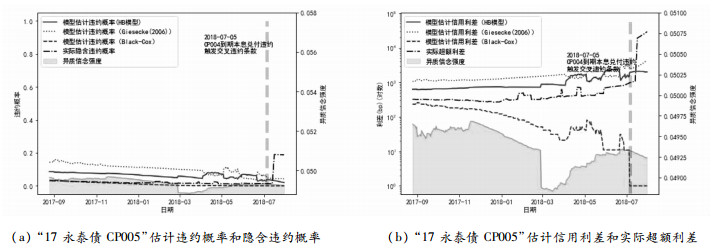
图 11给出了永泰SCP005的估计和比较结果。永泰SCP005短融债交易量小, 市场价格波动小, 隐含违约概率也一直在0附近, 投资者异质信念的强度波动也很小。其中, HB模型和Giesecke(2006)计算结果一直高于市场隐含违约概率, 且于发生交叉违约事件的三个月之前就出现了违约概率上的突增(2018年4月3日的7.07%至两个交易日后的2018年4月10日, 20.88%), 对应的信用利差也出现了增长。值得注意的是, 因为“永泰能源SCP005”只是触发了交叉违约条款, 实际兑付方案并未违约, 并不是的“资不抵债”式的违约, 因此完全依赖于企业财务杠杆状况的Black-Cox模型无法预警违约, 违约前夕概率预测依旧为0, 我们的模型给出了41.2%的条件违约概率。为了区分不同模型的计算结果, 信用利差示意图我们使用对数轴, 数值小的区域在图中会体现出较大的波动, 永泰SCP005期限短, 因此Black-Cox模型结果看似差异较大, 但其实来自于计算中的微小变动, 违约概率始终接近于0, 信用利差也接近于0。考虑到永泰能源在同时期发行了数十只信用债产品, 均含有交叉违约条款, 因此增大了单个信用债发生违约事件的可能性。而从建模的角度上考虑该要素比较困难, 模型估计的绝对值会低估违约的概率, 但HB模型与Giesecke(2006)和Black-Cox模型相比, 捕捉到投资者异质信念的变化而给出预警信号, 依旧具有占优的预警效果。
|
图 11 “17永泰债”的模型计算结果和实际数据 |
本文实证的两个信用案例分别由企业偿付困难和交叉违约条款触发, 对于前者, 模型给出了良好的预测精度, 后者给出了较好的预警效果, 均体现出了模型的实际应用价值。
(六) HB模型预警能力稳健性分析
在前文数值分析的部分, 我们已经通过一个模拟的参数集讨论了考虑投资者异质信念时, 不同企业基本面、信用债条款下, 信用债条件违约概率的数值结果与变化, 并通过列举极端情况, 说明了HB模型的有效性。量化模型的建立是为了提供评估信用风险的工具, 为风险事件的定性分析提供基础, 因此, 模型的预警能力尤为重要。为了更好地说明模型预警能力的稳健性, 基于我们的实证案例, 我们计算了在企业基本面、信用债条款不变的情况下, 异质信念的强度参数变化下HB模型的结果, 检验其稳健性。异质信念的强度由投资者企业违约阈值分布的方差的乘数控制σBetaκ2(ξ)=ξσBetaκ2。
图 12(a)给出了“11超日债”的预警稳健性分析。可以看出, 市场中投资者异质信念变化的情况下, 模型结果中的突增也得以保留, 可以给出较好的预警效果。且与我们数值分析结果一致, 在企业的资产负债结构较为合理, 条件违约概率较低的时期, 高投资者异质信念强度会高估违约概率, 而在2013年1月附近, HB模型给出违约概率的突增后, 高投资者异质信念低估违约概率。值得指出的是, 虽然我们的模型输入中没有债券价格的数据, 但是因为投资者异质信念的引入, 我们的模型给出了明确的信号:在2013年7月8日, “11超日债”因2011年、2012年连续两年亏损暂停上市后, 模型估计的条件违约概率没有发生突变, 但在稳健性分析中给出了高投资者异质信念高估违约概率, 低投资者异质信念低估违约概率的结果。这样反转的现象我们认为来自于投资者的刚性兑付预期的变化:由企业连年亏损触发企业债暂停上市, 投资者刚性兑付的预期降低, 因此造成条件违约概率的增加, 投资者异质信念越强(3倍投资者异质信念), 这样的增加的水平越多;而投资者异质信念影响被忽视时(0.3倍投资者异质信念), 违约概率会被低估。

|
图 12 HB模型应用违约估计概率稳健性分析 |
图 12(b)利用“17永泰债CP005”的数据对模型的稳健性进行检验。如前文分析, 该债券并非“资不抵债”式的违约, 短期限内企业的资产状况变化较小, 很难根据企业杠杆变化预测违约, 投资者异质信念的引入就显得尤为重要。可以看出, 该实证案例中, 条件违约概率对异质信念强度的变化非常敏感, 在企业财务杠杆水平正常时, 投资者异质信念高, 对应条件违约概率也会增高。但异质信念强度的变化不影响数值上突增变化带来的预警功能, 依旧体现了模型预警能力的稳健性。
六、结论与启示在信用债风险量化中, 结构化模型便于利用实际数据进行测算, 但模型假设与现实有差距, 强度模型具有良好假设, 但模型参数较难具有直观的经济含义对应。本文提出的HB模型结合了两类模型的优点, 并结合我国债券市场的特点, 考虑了来自发行主体财务状况、市场信息、投资者信心的多重信息的因素, 提出了一个考虑投资者异质信念的债券风险量化模型, 获得了企业条件违约概率、信用价差的理论计算公式。投资者异质信念是投资者对于信用债发行人违约的意见分歧, 取决于投资者对于企业信息披露和经营发展的信心, 通过数值分析我们发现:一, 投资者异质信念对短中期信用债影响较大, 异质信念越高, 信用利差越大, 短中期债券信用利差的非零现象来自于投资者对信用债发行人违约的意见分歧而要求的风险补偿;二、距离到期日较远、资产水平较好时, 违约可能性较低, 异质信念的存在会高估违约概率;而违约可能性升高时, 异质信念越高, 越容易造成市场对违约概率的低估, 进而使得信用事件对市场的冲击更大。三、“刚性兑付”预期会造成投资者对企业资产价值变动不敏感, 预期违约剩余价值越高, 模型估计违约概率越低。本文的模型含有内生的违约概率, 且参数均具有实际经济含义。我们通过使用历史的股价数据和财务数据, 对我国信用债市场已发生的信用事件进行了实证检验, 且与Giesecke(2006)、Black-Cox模型进行了比较, 检验结果说明HB模型可以较早的预警违约风险, 较高的精度预测信用利差, 为帮助评估风险和进行投资提供参考价值。
债券市场违约风险事件的发生确实会带来多方面的负面结果, 企业信用受损、企业及其关联企业经营利润受损、投资者收益减少。但需要强调的是, 债券市场违约是市场经济条件下企业信用风险释放的自然反应, 是市场进行资源配置的体现。我们需要防范的是市场系统性风险的发生。从宏观来看, 系统性风险事件的发生最主要来源于违约前夕对于信用风险的低估, 价格发现的延迟造成断崖式的价格下降, 通过资产负债关系联动的企业、金融机构出现的资产风险、平仓压力可能导致其陷入流动性危机, 形成对市场的秩序冲击。因此, 引导市场合理定价, 提升债市资源配置效率, 是监管部门和市场参与者共同的发展目标。
本文的分析结论对建设我国信用债市场具有较强的政策意义。通过本文的案例检验可以看出, 我国的信用债市场尚不活跃, 市场价格发现延迟, 实际市场反应较模型相比有明显的时滞, 市场的隐含违约概率及隐含信用利差存在低估的现象, 且因暂停上市严重影响了违约债券的流转和市场定价;本文的模型也指出, 信用债市场违约事件造成的价格断崖式下降现象, 来源于违约前夕, 投资者异质信念和“刚性兑付”的预期造成的违约概率的低估。因此, 我们从市场监管和市场参与者两个角度得到以下启示:从市场监管与建设的角度来说, (1)应加强信息披露的及时性与真实性监管, 提升信息透明度, 提升投资者对信息披露的信心;(2)有必要改变当前违约债券暂停上市的机制, 加强违约债券的流转机制, 更好地化解金融风险;(3)推进优化和完善信用衍生品的设计, 鼓励信用衍生品的交易, 完全市场信用风险定价生态;(4)加大违约处置中损害投资人利益的违法违规行为的打击力度, 维护信用债市场秩序。从市场参与者来说, (1)在宏观经济趋缓、融资环境收紧的情况下, 企业应有正确的经营和风险意识, 借助信用扩张时应更为审慎, 避免进入过度投资、过度担保、借新还旧和短贷长投的流动性陷阱, 避免陷入债券违约困境;(2)违约事件频发的背景下, 企业更应积极与市场的正面沟通, 加强企业诚信建设, 增强投资者对发行人的信任;(3)投资者也要在“违约常态化”中培育风险意识, 加强对投资标的的研判, 积极利用衍生工具对冲风险。
| [] |
陈秀梅, 2012, “我国债券市场信用风险管理的现状及对策建议”, 《宏观经济研究》, 第 2 期, 第 63-66 页。 |
| [] |
狄灵瑜、步丹璐, 2019, “债务违约、社会责任与政府支持”, 《南方经济》, 第 11 期, 第 72-93 页。 |
| [] |
黄世忠, 2019, "回归本源守住底线——审计失败的伦理学解释", 《新会计》, 第10期, 总第130期, 第8-13页。 |
| [] |
王芳, 2013, “我国债券市场信息披露的现状、问题与对策”, 《证券市场导报》, 第 2 期, 第 66-73 页。 |
| [] |
吴建华、张颖、王新军, 2017, “信息披露扭曲下企业债券违约风险量化研究”, 《数理统计与管理》, 第 36 期, 第 175-190 页。 |
| [] |
杨世伟、李锦成, 2015, “信用风险度量、债券违约预测与结构化模型扩展”, 《证券市场导报》, 第 10 期, 第 41-48 页。 |
| [] |
张维、张永杰, 2006, “异质信念、卖空限制与风险资产价格”, 《管理科学学报》, 第 9 期, 第 58-64 页。 |
| [] |
张永东, 2019, "基于非均衡样本的信用债违约风险预警研究", 《南方金融》, 第1期, 总509期, 第5-14页。 |
| [] |
Anderson R., Sundaresan S., 2000, "A comparative Study of Structural Models of Corporate Bond Yields:An Exploratory Investigation". Journal of Banking & Finance, 24, 255–269.
|
| [] |
Anderson R., Sundaresan W., S., 1996, "Design and Valuation of Debt Contracts". Review of Financial Studies, 9, 37–68.
|
| [] |
Black F., Cox J. C., 1976, "Valuing Corporate Securities:Some Effects of Bond Indenture Provisions". The Journal of Finance, 31, 351.
|
| [] |
Black F., Scholes M., 1974, "The Dffects of Dividend Yield and Dividend Policy on Common Stock Prices and Returns". Journal of Financial Economics, 1, 1–22.
|
| [] |
Boswijk H P, Hommes C H, 2007, "Manzan S. Behavioral Heterogeneity in Stock prices". Journal of Economic Dynamics and Control, 31(6), 1938–1970.
|
| [] |
Çetin U., Jarrow R., Protter P., Yildirim Y., 2004, "Modeling Credit Risk With Partial Information". Annals of Applied Probability, 14, 1167–1178.
|
| [] |
Chiarella C, ter Ellen S, He X Z, et al., 2015, "Fear or Fundamentals? Heterogeneous Beliefs in the European Sovereign CDS market". Journal of Empirical Finance, 32, 19–34.
|
| [] |
Collin-Dufresne P., Goldstein R., Hugonnier J., 2004, "A General Formula for Valuing Defaultable Securities". Econometrica, 72, 1377–1407.
|
| [] |
David A, 2008, "Heterogeneous Beliefs, Speculation, and the Equity premium". The Journal of Finance, 63(1), 41–83.
|
| [] |
Duffie D., Lando D., 2001, "Term Structures of Credit Spreads with Incomplete Accounting Information". Econometrica, 69, 633–664.
|
| [] |
Feldhütter P., Schaefer S. M., 2018, "The Myth of the Credit Spread Puzzle". The Review of Financial Studies, 31, 2897–2942.
|
| [] |
Gao X, Wang X, Tian F., 2019, "Do Significant Risk Warnings in Annual Reports Increase Corporate Bond Credit Spreads? Evidence from China". China Journal of Accounting Research, 12(2), 191–208.
|
| [] |
Geske R, 1977, "The Valuation of Corporate Liabilities as Compound Options". The Journal of Financial and Quantitative Analysis, 12, 541.
|
| [] |
Geske R., Johnson H. E., 1984, "The Valuation of Corporate Liabilities as Compound Options:A Correction". The Journal of Financial and Quantitative Analysis, 19, 231.
|
| [] |
Guo X, Jarrow R A, Zeng Y, 2009, "Credit Risk Models with Incomplete Information". Mathematics of Operations Research, 34(2), 320–332.
|
| [] |
Giesecke K, 2004, "Correlated Default with Incomplete information". Journal of Banking & Finance, 28, 1521–1545.
|
| [] |
Giesecke K, 2006, "Default and Information". Journal of Economic Dynamics and Control, 30, 2281–2303.
|
| [] |
Hong H, Stein J C, 2007, "Disagreement and the Stock market". Journal of Economic Perspectives, 21(2), 109–128.
|
| [] |
Jarrow, R. A.and P. Protter, 2015, "Structural versus Reduced-Form Models: A New Information-Based Perspective", Credit Market Handbook, pp. 118-131. Hoboken, NJ, USA: John Wiley & Sons, Inc.
|
| [] |
Jarrow R. A., Turnbull S. M., 1995, "Pricing Derivatives on Financial Securities Subject to Credit Risk". The Journal of Finance, 50, 53–85.
|
| [] |
Karatzas I, Shreve S E. Brownian motion, 1998, Brownian Motion and Stochastic Calculus. Springer, New York, NY, 47-127.
|
| [] |
Jeulin, T. and M. Yor., 1978, "Grossissement d'une Filtration et Semi-martingales: Formules Explicites", pp.78-97. Springer, Berlin, Heidelberg.
|
| [] |
Leland H. E, 1994, "Corporate Debt Value, Bond Covenants, and Optimal Capital Structure". The Journal of Finance, 49, 1213–1252.
|
| [] |
Leland H. E., Toft K. B., 1996, "Optimal Capital Structure, Endogenous Bankruptcy, and the Term Structure of Credit Spreads". Journal of Finance, 49, 1213–1252.
|
| [] |
Merton R. C, 1974, "On The Pricing of Corporate debt:The Risk Structure of Interest Rates". The Journal of Finance, 29, 449–470.
|
| [] |
Yan H, Xiong W, 2010, "Heterogeneous Expectations and Bond Markets". The Review of Financial Studies, 23(4), 1433–1466.
|



