尽管在全球化过程中全球经济的产业结构“脱实向虚”趋势明显,但实体产业仍然是各国或地区国民经济的“脊梁”。以美国为例,根据《National Association of Manufactures》数据源显示,制造业GDP占到国家比重虽然只有12%,但在该国出国产品的结构中制造业所占比例则高达59.8%;制造业对美国的投资回报率更是达到了289%,即对制造业一美元的投入可以获得将近3美元的经济回报,横向与其他行业的回报率相比,制造业的表现名列前茅;在就业创造方面,根据统计学家的计算,一个制造业装配线上的岗位增加,会在国家社会经济层面各个领域增加近10个就业人口,从这个角度来看,在高科技服务业发展的当下,制造业的发展仍然是关乎国计民生的根本。但在当下,部分国家那种单纯靠资本投入或是人口红利以拉动生产率提升的粗放式发展时期即将过去。全球制造业的GDP增长将面临着前所未有的挑战,各国面对国际市场上激烈的竞争环境,通过巨大的资本投入却无法换来相应的产出、生产率与产业竞争力的低下,或是资源浪费等问题,会直接影响未来很长时期内制造业的稳定发展。
与此同时,在提升制造业产业效率的同时如何防污减排以力图维系可持续发展模式也是当下世界各国所希望实现的总体目标,粗放式的发展模式固然可以推动产业的发展,但付出的代价则是巨大的,产业发展过程中引致的能源消耗以及温室气体排放问题也日趋严重。在低碳经济成为全球共识的今天,不仅是产业全要素生产率,环境生产率更应当成为研究者与决策层所重点关注的问题(Mulder et al., 2014)。换言之,在对世界各国各经济体进行生产效率方面加以考察之时,不考虑能耗污染问题是否会对生产率水平做出有失准确的评估?导致对于社会福利以及经济发展绩效做出扭曲的评价。另外,全球各经济体之间的制造业以及细分产业之间的两类生产效率(即传统生产率以及环境生产率)又表现出怎样的地区差异和行业差异?全球及不同类型经济体的制造业生产率是否存在收敛趋势?对制造业生产率变化的诱因主要有哪些?有鉴于此,除了通过Malmquist指数计算制造业传统全要素生产率之外,本文在全要素生产率变化的研究中还纳入污染排放项,利用Malmquist-Luenberger指数测算世界主要经济体以及细分行业的两类TFP变化指数,对服务业分经济体乃至分行业的两类TFP进行收敛性检验与比较分析,进而对全球制造业近年来的发展进行更直面性的审视,采用WIOD提供的分经济体分行业数据构建面板,试图合理评价2000-2009年期间全球主要经济体的制造业总体以及细分行业的两类生产效率进行比较分析。在此基础上分别对分经济体和分行业的两类生产率进行δ以及β收敛性检验。
二、文献评述学术界针对产业全要素生产率收敛性的研究可以追溯到新古典增长理论模型中的Solow-Swan模型(Solow, 1956; Swan, 1956),模型指出不同观测对象之间如人力资本、资源禀赋等方面的初始差异在长期中会随着经济的增长而逐步趋同,经济走向最初回归稳态。内生经济增长理论认为通过国际贸易以及国与国之间的资源互通,依赖于知识的外溢使得落后国家可以实现后发优势,从而缩小国与国之间产业效率的差距(Gerschenkron, 1962)。但截然相反的观点也大量存在,由于学习效应以及外部性等市场失灵问题,或是由于国际贸易专业化的趋势推动下,也可能出现背道而驰的现象,经济体之间经济增长速度的拉大(Grossman and Helpman, 1991)。因此,国与国之间的生产率是走向收敛还是扩张是一个存在争议的问题,这也引发了学者们对观测对象之间的生产率的收敛性进行实证检验的热情(Islam, 2003),诸多研究关注于各经济体各行业内的产业生产率的表现(Van Ark and Craft, 1996; Miller and Upadhyay, 2002; 彭国华,2005;杨翔等,2015)。但这种单纯的生产率探讨已经不足以对行业或国家产能发展状况做出准确且清晰的判断,随着全球气候变暖,温室气体排放问题以及不可再生能源的短缺愈发受到各界的关注与重视,关于如何对天然气体排放的管控问题成为多次国际论坛会议讨论的焦点,一国或经济体的产业效率中如果漠视污染排放的因素,势必做出错误的判断,而碳排放、硫排放与能源全要素生产率等领域的演化趋势以及收敛性检验也由之成为了学术研究的热点。Strazicich and List(2003)最早将数学收敛的思想引入到针对OECD国家之间碳排放水平上,研究指出,在1960-1997年之间的CO2排放呈现收敛的趋势。但在OECD以外的国家之间,根据一些学者的研究表明碳排放量则存在扩张的趋势(Aldy, 2006)。但在同类研究中,Westerlund and Basher(2008)将样本国家分为发达国家以及发展中国家两类,两类国家之间的CO2排放均具有收敛性。而在近些年内,学者们开始将污染气体排放融入到对于产业效率的研究之中,Miketa and Mulder(2005)针对全球56国制造业部门的研究发现各国之间的能源生产效率也出现了收敛的态势,换言之,环境生产率较低的国家拥有更高的增长速度。Mulder and Groot(2012)的后续研究也进一步证实了落后国家在多数产业部门内可以实现对领先国环境生产率的追赶。国内这个领域的研究近年来也在逐步的丰富,文献集中于对制造业传统生产率以及环境生产率水平的测算或是收敛性的检验, 沈能(2006)对1985-2003年中国制造业TFP的动态变化研究发现,我国制造业TFP年均增长主要得益于技术进步而非效率的提升,我国东中西部地区制造业TFP以及技术进步水平并没有表现出收敛性,地区TFP差距的扩大很大程度上可以由地区技术进步程度来解释。魏楚、沈满洪(2007)的研究也指出我国整体工业TFP在1995-2004年期间大多省份能源效率符合“先升后降”的特征,各省之间的能源效率差距在2000年后逐渐扩大, 不具有趋同性。且在我国不同地区间能源效率存在的显著差异在逐年降低, 即地区间能源效率存在一定的趋同性。张少华、蒋伟杰(2014)采用基于投入冗余的全要素生产率指数来测度中国1985-2009年的TFP,研究指出我国所有省份在样本期内都实现了TFP提升, 2005年之后逐渐有更多的省份成为“创新者”, 而省际之间追赶效应表现得并不是十分明显。针对国内分地区各种行业生产率的研究可以说非常的丰富,但国内文献中的观察维度大多也被局限于此。王许亮、王恕立(2018)则将研究的视角对准了OECD经济体服务业的环境生产率,他们的研究表明在1995-2009年期间发达经济体服务业环境生产率整体呈增长态势,发展中国家则在此期间出现了小幅下滑,第三产业环境生产率在不同经济体以及行业之间的发展存在很大的异质性,服务业总体上存在绝对以及条件β收敛,但却不存在δ收敛。
纵观多年以来的研究,尽管在全球经济一体化以及各国政府对于污染防控的重视程度提升的双重背景下,学者们也意识到了环境因素在核算一国或行业TFP动态变化中的作用,但在分析过程中罕有对两类生产率之间进行的直观比较。而对于收敛性检验,更多的也只是针对其中的一类TFP(传统或环境)进行,无法通过对两类生产率变化收敛性的检验与比较分析、归纳与总结出规律性的结论,并藉此提出相关政策。而在技术方法上,传统意义上对于TFP动态变化的计算采用方法是DEA-Malmquist指数, 将生产效率的变化率分解为技术进步和技术效率等部分,进而详细考察国家产业效率变化的根源。但随着碳与硫以及烟尘等污染气体排放量以几何级数的速度在增长,这种“非期望产出”的规模扩张需在生产率核算中予以考虑,而传统的DEA-Malmquist分析方法存在一定的不足之处,无法准确反映出世界经济体的产业绩效变化。国内的一些文献在计算能源生产率时简单的采用行业增加值与能源消费量的比值加以表征。这种方法虽然在解决了购买力平价的基础上可行,但无法传统生产率进行对照式的比较分析。在技术上,对于这种非期望产出的问题,Chung et al.(1997)提出了Global Malmquist Luenberger指数方法,基本思想是在非参数生产率核算模型中纳入污染气体排放量作为非期望产出的表征,从而核算出环境生产率,这是一种在考虑环境约束条件下计算出的观测对象生产率的变化,可以有效的对可持续发展这一全球性主题进行考察。
三、研究方法与数据处理 (一) 研究方法有鉴于DEA-Malmquist指数(以下简称DM指数)方法已基本成熟,此处仅简要阐述Global Malmquist Luenberger指数(以下简称GML指数)方法,GML技术实质上是对传统DM指数方法的一种修正,承前所述这是由于传统的DM指数中无法无法将污染气体排放等非期望产出纳入研究体系。DM的计算依据是产出距离的函数,GML指数则在此基础上将方向性距离引入到函数计算之中,可以在添加预期产出的同时减少非预期的产出,而这是传统产出距离函数无法满足的,GML首先构造的决策单元的最优生产前沿面,然后利用“方向性距离函数”计算出各决策单元与最优前沿面之间的距离,最后测度各决策单元与“预期”与“非预期”前沿面之间的距离,从而核算出对应时段的GML值。
DM指数是由Shephard(1970)所提出的一种线性产出距离函数,基本表达式为:
| $ D_{0}(x, y, f)=\inf \{\theta:((y, f) / \theta \in p(x))\} $ | (1) |
Shephard将其产出距离函数定义为按找相同比例变化的“预期”与“非预期”等两类产出值,但该函数中没有考虑到对于污染气体排放的控制,此处引入产出距离的函数进行替代,藉此可以对“预期”与“非预期”两类产出变化时的综合绩效进行衡量,参考Chung(1997)所设计的考虑环境能源因素限制下的GML指数,测度模型可通过下式表达:
| $ \bar{D}_{0}(x, y, f ; g)=\sup \{\beta:(y, f+\beta g) \in p(x)\} $ | (2) |
(2) 式中g是同比例与最终产出变化的变量,当g=(y, -f)时表明预期产出在正向变化,同时非预期产出则在负向变化。总体上Shephard函数只能定位于分析预期以及非预期两类产出的共同增加,该函数通过以预期产出的增长以及非预期产出的减少衡量决策单元的效率变化。为考虑方向上的距离函数,可以推导出以下公式:
| $ \begin{aligned} \bar{D}_{0}(x, y, f ; g) &=\sup \left\{\beta: D_{0}(y, f)+\beta(y, f) \leqslant 1\right\}=\sup \left\{\beta:(1+\beta) D_{0}(x, y, f) \leqslant 1\right\} \\ &=\sup \left\{\beta: \beta \leqslant D_{0}(x, y, f)^{-1}=1 / D_{0}(x, y, f-1)\right. \end{aligned} $ | (3) |
(3) 式中的Shephard产出距离函数实质上可视作为直接距离函数的一种特例,具体的关系可以D0(x, y, f; g)=(1/D0(x, y, f))-1进行表述。
事实上,GML为考虑了“非预期产出”的基础上对DM指数进行的一种拓展。一般意义上,DM指数可以分解为:
| $ \begin{array}{l} {M^{t, t-1}\left(x^{t+1}, y^{t+1}, f^{t+1}, x^{t}, y^{t}, f^{t}, \right)=\left[\frac{d_{0}^{t}\left(x^{t+1}, y^{t+1}, f^{t+1}\right)}{d_{0}^{t}\left(x^{t}, y^{t}, f^{t}\right)} \times \frac{d_{0}^{t+1}\left(x^{t+1}, y^{t+1}, f^{t+1}\right)}{d_0^{t+1}\left(x^{t}, y^{t}, f^{t}\right)}\right]^{1 / 2}} \\ {=\frac{d_{0}^{t}\left(x^{t+1}, y^{t+1}, f^{t+1}\right)}{d_{0}^{t}\left(x^{t}, y^{t}, f^{t}\right)} \times\left[\frac{d_{0}^{t}\left(x^{t+1}, y^{t+1}, f^{t+1}\right)}{d_{0}^{t+1}\left(x^{t+1}, y^{t+1}, f^{t+1}\right)} \times \frac{d_{0}^{t}\left(x^{t}, y^{t}, f^{t}\right)}{d_{0}^{t+1}\left(x^{t}, y^{t}, f^{t}\right)}\right]^{1 / 2}} \\ {=E F F C H^{t, t+1} \times T E C H C H^{t, t+1}} \end{array} $ | (4) |
式中d0t(xt, yt, ft)与d0t(xt+1, yt+1, ft+1)为以t时刻前沿生产技术计算出的t与t+1时段内的产出距离函数,而d0t+1(xt, yt, ft)与d0t+1(xt+1, yt+1, ft+1)则为以t+1时刻的前沿生产技术为参考的t和t+1时刻的产出距离函数。Mt为以t期的技术为参照计算出的DM指数,x、y和f分别为资本、劳动力等投入要素以及产出(包含“预期”与“非预期”的产出)。上式将DM指数分为技术效率(EFFCH)与技术进步(TECHCH)。技术效率指决策单元向最佳生产前沿面的接近,是一种“追赶效应”,目前状态与最大潜在生产能力之间的距离。技术进步指最佳生产状态界向外的平移,测度了最大潜在生产能力在相邻时段之间的移动情况,是为一种“增长效应”的表征。
由于只要置入投入产出的数据,就可以通过DM指数计算观测对象的全要素生产率水平,当然这也可以通过在产出项中置入污染气体的排放数据实现模型的拓展。但由于现有指数采用的是较为单一的距离函数,使得体系中决策对象的污染气体排放问题无法被涉及。因此此处使用直接距离函数替换DM的产出距离函数,距离函数中纳入向量g=(y, -f),实现与DM指数比较,藉此可以该函数转化为GML生产率形式。此处如果将向量定义为g=(y, f)时,此时GML指数与DM指数是完全一致的,但由于前文提到向量公式定义为g=(y, -f),此时的全要素生产率参数计算中同时纳入了“预期”与“非预期”产出的效率,也可以进一步分解出GML指数下的技术效率(MLEFFCH)以及技术进步(MLTECHCH)指标,GML函数式及其分解方式为:
| $ \begin{aligned} &G M L^{t, t+1}\left(x^{t+1}, y^{t+1}, f^{t+1}, x^{t}, y^{t}, f^{t}\right)=\left[\left(\frac{1+\bar{d}_{0}^{t}\left(x^{t}, y^{t}, f^{t} ; y^{t}, -f^{t}\right)}{1+\bar{d}_{0}^{t}\left(x^{t+1}, y^{t+1}, f^{t+1} ; y^{t+1} , -f^{t+1}\right)}\right.\right.\\ &\left.\left.\times \frac{1+\bar{d}_{0}^{t+1}\left(x^{t}, y^{t}, f^{t} ; y^{t}, -f^{t}\right)}{1+\bar{d}_{0}^{t+1}\left(x^{t+1}, y^{t+1}, f^{t+1} ; y^{t+1}, -f^{t+1}\right)}\right)\right]^{1 / 2}=\frac{d_{0}^{t}\left(x^{t+1}, y^{t+1}\right)}{d_{0}^{t}\left(x^{t}, y^{t}\right)}\\ &\times\left[\frac{d_{0}^{t}\left(x^{t+1}, y^{t+1}\right)}{d_{0}^{t+1}\left(x^{t+1}, y^{t+1}\right)} \times \frac{d_{0}^{t}\left(x^{t}, y^{t}\right)}{d_{0}^{t+1}\left(x^{t}, y^{t}\right)}\right]^{1 / 2}=M L E F F C H^{t, t+1} \times M L T E C H C H^{t, t+1} \end{aligned} $ | (5) |
本文所采用数据皆来自于世界投入产出数据库(WIOD),WIOD包含全球40个世界主要经济体的数据,我们通过反复遴选,剔除了部分数据缺失比较严重的卢森堡,因此保留了39个经济体,包括澳大利亚、奥地利、比利时、保加利亚、巴西、加拿大、中国大陆、塞浦路斯、捷克、德国、丹麦、西班牙、爱沙尼亚、芬兰、法国、英国、希腊、匈牙利、印尼、印度、爱尔兰、意大利、日本、韩国、立陶宛、拉脱维亚、墨西哥、马耳他、荷兰、波兰、葡萄牙、罗马尼亚、俄罗斯、斯洛伐克、斯洛文尼亚、瑞典、土耳其、中国台湾、美国,其中有28个OECD国家以及11个非该组织的国家。在WIOD数据中,对于制造业的分行业细分标准是NACE Rev.1,代码是C10-C33之间,但是现标准C33定义为“机器设备维修保养”,这个严格意义上应当是属于服务业的范畴,因此也予以剔除,NACE Rev.1中C10-C12分别表示的是食品、饮料以及烟草,编排时放置在一起进行汇报,类似的情况还有很多。而在汇报污染气体排放的数据表Environmental Accounts中,行业的编码即行业划分口径与WIOD数据也略有出入,譬如WIOD中丝织品与皮革产品制造整合在一起,但在Environmental Accounts中是分开汇报的。因此,我们手工对两组口径下的分行业进行比对,最终确定了12个制造业的分行业部门,分别是食品、饮料和烟草,丝织品、皮革,木制品,造纸业,汽油及焦炭能源,化工产品,橡胶及塑料,非金属制品,金属及人造金属制品(除机器设备),计算机及电子光学设备,机器设备,汽车、拖车及半拖车等交通设备。其中前9个部门定义为轻工制造业,而后三个则归入重工制造业。本文将计算这39个经济体以及12个制造业分行业纵横之间两类TFP变化进行收敛性的检验。从上述数据源中我们获取各经济体以及分行业的产出、污染气体排放量、就业人口以及资本投入等相关数据。
(1) 制造业产出:采用WIOD数据库中公布的各经济体制造业分行业增加值来衡量产业的产出。承前所述,涉及到39个经济体12个手工整合后的行业部门数据,并将各年数据折算为2000年的不变价,后文中所提的资本存量采用同样方法处理。
(2) 污染气体排放量:此处将污染气体排放做为非期望性产出,与期望性产出一起引入到GML核算过程。但需要特别说明的是,该数据只是在计算在GML指数时需要纳入,而在计算DM指数时不需要。Environmental Accounts数据源中包含了多种类型的污染气体排放值,包括二氧化碳、甲烷、笑气(一氧化二氮)、氮氧化物、硫化物、一氧化碳、非甲烷挥发性有机物(NMVOC)以及氨气等。如果将多种污染气体数据纳入会使得计算变得比较复杂,事实上,各经济体或行业中不同污染气体对于民众生产生活的影响是存在一定差异的,但现有的污染程度核算体系下,难以为各种污染气体赋予统一或是单独的权重加以计算。因此,本文考虑采用其中最具代表性的二氧化碳排放量作为污染气体排放量的表征。但有一个前提,即二氧化碳对于整体污染气体排放的代表性如何,表 1中我们提供了二氧化碳与其他污染排放气体在样本期内的pearson相关系数。可以看出,总体上二氧化碳与其他七类污染气体中的甲烷,一氧化氮,硫化物以及一氧化碳的排放量相关度较高,而与其他几种气体排放的相关性一般,但事实上,工业排放的主体是碳硫类气体,因此以二氧化碳排放为代表性的污染气体排放量是很有价值的。而在具体到经济体与行业来看,整体上在各国(地区)以及行业范围内,这种碳硫气体排放量之间高相关性也基本得到了证实。这也表明,尽管各国能源消费结构迥异,但二氧化碳排放量仍是其中比较具有代表性的一类。
| 表 1 2000-2009年制造业其他污染气体排放量与CO2排放量的相关系数 |
(3) 资本投入:资本投入量采自于各经济体历年的名义资本存量,数据来自于WIOD数据库的Socio Economic Accounts,承前所述,对各年投资额进行了2000年的不变价的处理。
(4) 劳动投入:关于不同经济体以及行业内就业人口指标同样采自于Socio Economic Accounts,该表中就业方面的数据包括了就业人口数(EMPE)以及工作总时间(H_EMPE)两类,考虑到由于各国(地区)之间社会文化意识等方面的差异,东方国家职工工作时间存在很大的差异,社会的幸福感与所工作时间高度相关(吴伟炯,2016)。因此采用总工时可以更为准确的评估出观测对象在劳动方面的投入。
在完成了对上述几组投入产出数据采集基础上,本文将通过DM指数计算全球各经济体以及制造业各行业部门的传统全要素生产率,再纳入二氧化碳排放量计算GML指数。前者涉及的“投入—产出”项包括产业增加值、资本以及劳动投入,而后者则在产出项中增加二氧化碳排放量。继而,本文从纵横交错两个维度的比较分析各经济体及各行业部门之间传统以及能源生产率的变化以及检验彼此之间的收敛性。
四、两类全要素生产率的测算本文通过图 1绘制了根据WIOD数据生成的分年度以及经济体两类生产率在样本期内走势曲线的对照图,可以明显看到,在样本期内,DM指数始终高于GML指数。这表明,在不考虑污染气体排放的状况下,传统的TFP计算方法的确会对实际产能输出能力做出高估性的判断,这与之前针对我国产业样本进行的一些类似研究结论相吻合(庞瑞芝,2014;王恕立等,2015)。但需要指出的是,无论何种产业效率,在该时期内总体都呈现出了下滑的趋势。传统TFP年均下滑1.16个百分点,而能源TFP则下滑1.22个百分点。换言之,能源生产率下滑幅度略高于传统生产率,全球主要经济体制造业在整体上没有在产业增长的同时实现污染排放的控制,制造业的发展伴随着能源的过度消耗以及环境的破环。继而在表 2中展示了39个经济体以及12个细分行业部门的两类TFP变化的对照。根据前文所述,此处区分发达与发展中经济体以及轻重工制造业①,表 2的结果进一步证明了传统DM方法高估了实际产业效率的结论。其中,在发展中经济体产业效率高于发达经济体的效率,但印尼、土耳其、俄罗斯等国的TFP变化率在样本中领跑。而在考虑能源消耗的情况下,发展中国家或地区产业效率损失更为严重,样本期内的实际产业效率损失率达到了3.3%(1.059-1.014/1.059),远高于发达经济体的1.4%,这也表明在经济发展欠发达的发展中经济体。制造业的产业发展更多的依赖于能源等要素投入拉动的粗放式发展模式。从分经济体来看,全球不同国家与地区之间制造业的两类产业效率的差异也存在较大的地区异质性,其中差异最大的土耳其,在考虑污染气体排放基础上的生产率损失亦达到了15.3%,印尼达到8.3%,而样本中仅有的几个能源效率高于传统效率的国家均是欧洲国家希腊、拉脱维亚、爱尔兰以及斯洛伐克。同样,从表 2可以解读的是TFP值较低的也都是欧洲经济较为发达的国家,而发展中经济体的制造业在降耗方面所面临的困难更为严峻。从行业部门角度来看,如果以传统生产率衡量,WIOD经济体的轻重工业在样本期内表现大致相仿,但在考虑污染气体排放的基础上,实际产业效率上,重工业的损失略大于轻工业,这也表明重工业更依赖于能源消耗而发展。其中计算机与电子光学产品以及汽车、轮船等交通设备制造等行业在考虑污染排放的基础上,产业效率损失达到了4.1%与3.6%,领跑于所有的产业部门,而同类指标中最低的汽油焦炭以及非金属制品行业的能源生产率较之于传统效率损失0.7与1.2个百分点。在发展中经济体国家(地区),轻重工业的两类效率差异度相差无几,但在发达国家,重工业由于污染气体排放带来的产能损失相比于轻工业更为突出。直观的感受是,不同经济体之间的传统与能源生产率之间的异质性明显,这也使得在考虑能耗的情况下,产业效率低估的问题在各经济体之间差异普遍存在。
① 根据世界银行公布的各国人均GDP数据本文将所涉及的样本地区分为发达与发展中经济体,其中发达经济体包括澳大利亚、奥地利、比利时、加拿大、丹麦、德国、西班牙、芬兰、法国、英国、希腊、爱尔兰、意大利、日本、韩国、荷兰、葡萄牙、瑞典、美国、斯洛文尼亚、捷克、匈牙利、拉脱维亚、斯洛伐克、马耳他、爱沙尼亚等26国,发展中经济体包括中国大陆、中国台湾、巴西、印度、俄罗斯、立陶宛、波兰、塞浦路斯、保加利亚、印尼、墨西哥、罗马尼亚、土耳其等13国。需要特别指出的是,按标准中国台湾地区属于高收入经济体,但在西方学者的研究中,多数情况下将其作为发展中经济体处理,本文因循这种成例。
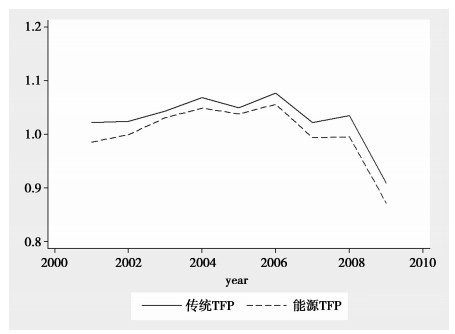
|
图 1 全球制造业传统及能源TFP变化走势对照图 |
| 表 2 各经济体/行业制造业两类TFP变化 |
进而,图 2与图 3展示的是在样本时期内两类生产率在经济体以及行业之间的核密度变化分布曲线,可以很明显的看出两类生产率在样本期内出现了一定幅度的波动,在2000-2005年期间生产率有一定幅度的提升,但在样本期末则总体出现明显下滑,这与当时出现的全球性金融危机有关。而在离散程度上,在分经济体之间,样本期内的前半部分总体上略有收敛,但后半部分则明显发散,不同国家(地区)之间的生产率差异度拉大,但直观感受是能源生产率的发散程度略小于传统生产率。总体上,如果以分经济体为研究维度,两类生产率的变化走势特征差异不大。但在分行业上,传统及能源两组生产率变化的差异则较大,传统生产率在样本期内一直在下滑,能源生产率仍是“先升后降”,而在行业之间生产率的发散程度没有太明显的变化,这意味着,在分行业间如果考虑污染气体排放问题,原有关于生产率的认知会出现些许差异。制造业在高速发展的过程中,应当在鼓励能耗节约的同时着手促进行业以及地区间的协调发展。
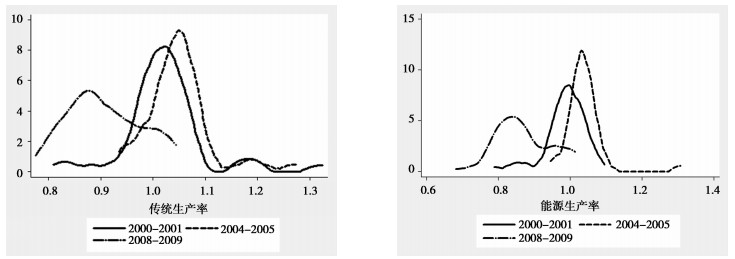
|
图 2 全球制造业传统及能源TFP不同经济体之间核密度分布图 |
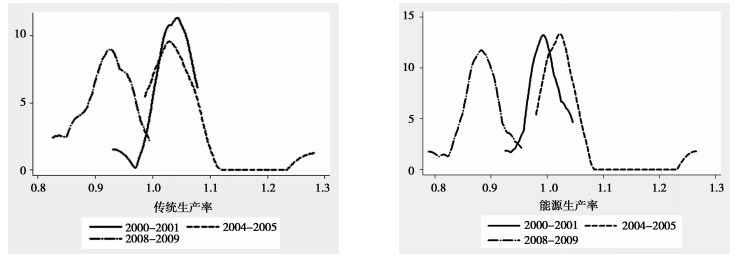
|
图 3 全球制造业传统及能源TFP不同行业之间核密度分布图 |
针对两类生产率计算结果的展示与分析表明,全球经济体以及行业之间两类生产率存在较大的地区以及行业差异,为了进一步考察地区以及行业之间差异性的变化趋势以及动态特征。本文采用常规性的δ收敛以及绝对和相对β收敛分析方法对样本中所涉及的行业与经济体之间进行纵横两个维度的两类生产率变化检验。
五、制造业两类生产率经济体及地区间收敛性检验数据和图形的报告可以大体上反映出制造业传统以及能源生产率在全球经济体以及各行业部门之间的变化趋势,本部分通过收敛性检验进一步加以论证,收敛理论为基于边际报酬递减和规模报酬不变等前提条件提出的理论,用于研究不同观测对象之间指标动态变化的趋势。最为常见的收敛类型包括了δ收敛以及β收敛检验方法(Barro, 1986),其中β收敛又可以区分为绝对β收敛以及条件β收敛。δ收敛检验的是不同经济体和行业之间生产率的离散程度是否会随时间而逐步减小。绝对β收敛同样进行的是绝对收敛性的检验,不同经济体和行业的环境与传统生产率如能实现完全相同的稳态就被认为实现了绝对收敛,而条件β收敛则是检验不同经济与和行业的两类生产率指数是否只能接近于不同的稳态。
(一) δ收敛检验δ收敛是根据不同观察之间生产率变化指标的变异系数来判断是否收敛的方式,变异系数以标准离差率来表征,参考王恕立、刘军(2014)的做法,其计算方式设定为:
| $ C V=\delta / \mu $ | (6) |
上式CV为标准离差率,δ为内观测对象(经济体或行业)DM以及GML指数之间的标准差率①,而μ则为生产率指数的均值。本文在图 4中展示制造业在经济体与行业部门之间两类生产率指数之间的变异系数的走势图,我们试图在几张图中寻找出收敛性的变化规律:第一,样本期内制造业两类生产率的差异度曲线总体上呈现出交织在一起的特征,而且在时段内,无论是分经济体还是分行业部门之间都没有表现出明显的收敛性特征,值得一提的是分行业间的两类TFP个别年份出现了标准离差率的峰值,而在针对发达经济体以及发展中经济体的研究中也同样存在类似的高峰值。但在分经济体之间,这种差异性则没有出现那么明显的变化和波动;第二,发达与发展中经济体之间生产率呈现出一些扩张拉大的趋势。在发达经济体内,除了个别年份,分经济体以及分行业间传统以及能源生产率之间标准离差率并没有出现明显的差异。但在发展中经济体内,无论是经济体之间还是分行业之,能源生产率的标准离差率都明显大于传统生产率的,这意味着在经济欠发达的地区,各国或地区为发展实体经济所付出的环境污染代价是存在差异的,或者说对于污染排放的控制力度也是不同的,有的国家或地区内政府对污染的管控更为严苛,但部分国家则不然,在不同行业内所实施的管控力度可能也存在差距,这是造成能源效率异质性明显大于传统效率的一种解释。总体上,在行业总体以及发达发展中经济体内,制造业在地区以及分部门之间都没有出现δ收敛;第三,在轻工业领域内,两类生产率的标准离差率也没有出现δ收敛,而且能源效率也没有明显的高于或低于传统效率,这也说明轻工业领域污染气体排放对于真实生产率产生的误判并不是很严重,轻工业所导致的污染气体排放问题也并不是很突出。但在重工业领域内,能源效率的异质性略大于传统效率且出现了一定的δ收敛趋势,而且能源效率的标准离差率差异也大于传统效率的差异程度,无论是在地区间还是行业之间都是如此,这也表明了不同行业以及经济体之间污染气体排放的水平由于政府管控以及技术水平的因素而存在一定落差;第四,在发达经济体内轻重工业的两类生产率的走势都是处于交织状态,轻工业走势波动没有出现收敛,重工业领域内差异度则略有减小。但在发展中经济体内轻重工业的能源效率异质性除个别年份整体上大于传统效率,轻工业走向略显发散,而重工业也出现了δ收敛的趋势。根据图线简单判断较为粗糙,有些行业或经济体内的生产率异质性趋势变化并不明确,如果结合总体趋势来看可能结论是有所不同的,而且为节约篇幅,本文没有对具体国家(地区)或是行业部门为更准确地考察,对于经济体或行业间两类生产率变化的收敛情况需要进行量化程度更高的β收敛检验。
① 即各观测值生产率之间的标准差与均值之商。
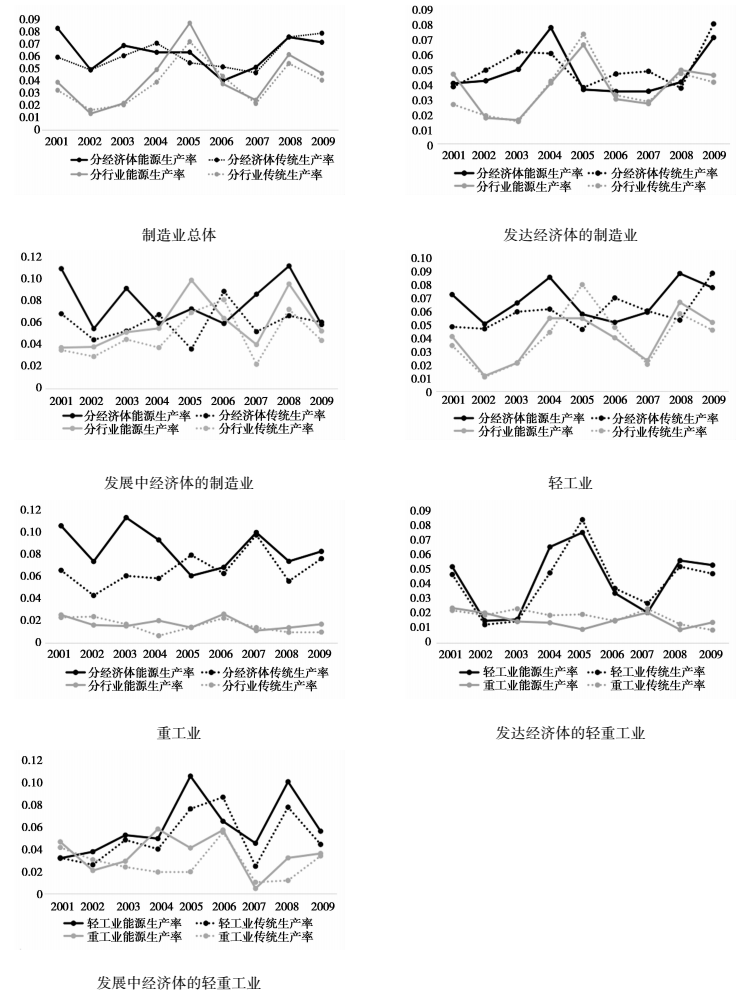
|
图 4 主要经济体制造业传统及能源生产率经济体及细分行业部门之间δ收敛检验 |
β收敛检验由Bernard et al.(1996)提出,本文用于分析所研究单元(经济体/行业)的生产率变化能否最终实现相同的稳态,进而分析判断产业效率发展相对滞后的的经济体或是行业能否最终追赶上领跑者。根据Barro(1986)的研究,观测单元指标变化趋势一般表现为对数线性形式,此处以DM指数为例,GML的情况可以同样的方式导出,绝对β收敛表述如下:
| $ \left[{Ln}\left(D M_{i, j, t}\right)-{Ln}\left(D M_{i, j, 0}\right)\right] / t=\alpha+\beta L n\left(D M_{i, j, 0}\right)+\varepsilon $ | (7) |
上式中的[Ln(DMi, j, t)-Ln(DMi, j, 0)]/t是指经济体i的行业部门j在时间t内的DM指数均值,参考刘兴凯和张诚(2010)的方法构建DM与时间项以及常数项的估计方程,α即常数,而Ln(DMi, j, 0)为经济体i的行业部门j在期初DM指数的自然对数,β为对应系数,ε为残差项,通过OLS的估计,如果β < 0且显著,绝对β收敛就是存在的。其收敛的速度λ可通过下式计算:
| $ \beta=-\left(1-\mathrm{e}^{-\lambda t}\right) $ | (8) |
根据(7)-(8)式,本文对DM以及GML指数在分经济体以及分行业之间的β值和对应的收敛速度λ进行计算,本文通过表 5展示了全样本下的两组计算结果,结果显示大部分分行业部门以及经济体之间都存在绝对的β收敛,这也就意味着不同经济体以及行业之间的生产率具有趋同的变化态势。但分经济体之间的能源生产率(即GML指数)的收敛速度远低于传统生产率(即DM指数),这也意味着在考虑污染气体排放的能源约束下,各国或地区之间的污染排放水平存在鸿沟,这也使得彼此间的能源效率收敛的速度明显低于传统算法算出的生产率。在细分行业中,各经济体之间的轻工业生产率领域内,多数部门的能源生产率收敛速度也低于传统生产率。但在后面三个重工业部门内,各经济体之间能源效率的收敛速度却超过了传统生产率,这大概也说明,各国对于重工业污染排放的关注度更高,管控力度更为严格,但在轻工业领域的排放监管上则似乎管制强度存在较大的差异。而行业之间的考察论证结果则表明,总体上轻工业的收敛速度高于重工业,不同行业领域内的监管力度同样存在差距,这也使得WIOD数据库所涵盖经济体不同行业之间的能源效率收敛速度低于传统生产率。轻工业的表现同样如此,但在重工业领域,实证结果显示传统效率没有出现明显的收敛态势,源自于β值并不显著,但其在能源效率上则以较高的速度实现收敛,这可能表明各行业部门对于污染排放进行的严格管控使得彼此在考虑了环境约束条件下的真实效率产生了趋同的态势。
| 表 5 全样本两类TFP增长率绝对收敛检验结果(固定效应模型) |
进一步的,在表 6和表 7中又展示了发达与发展中经济体的两类生产率指标变化比较,可以很明显的发现,发达经济体之间两类生产率的收敛速度远高于发展中国家或地区之间。尤其在传统生产率上,其收敛速度甚至达到了发展中国家速度的两倍以上,而且能源生产率的收敛速度都低于传统效率,这也进一步说明了经济体之间污染排放水平的差异性,这使得能源效率不及传统效率的收敛速度。而在具体行业部门上,有八个行业部门的分经济体能源生产率收敛速度要快于传统生产率,有四个部门的能源生产率收敛速度低于传统效率,其中,但由于木制品等少数行业的能源效率收敛速度大大低于传统效率的收敛速度,还是影响到了整体制造业能源效率的收敛速度。而在发展中国家内,情况则不尽相同,一方面,发展中国家之间的两类效率收敛速度都明显的低于发达国家之间,这样反映出发展中国家经济产业发展的差异性,远不如发达经济体在样本时段内发展的同步性强烈。但其整体制造业在两类效率的收敛速度相差并不大,能源效率收敛速度快于传统效率的行业部门只剩下了四个,有多达八个部门内,能源效率收敛速度不及传统效率。在两类经济体之间,只有木制品、造纸、橡胶塑料等少数行业内,能源效率与传统效率的收敛速度大小关系是一致的,这也反映出在经济发展水平不同的经济体之间,其产业发展模式存在较大的差异。
| 表 6 发达经济体两类TFP增长率绝对收敛检验结果(固定效应模型) |
| 表 7 发展中经济体两类TFP增长率绝对收敛检验结果(固定效应模型) |
两组经济体在分行业的两类生产率上的表现则是较为类似的,制造业所有分行业以及轻工业分行业之间的能源生产率低于传统生产率,而且发达经济体的上述两类生产率高于发展中国家及地区的表现,而重工业上能源效率则高于传统效率,其中发达国家重工业之间的传统效率没有出现显著的收敛态势。
结合δ收敛的结果来看,虽然大多数行业没有出现δ收敛,但表 5-表 7的结果显示,除了全样本以及发达经济体的传统重工业生产率没有出现显著的β收敛,其他所得分行业或是分经济体之间都出现了β收敛态势。,这表明跨经济体或是跨行业部门的变异系数的下降可能意味着初始两类生产率水平较低的经济体或是行业增长速度可能更快(Quah, 1993)。两类生产率之间都出现了明显的绝对β收敛的特征,无论是分经济体还是分行业之间,传统生产率都比能源效率收敛的速度更快。但在一些具体行业的分经济体效率的变化特征情况则有所差异,因此无法获得两类生产率收敛速度的较为一致性的结论。
(三) 条件β收敛检验本文中条件β收敛考察的是分经济体以及分行业部门之间的两类生产率是否收敛于各观测对象自身的稳态水平,其核心思想是认为产业效率较低的经济体或是行业部门与表现较好的观测对象之间可能存在稳定的长期差距,林毅夫、刘明兴(2003)的研究指出无论是否存在绝对β收敛,但在置入生产率增长率滞后项后改变β系数的方向或是显著性,换言之这种β收敛是依据条件而存在的。每种观测对象其稳态水平依赖于其自身基本特性,因此必然存在差异,条件β收敛检验要通过面板数据来进行核算,本文采用截面与时间双重固定效应模型来进行检验,在固定效应模型中观测效应与解释变量存在关联性,条件收敛的定义是各观测对象的生产率收敛于各自的稳态水平,因此控制变量在模型中并非不可或缺的(Miller and Upadhyay, 2002),仍然以DM指数为例,本文构建的β收敛模型为:
| $ Ln \left(D M_{i, j, t}\right)-{Ln}\left(D M_{i, j, t-1}\right)=\alpha+\beta Ln \left(D M_{i, j, t-1}\right)+\varepsilon_{i} $ | (9) |
上式中α为固定效应项,其他i, j, t的含义与前面公式一致,其对应的是不同主体(经济体/行业)其各自的稳态水平,Ln(DMi, j, t)-Ln(DMi, j, t-1)刻画的是本期与前期的DM指数的变化,β为前期DM指数的估计系数,此处为负且显著就意味着条件β收敛是存在的,即观测对象的传统生产率将收敛于其稳态水平。此处的收敛速度λ也可以同样通过(8)式进行计算。
在控制了截面以及时间固定效应的基础上,可以看到表 8-表 10的估计结果表明三表中除了部分重工业传统分行业之间没有出现条件β收敛,其他几乎所有的系数都是显著且显著性水平都达到达到了1%,换言之分经济体以及行业之间的两类产业效率变化都存在着明显的β条件收敛特征,传统及生产率都在动态中趋向其自身的稳态,而这也就表明产业发展过程带来的污染排放问题在样本期内没有有效的实现“破局”进而改变全球经济体的能源消费结构,污染防控仍是任重道远。在全行业的分经济体收敛性检验中,总体上能源生产率的β收敛速度要快于传统生产率。这与之前传统β收敛的检验结果相反,那就意味着各个经济体在能源消费领域内其污染排放水平对于过往水平较为依赖,产业效率可能出现波动,但其内在的能耗水平显然不会因为经济发展的起落出现大的变化,相对更为稳定。结合表 5的结论可知,样本期内不同国家地区之间污染排放水平差异较大,但各经济体污染气体排放量却遵循其既有能源消费的惯性而呈现出收敛的态势。能源消费上趋向于稳定,这可能与各国或地区能源消费结构相关;而各行业部门情况来看,在多数行业两类生产率条件β收敛速度相差并不大,造成能源生产率条件β收敛速度较快的主要原因是橡胶塑料以及木制品等少数行业内能源生产率自我收敛速度较大幅度的高于这些行业内的传统生产率收敛速度,那也就意味着全球范围内这些行业的污染排放量相比于产业发展效率的波动而言要更为稳定。需要特别指出的是在重工业的三个行业部门内,其能源效率收敛速度都不高于传统效率的收敛速度,这也就表明这些行业部门内各经济体的污染排放水平的波动性影响了各经济体产业收敛速度的稳定性;对于分行业之间全行业以及轻工业之间的两类条件β收敛速度相差无几,换言之,在大部分行业内污染气体排放量与产业效率发展基本属于同步的节奏,只有在重工业体系内,传统生产率没有出现向自身稳态水平收缩的态势,但能源效率则实现了缓慢的自我收敛趋势(收敛速度值λ不高),那可能意味着重工业行业之间污染排放“路径依赖”的趋势比较突出,这也使得原本未能实现条件β收敛的传统生产率在考虑了能源问题之后也出现了收敛的特征。
| 表 8 全样本两类TFP增长率条件收敛检验结果(固定效应模型) |
| 表 9 发达经济体两类TFP增长率条件收敛检验结果(固定效应模型) |
表 9与表 10列示的是发达经济体以及发展中经济体两类生产率的条件β收敛检验结果,发达与发展中经济体能源生产率的条件β收敛收敛速度都高于传统效率的速度,这与表 8的结果是一致的,其中发展中经济体内,能源生产率自我收敛速度领先的幅度更大,这也表明发展中经济体污染排放水平的“路径依赖”性更强,在发达经济体内,传统生产率收敛速度大幅度领先能源生产率的行业为食品饮料烟草业以及造纸业,而反之的则包括木制品、橡胶塑料,其他各行业相差不大。发展国家内传统生产率收敛速度大幅度领先能源生产率的行业只有造纸业,而相反情况的则包括了丝织品皮革、汽油焦炭能源以及橡胶及塑料等多个行业。由此观之,除了造纸业等少数行业,在诸多轻工业领域内,其污染气体排放水平比生产率的走势更为稳定。在重工业领域,可以看到发达经济体几个行业部门的两类生产率的条件β收敛速度差异不大,但发展中国家或地区内重工业统一类型指标比较的差异度则较大;在分行业之间条件β收敛速度表现上看,两类经济体的能源生产率自我收敛向稳态水平的速度都快于传统生产率,且发达经济体内能源效率的条件β收敛速度领先传统生产率的幅度更大,这表明发达国家各行业污染排放的水平在样本期内变化态势较之于分行业的发展更为稳定,但发展中经济体分行业两类生产率的条件β收敛速度均快于发达国家,轻工业分行业同样如此,但发达国家重工业的传统生产率没有出现条件β收敛态势,但能源生产率存在。而发展中国家的重工业分行业部门之间的两类生产率条件β收敛的速度相差不大。总体来看,发展中经济体在制造业总体以及轻工业领域分行业的条件β收敛速度稍具优势,重工业领域内分行业则没有出现明显的规律性特征。本文进行两组条件β收敛检验结果表明,全球主要经济体制造业在分经济体以及分行业大部分情况下既存在绝对β收敛,也存在条件β收敛。而且多数情况下,能源生产率的β收敛速度更快。
| 表 10 发展中经济体两类TFP增长率绝对收敛检验结果(固定效应模型) |
实体产业走上绿色经济发展通道已经成为世界性的共识,而提高能源生产率也是实现经济发展以及环境保护两大主题协调共进的方式之一。本文通过对2000-2009年全球主要经济体制造业细分行业的传统以及能源生产率的变动趋势以及收敛性检验,立足于WIOD数据,分析全球范围主要经济体以及具体行业部门的传统生产率以及能源生产率的变化特征以及收敛态势,进而通过对两类生产率的比较析出其中的规律性特点。而通过在传统这生产率的计算中加入反映污染气体排放的能源性因素,这样测算出来的能源生产率与传统生产率的比较可以更加深刻的反映全球性产业发展特点,而以全球数据进行制造业的生产率比较核算,这种研究所涉题材在学术界较为缺乏。本文得出以下主要结论:
1.全球主要经济体制造业的两类生产率在样本时段内呈现出现先小幅增长后大幅下滑的态势,且两类生产率的走势形状高度相关,表明了在总体上,制造业产业发展与所付出的环境污染代价基本保持了较为稳定一致的投入产出比例,样本期内并没有实现以节能减排为方式的加速发展。
2.样本期内,不同经济体之间的两类生产率都呈现出产业效率的差异先收敛后扩张的趋势,不同经济体之间生产率的差异度在样本时段后期有所放大,能源效率的发散程度小于传统生产率。而在分行业上,两类生产率的走势则有所差异,但发散程度变化不大。换言之,如果从分经济体以及分行业两个维度考察样本期两类生产率变化,结果将有较大差异。
3.从两类生产率的δ收敛检验结果来看,样本期内无论传统生产率还是能源生产率都没有表现出明显的收敛性特征,变化趋势曲线更多的是以交织为主要特点。在发达与发展中经济体之间生产率略显扩张拉大的态势,发达经济体内两类生产率变异系数相差不大,但在发展中经济体中,能源生产率变异指数都明显大于传统生产率。轻工业所导致的污染气体排放问题也并不是很突出,但在重工业领域内,能源效率的异质性略大于传统效率且出现了一定的δ收敛,行业以及经济体之间两类生产率的变化态势由于外部因素的作用会表现出一定的差异。
4.从β收敛检验结果来看,尽管在直观感受上经济体以及行业之间没有出现δ收敛态势,但数理检验结果表明,除了全球重工业分行业部门领域的传统生产率,其他分行业以及分经济体的β检验都表明,两类生产率都出现了绝对以及条件β收敛,但分经济体之间的能源生产率收敛速度远低于传统生产率,各国(地区)之间的污染排放力度存在差异。这应当与各国产业结构有关,也和政府监管力度的差异相关联。轻工业领域内,多数部门的能源生产率β收敛速度低于传统生产率,但在重工业领域内则正好相反,各国的重工业能源效率在以更快的速度趋同,这表明全球国家对于重工业污染排放问题的关注程度高于轻工业。
5.条件β收敛检验表明各经济体两类生产率在动态的向其自身稳态趋近,总体上没有能够在发展过程中真正意义上提升自己的能源利用效率。在诸多轻工业领域内,其污染气体排放水平比生产率的走势更为稳定。在重工业领域,发达经济体行业部门的两类生产率的条件β收敛速度差异不大,但发展中国家或地区内重工业统一类型指标比较的差异度则较大;总体来看,发展中经济体在制造业总体以及轻工业领域分行业的自我收敛速度稍具优势,重工业领域内分行业则没有出现明显的规律性特征。发达的经济体或是行业与落后者之间在考虑污染排放的基础上,彼此间产业效率差距可能长期存在,全球国家或行业之间的均衡性发展在纳入环境因素之后显得更为突出和严重。
本文研究所蕴含的政策含义是,各经济体在实体产业发展过程中对于环境管控工作成效上存在差异,发展中经济体的产业发展在更大程度上是以环境破环为代价的一种粗放模式。提升产业的科技含量,推动产业效率的提升,避免走粗放式的增长模式而带来的环境压力,并充分挖掘出实体产业现有的资源与技术潜力从而改善产业发展的模式,加快以高科技、低能耗为依托的智能制造产业是全球产业链布局优化的重点。全球特别是发展中经济体,应当结合自身条件将提升实体产业作为发展战略的核心,在淘汰落后产能的同时提高创新转化效率,改变其传统的能源结构,破除能源消费的路径依赖惯性。加强可再生的风能、太阳能以及新能源的开发与利用,在推在产业进步的过程中处理好资源环境和产业促进之间的关系,实现全球各经济体以及不同行业部门间的协调发展,减小各经济体之间以及行业之间发展上的差距。
| [] |
彭国华, 2005, “中国地区收入差距、全要素生产率及其收敛分析”, 《经济研究》, 第 9 期, 第 19-29 页。 |
| [] |
杨翔、李小平、周大川, 2015, “中国制造业碳生产率的差异与收敛性研究”, 《数量经济技术经济研究》, 第 12 期, 第 3-20 页。 |
| [] |
沈能, 2006, “中国制造业全要素生产率地区空间差异的实证研究”, 《中国软科学》, 第 6 期, 第 101-110 页。DOI:10.3969/j.issn.1002-9753.2006.06.014 |
| [] |
张少华、蒋伟杰, 2014, “中国全要素生产率的再测度与分解”, 《统计研究》, 第 3 期, 第 54-60 页。 |
| [] |
王许亮、王恕立, 2018, “服务业能源生产率变迁及收敛性分析——基于全球40个经济体细分行业数据的经验研究”, 《数量经济技术经济研究》, 第 1 期, 第 42-59 页。 |
| [] |
吴伟炯, 2016, “工作时间对职业幸福感的影响——基于三种典型职业的实证分析”, 《中国工业经济》, 第 3 期, 第 130-145 页。 |
| [] |
庞瑞芝、邓忠奇, 2014, “服务业生产率真的低吗?”, 《经济研究》, 第 12 期, 第 86-99 页。 |
| [] |
王恕立、滕泽伟、刘军, 2015, “中国服务业生产率变动的差异分析——基于区域及行业视角”, 《经济研究》, 第 8 期, 第 73-84 页。 |
| [] |
王恕立、刘军, 2014, “中国服务企业生产率异质性与资源再配置效应——与制造业企业相同吗?”, 《数量经济技术经济研究》, 第 5 期, 第 37-53 页。 |
| [] |
刘兴凯、张诚, 2010, “中国服务业全要素生产率增长及其收敛分析”, 《数量经济技术经济研究》, 第 3 期, 第 55-56+95 页。 |
| [] |
林毅夫、刘明兴, 2003, “中国的经济增长收敛与收入分配”, 《世界经济》, 第 8 期, 第 3-14+80 页。 |
| [] |
Mulder P, Groot H L F D, Pfeiffer B., 2014, "Dynamics and Determinants of Energy Intensity in the Service Sector:A Cross-country Analysis, 1980-2005". Ecological Economics, 100(100), 1–15.
|
| [] |
Solow R M., 1956, "A Contribution to the Theory of Economic Growth". Quarterly Journal of Economics, 70(1), 65–94.
|
| [] |
Swan T W., 1956, "Economic Growth and Capital Accumulation". Economic Record, 32(5), 334–361.
|
| [] |
Gerschenkron A., 1962, "Economic Backwardness in Historical Perspective"//Economic backwardness in historical perspective, The Belknap Press of Harvard University Press: 383-385.
|
| [] |
Grossman G M, Helpman E., 1991, "Innovation and Growth in the Global Economy"//Innovation and growth in the global economy. MIT Press: 323-324.
|
| [] |
Islam N., 2003, "Productivity Dynamics in a Large Sample of Countries a Pane l Study". Review of Income and Wealth, 49(2), 247–272.
DOI:10.1111/1475-4991.00085 |
| [] |
Van Ark H H, Crafts N F R., 1996, "Convergence and Divergence in the European Periphery". Cambridge Books, 2009(218), 83–85.
|
| [] |
Miller S M, Upadhyay M P., 2002, "Total Factor Productivity and the Convergence Hypothesis". Journal of Macroeconomics, 24(2), 267–286.
DOI:10.1016/S0164-0704(02)00022-8 |
| [] |
Strazicich M C, List J A., 2003, "Are CO2, Emission Levels Converging Among Industrial Countries?". Environmental & Resource Economics, 24(3), 263–271.
|
| [] |
Aldy J E., 2006, "Per Capita Carbon Dioxide Emissions:Convergence or Divergence?". Environmental & Resource Economics, 33(4), 533–555.
|
| [] |
Westerlund J, Basher S A., 2008, "Testing for Convergence in Carbon Dioxide Emissions Using a Century of Panel Data". Environmental & Resource Economics, 40(1), 109–120.
|
| [] |
Miketa A, Mulder P., 2005, "Energy Productivity Across Developed and Developing Countries in 10 Manufacturing Sectors:Patterns of Growth and Convergence". Energy Economics, 27(3), 429–453.
DOI:10.1016/j.eneco.2005.01.004 |
| [] |
Mulder P, Groot H L F D., 2012, "Structural Change and Convergence of Energy Intensity Across OECD Countries, 1970-2005". Energy Economics, 34(6), 1910–1921.
DOI:10.1016/j.eneco.2012.07.023 |
| [] |
Chung R.J., Fare R., Grosskopf. S., 1997, "Productivity and Undersirable Outputs:A Directional Distance Function Approach". Journal of Environmental Management, 51(3), 229–240.
DOI:10.1006/jema.1997.0146 |
| [] |
Barro R., 1986, "Reputation in a Model of Monetary Policy with Incomplete Information". Journal of Monetary Economics(17), 3–17.
|
| [] |
Bernard A, Jones C., 1996, "Comparing Apples to Oranges:Productivity Convergence and Measurement across Industries and Countries". American Economic Review, 86(5), 1216–1238.
|
| [] |
Quah D., 1993, "Empirical Cross-section Dynamics in Economic Growth". Discussion Paper, 37, 426–434.
|



