户籍改革的最终方向和目的是取消现有户籍规定对人口流动的限制,允许所有公民根据自己的意愿和能力迁移到任何地方生活和工作,自动获得当地居民的身份并享受与当地居民同等的公共权利和义务①。
① 中国社会科学院发布的《中国城乡统筹发展报告(蓝皮书)》。
中国改革开放以来取得了经济上的飞速发展, 人口流动成为一种趋势,进城挣钱和定居城市成为很多农村人的选择。然而为解决城市交通拥堵、人口多的问题,国家对农村人口进城进行了人为控制,比如户籍制度管制,医疗保障等方面的限制政策,再加上高住房成本使得农村人口移民城市变得越来越困难。随着经济、文化、社会的迅速发展,越来越多的流动人口进入了城市,这也给政府带来了很大的管理和服务挑战,面对中国如此庞大的流动人口,政府的流动人口管制是否会对经济产生一定影响?
目前国内关于人口流动对中国宏观经济波动影响的研究还相对较少。人口流动涉及到经济的方方面面,因此其对经济波动的影响不容忽视。本文结合中国流动人口的特点,从异质性技能的视角研究了流动人口对经济波动的影响。流动人口基本都是从农村流入城市,且大多数都属于低技能工人,因此,关于流动人口的冲击从理论模型上可以理解为低技能劳动的冲击。
本文的理论框架是在RBC模型基础上讨论了人口流动对经济波动的影响,模型中用低技能供给冲击来刻画人口流动,通过参数校准和贝叶斯估计出高低技能相关参数,在包含高低技能居民的RBC模型中,受到低技能劳动供给的冲击(流动人口)使得低技能工资上升,高技能工资下降,总产出和消费都有所回落,不利于经济的增长,而且人口流动冲击会导致不同技能的福利会有所减少。因此,国家的限制人口流动政策不利于经济发展和人民福利水平的提高。
上世纪80年代以来,国内外专家学者对流动人口与经济波动的关系进行了一系列的研究。Glomn.G(1992)研究了人口迁移与人均收入的关系,发现人口迁移对人均收入有着正向的影响; 左学金(1995)认为人口迁移能有效提高迁出地人口的收入水平,从而对迁出地经济产生正向影响,同时能够缓解迁入地劳动力不足的困境; 王桂新(1996)则从区域经济发展的角度进行了研究,发现人口迁移为东部地区的经济增长贡献了15%左右; ;Johnson(2003)通过研究发现,在农村劳动力流动人口不受限制时,人口流动会减少农村与城市收入差距;董栓成(2004)通过实证分析得出,单流入人口增长对经济增长存在正向作用; 段平忠(2005)通过对不同时间段东、中、西部地区经济增长的研究,发现劳动力增长对地区经济增长的作用是长效的,人口流动也确实存在使区域经济增长收敛的作用,人口流动的制度障碍能减弱人口流动对经济增长的这一影响。彭玉兰(2015)通过引入人口聚集效应的影响,表示当人口迁移量足够大时,人口流动将会使迁入地的经济处于长期增长状态,大规模的人口流动存在规模经济和知识溢出效应,从而不断促进迁入地的经济增长。综上所述,学者们认为人口流动将促进经济增长,有利于缩小区域间经济发展水平的差距。然而,目前国内还少有学者从理论上系统研究人口流动冲击对经济波动和不同居民的福利影响。
本文主要是在RBC的模型框架下进行的。选用RBC模型来研究我国人口流动对经济波动的影响主要有两个原因:第一,RBC模型是一个包含了不同部门进行利益或者福利最大化决策的过程,可以很好地综合考虑人口流动管制对不同技能工人变量的影响,丰富了人口流动对宏观经济波动的理论研究;第二,人口流动通常具有全面性和整体性,统计的数据主要是时间序列数据,加上统计时间短,在我国很难或者无法用人口流动的面板数据进行实证分析,倘若采用实证分析,不仅缺乏理论基础且存在强烈的内生性问题。对RBC模型在分析人口流动对经济波动问题的适用性方面,本文结合已有文献的参数校准方法并基于实际数据对模型参数进行了贝叶斯估计,以此来分析人口流动管制对异质性技能对我国经济波动的影响。
本文的主要创新和可能的贡献有:第一,本文在RBC模型中引入低技能劳动供给冲击来刻画流动人口管制对经济波动的影响,而不是采用目前普遍的总劳动供给;第二,劳动人口流动管制对总产出和消费都有负的影响,即不利于我国经济的长期增长,同时人口流动管制会使得低技能工人工资上升,高技能工资下降, 总有效劳动量下降,居民福利减少;第三,资本质量冲击、政府购买冲击都会使得消费、工资及福利下降。其中政府购买冲击会使居民福利下降最大,低技能总福利损失大于高技能总福利损失;第四,随着经济整体高技能比重加大,会加大人口流动管制对总福利的影响,高技能社会越离不开低技能的互补。
本文的结构安排如下:第一部分为引言;第二部分描述了我国人口流动趋势和特征事实;第三部分构建了一个带有流动人口管制冲击的异质性技能劳动RBC模型;第四部分对模型参数进行校准和贝叶斯估计,并进行相应冲击的动态分析;第五部分为方差分解及福利分析;第六部分为结论及政策建议。
二、经验事实中国的流动人口总量一直都处于居高不下的状态,数量从2010年的22100万增长到2017年的24400万,流动人口占总人口的比重从16.48%到17.55%。2014年,我国流动人口总量一度高达25300万,占总人口的18.5%,如此庞大的流动人口总量无疑对我国经济产生深远影响。
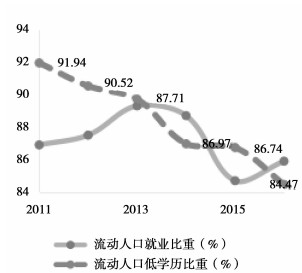
图 2.1可以发现,2010年到2016年中国流动人口还是以就业为主要目的。流动劳动人口就业占比从2010年的86.9%发展到2016年的85.9%,说明了我国流动人口进入发达城市或地区还是主要以找工作为目的。通过进一步统计流动人口的受教育程度分布情况,我们发现流动人口基本都属于教育水平比较低下的人群,80%以上的人口受教育水平程度为初中及初中以下。教育水平低意味着流动人口绝大部分都是低技能人群, 这也是本文采用低技能供给冲击来刻画流动人口对经济波动影响的主要原因,同时也能说明本文运用低技能供给冲击反映人口流动冲击是合理的,符合现实经济情况。
|
图 2.1 中国流动人口劳动比例和教育程度 数据来源:笔者根据中国流动人口数据平台整理① |
① 流动人口低学历比重是以初中及以下学历为低学历人群占总流动人口比重(%)。
21世纪以来,中国经济处于持续增长状态,但是经济增长率开始缓慢下降。
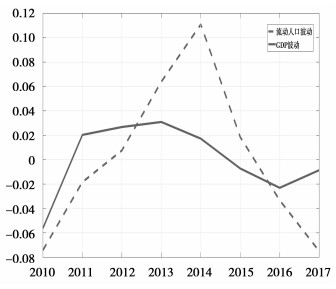
2007年,我国经济增长率达到历史最高的14.2%,之后开始缓慢下降,2017年经济增长率下降到6.9%。为了更加直观地看到近些年来的经济波动情况,对经济总量进行了对数HP滤波处理。根据趋势线提取了经济波动项,同时也通过同样方法提取了人口流动波动项。图 2.2中两变量的波动趋势协同性较高,通过进一步相关性检验发现人口流动和GDP波动显著相关,因此本文提出一个简单假设,认为在各种经济体制的障碍背景下,人口流动迁移受到阻碍,是我国经济增长速度放缓的一个特别重要的原因。
|
图 2.2 中国流动人口与GDP波动比较 数据来源:中经网整理② |
② 由于流动人口数据的可得性,时间长度不是很长,通常如果使用季度数据,lamada为1600,而年度数据则为400。
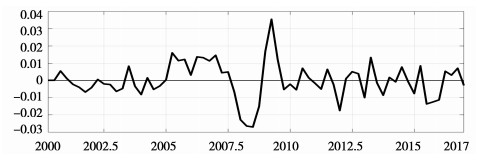
人口流动管制是一个很抽象和复杂的综合概念,目前国内还没有对人口流动管制程度数据进行时间序列统计。本文的人口流动管制是指所有能影响到低技能劳动供给政策外生冲击的变量,包括户籍制度变动对流动人口的限制、大城市对技能劳动的排挤政策、低技能社保、医疗、住房等,这些政策变动都会影响到流动人口的流动。虽然实际流动人口管制数据很难统计得到,但是通过贝叶斯方法①使其成为可能,本文基于已有的宏观变量有限信息可以估计出人口流动管制的时间序列波动,这种方法是目前很多宏观文献中估计不可观测变量的主流方法。例如,郭长林(2016)用贝叶斯方法估计出我国历年国有企业和民营企业资本利用率的季度时间序列数据②。贝叶斯估计结果发现金融危机期间流动人口管制波动很大,图 2.3中人口流动的时间序列可以发现:在2008年金融危机时期,经济不景气,流动人口的管制波动有一个向下的剧烈波动,2009年中国颁布了《全国流动人口管制条例》,从很多方面加强保障了流动人口的权利,出现了人口流动管制波动的放松阶段,接着是2015-2016年中国的很多城市出现了住房和租房的剧烈上升,增加了流动人口的经济成本,从而出现了人口流动管制的向下波动。因此,图 2.3很好的反映了人口流动管制的时间序列变化。从时间段上我们可以发现,人口流动管制加强(特别是金融危机期间)会对我国经济增长有一定的抑制作用,随后的放松管制会促进经济增长。此外,2010-2017年8年时间的人口流动管制波动均值为负数,说明近几年来我国的人口流动管制平均而言是在加强。
|
图 2.3 2000-2017年季度流动人口管制时间序列图 |
①文中的第四部分的参数贝叶斯估计和变量动态模拟。
②关于动态贝叶斯方法的相关理论描述,请参见An&Schorfheide(2007)。
这部分主要是基于人口流动和经济波动的经验事实,总结我国的流动人口有三大特点:第一,流动人口数量越来越多,占总人口比重越来越大;第二,流动人口主要目的是为了解决就业问题,普遍学历比较低,属于低技能人群;第三,数据统计上发现流动人口波动与经济产出波动有正的相关性,而且在百分一置信区间内显著;第四,通过有限信息的贝叶斯估计我国历年季度的人口流动管制时间序列趋势,发现近些年来我国的人口流动管制程度在加强。因此,为了能从理论上解释人口流动对经济波动的影响,本文构建了异质性技能劳动的RBC模型分析人口流动管制会对经济波动带来的各方面影响。
三、异质技能的DSGE模型本部分是基于标准的RBC一般均衡的理论框架下,引入了低技能劳动供给的冲击,以分析人口流动对经济波动的影响。我们假设经济体中有两种不同技能居民,记为高技能和低技能居民。模型中包含了厂商、居民和政府部门三个代表性部门,整个经济体运作是不同主体根据效应或者福利最大化做出决策。下面本文就具体分析每个经济体的厂商、不同居民和政府的行为,为了方便描述,本文将i∈{1,2}的变量用i表示。
(一) 异质性技能居民参照Federico S.et al., (2012)异质性技能居民家庭的效用函数可以得出总表达式:
| $ \max E_{t} \sum\limits_{s=t}^{\infty} \beta^{t}\left\{\phi s U\left(c_{h, t}, l_{h, t}\right)+(1-\phi)(1-s) U\left(c_{l, t}, l_{l, t}\right)\right\} $ | (3.1) |
| $ u_{t}=\left(\frac{C_{i, t}^{1-\theta}}{1-\theta}-\zeta_{t}^{u} \frac{\psi_{i}}{1+\varphi} l_{i, t}^{1+\varphi}\right) $ | (3.2) |
居民预算约束为:
| $ s w_{h, t} l_{h, t}+(1-s) w_{l, t} l_{l, t}+r_{t} k_{t} \geqslant s c_{h, t}+(1-s) c_{l, t}+I_{t} $ | (3.3) |
其中,ch为高技能消费,cl为低技能的消费,lh为高技能劳动时间,ll低技能劳动时间,wh技能工资收入,wl为u低技能工资收入,ψi为不同技能劳动的效用权重大小,ζtu为低技能劳动供给冲击,ϕ为高技能的相对效应权重,s为高技能占总技能比重,θ为消费的替代弹性,φ为劳动的替代弹性,It是居民的实物投资,kt为居民拥有资本,rt为资本的报酬率。
通过等式(3.3)约束下最大化(3.1),一阶段求导C, L,K,其中ζt拉格朗日乘子:
| $ \frac{\phi_{t}^{d}}{c_{h, t}}=\frac{(1-\phi)}{c_{l, t}}=\zeta_{t} $ | (3.4) |
| $ \frac{{{w_{h,t}}}}{{{c_{h,t}}}} = \mathsf{{ψ}_h}l_{h,t}^\varphi ,\frac{{{w_{l,t}}}}{{{c_{l,t}}}} = \mathsf{{ψ }_l}l_{l,t}^\varphi ,$ | (3.5) |
| $ 1=\beta E_{t}\left\{\frac{\zeta_{t+1}}{\zeta_{t}} r_{t+1}+1-\delta\right\} $ | (3.6) |
假设企业生产是由资本及不同技能劳动进行生产,生产函数的劳动是复合劳动,由低技能劳动和高技能劳动进行生产,另外假设中生产厂商生产函数表示为:
| $ y_{t}=A_{t}\left(F_{t} k_{t}\right)^{\alpha} n_{t}^{1-a} $ | (3.7) |
其中nt为生产的高技能总劳动Nh, t和低技能总劳动Nu, t的复合生产劳动:
| $ n_{t}=\left\{s^{\frac{1}{r}}\left(\zeta N_{h, t}\right)^{\frac{r-1}{r}}+(1-s)^{\frac{1}{r}}\left(N_{u, t}\right)^{\frac{r-1}{r}}\right\}^{\frac{r-1}{r}} $ | (3.8) |
根据生产厂商的利润最大化条件进行一阶段最优,分别计算出生产的高技能工资、低技能工资和资本利率的表达式:
| $ w_{h, t}=A *(1-a) *(1-1 / v) * \zeta^{(1-1 / v)} * \frac{y_{t}}{n_{t}} *\left(\frac{n_{t}}{N_{h, t}}\right)^{\frac{1}{r}} $ | (3.9) |
| $ w_{u, t}=A *(1-a) *(1-1 / v) * \frac{y_{t}}{n_{t}} *\left(\frac{n_{t}}{N_{u, t}}\right)^{\frac{1}{v}} $ | (3.10) |
| $ r_{t} k_{i t}=a \frac{y_{t}}{n_{t}} $ | (3.11) |
其中s为高技能占高低技能人口比重,ζ为高技能的生产效率,ν为高低技能的替代弹性,Ft为资本质量冲击。
(三) 政府部门本模型并没有考虑货币政策影响,因为基于RBC模型的货币政策并不能对实体经济产生作用,基于本文研究的问题和模型设定,本文只考虑了政府财政部门,为了简单起见,假设政府购买支出冲击进行如下设定:
| $ G_{t}=\eta_{t} * y_{t} $ | (3.12) |
其中ηt为政府购买的与总产出的占比的冲击变量以刻画政府购买冲击对经济变量的影响。
(四) 市场出清条件| $ Y_{t}=s c_{h, t}+(1-s) c_{u, t}+I_{t}+G_{t} $ | (3.13) |
为考察低技能劳动供给冲击的宏观经济影响,在文章基准模型中低技能劳动供给冲击、技术冲击、金融冲击、政府购买冲击服从AR(1)过程,它们的持续性系数为{ρl ρa ρf ρG},外生冲击项分别为{σi, σa, σf, σG},服从具有标准差的标准正态分布。
(五) 一般均衡与动力系统整个经济的一般均衡由如下条件确定:(1)不同技能家庭和厂商最大化各自的目标函数; (2)劳动市场和资本市场出清; (3)不同技能家庭的资源约束条件成立。
四、参数的校准与动态分析 (一) 参数校准本文的主观贴现因子参照陈昆亭等(2004a, 2004b), 黄赜琳、朱保华(2015)研究选取了0.97;不同技能效应权重参照Federico S.et al., (2012),高技能效应选取为0.6①;资本比例参照张军等(2002, 2003)和陈昌兵(2015)选择为0.5;资本折旧参照张军等(2004)和张健华、王鹏(2012)综合比较选择为0.025;劳动时间参照许志伟(2011)的稳态为0.33,假设工作时间一天为1单位的话,按照中国8小时的工作时间,刚好稳态也是三分之一;高低技能替代弹性参照陈利锋(2018)为1.5;高低技能比值参照陈利锋(2018)综合选取为0.10;高技能的技术效率结合中国特点然后参照Federico S.et al., (2012)设置为3;冲击自相关系数参照朱军(2018)设置先验均值。其它参数参照其它相关文献进行了相应的校准。
① 通过不同高技能效应权重大小,发现并不影响本文的主要结论。
(二) 部分贝叶斯估计为了刻画最真实的估计参数,参照陈小亮等(2016)和朱军(2018)的研究,采取参数校准与估计相结合的方法。第一类参数是与稳态相关的参数,在计算模型稳态的基础上,利用已有研究或与可观测变量“矩条件匹配方法”进行校准(表 4.1);第二类是与转移动态的相关参数,使用“贝叶斯”计量方法估计。动态参数依据数据样本均为2000年1季度至2016年4季度数据,所有数据均来自CQER数据库①。选取投产出与消费两个主要宏观变量作为观察值, 一方面避免变量选取的多重共线;另一方面也满足了实际观察值变量比冲击变量少的要求。另外对选取的变量进行季节调整,然后利用HP滤波去趋势以分离这些变量时间序列中的经济周期部分,再使用“贝叶斯”估计得到相关参数。贝叶斯估计借鉴SW(2007)和朱军(2018)使用贝叶斯的后验均值作为先验均值,参照文献找出参数的先验分布和标准差,然后通过贝叶斯进行估计他们的后验均值进行模型动态分析。
| 表 4.1 参数校准情况 |
| 表 4.2 贝叶斯估计结果 |
① 参见https://www.frbatlanta.org/cqer.aspx的中国宏观数据。
(三) 实际数据和真实比较为了对模型的可靠性进行分析,通过参照林仁文(2014)和朱军等(2018),对主要的宏观经济变量的模型的标准差和相关性特征与真实数据进行比较。表 4.3可以发现模型的产出、投资与消费对应的Kydland-Prescott(KP)方差比率分别为90.25%、77.56%与28.69%,说明本模型设定的冲击能解释70%以上的产出和投资波动以及五分之一以上的消费波动。这是因为模型不可能穷尽所有的冲击,包括影响消费的偏好冲击、政府支出冲击等等。模型中的产出波动的标准差为2.50个百分点,真实数据的产出波动标准差2.77个百分点, 产出波动的拟合能力90%;模型中投资的标准差为5.60个百分点,真实数据的消费标准差为7.22个百分点,KP方差比为77.56%。模型的消费标准差为1.03个百分点,实际消费的标准差为3.59个百分点,模型拟合能力是28.69%,另外模型中的投资与收入波动相关性为0.85,实际数据中投资与收入的相关性为0.73,投资一阶自相关中模型为0.67,实际数据为0.73。模型中的消费与收入相关性为0.50,实际数据中消费与收入的相关性为0.86。因此,模型总体上能够较好拟合经济产出的波动,综合分析说明模型可以反映经济波动的主要特征。
| 表 4.3 模型与真实数据比较 |
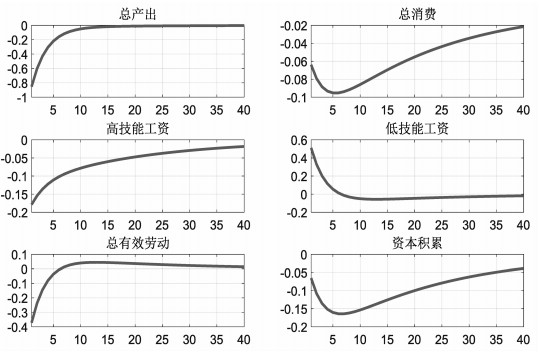
首先分析了负向低技能供给冲击对宏观经济变量的影响。图 4.1发现低技能劳动供给冲击会使得经济产出下降,总消费减少,高技能工人工资是先下降后逐渐向稳态靠近,低技能工人工资是先上升后逐渐向稳态靠近,人口流动管制对低技能工资影响明显高于对高技能工资的影响。由于低技能的工资增加使得高技能劳动增加,同时人口流动管制使得投资下降,资本积累降低,低技能劳动供给的冲击使得总生产劳动供给降低、总需求降低、总消费下降,导致总产出减少。据图 4.1可以发现单位低技能劳动供给冲击使得总产出下降0.8%, 消费减少0.06%,资本积累下降0.5%,高技能工资减少0.16%,低技能工资上升0.6%。说明人口流动管制不利于我国的经济增长和消费,反之,人口流动放松会促进经济增长。随着人口流动管制的加强,经济活动中的低技能劳动就会相对减少,而随着经济活动对低技能劳动需求的增加,低技能劳动的工资水平就会上升。例如,经济社会中低技能劳动逐渐减少时,城市中类似工人、保姆等职业的低技能劳动工资水平就会出现上升,究其原因可能是,当经济体中受到低技能劳动供给冲击时,一部分高技能劳动会选择一些社会必须的低技能劳动,说明高技能和低技能劳动在经济中的确存在相互替代性。这种人口流动管制使得高技能居民牺牲劳动高工资去做低技能的工人工作,技能错配使得总有效劳动下降,不利于整体经济的增长。
|
图 4.1 低技能劳动供给冲击对各变量动态 注:纵轴为偏离稳态的百分比(%),横轴为季度,以下相同。 |
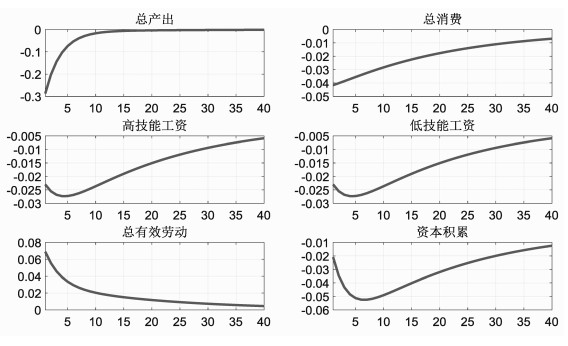
考虑到我国面临金融市场不发达的情况,再加上我国投资过剩现象严重,使得企业的资本不能充分利用,当引入了资本质量(资本利用率)冲击后,模拟分析了资本质量冲击对我国经济波动的影响。图 4.2发现资本质量的负冲击会使得经济产出下降0.3%,然后经过10期逐渐回到稳态,总消费下降0.04%,资本积累减少0.02%,工资下降0.02%。分析可能原因是资本质量冲击使得有效投资效率开始降低,资本积累开始减少,总产出下降,经济的不景气使得不同技能的工资出现下滑,最后导致消费也下降。说明了资本质量冲击是不利于我国的宏观经济增长,特别是在我国目前产能过剩、投资效率低下背景下,资本质量冲击会进一步恶化宏观经济影响。因此,我国应该加强资本质量管理,提高投资效率,减少产能过剩问题,以此来逐步提高经济发展水平。
|
图 4.2 资本质量冲击对各变量动态反应 注:纵轴为偏离稳态的百分比(%),横轴为季度,以下相同。 |
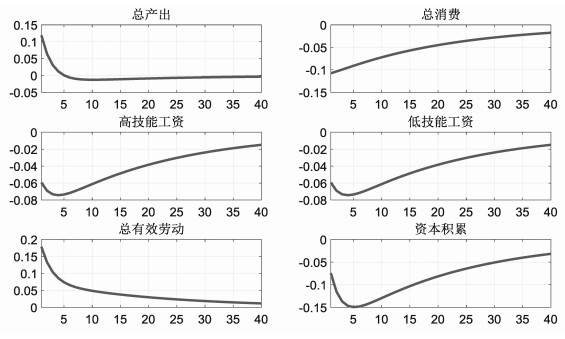
图 4.3模拟我国政府购买支出对宏观经济变量的影响,可以发现单位政府购买冲击会增加总产出,但会挤出私人总消费,从而使得消费水平下降。单位政府购买冲击使得总产出增加0.1%,持续时间大概在4期左右,说明政府购买冲击对经济总产出持续性时间较短,可能的原因是政府购买支出大多数是消费性公共支出。政府购买支出会挤出私人总消费,从下图 4.3的脉冲结果可以发现,单位的政府购买冲击会使得总消费先下降0.1%,后期会逐渐回归稳态,对消费的挤出时期较长,说明单位的政府购买冲击会使得私人总消费持续减少,不利于人们福利水平的提高。同时资本积累也是先下降后上升,慢慢回到稳态。政府购买冲击对技能劳动工资都有减少,技能工资是先下降0.06%,然后逐渐上升,经过很长时期回到稳态水平。进一步分析发现,政府购买的冲击对技能工资的影响主要是通过影响了私人投资进而影响了资本积累的水平,投资效率低下,使得工人的边际劳动效率工资下降,为了维持以前的产出水平会使得总有效劳动时间上升。
|
图 4.3 政府购买冲击对各变量动态反应 注:纵轴为偏离稳态的百分比(%),横轴为季度,以下相同。 |
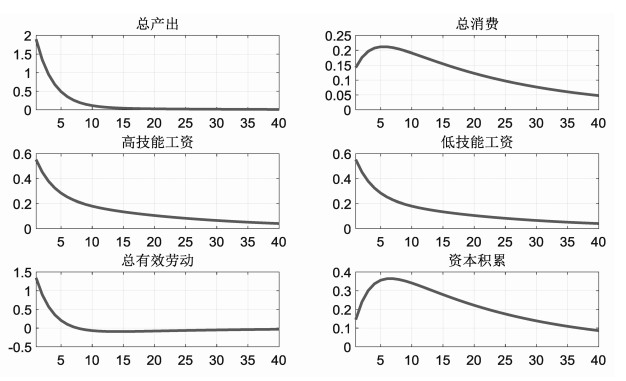
最后模拟分析的是技术冲击对我国各经济变量的影响,图 4.4模拟结果显示单位技术冲击会使得经济产出增加, 消费上升,高技能和低技能的工资增加, 劳动增加, 同时使得总有效劳动在增加, 资本利率也上升。具体分析如下:1单位的技术冲击使得总产出增加1.8%,持续时间大概在十个季度左右,说明了技术冲击对经济总产出持续性时间较长,技术进步能给经济带来持续的经济增长。从下图的脉冲结果可以发现,单位技术冲击会使得总消费上升0.15%,后期会逐渐回归稳态,对消费的促进作用时期也较长,总消费持续增加10年左右,同时资本积累在上升,慢慢回到稳态;单位技术冲击会使得技能工资增加0.6%,影响持续性大概也有10年,其中影响最大的是前5个季度,后面影响会慢慢减弱。观察其它相关变量发现单位技术冲击使得总有效劳动持续的增加,劳动工资有持续正的影响。总之,技术冲击会使投资增加,工资上升,消费增加,最后影响总产出也上升。
|
图 4.4 技术冲击对各变量动态反应 注:纵轴为偏离稳态的百分比(%),横轴为季度,以下相同。 |
本文通过真实数据贝叶斯估计,关于不同外生冲击对产出的影响进行了方差分解。通过产出的方差分解,发现技术冲击能解释产出的61.6%,能解释经济波动一半以上,和许多文献结论一致(祝梓翔等,2017)。低技能劳动(流动人口)冲击能解释产出波动7.83%,财政政策冲击能解释产出波动的5.59%,资本质量冲击(资本利用率)能解释产出波动的24.98%,说明我国的资本质量冲击对产出波动有1/4的影响。从投资方差分解方面,低技能劳动冲击能解释产出的5.60%,技术冲击能解释投资的42.10%波动,财政政策冲击能解释50.20%,资本质量的冲击能解释投资2.05%,由于我国投资过度出现产能过剩现象导致资本质量冲击对投资影响比较小。
| 表 5.1 产出的方差分解 |
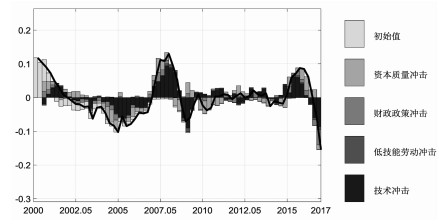
图 5.1对我国产出进行了历史方差分解,可以发现本轮经济增速下滑的重要原因是技术冲击。说明之前我国经济增长主要靠模仿学习等方式促进经济快速增长,之后缺乏自主创新使得技术进步促进经济增长越来越难,因此国家要进行经济结构调整,鼓励创新,这也符合RBC模型中技术冲击是驱动经济波动的最重要因素。而人口流动管制的低技能劳动供给对我国的产出影响有限,从历史的方差分解来看,低技能劳动供给冲击会减少产出,特别在经济不景气的时候低技能劳动冲击会进一步加大经济下滑压力。总体来说低技能劳动冲击不利于经济增长;反之,放松人口流动会促进经济增长。
|
图 5.1 产出的历史方差分解(2000-2017) |
根据图 5.2显示,我国最近几年的投资波动在上升,方差分解分析主要是由政府财政政策影响了投资,说明目前我国的投资更多是财政政策驱动的。同时低技能劳动供给冲击会减少投资,技术水平的负面冲击对投资有抑制作用。同样从历史方程分解来看低技能劳动冲击对投资有负面的影响,但影响比较有限。投资的波动主要是由政府财政政策和技术对投资的共同作用的结果。
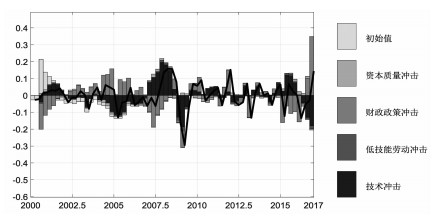
|
图 5.2 投资的历史方差分解(2000-2017) |
以上部分是从人口流动管制冲击和其它冲击对经济变量的动态影响,为了进一步说明人口流动对经济波动的福利影响,本文对福利分析进行两部分展开,第一部分是考察不同冲击对不同技能劳动福利的影响。第二部分以消费弥补的大小进行衡量,随着国家高技能比重增加,考察人口流动冲击对社会福利的影响。两部分对不同冲击从不同的角度进行了福利分析。
首先从整个福利动态分析,考察冲击波动如何影响高低技能福利水平。具体地,本文定义不同技能劳动福利水平变化满足如下等式
| $ W_{i}\left(A_{t}, K_{t}\right)=W_{i}^{c}\left(A_{t}, K_{t}\right)+W_{i}^{N}\left(A_{t}, K_{t}\right) $ |
| $ W_{i}\left(A_{t}, K_{t}\right)=E_{t} \sum\limits_{j=0}^{\infty} \beta^{j}\left(\frac{(1+\lambda) c_{i}^{1-\theta}}{1-\theta}-\phi \frac{N_{i, t}^{1+\phi}}{1+\phi}\right)+\beta W_{i+1}\left(A_{t}, K_{t}\right) $ |
根据以上推导的福利公式模拟出不同冲击对福利的动态影响。图 5.3分别模拟低技能劳动供给冲击、金融冲击和政府购买冲击对福利动态的影响,可以发现低技能劳动供给冲击对低技能总福利损失比高技能福利损失大,单位低技能劳动供给的冲击会使高技能劳动的福利损失迅速下降0.4%,对低技能劳动的福利损失下降为1%,高于对高技能劳动福利损失的0.6%,总福利下降1.5%。金融冲击方面,单位的负资本质量冲击使得高技能劳动福利损失下降0.4%, 低技能劳动的福利损失下降2.3%,总福利下降2.6%。另外金融冲击对低技能福利影响最大,可能的原因在于资本质量冲击使得产出下降,工资减少,低技能劳动者对消费下降反应更敏感。最后模拟的政府购买冲击对不同技能劳动者的福利影响,单位政府购买冲击使得不同技能劳动者福利都减少,同样对低技能劳动者的福利影响更大。政府购买增加挤出私人消费,工资降低使得低技能劳动者替代效应大于财富效应,进一步加大了福利损失。
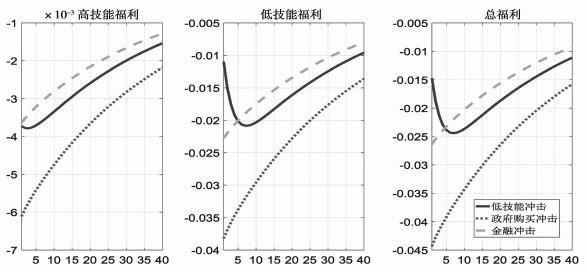
|
图 5.3 不同冲击对不同技能居民福利动态反应① |
① 包括三种冲击:低技能冲击、政府购买冲击、资本质量冲击。
(四) 消费补偿效应这部分是从横向进行福利比较,当经济体中高技能比重加时,之前的消费要增加多少倍才能弥补现在的福利水平,即经济体中高技能比重的增加,单位人口流动管制(低技能劳动冲击)会产生怎样的福利效果。从福利公式推导出消费补偿值的推导过程。具体地,总福利函数是由两部分组成,一部分是消费带来的福利部分,另外一部分是劳动带来的福利部分,两部分共同组成了居民的总福利函数。
| $ W_{i}\left(A_{i}, K_{i}\right)=W_{i}^{x}\left(A_{i}, K_{t}\right)+W_{i}^{N}\left(A_{t}, K_{t}\right) $ |
消费部分的福利函数表达,参照标准的消费函数基本设定形式为:
| $ W_{i}^{c}\left(A_{t}, K_{t}\right)=E_{t} \sum\limits_{j=0}^{\infty} \beta^{j}\left(\frac{c_{i, t}^{1-\theta}-1}{1-\theta}\right) $ |
劳动供给部分的福利函数设定参照标准的函数形式,其中的φ的值不同技能劳动者的比值是不同。
| $ W_{i}^{N}\left(A_{t}, K_{t}\right)=E_{t} \sum\limits_{j=0}^{o o} \beta^{j}\left(-\phi \frac{N_{i, t}^{1+\phi}}{1+\phi}\right) $ |
比较变化前后的不同比例高技能福利无差异必须要满足如下条件:
| $ W_{i}\left(A_{t}, K_{t}\right)=E_{t_{j}=0}^{o o} \beta^{j}\left(\frac{(1+\lambda) c_{h}^{1-\theta}}{1-\theta}-\phi \frac{N_{h, t}^{1+\phi}}{1+\phi}\right) $ |
最后求解出:
| $ \lambda=\left(\frac{W_{l}\left(A_{t}, K_{t}\right)-W_{h}^{N}\left(A_{t}, K_{t}\right)+\frac{1}{(1-\theta)(1-\beta)}}{W_{h}^{c}\left(A_{t}, K_{t}\right)+\frac{1}{(1-\theta)(1-\beta)}}\right)^{\frac{1}{1-\theta}}-1 $ |
根据以上的福利公式,λ的值为消费补偿变化值,也可以表示为福利的变化。发现随着我国经济中高技能工人比重的提高,单位低技能工人供给冲击会使得福利损失加大,当经济体中高技能比重增加到0.12时候,人口流动冲击会使得高技能的消费补偿损失为-1.78%,低技能消费补偿为-0.74%,总消费补偿为-0.86%,即是当经济体高技能比重为0.12时,低技能供给冲击会使得总福利下降0.86%,随着高技能比重增加,总福利损失也就越大,进一步细分发现高技能福利损失要大于低技能福利损失。综合说明了经济体中高技能比重越大,人口流动管制政策越不利于整体经济福利水平的提高,高技能比重提高就越应该鼓励人口流动,越离不开低技能工人的互补。
| 表 5.2 低劳动供给冲击随着高技能比重增加的福利效应 |
目前,鲜有文献从理论上讨论人口流动管制对我国宏观经济的综合效应。本文将异质性技能劳动概念引入RBC模型中,分析流动人口的供给冲击对经济波动的影响。通过区分高技能和低技能劳动,分别考察低技能劳动供给冲击(人口流动管制)、资本质量冲击、政府购买冲击和技术冲击对宏观经济的动态影响。模型经过参数校准和贝叶斯估计,异质性技能模型可以解释约90.25%的宏观经济波动,研究发现人口流动管制会使得低技能工资提高,高技能工资降低,总消费减少,总产出下降。单位人口流动管制冲击使得产出下降0.8%左右,这是低技能的人口流动管制使得总有效劳动、消费和投资都下降共同作用的结果。对于不同技能福利方面,发现低技能劳动供给冲击使得不同技能劳动的福利都有下降,高技能福利影响更大。同时还发现资本质量冲击和政府购买冲击同样对不同技能劳动的总福利都有负的影响,另外研究也表明随着高技能比重提高就越应该鼓励人口流动,就越离不开低技能的互补。
有鉴于此,政府对人口流动的管制,特别是限制低技能劳动的做法不利于我国社会整体经济的增长。一个城市的发展离不开任何一个行业的技能工人,随着我国工业化进程和服务业的不断提升与发展,对于低技能工人的需求还在不断扩大,而为了促使我国产业结构均衡发展,政府应当鼓励和支持低技能工人的流入。人口的自由流动不仅能够使城市的不同行业之间技能互补,同时也能够促进行业间的有效竞争。资本质量冲击会使不同技能工人的工资减少,进而对总体消费产生一定的影响,因此,政府应当加快我国金融体系建设,促进我国金融业的快速发展。政府购买冲击虽然能够促进总产出,但却会带来私人消费与福利的下降,因此,政府应当合理进行购买管理,避免过多的购买支出影响消费和福利水平的提高。随着我国经济社会中高技能比重的不断扩大,和高技能福利损失大于低技能福利损失的结论,人口流动管制政策将不利于实现我国整体经济福利水平的提高,因此,政府应当促进和鼓励人口流动。综上所述,政府应当采取鼓励人口流动、加强资本质量管理、合理进行投资从而保证资本利用率和合理增加政府支出等一系列措施,实现我国经济的平稳发展和增长。
| [] |
彭玉兰, 2015, “集聚效应、人口迁移与经济增长”, 《湖南商学院学报》, 第 3 期, 第 27-32 页。DOI:10.3969/j.issn.1008-2107.2015.03.004 |
| [] |
董栓成, 2004, “人口流动与区域经济发展的实证分析”, 《市场与人口分析》, 第 5 期, 第 23-32 页。DOI:10.3969/j.issn.1674-1668.2004.05.004 |
| [] |
蔡昉, 2004, “边缘化的外来劳动力”, 《开放导报》, 第 6 期, 第 37-40 页。DOI:10.3969/j.issn.1004-6623.2004.06.006 |
| [] |
段平忠、刘传江, 2005, “人口流动对经济增长地区差距的影响”, 《中国软科学》, 第 12 期, 第 99-110 页。DOI:10.3969/j.issn.1002-9753.2005.12.015 |
| [] |
王桂新, 1996, “中国人口迁移与区域经济发展关系之分析”, 《人口研究》, 第 6 期, 第 9-16 页。 |
| [] |
左学金, 1995, “人口迁移与经济发展:理论模型及政策含义”, 《上海社会科学院学术季刊》, 第 4 期, 第 101-109 页。 |
| [] |
陈利锋, 2018, “部门差异、不平等与货币政策”, 《当代财经》, 第 6 期, 第 3-13 页。 |
| [] |
黄赜琳、朱保华, 2015, “中国的实际经济周期与税收政策效应”, 《经济研究3》, 第 3 期, 第 4-17 页。 |
| [] |
陈昌兵, 2015, “城市化、房地产与宏观调控”, 《经济学动态》, 第 1 期, 第 29-41 页。 |
| [] |
陈昌兵, 2014, “可变折旧率估计及资本存量测算”, 《经济研究》, 第 12 期, 第 72-85 页。 |
| [] |
张健华、王鹏, 2012, “银行风险、贷款规模与法律保护水平”, 《经济研究》, 第 5 期, 第 18-30 页。 |
| [] |
许志伟、薛鹤翔、罗大庆, 2011, “融资约束与中国经济波动——新凯恩斯主义框架内的动态分析”, 《经济学(季刊)》, 第 1 期, 第 83-110 页。 |
| [] |
陈昆亭、周炎、龚六堂, 2004, “中国经济周期波动特征分析:滤波方法的应用”, 《世界经济》, 第 10 期, 第 47-56+80 页。 |
| [] |
陈昆亭、龚六堂、邹恒甫, 2004, “什么造成了经济增长的波动, 供给还是需求:中国经济的RBC分析”, 《世界经济》, 第 4 期, 第 3-11 页。 |
| [] |
张军、章元, 2003, “对中国资本存量K的再估计”, 《经济研究》, 第 7 期, 第 35-43+90 页。 |
| [] |
张军、施少华, 2003, “中国经济全要素生产率变动:1952-1998”, 《世界经济文汇》, 第 2 期, 第 17-24 页。DOI:10.3969/j.issn.0488-6364.2003.02.002 |
| [] |
朱军、李建强、张淑翠, 2018, “财政整顿、'双支柱'政策与最优政策选择”, 《中国工业经济》, 第 8 期, 第 24-41 页。 |
| [] |
林仁文、杨熠, 2014, “中国市场化改革与货币政策有效性演变——基于DSGE的模型分析”, 《管理世界》, 第 6 期, 第 39-52 页。 |
| [] |
祝梓翔、邓翔, 2017, “时变视角下中国经济波动的再审视”, 《世界经济》, 第 7 期, 第 5-29 页。 |
| [] |
郭长林, 2016, “财政政策扩张、纵向产业结构与中国产能利用率”, 《管理世界》, 第 10 期, 第 13-33 页。 |
| [] |
Everett S.Lee, 1966, "A Theory of Migration", Demography, 23(1): 47-57.
|
| [] |
Glomm.G, B.Ravikumar, 1992, "Public Versus Private Investment in Human Capital:Endo-genous Growth and Income Inequality", Public Versus Private Investment in Human Capital, 12(9):818-834.
http://cn.bing.com/academic/profile?id=a41612c249b89d2bc0c5a2c278506e6d&encoded=0&v=paper_preview&mkt=zh-cn |
| [] |
Johnson D G., 2003, "Provineial Migration in China in 1990". China Economic Review, 15(14), 22–31.
|
| [] |
Lewis, W Arthur, 1954, "Economic Development with Unlimited Supplies of Labour", The Manchester School, 22(2):139-191.
http://cn.bing.com/academic/profile?id=18fb5ffbe436d5d388b0b68fee1f4f97&encoded=0&v=paper_preview&mkt=zh-cn |
| [] |
Mandelman, Federico S. & Zlate, Andrei, 2012, "Immigration, Remittances and Business Cycles", Journal of Monetary Economics, Elsevier, vol, 59(2):196-213.
https://www.researchgate.net/publication/46451860_Immigration_Remittances_and_Business_Cycles |



