我国出口商品外币价格在人民币贬值时降得多,还是人民币升值时涨得多?相比人民币1%的贬值,2%的贬值会使出口价格成倍下降吗?对这个问题,“依市定价”等汇率传递经典理论隐含的答案是升值涨多少,贬值就降多少。直到最近,关于汇率传递的宏微观理论都基于对称性假设,即升值和贬值会以同等幅度、同等速度被传递到贸易品价格和国内消费者物价水平上。然而实证中发现并非如此,这使得汇率传递的对称性假设显得过于理想主义(Delatte and López,2012)。因而,相关研究出现一个新的趋势,即放松对称性假设,转向升贬值不同的影响机理,并由此延伸至汇率波动对物价水平的不对称影响。
面临外部冲击时,价格是涨多跌少还是相反,并非汇率传递领域独有的现象。Bacon(1991)曾用“火箭和羽毛”形容英国零售汽油价格涨得快,降得慢,反映成本冲击对销售价格影响的不对称性:正向的成本冲击引致价格上涨得又快又多,负向冲击引致的价格下降又慢又少。实际上,货币升贬值可以被视为成本冲击的一种。例如,对于用外币定价的出口厂商来说,出口国货币贬值意味着一个负向冲击,因为以外币计算的成本下降了;反之,升值意味着正向冲击,这时外币计算的成本上升。如果厂商在面对成本上升和下降时,做出不同反应,那么汇率传递也应该具有非对称性。
自2005年7月人民币汇率形成机制经历多次改革,人民币兑美元从单边升值转为双向波动,对其他主要货币的弹性也大幅增强。例如自2015年8月11日起,人民币兑美元一年内贬值8.3%。人民币兑日元更早出现较大幅的波动,例如2005年到2008年人民币相对日元升值23%,2009年到2011年则贬值31.5%,2012年至2015年更是升值38.8%。在双向波动加大的趋势下,如果汇率升贬值对价格的影响具有不对称性,即使汇率若干年累积变化为0,但期间的波动可能导致出口价格实际下降或者上升,进而改变贸易条件。非对称传递还将导致升贬值对出口商利润率的不对称影响和升贬值向国内物价的不对称传递。
本研究对其它类型的成本冲击,如关税增减、主要原材料价格涨跌等,也有一定的借鉴价值。以关税为例,提高关税与出口国货币升值均可能导致出口商品外币价格上升,只是两者影响程度不同。Fitzgerald and Haller(2018)发现关税对贸易总额的影响系数是真实汇率的6倍。不过,关税的调整不经常发生,而汇率时时波动,很容易观测。因而研究汇率向出口价格的非对称传递有助于预测关税调升或调降对贸易品价格和总值的影响。
本文首先从理论上得出汇率传递非对称应为常态的结论,并论证在一定前提下,依市定价的出口厂商面临的商品需求价格弹性越大,越有可能出现本币贬值出口价格降得多的现象。本文进而采用2000年1月至2011年12月966种中国出口至日本商品的价格数据构造面板模型,实证检验了人民币汇率向日元价格传递的非对称性,发现我国出口价格降得多,升得少,但在人民币大幅升值时,厂商也不得不较大幅度地提高日元售价。
2013年之后,我国向日本出口总额结束一路上行走势,趋于稳定。但日本从中国台湾、韩国、越南等地的进口增幅却明显提高,说明日本市场上的竞争格局悄然变化。此外,2012年至2015年日元相对人民币贬值幅度显著高于前期。因此,为了覆盖更长的研究时间段,保证研究结果的可靠性,本文采用2000年至2018年9月七大类日本从中国进口单位价值指数进行稳健性检验,结果支持上述采用细分数据得出的主要结论。
本文的结构安排如下:第二部分总结汇率传递非对称性的理论和实证研究进展,并提出本研究特殊之处;第三部分扩展Yang(2007)的理论模型,探讨汇率传递不对称性的微观来源;第四部分实证检验汇率传递在人民币升贬值方向和幅度上的非对称性;第五部分为结论和政策启示。
二、文献综述汇率传递是指汇率变化引起贸易品以销售地的货币计价其价格变化的程度,通常用汇率传递率来衡量一单位汇率变化引致的价格变化量。例如,当本币贬值1%时,进口商品本币价格上涨的百分比被称为汇率向进口价格的传递率①。
① 由于本文关注的大部分文献从进口商角度考虑,为表述方便,如无特别说明,本部分所指升贬值均统一为进口国货币升贬值,价格为进口国货币计算的进口价格或进口国物价水平。
正如商品的采购成本经常变化,但售价却不经常变化(Ravn et al., 2010),大量研究表明,汇率波动也通常不会完全传递到价格上,这种现象被称为不完全传递。Krugman(1987)发现80年代中早期美元实际升值中仅有60%~65%被传递到美国进口商品价格上,这是外国企业在不完全竞争的美国市场上“依市定价”的结果。依市定价模型暗示升贬值对进口价格的影响是对称的,企业的策略是通过调整加成实现利润的跨时平衡,有效地稳定销售价格。
但是,具有一定市场力量的进口厂商真的会无视本币贬值对利润的侵蚀吗?Peltzman(2000)指出价格具有向下刚性,即价格涨得快,降得慢,并且不论在低通胀还是高通胀期,这种不对称性都广泛、持续地存在。Tappata(2009)用消费者搜寻模型证明,即使在高度竞争的市场中,持续的成本变化也将导致产出价格上升快于下降。近年不少实证研究也揭示汇率波动向价格传递具有不对称的特点(Brun-Aguerre et al., 2017)。
(一) 方向非对称性的理论解释对于升贬值方向上的非对称性的理论解释并不多,综合Pollard and Coughlin(2004)以及Bussière(2013),我们发现从不同视角出发,价格涨得多或降得多,均能获得理论支持。
贬值向进口价格传递高于升值,可能是由于价格向下刚性,即进口商不愿因进口国货币贬值而损失利润,积极提价,而升值时进口商不降价,宁愿安享利润增厚;也可能是由于出口数量向上刚性,即受产能限制或者贸易壁垒的影响,销量难以扩大,升值时进口商不愿意降价,因为即使降价了,销量也无法提升。
相反,如果贬值向进口价格传递低于升值,则可能是由于厂商关心市场份额,担心提价导致市场份额损失,而乐于降价抢夺市场份额;也可能因为出口厂商可以自由转换原料采购地,出口国货币贬值时采用本国原料,使外币售价下降,升值时采用外国原料,保持售价不变。站在进口国立场上,反映为升值传递率高于贬值。
可见发生汇率冲击时,价格有可能涨得多,也有可能降得多,并无定论。现有文献在升贬值传递的非对称性特征和微观成因方面,理论关注依然不足。
(二) 方向非对称性的实证检验实证研究相对理论分析丰富一些,但基于微观数据的研究并不多,得出的结论也相去甚远。
支持贬值升得多的包括:Kadiyali(1997)研究了美国摄影行业从日本进口价格,Goldberg(1995)检验了美国汽车行业从德国、日本的进口价格,两者都发现美元贬值的传递率是更高的。Webber(2000)研究了7个亚洲国家的进口价格,发现5个国家进口价格在贬值后上升得快,升值后下降得慢。Bussière(2013)发现在化学品和汽油行业存在销量受限,因而进口商在本币升值时宁愿保持价格稳定,而不是降价。
相反,支持升值降得多的包括:Mckinnon and Ohno(1997)研究了美元经历贬值转而升值的过程,得出美元升值对美国进口总体价格水平传递效应较大的结论(即降得快,升得慢)。Wickremasinghe and Silvapulle(2004)研究了日本进口制造业产品价格,发现长期升值传递率高于贬值。Campa et al.(2008)在行业层面研究了欧盟国家进口价格,发现在制造业中,本币升值传递率快于贬值,可能源于外国厂商希望维持市场份额。
也有学者同时提供了两个方向的证据。Bussière(2013)发现意大利进口价格向下刚性显著,贬值涨得多;日本出口商似乎更关心市场份额,贬值涨得少,升值降得多。Yang(2007)以1985年3月为界,在少量行业中发现了美元升贬值向美国进口价格传递的非对称性,但具体特征因行业而异。
(三) 幅度非对称性的理论和实证至于汇率波动幅度的非对称性影响,理论解释和实证证据均比较集中地支持汇率波动幅度越大,汇率沿同一个方向持续时间越久,传递率越高(Gaulier et al., 2008)。此外,Pollard and Coughlin(2004)认为菜单成本的存在使得大幅升贬值传递率更高;Bussière(2013)认为消费者的转换成本也会导致同样的结果。实证方面,早期Ohno(1989)的研究即发现日本出口价格在汇率波动大的时候变化更明显。Frankel et al.(2012)发现当贬值幅度达到25%的门槛值,传递率显著提高。Bussière(2013)认为较大幅度的货币升值很难用调整加成来吸收,会触发更高的汇率传递。
(四) 国内研究进展国内尚无关于汇率传递非对称性的理论研究。实证检验则通常采用高度整合的数据,如进出口价格指数或物价指数等。得出的实证结论有的支持涨得多,降得少,如谢博婕(2014)发现人民币贬值向国内物价指数传递程度更大,汇率变动幅度较大时,传递程度更显著;曹伟、倪克勤(2010)发现人民币贬值对进口价格指数存在较高的传递效应,汇率波幅越大,传递效应越大。而有的研究则支持降得多,升得少,例如姜昱等(2010)利用中国17个贸易伙伴1994-2008年数据的研究发现,人民币升值向进口价格指数传递效应较强,而贬值较弱。胡冬梅等(2014)采用日本商品出口价格指数的测算结果是日元贬值传递率低,但结果显著度不高。
本文将在现有研究基础上做出以下贡献:(1)现有理论研究虽然认为不同的市场竞争结构是不对称性的来源,但对于不对称特征及其与竞争结构之间的关系缺乏具体衡量和深入分析。本文以出口厂商在目标市场面临的需求弹性及其变化为维度,阐明汇率不对称传递的条件和特点,并证明随着价格上涨需求曲线变得更有弹性,汇率传递将是不完全和不对称的;在一定的条件下,如果出口商面临非常富有弹性的需求曲线,那么出口国货币贬值传递率将超过升值传递率。(2)国内现有实证研究仍较少,且测算结果分歧较大,充分说明采用高度分解数据进行研究的必要性。本文以中日贸易为例,采用966种HS8位编码①商品的月度出口单价作为研究基础,其它对厂商定价行为的解释因素也尽可能落实到最细分的层面上。
① HS是世界海关组织《商品名称及编码协调制度》的简称。
三、汇率传递不对称性的理论分析本文以中日贸易为例,扩展Yang(2007)的厂商定价模型,探讨汇率传递不对称的特点和成立条件,并用一个简单的数字模拟分析需求弹性大小如何影响升贬值的不对称效应。需求弹性是重要的分析维度,因其可以被视为需求方因素的汇总。例如,Pollard and Coughlin(2004)的市场份额理论隐含假设是降价将带来明显的销量扩大,所以升值降得多的商品面临的需求弹性应该是比较大的。Tappata(2009)认为消费者搜寻决策影响厂商面临的需求弹性,进而影响到成本传递。
设中国为出口国,货币以RMB表示,日本是进口国,货币以YEN表示。在日本市场销售的中国商品价格为Pyen=Prmb/ermb/yen,其中e为名义汇率,即1单位日元可兑换的人民币数量。
出口商面临汇率波动,究竟如何制定价格策略?基于Yang(2007)的模型,假设中国垄断竞争出口厂商生产和出口单一产品至日本,产品具有一定差异性,因此出口厂商享有一定的定价权。为简单起见,假设人民币计算的边际成本MC恒定。出口厂商在日本市场面临的需求函数为P(Q),需求弹性为ε,对于普通商品而言取值为负,且需求弹性随Pyen的变化而发生改变。中国出口商以人民币计算的利润函数为:
| $ \pi_{r m b}=e_{rm b/ y e n} \cdot P_{y e n}(Q) \cdot Q-C_{r m b}(Q) $ | (1) |
厂商基于人民币利润最大化决定在日本市场上的日元销售价格:
| $ P_{ {yen }}=\frac{M C_{ {rmb}}}{e_{ {rmb} / {yen}}} \cdot\left(\frac{\varepsilon}{1+\varepsilon}\right) $ | (2) |
日元价格包含两个部分,日元边际成本和成本之上的加成。文献中常将汇率变化看成一种成本冲击。例如人民币升值使得以日元计价的成本上升,所以为正向或不利冲击,反之人民币贬值为负向或有利冲击。这里,加成的幅度反向取决于需求弹性,如果需求特别有弹性,价格将非常接近边际成本。
根据汇率传递率的定义,令传递率
① 推导过程备索。
| $ \tau=\frac{d ln P_{yen}}{d ln e_{rmb/yen}}=-\left[1-\frac{d \varepsilon}{d P_{yen}} \cdot \frac{P_{y e n}}{\varepsilon} \cdot \frac{1}{1+\varepsilon}\right]^{-1} $ | (3) |
根据τ可判定汇率传递为完全传递(τ=-1)、不完全传递(-1 < τ < 0)或过度传递② (τ < -1)。而τ的大小又取决于dε/dP的正负号和ε的取值。dε/dP < 0意味着随着价格上升,需求更富有弹性,而随着价格下降,需求变得缺乏弹性,dε/dP>0的情形则相反。对于一般的需求曲线而言,需求弹性随着价格的上升通常变得富有弹性,所以dε/dP < 0比较符合一般的情形。不妨考虑在垄断竞争市场上,对于有一定差异性的商品而言,当其他竞争性商品价格不变,此商品单价上升,很可能面临更富有弹性的需求;反之,若仅此商品单价下降,很可能吸引较多的需求,并且由于价格已低于同类商品,价格再发生微小变化,消费者的敏感度也相应下降。在dε/dP≤0的条件下,τ的取值有以下三种可能③:
② 笔者与纺织服装行业出口商的访谈中,因汇率出现大幅波动,厂商借机调整定价策略,抢夺市场份额的情况经常被提及。
③更完整的分析包含8种情形,备索。
(1) 若τ = -1,此时为完全传递。条件是
(2) 若-1 < τ < 0,此时为不完全传递。条件是ε < -1且dε/dP < 0,需求富有弹性,随着价格上升更富有弹性,而随着价格下降则变得缺乏弹性。
(3) 若τ < -1,此时为过度传递。条件①是-1 < ε < 0且dε/dP < 0,需求缺乏弹性,但随着价格上升,需求变得富有弹性,而随着价格下降则更缺乏弹性。
① τ < -1意味着
以上分析得出两个结论:(1)完全传递需要满足比较严格的条件,即要求ε为常弹性,不随价格变化。(2)在dε/dP < 0的情况下,富有弹性的商品因竞争厂商众多,为避免失去市场份额,厂商不愿轻易调整报价,因而多为不完全传递。而缺乏弹性的商品更容易发生过度传递,因为厂商拥有较强的定价权,并有能力将汇率预期带入定价,以规避汇率风险,从而对当期汇率变动产生过度反应。
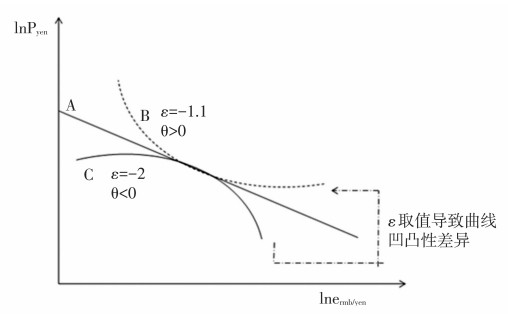
Yang(2007)对非对称性的讨论止步于此。本文进一步详细分析出口厂商在面临有利的汇率冲击(人民币贬值)和不利的汇率冲击(人民币升值)时,外币定价行为是否不同?以及有何不同?lnPyen对lnermb/yen继续求二阶导数,可根据图 1中价格-汇率曲线的凹凸性,判断不同的汇率冲击下厂商定价行为的不对称性。为表述简便,省去下标,令:
|
图 1 价格-汇率曲线 |
| $ \theta=\frac{d \tau}{d ln e}=\frac{d(d ln P / d ln e)}{d ln e} $ | (4) |
并令:
| $ \omega=\frac{d \varepsilon}{d P} \cdot \frac{P}{\varepsilon} $ | (5) |
推导可得:
| $ \theta=\frac{d(d ln P / d ln e)}{d ln e}=\frac{\tau^{2} \omega^{2}\left(\frac{d P}{d \varepsilon} \cdot \frac{\varepsilon}{d P}-1-\frac{\varepsilon}{1+\varepsilon}\right)}{1+\varepsilon-\frac{d \varepsilon}{d P} \cdot \frac{\rm P}{\varepsilon}} $ | (6) |
若θ=0,则如图 1中的直线A所示,对应于任何汇率,传递率始终不变,不存在汇率传递的非对称性。若θ≠0,则如曲线B或C所示,汇率上升或者下降对应不同的汇率传递率,即存在非对称性。
第一种情形(直线A):汇率传递无不对称性,此时dε/dP=0,τ=-1,θ=0。可见升贬值对称传递需要满足严格的条件,此时汇率波动完全传递到商品售价上。
第二种情形(曲线B):因θ>0,同等幅度的人民币升值带来日元价格的上涨幅度大于人民币贬值带来日元价格的下降幅度,也就是涨得多,降得少。在商品缺乏弹性或富有弹性时有如下可能:
(1)-1﹤ε﹤0(缺乏弹性),dε/dP < 0,τ﹤-1(过度传递)且
(2)ε﹤-1(富有弹性),dε/dP < 0,-1﹤τ﹤0(不完全传递)且
第三种情形(曲线C):也存在汇率传递不对称现象,但因θ﹤0,同等幅度的人民币升值带来的日元价格上涨幅度小于人民币贬值带来的日元价格下降幅度,也就是涨得少,降得多。在商品缺乏弹性或富有弹性时有如下可能:
(1)-1﹤ε﹤0(缺乏弹性),dε/dP < 0,τ﹤-1(过度传递)且
(2)ε﹤-1(富有弹性),dε/dP < 0,-1﹤τ﹤0(不完全传递)且
大量文献表明汇率不完全传递广泛存在。因此重点考察-1﹤τ﹤0(不完全传递)的两种情形,即第二和第三种情形中的(2)。只要满足ε﹤-1,dε/dP < 0,就存在汇率不完全传递,即-1﹤τ﹤0。但这时θ>0还是θ < 0,取决于
| 表 1 汇率不完全传递下ε取值对θ的影响 |
其他条件不变,随着ε的取值下降(即更加富有弹性),θ由正转负,价格-汇率曲线也从凸向原点变为凹向原点。当需求价格弹性较小,如表中ε=-1.1时,θ﹥0,表明出口厂商面临升值压力时加价多于面临贬值压力时的降价,即涨得多,降得少。而当需求弹性较大,如表中ε=-2时,θ<0,表明厂商面临升值压力时加价少于贬值时的降价,即涨得少,降得多。
数字模拟说明,当出口商在目标市场上面临的需求弹性大于1时,厂商部分吸收汇率冲击,表现为汇率的不完全传递。在此前提下,当需求弹性相对较小(绝对值上比较接近于1)时,厂商有较强烈的加价动机,因为加价并不会带来需求量太大的下降,对市场份额影响有限;而厂商降价的动机相对较弱,因为降价也不会带来需求量足够大的上升,不如安享利润增厚。相反地,当面临的需求弹性相对较大(绝对值上远离1)时,厂商有较强烈的降价动机,因为这时降价可以较明显地增加需求量,有助于提高市场份额。而加价却要承受需求量大幅下降、甚至可能丢失市场份额的后果。因此,商品需求弹性越大,越可能呈现出口国货币贬值传递率高而升值传递率低的非对称性。
综上,本部分有以下主要发现:(1)对称传递需要满足比较严格的条件,如需求弹性ε为常数,不随价格变化等。放松假设条件后,可以证明现实中更常见的是非对称的汇率传递。(2)非对称的汇率传递包含两种情形,出口国货币贬值时售价降得多、升值时涨得少,或者相反。在不完全传递的条件下,通过一个简单的数字模拟,发现厂商面临的需求越富有弹性,越可能出现贬值降得多而升值难以涨价的非对称特征。
以下将采用中日贸易数据检验人民币升、贬值向日元售价的传递是否存在非对称性,呈现怎样的非对称特征,并尝试结合理论部分对非对称特征进行解释。
四、关于非对称传递的实证检验与人民币兑美元不同,人民币兑日元汇率长期以来存在较大的波动。例如2000年1月至2011年12月,人民币相对日元经历了两个完整的升贬值周期,为本文研究提供了很好的机会。同时,日本一直是中国最主要的出口目的地国,使得我们能够找到足够多的细分商品构造面板数据,并保证这些商品从2000年1月开始就有连续的月度单价。
本部分首先基于线性方程估计汇率传递率,然后运用面板门限模型,检验汇率波动对价格的影响是否存在非对称性,以及具体的非对称特征。最后采用两种方案进行稳健性检验。
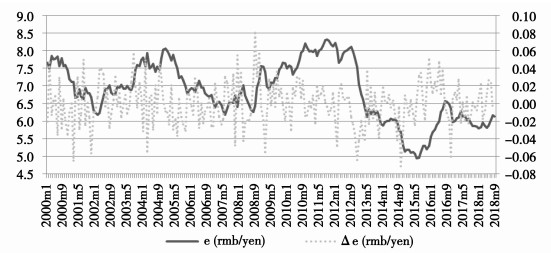
|
图 2 日元汇率与汇率波动 |
中国出口日本的7000多种HS8位编码商品中,根据以下标准,筛选出966种具有连续月度单价的商品:(1)仅选择以一般贸易方式出口的商品,以剔除进口中间品比例等对汇率传递率的影响;(2)各月单价的标准差/平均值< 0.5,目的是删除单价存在极端值的商品;(3)至少具有140个月的月度数据,目的是删除价格缺失值较多的商品。为了构建平衡面板,对于极少量存在缺失值的样本,用前后两期平均的方法补上缺失值。样本的品种分布较平衡,覆盖98章中的大部分,其中分布较密集的为服装鞋帽、机电产品、金属制品和化学品。商品合计占我国出口日本总金额的30%左右,样本具有较好的代表性①。
①样本商品的行业分布备索。
数据来源于中国海关总署,研究时间段为2000年1月至2011年12月。用商品出口金额除以数量,得到月度单位价值,以此作为商品单价的代理变量。
(二) 线性模型对传递率的估计根据式(3),我国出口商品的日元价格由人民币成本、汇率和成本之上的加成决定。加成数据难以获得,但通常认为加成与市场竞争程度有关(Dornbusch,1987),因此本文用日本同类商品价格指数来控制行业竞争程度。此外,厂商定价是一个动态、连续的过程,因此,将滞后一期价格作为解释变量纳入模型,实证结果也表明,动态方程拟合优度大幅提高。用于估计的线性对数方程如下:
| $ \ln p_{i t}=\beta_{0}+\beta_{1} \ln p_{i t-1}+\beta_{2} \ln m c_{i t}+\beta_{3} \ln c p_{i t}+\beta_{4} \ln e_{t}+\mu_{i}+\varepsilon_{i t} $ | (7) |
其中,被解释变量pit为HS8位编码商品的日元价格。海关统计的出口商品均以美元标价,按IMF月平均汇率换算成日元价格。β0是回归方程的截距项,μi反映商品的个体固定效应,εit为随机误差项。
解释变量e为间接标价法双边名义汇率,e上升表示日元升值,人民币贬值。β4为汇率传递率,估计值若为0表示无传递,为-1表示完全传递,介于0和-1之间为不完全传递。
mc表示边际成本,本文选用各类商品对应的分行业工业品出厂价格指数(PPI)作为代理变量。PPI月环比和同比数据来源于广东省和国家统计局。以2001年12月为基期套算得到分行业PPI月度定基指数。cp为同类日本商品价格指数,用于控制在日本市场上销售的竞争品价格。其中消费品的价格来自日本财务省发布的月度对应商品的消费者价格指数(cpi),工业品的价格来自日本央行发布的月度生产者价格指数。
单位根检验①表明lnp为平稳过程,lncp、lnmc和lne未能通过全部检验。在变量非平稳的情况下,实证中经常使用对数差分方法,虽然一阶差分会删除重要信息,并改变系数的经济学含义,但为了模型估计结果的稳健性,本文对上述变量全部或部分差分,基于以下两式重新估计模型参数:
① 限于篇幅, 检验结果备索。
| $ \varDelta \ln p_{i t}=\beta_{0}+\beta_{1} \varDelta \ln p_{i t-1}+\beta_{2} \varDelta \ln m c_{i t}+\beta_{3} \varDelta \ln c p_{i t}+\beta_{4} \varDelta \ln e_{t}+\mu_{i}+\varepsilon_{i t} $ | (8) |
| $ \ln p_{i t}=\beta_{0}+\beta_{1} \ln p_{i t-1}+\beta_{2} \varDelta \ln m c_{i t}+\beta_{3} \varDelta \ln c p_{i t}+\beta_{4} \varDelta \ln e_{t}+\mu_{i}+\varepsilon_{i t} $ | (9) |
为简化表述,所有方程的随机误差项均写为εit,但需注意的是,差分后随机误差项的分布已经发生改变。此外,方程系数的含义也有所不同。以本文关心的β4为例,在方程(2)中,β4表示日元波幅每变化1%,日元价格波幅变化的百分比;而在方程(3)中,β4表示日元波幅每变化1%,日元价格变化的百分比。
Huasman检验表明,不论采用哪种模型设定,固定效应模型均优于随机效应模型。表 2显示三种模型设定的估计结果。
| 表 2 固定效应模型估计结果 |
模型估计结果的稳定性很好,系数显著度高,且三个方程的系数方向基本一致。控制变量中,成本对当期价格有明显的正向影响,说明国内成本上升将部分传递到日元出口价格上;日本当地竞争价格对出口价格存在少许负向影响,可能占据和保持市场份额是我国出口商的一个较为重要的战略,并不会跟随日本本地商品调价。
根据方程(1)的估计结果,汇率传递率为-0.327,即日元升值(人民币贬值)1%,仅带来日元价格下降0.327%,其余部分反映为中国出口厂商的加成增加。日元贬值的情形相反。中国出口厂商通过调整加成,吸收大部分的汇率波动,仅将小部分汇率波动传递到日元价格上。
一阶差分方程的估计结果相似,其中β4的估计值为-0.57和-0.315,以升值为例,分别反映日元升值幅度上升带来日元价格下降和价格增幅的下降。不过,正如前文指出的,方程(1)的系数值可以直接理解为汇率传递率,而Δlne前的系数则反映升贬值幅度的变化带来的影响。接下来进一步构建面板门限模型,将两者的影响综合起来,探讨升贬值和汇率波幅对汇率传递率的非对称性影响。
(三) 汇率传递非线性估计在非线性回归中,运用较为广泛的是Hansen(1999)提出的“门限回归”,以严格的统计推断方法对导致影响机制发生改变的门限值进行参数估计和假设检验。参考Hansen(1999)的做法,本文的双重门限面板模型设定为:
| $ \begin{array}{l}{\ln p_{i t}=\beta_{0}+\beta_{1} \ln p_{it-1}+\beta_{2} \ln m c_{i t}+\beta_{3} \ln c p_{i t}+\beta_{4} \ln e_{t} \cdot I\left(\varDelta \ln e_{t}<\gamma_{1}\right)} \\ {\quad+\beta_{5} \ln e_{t} \cdot I\left(\gamma_{1}<\varDelta \ln e_{t}<\gamma_{2}\right)+\beta_{6} \ln e_{t} \cdot I\left(\gamma_{2}<\varDelta \ln e_{t}\right)+\mu_{i}+\varepsilon_{i t}}\end{array} $ | (10) |
其中,I(·)为示性函数,若括号中的表达式为真,取值1;反之取值0。Δlne为门限变量,γ1和γ2为导致汇率传递影响机制发生改变的门限值。在实际检验中,依次估计了单一门限、双重门限和三重门限模型,门限估计值及相关统计量如表 3和图 3。
| 表 3 门限估计值Threshold estimator(95%置信区间) |
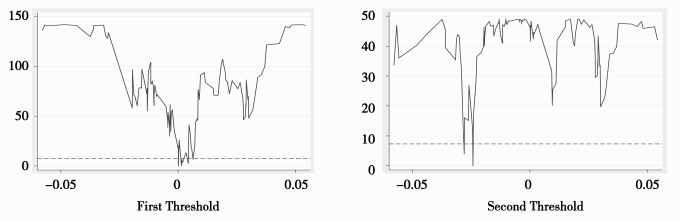
|
图 3 门限值及似然比(LR)统计量 |
由于依次拒绝了线性回归和单一门限假设,而接受双重门限假设,因此汇率向日元价格传递为非线性,存在两个门限值。按照双重门限估计结果,应该分三种情形讨论汇率波动向价格的传递效应:人民币大幅升值(Δlne < -0.0243)、人民币较小幅升值(-0.0243≤Δlne < 0.0001)和人民币贬值(Δlne≥0.0001),三种情形对应的月份数分别为22、52和69个月。尽管从统计推断的角度,双重门限模型优于单一门限,但也将单一门限的参数估计结果一并呈现于表 4。
| 表 4 面板门限模型估计结果 |
根据双重门限模型的估计结果,有以下主要发现:
1) 人民币升贬值的非对称影响。由于γ2恰好等于0.0001,所以Δlne≥0.0001的月份几乎包含了所有人民币贬值的月份。若当月人民币贬值1%,日元价格将下降0.3135%;相反,若人民币升值1%,当月日元价格将上升0.3045%。尽管传递率估计值在数值上差异很小,但差异显著存在。人民币贬值比升值传递率高,即人民币贬值日元价格下降较多,人民币升值日元价格上升较少。
2) 汇率波动幅度的非对称影响。γ1为-0.0243,Δlne < -0.0243的月份为人民币出现较大幅度升值的月份。若当月人民币升值幅度比较大,即Δlne超越了-0.0243的临界值,传递率又会有所上升,即从0.3045%上升到0.3128%。尽管日元价格易跌难涨,但若人民币大幅升值,导致成本显著上升、利润被明显挤压,厂商不得不适当提高日元价格,转嫁更多的不利冲击。
结合上文的理论分析,我国出口商在日本市场的定价行为符合图 1曲线C的描述,即人民币贬值的传递率显著高于人民币升值的传递率,反映中国出口商品在日本市场面临的需求弹性较大,产品可替代性较高,竞争较为充分。汇率传递的非对称性还表现在,如果人民币升值幅度过大,导致出口厂商成本上升较多,也会迫使厂商适度调高日元价格,以减少利润损失。我国出口商在日本市场的销售利润较薄,可能是升值幅度较大时汇率传递率突然提高的重要原因。
(四) 稳健性检验首先采用主观设定哑变量的方法,对门限模型结果进行检验。其次,采用七大类日本从中国进口单位价值指数,将研究时间段拓展到2018年9月,检验上文得出的非对称性在更长时间段内是否成立。
1.主观设置虚拟变量方法
面板门限模型对门限值的选择由程序搜索完成,但汇率是波动十分频繁的变量,在一定幅度内波动通常被视为汇率平稳,所以多大幅度的波动应被视为贬值或升值,常依据主观判断。在本文研究时间段内,人民币兑日元月度波幅均值0.0004,标准差0.025。月度汇率上升或下降不超过半个标准差(约1%)可以被视为汇率稳定,因此,若主观设定门限值为±0.01,Δlne>0.01可视为人民币贬值,Δlne < -0.01为人民币升值,其余为汇率平稳。人民币升值、贬值和稳定的月份数基本相当,分别为52、44、47个月。
主观设置门限值有一个优点,即可以通过不断调整门限值,观测系数估计值相应变化的趋势,因此本文从±0.01开始,逐步放大门限值,直至±0.024。用于估计的实证方程(差分方程相似)如下:
| $ \ln p_{i t}=\beta_{0}+\beta_{1} \ln p_{i t-1}+\beta_{2} \ln m c_{i t}+\beta_{3} \ln c p_{i t}+\beta_{4} \ln e_{t}+ \\ \beta_{5} d_{1} \times \ln e_{t}+\beta_{6} d_{2} \times \ln e_{t}+\mu_{i}+\varepsilon_{i t}\\ d_{1}=\left\{\begin{array}{l}{1, \varDelta \ln e <-0.01} (人民币升值)\\ {0, \varDelta \ln e>-0.01 (其他)}\end{array}\right. \;\;\;\;\;\;\;\;d_{2}=\left\{\begin{array}{l}{1, \varDelta \ln e>0.01} (人民币升值)\\ {0, \varDelta \ln e <0.01 (其他)}\end{array}\right. $ | (11) |
β4的估计值为人民币汇率平稳月份的传递率,β4+β5为升值月份的传递率,β4+β6为贬值月份的传递率。表 5报告了部分门限取值的估计结果。对数差分的估计结果参阅表 6。
| 表 5 对数方程估计的非对称性 |
| 表 6 差分方法估计的非对称性 |
主观设置门限值的方法得出的结论与面板门限模型一致。1)表 5中两个哑变量系数估计值虽然数值很小,但均在99%的置信区间内显著,说明汇率传递具有非对称性;2)人民币升值期传递率为0.3146,贬值期为0.3199,人民币贬值传递率较高。对数差分的估计结果(表 6)进一步支持上述结论。
主观设置门限值还得出一个有趣现象:表 6显示β5的估计值从显著为正,逐步变为与零无差异,再转变为显著为负。表现出随着人民币升值幅度的加大,升值传递率在慢慢上升。这是对门限模型关于非线性发现的一个动态补充,反映出口商尽管在人民币升值时倾向于少加价,但由于利润较薄或其他原因,随着升值幅度加大,利润空间被逐步挤压,这时厂商不得不提高传递率。这种现象在人民币贬值时并没有明显的表现。
由于上述模型均引入被解释变量的滞后期,为消除内生性问题对模型估计可能造成的偏误,我们也采用系统GMM方法进行了检验①,汇率传递率的估计值与上述估计结果相近,支持模型结论的稳健性。
① 限于篇幅,估计结果备索。
2.采用单位价值指数的进一步检验
日本财务省定期发布日本从中国进口单位价值定基指数,时间覆盖性非常好,可弥补高度细分数据在时间跨度上的不足,因此本文采用该数据进行稳健性检验。当然,由于指数为整合数据,可能存在“整合偏差”(Yoshida,2010)。本文采用食品、原材料、矿物燃料、服装、化学制品、金属、机械设备这7个大类单位价值指数构建面板模型,研究时间段为2000年1月至2018年9月。竞争性价格cp采用对应的日本分行业PPI,边际成本mc则用中国分行业PPI作为代理变量。数据分别来自于日本央行和中国国家统计局。
根据单位根检验,lnp和lncp为平稳过程,lnmc和lne未能通过全部检验,但变量之间存在长期协整关系。基于方程(7)至(9)估计对数、全部差分和部分差分模型。三个模型估计系数显著度均较高,且方向基本一致。差分和部分差分方程估计的传递系数分别为-0.348和-0.336,与细分数据估计结果非常相似。对数模型的汇率传递率为-0.084,低于细分数据估计的-0.327,但系数均显著为负。
进而分别采用面板门限模型、主观设置门限值、设置虚拟变量反映升贬值周期这三种方法研究非线性特征,估计结果依次报告如下:
首先,参照前文实证方程(10),依次估计单一门限和双重门限模型。单一门限假设被接受,双重门限假设被拒绝,因此汇率向日元价格传递依然为非线性,存在一个门限值Δlne=-0.0045。由于该值也非常接近于0,说明人民币升值(Δlne < -0.0045)与贬值(Δlne≥-0.0045)的传递率不同,且贬值传递系数0.071高于升值传递系数0.063,因而升贬值非对称性的结论得到支持。与前文不同的是,人民币大幅升值与其他情形间的差异未被检出,即汇率波动幅度的非对称性没有得到支持。单一门限的参数估计结果如表 7和表 8。
| 表 7 门限估计值Threshold estimator(95%置信区间) |
| 表 8 面板门限模型(单一门限)参数估计结果 |
其次,采用主观设置门限值的方法,重新估计汇率传递的非对称性。多次测试汇率波动幅度的非对称性,实证结果均不显著,但人民币升值与贬值对汇率传递的非对称影响得到进一步支持。实证方程(差分方程相似)如下:
| $ \ln p_{it}=β_{0}+β_{1}\ln p_{it-1}+β_{2}\ln mc_{it}+β_{3}\ln cp_{it}+β_{4}\ln e_{t}+β_{5}d×\ln e_{t}+μ_{i}+ε_{it} \\ d= \left\{ \begin{array}{l} 1, \varDelta \ln e>0(人民币贬值) \\ 0, \varDelta \ln e≤0(人民币升值) \end{array} \right. $ | (12) |
估计结果①显示,对数模型中β5的估计值为-0.005,显著异于0,且为负,说明贬值月份的平均传递率更高。不过,差分和部分差分模型的估计结果未能支持上述结论。
① 估计结果备索。
最后,由于该套数据覆盖时间长,本文得以划分出多达4个人民币升值和3个人民币贬值期,通过设置虚拟变量反映升贬值周期,尝试从另一个维度进行研究。实证方程(差分方程相似)如下:
| $ \ln p_{it}=β_{0}+β_{1}\ln p_{it-1}+β_{2}\ln mc_{it}+β_{3}\ln cp_{it}+β_{4}\ln e_{t}+β_{5}s×\ln e_{t}+μ_{i}+ε_{it} \\ s= \left\{ \begin{array}{l} 1, 2002m3-2004m12, 2008m9-2012m9, 2015m7-2016m8(人民币贬值) \\ 0, 2000m1-2002m2, 2005m1-2008m8, 2012m10-2015m6, 2016m7-2018m5(人民币升值) \end{array} \right. $ | (13) |
估计结果②显示,对数模型和差分模型中β5的估计值均显著异于0,且为负,说明贬值期间的平均传递率更高,与上文关于升贬值非对称性的结论吻合。
② 估计结果备索。
以上采用日本进口单位价值指数的研究较为充分地支持升贬值的非对称性,且人民币贬值传递率高于升值传递率,说明我国出口厂商在人民币贬值时降价幅度略高于升值时的涨价幅度。不过,汇率波动幅度的非对称性未能得到证实。考虑到升贬值的非对称性是研究重点,本文认为基于细分数据的主要结论放在一个更长的研究时间段内依然是稳健的。
五、结论和政策启示本文扩展了Yang(2007)的厂商定价模型,对汇率传递非对称性进行理论分析,得出如下结论:
(1) 汇率完全传递和对称的汇率传递均需要满足比较严格的条件,即ε为常弹性,不随价格变化等,所以不完全和非对称的汇率传递应为现实中的常态。不完全传递已经被正式引入新开放宏观经济学框架,而汇率传递的非对称性尚被多数理论和实证研究忽略。例如Auer et al.(2012)基于经典模型推论,产品质量越高,厂商加成越高,因此更能够吸收汇率冲击,不论升贬值传递率均较低。但有能力吸收汇率冲击,不代表厂商会这么做。若汇率波动为负向冲击,例如出口商本币贬值,厂商虽然有降价空间,但追求利润最大化的动机可能会阻止厂商降价。因此,若加入非对称性考量,应能大幅提高模型解释力。
(2) 在dε/dP < 0的前提下,富有弹性的商品因竞争厂商众多,为了避免失去市场份额,厂商不愿意轻易调整报价,因而多为不完全传递。在此条件下进一步分析发现,随着需求更加富有弹性,价格-汇率曲线也从凸向原点变为凹向原点。当需求价格弹性较小时,出口厂商面临升值压力时加价多于面临贬值压力时的降价,即涨多降少。当需求弹性较大时,厂商面临升值压力时加价少于贬值压力时的降价,即涨少降多。因此,在不完全传递的情况下,商品需求弹性越大,越可能呈现出口国货币贬值传递率高而升值传递率低的非对称性。
基于966种出口日本细分商品的价格数据,本文发现汇率传递存在升贬值方向上的和幅度上的不对称性。我国出口日本的实际价格-汇率曲线接近凹向原点的曲线C,升值涨得少,贬值降得多;但在升值幅度较大时,传递率有一个逐步抬升的过程。
(1) 人民币升值时,日元价格涨得少;人民币贬值时日元价格降得多。结合理论部分推测,我国出口商品需求弹性较大,在日本市场上面对的是一个强竞争结构,厂商定价时更多地考虑维持市场份额,不愿轻易涨价。
(2) 若人民币相对日元月升值幅度超过2.43%,传递率又会有所上升。尽管出口价格易跌难涨,但在大幅升值、厂商成本上涨较多的情况下,厂商会适当提高日元售价,转嫁更多的不利冲击。一个可能的原因是我国出口厂商利润较薄,吸收升值的能力有限。
研究结论具有明显的政策含义。从微观角度,出口价格易跌难涨,折射出我国出口商仍主要依赖价格竞争。一方面,出口企业规模相对较小,大量同质商品在海外市场互相倾轧,导致出口商利润不高,依市定价的能力有限,特别是人民币贬值时易引发价格战。产业政策应鼓励出口企业产品升级,突出品质、功能和品牌效应。另一方面,随着汇率制度改革的推进,汇率波幅有可能进一步加大。非线性的汇率传递说明,即使全年核算下来人民币汇率稳定,但期间发生的贬值或者升值本身就会对厂商利润产生侵蚀。因此从汇率政策上来看,在现阶段稳定的人民币汇率对我国出口企业仍是更为有利的。
从宏观角度,如果我国出口到其它国家也存在价格易跌难涨的情形,那么中国作为全球最大商品出口国,在过去若干年里对稳定贸易伙伴国的进口价格和物价是有贡献的。Bussière and Peltonen(2008)曾指出,发达国家传递率下降和物价平稳很大程度上归功于从中国大量地进口商品。但本研究表明,汇率传递具有非对称性,若我国出口价格向上刚性,而进口价格相反地具有向下刚性的话,汇率波动本身就可能导致我国贸易条件恶化。
| [] |
曹伟、倪克勤, 2010, “人民币汇率变动的不完全传递-基于非对称性视角的研究”, 《数量经济技术经济研究》, 第 7 期, 第 105-118 页。 |
| [] |
胡冬梅、郑尊信、谢帆, 2014, “商品质量是汇率传递异质性的来源吗-以中日贸易为例”, 《国际贸易问题》, 第 12 期, 第 144-156 页。 |
| [] |
姜昱、邢曙光、杨胜刚, 2010, “人民币汇率传递的不对称效应”, 《金融经济学研究》, 第 4 期, 第 14-21 页。 |
| [] |
谢博婕、西村友作、门明, 2014, “汇率传递与国内物价水平关系研究-基于非对称性视角”, 《北京工商大学学报(社会科学版)》, 第 2 期, 第 46-51 页。DOI:10.3969/j.issn.1009-6116.2014.02.007 |
| [] |
Auer R., T. Chaney, and P.U. Sauré, 2012, "Quality Pricing-to-Market", Globalization & Monetary Policy Institute Working Paper.
|
| [] |
Bacon R.W., 1990, "Rockets and Feathers:The Asymmetric Speed of Adjustment of UK Retail Gasoline Prices to Cost Changes". Energy Economics, 13(3), 211–218.
|
| [] |
Brun-Aguerre R.X., Fuertes A.M., Greenwood-Nimmo M.J., 2017, "Heads I Win, Tails You Lose:Asymmetry in Exchange Rate Pass-Through into Import Prices". Journal of the Royal Statistical Society:Series A (Statistics in Society), 180, 587–612.
DOI:10.1111/rssa.12213 |
| [] |
Bussière M., 2013, "Exchange Rate Pass-through to Trade Prices:The Role of Nonlinearities and Asymmetries". Oxford Bulletin of Economics & Statistics, 75(5), 731–758.
|
| [] |
Bussière M., and T. Peltonen, 2008, "Exchange Rate Pass-through in the Global Economy: The Role of Emerging Market Economies", ECB Working Paper Series, 951.
|
| [] |
Campa J.M., J.M. Gonzalez Minguez, and M. Sebastia Barriel, 2008, "Non-Linear Adjustment of Import Prices in the European Union", Bank of England Working Papers, 347.
|
| [] |
Delatte A.L., López-Villavicencio A., 2012, "Asymmetric Exchange Rate Pass-through:Evidence from Major Countries". Journal of Macroeconomics, 34(3), 833–844.
DOI:10.1016/j.jmacro.2012.03.003 |
| [] |
Dornbusch R., 1987, "Exchange Rate and Prices". The American Economic Review, 77(1), 93–106.
|
| [] |
Fitzgerald D., Haller S., 2018, "Exporters and Shocks". Journal of International Economics, 113, 154–171.
DOI:10.1016/j.jinteco.2018.04.005 |
| [] |
Frankel J., Parsley D., Wei S.J., 2012, "Slow Pass-through Around the World:A New Import for Developing Countries?". Open Economies Review, 23(2), 213–251.
DOI:10.1007/s11079-011-9210-8 |
| [] |
Gaulier G., Lahrèche-Révil A, Méjean I., 2008, "Exchange-Rate Pass-Through at the Product Level". Canadian Journal of Economics/revue Canadienne Déconomique, 41(2), 425–449.
DOI:10.1111/j.1365-2966.2008.00469.x |
| [] |
Goldberg P.K., 1995, "Product Differentiation and Oligopoly in International Markets:The Case of the U.S. Automobile Industry". Econometrica, 63(4), 891–951.
|
| [] |
Hansen B.E., 1999, "Threshold Effects in Non-dynamic Panels:Estimation, Testing, and Inference". Journal of Econometrics, 93(2), 345–368.
DOI:10.1016/S0304-4076(99)00025-1 |
| [] |
Kadiyali V., 1997, "Exchange Rate Pass-through for Strategic Pricing and Advertising:An Empirical Analysis of the U.S. Photographic Film Industry". Journal of International Economics, 43(3-4), 437–461.
DOI:10.1016/S0022-1996(97)00008-1 |
| [] |
Krugman P., 1986, "Pricing to Market When the Exchange Rate Changes", NBER Working Papers.
|
| [] |
Mckinnon R.I., Ohno K., 1997, "Dollar and Yen:Resolving Economic Conflict between the United States and Japan". Pacific Affairs, 1(3), 845–846.
|
| [] |
Ohno K., 1989, "Export Pricing Behavior of Manufacturing:a U.S. Japan Comparison". IMF Staff Papers, 36(3), 550–579.
DOI:10.2307/3867047 |
| [] |
Peltzman S., 1998, "Prices Rise Faster than They Fall". Journal of Political Economy, 108(3), 466–502.
|
| [] |
PollardS.P. and C.C. Coughlin, 2004, "Size Matters: Asymmetric Exchange Rate Pass-Through at the Industry Level", Working Papers, 2003-029C.
|
| [] |
Ravn M.O., Schmitt-Grohé S., Uribe M., 2010, "Incomplete Cost Pass-through under Deep Habits". Review of Economic Dynamics, 13(2), 317–332.
DOI:10.1016/j.red.2009.06.001 |
| [] |
Tappata M., 2009, "Rockets and Feathers:Understanding Asymmetric Pricing". Rand Journal of Economics, 40(4), 673–687.
DOI:10.1111/j.1756-2171.2009.00084.x |
| [] |
Webber A.G., 2000, "Newton's Gravity Law and Import Prices in the Asia Pacific". Japan & the World Economy, 12(1), 71–87.
|
| [] |
Wickremasinghe G.B. and P. Silvapulle, 2004, "Exchange Rate Pass-Through to Manufactured Import Prices: The Case of Japan", Param Silvapulle.
|
| [] |
Yang J.W., 2007, "Is Exchange Rate Pass-through Symmetric? Evidence from US Imports". Applied Economics, 39(2), 169–178.
|



