改革开放几十年来,中国经济保持了令人惊讶的增长速度,取得了举世瞩目的发展成就,而这一成就的取得是建立在中国工业企业快速成长基础上的。那么,中国工业企业快速成长的动能是什么?全要素生产率的增长差异是解释跨国收入差异的主要因素,而大量研究证实资源配置效率是阻碍发展中国家经济增长的重要原因。那么,中国工业企业的资源配置效率如何?最近几十年来,劳动收入份额的不断下降已经成为中国乃至全球的一个重要问题,那么,中国工业企业在快速成长的过程中,其要素投入的经济利润又如何?这不仅关系到经济增长的要素收入分配问题,而且关系到中国经济增长的潜力问题。
国家之间的贫富差距为什么如此普遍?起初,Klenow and Rodriguez-Clare(1997),Prescott(1998)和Hall and Jones(1999)等的开创性工作认为国家之间人均收入的差距关键在全要素生产率(TFP)水平。那么,TFP的差异又是如何形成的?资源配置效应。这可以说是近十几年来经济增长理论方面较为一致的发现与结论。尤其是随着异质性企业理论兴起和微观企业数据的大量出现,经济学家们开始从更为微观的视角来审视TFP的来源,关于资源错配对TFP的影响研究也从行业层面深入到了微观企业层面,从微观企业资源配置状况分析宏观经济效率的研究范式更是趋于成熟,为理解资源错配影响宏观经济效率的机制提供了很好的分析框架。该研究范式最早源于Hopenhayn(1992),经Melitz(2003)在理论上的完善以及Restuccia and Rogerson(2008)对实证的发展,到Hsieh and Klenow(2009)的应用已经非常成熟,为许多后续研究所借鉴。Restuccia and Rogerson(2008)认为,生产要素在企业之间的错配,可能是影响总体TFP高低的重要因素。Hsieh and Klenow(2009)发现,如果中国资源配置效率提高到美国的水平,则中国的宏观经济产出将提高30-50%。Brandt et al. (2012)认为如果资源从低效率的国有企业向高效率的民营企业流动,这种资源再配置将提高中国总体经济的生产效率。国内学者也逐渐在总量生产率增长分解框架下研究资源配置效率问题。李玉红等(2008)利用BHC方法分析技术进步和资源再配置在工业生产率变动中的作用,分别分析了存活企业,进入企业和退出企业在经济增长中的作用。聂辉华、贾瑞雪(2011)发现全要素生产率的增长主要源于企业的效率提升,企业间的资源配置效果为负,行业净进入效应接近于零。毛其淋、盛斌(2013)研究发现,企业更替对工业企业生产率具有重要的直接影响,企业更替还通过市场竞争效应对在位企业生产率的提高产生显著的间接促进作用。
这些国内外研究可以说是从微观企业层面对全要素生产率的增长源泉进行了有意探索,但是无法看到各种要素层面的资源配置情况。张少华、蒋伟杰(2014)采用一种新的分解技术,虽然可以识别要素层面的配置效率,但是分解过程停留在宏观层面。更需要强调的是,现有研究由于在分解过程中忽略价格因素,导致无法识别和分解经济利润,尤其是资本利润和劳动利润对TFP的贡献。
为此,本文借助1998-2007年中国工业企业数据库的数据,采用一个新的增长分解框架将产出增长分解为要素投入增长和全要素生产率增长,进一步从要素层面将全要素生产率增长分解为企业自身技术进步、资本在行业内企业间和行业间的重新配置、劳动在行业内企业间和行业间的重新配置、资本的经济利润和劳动的经济利润等七个方面,从而对全要素生产率增长的动力源泉进行了更加深入的分析。
本文主要贡献在于以下几个方面:首先,鉴于已有中国工业生产率分解的相关研究忽略了资本和劳动利润对全要素生产率增长的贡献,本文借鉴Basu and Fernald(2002)、Bollard et al.(2013)等提出的测算框架对中国工业增长的源泉进行分解。在该分解框架下,不仅可以分析技术进步和资源配置效率对全要素生产率的贡献,还可以更全面的考察资本和劳动利润对全要素生产率的影响,这对理解经济增长带来的经济福利至关重要。其次,以往的大多数分析都认为资源配置效率改善有利于中国工业生产率提升,但无法进一步考察究竟是哪种投入要素配置效率的改善带来了生产率的增进,该分解框架可以进一步区分资本和劳动的资源配置效率对中国工业生产率的影响。最后,基于大量稳健性检验和异质性分析,探讨中国工业企业增长动能和经济利润在区域、所有制、行业等方面的差异,异质性分析可以有效评价、识别和比较不同情形的增长动能差异,从而为进一步的政策制定提供参考。
研究发现:(1)中国工业企业的生产率增长是其产出增长的主要推动力量,这个结论在不同所有制、不同产业以及不同地区均适用。中国工业企业正逐渐由劳动密集型向资本密集型和技术密集型转移。(2)企业自身技术进步对全要素生产量增长的增进效应贡献最大,而且国有企业和民营企业的技术进步增长率明显高于外资企业。企业之间的资源配置效率显著抑制了全要素生产率的提升,而且其抑制作用抵消了企业技术进步的绝大部分。具体到资源配置效率程度大小来看,行业内部企业之间的资本配置效率年均恶化程度至少是劳动配置效率的两倍,而行业之间的资源配置效率对全要素生产率的影响微弱。(3)就要素获取的经济利润份额来看,资本利润是劳动利润的至少四倍,劳动利润的上升极为有限。民营企业、技术密集型企业以及中东部地区企业获取了更大的资本利润,而外资获得了更多的劳动利润,体现了外资进入中国的战略取向。
余下部分结构如下:第二部分介绍了一个全要素生产率增长分解框架。第三部分报告了全要素生产率增长率及其分解测算结果,并对不同所有制、不同行业、不同地区进行了测算以及稳健性进行了讨论。第四部分是结论与启示。
二、基于要素层面的增长分解框架总体全要素生产率增长等于总量增加值的增长减去总量投入的增长。借鉴Basu and Fernald(2002),Bollard et al.(2013)等的做法,将总体全要素生产率增长分解为企业自身技术进步、生产要素在行业内企业间和行业间的重新配置以及要素的经济利润。这种方法的优势在于,可以借助微观企业数据,分解出企业的技术进步水平、要素层面的资源配置效率和经济利润。具体的分解方法如下:
假设一个经济体中有N个企业,企业i通过雇佣劳动Li单位的劳动,使用Ki单位的资本进行生产,劳动的价格为Wi,资本的价格为Ri,具体来看,代表性企业的生产函数是标准的柯布道格拉斯形式:
| $ Y_{i t}=A_{i t} K_{i t}^{\alpha} L_{i t}^{\beta} $ | (1) |
其中,Yit表示企业i在时间t的增加值,Ait表示企业i在时间t的全要素生产率,Kit表示企业i在时间t使用的资本存量,Lit表示企业i在时间t使用的劳动存量,α表示资本弹性,β表示劳动弹性,且0<α<1,0<0<β<1。企业前一期的生产函数为:Yit-1=Ait-1Kit-1αLit-1β,将两期的生产函数取对数后相减可得:
| $ \ln Y_{i t}-\ln Y_{i t-1}=\ln A_{i t}-\ln A_{i t-1}+\alpha\left(\ln K_{i t}-\ln K_{i t-1}\right)+\beta\left(\ln L_{i t}-\ln L_{i t-1}\right) $ | (2) |
由lnXit-lnXit-1=dX可知式(2)可以转化为:
| $ d A_{i}=d Y_{i}-\alpha d K_{i}-\beta d L_{i} $ | (3) |
上式的含义是全要素生产率的增长率可以用产出的增长率减去要素投入的增长率,在不引起歧义的情况下,如无必要,余下部分将不带时间t的下标。
经济体中的资本和劳动的总量分别为为
用dY表示总产出(即总量增加值)的增长率,将总产出的增长率用各个企业i产出增长率的加权平均表示,权重是企业名义产出占总名义产出的比重,即:
| $ d Y=\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y} d Y_{i} $ | (4) |
用类似的方法可以定义总的全要素生产率和要素投入增长率。其中,总的全要素生产率的增长率可以表示为:
| $ d A=\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y} d A_{i} $ | (5) |
每个企业每种要素的弹性定义为每种要素的使用成本占增加值的比重,因此总要素投入的增长率dX可以用企业i的要素增长率乘以要素弹性的加权平均表示,权重是企业名义产出占总名义产出的比重,即:
| $ d X=\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y} \frac{P_{K} K_{i}}{P_{Y} Y_{i}} d K_{i}+\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y} \frac{P_{L} L_{i}}{P_{Y} Y_{i}} d L_{i} $ | (6) |
在上述定义下,基于企业层面的总量全要素生产率的增长率可以表示如下:
| $ d A=d Y-d X=\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y} d Y_{i}-\left(\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y} \frac{P_{K} K_{i}}{P_{Y} Y_{i}} d K_{i}+\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y} \frac{P_{L} L_{i}}{P_{Y} Y_{i}} d L_{i}\right) $ | (7) |
其中, dYi=ΔYi/Yi,dKi=ΔKi/Ki,dLi=ΔLi/Li。式(7)经过简单的变化可以分离出企业水平的技术效率加权增长率:
| $ \begin{aligned} d A &=\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y}\left(d Y_{i}-\alpha d K_{i}-\beta d L_{i}\right)+\sum\limits_{i=1}^{N}\left(\frac{P_{Y} Y_{i}}{P_{Y} Y} d K_{i}\right.\\ &+\frac{P_{Y} Y_{i}}{P_{Y} Y} d L_{i}-\frac{P_{K} K_{i}}{P_{Y} Y} d K_{i}-\frac{P_{L} L_{i}}{P_{Y} Y} d L_{i}) \end{aligned} $ | (8) |
上式第一项是企业效率水平增长率的加权平均, 即企业技术效率项,权重是企业增加值占总增加值的比重,第二项是技术效率余项。第一项可以说明企业自身技术进步。我们可以把第二项分别分解为与利润相关的增长率和资源再配置的增长率,即将式(8)加上和减去(PKKi/PKK)dKi和(PLLi/PLL)dLi:
| $ \begin{aligned} d A &=\sum\limits_{i=1}^{N} \frac{P_{Y} Y_{i}}{P_{Y} Y}\left(d Y_{i}-\alpha d K_{i}-\beta d L_{i}\right)+\left(1-\frac{P_{K} K}{P_{Y} Y}\right) d K+\left(1-\frac{P_{L} L}{P_{Y} Y}\right) d L \\ &+\sum\limits_{i=1}^{N}\left(\frac{P_{Y} Y_{i}}{P_{Y} Y}-\frac{P_{K} K_{i}}{P_{K} K}\right) d K_{i}+\sum\limits_{i=1}^{N}\left(\frac{P_{Y} Y_{i}}{P_{Y} Y}-\frac{P_{L} L_{i}}{P_{L} L}\right) d L_{i} \end{aligned} $ | (9) |
其中,
式(9)中的第四项和第五项反映的是要素投入被重新配置给产出份额Yi/Y比要素投入份额Xi/X(X表示K或者L)更大的从而也是更具生产效率的企业,即资本和劳动重新配置,分别表示资本和劳动的配置效率。另外一种表示资源重新配置收益的方法是生产率差距。设企业i的资本和劳动的平均产品值分别为VAPKi=PYYi/Ki和VAPLi=PYYi/Li,整个经济体资本和劳动的平均产品分别是VAPK=PYYi/K和VAPL=PYYi/L。接下来,资本重新配置项可以重新表示为:
进一步把资本和劳动重新配置项, 即式(9)中的第四项和第五项分别分解为行业内企业间资本投入的重新配置、行业间资本投入的重新配置以及行业内企业间劳动投入的重新配置、行业间劳动投入的重新配置四项。设VAPKs=PYYs/Ks表示行业s内的资本投入K的平均产品,VAPLs=PYYs/Ls表示行业s内的劳动投入L的平均产品。分别在资本和劳动重新配置项中加入(PYYs/Ks)(Ki/PYY)和PYYs/Ls)(Li/PYY),可以得到:
| $ \sum\limits_{i=1}^{N}\left(\frac{P_{Y} Y_{i}}{P_{Y} Y}-\frac{P_{K} K_{i}}{P_{K} K}\right) d K_{i}=\\ \sum_{S} \sum_{i \in S}\left(\frac{P_{Y} Y_{i}}{K_{i}}-\frac{P_{Y} Y_{s}}{K_{s}}\right) \frac{\varDelta K_{i}}{P_{Y} Y_{i}}+\sum_{S} \sum_{i \in S}\left(\frac{P_{Y} Y_{s}}{K_{s}}-\frac{P_{Y} Y}{K}\right) \frac{\varDelta K_{i}}{P_{Y} Y_{i}}\\ =\sum\limits_{s=1}^{S} \frac{P_{Y} Y_{s}}{P_{Y} Y} \sum_{i \in S}\left(\frac{P_{Y} Y_{i}}{K_{i}}-\frac{P_{Y} Y_{s}}{K_{s}}\right) \frac{\varDelta K_{i}}{P_{Y} Y_{s}}+\sum\limits_{s=1}^{S}\left(\left(\frac{P_{Y} Y_{s}}{K_{s}}-\frac{P_{Y} Y}{K}\right) \frac{\varDelta K_{s}}{P_{Y} Y}\right) $ | (10) |
| $ \sum\limits_{i=1}^{N}\left(\frac{P_{Y} Y_{i}}{P_{Y} Y}-\frac{P_{L} L_{i}}{P_{L} L}\right) d L_{i}= \\ \sum_{S} \sum_{i \in S}\left(\frac{P_{Y} Y_{i}}{L_{i}}-\frac{P_{Y} Y_{s}}{L_{s}}\right) \frac{\varDelta L_{i}}{P_{Y} Y_{i}}+\sum_{S} \sum_{i \in S}\left(\frac{P_{Y} Y_{s}}{L_{s}}-\frac{P_{Y} Y}{L}\right) \frac{\varDelta L_{i}}{P_{Y} Y_{i}}\\=\sum\limits_{s=1}^{S} \frac{P_{Y} Y_{s}}{P_{Y} Y} \sum_{i \in S}\left(\frac{P_{Y} Y_{i}}{L_{i}}-\frac{P_{Y} Y_{s}}{L_{s}}\right) \frac{\varDelta L_{i}}{P_{Y} Y_{s}}+\sum\limits_{s=1}^{S}\left(\left(\frac{P_{Y} Y_{s}}{L_{s}}-\frac{P_{Y} Y}{L}\right) \frac{\varDelta L_{s}}{P_{Y} Y}\right) $ | (11) |
其中,ΔKs=∑i∈SΔKi,ΔLs=∑i∈SΔLi。式(10)中的第一项是行业内部企业间的资本投入重新配置,第二项是行业间资本投入重新配置;式(11)中的第一项是行业内部企业间的劳动投入的重新配置,第二项是行业间劳动投入的重新配置。需要说明的是:为了避免总产出和总量TFP增长估计的重复计算,本文用到的是增加值而不是总产出;此外,Brandt et al.(2012)认为中国工业企业真实资本成本介于10%到15%之间,本文按照Bollard et al.(2013)的做法在实证部分将资本成本设定为15%,同时在后面的稳健性讨论部分,将资本使用成本设定为10%进行了分析(Hsieh and Klenow, 2009),结果表明资本成本的设定并不会对研究结果产生较大影响。
三、分解结果与分析 (一) 数据处理说明企业层面数据源于中国工业企业数据库,该数据库涵盖了所有的国有工业企业和销售收入在500万元以上的非国有工业企业,全部样本数量200多万,时间范围是从1998年到2007年。相比其他使用上市公司数据的研究,该样本包含了大量的非上市企业和中小企业,更有利于识别企业异质性信息。中国工业企业数据库样本企业的产值大概占中国工业总产值的85%左右,是目前可以获得的最大中国微观企业数据。然而,由于该数据库并不是由学术机构发布,因此存在样本匹配混乱、变量大小异常、测量误差明显和变量定义模糊等问题(聂辉华等,2012;邵宜航等,2013),参照Brandt et al. (2012)的处理方法对数据进行整理,他们的处理方法被广为借鉴,具体包括样本匹配、名义变量的价格平减以及样本筛选等关键环节。结合研究需要,具体对样本进行了如下处理:(1)删除了企业增加值、固定资产净值、从业人员、工资等缺失、等于或小于零的企业观测值,删除了企业识别代码、企业成立年份、四位数行业代码等为空的观测值;(2)剔除了一些明显不符合会计原则的观测值,包括总资产小于流动资产,总资产小于固定资产净值,或者从业人员数少于8人,或者累计折旧小于当期折旧的观测值;(3)删除了企业增加值、固定资产净值以及员工工资首尾两端1%的极端值,以排除异常值对测算结果的干扰。
企业增加值、员工工资和从业人员变量均可直接或间接从数据库中获得,其中企业增加值使用企业所在行业的工业品出厂价格指数平减。理想情况下,估计企业资本存量的实际值需要获得企业的历史投资记录及资本处置情况,但企业在中国工业企业数据库之外年份的相关信息基本无法获得,只能对其进行大致的估计。由于企业历史信息缺失,大部分研究都以中国工业企业数据库的起始年份1998年为基期进行价格平减,忽略资本存量中1998年之前的价格因素。只有Brandt et al.(2012)尝试通过拟合企业名义资本存量增长率消除企业资本存量中1998年之前的价格因素。本文在Brandt et al.(2012)估算思想的基础上,通过区分固定资产原值与固定资产净值、改进企业名义资本增长率估计方法和纳入更丰富的数据信息,尝试将企业名义资本存量向真实的资本存量方向调整,以期获得更为准确的企业实际资本存量。另外,数据库中包含劳动报酬的变量有从业人员数、工资、雇员补贴以及失业保险等。2003年以后出现退休和健康保险等变量,2004年出现住房补贴变量。根据连贯性的原则,一般使用工资、雇员补贴和失业保险作为整个样本期的工资指标。然而,数据库中劳动所得占增加值总额的份额与宏观统计数据有较大的冲突。根据计算,中国工业企业数据库中劳动所得占增加值的份额只有34.2%,而国民收入核算中工业行业的劳动所得份额大概为55%,工业企业报告的劳动报酬可能低估了支付给劳动的份额。因此,Hsieh and Klenow(2009)在对生产率估计时,将所有企业的劳动工资份额等比例调整至与国民核算中的份额一致,以纠正该偏差。经过上述处理后,得到了覆盖28个行业工业企业的有效观测值约164.56万个。
(二) 增长动能分析1.总体分析
基于前述数据和分解方法,本部分计算了1998-2007年中国工业企业的整体全要素生产率增长情况,并分所有制、行业和区域角度进行讨论。
首先看中国工业企业整体的全要素生产率增长情况。表 1汇报了总量全要素生产率增长的估计结果。从表 1可以看出,产出增长率由1999年的6%提升到2007年的13.8%,整个样本期保持了年均9.25%的增长速度,说明在整个样本期间,产出增长出现了加速态势,最后一年的增长速度是第一年的两倍以上,考虑到基数不断扩大,这无疑说明了中国工业企业呈现出一个加速发展的趋势。通过全要素生产率6.8%的年均增长速度可以看出,产出增长的2/3是由全要素生产率的增长所贡献,要素投入增长贡献部分较少(年均2.4%的增长速度),而在要素投入增长中,资本投入增长的贡献(5.5%)要远超过劳动投入(0.8%)。上述结果说明,样本期间中国工业企业取得了长足发展,以资本投入增长为主的要素投入驱动对产出增长的贡献要远小于全要素生产率增长,中国工业企业无论是从数量还是质量方面都呈现高速增长的态势。
| 表 1 中国工业企业产出增长贡献分析 |
图 1是产出、生产率和投入的累计增长率。可以看出,产出的累计增长率接近85%,全要素生产率累计增长了60%左右,而从资本和劳动投入的增长情况来看,资本的累计增长率超过50%,劳动投入的累计增长率不到10%。总体来说,中国工业企业在1998年到2007年的十年间呈现出高速增长态势,增长的重要源头来自企业全要素生产率的提升,要素投入增长的贡献较小,并且相对于资本投入增长来说,劳动投入增长几乎处于停滞状态。
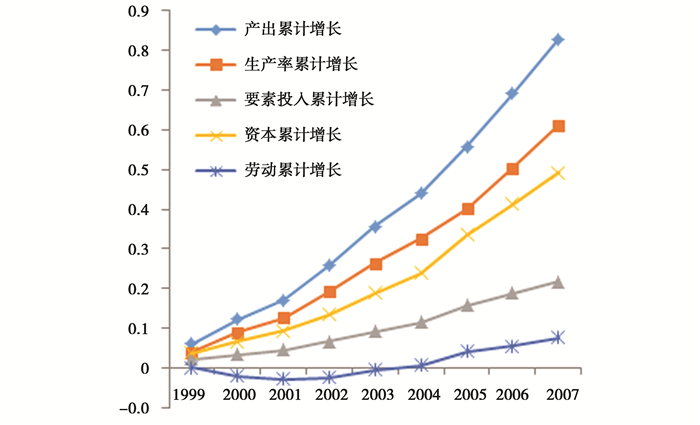
|
图 1 1998-2007年间工业企业的累计增长率水平 数据来源:中国工业企业数据库 |
2.不同所有制
接下来是不同所有制企业的全要素生产率增长情况(表 2)。按照Konings et al.(2005)对企业所有制类型的划分,本文将国有资本占注册资本比重超过50%的企业定位为国有企业,将港澳台资本和外商资本占注册资本比重超过50%的企业定位为外资企业,剩下的所有企业定位为民营企业。从不同所有制类型来看,各类所有制企业的产出增长率都为正,并在1998-2007年间呈现总体上升的态势,但不同所有制增长幅度呈现出明显差异,表现为民营企业的产出增长率高于外资企业,外资企业产出增长率高于国有企业(9%>8.4%>5.3%),这从微观层面证明了民营经济在中国经济发展中的重要地位。尽管全要素生产率增长率在不同所有制之间也呈现民营企业大于外资企业,外资企业大于国有企业的特点,但是三者之间的差距并不像产出增长率悬殊。从要素投入增长与全要素生产率增长对产出增长的贡献来看,国有企业全要素生产率增长尽管绝对水平最低,但其对产出增长的贡献要大于外资和民营企业。此外,各类所有制的资本投入增长都要高于劳动投入增长,其中国有企业的劳动投入增长在样本期间一直为负,而外资企业的劳动投入增长是民营企业的两倍左右。
| 表 2 不同所有制工业企业的产出增长贡献分析 |
3.不同产业
同时我们也测算了不同产业下的全要素生产率增长(见表 3)。从产出增长率来看,三大产业的产出增长率都呈现上升的趋势,但增长差异明显,技术密集型产业增速高于资本密集型产业,资本密集型产业增速高于劳动密集型产业,说明中国工业企业正逐渐由劳动密集型向资本和技术密集型转移,与中国工业企业转型的方向吻合。
| 表 3 不同产业工业企业的产出增长贡献分析 |
全要素生产率增长的差异与产出增长差异相类似,技术密集型产业和资本密集型产业大于劳动密集型产业,考虑到技术密集型产业的全要素生产率绝对水平本身就高于其他两大产业,这意味着三大产业的生产率差距呈现不断加大的态势,不过从其对产出增长的贡献来看,资本密集型产业的全要素生产率增长对产出增长的贡献最高,劳动密集型次之,技术密集型最低;从投入增长来看,三大类产业的差异并不太大。值得注意的是在要素投入增长中,占据主要份额的是资本投入增长(技术密集型最高,资本密集型次之,劳动密集型最低),劳动投入增长占的比重较小,这与宏观层面居高不下的资本投资率也十分吻合。其中,资本密集型产业的劳动投入增长接近于零,劳动密集型和技术密集型产业的劳动投入增长年均为1%左右。
4.不同区域
不同区域的全要素生产率增长也呈现出差异,表 4报告了不同区域的全要素生产率分解情况。
| 表 4 不同区域工业企业的产出增长贡献分析 |
从产出的年均增长率来看,东中西部地区的差异并不明显;从变化趋势可以看出,东部地区的产出增长率在样本早期要高于中西部地区,但在样本后期,中西部地区的增长率要明显快于东部地区,说明三大区域的增长差距出现了收敛的态势,这可能与国家出台的“西部大开发”战略和“中部崛起”战略有关。从全要素生产率增长水平来看,中西部地区也要高于东部地区,同样地,中西部地区的全要素增长率在样本初期要低于东部地区,但在样本后期出现了加速增长的态势,增长率远高于东部地区,而且全要素生产率增长对中西部地区的产出增长贡献也要高于东部地区,上述结果表明产出增长率收敛的原因主要由于全要素生产率增长收敛。从要素投入增长来看,三大区域的差距较小,东部地区要略高于中西部地区,中西部地区相差无几。具体到劳动和资本投入增长情况,东部地区的资本投入和劳动投入增长均要高于中西部地区,而且中西部地区的劳动投入增长在整个样本期间的年均增长为负,体现了现实中存在的中西部地区民工向东部地区流出的现象。
(三) 配置效率与经济利润分析1.总体分析
上述测算结果表明产出增长的源泉主要来自于全要素生产率的提升,那么,全要素生产率增长又由哪些因素导致?更具体地,技术进步、资源配置效率以及经济利润增长在全要素生产率增长中扮演了何种角色?借助第一部分提供的测算框架,本部分将全要素生产率增长分解为:技术进步、资本利润、劳动利润、行业内部企业间资本配置效率、行业间资本配置效率、行业内部企业间劳动配置效率以及行业间劳动配置效率等七项,以探查各因素对全要素生产率增长的贡献。
表 5报告了全样本下全要素生产率增长分解结果。从全要素生产率增长分解结果来看,技术进步增长贡献最大,且在样本期间较为稳定,年均增长率为22.9%,而资源配置效率对全要素生产率增长的抑制作用在数值上略小于技术进步增长的贡献,其年均增长率为-20%,几近抵消技术进步增长,其中资本配置效率的抑制作用为年均-14.3%,劳动配置效率的抑制作用为年均-5.7%。行业内企业间资本配置效率增长对全要素生产率增长具有较强的负向影响,即抑制了全要素生产率增长,同样地,行业内企业间的劳动配置效率也抑制了全要素生产率增长,但其抑制作用要小于资本配置效率,仅相当于资本配置效率的40%左右(0.057/0.144)。
| 表 5 中国工业企业的全要素生产率增长分解 |
全要素生产率增长的另一个来源是资本利润和劳动利润的提升,其中,资本利润增长为3.2%,劳动利润增长为0.7%,表明经济利润的绝大部分越来越多地被资本所攫取,劳动报酬占据的份额增长缓慢,这与国内外学者研究发现中国劳动收入份额在最近十几年不断下降的事实相吻合。由于政府片面追求GDP指标、广泛存在干预政策以及要素价格扭曲,中国在技术选择方面呈现出资本偏向的逆资源禀赋趋势(周其仁,1997;林毅夫等,1999),使得政府投资集中在就业吸纳能力较弱的资本密集型行业(蔡昉等,2004),即“资本偏向型技术进步”。而资本偏向型技术进步策略是制造业部门劳动收入份额增长缓慢或者说长期在低位徘徊的主要原因(黄先海、徐圣,2009;陈宇峰等,2013)。此外,上述测算还发现行业间的资本和劳动配置效率对全要素生产率增长的影响较为有限,年均贡献保持在0左右,尽管这意味着可以进一步提升行业间资源配置效率,以改善其对全要素生产率的提升作用,但考虑到企业间资源配置效率相对于行业间呈现出的对全要素生产率增长的更强抑制作用,下一步经济增长的动能可能更多地会来自于异质性企业间资源配置效率的改善。
总之,上述结果表明,全要素生产率增长主要来自于企业自身技术进步,技术进步对全要素生产率的增进效应绝大部分被资源配置效率的恶化所抵消,即资源配置效率、尤其是行业内的资源配置效率严重阻碍了全要素生产率的进一步提升。上述结果带来的启示是,为了促进中国工业全要素生产率增长,一方面,应该进一步提升企业自身的技术进步水平,但随着中国工业企业技术水平距离世界前沿越来越近,引进、学习、消化、吸收先进技术的难度会逐步加大,技术进步会越来越多地依赖于我国企业的自主研发,这也是中国提出工业企业转型发展战略的原因;另一方面,应该坚持市场配置资源为主的要素投入方式,打破影响资本和劳动合理流动的各种体制机制障碍,不断提升要素投入的配置效率,尤其是资本在企业间的配置效率。此外,应该努力提升劳动利润,使得经济发展成果更多地为国民所分享,在投资上通过产业升级来实现,短期内借助二次收入分配来调节。
2.不同所有制
表 6报告了不同所有制下全要素生产率增长的分解结果。从表 6可以看到技术进步对全要素生产率增长的贡献在不同所有制中都是最高的,但也表现出一定的差异,国有企业和民营企业的技术进步增长率要明显高于外资企业,说明本土企业的技术创新能力正在赶超外资企业。国有企业的资本利润为1.3%,外资企业为2.4%,民营企业为3.4%。外资企业的劳动利润最高(3.0%),民营企业次之(1.4%),国有企业最低(-3.3%),说明外资企业成长的成果越来越多地为劳动者所分享,这也说明了为什么外资企业的职工工资更高,而国有企业劳动利润增长为负的一个原因可能在于国有企业职工享有更高的不包含在工资中的隐形福利。从行业内企业间的资本配置效率来看,三类企业的资本配置效率都出现了恶化的态势,其中,样本前期的外资企业和其他内资企业的资本配置效率恶化呈现缓解态势,但后期又重新恶化,总体来说,民营企业和外资企业的资本配置效率恶化程度要高于国有企业;从行业内企业间的劳动配置效率来看,包括国有企业在内的内资企业的劳动配置效率年度增长率为负,且要高于外资企业(-3.3%),可见,民营企业间资本配置效率和劳动配置效率都是最低的。此外,资本和劳动在行业之间的配置效率增长集中在零附近,对全要素生产率的增长影响较为微弱。
| 表 6 不同所有制企业的全要素生产率增长分解 |
3.不同产业
对不同产业类型全要素生产率增长分解对于理解中国工业转型具有重要的现实意义,表 7是不同产业类型下全要素生产率增长的分解结果。
| 表 7 不同产业工业企业的全要素生产率增长分解 |
从表 7可以看出,三大产业中对全要素生产率增长贡献最大的依然是技术进步提升,其中资本密集型产业的技术进步增长最高(27.6%),劳动密集型产业次之(22.6%),技术密集型产业最低(15.5%)。三大类产业的资本利润增长在整个样本期间呈现一个上升的态势,不同产业之间尽管呈现一定的增长差异,但差异较小,劳动密集型小于资本密集型(2.8% < 3.0%),资本密集型小于技术密集型(3.0% < 3.3%)。相对于资本利润较高的增长率,劳动利润在整个样本期间几乎处于停滞状态,这与总体测算中表现的国民财富增长中被劳动者所分享的份额一直没有发生较大改变相一致,尽管如此,劳动密集型产业和技术密集型产业的劳动利润仍然保持了较低的稳定增长势头,年均增长率达到了1%左右,这可能体现了低技能劳动者和高技能劳动者在这两个产业的配置情况。
从行业内部企业间的资本配置效率来看,资本密集型产业和劳动密集型产业的配置效率对全要素生产率提升的抑制作用在样本前期较强,在样本后期逐渐减弱,而技术密集型产业的资本配置效率则是在样本后期恶化,总体来看,资本密集型产业的企业间资本配置效率恶化趋势最为严重(-19.6%),劳动密集型产业次之(-13.1%),技术密集型产业最小(-8.6%),中国长期以来推行的重工业赶超战略可能是造成这一结果的重要原因。从行业内部企业间的劳动配置效率来看,三大类产业的劳动配置效率都对其全要素生产率增长具有较强的抑制作用,从劳动配置效率恶化的年度均值来看,劳动密集型产业的恶化最为严重(-7.6%), 资本密集型和技术密集型产业的恶化作用相差不多,而且要明显小于劳动密集型产业,同样地劳动配置效率对全要素生产率增长的抑制作用要小于资本。值得注意的是,资本密集型产业的企业间资本配置效率最低,劳动密集型产业的企业间劳动配置效率最低。此外,行业间的资本和劳动配置效率的年均增长率接近于零,说明行业间的资源配置效率在整个样本期间基本没有发生变化,对全要素生产率的增进效应极为有限。
4.不同区域
表 8汇报了不同区域的全要素生产率分解结果。从技术进步增长率来看,中部地区的技术进步增长率最快,保持了年均28.6%的增长速度,东部地区和西部地区的技术进步增长相近,说明全要生产率增长主要是由于技术进步增长所致。中东部地区获取的资本利润大于西部,而中西部地区的劳动利润增长在样本前期为负,到了样本后期有所改善,总体依然保持了较弱的负增长态势,东部地区的劳动利润增长一直较为稳定,年均增长速度为1.5%, 一定程度上说明劳动力由中西部地区流向东部地区的重要原因可能在于东部地区的劳动者能够更多地分享地区经济增长的成果。中部地区行业内部企业间的资本配置效率一直呈现恶化态势,年均增长率为-18.7%,要高于东部地区的13.6%和西部地区的12.7%,由此可知,尽管中部地区的技术进步速度最高,但是其对区域全要素生产率的增进效应大部分被资本配置效率的低下所抵消。从劳动在行业之间的配置效率来看,东部地区的劳动配置效率对全要素生产率的抑制作用最为强烈,达到了年均-6.1%,中部地区次之,西部地区为3.8%,可见尽管东部地区作为劳动力流动的重要目的地,但是劳动在不同企业之间的配置效率最低,显著抑制了该区域的全要素生产率增长。此外,与前文的分析相类似,资本和劳动在行业之间的配置效率增长一直维持了0附近,说明其对全要素生产率增长的贡献较为微弱,这一效应在不同区域之间也不存在明显差异。
| 表 8 不同区域工业企业的全要素生产率增长分解 |
1.存续样本检验
中国工业企业数据库在2004年进行了统计标准的调整,有大量的企业在2004年进入了数据库(图 2),通过整理后的数据库可以看出,企业数量由2003年的不足15万家,猛增到2004年的21万多家,如此大规模的样本数量变化可能会影响估计结果的稳健性,因此本文采用1998年到2007年期间持续存续的企业为样本,按照第二部分的测算方法重新测算全要素生产率增长,并对其进行了分解,分解结果汇报于表 9。通过表 1、表 5与表 9的比较可以看出,产出增长率都保持了年均9%左右,生产率增长速度不到7%,说明即使考虑到2004年有大量新企业进入数据库的情形,本文的增长测算结果也是稳健的。从对全要素生产率增长的贡献来看,存续样本的检验同样表明,技术进步效率对全要素生产率增长的贡献最大,行业内部企业间资本和劳动的配置效率对全要素生产率增长具有较强的抑制作用,使得技术进步对全要素生产率增长的贡献大部分被抵消。此外,与全样本测算相一致,行业内部企业间的资本配置效率恶化程度要高于劳动配置效率。总体来说,采用存续样本进行测算的结果表明,2004年出现的大量企业进入数据库的情况,并没有影响到全要素生产增长估计和分解测算的主要结论。
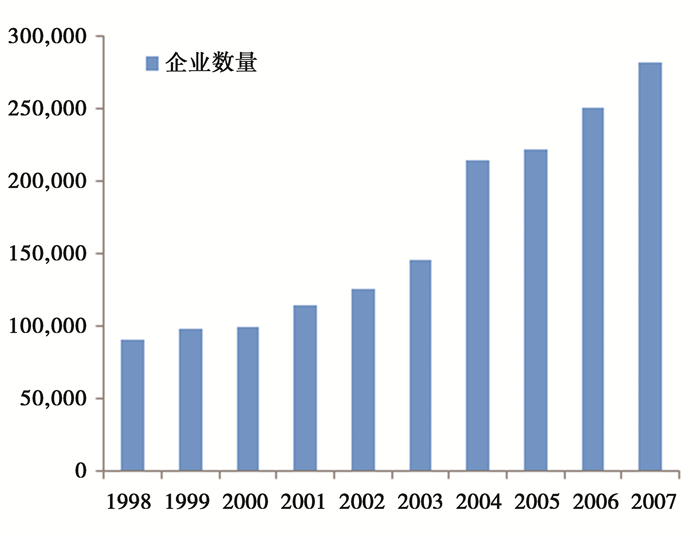
|
图 2 中国工业企业年度企业数量 数据来源:中国工业企业数据库 |
| 表 9 存续样本下的检验 |
2.资本使用成本的影响
在前文的测算中假定资本成本为0.15,考虑到资本成本可能会对研究结果产生影响,我们按照Hsieh and Klenow(2009)关于中国工业企业资本使用成本的设定,将资本成本设定为0.10,利用全样本数据和第二部分的测算方法进行了重新估计,估计结果汇报于表 10。
| 表 10 资本使用成本差异下的检验 |
从表 10的估计结果可以发现,产出增长率和全要素生产率增长率与表 1的测算结果并没有较大差异,将全要素生产率增长进一步分解表明,技术进步增长对全要素生产率增进贡献最大,企业间的资本和劳动配置效率起到了较大的抑制作用,几乎抵消了技术进步的全要素生产率增进效应,其中资本配置效率要高于劳动配置效率,行业间的资源配置效率对全要素生产率的影响较为微弱,这与前面的研究结论相一致,说明资本成本的设定并不会对全要素生产率的增长估计和分解测算产生较大影响,本文研究结论是稳健的。
3.不同时间段的检验
根据中国宏观经济景气周期和数据状况,我们分1998-2003年和2004-2007年两个时段进行了比较分析。
从前面的分析可以发现,样本后期的全要素生产率增长速度要高于样本前期,这一结论不论是采用全样本测算还是使用十年存续样本测算都是成立的,为了防止企业数量变化对该结论可能产生的影响,我们进一步分别使用1998-2003年和2004-2007年两个样本区间分别存续的样本进行了重新测算,两个时间段的测算结果汇报于表 11。其中,第三列和第四列分别是全样本测算的1998-2003年和2004-2007年两个样本区间的年均增长率,第五列和第六列分别是十年存续样本测算的1998-2003年和2004-2007年两个样本区间的年均增长率,第七列和第八列分别是1998-2003年和2004-2007年两个时间段分别存续企业测算的年均增长率。
| 表 11 不同时间段的检验 |
从表 11可以看出,在三种样本划分方法下,产出增长率在样本后期出现大幅度提升的主要原因在于全要素生产率增长的贡献。进一步对增长进行分解后发现,后一时间段的资本利润增长、行业内企业间资本配置效率和劳动配置效率的改善是全要素生产率出现较大提升的主要原因,而技术进步增长速度出现了一定幅度的下滑,这也说明随着中国工业企业与世界先进技术前沿面距离的不断趋近,靠引进发达国家的先进技术、提升中国的技术进步来驱动全要素生产率增长的难度日益加大,中国工业经济发展质量提升的下一步驱动力来自于资源配置效率的改善。
四、结论与启示基于中国工业企业数据库,本文根据一个新的测算框架对中国工业企业的全要素生产率增长进行了估计与分解测算。该研究框架以企业异质性理论为基础,将工业整体全要素生产率增长分解为企业自身技术进步、资本利润、劳动利润、行业内部企业间的资本配置效率、行业间的资本配置效率、行业内部企业间的劳动配置效率以及行业之间的劳动配置效率等七项,一方面,弥补了大多数研究只能分解出资源配置效率,而无法分别识别资本和劳动资源配置效率的缺陷;另一方面,该框架可以进一步识别资本和劳动利润对全要素生产率的贡献,突破了以往忽视经济利润对全要素生产率增长的影响。
文章的主要发现有以下几个方面:
(1) 中国工业经济总产出在1998年到2007年的整个样本期间呈现出高速增长态势,增长的重要源头来自工业整体全要素生产率的提升,要素投入增长的贡献较小,并且相对于信贷投放推动的资本投入增长来说,受限于适龄劳动人口增长缓慢和人口老龄化问题的日益严重,劳动投入增长在整个样本期间几乎处于停滞状态。所有制层面,民营企业的产出增长率高于外资企业,外资企业产出增长率高于国有企业,而产出增长的主要差异是由于要素投入造成,受到大规模的国有企业改制的影响,国有企业的劳动投入增长在样本期间一直为负,而外资企业的劳动投入增长是民营企业的两倍左右;区域层面,三大区域全要素生产率增长收敛带来了产出增长率的收敛,而要素投入增长差距较小,东部地区的资本投入和劳动投入增长均要高于中西部地区,体现了中西部地区民工向东部地区流出以及资本向经济发达地区集聚的现象;产业层面,三大产业全要素生产率增长的差异体现了产出增长差异,技术密集型产业增速高于资本密集型产业,资本密集型产业增速高于劳动密集型产业,说明中国工业企业正逐渐由劳动密集型向资本和技术密集型转移,与中国工业企业转型的方向吻合。
(2) 企业自身技术进步对全要素生产量增长的增进效应贡献最大,说明中国工业企业在样本期间主要通过引进、学习、消化、吸收国外的先进技术取到了长足发展,企业自身成长是中国工业企业高速发展的一个重要原因。企业之间的资源配置效率显著抑制了全要素生产率的提升,从抑制效应大小来看,其抑制作用抵消了企业技术进步的绝大部分,具体到资源配置效率来看,行业内部企业之间的资本配置效率年均恶化程度至少是劳动配置效率的两倍,而行业之间的资源配置效率对全要素生产率的影响微弱。资本利润是劳动利润的至少四倍,说明中国工业企业的发展程度较大部分被资本所攫取,劳动者所得份额的上升较为有限。所有制层面看,内资企业的技术进步率要高于外资企业,而其资源配置效率要低于外资企业;从三大产业来看,资本密集型产业的技术进步增长率最高,技术密集型产业最低,技术密集型资本利润最高,资本密集型产业的资源配置恶化趋势最强,劳动密集型行业和技术密集型行业的劳动利润保持了较低的稳定增长势头;分区域来看,中部地区的技术进步增长率最快,但同时其行业内部企业间的资本配置效率一直呈现恶化态势,此外,东部地区获取的资本利润最高,而中西部地区的劳动利润增长在样本前期为负,东部地区的劳动利润增长一直较为稳定。
(3) 考虑样本期间企业大量进入数据库和资本使用成本不同的情况后,上述研究结论依然没有产生较大差异,值得注意的是不管使用十年存续期企业,还是两个时间段分别存续企业,亦或者是全部企业的样本,分时间段的分析都表明,后一时间段的资本利润增长、行业内企业间资本配置效率和劳动配置效率的改善是全要素生产率出现较大提升的主要原因,而技术进步增长速度出现了一定幅度的下滑,说明进一步经济增长的驱动力可能会更多的来优化资源配置效率。
基于以上相关研究结论,本文提出以下政策建议:
(1) 为了促进中国工业企业全要素生产率增长,应该进一步提升企业自身的技术进步水平,随着中国工业企业技术水平距离世界前沿越来越近,引进、学习、消化、吸收先进技术的难度会逐步加大,技术进步会越来越多的依赖于我国企业的自主研发。当前紧张激烈的中美贸易战本质上是美国在高技术层面对中国崛起的封锁,这更提醒我们必须走自主创新的道路。
(2) 应该坚持市场配置资源为主的要素投入方式,打破影响资本和劳动合理流动的各种体制机制障碍,不断提升要素投入的配置效率,尤其是资本在企业间的配置效率。如果说提高企业自身技术水平是一种长期战略的话,那么,坚持市场化改革提高资源配置效率,可以说是保持中国经济高质量增长的短期有效举措。
(3) 应该努力提升劳动利润,使得经济发展成果更多地为国民所分享,在投资上通过产业升级来实现,短期内借助二次收入分配来调节。劳动利润的提升可以帮助中国居民消费升级,而消费升级会促进中国企业的产业升级和技术进步,这可以说是从需求侧和供给侧两端为新时代中国经济的高质量增长“保驾护航”。
| [] |
蔡昉、都阳、高文书, 2004, “就业弹性、自然失业和宏观经济政策——为什么经济增长没有带来显性就业?”, 《经济研究》, 第 9 期, 第 18-25+47 页。 |
| [] |
李玉红、王皓、郑玉歆, 2008, “企业演化:中国工业生产率增长的重要途径”, 《经济研究》, 第 6 期, 第 12-24 页。 |
| [] |
林毅夫、蔡昉、李周, 1999, “比较优势与发展战略——对东亚奇迹的再解释”, 《中国社会科学》, 第 5 期, 第 4-20+204 页。 |
| [] |
毛其淋、盛斌, 2013, “中国制造业企业的进入退出与生产率动态演化”, 《经济研究》, 第 4 期, 第 34-37 页。 |
| [] |
聂辉华、贾瑞雪, 2011, “中国工业企业企业生产率与资源误置”, 《世界经济》, 第 7 期, 第 25-46 页。 |
| [] |
聂辉华、江艇、杨汝岱, 2012, “中国工业企业数据库的使用现状和潜在问题”, 《世界经济》, 第 3 期, 第 142-158 页。 |
| [] |
邵宜航、步晓宁、张天华, 2013, “资源配置扭曲与中国工业全要素生产率——基于工业企业数据库再测算”, 《中国工业经济》, 第 12 期, 第 39-51 页。 |
| [] |
王志华、董存田, 2012, “我国制造业结构与劳动力素质结构吻合度分析——兼论'民工荒'、'技工荒'与大学生就业难问题”, 《人口与经济》, 第 5 期, 第 1-7 页。 |
| [] |
杨汝岱, 2015, “中国制造业企业全要素生产率研究”, 《经济研究》, 第 2 期, 第 61-74 页。 |
| [] |
张少华、蒋伟杰, 2014, “中国全要素生产率的再测度与分解”, 《统计研究》, 第 3 期, 第 54-60 页。DOI:10.3969/j.issn.1002-4565.2014.03.008 |
| [] |
周其仁, 1997, “机会与能力——中国农村劳动力的就业和流动”, 《管理世界》, 第 5 期, 第 81-101 页。 |
| [] |
Bollard A., Peter J. Klenow, Gunjan Sharma, 2013, "Indias Mysterious Manufacturing Miracle". Review of Economic Dynamics(16), 59–85.
|
| [] |
Baily M.N., Hulten C., Campbell D., 1992, "Productivity Dynamics in Manufacturing Plants". Brookings Papers on Economic Activity:Microeconomics, 187–267.
|
| [] |
Basu, Susanto, Fernald, John G., 2002, "Aggregate productivity and aggregate technology". European Economic Review, 46(6), 963–991.
DOI:10.1016/S0014-2921(02)00161-7 |
| [] |
Brandt L., Van Biesebroeck J., Zhang Y., 2012, "Creative Accounting or Creative Destruction? Firm-Level Productivity Growth in Chinese Manufacturing". Journal of Development Economic, 97(2), 339–351.
DOI:10.1016/j.jdeveco.2011.02.002 |
| [] |
Foster, Lucia, Haltiwanger, John, Syverson, Chad, 2008, "Reallocation, firm turnover, and efficiency:Selection on productivity or profitability?". American Economic Review, 98(5), 394–425.
|
| [] |
Hall R., Jones C., 1999, "Why do some countries produce so much more output per worker than others?". Quarterly journal of economics, 114(1), 83–116.
DOI:10.1162/003355399555954 |
| [] |
Hopenhayn H. A., 1992, "Entry, Exit, and Firm Dynamics in Long-Run Equilibrium". Econometrica, 60(5), 1127–1150.
DOI:10.2307/2951541 |
| [] |
Hsieh C.T., Klenow P.J., 2009, "Misallocation and Manufacturing TFP in China and India". The Quarterly Journal of Economics, 124(4), 1403–1448.
DOI:10.1162/qjec.2009.124.4.1403 |
| [] |
Klenow P., Rodriguez-Clare A., 1997, "The neoclassical revival in growth economics:has it gone too far?". NBER Macroeconomics Annual(12), 73–103.
|
| [] |
Konings J, Cayseele P.V., Warzynski F., 2005, "The effects of privatization and competitive pressure on firms' price-cost margins:Micro evidence from emerging economies". Review of Economics and Statistics, 87(1), 124–134.
DOI:10.1162/0034653053327603 |
| [] |
Melitz M.J., 2003, "The impact of trade on intra-industry reallocations and aggregate industry productivity". Econometrica, 71(6), 1695–1725.
DOI:10.1111/ecta.2003.71.issue-6 |
| [] |
Prescott, Edward C., 1998, "Lawrence R. Klein lecture 1997:Needed:A theory of total factor productivity". International economic review, 39(6), 525–551.
|
| [] |
Restuccia D., Rogerson R., 2008, "Policy distortions and aggregate productivity with heterogeneous establishments". Review of Economic Dynamics, 11(4), 707–720.
DOI:10.1016/j.red.2008.05.002 |




