最近几年,中国爆发了多起金融风险事件,如2014年“钱荒”事件,2015年“股灾”事件,2015-2016年债券违约事件,2016年严重的资本外流和房价疯涨事件。这些事件使得防范金融风险、维护金融稳定成为中国决策层和学术界关注的热点和焦点。同时,习总书记在2017年10月18日召开的十九大报告中,明确提出“守住不发生系统性金融风险的底线”,并将“防范化解重大金融风险”列为全面建成小康社会三大攻坚战之首。同年11月国务院金融稳定发展委员会获批成立,旨在加强央行宏观审慎管理与系统性风险防范职责,加强金融监管部门问责,确保国内金融市场的稳定与发展。这说明无论是中国金融决策和监管部门还是金融实体经济部门都已经充分认识到金融稳定在宏观决策中的重要性。但金融稳定职责由谁来承担仍存在很大的争议,总的来看主要有两种观点:第一,中央银行承担金融稳定职责,从而其货币政策应考虑金融稳定;第二,成立专门的金融稳定机构承担金融稳定职责,该机构与中央银行一起组成“双支柱”宏观调控体系。虽然中国已经成立金融稳定发展委员会,但目前该机构主要定位是一个统筹协调机构,而不是专职履行金融稳定职责的独立机构。因而,在中国现行金融监管体系下,中国人民银行还是具体承担金融稳定职责的主体。基于目前我国金融风险事件多发的实际背景和金融监管部门大力加强金融稳定监管的宏观背景,研究金融稳定是否纳入货币政策目标有重大的理论与现实意义。
国内外学者对“金融稳定是否要纳入货币政策目标”展开了一系列的研究,并取得丰富的成果。根据使用同频还是混频模型展开研究,本文将这些研究大致分为以下两类,展开文献综述。(1)基于同频模型的研究。根据实证分析遵循的基本框架不同,该类研究又可进一步分为以下两种研究思路:①根据金融稳定是否与货币政策其他主要目标存在某种关联关系来决定金融稳定是否应纳入货币政策目标。Bernake and Gertler(1999)、Cecchetti et al.(2000)就这个问题存在很大的争议,并得出完全相反的结论。Bernake and Gertler认为金融稳定与物价稳定之间具有一致性,以利率规则为指导的货币政策已关注物价稳定,再引入金融稳定只会加剧经济波动,因而无需考虑金融稳定。相反,Cecchetti et al.却指出,历史上影响较大的金融危机都出现在物价稳定期,因此央行货币政策要考虑金融稳定;马勇等(2017)从金融周期视角研究发现包含金融稳定因素的货币政策有助于在正常时期维护实体经济和金融的“双稳定”;朱军(2018)进一步使用NK-DSGE模型分析发现构建“宏观审慎双支柱+财政整顿政策”的大宏观审慎政策有利于使经济达到有效均衡状态,从根本上提高社会福利水平。相关方面的研究还包括,Dhal(2011)、林珏、杨荣海(2011)、戴金平、刘东坡(2015)、徐国祥、郭建娜(2017)、张龙、金春雨(2018)等。上述文献尽管在研究对象与研究区间上存在差异,但都应用同频季度数据模型进行实证研究,且基本上认为金融稳定与产出和物价的稳定具有某种关联性,同时也有自己独特的运行规律,从而说明三者之间存在时变而非固定的关联性,因此基本得出货币政策应考虑金融稳定的结论。②基于最小化货币政策损失函数标准判断是否应将金融稳定纳入货币政策目标。唐齐鸣、熊洁敏(2009)认为上述争论的本质差异在于二者人为设定了不同的利率规则,然而这两种利率规则可能均为次优而非最优,并进一步提出从模型出发,在相关约束条件下通过最小化货币政策损失求解利率规则才是正确的分析方法。国内外学者主要使用IS-Phillips方程和DSGE模型等方法,通过最小化货币政策目标缺口损失函数,实证分析发现纳入金融稳定后,货币政策损失对比未纳入时显著减小,因此认为货币政策应该关注金融稳定(Kontonikas and Montagnoli, 2006;马勇,2013;Nisticò,2014;马亚明、刘翠,2014;朱军等,2018)。然而,也有少量学者得出相反的结论(谭政勋、陈怡君,2015)。另外,Taylor(2010)和Svensson(2010)则认为货币政策目标和金融稳定分属不同范畴,则应分别由其责任机关——货币当局和金融监管机构进行针对性调控,只有在金融稳定严重影响宏观经济或金融崩溃被提前发现时,货币当局才应将金融稳定纳入调控范围。总之,国内外学者均采用同频模型对这个问题展开研究,大多认为纳入金融稳定可以显著减少货币政策损失,货币政策应该关注金融稳定。
(2) 基于混频模型的研究。虽然大多数基于同频模型的实证分析支持货币政策应该关注金融稳定,但还是存在较大争议,结论也不一致。究其原因,本文认为在于没有考虑货币政策目标统计频率的差异性。同频模型通过人为的降频或升频导致信息损失或误增进而导致信息失真,影响了货币政策的实时性和真实敏感度。最近几年来,随着混频模型的兴起,学者们探索了其在金融经济研究中的应用,目前主要用于构建混频金融状况指数(周德才等,2017;周德才等,2018)和经济景气指数(Camacho,2013;郑挺国、王霞,2013);同时也有少量学者应用MF-VAR等混频模型分析货币政策冲击及其经济效应(Bacchiocchi et al., 2016;Marcellino and Sivec, 2016),以及货币政策规则(刘金全等,2016),发现混频模型比同频模型更适合研究货币政策。考虑到目前还没有学者使用混频模型研究货币政策目标选择问题,本文拟对此进行一个初步的探讨。
综上,关于金融稳定能否纳入货币政策目标这一问题,学术界无论在分析框架还是在研究结论上均已做了广泛且有益的探讨,并为相关政策制定者提供了充足的实证与理论支持。但现有研究仍然处于基于同频样本数据使用同频模型进行实证分析阶段。由于GDP是季度的,金融变量一般是月度的,为了使得二者频率一致,传统的同频方法一般是使用平均法由高频向低频转换,或者使用频率分解器由低频向高频转换,这两种方法会导致样本数据信息的人为的丢失和人为的虚增,从而不利于充分利用全部真实的样本数据信息,使用这样的样本数据进行实证分析可能会得到错误的结论。这种忽略样本变量统计频率差异的做法可能会使得无论在金融稳定测度还是货币政策问题研究上都缺乏真实可靠性和实时灵敏性。鉴于此,本文拟作以下一些有益的探索,也可能是本文的边际贡献:第一,构建中国首个混频金融稳定指数(MF-FSI)。本文选择1998年1月至2017年12月不良贷款率等15个月季混频金融变量,应用MF-DFM模型构建了中国首个混频金融稳定指数;第二,构建混频IS-Phillips模型,在这个模型基础上实证分析金融稳定是否应纳入货币政策目标,并进行货币政策目标选择和时效选择的敏感性分析。
二、构建混频IS-Phillips模型 (一) 推导IS-Phillips的数理模型宏观经济中的经济变量一般存在较强的滞后效应,即当期数值常常与前一期甚至前几期存在较大的相关性。毫无疑问,受制于棘轮效应的影响,社会总需求也往往较大地受到前期总需求量的影响。同时,考虑到严格执行货币政策规则过程中,过于频繁地调整中介目标加剧经济波动的可能,货币当局在执行货币政策规则时,通常承认经济变量适应性预期的特点,从而使得货币政策呈现出明显的平滑倾向。鉴于以上原因,本文构建如下后顾型的IS-Phillips模型并以此推导后顾型的利率反应函数。
| $ \pi_{\mathrm{t}+1}=\pi_{t}+\alpha y_{t}+\varepsilon_{t+1} $ | (1) |
| $ y_{t+1}=\beta_{1} y_{t}-\beta_{2} r_{t}+\beta_{3} f s_{t} $ | (2) |
上式中,t表示时间;π表示通货膨胀率;y表示产出缺口,即实际产出与潜在产出的偏差;r表示实际利率缺口,即实际利率与其均衡值的偏差,假定费雪方程成立,则rt=i-πt;fs表示金融稳定缺口,即金融稳定与其长期平均水平的偏差。εt+1、vt+1分别表示在t+1时期对通货膨胀及产出缺口的冲击,二者独立且均服从正态分布,即εt+1~NIID(0, σε2),υt+1~NIID(0, συ2)。由于式(1)、(2)中的变量的缺口是各变量与其长期均衡水平的偏差,故方程不设常数项。
式(1)为Phillips曲线,表征总供给,表示为惯性作用下自身滞后1阶、产出缺口滞后1阶与当期冲击的函数。式(2)为修正的IS曲线,表征总需求。本文通过将经济增长(y)、物价稳定(π),金融稳定(fs)三个货币政策目标纳入到改进的IS曲线理论模型,以便于对货币政策最终目标进行分析。金融稳定无论引入IS亦或Phillips方程在经济意义上都是可行的,本文将金融稳定引入IS方程主要基于两点考虑。一是,现有文献仅存在2篇将金融稳定引入Phillips方程的实践,数量上可以看出学术界更认同将金融稳定引入IS方程;二是,统计上倾向于将金融稳定引入IS方程。FSI同GDP、CPI的Granger因果关系检验结果表明,FSI与CPI存在双向Granger因果关系,而FSI与GDP仅存在FSI对GDP的单向Granger因果关系。故本文将金融稳定引入IS方程而非Phillips方程。参照唐齐鸣、熊洁敏(2009)的做法,均将三个货币政策目标的代理变量设置为滞后1阶的形式。这里需要特别说明,金融稳定对总需求的影响有多种传导渠道:一方面,如大多数学者(Goodhart and Hofmann, 2002;Elbourne,2008;马亚明、刘翠,2014)使用资产价格代理金融稳定时指出,资产价格通过财富和资产负债表效应对经济产出产生同方向影响;另一方面则表现为不同金融稳定程度下,投资环境的利好和利空对投资者信心的影响,从而传导到总需求的变化。
在上述总供给和总需求模型的约束下,本文通过最小化央行货币政策损失函数来求解利率反应函数。学术界关于货币政策应采用规则型还是相机型莫衷一是,Svensson (1997)认为盯住通胀的货币政策兼具二者优势,且国内学者在研究本国货币政策时多采用盯住通胀的货币政策,因此,本文同样采取此种方法构建如下货币政策损失函数:
| $ L=\frac{1}{2}\left[\left(\pi-\pi^{*}\right)^{2}+\lambda\left(y-y^{*}\right)^{2}\right] $ | (3) |
式(3)中,L表示央行货币政策损失函数,λ表示货币当局给予经济增长这一货币政策目标的权重,π*、y*分别为通胀和产出缺口的目标值。中央银行通常希望经济稳定增长,因此令y*=0,而实际操作中,货币当局一般会将π*设定某个正值。这样,损失函数就可以表示为如下形式:
| $ L=\frac{1}{2}\left[\left(\pi-\pi^{*}\right)^{2}+\lambda y^{2}\right] $ | (4) |
央行制定货币政策的目标是使得社会福利损失最小,即损失函数取最小值。因此,构建如下值函数:
| $ V\left(\pi_{t+1 | t}\right)=min \left\{\frac{1}{2}\left[\left(\pi_{t+1| t}-\pi^{*}\right)^{2}+\lambda y_{t+1 | t}^{2}\right]+\theta E_{t} V\left(\pi_{t+2 | t+1}\right)\right. $ | (5) |
式(5)中,θ表示折现因子,且θ∈[0, 1],πt2|t1表示基于t1期的信息集对t2期通货膨胀的预测,Et(·)表示对应变量在t期的期望值。
参照Svensson (1997)的处理方法,基于式(1)、(2)的约束,对式(5)求解关于实际利率ti的偏导的一阶条件为:
| $ \pi_{t+2| t}-\pi^{*}=-\frac{\lambda}{\theta \alpha k} y_{t+1 | t} $ | (6) |
其中,
将式(1)提前一期并表示成基于t期信息集的形式,将其带入式(6),则可消去yt+1|t,得到表达式(7)。
| $ \pi_{t+2 | t}=\pi^{*}+\omega\left(\pi_{t+1| t}-\pi^{*}\right) $ | (7) |
其中
式(6)与式(2)联立即可求得利率反应函数:
| $ r_{t}=c_{1}\left(\pi_{t+2 |t}-\pi^{*}\right)+c_{2} y_{t}-c_{3} f s_{t} $ | (8) |
其中,
将式(1)进行2次迭代,可得到πt+2|t的表达式:
| $ \pi_{t+2| t}=\pi_{t}+\alpha\left(1+\beta_{1}\right) y_{t}-\alpha \beta_{2} r_{t} $ | (9) |
因此,式(8)亦可表述为以下形式:
| $ r_{t}=\tilde{c}_{1}\left(\pi_{t}-\pi^{*}\right)+\tilde{c}_{2} y_{t}-\tilde{c}_{3} f s_{t}-\tilde{c}_{4} u_{t} $ | (10) |
其中,
式(10)意味着,中央银行根据利率规则制定货币政策时,除了稳物价与稳增长的目标外,还要将金融稳定状况考虑在内,这样才能实现货币政策损失函数的最小化。
(二) 构建混频IS-Phillips计量模型基于新建的中国首个混频金融稳定指数,本文使用IS-Phillips的混频计量模型,实证分析了中国金融稳定是否应纳入货币政策目标。该计量模型的详细构建过程具体如下:
1.构建IS-Phillips的混频计量模型的一般形式
在上文推导利率规则过程中,为方便起见,均将变量间的滞后影响设置为滞后1阶,然而在实际处理过程中,所选数据区间和频度的不同都会影响到变量的滞后阶数。本文选择一般到特殊的分析方法确定变量滞后阶数:首先,设定变量的滞后阶数最大为4阶,然后,结合极大似然值和系数显著性去掉一定滞后阶数的变量。因此IS-Phillips的混频计量模型可表示为式(11)、(12)的形式,其中lmn≤4lmn≤4。
| $ \pi_{t}^{m}=\alpha_{0}+\sum\limits_{i=1}^{l_{11}} \alpha_{1, i} \pi_{t-i}^{m}+\sum\limits_{j=1}^{l_{12}} \alpha_{2, j} y_{t-j}^{q m}+\varepsilon_{t} $ | (11) |
| $ y_{t}^{q m}=\beta_{0}+\sum_{p=1}^{l_{21}} \beta_{1, p} y_{t-p}^{q m}-\sum_{k=1}^{l_{22}} \beta_{2, k} r_{t-k}^{m}+\sum_{s=1}^{l_{23}} \beta_{3, } f s_{t-s}^{m}+v_{t} $ | (12) |
其中
2.构建IS-Phillips的混频计量模型的状态空间模型的一般形式
上述IS-Phillips的混频计量模型一般形式可表示为状态空间模型的形式,从而可通过卡尔曼滤波方法估计出相关系数,则IS-Phillips的混频计量模型的状态空间形式表示为:
| $ 量测方程:Y_{t}^{m f}=\alpha+H Z_{t}^{m}+\varepsilon_{t} $ | (13) |
| $ 状态方程:Z_{t}^{m}=u+A X_{t-1}^{m}+B Z_{t-1}^{m}+v_{t} $ | (14) |
其中,Ytmf=[ πtm ytqm ]为可观测的混频数据向量;α和H是量测方程的截距项和斜率系数项;Ztm为无法观测的状态变量向量;εt~NIID(0, σεt2)为量测方程的误差项;u、A和B分别是状态方程的截距项、外生变量和状态变量的斜率系数;υt~NIID(0, συ2)。
3.构建IS-Phillips的混频计量模型的状态空间模型的具体形式
在构建IS-Phillips的混频计量模型状态空间模型的具体形式中,本文选择季度GDP缺口(GDPgap)和月度通货膨胀缺口(CPIgap)作为内生变量,利率缺口(r)和金融稳定(fs)作为外生变量。本文全部数据都是标准化的,从而构建该模型无截距项。经过检验,本文发现在IS方程的自变量中GDPgap滞后1-3阶、利率缺口(r)滞后2阶和金融稳定(fs)滞后1阶,同时在Phillips方程的自变量中,GDP缺口(GDPgap)滞后1阶、通货膨胀缺口(CPIgap)滞后1阶,似然函数值最大,且给出的估计效果最好。因此,该模型具体形式如下:
| $ 量测方程:\underbrace {\left[ {\begin{array}{*{20}{c}} {CPI_t^m}\\ {GDP_t^{qm}} \end{array}} \right]}_{Y_t^{mf}}{\rm{ = }}\underbrace {\left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0\\ {\frac{1}{3}}&0&{\frac{1}{3}}&0&{\frac{1}{3}}&0 \end{array}} \right]}_H\underbrace {\left[ {\begin{array}{*{20}{c}} {Y_t^m}\\ {Y_{t - 1}^m}\\ {Y_{t - 2}^m} \end{array}} \right]}_{Z_t^m} + \underbrace {\left[ {\begin{array}{*{20}{l}} {{{\varepsilon}_{t, 1}}}\\ {{\varepsilon _{t, 2}}} \end{array}} \right]}_{{\varepsilon _t}} $ | (15) |
| $ 状态方程:\\ \begin{array}{l} \underbrace {\left[ {\begin{array}{*{20}{c}} {Y_t^m}\\ {Y_{t - 1}^m}\\ {Y_{t - 2}^m} \end{array}} \right]}_{Z_t^m} = \underbrace {\left[ {\begin{array}{*{20}{c}} 0&0&{{0_{1 \times 4}}}\\ {{\alpha _1}}&{{\alpha _2}}&{{0_{1 \times 4}}}\\ {{0_{4 \times 1}}}&{{0_{4 \times 1}}}&{{0_{4 \times 4}}} \end{array}} \right]}_A\underbrace {\left[ {\begin{array}{*{20}{c}} {{r_{t - 2}}}\\ {{f_{{s_{t - 1}}}}}\\ {{0_{4 \times 1}}} \end{array}} \right]}_{{X_{t - 1}}} + \\ \underbrace {\left[ {\begin{array}{*{20}{c}} {{\beta _{11}}}&{{\beta _{12}}}&0&0&0&0\\ {{\beta _{21}}}&0&{{\beta _{22}}}&0&{{\beta _{23}}}&0 \end{array}} \right]}_B\underbrace {\left[ {\begin{array}{*{20}{c}} {Y_{t - 1}^m}\\ {Y_{t - 2}^m}\\ {Y_{t - 3}^m} \end{array}} \right]}_{Z_{t - 1}^m} + \underbrace {\left[ {\begin{array}{*{20}{c}} {{v_{t, 1}}}\\ {{v_{t, 2}}}\\ {{0_{4 \times 1}}} \end{array}} \right]}_{{v_t}}\\ \end{array} $ | (16) |
其中,Ytm=[ CPIgap, tm GDPgap, tm ]′表示第t期全部状态变量向量;当不纳入金融稳定时,α2=0;I4×6表示4×6维的单位矩阵。
(三) 简单构建MF-DFM模型本文在实证分析过程中,首先使用混频动态因子模型(MF-DFM)测度中国首个混频金融稳定指数,用于检验金融稳定是否应纳入货币政策目标,因此本文需要简单构建MF-DFM模型。在相关文献中一般选择单个金融稳定指标或者构建综合性的金融稳定指数来表征金融稳定。为了更加全面地刻画我国金融稳定状况,本文选择金融稳定指数来表征。考虑到构成金融稳定指数各个指标的统计频率不尽相同,同时为了实证分析结果的准确性、实时性以及跨期分析的期限敏感性,故本文应用MF-DFM模型构建中国混频金融稳定指数。
1.构建MF-DFM模型的一般形式
MF-DFM模型的一个主要特点是对不同频率的数据进行分析。定义
| $ \left(\begin{array}{c}{\mathrm{Y}_{\mathrm{t}, 1}^{\mathrm{qm}}} \\ {\mathrm{Y}_{\mathrm{t}, 2}^{\mathrm{m}}}\end{array}\right)=\mathrm{a}+\mathrm{b} \mathrm{f}_{\mathrm{t}}+\mathrm{u}_{\mathrm{t}} $ | (17) |
| $ \phi_{f}(L) f_{t}=\mu+v_{1, t}, \phi_{u}(L) u_{t}=v_{2, t} $ | (18) |
| $ \left(\begin{array}{c}{\mathrm{v}_{1, \mathrm{t}}} \\ {\mathrm{v}_{2, \mathrm{t}}}\end{array}\right) \sim \mathrm{NID}\left(0, \quad\left(\begin{array}{cc}{\sigma_{1}^{2}} & {0} \\ {0} & {\sum_{22}}\end{array}\right)\right) $ | (19) |
其中,式(17)的常数项是a=(a′1, a′2),低频和高频变量的常数项分别是a1和a2;b为N×1阶因子载荷阵;ft是平稳共同因子;ut=(u′t, 1, u′t, 2), 为N×1维平稳的特定因子;f(·)阶多项式;ϕu(·)是N维空间上q阶多项式;L为滞后算子。同时,为了模型可识别,本文参考相关文献的常见处理方法,对模型施加2个可识别条件:(1)假定因子载荷阵b的首个元素是1;(2)假定ϕu(·)与Σ22都是对角阵,即各指标的特定因子间无相关性,并记∑22的主对角元素是σ2, i2, i=1, 2,…, N。
借鉴郑挺国、王霞(2013)的方法,式(17)可以改写成式(20):
| $ \left(\begin{array}{c}{\mathrm{Y}_{\mathrm{t}, 1}^{\mathrm{qm}}} \\ {\mathrm{Y}_{\mathrm{t}, 2}^{\mathrm{m}}}\end{array}\right)=\mathrm{a}+\left(\begin{array}{c}{\frac{1}{3} \mathrm{b}_{1}\left(\mathrm{f}_{\mathrm{t}}+\mathrm{f}_{\mathrm{t}-1}+\mathrm{f}_{\mathrm{t}-2}\right)} \\ {\mathrm{b}_{2} \mathrm{f}_{\mathrm{t}}}\end{array}\right)+\left(\begin{array}{c}{\frac{1}{3} \mathrm{u}_{1, \mathrm{t}}+\frac{1}{3} \mathrm{u}_{1, \mathrm{t}-1}+\frac{1}{3} \mathrm{u}_{1, \mathrm{t}-2}} \\ {\mathrm{u}_{2, \mathrm{t}}}\end{array}\right) $ | (20) |
其中,(b′1, b′2)′:=b(u′1, t, u′2, t):=ut。
2.构建MF-DFM的状态空间模型形式
对前文介绍的MF-DFM模型,可将其表示为以下状态空间模型形式:
| $ 量测方程:Y_{t}=a+H S_{t} $ | (21) |
| $ 状态方程:S_{t}=\mu+F S_{t-1}+G v_{t}, v_{t} \sim N I D \quad\left(0, \Sigma_{\mathrm{v}}\right) $ | (22) |
量测方程,描绘了观测变量Yt和无法观测的状态变量St间相互依存的关系;状态方程,则描绘了St的动态路径。其中,Yt=[Yt, 1qm, Yt, 2qm],且Yti是第i个变量在t期的观测值,St是由不可观测共同因子组成的矩阵。
在式(21)和式(22)中,Yt, a, St, vt, F, G, H分别为相应的系数向量与矩阵,它的详细表达式可参考郑挺国、王霞(2013)一文。
三、构建中国混频金融稳定指数 (一) 指标的选取和来源关于金融稳定状况的测度,方法上包括单指标、多指标和金融稳定指数3种形式,相比而言,后者能够综合金融市场的各个金融变量全方面衡量金融市场稳定状况,从而成为近几年认可度较为高的做法。因此本文选择金融稳定指数作为金融稳定的代理变量。然而,由于不同学者对金融稳定的含义解读各异,因而在指标选取和指标数量上存在较大差异。国际上较为权威且成熟的金融稳定评估体系主要是IMF编制的金融稳健性指标评估体系(FSIs),本文主要参考FSIs中所选用的指标,从金融机构、金融市场、经济环境三个层面构建中国金融稳定指数(FSI),具体指标如表 1所示。
| 表 1 不平衡混频样本数据选取说明 |
1.实际化处理。为剔除价格因素的影响,本文对GDP和名义利率进行了实际化处理。其中,实际GDP通过使用同期CPI调整得到,实际利率=名义利率-同期通货膨胀率。
2.季节性调整。本文采用X-12方法对存在明显季节性变化的月度变量和季度变量进行季节性调整。
3.对数化处理。本文对经实际化和季节性调整后的样本数据进行对数化处理以消除异方差影响。
4.缺口值计算。对于实际利率,借鉴唐齐鸣、熊洁敏(2009)的做法,本文采用实际利率减去其平均值的做法作为实际利率的缺口值;其余数据均采用HP滤波法计算其缺口值。
5.标准化处理。旨在消除各变量量纲差异。
6.指标同向化处理。考虑到各金融指标对金融稳定的影响存在正负方向的差异,本文参考任重等(2016)的处理方法,对负向指标的标准化数值做相反数处理,旨在通过MF-DFM萃取出金融稳定状况的同向共同成分因子。
(三) 基于MFM-DF模型的中国混频金融稳定指数构建1.中国混频金融稳定指数的测度
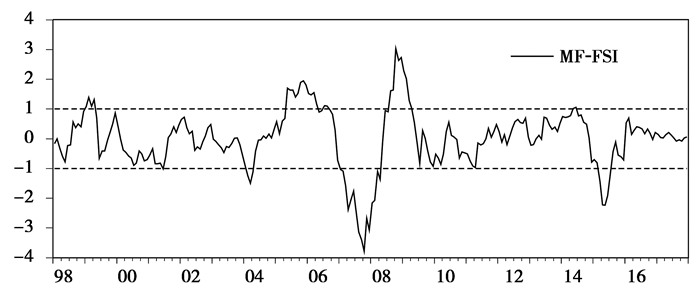
运用Matlab软件运行混频动态因子模型(MF-DFM)程序,求得共同因子f的估计结果。由于本文构建的混频金融稳定指数为一致指数,同时共同因子f集聚了所选取的金融变量的共同波动成分,故f可直接作为混频金融稳定指数,记为MF-FSI。纵观MF-FSI的构建原理,由于对各指标进行了标准化处理,致使得到的指数值不是绝对值而是相对值,因此可通过其相对大小比较金融稳定程度。综合考虑FSI的水平与波动状况,我国金融环境状况表现为长期稳定短期波动的态势。局部来看,直观上可认为FSI向上波动表征金融稳定状况提高,FSI向下波动表征金融稳定状况下降。Van den End(2006)认为合理范围内的FSI金融市场即可平稳运行,因此建议使用具有边界的FSI测度金融市场环境。因此,本文借鉴郭红兵、杜金岷(2014)的做法,用所选样本区间内FSI的均值加减一个标准差作为其上下边界,即:TH下限=μ-σ,TH上限=μ+σ,其中:TH、μ、σ分别为样本区间内FSI的阈值、平均值和标准偏差。以此为判断标准,则TH下限 < FSI < TH上限,认为金融稳定状况处于合理范围之内,FSI>TH上限,认为金融状况处于“金融失衡”状态,FSI < TH下限,认为金融状况处于“金融不稳定”状态。基于MF-DFM构建的中国混频金融稳定指数及其边界见图 1。
|
图 1 中国混频金融稳定指数及其边界 |
2.MF-FSI的历史经验分析
图 1表明自1998年以来,代表中国金融稳定状况的混频金融稳定指数(MF-FSI)主要经历了3次金融失衡时期和3次金融不稳定时期。金融失衡时期主要表现在:(1)1999年1月-1999年5月。亚洲金融危机发生后,亚洲等国家经济动荡,同时中国经济也遭受了巨大冲击,出现了明显的经济衰退,为此中国人民银行采取了7次降息和征收利息税等一系列扩张性货币政策,超出了实际需要,导致了金融失衡情况。(2)2005年5月-2006年11月。为了减缓“非典”和股市大熊市给经济造成的冲击,中国金融监管部门采取扩张性的货币政策, 特别是信贷增速超出实际需要,在一定程度上导致了金融失衡。(3)2008年8月-2009年4月。为了应对爆发于美国的世界金融危机对中国经济的巨大冲击,中国政府部门推出了“四万亿”经济刺激计划,央行实施了天量货币供应和信贷供应等前所未有的货币政策,大大超出了实时部门的需要,导致了特别严重的金融失衡,达到了全局的最高峰。
金融不稳定主要表现在:(1)2004年2月-2004年5月。2003年爆发的“非典”对金融市场的影响逐步显现,超过了金融市场正常情况所能承受的,出现了金融不稳定状况。(2)2007年10月-2008年7月。为了应对这个期间的经济过热,中国金融监管部门实施了诸如通过6次上调存款准备金率最终达到超高的21.5%等一系列的严格的紧缩货币政策,给金融市场造成了下行冲击,再加上股票由大牛市转为大熊市,大大超出了金融市场的正常承受能力,导致了特别严重的金融不稳定,达到了全局的最低谷。
3.MF-FSI的实时性分析
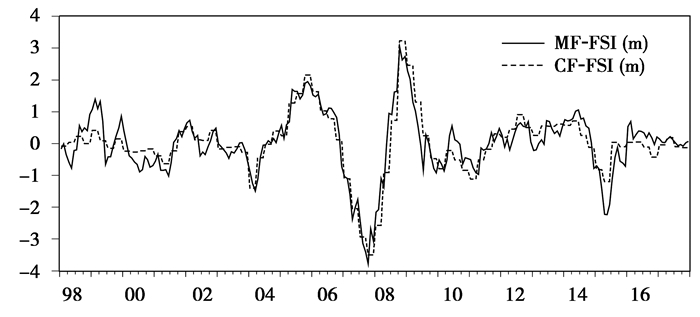
借鉴传统的测算金融稳定指数的方式应用因子分析法得到季度同频金融稳定指数(CF-FSI(q)),同时利用Eviews8.0的频率转化器将季度同频金融稳定指数(CF-FSI(q))转化为月度同频金融稳定指数(CF-FSI(m))。图 2呈现了月度混频金融稳定指数(MF-FSI(m))与月度同频金融稳定指数(CF-FSI(m))的对比结果。可以发现,二者整体走势趋于一致,但同频指数更为光滑,混频指数波动更为频繁,且在金融稳定状况的非合理区间内,混频指数的波动幅度较大,说明MF-FSI(m)相较CF-FSI(m)更具实时性和灵敏性。
|
图 2 MF-FSI(m)与CF-FSI(m)对比图 |
金融稳定与经济增长的关系一直受到学术界的高度关注,特别是在08年金融危机,多数学者认为需将金融稳定作为新的货币政策目标制定相关政策。基于前文IS-Phillips的数理模型中关于金融稳定对总需求影响的探讨,下文将从动态相关角度分析MF-FSI代表的金融稳定同GDP缺口之间的关系。
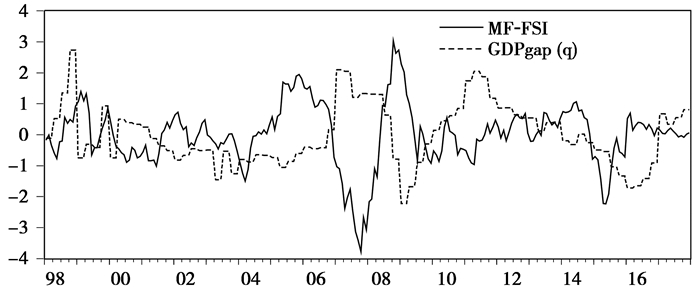
(1) MF-FSI与GDP缺口的图形相关性分析。图 3呈现了考察区间内MF-FSI与GDP缺口的折线图,从图中可以看出MF-FSI与GDP缺口整体走势轨迹趋于一致,通过几个显著的波峰波谷的比较,可以发现MF-FSI显著领先GDP缺口约4-9个季度。首先进行波峰比较:MF-FSI在2005年第4季度处于阶段峰值,而GDP缺口于2007年第2季度达到阶段峰值,MF-FSI提前GDP缺口4个季度;其次进行波谷的比较:第一个波谷,MF-FSI出现在2007年第4季度,而GDP缺口出现在2009年第1季度,MF-FSI提前GDP缺口5个季度。第二个波谷,MF-FSI出现在2015年第2季度,而GDP缺口出现在2016年第1季度,MF-FSI提前GDP缺口3个季度。综合MF-FSI和GDP缺口在波峰波谷的表现,可认为MF-FSI对于GDP缺口具有一定的预测能力,可以视为GDP缺口的先行指标,预测时间大致为5-18个月,约2-6季度。
|
图 3 MF-FSI与GDPgap折线图 |
(2) MF-FSI与GDP缺口的Granger因果关系检验。为考察金融稳定与经济增长之间的关系,本文应用算术平均法将月度FSI调整为季度FSI的形式,表示为FSI(q)。表 2呈现了FSI与GDP缺口的Granger因果关系检验,结果表明FSI(q)是GDP缺口的格兰杰原因,而GDP缺口并非FSI(q)的格兰杰原因,说明FSI(q)对GDP缺口,从而对GDP有一定的预测能力。
| 表 2 FSI(q)与GDP的Granger因果关系检验 |
综合前文对混频金融稳定指数和经济增长的动态相关性分析可得出以下结论:在考察期样本内,金融稳定状况与经济增长走势轨迹趋于一致,且在短期内MF-FSI对GDPgap有良好的预测效果。Castro(2011)认为,金融稳定是否对产出具有预测能力是判断金融稳定能否纳入货币政策的标准。因此,可初步判断金融稳定应该纳入到中国货币政策考虑范畴。
四、实证分析 (一) 样本数据的单位根检验为防止实证分析中存在伪回归现象,需对时间序列进行单位根检验。结果如表 3所示。由表 3可知,ADF检验与PP检验都表明全部缺口值则均在1%的显著性水平下拒绝原假设。因此,在1%的显著性水平下,样本数据均为平稳时间序列,可用来进行回归分析。
| 表 3 单位根检验 |
基于上文构建的混频IS-Phillips模型,使用基于状态空间模型和卡尔曼滤波算法的极大似然估计法,分别对是否纳入金融稳定指数(FSI)的混频IS-Phillips模型进行估计,估计结果如下表所示:
从表 4可知,无论纳入金融稳定(FSI)还是不纳入金融稳定(FSI)这两个模型下,混频IS-Phillips模型系数估计值都在1%的水平上显著;两个模型的系数联合显著检验都在1%水平上拒绝原假设,表明该模型系数不全部为零;两个模型估计残差的异方差检验(即ARCH LM检验)在滞后1-3阶上都以很高概率接受不存在异方差的原假设,表明模型估计残差不存在异方差,篇幅所限,只列出滞后2阶的检验结果;两个模型估计残差的序列相关检验(即LBQ检验)在滞后1-3阶上都以很高的概率接受不存在序列相关的原假设,表明模型估计的残差无序列相关。总之,这些都说明了本文对混频IS-Phillips模型的系数估计是很合理的。
| 表 4 混频IS-Phillips模型估计结果及相关检验 |
由上述回归结果可知,在考察的样本区间内,就Phillips方程而言,通货膨胀除受自身滞后值的影响外,还受到滞后1阶的产出缺口的显著性正向影响。至于总需求IS方程,除受自身滞后的影响外,滞后2阶实际利率缺口与滞后1阶金融稳定缺口对其都具有非常显著性的负向影响。此外对比IS方程(1)与IS方程(2),去掉金融稳定缺口对产出缺口的影响后,Phillips方程回归结果拟合优度有所下降,IS方程回归结果拟合优度有所上升。但是,这并不意味着加入金融稳定后加大了产出缺口,因为本文利用状态空间模型对混频IS-Phillips模型进行估计时是把两个方程放在一起进行联合估计的,两个方程之间存在一定程度的相互影响。同时,还可以看到IS方程(2)相较于IS方程(1),利率缺口对产出缺口的负向影响程度有了较大的提高,这是因为实际利率缺口与金融稳定缺口之间存在负向关系,而二者对产出缺口的影响是同向的,从而加强了利率缺口对产出缺口影响的绝对值。进一步表明,将金融稳定纳入货币政策有利于发挥利率传导机制的作用。
就模型估计结果而言,加入金融稳定后模型的各项检验值均有了较大的提高,可以初步判定考虑金融稳定的货币政策效果优于忽略金融稳定的货币政策效果。根据损失函数表达式:
| 表 5 损失函数值 |
央行利用利率规则进行最优货币政策目标选择时,除进行上述IS-Phillips方程的估计外,还要根据其计算结果,通过最小化央行福利损失得出利率反应规则的表达式。考虑到不同的贴现因子θ和产出权重λ对利率规则表达式的影响存在较大差异,对于θ,本文借鉴马亚明和刘翠(2014)的做法,令θ=0.95;对于λ,鉴于我国制定货币政策时兼顾对物价稳定与经济增长的调控,故令λ=1。在上述参数设定下,计算出利率规则反应函数:
| $ r_{t}=7.542 \pi_{t}+14.002 y_{t}-1.489 f s_{t} $ | (23①) |
① 式(23)的参数估计结果同传统泰勒规则差异较大,同时本文类比其他同类研究发现也存在此类问题,因此本文认为这是由中国基本国情与研究差异导致的。传统泰勒规则是基于美国经济运行经验得出的,同美国相比,我国利率市场化尚未成熟且存在利率管制的情况,同时,本文所选的研究区间为1998M1-2017M12,时间跨度较长,期间涉及经济转型、利率改革等大型经济事件。
式(23)表明,根据利率规则,通货膨胀、经济增长和金融稳定的系数大小分别为:7.542、14.002和-1.489。系数的绝对值衡量了3个目标在货币政策目标选择中的重要程度,因此,根据上述利率规则,货币政策目标的选择次序依次为:经济增长、物价稳定、金融稳定。显然,经济增长和物价稳定仍是我国货币当局的主要目标,但考虑到金融稳定在利率规则中亦占有较大的比重,因此货币当局也应适当侧重对金融稳定的调控。特别在货币政策与宏观审慎政策“双支柱”宏观调控的背景下,二者在金融稳定方面采取宏观调控与微观监控的互补措施,才更有益于整个金融市场的稳定。
(三) 敏感性分析λ和θ反映了货币当局货币政策调控意图和预期偏好的差异,尽管前文中求取利率反映规则函数时,赋予了λ和θ特定的值,但根据最小化货币政策损失函数求取利率规则的基本数学推理,很明显随两个参数的不同取值,利率规则会发生较大的改变。为了反映这种变化,本文基于最优货币政策目标的选择,进行了利率规则关于λ和θ两参数的敏感性分析。
1.经济增长权重λ的变化对最优货币政策目标选择的敏感性分析
为简化计算量,给定θ=1,分别计算λ取0.1、0.5、1、2四种状态时,利率规则表达式中各货币政策目标系数的改变。直观上可认为,随λ的增大,货币当局更倾向于考虑经济增长目标降低对物价稳定的关注。按此逻辑,λ=0代表货币政策目标仅为物价稳定,但一国货币当局不可能完全忽视经济增长,因此λ=0.1更符合现实情况,且能够反映货币当局对物价稳定的高度重视,故本文以λ=0.1为起点分析利率规则对λ的敏感性,结果如表 6所示。由表 6可知,随货币当局对经济增长目标赋权加大,产出缺口和通胀缺口系数不断减小,且通胀缺口减小的速度远大于产出缺口,而金融稳定缺口系数没有发生变化。这说明,货币当局货币政策目标由关注物价稳定转向关注经济增长时,对产出缺口和通胀缺口的关注度都要有所减少,且对产出缺口维持在更为稳定的较高关注度,要显著降低对通胀缺口的关注度,同时时刻保持对金融稳定缺口的关注。
| 表 6 λ敏感性分析(θ=1) |
2.货币政策预期偏好θ的变化对最优货币政策目标选择的敏感性分析
同样,类比λ的分析过程,本文令θ=0.1、0.2、0.5、0.90、0.95和1等六种状态时,利率规则表达式中各货币政策目标系数的改变。学术界一般认为,θ越大,货币当局在制定货币政策目标时更加关注对远期预期的影响,货币政策影响时间越长。表 7呈现了θ的敏感性分析结果。由表 7可知,随货币政策预期偏好的增加,仅从数值上来看产出缺口和通胀缺口系数不断增大,且通胀缺口增大的速度远大于产出缺口,而金融稳定缺口系数没有发生变化。然而从绝对值层面来看,通胀缺口系数发生了结构性的改变,即当θ处于低位时,通胀缺口与实际利率缺口之间为负向关系,且通胀缺口对宏观经济的影响远大于其余缺口变量,而当θ处于高位时,除为1的极端情况外,通胀缺口与实际利率缺口之间为正向关系,且通胀缺口对宏观经济的影响小于产出缺口。这表明,货币政策预期偏好会影响货币政策目标的选择,若货币当局想延长货币政策影响时间,则要不断增加对通胀缺口和产出缺口的关注,重点考虑产出缺口对宏观经济的影响,同时维持对金融稳定的关注。若货币当局只为解决短期经济问题,则应首先关注通胀缺口的影响,其次为产出缺口,此时仍要保持对金融稳定的关注度。
| 表 7 θ敏感性分析(λ=1) |
综合表 6和表 7,观察各目标值系数的绝对值,可见除极端情况外,通胀缺口和产出缺口都显著高于金融稳定缺口,表明物价稳定和经济增长仍为中国主要货币政策目标;此外,无论货币当局调控意图是稳增长还是稳物价,也无论货币政策预期偏好是长期性的还是暂时的,货币当局都要在一定程度上保持对金融稳定的关注度,不能因为政策意图及偏好的改变而消减或增大其影响,其原因在于货币政策对金融稳定的调控力度和手段是有限的,单纯为调控金融市场状况而应用利率规则会对国民经济产生剧烈的影响,因此必须匹配金融发展委员会的宏观审慎政策进行互补性调控才能保证我国经济的平稳运行。
五、简要结论及政策建议 (一) 简要结论本文基于1998.1—2017.12这一时间区间的不平衡混频样本数据,构建了我国首个混频金融稳定指数作为金融稳定的代理变量,并在此基础上探讨金融稳定是否应纳入货币政策。实证研究表明:(1)本文首次构建的中国混频金融稳定指数是金融稳定的一个具有实时性的有效测度指标。(2)与不纳入金融稳定相比,纳入金融稳定的货币政策能够有效减少央行福利损失, 中国货币政策目标应纳入金融稳定。(3)无论中国货币政策目标偏好和预期偏好怎样变化,央行都应给予金融稳定固定且不可忽略的关注度,但物价稳定和经济增长仍为主要货币政策目标。
(二) 政策建议第一,定期构建中国混频金融稳定指数,并进行金融风险预警。中国混频金融稳定指数综合了金融机构、金融市场和经济环境三层面的金融经济波动,同时充分考虑到了各个金融稳定变量的信息及时性,克服了传统同频金融稳定指数人为因素影响及无法充分利用信息的缺点,具有很强的操作性。因此,央行可指定专门的机构部门对中国混频金融稳定指数进行跟踪测算并定期公布,真实透明地反映中国金融稳定状况。对于实体经济中的任一冲击,及时发现波动来源的层面,对症下药。同时对中国未来的金融经济稳定情况进行预测,以及对金融风险进行预警,尽量减少因金融和经济的不稳定性而给各经济主体带来的经济损失,促进中国经济可持续发展。
第二,建议央行将金融稳定纳入中国货币政策目标。中国央行在制定货币政策时,不能忽略金融稳定对经济产出与通胀的影响,应及时利用各类货币政策工具对金融稳定状况的非正常状况进行调控,以加强金融服务实体经济的职能,并将金融稳定纳入货币政策目标达到最小化央行福利损失的目的。但仍须明确,货币政策通过金融稳定控制宏观经济波动得益于利率等有效传导机制。利率根据货币政策目标的偏离程度进行灵活调整要求央行加大公开市场业务操作,加强利率调整的灵敏性。因此,在调控偏好上,央行应改变过去对金融市场的行政手段的调控倾向,转向市场化调控和监管的模式。
第三,尽快明确中国金融稳定发展委员会职能的具体分工,建设并完善好中国金融监管的“双支柱”宏观调控体系。央行维持金融稳定的能力和手段是有限的,且货币政策的实施对整个宏观经济的冲击效果是强烈的,若为维持金融稳定而进行过多的操作并不利于宏观经济的平稳运行。金融稳定发展委员会建立的初衷是强化金融监管协调,补齐央行在宏观审慎管理和系统性风险防范中的监管短板,但该机构各个层次职能的具体分工,至今还没有细则。而随着中国金融市场不断深化,各类创新型金融产品复杂化和跨部门化特征显著,导致潜在金融风险加剧,相关风险调控和监管难以依靠单一金融机构完成。如何协调不同层面的监管,避免监管交叉或失空,是金融发展委员会需要重点考虑的问题。因此,防控金融风险和创新金融调控思路需形成“一盘棋”模式——“双支柱”宏观调控体系。货币政策应保持连续性和稳定性,央行要通过实时有效的评估,引导各类金融机构强化内部约束,实现稳健经营、金融服务实体经济的可持续性的目标。此外,金融发展委员会应协调好各类金融机构的监管面,强化宏观审慎政策的协同作用,搭配宏观审慎工具在各金融市场开展逆周期调节,以稳定市场预期。
| [] |
戴金平、刘东坡, 2015, “金融稳定与物价稳定、经济增长的动态关联性”, 《财经科学》, 第 10 期, 第 14-25 页。DOI:10.3969/j.issn.1000-8306.2015.10.002 |
| [] |
郭红兵、杜金岷, 2014, “中国金融稳定状况指数的构建”, 《数量经济技术经济研究》, 第 5 期, 第 100-116 页。 |
| [] |
刘金全、解瑶姝、龙威, 2016, “'新常态'下中国财政政策与货币政策选择的新视角”, 《经济问题》, 第 3 期, 第 14-21 页。 |
| [] |
林珏、杨荣海, 2011, “金融稳定性与经济增长的机制分析——基于新兴市场国家和发达国家的两组数据”, 《财经研究》, 第 2 期, 第 49-59 页。 |
| [] |
马勇, 2014, “植入金融因素的DSGE模型与宏观审慎货币政策规则”, 《世界经济》, 第 7 期, 第 68-92 页。 |
| [] |
马勇、张靖岚、陈雨露, 2017, “金融周期与货币政策”, 《金融研究》, 第 3 期, 第 33-53 页。 |
| [] |
马亚明、刘翠, 2014, “房地产价格波动与我国货币政策目标制的选择——基于IS-Philips模型的分析”, 《南开经济研究》, 第 6 期, 第 138-150 页。 |
| [] |
唐齐鸣、熊洁敏, 2009, “中国资产价格与货币政策反应函数模拟”, 《数量经济技术经济研究》, 第 11 期, 第 104-115 页。 |
| [] |
谭政勋、陈怡君, 2015, “货币政策反应规则与房价波动的实证研究”, 《金融论坛》, 第 7 期, 第 27-36 页。 |
| [] |
王自力, 2005, “金融稳定与货币稳定关系论”, 《金融研究》, 第 5 期, 第 1-11 页。 |
| [] |
徐国祥、郭建娜, 2017, “金融稳定目标下中国货币政策规则研究”, 《财经研究》, 第 10 期, 第 18-30 页。 |
| [] |
尹继志, 2012, “金融调控中的物价稳定与金融稳定:从分离到融合的逻辑演进”, 《南方金融》, 第 3 期, 第 7-13 页。DOI:10.3969/j.issn.1007-9041.2012.03.003 |
| [] |
印重、刘金全、张小宇, 2016, “包含金融稳定因素的货币政策规则研究”, 《数量经济研究》, 第 2 期, 第 1-19 页。 |
| [] |
周德才、邓姝姝、左玥, 2018, “中国金融状况指数混频编制与应用研究——基于MS-MF-VAR模型的一个经验分析”, 《南开经济研究》, 第 2 期, 第 1-9 页。 |
| [] |
周德才、燕洪、钟佳敏, 2017, “中国混频金融状况指数的构建”, 《统计与决策》, 第 15 期, 第 5-10 页。 |
| [] |
朱军、李建强、张淑翠, 2018, “财政整顿、双支柱政策与最优政策选择”, 《中国工业经济》, 第 8 期, 第 24-41 页。 |
| [] |
张龙、金春雨, 2018, “数量型和价格型货币政策工具的有效性对比研究”, 《中国工业经济》, 第 1 期, 第 119-136 页。 |
| [] |
郑挺国、王霞, 2013, “中国经济周期的混频数据测度及实时分析”, 《经济研究》, 第 6 期, 第 58-70 页。 |
| [] |
Bacchiocchi E, Bastianin A, Missale A, Rossi E., 2016, "Structural analysis with mixed frequencies:monetary policy, uncertainty and gross capital flows". Working Papers, 11, 1–44.
|
| [] |
Bernanke B S, Gertler M., 1999, "Monetary policy and asset price volatility". Federal Reserve Bank of Kansas City, 18–51.
|
| [] |
Castro V., 2011, "Can central banks' monetary policy be described by a linear (augmented) Taylor rule or by a nonlinear rule?". Journal of Financial Stability, 7(4), 228–246.
DOI:10.1016/j.jfs.2010.06.002 |
| [] |
Camacho M., 2013, "Mixed-frequency VAR models with Markov-switching dynamics". Economics Letters, 121(3), 369–373.
DOI:10.1016/j.econlet.2013.09.010 |
| [] |
Dhal S., 2011, "Financial Stability, Economic Growth, Inflation and Monetary Policy Linkages in India:An Empirical Reflection". Reserve Bank of India Occasional Papers, 32(3), 1–35.
|
| [] |
Durré A., 2000, Asset Prices and Central Bank Policy, ICMB and the CEPR Press.
|
| [] |
Elbourne A., 2008, "The UK housing market and the monetary policy transmission mechanism:An SVAR approach". Journal of Housing Economics, 17(1), 65–87.
|
| [] |
End J W V D., 2006, "Indicator and boundaries of financial stability". Dnb Working Papers(No.097).
|
| [] |
Goodhart C, Hofmann B., 2002, "Asset Prices and the Conduct of Monetary Policy". Royal Economic Society, 1–20.
|
| [] |
Kontonikas A, Montagnoli A., 2006, "Optimal Monetary Policy and Asset Price Misalignments". Scottish Journal of Political Economy, 53(5), 636–654.
DOI:10.1111/sjpe.2006.53.issue-5 |
| [] |
Marcellino M, Sivec V., 2016, "Monetary, fiscal and oil shocks:Evidence based on mixed frequency structural FAVARs". Journal of Econometrics, 193(2), 335–348.
|
| [] |
Nisticò S., 2006, "Optimal Monetary Policy and Financial Stability in a Non-Ricardian Economic". Journal of the European Economic Association, 14(5), 1225–1252.
|
| [] |
Svensson, Lars E. O., 2010, "Inflation Targeting after the Financial Crisis". Speech Prepared for the Reserve Bank of India's International Research Conference.
|
| [] |
Svensson L E O., 1997, "Inflation forecast targeting:Implementing and monitoring inflation targets". European Economic Review, 41(6), 1111–1146.
DOI:10.1016/S0014-2921(96)00055-4 |
| [] |
Stock J, Watson M., 1989, "New Indexes of Coincident and Leading Economic Indicators". NBER Macroeconomics Annual, 351, 393.
|




