在2007年底美国次级贷款危机爆发前,全球经济经历了一个高增长、低通胀的“大缓和”时代。长期的低利率与宽松的信贷环境使得金融市场高速发展,资产价格不断走高。作为中央银行对宏观经济进行调控的重要手段,传统的货币政策以产出与价格水平为核心决策变量,并未对金融市场给予过多的关注。但是,以稳定通胀和产出为政策目标的各国央行却忽视了不断累积的金融风险。危机之前,经济高速增长,价格水平保持稳定,而与之相伴的信贷扩张以及资产价格飙升却没有得到货币当局应有的重视,金融市场的过度繁荣使得风险不断积累并最终导致危机爆发。这一点无论是在2008年的美国次级贷款危机,还是在1997年的亚洲金融风暴当中都体现地尤为明显。
随着金融市场的不断深入发展,金融体系在货币政策的传导过程中也发挥着日益重要的作用。货币政策除了能够对宏观经济产生直接的影响之外,还会通过金融系统间接传导到实体经济。当金融体系运行稳定时,金融市场资源配置效率较高,货币政策通过金融市场影响实体经济的效果较好。而当金融市场出现剧烈波动时,货币政策往往无法通过金融渠道对宏观经济进行调控。此外,中央银行进行政策调控的有效性在很大程度上取决于其对于未来经济形势的预判,如果预期资本市场的波动会影响产出和通胀,那么金融体系的运行状况就为政策制定者提供了重要的信息,将金融稳定纳入货币政策规则就成为了央行自然的选择。
因此,为了考察拓展的泰勒规则在我国的适用性、准确刻画货币当局的实际政策操作,后文安排如下:首先对该领域内相关文献进行回顾。随后构建我国金融稳定指数。之后通过线性模型对比分析传统货币政策规则与包含金融稳定目标的货币政策规则。最后,本文将金融稳定目标加入货币政策框架,利用包含随机波动率的时变参数向量自回归(TVP-SV-VAR)模型考察金融稳定与规则性货币政策的动态关联机制并给出政策建议。
二、相关文献回顾目前有关金融稳定与规则型货币政策之间关联机制的研究正在深入进行,其主要围绕如下三个方面展开:(1)次级贷款危机之后政策制定者对金融稳定以及传统货币政策的反思与总结;(2)对于金融稳定目标下规则型货币政策的研究;(3)规则型货币政策的估计方法及其演变过程。
传统的观点认为,货币政策的核心是稳定价格水平和产出,因此不应该对金融市场或资产价格给予过多的关注。一方面,中央银行无法准确判断金融市场的具体运行状况(Bean,2004);另一方面,央行也缺乏直接干预金融市场与资产价格的政策工具(Mishkin,2001)。而在本轮危机过后,研究者和政策制定者逐渐意识到金融体系对于货币政策的有效传导具有重要意义,大量研究表明资本市场能够通过财富效应以及资产负债表效应对货币政策的传导过程产生显著的影响(Gilchrist et al., 2002;徐宁等,2017)。而伴随着金融自由化和全球化的不断发展,货币政策与金融体系之间的关联机制开始发生悄然转变,金融不稳定也直接地影响到货币政策向实体经济的传导过程(Smets,2014)。Borio (2014)的研究结果进一步表明,金融稳定是货币稳定的重要组成部分,金融体系的波动与不稳定会通过投资以及消费等宏观经济变量的传导作用削弱货币政策的调控效果,因此货币政策有必要对金融市场的稳定状况给予关注。针对金融体系的不稳定性,余辉、余剑(2013)采用时变参数状态空间模型构建了我国金融状况指数,其研究结果表明金融状况不仅包含了未来的宏观经济信息,同时也能够对通胀做出有效的预测,金融市场的运行状况在很大程度上成为了通货膨胀和实体经济运行的指示器。因此,货币当局应当适当关注金融稳定对货币政策传导的影响以提升货币政策的有效性。
鉴于传统的货币政策框架已不能满足当前经济形势和金融环境的要求,金融稳定开始逐渐步入货币当局的决策视野。早期文献大多认为货币政策中可以考虑纳入资产价格等单一变量。例如,伍戈(2007)利用Bordo-Jeanne理论框架分析了美联储在资产价格膨胀背景下的货币政策操作,同时结合我国金融系统运行状况指出,资产价格不但能够作为货币政策的传导渠道,同时其本身也可以作为货币政策的调控目标。不过,由于资产价格难以衡量金融市场整体的运行状况,研究者的焦点逐渐转向合成金融稳定指数并考察其对货币政策传导的影响(戴国强、张建华,2009;Sousa et al., 2011)。而在本轮危机过后,政策制定者逐渐意识到价格水平稳定并不一定导致金融稳定(雷蕾、彭孙琥,2016),并进一步在价格稳定与金融稳定的双重视角下重新审视现有的货币政策框架。Woodford (2012)的研究表明,金融市场运行状况不仅会对货币政策的传导产生影响,其也蕴含着未来宏观经济走势的重要信息,盯住金融状况的货币政策能够有效纠正金融市场失衡以避免实体经济出现剧烈波动。持相似观点的研究还包括Teranishi (2012)以及Kafer and Benjamin (2014)等。马勇等(2017)的研究结果表明,包含金融稳定的货币政策不仅有助于保持宏观经济与金融体系的双重稳定,同时其在危机时期能够有效对冲金融冲击对实体经济所产生的不利影响。而相关的经验研究也表明各国央行在实施货币政策时的确对金融系统的运行状况有所关注,金融稳定在一定程度上已经成为了中央银行的决策变量(Albulescu et al., 2013;Cukierman,2013)。
与此同时,研究者也开始尝试从福利增进的视角论证将金融稳定目标加入货币政策的合理性,Agur and Demertzis (2010)从商业银行风险承担的角度出发对这一问题进行了考察,其理论模型显示,仅关注价格水平的货币政策虽然在短期内能够保持通货膨胀的稳定,但是也会忽视金融体系内不断积累的风险,并导致长期更高的福利损失。而马勇(2017)的研究从中央银行的福利损失函数出发,推导出最优货币政策规则,论证了利率规则中关注金融稳定状况的合理性。
就研究方法层面而言,Taylor (1993)通过一个简洁的线性模型刻画了美联储的货币政策操作,这即是著名的“泰勒规则”。后续研究也一般采用线性模型对泰勒规则进行估计。不过,由于金融系统具有天生的不稳定性,资本市场的周期运行表现出缓升陡降的非对称特征。特别是我国资本市场频繁受到宏观经济政策的干预,这导致金融市场往往在短期发生大幅波动。在此背景下,中央银行自然需要随着金融状况与宏观经济形势的更迭不断调整货币政策,表现在利率规则上即是对不同核心政策变量的非对称调整(王少林,2015)。在这种情况下,采用传统的常系数模型对参数进行估计存在较大的困难和障碍,研究者开始采用非线性模型对问题展开研究。Castroa (2011)通过平滑迁移模型研究发现,欧洲央行在实施货币政策时考虑了金融状况,而美联储与英格兰银行则不然,这一差异可能正是导致美国房地产市场出现危机并迅速传导至英国的重要原因。国内学者的研究同样表明,中央银行在执行货币政策时不仅具有非线性的特征,同时,相比于传统的泰勒规则,纳入金融稳定的非线性货币政策规则能够更好地拟合货币当局的实际政策操作(耿中元等,2016;徐国祥、郭建娜,2017)。
对比现有文献,本文主要贡献体现在以下两个方面:首先,国内外大部分研究对于金融稳定状况的衡量都侧重于资产价格方面,维度比较单一。而本文构建的中国金融稳定指数包含23个指标,涵盖4个维度,能够更加全面地刻画我国金融稳定状况。其次,目前对于这一领域的非线性方法多集中在平滑迁移模型以及马尔可夫区制转移模型。但是这些模型并无法准确刻画货币政策规则在不同时点的动态调整过程。而时变参数模型改进了以往传统非线性模型的局部线性缺陷,能够更加准确地识别货币当局的实际政策操作,捕捉到货币政策规则与金融稳定之间的动态关联机制。
三、中国金融稳定指数的构建 (一) 指标选取与数据预处理本节将构建一个包含金融发展程度、宏观经济形势、金融市场运行状况以及世界经济形势四个维度、二十三个指标的金融稳定指数,指标选取的标准主要参考Albulescu (2010)以及IMF (2011)。
金融发展程度包括4个指标:信贷余额/GDP、债券市值/GDP、保费收入/GDP以及股票市值/GDP,这些指标可以全面地衡量银行业、股票市场、债券市场与保险业的发展状况。这4个指标对金融稳定均具有正向影响。
宏观经济形势包含5个指标:通货膨胀率、财政赤字/GDP,经常账户赤字/GDP,短期外债/外汇储备以及GDP增长率。这些指标可以较好地刻画我国宏观经济的运行状况,其中除去GDP增长率对金融稳定具有正向影响外,其余指标均对金融稳定指数具有负向影响。
金融市场运行状况包括8个指标:存款/M2、银行不良贷款率、贷款/存款、(准备金/存款)/(M0/M2)(该指标分子反映商业银行对挤兑风险的应对能力,分母反映经济中的流动性偏好)、银行间7天同业拆借利率(该指标越高,说明市场流动性越紧张)、证券市场平均换手率(该指标能够衡量股票市场的流动性)、汇率波动率以及国房景气指数(该指标越高,表明房地产市场过热,资金难以流入实体经济)。其中,存款/M2、(准备金/存款)/(M0/M2)以及证券市场平均换手率对金融稳定具有正向作用,其余指标均对金融稳定具有负向影响。
世界经济形势包括6个指标:世界经济增长率、世界通货膨胀率、石油价格指数、伦敦同业拆借利率、实际美元指数以及世界经济景气指数。其中,世界经济增长率、实际美元指数以及世界经济景气指数对金融稳定具有正向影响,其余指标对金融稳定具有负向影响。
以上23个指标的来源为Wind数据库、银监会网站、IMF以及CESifo。数据起止时间为2003年第2季度至2017年第3季度,数据均为季度数据。为了消除数据中包含的季节因素,所有数据均首先通过X12方法进行季节调整。随后通过Min-Max标准化方法对数据进行标准化处理,具体公式如下,
| $ {I^s_{it}} = \frac{{{I_{it}} - Min\left({{I_i}} \right)}}{{Max\left({{I_i}} \right) - Min({I_i})}} $ | (1) |
上式中,Iits代表指标i在时期t标准化之后的值,Iit代表指标i在时期t标准化处理前的值,Max(Ii)代表指标i在样本区间内最优的值,Min(Ii)代表指标i在样本区间内最差的值。具体而言,对金融稳定状况具有正向影响的指标,最优值指的是其在样本区间内的最大值;而对于与金融稳定状况呈负相关的指标,最优值指的其是在样本区间内的最小值。进行标准化处理的主要目的是防止正负指标之间相互抵消。标准化处理后的数据均落在[0,1]区间,数值越大,代表金融稳定程度越高。
(二) 中国金融稳定指数的合成本节在上一节的基础上,采用因子分析法合成金融稳定指数FSI。首先对数据进行Bartlett以及KMO检验,检验结果显示Bartlett检验sig值为0.00,小于0.01的显著性水平。同时,KMO值为0.704,大于0.6。这表明之前选取的金融稳定指标能够进行因子分析。随后构建因子分析模型,提取出方差贡献度较高的因子对中国金融稳定指数进行合成。本文通过最小平均偏相关法提取前6个因子,模型结果显示,提取的因子累计方差贡献率超过85%,仅有少量信息丢失,模型估计效果较好。最后,以各个因子的方差贡献率为权重,通过加权平均法合成金融稳定指数。表 1显示了各因子的特征值以及方差贡献。篇幅所限,因子载荷矩阵未列出,备索。
| 表 1 因子特征值与方差贡献 |
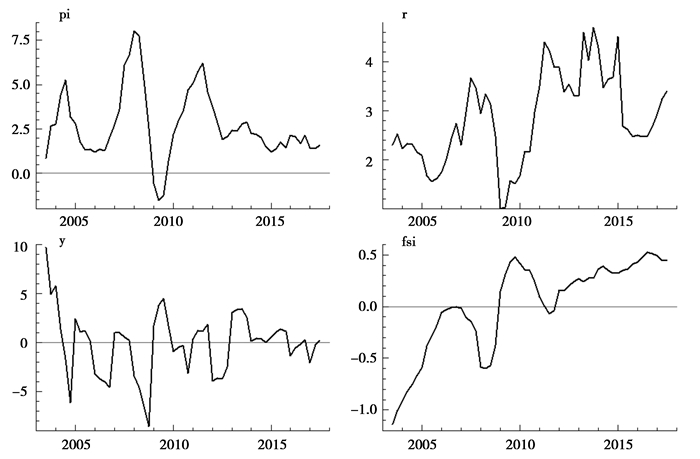
图 1显示了本文合成的金融稳定指数,可以发现我国金融稳定指数总体上处于稳步上升的趋势,特别是2003年至2006年,其间中国人民银行通过汇金公司向中国建设银行、中国工商银行以及中国银行进行注资,同时四大国有资产管理公司对银行坏账进行收购和剥离,商业银行不良贷款率显著下降,我国金融风险得到了极大程度的缓解。同时,伴随着证券业和保险业等产业的迅速发展,我国金融体系市场化程度也在不断加深,而财政收入与外汇储备的稳步增长也为我国抵御外部风险构筑了坚实的防线。这表明,随着我国金融市场的不断发展以及金融体系改革的不断深入,我国的金融稳定状况有了长足的提升。但是,我国金融稳定指数在2008年与2011年左右也出现了一定程度的下跌,其中2008年下滑幅度较大,这主要是由于美国次贷危机对全球经济造成了巨大的冲击,我国宏观经济运行出现较大的下行压力,此外,在此期间我国股票市场出现大幅波动,资产价格剧烈震荡,金融系统的稳定性也受到了一定程度的削弱。而2011年国内资金面持续紧张,银行间利率持续攀升,对金融市场情绪产生了负面影响。与此同时,欧债危机全面爆发,内外部冲击结合导致我国金融稳定状况受到一定程度的不良影响。总体而言,本文合成的金融稳定指数能够较好地拟合我国金融系统的运行状况,同时也可以捕捉到重大外部冲击对我国金融稳定状况的影响,因而具有较好的适用性,能够用于下文的实证分析。
|
图 1 通货膨胀率、名义利率、产出缺口以及金融稳定指数 |
在传统的泰勒规则中,中央银行根据产出缺口和通货膨胀率对名义利率进行调整,即名义利率由下式决定:
| $ i_t^* = {\beta _0} + {\beta _1}\left({{\pi _t} - {\pi ^*}} \right) + {\beta _2}{y_t} $ | (2) |
上式中,it*代表均衡利率,πt代表通货膨胀率,π*代表目标通货膨胀率,yt代表产出缺口,β0代表常数项,β1和β2分别代表通胀和产出的调整系数。
不过,(2)式中假定货币当局会对名义利率进行即时的调整,而Clarida et al. (2000)指出,货币政策的短期大幅调整将削弱中央银行的政策可信度,因此其在泰勒规则当中引入了货币当局的平滑意愿:
| $ {i_t} = \left({1 - \rho } \right)i_t^* + \rho {i_{t - 1}} + {\mu _t} $ | (3) |
其中,ρ代表平滑系数,该系数越大,表明中央银行对利率的调整越依赖于上一期的利率。将(2)式代入(3)式可以得到:
| $ {i_t} = \left({1 - \rho } \right)\left[ {{\beta _0} + {\beta _1}\left({{\pi _t} - {\pi ^*}} \right) + {\beta _2}{y_t}} \right] + \rho {i_{t - 1}} + {\mu _t} $ | (4) |
进一步化简得到:
| $ {i_t} = c + {\beta _\pi }{\pi _t} + {\beta _y}{y_t} + \rho {i_{t - 1}} + {\mu _t} $ | (5) |
式(5)即为传统的泰勒规则(以下简称为模型1)。
进一步地,将金融稳定目标fsit纳入中央银行的货币政策框架式(2),并同样按照上述(2)式至(5)式的推导过程即得到纳入金融稳定指数的泰勒规则(以下简称为模型2):
| $ {i_t} = c + {\beta _\pi }{\pi _t} + {\beta _y}{y_t} + {\beta _f}fs{i_t} + \rho {i_{t - 1}} + {\mu _t} $ | (6) |
本文中数据包括2003年第2季度至2017年第3季度的名义利率、通货膨胀率、产出缺口以及金融稳定指数。利率反应了金融市场中使用资金的成本,发达国家往往采用国债利率作为基准利率,但是我国国债市场规模较小,市场化程度不高,因此现有研究一般选取7天银行间同业拆借利率作为代理变量,并以各月交易量为权重,将月度数据加权平均为季度数据。通货膨胀率选取中国居民消费价格指数CPI作为代理变量,并将各月CPI数据的算术平均值作为季度CPI。最后通过公式πt=(CPIt-100)×100%,得到季度通货膨胀率。产出缺口计算过程如下,首先利用实际GDP累积同比增长率和2000年的名义累积GDP计算出以2000年为基期的实际累积GDP。随后将实际累积GDP转化为实际季度GDP。然后利用X12季节调整方法剔除实际季度GDP当中的季节成分。最后通过HP滤波方法测算出潜在产出Yt*,并通过公式yt=100×ln(Yt/Yt*)得到产出缺口。以上所有数据均来源于Wind数据库。金融稳定指数上一节已经做过介绍,不再赘述。
之后对变量的平稳性进行检验,ADF检验结果显示,各个变量的水平值均不是平稳时间序列,但是所有变量在一阶差分之后均在5%的显著性水平下为平稳时间序列,即各变量均为一阶单整序列。随后对变量进行协整检验,迹检验和最大特征根检验结果均表明变量之间存在协整关系,因此无需对数据进行进一步处理,可以直接利用原始数据进行建模,相关检验结果备索。图 1中分别显示了本文建模利用的名义利率、通货膨胀率、产出缺口以及金融稳定指数等数据。后续TVP-SV-VAR模型使用的数据与OLS模型相同,下文不再赘述。
(三) 包含金融稳定指数泰勒规则的再估计在利用TVP-SV-VAR模型对问题进行分析之前,本文首先通过OLS方法对泰勒规则进行估计,同时为了解决模型中可能存在的内生性问题,本文也报告了GMM的回归结果。表 2分别列出了模型1和模型2的估计结果。模型1中未加入金融稳定指数,可以看到OLS与GMM估计中利率平滑系数与通胀反应系数均显著,但是产出缺口反应系数不显著,GMM估计结果中各个系数的估计值存在一定变化,不过系数估计值的符号方向均未发生改变。而在加入金融稳定指数的模型2中,所有变量估计结果的显著性相比于模型1均有一定改善,而且无论是通过OLS估计还是GMM估计,新加入的金融稳定指数估计结果均显著为正,这也表明金融稳定与名义利率之间的正相关关系较为稳健。同时,相比于模型1,包含金融稳定的货币政策规则能够更好地拟合中央银行的货币政策操作,不论采用哪一种估计方法,模型2的拟合优度均显著提高。这表明,在纳入金融稳定指数的泰勒规则中,利率不仅能够对产出缺口和通货膨胀做出更好的反应,同时也可以较好地对金融稳定状况进行调控,中央银行在制定和执行货币政策时,不但关注价格水平与产出缺口,同时也力图维持金融领域的稳定和平衡。此外,在模型1和模型2中,利率平滑参数均大于0.6,且高度显著,这表明中央银行对名义利率的调整存在显著的平滑特征。
| 表 2 线性泰勒规则估计结果 |
不过,虽然加入金融稳定因素的泰勒规则对通胀的反应有了明显的改善,但是无论采用何种估计方法,模型1以及模型2中通胀调整系数均小于1,这表明我国的货币政策并不稳定。当通货膨胀上升时,名义利率也会提高,但是上升幅度小于通货膨胀。这导致实际利率下降,并进一步刺激总需求,从而造成价格水平的进一步上升。而当价格水平下降时,名义利率向下调整,但是下降幅度小于通胀,因此导致实际利率上升,抑制总需求,并进一步加剧通货紧缩风险。
模型2中新加入的金融稳定指数系数估计值显著为正,且产出和通胀反应系数有了显著的提高。这一方面说明中央银行在执行货币政策时对金融稳定状况有所关注。另一方面也表明,相比于传统的泰勒规则,包含金融稳定因素的货币政策中利率规则值往往更高。这与马勇(2013)的研究结果相同,其中的原因主要在于,中央银行的货币政策操作不仅会对实体经济产生重要影响,同时也改变了整个金融体系的风险承担(risk taking)倾向。忽视金融稳定的货币当局往往制定相对较低的名义利率,这导致金融机构的风险偏好发生改变并进一步催生资产价格泡沫。因此,资产价格等金融变量实际上反映了金融中介部门的风险偏好。而关注金融稳定的中央银行需要制定一个更高的利率水平以对冲金融机构过度的风险承担,以保证中长期内金融市场的稳定。如果中央银行在执行货币政策时仅仅考虑产出缺口和通货膨胀,那么将会导致名义利率出现系统性的低估,这一方面刺激金融机构提高其风险偏好,同时也为长期的系统性风险与金融不稳定埋下了隐患。
五、引入金融稳定指数货币政策的时变反应机制分析 (一) 非线性检验前文的文献综述部分表明,在金融系统不稳定的背景下,如果采用普通常系数模型可能会造成模型设定误差,无法捕捉到变量之间的动态关系。而在利用非线性模型对问题展开分析之前,有必要首先对变量之间的非线性关系进行检验。同时,为了保证结果的稳健性,本文分别采取参数方法(RESET检验)和非参数方法(BDS检验和Ljung-Box检验)进行分析。首先通过VAR模型去除变量之间存在的线性成分,随后利用剩余残差进行非线性检验。检验结果在表 3中,可以看到,除去利率残差的Ljung-Box检验以及通胀残差的RESET检验之外,其余结果均通过非线性检验。因此,无论是哪种检验方式,均拒绝变量之间存在线性关系的原假设。
| 表 3 VAR模型回归残差非线性检验结果 |
而就非线性模型的选择而言,可以选择门限模型、平滑迁移模型以及马尔可夫区制转移模型,不过这些模型均假定变量之间的关联机制具有一定的跃迁特征。而在实际的政策操作中,为了避免政策在短期内大幅调整对其公信力产生影响,中央银行的政策转变是一个渐进的动态调整过程。因此上述非线性模型并无法全面刻画变量之间关系的时变特征,从这个角度出发,本文选择TVP-SV-VAR模型对问题展开研究。
(二) 金融稳定视角下时变参数模型的构建与模型参数估计为了准确刻画变量之间的非线性关系,灵活反映中央银行对产出缺口、通货膨胀和金融稳定的调控偏好,识别了不同时期货币当局的核心政策目标。本文在前文非线性检验的基础上,将名义利率、产出缺口、通货膨胀与金融稳定指数纳入统一模型,采用TVP-SV-VAR方法对问题展开研究。TVP-SV-VAR模型由结构向量自回归模型发展而来,其假定模型中所有参数均随时间发生变化。鉴于该模型研究比较成熟,本文在此不再对模型展开具体叙述,模型的具体细节与进一步阐述参考Primiceri (2005)和Nakajima (2011)。
在进行模型估计之前,本文首先参照Nakajima (2011)的研究结论对TVP-SV-VAR模型的时变参数初始值进行设定。具体而言,分别设定
表 4中显示了参数具体估计结果。其中Geweke统计量和无效因子均是判断模型估计效果的重要指标,其中前者用于衡量马尔科夫链的收敛性,后者则用于计算模型模拟所产生的不相关样本个数。从表 4中可以看出,所有参数估计结果的无效影响因子均较小,即使以最大的89.15计算,也至少可以产生10000÷89.15≈112个不相关样本,这已经足够进行有效的后验推断。综合考虑上述两个指标,本文模型估计结果较为良好。
| 表 4 模型参数估计结果 |
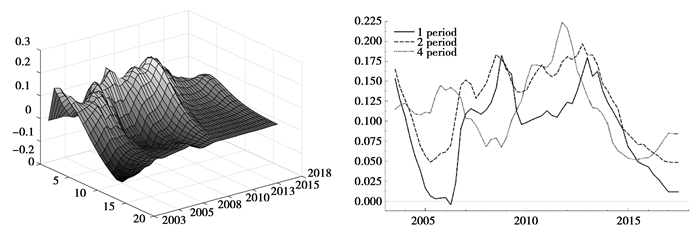
利用TVP-SV-VAR模型能够生成两种不同类型的脉冲响应函数,分别为时点脉冲响应函数和等间隔脉冲响应函数。图 2至图 4显示了通胀、产出缺口与金融稳定冲击对利率的全时点三维立体图。在右侧横轴不同时期取截面,可以得到不同时期的时点脉冲响应函数,时点脉冲响应函数指的是因变量在特定时点受到一单位外生冲击后的响应函数,同时时点可以根据研究的需要灵活选择。而在左侧横轴不同滞后时期取截面,可以得到不同滞后时期的等间隔脉冲响应函数,等间隔脉冲响应函数指的是因变量在受到一单位外生冲击后,在相等时间间隔后的脉冲响应,其可以详尽刻画整个样本区间内因变量对外生冲击的反应,捕捉到经济系统中的结构性变化。综合对比分析两种脉冲响应函数,有助于理解我国名义利率的动态调整过程,分析货币当局实际政策操作与政策取向。
|
图 2 名义利率对产出缺口冲击的脉冲响应函数 |
|
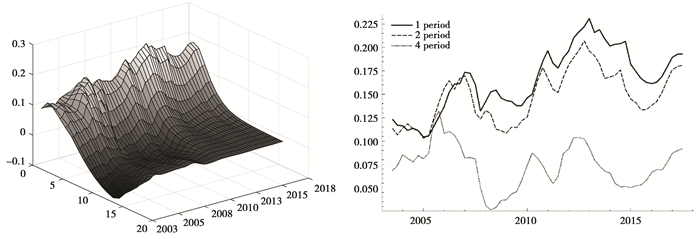
图 3 名义利率对通货膨胀冲击的脉冲响应函数 |
|
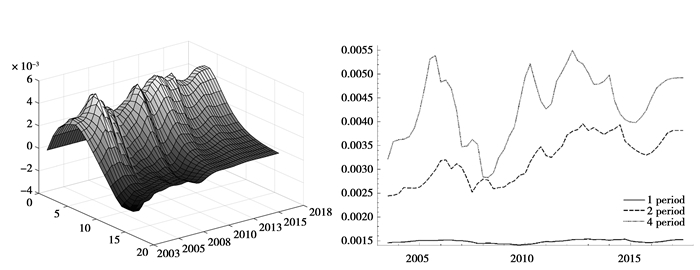
图 4 名义利率对金融稳定冲击的脉冲响应函数 |
图 2至图 4分别显示了产出缺口、通货膨胀以及金融稳定对名义利率的全时点三维立体图以及等间隔脉冲响应函数。图中,实线、长虚线与短虚线分别代表短期(滞后1期)、中期(滞后2期)与长期(滞后4期)的脉冲响应函数。可以看到,三者对货币政策的冲击均具有显著的时变性特征。同时,三组响应函数走势比较一致,说明模型估计结果较为稳健。
利率对产出缺口的三条脉冲响应函数均位于零线上方,这表明我国的货币政策能够有效稳定产出,当实际产出高于潜在产出时,利率上升抑制总需求,从而防止产出缺口的进一步扩大,而当实际产出低于潜在产出时,利率会下降刺激总需求,从而减小产出缺口。此外,产出缺口对利率的冲击效果在2008年和2014年两个时间节点出现了阶段性峰值,而这两个时点也对应我国宏观经济的收缩时期。2007年底美国次级贷款危机爆发,危机迅速蔓延并对世界各国经济产生重要影响。面对危机,我国政府迅速出台措施防止经济进一步下滑,中国人民银行在2008年下半年连续5次降息,其频率和幅度均创历史水平。此后在2011年至2013年的后危机时代,名义利率对产出缺口的响应函数始终在高位盘桓,这表明货币当局对于整个宏观经济的全面复苏仍然持谨慎态度,名义利率在很大水平上仍然盯住产出缺口。而在经济步入“新常态”之后,我国面临经济结构调整的阵痛期,在去产能和去杠杆的大背景下,宏观经济运行呈现出明显的收缩态势,此时货币当局的偏好再次转向产出缺口,利率对产出缺口的响应函数又一次呈现上升态势。不难发现,货币当局对名义利率的调整具有显著的反周期特征,当经济出现下行压力时,中央银行对货币政策的调整会向产出缺口倾斜,增加对货币政策的调整力度。
就通货膨胀而言,中央银行对其的调控较为稳健,通胀对名义利率的冲击效果始终维持在较高水平。在2007年之前,我国经济发展处于高速扩张阶段,GDP年均增速超过10%,而通货膨胀率也有抬头的倾向,因此中央银行并未对产出缺口给予过多的关注,而是主要依据通货膨胀对名义利率进行调整,在此阶段,名义利率对通货膨胀的响应保持在较高的水平。不过,利率对通胀的响应在2008年左右出现了阶段性的下降,其中的原因主要在于,次贷危机对我国经济造成了巨大的冲击,因此货币当局核心政策目标转换为产出缺口,提高了对通货膨胀的容忍程度。尽管如此,相比于产出缺口,名义利率对通货膨胀的脉冲响应函数波动幅度明显较小。这说明治理通货膨胀始终是货币当局的工作重心,毕竟,宏观经济的健康稳定发展是各个部门联合发力的结果,而如果一国价格水平在短期发生大幅度的波动,则中央银行难辞其咎。
图 4显示了利率对金融稳定的响应函数,可以看到,金融稳定对名义利率的冲击效果显著为正,这也与上文OLS模型的估计结果相一致。当金融稳定指数提高时,利率规则值也会随之上升以对冲金融机构过度的风险承担,抑制金融市场过度繁荣。而当金融稳定指数下降时,货币当局会下调名义利率并放松银根,以防止市场出现流动性紧张。同时,货币政策对金融稳定的调控机制存在显著的时变性特征,其脉冲响应函数走势与通货膨胀水平高度耦合。这表明,相比于低通货膨胀时期,货币当局在高通货膨胀时期更加关注金融稳定状况。这也较为符合理论,因为较高的价格水平正是导致金融系统不稳定的原因之一。而在2008年之后,脉冲响应函数始终处于高位,说明中央银行在此次金融危机之后明显加强了对金融稳定状况的关注。此外,金融稳定的波动对名义利率的影响具有显著的时滞性,在图 4中表现为长期脉冲响应函数显著高于短期脉冲响应函数。不过,通过对比图 2至图 4中的纵坐标可以发现,相比于产出缺口和通货膨胀,金融稳定对名义利率的冲击效果较小。这表明尽管货币当局对金融市场的运行状况有所考虑,但是其在中央银行的决策中所占权重较小,目前阶段货币当局的核心政策变量主要还是产出缺口与通货膨胀。
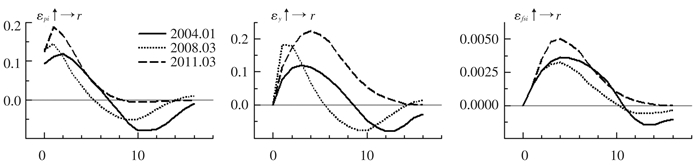
图 5显示了产出缺口、通货膨胀以及金融稳定对名义利率的时点脉冲响应函数,本文选取时点为2004年第1季度、2008年第3季度与2011年第3季度,分别代表我国经济高增长低通胀、低增长低通胀以及高通货膨胀的三种运行状况。
|
图 5 时点脉冲响应函数 |
估计结果表明,无论是产出缺口、通货膨胀还是金融稳定对名义利率的冲击均表现出较为明显的时变特征,同时脉冲响应函数均呈现出先上升后下降最终收敛至稳态的驼峰状形态。首先,一单位正向通胀冲击导致名义利率上升,同时在高通货膨胀时期(2011年第3季度),冲击对利率的冲击效果更为显著。其次,正向产出冲击同样导致央行提高名义利率,而相比于经济高速增长时期(2004年第1季度),当经济存在较大下行压力时(2008年第3季度和2011年第3季度)冲击效果较为显著。这说明货币当局存在明显的规避经济收缩的偏好,当实际产出低于潜在产出时,其会增加对产出缺口的关注。最后,利率对金融稳定的脉冲响应显著为正,同时冲击效果在2008年次贷危机过后更为显著。这表明金融危机之后央行的政策取向发生一定程度的转变,其对金融稳定目标进行了适当的关注。
综合而言,中央银行对于名义利率的调整并不是一成不变的,随着经济周期和金融稳定状况的更迭,中央银行也会不断动态调整其核心政策目标。同时,无论是对于利率上调期(2005年至2007年、2009年至2011年)还是利率下调期(2008年、2013年至2015年),引入金融稳定的时变参数泰勒规则均能够较好地拟合我国名义利率的演变过程。这表明,中央银行在制定和执行货币政策时,不但关注价格水平与产出缺口,同时也力图维持金融领域的稳定和平衡。
六、结论与政策涵义在当今经济金融体系中,货币政策与金融稳定之间的联系不断深化,中央银行理应在防范金融市场系统性风险当中发挥重要的作用,本文正是以此为切入点对问题展开研究,并得到以下研究结论:(1)中央银行的确对金融稳定状况有所关注,相比于传统泰勒规则,纳入金融稳定指数的泰勒规则中,通胀系数与产出缺口系数均有显著改善,其也能够更好地拟合中央银行的实际政策操作;(2)金融稳定会对名义利率产生显著的正向冲击,当金融稳定指数提高时,利率规则值也会随之上升以对冲金融机构过度的风险承担,抑制金融市场过度繁荣。此外,金融稳定冲击效果在次级贷款危机过后更为显著,说明货币当局在本次金融危机之后显著增强了对金融稳定目标的关注;(3)在样本期间内,通货膨胀波动对利率的冲击效果并未发生较大变化,表明货币政策对通货膨胀的调控不存在明显的惰性区域,控制通胀始终是中央银行工作的重心。同时,中央银行存在规避经济收缩的偏好,在经济下行时期其对货币政策的调整会向产出缺口倾斜。
基于以上结论,本文得到如下的政策启示:首先,忽视金融稳定因素的货币政策有可能导致金融失衡与系统性风险。中央银行应当优化货币政策目标体系,加强金融稳定与宏观审慎监管,并着力构建包含金融稳定的货币政策框架,弱化金融市场的顺周期属性。其次,鉴于单一变量往往无法综合反映金融市场的整体运行状况,因此可以考虑构建我国金融稳定指数,这不仅有助于实时监控识别金融体系的系统性风险,也有利于货币当局及时采取反周期调控和动态预防措施。最后,我国利率长期处于管制状态,利率水平并不能完全由市场竞争所决定。虽然近些年放开了对于存贷款利率的限制,但是利率市场还是频频受到政策的掣肘。因此,政府应该继续推进利率市场化进程,完善货币政策传导机制,为规则型货币政策营造更为良好的政策环境。
| [] |
戴国强、张建华, 2009, “中国金融状况指数对货币政策传导作用研究”, 《财经研究》, 第 7 期, 第 52-62 页。DOI:10.3969/j.issn.1001-9952.2009.07.005 |
| [] |
耿中元、李薇、翟雪, 2016, “基于金融稳定的非线性泰勒规则——中国的经验证据”, 《经济理论与经济管理》, 第 9 期, 第 12-24 页。DOI:10.3969/j.issn.1000-596X.2016.09.002 |
| [] |
雷蕾、彭孙琥, 2016, “价格稳定与金融稳定相关性研究——基于中国2002-2015年数据实证研究”, 《南方经济》, 第 2 期, 第 106-117 页。 DOI:10.3969/j.issn.1000-6249.2016.02.008 |
| [] |
马勇, 2013, “基于金融稳定的货币政策框架:理论与实证分析”, 《国际金融研究》, 第 11 期, 第 4-15 页。 |
| [] |
马勇, 2017, 《DSGE宏观金融建模及政策模拟分析》, 北京: 中国金融出版社。 |
| [] |
马勇、张靖岚、陈雨露, 2017, “金融周期与货币政策”, 《金融研究》, 第 3 期, 第 33-53 页。 |
| [] |
王少林, “双重时变'泰勒规则'在中国货币政策操作中的检验”, 《南方经济》, 第 6 期, 第 67-83 页。 |
| [] |
伍戈, 2007, “货币政策与资产价格:经典理论、美联储实践及现实思考”, 《南开经济研究》, 第 4 期, 第 90-105 页。DOI:10.3969/j.issn.1001-4691.2007.04.008 |
| [] |
徐国祥、郭建娜, 2017, “金融稳定目标下中国货币政策规则研究”, 《财经研究》, 第 10 期, 第 18-30 页。 |
| [] |
徐宁、刘金全、于洋, 2017, “理解我国名义利率传导机制有效性的时变特征——基于DSGE模型的理论分析与TVP-VAR模型的实证检验”, 《南方经济》, 第 7 期, 第 70-84 页。 DOI:10.3969/j.issn.1000-6249.2017.07.005 |
| [] |
余辉、余剑, 2013, “我国金融状况指数构建及其对货币政策传导效应的启示——基于时变参数状态空间模型的研究”, 《金融研究》, 第 4 期, 第 85-98 页。 |
| [] |
Agur, I. and Demertzis, M., 2010, "Excessive Bank Risk Taking and Monetary Policy", De Nederlandsche Bank Working Papers, No. 271.
|
| [] |
Albulescu C. T., 2010, "Forecasting the Romanian Financial System Stability Using a Stochastic Simulation Model". Romanian Journal of Economic Forecasting, 13(1), 81–98.
|
| [] |
Albulescu C. T., Goyeau D. and Pepin D., 2013, "Financial Instability and ECB Monetary Policy". Economics Bulletin, 33(1), 388–400.
|
| [] |
Bean C. R., 2004, "Asset Prices, Financial Instability, and Monetary Policy". American Economic Review, 94(2), 14–18.
DOI:10.1257/0002828041301795 |
| [] |
Borio, C., 2014, "Monetary Policy and Financial Stability: What Role in Prevention and Recovery?", BIS Working Papers, No. 440.
https://socionet.ru/publication.xml?h=repec:bis:biswps:440 |
| [] |
Castro V., 2011, "Can Central Banks' Monetary Policy Be Described by a Linear (Augmented) Taylor Rule or by a Nonlinear Rule?". Journal of Financial Stability, 7(4), 228–246.
DOI:10.1016/j.jfs.2010.06.002 |
| [] |
Clarida R., Gali J. and Gertler M., 2000, "Monetary Policy Rules and Macroeconomic Stability:Evidence and Some Theory". Quarterly Journal of Economics, 115(1), 147–180.
|
| [] |
Cukierman A., 2013, "Monetary Policy and Institutions Before, During, and After the Global Financial Crisis". Journal of Financial Stability, 9(3), 373–384.
DOI:10.1016/j.jfs.2013.02.002 |
| [] |
Gilchrist S., Leahy J. V., 2002, "Monetary Policy and Asset Prices". Journal of Monetary Economics, 49(1), 75–97.
DOI:10.1016/S0304-3932(01)00093-9 |
| [] |
IMF, 2011, "People's Republic of China: Financial System Stability Assessment", IMF Country Reports, No. 11/321.
|
| [] |
Kafer B., 2014, "The Taylor Rule and Financial Stability:A Literature Review with Application for the Eurozone". Review of Economics, 65(2), 159–192.
|
| [] |
Mishkin, F. S., 2001, "The Transmission Mechanism and the Role of Asset Prices in Monetary Policy", NBER Working Paper, No. 8617.
http://cn.bing.com/academic/profile?id=a884f09e783ee468c0c2b3a3dd80fee8&encoded=0&v=paper_preview&mkt=zh-cn |
| [] |
Nakajima J., Kasuya M. and Watanabe T., 2011, "Bayesian Analysis of Time-Varying Parameter Vector Autoregressive Model for the Japanese Economy and Monetary Policy". Journal of the Japanese & International Economies, 25(3), 225–245.
|
| [] |
Primiceri G. E., 2005, "Time Varying Structural Vector Autoregressions and Monetary Policy". Review of Economic Studies, 72(3), 821–852.
DOI:10.1111/j.1467-937X.2005.00353.x |
| [] |
Smets F., 2014, "Financial Stability and Monetary Policy:How Closely Interlinked?". International Journal of Central Banking, 3(2), 121–160.
|
| [] |
Sousa J., Gameiro I. M. and Soares C., 2011, "Monetary Policy and Financial Stability:An Open Debate". Banco de Portugal Working Paper, 17(1), 7–25.
|
| [] |
Taylor J. B., 1993, "Discretion versus Policy Rules in Practice". Carnegie-Rochester Conference Series on Public Policy, 39(1), 195–214.
|
| [] |
Teranishi Y., 2012, "Credit Spread and Monetary Policy". Economics Letters, 114(1), 26–28.
|
| [] |
Woodford, M., 2012, "Inflation Targeting and Financial Stability", NBER Working Papers, No. 17967.
https://www.nber.org/papers/w17967.pdf |



