系统性风险一直是金融领域的热点问题,尤其在2008年金融危机后各国对系统性风险愈加重视。对我国金融市场而言,银行业的不良贷款、影子银行业务以及房地产的风险积聚等诸多因素都可能成为系统性风险爆发的导火索,但危机事件的生成不代表系统性风险的必然发生,普通风险的潜移默化也可能会对金融市场的稳健发展产生灰犀牛效应。金融市场的内在运行机制对风险传染的控制能力才是实现个体风险向系统性风险转变的关键,因此从金融机构间的关联度视角分析金融风险的交叉传染对系统性风险的形成具有重要的理论和实践价值。
我国金融市场的发展一直以来都是以银行为主导的间接融资模式,在银行稳健经营的条件下爆发系统性风险的可能性较低。但随着金融市场化的改革以及新型金融公司的冲击,以影子银行、第三方支付为代表的金融创新结合了科技金融和模糊监管的双重优势而获得投资者的认可,直接冲击了银行的市场主导地位。为了挽回颓势,银行通过与证券、保险、基金、信托等多类金融机构的业务合作来增强市场的竞争力。作为金融市场中最为重要的金融机构,银行通过多元化合作提高资金流动性和回报率的同时延伸了金融服务的资金链,将金融风险由银行内部逐渐向金融市场转移,由此导致系统性风险更易于在风险管理相较薄弱的非银行金融机构中爆发,并通过信用传导的形式在金融体系中扩散。与此同时,经济领域下行压力和改革矛盾也以外部冲击的形式将风险积聚在金融体系的内部,多途径的金融风险来源以及风险的交叉传染方式使得金融风险的系统化趋势愈加明显。为了实现“不爆发系统性风险”的监管目标,本文选择从金融网络的角度分析金融机构的风险关联性和动态传染性对系统性风险的影响,希望能够提高金融机构风险管理的效率,增强金融市场的风险包容能力。
二、文献综述风险起源的多元化和传导过程的交叉重构会在金融系统内通过某一冲击的触发,以相继形式形成一种复杂的互动与反馈回路,继而威胁系统稳定与公众信任。如果将金融市场视为一个网络,将市场中的金融机构作为构成金融网络的微观主体,那么系统性风险就是关于微观主体承担负外部效应所导致的整体风险损失。在此过程中金融市场的中介职能混乱,不能引导金融体系及时有效地服务实体经济(胡海峰、代松,2012)。金融机构的关联性对系统性风险的影响途径主要有金融机构间的相互风险敞口、共同风险敞口、间接风险敞口和信息传染等四种方式(胡锡亮、吴恒煜,2016),在此过程中形成的风险传染的网状结构可以根据金融机构之间的金融创新、同业拆借、影子银行业务、金融衍生品等业务得到巩固和完善。两两关联的金融网络结构证明了系统性风险的大小不仅对个体金融机构的财务状态产生影响,也会对金融体系的稳健发展产生影响(Lenzu, 2012;Acemoglu et al., 2015)。风险传染作为系统性风险形成的主要方式,是将个体机构的违约或破产事件通过流动性、资产价格等因素的影响传染给健康的金融机构,同时也将破产风险延伸至整个金融体系,最终影响经济社会的正常运行(Kreis and Leisen, 2017; Aldasoro et al., 2016)。总结已有学者对此类问题的探讨主要有两种途径,一是从微观角度分析金融机构的关联度对系统性风险的个体贡献,二是从宏观角度分析金融网络的结构特征对系统性风险的影响。
微观视角的系统性风险研究已经取得较为丰富的成果。早期研究主要集中于金融机构的系统性风险贡献度分析,对金融机构之间的风险关联性和系统性风险形成的作用机制研究还不充分。近年来有学者针对上述问题进行了深入研究,李建军、薛莹(2014)从影子银行业务的视角证实了风险关联度可以通过业务往来中的会计账户渠道得以实现,并在市场心理和投资者选择的过程中被放大,逐步形成系统性风险。杨有振、王书华(2013)从分位数回归的CoVaR模型出发,分析单个银行的风险溢出效应对系统性风险的贡献率。梁琪等(2013)通过SRISK法计算金融机构破产对金融市场服务职能的影响。尽管学者们对系统性风险的研究角度、实证方法和研究结论都不尽相同,但他们都一致认为微观金融机构的风险管理体系对风险的包容能力可以对系统性风险产生显著影响,同时风险的溢出效应和系统性风险的测量应具有时变特征,对系统性风险的判断应考虑个体效应和时间效应。在此基础之上,李志辉等(2016)基于SCCA技术提出了风险相依结构的J-VaR指标,得出基于金融机构违约风险动态相依性的系统性风险评价指标。Drehmann and Tarashev(2013)基于Shapley法的广义贡献法(GCA)得出一个银行的系统重要性就是其对所有子系统的风险贡献的均值,其实证结果支持了银行间的风险关联性对衡量单个银行的系统重要性的关键作用。已有研究的局限性在于对系统性风险形成的微观传染机制还未能做出充分解释,同时没有考虑到非银行金融机构作为金融市场的参与方对系统性风险传染的冲击和影响,由此得出的系统性风险的特征偏颇,且不具有代表性。
在微观分析的基础之上,有学者从宏观视角将金融市场视为一个金融网络,将金融机构视为网络中的行动者,通过分析因网络行动者之间的投资、业务、信息关系所形成的相互影响、相互制约的风险传染结构对自身经营行为的差异化影响。张英奎等(2013)通过风险传染的动力学研究方法,仿真模拟并比较了不同金融网络的拓扑结构对系统性风险传染的差异化影响,但是仿真模拟模型对于关联矩阵的获取依赖作者对市场风险关系的专业判断,实证结果的客观性不足。Engle(2015)和Caballero(2015)通过对金融危机后系统性风险形成原因的分析,得出金融网络的关联度、中心度和凝聚度能够体现金融一体化发展的水平,并能解释系统性风险在金融市场中发挥重大影响力的原因。金融机构之间的风险传染随着网络体系复杂性与同质性的增加而增强,金融机构的风险反馈效应则会进一步增强这种网络风险传播,由此形成金融网络的动态结构。Daron Acemoglu et al. (2017)的研究证明了当负面冲击超过一定的阙值以后,原本使金融网络结构更加稳定的积极因素可能会转变成使系统性风险增强、金融市场不稳定的消极因素,从而使金融网络呈现既稳健又脆弱的结构特征,进一步证明金融市场的风险传染具有动态特性,同时强调了风险演变的历史阶段对风险管理策略的效用。王占浩等(2016)分析了资产价格的网络隐形传染对银行间风险传染的重要作用,并通过实证比较得出资产价格可以作为评估是否爆发银行系统性危机的重要参考指标,此结论为下一步的实证分析提供了数据选择的理论依据。总结已有文献关于风险传染的网络结构分析还处于理论模拟阶段,不能将我国金融市场的实际结构特征引入网络模型中,因此所得结论和建议不具有现实指导性。
针对上述不足,本文进行了如下创新:理论上,通过金融网络中关于风险传染的宏微观综合效用分析金融风险的微观基础和宏观传染结构对系统性风险的动态影响。在系统性风险的分析中考虑金融机构的业务关系导致的交叉性风险传染,将金融机构的破产行为从外生的金融冲击转化为内生的金融网络压力。实证中,通过DCC-MGARCH模型构建基于多元市场主体的动态条件相关的风险关联度分析,将金融机构间的关联度作为金融网络中的节点连接线,从风险传染的角度分析系统性风险的形成机制。
三、研究方法 (一) 理论分析大多学者认为金融机构的破产是系统性风险生成的起因。金融机构面对风险损失的策略首先是风险承担,如若资不抵债,则金融机构破产,风险外溢,导致其他相关金融机构承担这部分风险损失,其他金融机构重复上述过程形成破产风潮,最终导致系统性风险爆发。但本文认为金融机构的理性人思维将决定其对风险的态度是转嫁优于自我承担。加之宏观审慎监管要求不断提升,金融机构风险承担的现实压力也会促使金融机构通过业务合作和风险共担的形式降低自身承担的风险损失。
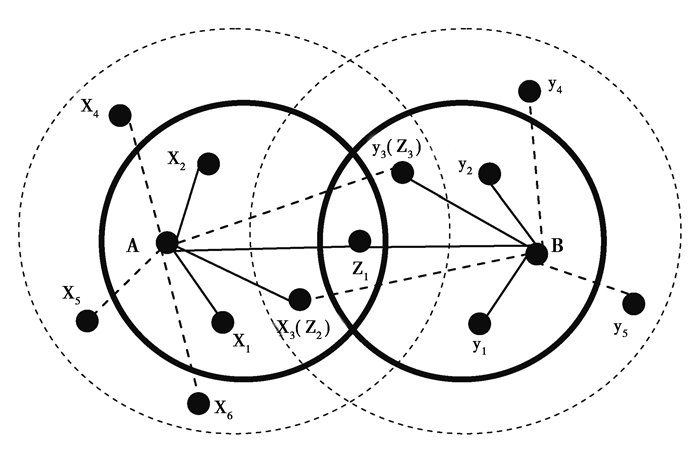
本文以出现违约风险的金融机构A、B为例,说明金融机构间的关联度对系统性风险的作用过程。金融机构通常会选择分散化投资来降低风险,但同时会增强风险在机构之间的转移和扩散能力。假设金融机构A、B共同投资的某一金融产品出现了违约,作为投资方的A和B出现了流动性风险R(A)、R(B),他们打算将比例为α的风险转移,剩余风险自行承担。
金融机构在寻求流动性支持时通常会选择周边熟悉的机构进行交易,这样能够有效控制资金成本。金融机构A选择的交易机构组合为X(x1、x2、…、xn)满足α*R(A)的流动性补充需求,金融机构B选择的交易机构组合为Y(y1、y2、…、ym)满足α*R(B)的流动性补充需求。金融市场的混业经营模式使得金融机构之间的联系是多重性的,因此假设组合X和Y存在一个重合的机构z1,且z1提供的流动性供给小于市场需求。对此,机构A和B的对策都是增加新的交易机构,补充流动性缺口,形成扩大了的交易机构组合X'(x1、x2、…、xn、xn+1、xn+2、…、xn+p)、Y'(y1、y2、…、ym、ym+1、ym+2、…、ym+q)。
对机构z1而言,可进行交易的流动性有两种分配方式:1.处于自我保护以及对于未来风险的谨慎估计,选择流动性囤积;2.与其他机构交易。假设金融机构提供的流动性是有限的,即金融机构的流动性总量不能同时满足自身和其他金融机构的需求总和。如果机构z1选择保证自身流动性的充足,则与其他机构交易的流动性则不能满足市场需求,A、B中可能存在流动性不足导致的资不抵债,进而机构破产。如果机构z1选择交易最大化,则自留的流动性不足,从而增加引致破产的可能性。当一家金融机构需要同时为两家金融机构提供流动性支持时,至少存在一家机构的风险补充将会减少,这将使原本无交叉关系的A、B机构因为z1形成了一个简单的网络。组合X'和Y'之间存在的重合机构也将扩大到z1、z2、z3,重复上述供给与需求的比较过程,可形成扩大的重合机构组合Z(z1、z2、…、zk)。重合机构的存在会增加流动性获取的不确定性,同时将机构A、B的风险扩大到对方的影响区域,实现了金融风险的区域性传导。
将机构A、B间的风险传导机制拓展到多个金融机构,可实现关于金融系统风险传染的网络型结构。通过金融机构之间的往来深入化,系统性风险的传染机制将更为复杂,个体风险的冲击通过流动性供求的网络化交易活动传递到金融市场的各个角落,最终形成不可抵消的系统性风险。金融机构在向市场转移个体风险的同时,作为金融市场的微观组成,也将遭受系统性风险的冲击,由此形成风险水平才是真正由金融机构个体承担。当金融机构不能承受风险损失,出现资不抵债的情况时,破产产生,此过程体现了金融机构破产的内生性。
|
图 1 系统性风险的形成机制 |
首先,构建关于金融机构动态关联度的DCC-MGARCH模型,获取机构间风险传染的动态相关性系数。MGARCH模型优于GARCH模型的原因在于包含了由多元变量时间序列的时变协方差矩阵,体现出关于市场信息的价值取向。考虑到模型构建的效率和可操作性,本文选择多元GARCH(1,1)模型作为实证的基础方程。然后,将金融机构之间的动态相关性系数作为风险关联度带入整体网,从网络密度的角度分析金融网络的风险关联性和传染机制对系统性风险的非线性影响。最后,根据金融机构在风险传染过程中的网络位置和中介作用,分析各类金融机构对系统性风险形成的贡献度,进而得出基于风险传染视角的系统性重要金融机构。模型构建的具体过程如下所述:
1.金融机构间的关联度构建
(1) 对数据进行“去GARCH化”处理,得到标准化残差和收益率的波动率。
rn, t是第n个金融机构在t时刻的股票对数收益率(以股票价格逐日变化表示金融机构承受的风险程度)
| $ {r_{nt}} = 100 * \ln \left({{p_t}/{p_{t - 1}}} \right)\left({{\rm{n}} = 1、2 \cdots \cdots } \right) $ | (1) |
将每个金融机构的对数收益率rnt按照股本比例∂i进行加权平均,求得各类金融机构的对数收益率rit和条件协方差矩阵Ht。
| $ {r_{it}} = \sum\limits_{n \in i}^{} {{\partial _i} * {r_{nt}}} \;\;\;\;\left({{\rm{i}} = 1、2 \cdots \cdots } \right) $ | (2) |
| $ {H_t} = {V_{t - 1}}({r_t}) $ | (3) |
由条件协方差矩阵Ht推出条件相关系数矩阵Rt、条件方差矩阵Dt2和标准化残差ui, t。
| $ {R_t} = D_t^{ - 1}{H_t}D_t^{ - 1} $ | (4) |
| $ D_t^2 = diag[{H_t}] $ | (5) |
| $ {u_{i, t}} = {e_{i, t}}{\rm{/}}\sqrt {{H_{i, i, t}}} $ | (6) |
(2) 通过均值回复模型得到似相关系数矩阵。
基于标准化残差ui, t,获得标准化收益序列的动态似相关系数矩阵:
| $ {Q_{i, j, t}} = \Omega + {\lambda _1} * {u_{i, t - 1}}{u'_{j, t - 1}} + {\lambda _2} * {Q_{i, j, t - 1}} $ | (7) |
其中,截距项矩阵Ω中存在Nx(N-1)/2个参数,λ1、λ2是两个未知的动态参数。为降低参数的个数,通过相关系数靶向法获取估计截距项参数的简易方式,使得未知参数仅为λ1和λ2。其简易估计量如下:
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \Omega } = \left({1 - {\lambda _1} - {\lambda _2}} \right) * \bar R, \;\;其中\bar R = \frac{1}{T}\sum\limits_{t = 1}^T {{u_t}{{u'}_t}} $ | (8) |
得到均值回复DCC-MGARCH模型的基本表达式为:
| $ {Q_{i, j, t}} = \bar R + {\lambda _1}({u_{i, t - 1}}{u'_{j, t - 1}} - \bar R) + {\lambda _2}({Q_{i, j, t - 1}} - \bar R) $ | (9) |
上式中,λ1、λ2、(1-λ1-λ2)全为正数且初始矩阵Q1正定,则Q矩阵为正定矩阵,存在时变的相关系数。
(3) 调整似相关系数矩阵,得到真实的相关系数矩阵。相关系数表达式为:
| $ {\rho _{i, j, t}} = \frac{{{Q_{i, j, t}}}}{{\sqrt {{Q_{i, i, t}}{Q_{j, j, t}}} }} = \frac{{(1 - {\lambda _1} - {\lambda _2}){{\bar R}_{{\rm{i, j}}}} + {\lambda _1}{u_{i, t - 1}}{u_{j, t - 1}} + {\lambda _2}{Q_{i, j, t - 1}}}}{{\sqrt {(1 - {\lambda _1} - {\lambda _2} + {\lambda _1}u_{i, t - 1}^2 + {\lambda _2}{Q_{i, i, t - 1}})(1 - {\lambda _1} - {\lambda _2} + {\lambda _1}u_{j, t - 1}^2 + {\lambda _2}{Q_{j, j, t - 1}})} }} $ | (10) |
2.基于整体网的系统性风险分析
将按类划分的金融机构作为金融网络中的节点,金融机构之间的风险关联度作为节点间“线”(节点间的相互关系)的权重,从网络的动态关联视角考虑系统性风险对金融市场的传染程度和影响能力。参照李政等(2016)关于金融市场关联网络的模型及实证方法,分析由机构间的相互关联性构成的系统性风险以及金融机构的网络压力。
网络密度是对网络中“线”的完备性度量。在金融市场上金融机构的风险关联度越大、传染性越强,由此形成的整体网络的密度就越大,该网络对于各类金融机构的风险行为产生的影响也越大。该定义符合本文对于系统性风险的界定,因此可以用整体网密度指标表示系统性风险的动态变化。
根据上文得到的金融机构间收益率的关联度数据,可以判断金融市场符合无向有权的网络结构。假设网络中有P个行动者,那么理论上包含的网络关系线条数的最大值为N①,Xn(n=1,2,……,N)为理论上存在的第n组机构间关系。
| $ {X_n} = \left\{ \begin{array}{l} 1, \;\;网络中实际上包含第{\rm{n}}组关系\\ 0, \;\;网络中实际上不包含第{\rm{n}}组关系 \end{array} \right. $ | (11) |
① N=P(P-1)/2
实际包含的网络关系线条数为
| $ {D_t} = \frac{{实际包含的网络关系}}{{理论包含的网络关系最大值}} = \frac{{\sum\limits_{n = 1}^N {{\rho _{i, j, t}}} * {X_n}}}{{\sum\limits_{\left({{\rm{i, j}}} \right) \in {\rm{N}}} {{\rho _{i, j, t}}} }} $ | (12) |
3.金融机构的系统重要性判断
金融机构的中心度是其在金融网络中的权力,具体指行动者x在网络中可以通过控制资源信息的传递而影响周边行动者,将风险从一个金融机构传导到另一个金融机构并对网络的系统性风险产生冲击的影响力。因此中心度较高的金融机构在金融网络中的位置也比较重要,能够为风险传染提供有效的传导途径,扩大金融风险的影响力。本文采用特征向量中心度(Eigencector Centrality)来表示节点的重要性,其数值取决于节点的度和节点的重要性,具体表达式如下:
| $ \bar Rx = \lambda x $ | (13) |
| $ {C_{i, t}} = \frac{1}{\lambda }\sum\limits_{{\rm{g}} \in G\left({j, t} \right)}^{} {{\rho _{i, j, t}}} {x_g} $ | (14) |
我国金融市场的发展已经呈现出多元化、多层次的结构特点,银行、非银行金融机构对金融体系和系统性风险的影响都在不断深入,因此本文选择银行、证券、保险和其他多元金融公司作为金融网络中的节点,分析不同类型的金融机构对系统性风险的动态影响。考虑到不同性质的银行存在风险偏好和风险管理水平的差异,可将银行细分为国有银行、股份制银行和城商行,由此共形成6类金融机构作为金融网络中的6个节点进行DCC-MGARCH模型和网络模型的实证分析。每个网络节点的数据来源于各个网络节点所包含的上市公司①2011年1月5日至2017年3月30日日收盘价的加权平均值,具体分类见表 1。选择股票市场价格作为风险衡量指标的优势在于股价的变动表达了市场对于金融机构经营风险和未来获利能力的综合评价,其前瞻性、连续性的数据特点能够及时有效地反映金融市场中的风险传染和积累程度。相关数据来自wind数据库,数据分析软件为STATA14.0和UCINET6.0。
① 6类金融机构共包含42家2011-2017年间主营业务均属于金融行业的上市公司。
| 表 1 金融机构分类 |
对上述数据进行自相关、异方差和单位根的检验,以判断是否存在ARCH效应。表 2第一、二列数据说明所选样本向量在时间序列上都是平稳的,不会出现“伪回归”现象。第三、四列数据通过ARCH-LM检验,说明在滞后4期的情况下,在10%的显著性水平上存在ARCH效应。第五、六、七列通过正态分布、偏度、峰度的检验得出样本数据不符合正态分布,呈现出尖峰肥尾的样本特征。因此所选数据通过上述检验,能够进行DCC-MGARCH的模型分析。
| 表 2 ARCH效应检验结果 |
通过DCC-MGARCH(1,1)的方程进行统计分析,得到6类金融机构的条件相关系数(如表 3所示)。其中,3类银行之间的关联性普遍高于其他金融机构,多元金融公司与其他5类金融机构的关联性普遍偏低。总体而言,6类金融机构之间具有较为显著的关联关系。
| 表 3 金融机构的条件相关系数 |
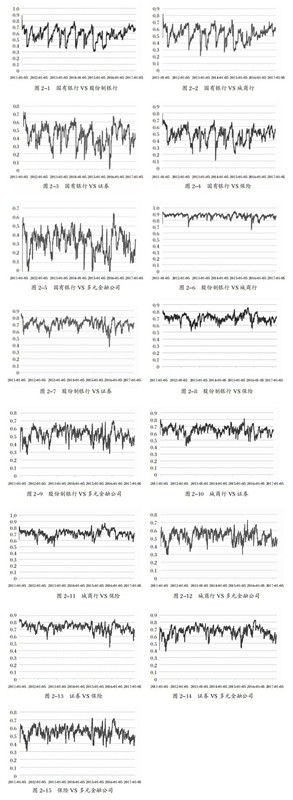
此外,还可得到动态参数λ1、λ2的数值,即:λ1=0.0228372,λ2=0.9251531,λ1+λ2<1。据此说明收益率风险的滞后期残差对风险关联度的影响较小,金融市场对风险关联度的影响较大,风险关联度的变化具有明显的动态共振特征。将上述条件相关系数和参数值带入方程(10),得到6类金融机构之间的动态关联度(如图 2所示)。比较下图中的动态相关系数可知,除股份制银行与城商行之间具有稳定的关联度以外,其他金融机构间的关联度均具有显著的时间效应,国有银行与其他5类金融机构的相关度随时间变化的幅度最大、频率最高。
|
图 2 金融机构的动态关联度 |
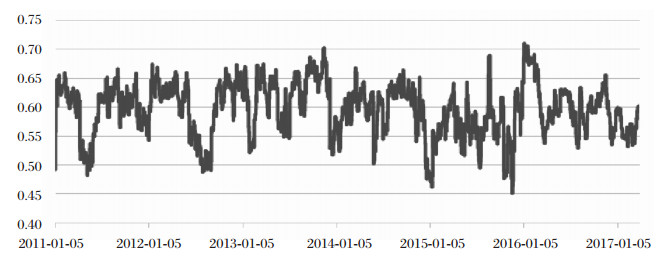
根据DCC-MGARCH模型结果,将所得金融机构间的关联度数据带入以6类金融机构为节点的无向有权网络中,通过金融机构之间的非线性网络关系,得到关于金融市场系统性风险的动态演变过程(如图 3所示)。
|
图 3 系统性风险的动态演变图 |
受2008年至2010年大规模金融救助和非常规政策的影响,2011-2017年间金融市场面临的不确定冲击及其深层次影响还在持续发酵。在样本期内,系统性风险的均值为0.5948,约有73%的数值在(0.55, 0.65]的范围内,超出此范围的极值多集中于2015年以后。其中,最高值出现在2016年1月8日,当日的系统性风险为0.7091;最低值出现在2015年11月23日,当日的系统性风险为0.4505。需要特别指出的是2013年下半年金融市场的流动性紧张以及2016年第一季度的新金融行业洗牌都使得金融系统的整体风险处于高值水平上。2015年将互联网金融纳入监管体系能够有效降低金融市场的整体风险,但在此期间系统性风险的波动性强。图 3中系统性风险的走势能够体现金融市场的发展实际,说明基于金融网络关联度的风险传染能够对系统性风险进行较好的解释。
根据系统性风险的变化趋势可以将2011年1月至2014年12月视为较为稳定的第一阶段,2015年1月至2017年3月视为波动较大的第二阶段。在第一阶段中,经济发展处于危机后的恢复期,金融市场间的监管严格,业务创新不充分,同时市场化改革刚刚起步,有效抑制了系统性风险的网络传染能力。2015年后系统性风险的变化进入第二阶段,该阶段风险变化频率快、幅度大。分析其可能原因是经济进入“新常态”,传统银行业受到资本监管和收益水平的束缚,科技金融、互联网金融、影子银行等业务主体则积极参与市场竞争,吸引各类社会资本进入,由此导致金融市场规模的扩大和金融机构关联度的提高,在共振效应的影响下形成波动性较大的系统性风险。
在了解系统性风险变化趋势后,还可以从金融网络的宏观视角分析金融机构的微观价值。本文选择特征向量中心度指数对各类金融机构在整体网中的中介地位进行比较,得出整体网密度和整体网中心度的相关系数为-0.7865,说明系统性风险与金融机构的网络权力存在显著的负相关关系。在不同程度的系统性风险水平上,金融机构的网络重要性如表 4所示。
| 表 4 金融机构的网络重要性分析 |
整体网密度与整体网中心度的负相关关系说明具有风险积聚特征的金融网络结构可以通过关键节点的中介作用增加风险传染的包容性和市场分担能力,从而降低系统性风险。比较表 4第一列和第六列的数据可知,在系统性风险小的网络结构中,金融机构作为风险传染关键节点的作用效果存在显著差异,但随着系统性风险的增加各类金融机构的中心度差异会逐渐降低。因此可以认为非均衡化的无标度网络风险传染机制能够有效降低我国金融市场的系统性风险生成概率,强调关键节点的风险态度与风险管理能力能够提高整体网络的风控效率。
对金融机构网络中心度的评价是基于风险传染的视角,中心度高的金融机构对风险传染的影响力大,更易于吸收和传播在经营活动中接触的金融风险。比较表 4的横向数据可知,各类金融机构的网络中心度由强到弱排序:城商行>保险>证券>股份制银行>国有银行>多元化金融公司。总体而言,保险部门的风险贡献率高于证券、银行和其他金融公司,其中银行部门的风险贡献率高低不等,风险管理各具特色。比较表 4的纵向数据可知,降低银行部门中的国有银行、多元金融公司风险传染的网络中介地位可以有效降低系统性风险;提高银行部门中的股份制银行、城商行、证券、保险等金融机构的网络中介地位可以在一定程度上降低系统性风险,除城商行的中心度变化对系统性风险的作用较为显著以外,其他金融机构的中心度变化并不显著。
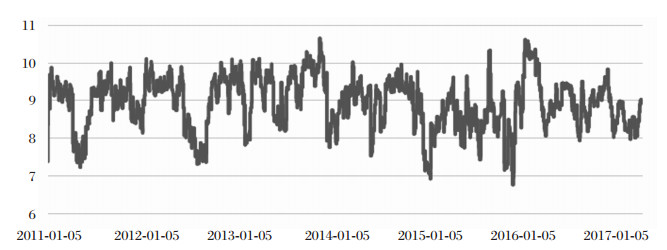
(五) 稳健性检验将DCC-MGARCH模型中得到的关于6类金融机构的动态关联度通过公式(15)、(16)分别计算得出基于线性关系的系统性风险系数Dt'和金融机构的网络重要性系数Ci, t'(具体结果见图 4、表 5),将所得结果与实证结果进行比较,判断实证结果是否具有稳健性。
| $ {{D'}_t} = \sum\limits_{\left({i, j} \right) \in N}^{} {{\rho _{i, j, t}}} $ | (15) |
| $ {{C'}_{i, t}} = \frac{{\sum\limits_{j = 1}^J {{\rho _{i, j, t}}} }}{{\sum\limits_{\left({i, j} \right) \in N}^{} {{\rho _{i, j, t}}} }} $ | (16) |
|
图 4 系统性风险的稳健性检验 |
| 表 5 金融机构网络重要性的稳健性检验 |
由于两种检验方法的表达式不同,因此稳健性检验的结果在数值上与实证结果存在差异,但图 3和图 4中关于系统性风险的动态变化趋势基本一致,因此可以证明系统性风险的实证结果具有稳健性。
比较表 4和表 5可知,在稳健性检验的结果中,6类金融机构的中心度与系统性风险的变化趋势与实证结果一致,仅有国有银行、城商行的中心度变化幅度相较实证结果发生了较大差异,可能原因是金融机构中心度的衡量受到金融网络中直接因素和间接因素的双重影响,而在稳健性检验中只包含直接因素的影响,忽略了间接因素,因此产生了变化幅度的差异,但整体而言,金融机构网络重要性的实证分析结果具有稳健性。
五、结论及政策建议本文通过DCC-MGARCH模型和无向有权型网络阐述了金融机构的风险关联度对金融系统风险的作用机制,将金融机构的破产问题从外生转为内生。在对系统性风险的评价中,创新地选取宏微观相结合的网络关联度视角,摆脱传统研究中关于线性关系和个体效应的不足。此外,本文拓展了已有文献多针对银行系统性风险研究的市场限制,通过具有预测作用的资本市场数据分析包括银行、证券、保险和其他金融机构在内的较为完整的金融体系中的风险传染机制。
综上,本文得出以下结论:中国金融市场的系统性风险在样本期内多处于较高水平,且自2015年1月起系统性风险的波动幅度增强,波动速度增加。目前我国金融市场风险传染的网络关系符合无标度网络的结构特征,非均衡的网络结构有助于控制金融风险的传染和扩散,因此处于关键节点的金融机构对系统风险的传染作用应被重视。在对具体的金融机构进行日常风险监管时,应按照金融机构的风险贡献度重点关注银行部门中的城商行、保险部门等机构的风险包容性和风险传染力。当系统性风险在金融市场的变革之中有变小的趋势时,应注重对城商行的业务创新风险和风险偏好的有效引导和监督,降低城商行在网络结构中风险传染的节点作用;而当系统性风险有变大的趋势时,应注重国有银行和多元化金融公司在这一阶段风险传染和蔓延的新特征,尤其需要加强对新型金融公司的创新监管,如此才能在金融创新及市场变革的波动中有效控制风险传染的渠道,降低系统性风险的生成概率。
根据上述结论,提出如下政策建议:
1.强调金融机构的网络属性,提高宏观审慎监管效率。同一金融机构所处网络结构的差异性将影响其风险传染的选择策略,进而形成异质化的系统性风险。因此,对系统性风险的辨析需要与其所对应的网络特征相结合,明确提出以宏观审慎监管为目标的具体监管措施、参与者和中期目标,增加系统性风险监管的可操作性。
2.在金融监管政策中加强对跨市场、跨行业业务的风险关联度指标的衡量和监测。近年来我国已基本放开了对非银行金融牌照的限制,金融机构之间的风险关联性对系统性风险的影响大大增强,因此将相应的关联度指标加入金融监管的政策中,可以有效预警各类金融机构之间的联动性、传染性、共振性对整个金融体系风险的影响。
3.加强影子银行业务的风险监管,有效控制金融风险的交叉传染。对诸如信托、基金等新型金融公司的业务创新应加强相应的影子银行业务监管,逐步引导并实现业务风险的主动承担,控制投机行为所导致的风险外溢及其负外部性损失。在提高金融市场活力的同时,增加金融市场的风险包容性。
| [] |
胡海峰、代松, 2016, “后金融危机时代系统性风险及其测度评述”, 《经济学动态》, 第 4 期, 第 41-61 页。 |
| [] |
胡锡亮、吴恒煜, 2016, “基于金融网络的系统性风险研究”, 《现代经济探讨》, 第 9 期, 第 59-62 页。DOI:10.3969/j.issn.1009-2382.2016.09.012 |
| [] |
李建军、薛莹, 2014, “中国影子银行部门系统性风险的形成、影响与应对”, 《数量经济技术经济研究》, 第 8 期, 第 117-130 页。 |
| [] |
李政、梁琪、涂晓枫, 2016, “我国上市金融机构关联性研究——基于网络分析法”, 《金融研究》, 第 8 期, 第 95-110 页。 |
| [] |
李志辉、李源、李政, 2016, “中国银行业系统性风险监测研究——基于SCCA技术的实现与优化”, 《金融研究》, 第 3 期, 第 92-106 页。 |
| [] |
刘军, 2016, 《整体网分析(第二版)——UCINET软件实用指南》, 上海: 格致出版社、上海人民出版社。 |
| [] |
梁琪、李政、郝项超, 2013, “我国系统重要性金融机构的识别与监管——基于系统性风险指数SRISK方法的分析”, 《金融研究》, 第 9 期, 第 56-70 页。DOI:10.3969/j.issn.1007-9041.2013.09.011 |
| [] |
王占浩、郭菊娥、薛勇, 2016, “资产负债表关联、价格关联与银行间风险传染”, 《管理工程学报》, 第 2 期, 第 202-209 页。 |
| [] |
杨有振、王书华, 2013, “中国上市商业银行系统性风险溢出效应分析——基于CoVaR技术的分位数估计”, 《山西财经大学学报》, 第 7 期, 第 24-33 页。 |
| [] |
张英奎、马茜、姚水洪, 2013, “基于复杂网络的银行系统风险传染与防范”, 《统计与决策》, 第 10 期, 第 149-153 页。 |
| [] |
Engle R.、王成璋(译), 2015, 《预见相关性: 风险管理新范例》, 北京: 机械工业出版社。 |
| [] |
Acemoglu D., Ozdaglar A. and Tahbaz-Salehi A., 2015, "Systemic Risk and Stability in Financial Networks". American Economic Review, 105(2), 564–608.
DOI:10.1257/aer.20130456 |
| [] |
Aldasoro I., Gatti D.D. and Faia E., 2016, "Bank Networks:Contagion, Systemic Risk and Prudential Policy". BIS Working Paper, No.597.
|
| [] |
Caballero J., 2015, "Banking Crises and Financial Integration:Insights from Networks Science". Journal of International Financial Markets, Institutions & Money, 34, 127–146.
|
| [] |
Drehmann M., Tarashev N., 2013, "Measuring the Systemic Importance of Interconnected Banks". Journal of Financial Intermediation, 22(4), 586–607.
DOI:10.1016/j.jfi.2013.08.001 |
| [] |
Kreis Y., Leisen D., 2017, "Systemic Risk in A Structural Model of Bank Default Linkages". Journal of Financial Stability, 05(online).
|
| [] |
Lenzu S., Tedeschi G., 2012, "Systemic Risk on Different Interbank Network Topologies". Physica A:Statistical Mechanics and its Applications, 391(18), 4331–4341.
DOI:10.1016/j.physa.2012.03.035 |