国家在不同的阶段会制定不同的发展战略,由于资源要素是稀缺的,制定产业发展战略的同时,会面临资源要素等各方面的约束。特别是在国际经济竞争程度日益增强的背景下,每个国家需要根据本国国情对发展哪些产业做出选择,这种选择的结果表现为产业发展模式,进而影响要素在不同产业间的配置。经济增长理论认为,资本、劳动力、技术进步是经济增长的源泉,要素在产业中的配置会影响产业发展模式进而影响经济增长。无论是资源配置是否合理,总会以某种方式呈现出来,而产业结构就是资源配置所形成的产业发展模式。按照配第-克拉克定理①,劳动力在不同部门间的转移,结果显示出三次产业的演进规律。因此,经济增长过程中,各种资源在不同部门间进行配置,无论这种配置是自发的还是人为的,是按照市场规律还是政府导向,最终会形成部门内部以及部门之间的替代。要素跨部门间的转移如果按照市场自发调节进行配置,根据新古典经济学的观点,最终会达到帕累托最优的配置,那么产业或者部门间也会达到一种均衡状态。然而,要素在产业发展或者产业结构的变化过程中并不一定是自发配置的,即存在“经济楔子”①。如果要素的自发转移受到某种干扰,比如市场环境、政府的干预、自然环境、地域限制等因素,要素并没有从低要素报酬部门向高要素报酬部门转移,那么会造成要素配置扭曲,表现出非均衡的产业发展模式。经济在实际发展过程中,是否会如新古典经济学所描述的那样,政府干预是无效的,甚至是“帮倒忙”?政府干预会造成要素配置的扭曲,但这种扭曲是否会造成产业发展不合理,是否不利于某些产业的发展?政府干预的发展战略影响产业结构变动,这种“结构效应”是否是经济增长中的“结构红利”?因此本文聚焦政府发展战略对资本和劳动投入在产业中配置的影响,建立发展战略影响产业发展的理论和实证模型,揭示发展战略在产业发展过程中的主导作用。
① 对40多个国家和地区不同时期三次产业的劳动投入产出资料进行了整理和归纳,总结出:随着经济发展和人均国民收入水平的提高,第一产业国民收入和劳动力的相对比重逐渐下降;第二产业国民收入和劳动力的相对比重上升,经济进一步发展,第三产业国民收入和劳动力的相对比重也开始上升。
① “经济楔子”是指阻碍市场自发配置的各种影响因素,会阻碍资源要素自发的配置。
二、文献综述我国已经实现了从落后的农业经济向工业经济的大转型,并已跨入工业化中期阶段②。在经济改革初期阶段,由于历史和现实发展状况,经济发展基础薄弱,因此国家实行有计划的市场经济,按照国家发展计划和战略,将有限的资源要素分配到国家规划中优先发展的部门和地区,形成了适应当时阶段的发展方式以及产业结构形式,劳动力、资本和自然资源等生产要素在不同部门间的供给及使用导致了产业结构的变动(Syrquin and Chenery, 1989;宋建、王静,2018)。产业结构的演进会受到政府的引导,取决于政府主导产业的变化和发展(张冰、金戈,2007)。
② 按照“霍夫曼工业化经验法则”划分不同的工业化阶段。
在实际经济发展中,政府可以根据发展战略制定行政命令来主导产业发展的路径,但是这种政府主导性的干预是否合理,或者是否有利于经济发展?学界对于该问题存在分歧,特别是进入21世纪,产业结构调整过程中政府和市场的关系成为讨论的焦点。一种观点认为政府发展战略在产业发展过程中会产生负面影响,不利于经济社会的发展。如果追求优先发展重工业的赶超战略,那么该国生产要素存量配置结构必将违背由本国的要素禀赋结构决定的比较优势,从而导致国内的赶超企业缺乏自生能力,因此政府必须以扭曲市场最优配置的方式保护补贴缺乏自生能力的企业(王坤宇,2017)。林毅夫将发展战略区分为两种,一种是符合地区比较优势的发展战略,另一种是违反地区比较优势的发展战略,其研究发现重工业优先发展战略导致了中国更差的经济绩效(Lin,2003)。中国的产业结构变化在要素配置上表现为越来越多的资源被配置到资本密集型部门和东部地区(林毅夫、陈斌开,2013)。这种集中力量办大事的发展战略,也造成了一定的要素配置和产业问题,政府鼓励重工业等资本密集型产业发展的各种战略政策导致该产业部门的资本密集程度过高(王金照,2010)。在产业结构转型的过程中,中国产业间、区域间存在的不协调,以及各产业内部的若干矛盾和问题不断凸显。特别是工业比重偏高和服务业发展不足、工业制造业低端化、重化工业比重偏大、产能过剩、公共性和生产性服务业发展不足、产业结构地区趋同等问题比较突出。这些产业发展过程中的突出问题很大程度上与国家发展战略有关(林毅夫、陈斌开,2013)。江飞涛、李晓萍(2010)指出,处于发展中和转型中的国家存在的所谓“市场失灵”,实则多是“政府失灵”或“制度失灵”,实施直接干预的产业政策只会使问题更为严重。Mcmillan et al.(2014)发现,与亚洲国家不同,拉丁美洲国家在1990-2005年以及非洲国家在1990-2000年期间,政府主导的产业结构调整对于经济增长率存在负向作用。另一种观点认为,由于市场不完善、市场失灵以及我国特殊国情等原因,政府干预在产业结构调整中的效果更为明显,政府发展战略有利于产业结构优化,并且所形成的产业发展模式对经济增长产生了很大的贡献。发展中国家由于市场体系和机制不完善,经济运行中普遍存在着非均衡现象,结构问题较为突出,加上技术相对落后以及国际竞争力差等原因,政府对产业结构的调整发挥着更大的作用(罗勤,2001)。王皓(2009)分析了2008年国际金融危机对我国产业结构的影响,肯定了政府对调结构的主导作用。要素在不同部门之间流动带来的生产率的提升可以称为“结构红利”,这种“结构红利”是经济持续增长的动力,因而产业结构优化升级可以促进经济增长(Peneder,2002)。Dietrich(2012)利用OECD国家数据,实证分析表明,产业结构对于经济增长有重要的促进作用。
上述研究表明了发展战略对于产业发展存在影响,但并没有明确提出对每个产业具体影响情况,虽然中国实施了大量促进产业发展的战略,但是关于政府的产业发展战略影响产业发展的具体机制与效应,一直缺乏详细的理论模型和实证分析。本文从政府主导的发展战略影响资本和劳动在不同产业中配置的视角,建立理论模型,并结合数据经验进行实证分析。文章力求弥补现有研究中的这些不足,从以下几个方面取得了进展:第一,构建理论模型,说明发展战略影响要素的配置,从而影响产业发展;第二,从理论模型中定义测度发展战略的指标以及其他相关变量;第三,通过实证分析,说明发展战略对于产业发展和产业结构调整的影响程度;最后,总结并提出结论。
三、理论框架与模型设定 (一) 要素配置影响产业发展的微观视角按照新古典经济学的观点,要素的报酬是要素在生产过程中的边际生产力价值,即资本的报酬r=P·MPK,劳动力的报酬w=P·MPL。在非均衡经济中①,要素在部门i的报酬小于要素在部门j的报酬,那么要素会从部门i转移到部门j。这种要素跨部门间的转移可以通过市场自发调节,如果这种自发调节受到某种干扰,比如市场环境、政府干预、自然环境、地域限制等因素,要素并没有从低报酬部门向高报酬部门转移,就会影响部门的发展,从而影响经济体中产业发展的模式。在中国,政府是影响投入要素流动的最主要的非市场因素之一,要素流动过程中由于政府干预或者政府主导产业发展进程,要素不能按照边际生产效率规律跨部门之间流动,从而形成了政府主导的产业发展模式。
① 非均衡经济是指一个经济体中不同部门或者产业的要素生产力或者回报率是不同的。
从微观视角来看,在一个竞争性的市场中,企业在一定技术水平下,面临成本预算约束,按照竞争市场的最优生产条件,厂商会在成本预算线与生产函数相切的位置选择生产要素的投入量进行生产。如果厂商生产两种产品,投入资本和劳动两种要素,在市场达到均衡时的条件为:λ1=λ2=r/MPK=w/MPL。其中,r、w分别为资本和劳动的要素价格,λ为拉格朗日乘数,一般表示单位投入所带来的效用或者报酬,此处为生产产品1和产品2投入要素的单位报酬,均衡时两者相等。
|
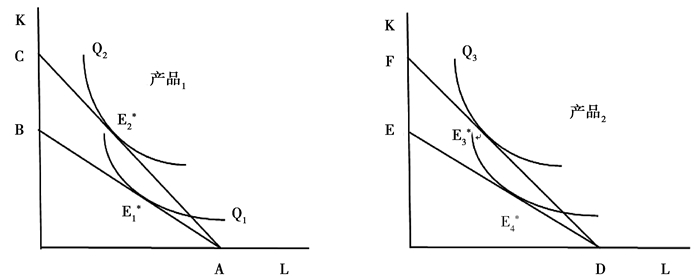
图 1 代表竞争性厂商生产两种产品比较静态变动图 |
具体来说,在图中设定代表性竞争厂商面临成本预算线AB,生产等产量线为Q1,投入要素为资本K、劳动L,达到均衡时,预算线与等产量线相切与E1*,在均衡处的条件为边际产出比等于要素价格比,具体形式可写为:MPK/MPL=r/w=λ1=λ2。
在某一时期T,如果市场中资本更多流向商品1的生产,那么对于商品1的生产中,资本K的价格r相对降低,那么竞争性厂商生产产品1面临的成本预算线会发生变化,由AB调整为AC,生产等产量线为Q2,那么厂商会改变要素投入,在E2*处达到均衡,可以证明在E2*处的产品产量要高于E1*处的产量。由于厂商生产产品1中投入的资本增多,那么生产产品2的时候资本就会相对减少①,而劳动投入相对增加,生产产品2时,成本预算线发生变化,由DF调整为DE,生产等产量线为由Q3变动为Q4,那么厂商会改变要素投入,在E4*处达到均衡。
① 此处假设经济体中投入要素总量不变。
通过上面的分析,从微观企业产品和要素市场分析引申到产业,如果政府按照发展战略,集中把更多的资本K投入到资本密集的产业生产中,把劳动投入要素更多的配置到劳动密集型产业中,那么资本密集型和劳动密集型产业就会因为符合本行发展的“技术优势”得到快速发展,产业在经济体中的份额逐渐提升,最终表现出政府主导的产业发展模式。
(二) 理论模型与方法为了分析政府“有形之手”所决定的发展战略对于产业发展以及产业结构调整的影响,引入总量生产函数,假设总量生产函数为规模报酬不变的柯布-道格拉斯生产函数(Cobb-Douglas Production Function),生产函数具体形式为:
| $ Y=A{{K}^{\alpha }}{{L}^{\beta }} $ | (1) |
其中,生产函数为一次齐次函数,即α+β=1,α和β分别为资本产出弹性、劳动产出弹性,Y表示产出,K表示资本投入量,L表示劳动投入量。A在一般情况下表示技术进步,也称为索洛剩余。根据总量生产函数设计各产业的生产函数模型,函数具体形式为:
| $ {{Y}_{j}}={{A}_{j}}K_{j}^{{{\alpha }_{j}}}L_{j}^{{{\beta }_{j}}} $ | (2) |
其中,j表示各产业,αj和βj分别为j产业的资本产出弹性与劳动产出弹性,Yj表示j产业的产出,Kj和Lj分别表示产业j中资本投入以及劳动投入量。各产业生产函数也遵循规模报酬不变的假设,即αj+βj=1。
公式(1)和公式(2)变形为人均形式:
| $ \frac{Y}{L}=A{{\left(\frac{K}{L} \right)}^{\alpha }}, \ \frac{{{Y}_{j}}}{{{L}_{j}}}={{A}_{j}}{{\left(\frac{{{K}_{j}}}{{{L}_{j}}} \right)}^{{{\alpha }_{j}}}} $ | (3) |
K/L表示为生产过程中两种投入要素资本与劳动的配置组合,也可以表示人均资本以及资本深化,不同的产业Kj/Lj是不同的,并且产业j的Kj/Lj与该地区的K/L的比值在不同地区也不同,从上文中的分析中,地区的发展战略不同,发展的产业存在差异,不同地区的资本投入与劳动投入在政府主导的产业发展战略中存在差异,因此,可以用PCI(Policy Choose Index)来测度发展战略影响资本与劳动在产业中配置的一种指标,反映地区政府为发展j产业所实施的发展战略选择。发展战略会影响资本与劳动在不同产业中的配置组合,一个产业的资本劳动比率与地区的资本劳动比率的比值,反映该产业的经济发展战略对自身比较优势的偏离程度,具体形式为:
| $ PC{{I}_{j}}=\frac{{{K}_{j}}/{{L}_{j}}}{K/L}={{\left(\frac{{{Y}_{j}}}{{{L}_{j}}} \right)}^{1/{{\alpha }_{j}}}}{{\left(\frac{Y}{L} \right)}^{-1/\alpha }}\left(\frac{{{A}^{1/\alpha }}}{A_{j}^{1/{{\alpha }_{j}}}} \right) $ | (4) |
公式(4)可以得到:
| $ \frac{{{Y}_{j}}}{{{L}_{j}}}~={{\left(PC{{I}_{j}} \right)}^{{{\alpha }_{j}}}}{{\left(\frac{Y}{L} \right)}^{{{\alpha }_{j}}/\alpha }}\left(\frac{{{A}_{j}}}{{{A}^{{{\alpha }_{j}}/\alpha }}} \right) $ | (5) |
| $ {{y}_{j}}={{y}^{{{\alpha }_{j}}/\alpha }}{{\left(PC{{I}_{j}} \right)}^{{{\alpha }_{j}}}}\left(\frac{{{A}_{j}}}{{{A}^{{{\alpha }_{j}}/\alpha }}} \right) $ | (6) |
yj表示产业j的劳动产出效率(j产业产出与j产业就业人口比值),y为地区人均产出,从公式(6)中可以发现,产业j的劳动产出效率受到该产业的资本-劳动组合(PCIj)、地区人均产出y以及技术进步的影响。在产出-资本弹性αj>0时,PCIj对于产业j的劳动产出效率有正向作用,也就是说政府主导的发展战略通过影响资本与劳动投入在不同产业中的配置,从而提升劳动生产率水平。发展战略的意义在于对一些产业进行扶持,改变该产业的资本-劳动比率,可以提高产出效率水平,大大增加该产业在国民经济中的比重,从而影响产业结构调整。
发展战略对产业发展的影响机制,同样也适用于地区经济范畴,在文中PCIj影响产业发展的作用机制可以引申为地区发展战略对于本地区产业发展的影响,国内区域经济发展态势和趋势具有明显差异,各地区在选择自身经济发展战略过程中也必然面临政策选择问题。地区经济如果选择的发展战略影响了要素在产业中的配置,使得扶持的产业部门发展速度高于其他部门,产业结构随之而变。为了研究的需要以及数据的可得性,可以建立一个基于省域面板数据的模型,来分析发展战略对地区产业发展的影响,定义具体形式为:
| $ PC{{I}_{ijt}}=\frac{{{K}_{ijt}}/{{L}_{ijt}}}{{{K}_{t}}/{{L}_{t}}} $ | (7) |
i表示省份,t为时间,j表示产业部门,公式(7)可以改写为:
| $ {{y}_{ijt}}={{\left(PC{{I}_{ijt}} \right)}^{{{\alpha }_{j}}}}{{\left({{y}_{t}} \right)}^{{{\alpha }_{j}}/\alpha }}\frac{{{A}_{j}}}{{{\left(A \right)}^{{{\alpha }_{j}}/\alpha }}} $ | (8) |
yijt表示地区i的产业部门j在时期t的劳动产出率,yt表示全国时期t劳动产出率,对于公式(8)两边取对数,可化简为线性回归方程等式:
| $ TS=\sum\limits_{\text{ }j=1}^{3}{{{y}_{j}}\times i={{y}_{j}}\times 1+{{y}_{j}}\times 2+{{y}_{j}}\times 3~} $ | (9) |
公式(9)中
该方程说明不同省份的各行业劳动产出率受到该地区各产业资本-劳动配置(PCIijt)、全国劳动产出率以及其他因素的影响。通过各省份和全国的GDP、资本投入和劳动投入数据,可以测算出回归方程中的参数,从而得到用资本-劳动组合测算的地区政府发展战略指标对于本地区产业发展的贡献程度。从公式(6)分析中,如果政府实施产业政策重点扶持某一产业,增加对该产业的资本投入,该产业的资本-劳动比率提升之后,就会使得该产业超过其他产业的发展速度,从而改变产业结构的演化路径,提升地区整体劳动产出效率水平,因此可以预期回归方程(9)中的参数β1为正。比如,2008年全球金融危机以后,面临GDP增速下降的问题,制定了大力发展战略性新兴产业的政策。①
① 2008年,全球金融危机爆发后,中国面临国际需求下降,出口压力增加,GDP增速下降,中国政府制定大力发展战略性新兴产业(光伏、LED等产业)的发展战略,采取金融支持,财政性支出投入以及其他补贴或者政策优惠等行政性手段,增加对发展产业的资本投入,使得重点扶持产业发展速度明显超过其他产业。
另外,随着整体的劳动产出效率提升,商品和要素市场更加完善,资本和劳动等投入要素在不同地区可以自由流动,全国劳动产出水平的提升对于国内不同省份的产出劳动效率也应该存在促进作用,所以回归参数β2在理论上也是正的。
(三) 模型设定根据上文的讨论,为了检验理论模型在实际经验中的应用,除了理论模型所涉及到的变量之外,从供给角度分析,投入要素配置是影响产业发展和产业结构演进最根本的因素,所以除了在模型中纳入用资本-劳动配置组合测度的政府发展战略的指标(PCIijt)之外,也将技术进步、金融发展、国际贸易、政府支出等因素纳入到模型之中,建立基础模型回归方程:
| $ {{y}_{ijt}}={{\beta }_{0}}+{{\beta }_{1}}PC{{I}_{ijt}}+{{\beta }_{2}}{{y}_{it}}+{{\beta }_{3}}financ{{e}_{it}}+{{\beta }_{4}}go{{v}_{it}}+{{\beta }_{5}}fd{{i}_{it}}+{{\beta }_{6}}trad{{e}_{it}}+\varepsilon ~ $ | (10) |
其中,PCI为测度发展战略影响资本与劳动投入在产业中配置的指标;y为整体劳动产出效率,此处可以描述为技术进步;finance为金融发展水平,gov表示政府支出,fdi为外商直接投资,trade表示贸易指数,ε为随机误差项。
考虑到产业发展以及结构变动是一种渐进的动态过程,所以要考虑这种动态效应,因此在实证分析中利用了GMM分析方法,GMM模型中涉及到滞后项和动态效应,建立GMM基础模型回归方程:
| $\begin{align} &{{y}_{ijt}}={{\beta }_{0}}+{{\beta }_{1}}{{y}_{ijt-1}}+{{\beta }_{2}}PC{{I}_{ijt}}+{{\beta }_{3}}{{y}_{it}}+{{\beta }_{4}}financ{{e}_{it}}+{{\beta }_{5}}go{{v}_{it}}+{{\beta }_{6}}fd{{i}_{it}}+ \\ &{{\beta }_{7}}trad{{e}_{it}}+{{\mu }_{it}}+{{\eta }_{it}}+{{\varepsilon }_{it}} \\ \end{align} $ | (11) |
其中,i表示省份,t为时期,j为产业部门,其他变量与模型公式(10)中的经济含义一致,ηit为时间效应,μit表示个体效应,εit为随机误差项。
四、指标选择、数据说明及描述 (一) 变量指标设定 1. 产业发展水平在理论模型公式(8)中,yit表示地区i在时期t的劳动产出效率,可以表示该地区某时期行业的发展水平,分别有三次产业的劳动产出效率。
2. 产业结构调整指标(1) 产业结构合理化
描述产业结构合理化程度,我们采用干春晖等(2011)使用的Theil指数来衡量,测算公式为:
(2) 产业结构高度化
采用学者李逢春(2012)测度产业结构高度化的方法,公式为:
其中yj为第j产业产值占GDP比重,TS的值越接近1,说明产业结构高度化层次越低,TS值越接近3,说明产业结构高度化层次越高。
(3) 有效产业结构调整指数
为了分析产业结构与经济增长的关系,设计了劳动力配置视角下的产业结构指标:有效产业结构调整指数ESC(Effective Structure Change Index)。
ESC是综合了偏离-份额法(Shift-share Method) ①和绝对价值法NAV(the Norm of Absolute Value Index) ②。两种指标,弥补了偏离-份额法中包含劳动力不合理配置的缺点,改善了NAV中不能体现部门劳动力生产率提高或者降低的弊端。该指标说明了产业结构调整对于经济增长存在的“结构效应”。ESC的测算公式为:
| $ ESC=0.5*\sum\limits_{i\in X}{\left| {{S}^{jT}}-{{S}^{j0}} \right|}X=\left\{ j \right\}\text{ }such\text{ }that\text{ }{{C}^{j}}>0 $ |
① 偏离-份额法SSM(shift-share method)包含两种效应,生产率效应和部门转移效应,公式为
② 绝对价值法NAV(the norm of absolute value index)的测算公式为:
在ESC测算公式中Cj>0时,才表示部门j对于经济增长的贡献。
3. 解释变量政府发展战略(PCI)为测度发展战略影响资本与劳动投入在产业中配置的指标,一个产业的资本劳动比率与地区的资本劳动比率的比值,反映该产业的发展战略对自身比较优势的偏离程度,反映地区政府为发展j产业所实施的产业发展战略。
| 表 1 模型中变量含义解释 |
模型中加入了一些控制变量,finance为金融发展水平的测度指标,利用年末金融机构各项贷款余额占GDP的比值测算;gov表示政府支出,地方公共财政支出占GDP的比重可以作为政府支出的测算指标;fdi为外商直接投资,用fdi与GDP的比值测算;trade表示贸易指数,用进出口总额与GDP比值测度;地区经济发展水平(pgdp),表示经济发展水平对产业发展以及产业结构的影响,产业结构作为经济增长的一种表现形式,所以产业结构要受到经济发展水平的影响。根据已有的研究成果表明,人均GDP能够表示经济增长,因此本文选取人均GDP作为衡量经济增长的指标,利用前一期为基期,剔除价格的影响。
(二) 数据说明 1. 数据来源文章采用中国省际面板数据,数据样本不包括港、澳、台地区的数据,全部数据样本为中国28省市1984~2015年数据,因为海南省、西藏自治区和重庆市三省市缺失数据,因此剔除了三省市的数据。各省的产业增加值、GDP指数、社会固定资本投资等各项数据来源于《中国科技统计年鉴》、《中国工业经济统计年鉴》、《中国统计年鉴》、各省的《统计年鉴》;劳动就业量来源于各省的《统计年鉴》、《中国统计年鉴》、《中国劳动统计年鉴》。资本存量的测算基础数据来源于《中国统计年鉴》、《中国国内生产总值核算历史资料》以及各省的《统计年鉴》。
2. 数据处理为了剔除价格波动的影响,对各产业的增加值以及各省的产值进行了平减,利用GDP指数,以1984年为基期,对产值进行了处理。
对于资本存量的测算,主要包括各省三次产业、各省总的资本存量以及全国的资本存量估算,借鉴了徐现祥(2007)的算法,利用各省三次产业固定资产投入以及折旧额,测算了1984-2002年的资本存量数据,2003-2014年由于缺少折旧额,测算时借鉴了单豪杰(2008)所采用的10.96%的折旧率对资本投资进行折旧扣除,鉴于可获得的数据,各省的资本存量和全国的资本存量是分开测算的。另外,在测算资本存量时,利用固定资本投资价格指数以1984年为基期进行了剔除价格因素影响的处理。对于劳动投入的数据,三次产业劳动投入利用三次产业就业人口进行代替,需要注意的是1990年由于统计口径发生变化,但是并不影响总体分析。
需要说明的是,测算指标中用到的价格指数,GDP价格指数与资本存量价格指数不同,总的资本存量价格指数为固定资产投资价格指数,由于各个产业并没有资本投资价格指数,因此根据不同产业利用各自的价格指数进行替代,第一产业资本存量价格指数为农产品生产者价格指数,第二产业资本存量价格指数为工业生产者出厂价格指数,第三产业资本存量价格指数为总的减去一二产业。
另外,在经验估计中,为了避免出现多重共线性、异方差等回归问题,比如人均GDP、劳动产出效率等绝对量进行取对数处理。
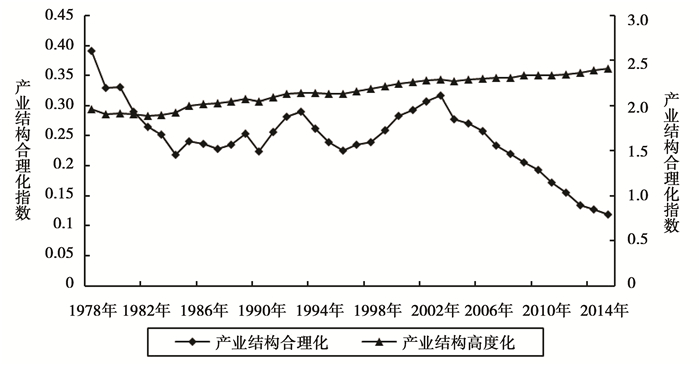
(三) 描述性分析图 2报告了我国1978~2015年产业结构调整过程中产业结构合理化与高度化的变动趋势,由图 2可以发现,改革开放初期,产业结构的泰尔指数下降明显,产业结构趋于合理化。从上世纪80年代到本世纪初,产业结构合理化出现大的波动,泰尔指数先上升后下降再上升,这一段时间是中国经济改革的关键时期,市场经济制度由探索到成熟的阶段,对中国产业变革产生重大影响。进入本世纪后,产业结构的泰尔指数开始下降,产业结构趋于合理化。图 2还报告了产业结构高度化指标,从产业结构高度化变动趋势可以看出,产业结构高度化呈现出缓慢增长的趋势,产业结构高度化水平持续提升。综合产业结构合理化与产业结构高度化的变动趋势可以看出,产业结构调整趋向越来越合理和越来越高级。
|
图 2 全国1978-2015年产业结构调整水平变动趋势 资料来源:根据国家统计局数据资料制图。 |
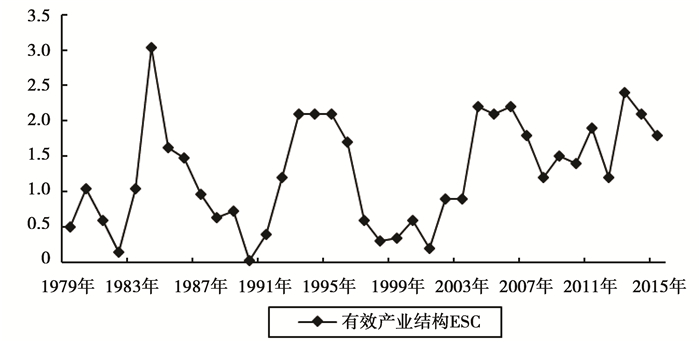
图 3描述了有效产业结构的变动情况,说明结构变动中,对于经济增长的贡献存在波动,特别是上世纪八十年代,有效产业结构指数较大,对于经济增长的贡献也较大,与图 2中产业结构变化相对应。随着近些年产业结构优化升级,产业发展中所形成的“结构效应”对于经济增长的贡献也逐渐提升,表现为图 3中有效产业结构(ESC)数值增长。
|
图 3 全国1978-2015年有效产业结构ESC变动趋势 资料来源:根据国家统计局数据测算。 |
不同省份的经济因素存在差异,政府发展产业的侧重点也不同,政府发展战略和各种因素对产业发展以及产业结构调整的影响可能也会有差异,所以考虑到不同地区间存在的异质性,在设计实证模型时引入了个体效应以及时间效应。
为了充分利用面板数据实证检验政府发展战略对于产业发展的影响,我们分别采用静态面板数据模型和动态面板数据模型。表 2中给出了模型选择检验结果,异质性检验中,从Honda检验结果表明模型中存在异质性,因此应选择个体效应。在固定效应和随机效应的Hausman检验中,从检验结果中来看,个体效应满足固定效应模型的假设,因此在静态回归模型中选择了固定效应回归结果。
| 表 2 模型设定检验 |
动态面板数据模型的解释变量中加入了被解释变量指标的滞后一期,而静态面板数据则不考虑被解释变量的滞后项。在静态面板数据模型中,考虑到可能存在异方差和序列相关等误差问题,我们采用FGLS估计方法,FGLS估计方法可以同时考虑到可能存在异方差和序列相关的问题。在动态面板数据中,由于加入了被解释变量的滞后一期作为解释变量,那么就会产生内生性的问题,利用Arellano and Bond(1991)提出的差分GMM估计方法可以较好地解决内生性和面板数据异质性造成的误差,另外本文采取两步法差分GMM估计,解决了面板数据存在的异质性问题。在回归结果中报告了误差项的自相关检验结果,同时利用Hansen-J过渡识别检验工具变量的有效性。
1. 对产业发展影响的静态面板估计表 3报告了各产业中,政府发展战略(PCI)对产业发展的影响,回归结果(1)、(2)、(3)中的因变量分别为第一产业劳动产出率avey1、第二产业劳动产出率avey2、第三产业劳动产出率avey3。从静态面板估计结果中,模型(1)、(2)、(3)投入要素资本-劳动配置组合(lnpci)对各行业的劳动产出率存在显著的影响,并且通过了1%的显著性检验。其中第一产业,如果lnpci对第一产业中投入要素的干预指数提升1个百分点,那么第一产业劳动生产效率会提升0.033个百分点,政府对第二产业的干预指数提高1%,第二产业的劳动生产效率会提高0.294%,第三产业中政府的干预指数作用为0.066%。从政府在不同产业中的发展战略对于不同产业的影响程度是不同的,特别是对于第二产业的作用最大,说明政府在过去的发展战略制定中,是有效的促进了第二产业的劳动产出率。地区产业劳动产出效率(lnavy)即技术进步对于三次产业的劳动产出率存在正向的促进作用,也就是说提升地区整体的劳动生产率(技术进步水平)可以提升每个产业的劳动生产率,并且在统计结果中通过了1%的显著性检验,对于第二产业的劳动生产率的影响是最大的,达到了0.789%,另外也在验证了模型中参数β1、β2在理论上的预测为正的假设。
| 表 3 发展战略影响三次产业发展的FGLS回归估计 |
控制变量中,各自变量对于三次产业的劳动生产率的影响都通过了显著性的检验,经济发展水平人均GDP(lnpgdp)与三次产业的劳动产出率存在非线性的关系,与第一产业存在“U”型关系,与第二三产业的劳动产出率存在倒“U”型关系,及随着经济水平的提升,第一产业的劳动产出率先下降后上升,第二三产业的劳动生产率先上升后下降,并且对于第二产业的劳动产出效率的影响最大,基本符合Kuznets对于经济发展过程中产业结构演变的理论①。其他的控制变量对于三次产业劳动产出率影响最大的是金融发展水平(finance)和贸易水平(trade),其中金融发展水平对于一三产业的劳动产出率存在负向作用,对于第二产业存在正向作用,贸易水平提升可以促进一二产业的劳动产出率,但是不利于第三产业的劳动产出效率。政府支出(gov)对于各产业的劳动生产率的贡献在数值上不大,外商直接投资(fdi)对一二次产业的劳动产出率的影响要大于第三产业。
① 发达国家在经济增长的过程中都发生了迅速的经济结构转变。一是经济活动从农业先转向非农业活动,再从工业活动转向服务业;二是企业从个体中、小型企业转向全国性或跨过性大公司;三是劳动从农业部门转向非农业部门,农业与非农业部门的劳动力人数比例在下降。而不发达国家的经济结构变化缓慢,结构因素对经济增长的贡献较小,传统的结构把劳动力大都束缚在传统的农业生产部门,传统的生产技术和生产组织方式又阻碍着经济的增长。
2. 对产业发展影响的动态面板模型估计在现实经济发展过程中,经济发展或者产业的发展存在内在的连惯性,一般存在影响的滞后性。很多国家或者地区产业的发展存在一定的动态演进过程,那么在实证模型中就要考虑这种动态影响,因此构建了包含因变量滞后项的动态实证模型。通过滞后期检验,本文选择滞后一期的估计结果,从Sargan检验结果来看,我们的设定是合理的。为了对GMM的权重矩阵有更好的估计,我们采用了2阶段估计方法,具体的回归估计如表 4所示。各因变量的滞后一期(L.)对于当期的影响是很显著的,分别为0.491、0.517、0.583,并且通过了1%的显著性检验,说明在产业发展过程中,本行业的劳动产出率存在这种动态特征。存在这种滞后影响的原因,一是政府干预改变了产业中当期的资本和劳动等生产要素的投入,要素投入之间的组合并不是立刻完成的,要素之间的组合需要时间进行最优配置,因此劳动产出率的提升具有滞后效应;二是因为劳动产出效率提升是劳动力素质的提升,劳动力素质的提升依赖劳动者的学习,这种学习效应并不是在当期就可以显现,就存在了一种滞后的动态效应。三次产业中政府发展战略(lnpci)对于一二产业的影响是显著地,对于第三产业的影响并不明显,并且政府行为对于第二产业的劳动产出效率影响最大。
| 表 4 发展战略影响三次产业发展的diff-GMM回归估计 |
表 5给出了政府发展战略对于产业结构调整的静态面板回归结果,回归方程估计结果(7)、(8)、(9)的被解释变量分别为产业结构合理化指数(Theil)的倒数TL①、产业结构高度化指数(TS)和有效产业结构指数(ESC),自变量中的政府发展战略测量数值不同于上文中所描述的三次产业各自的PCI,这里测度的是地区的整体发展战略。在回归结果中,政府发展战略促进了产业结构高级化,对于产业结构合理化与有效产业结构存在负向作用。因为产业结构高度化描述的是第一产业比重下降,第二产业比重先上升后下降,第三产业比重逐渐增加,政府发展战略正是按照三次产业演进的规律干预资本和劳动在不同产业中的投入。而产业结构合理化描述了要素在各产业中的配置组合是否合理,有效产业结构指数是指产业结构变动中对于经济增长存在促进作用的那部分产业结构变化,从实证结果来看,政府的行为对于要素在产业中的配置组合以及有效的产业结构变动存在负向作用。其他自变量对于产业结构合理化以及产业结构高度化的影响都通过了显著性检验,但是对于有效产业结构(ESC)的影响并不显著。
| 表 5 发展战略影响产业结构的FGLS回归结果 |
① 产业结构合理化指数Theil为TL,为上文中tl的倒数。
2. 影响产业结构调整的动态面板估计通过表 6给出的估计结果可以看出,各被解释变量的滞后项对于本身存在明显的影响,说明产业结构的变动是一种渐进的动态过程。存在这种滞后影响的原因,一是投入要素达到合理的配置需要一定的时间,二是产业结构的演进是基于前期产业结构的演进方式,因此存在这种动态影响机制。政策发展战略提升了产业结构高度化水平,不利于产业结构合理化以及有效产业结构。
| 表 6 发展战略影响产业结构调整的diff-GMM回归估计 |
由于政府政策存在外在时滞效应,所以在具体的经验分析过程中,要考虑这种外在滞后效应的影响。因此在实证分析中加入政府发展战略影响要素资本-劳动配置组合的滞后项,采用2SLS方法进行稳定性检验,并将解释变量的滞后项作为工具变量。表 7和表 8给出了实证结果,发现PCI对于各产业发展以及产业结构的影响没有发生变化,说明文章的实证结果是稳健的,并且政府政策确实存在外在时滞效应。
| 表 7 发展战略影响各产业发展的稳健性检验 |
| 表 8 发展战略影响产业结构调整的稳健性检验 |
本文通过建立理论模型,结合三次产业产值、就业人口、资本存量等数据构建了测算政府发展战略的指标,以及衡量产业结构调整的不同指标,利用1984-2015年中国28个省份的面板数据进行实证分析,得到如下结论:从理论模型推导来看,各产业中资本-劳动配置组合水平的提升会促进本产业劳动产出率水平,政府行为这种“经济楔子”的确可以通过发展战略影响资本-劳动在不同产业中的组合,从而影响各产业发展。从实证结果来看,验证了理论模型中变量政府发展战略(PCI)系数为正的推论。由于要素之间的组合需要时间进行最优配置以及劳动者的学习效应,使得产业的劳动产出效率的提升存在内部动态机制。从政府发展战略影响产业结构调整的实证结果中发现,发展战略对于提升产业结构高度化水平存在明显的促进作用,而对产业结构合理化与有效产业结构水平存在负向作用,说明资本以及劳动投入在产业间的流动并不是合理的配置组合,资本劳动比率的提升虽然有利于产业发展,但是不能够提升要素配置水平,反而对经济增长速度产生负向作用。动态面板的模型中产业结构调整也存在着动态滞后效应,产业结构的变化是对于前期结构的一种扬弃,在这种扬弃的过程中,结构的优化促进了产业发展中资本与劳动的耦合,这种耦合对于产业结构合理化、高度化以及有效产业结构也存在促进作用。
从模型以及实证结果看出,各产业资本劳动比率的提升虽然有利于产业发展,但是这种资本-劳动比率的提升并不一定是好的,会导致资源要素的错配,以及结构的不合理,反而不利于经济增长。只有在要素配置的合理以及结构优化的前提下,提升资本深化,才能提升产业的劳动产出率的同时促进经济增长。从中国以往发展经验来看,政府拥有过多的资源配置权力,中国政府制定发展战略的干预产业发展的行为,虽然促进了各产业发展,但是造成了要素配置结构的扭曲,从经济增速内部分解来看,政府的干预并没有提升促进经济增速的有效产业结构水平,反而存在不利影响。现阶段中国经济进入“新常态”,如何才能通过要素合理配置以及结构优化来提升经济增速,本文的结论为政府行为提供了参考。第一,虽然政府制定的发展战略有助于产业的发展,但是如果政府采取的“有保有压”和“有扶有控”的产业发展战略,有效的产业结构水平并没有提升,可能变得更为扭曲,从而造成了经济增速变缓,因此,要制定顺应市场、不限制竞争、谨慎干预、可评估的有效产业政策,根据“比较优势”以及要素配置规律有效引导资源配置。第二,资源配置过程中应该遵循市场规律,处理好政府与市场的关系,在不存在市场失灵的情况下,尽量通过市场作用实现资源的优化配置。第三,由于体制缺陷和政策偏差,政府没有办法判定什么样的结构才是好的结构,应避免以往利用政府行政手段来“调结构”的做法。
| [] |
干春晖、郑若谷、余典范, 2011, “中国产业结构变迁对经济增长和波动的影响”, 《经济研究》, 第 5 期, 第 4-16 页。 |
| [] |
江飞涛、李晓萍, 2010, “直接干预市场与限制竞争:中国产业政策的取向与根本缺陷”, 《中国工业经济》, 第 9 期, 第 26-36 页。 |
| [] |
罗勤, 2001, “论政府在产业结构调整中的作用”, 《社会科学辑刊》, 第 4 期, 第 97-99 页。 |
| [] |
林毅夫, 2011, “新结构经济学——重构发展经济学的框架”, 《经济学(季刊)》, 第 4 期, 第 1-32 页。 |
| [] |
林毅夫、陈斌开, 2013, “发展战略、产业结构与收入分配”, 《经济学(季刊)》, 第 3 期, 第 1109-1140 页。 |
| [] |
宋建、王静, 2018, “环境污染对产业结构变动的传导机制研究:基于国际细分行业全要素生产率视角”, 《世界经济研究》, 第 6 期, 第 109-122 页。 |
| [] |
王皓, 2009, "金融危机对产业结构的影响", 《中国社会科学报》, 第2期, 第7版。 |
| [] |
王金照, 2010, 《典型国家工业化历程比较与启示》, 北京: 中国发展出版社。 |
| [] |
王坤宇, 2017, “国家发展战略与能源效率”, 《经济评论》, 第 5 期, 第 3-13 页。 |
| [] |
杨大楷、孙敏, 2009, “公共投资与宏观经济结构的实证研究”, 《经济问题》, 第 4 期, 第 21-24 页。 |
| [] |
张冰、金戈, 2007, “港台产业结构变迁:模型与比较”, 《台湾研究》, 第 2 期, 第 44-49 页。 |
| [] |
郑若谷、余典范, 2010, “转型期中国经济增长的产业结构和制度效应——基于一个随机前沿模型的分析”, 《中国工业经济》, 第 2 期, 第 58-67 页。 |
| [] |
Dietrich A., 2012, "Does growth cause structural change, or is it the other way around? A dynamic panel data analysis for seven OECD countries". Empirical Economics, 43(3), 915–944.
DOI:10.1007/s00181-011-0510-z |
| [] |
Lin J.Y., 2002, "Development Strategy, Viability, and Economic Convergence". China Economic Quarterly, 51(2), 277–308.
|
| [] |
Lin J.Y., Chen B., 2011, "Urbanization and urban-rural inequality in china:a new perspective from the governmenta analysis for seven OE". 中国经济学前沿, 6(1), 1–21.
|
| [] |
Mcmillan M., Rodrik D. and Verduzco-Gallo íñigo, 2014, "Globalization, Structural Change, and Productivity Growth, with an Update on Africa". World Development, 63, 11–32.
DOI:10.1016/j.worlddev.2013.10.012 |
| [] |
Peneder M., 2003, "Structural Change and Aggregate Growth". Structural Change & Economic Dynamics, 14.
|
| [] |
Syrquin M., Chenery H., 1989, "Three Decades of Industrialization". World Bank Economic Review, 3(2), 145–181.
DOI:10.1093/wber/3.2.145 |




