1952年,Markowitz(1952)在他开创性的论文中建立了著名的均值-方差模型,奠定了现代投资组合选择理论的基石,使金融研究由定性描述走向定量分析。经典的Markowitz模型只考虑了单期静态情形,之后学者们致力于把它推广到更符合实际的多期及连续时间情形。其中Li and Ng(2000)、Zhou and Li(2000)利用嵌入法技术分别给出了多期和连续时间情形下均值-方差投资组合选择模型的解析解。随后,关于动态均值-方差投资组合选择的研究得到蓬勃发展,如傅毅等(2017)、Zhang and Chen(2016)、Chen et al.(2008)、Wei et al.(2013)。
但上述文献中均假定风险资产价格的随机过程为几何Brown运动,即随机扰动项服从正态分布。然而,大量的实证研究表明,风险资产的收益率并非是高斯分布的并且存在条件异方差(Christoffersen et al., 2009;Andersen et al., 2001)。因而一些学者提出了各种随机波动率的股价模型,如平均值回复模型(Heston,1993),带跳的随机波动率模型(Duffie et al., 2000;Barndorff-Nielsen and Shephard, 2001)和常方差弹性模型(Bakkaloglu et al., 2017;Li et al., 2017)。
另一方面,Lévy过程作为一类广义随机过程,它能够涵盖常见的连续扩散和随机跳跃(Papapantoleon,2005)。研究表明Lévy模型对资产价格的随机过程有着卓越的刻画能力,也可以用小跳跃取代连续扩散(Carr et al., 2002;Carr and Wu, 2004),因此不少学者展开了Lévy过程在金融保险中的应用研究。其中,吴恒煜等(2014)考虑股票收益与波动的负相关关系,建立了漂移率和波动率随条件变化的时变无穷纯跳跃Lévy过程。根据局部鞅测度变换方法,推导了条件Lévy过程的风险中性定价模型,并运用于恒生指数期权进行实证研究。De Vallière et al.(2016)在考虑交易费用的条件下研究了风险资产价格由Lévy过程驱动的最优消费投资问题。Nowak and Pawłowski(2017)考虑了基础资产价格服从Lévy过程的期权问题。Mitsui and Yoshio(2008)讨论了Lévy过程和多维Brown运动共同驱动的齐次随机系统的线性二次(linear quadratic,LQ)控制问题,并将所得结果应用于套期保值问题。
但上述关于Lévy过程在金融保险中的应用研究很少涉及到均值-方差模型的投资组合选择问题,因此本文在Zhou and Li(2000)与张伏等(2014)的基础上,将仅由Brown运动驱动的随机LQ控制问题推广至由Lévy过程和与之独立的多维Brown运动共同驱动的随机LQ控制问题,并将其应用到风险资产价格过程由Lévy过程和与之独立的多维Brown运动共同驱动的均值-方差型投资组合选择问题中。通过运用所得的随机LQ控制结果对模型进行求解,得到了模型的最优投资策略的解析式和有效前沿,最后通过数值算例分析了Lévy过程对最优投资策略和有效前沿影响。
二、模型假设 (一) 记号和准备工作设T≥0是一个固定的数值,(Ω, f,{ft}t≥0, P)是完备的概率空间,流域{ft}t≥0是由m-维Brown运动{W(t)=(W1(t), W2(t), …, Wm(t))′, 0≤t≤T}和一维Lévy过程{L(t), 0≤t≤T}生成的右连续的流域。Lévy过程在ℝ上的测度ν满足∫ℝ(1∧x2)ν(dx) < ∞。
参照张伏等(2014),用{Hi(t), 0≤t≤T}i=1∞表示与Lévy过程{L(t), 0≤t≤T}相关联的Teugles鞅,Hi(t)的定义如下:
| $ {H_i}\left( t \right) = {c_{i,i}}{Y^{\left( i \right)}}\left( t \right) + {c_{i,i - 1}}{Y^{\left( {i - 1} \right)}}\left( t \right) + \cdots + {c_{i,1}}{Y^{\left( 1 \right)}}\left( t \right), $ |
其中,对任意i≥1,Y(i)(t)=L(i)(t)-E[L(i)(t)],L(i)(t)是所谓的幂跳过程; L(1)(t)=L(t),对任意i≥2,L(i)(t)=∑0 < s≤t(ΔL(s))i,cij是多项式1, x, x2, …关于测度μ(dz)=z2ν(dz)+σ2δ0(dz)的正交化系数。关于Teugles鞅的更详细讨论,请读者参阅Nualart and Schoutens(2000)。
为了便于表述,本文引入下面的记号:
·ℝn:n-维欧式空间;
·M′:矩阵M的转置;
·
·Sn:ℝn×n中所有对称矩阵组成的空间;
·S+n:由Sn中所有非负定矩阵组成的子空间;
·C(0, T; X):由[0, T]上的取值于空间X的连续函数构成的巴拿赫空间,其范数为给定希尔伯特空间X上的最大值范数;
·LF2(0, T; X):由满足下列条件的φ={φ(t, ω):0≤t≤T}构成的空间:φ为[0, T]上取值于空间X的Ftt
-适应过程,其范数
在后文的表述中,我们用上述Teugles鞅{Hi(t)}i=1∞表示Lévy过程。
(二) 金融市场假设市场上有m+1种连续交易的资产,其中一种为无风险资产(如银行账户),其在t∈[0, T]时刻的价格过程P0(t)满足如下常微分方程:
| $ d{P_0}\left( t \right) = r\left( t \right){P_0}\left( t \right)dt,\;\;\;\;{P_0}\left( 0 \right) = {p_0} > 0, $ | (1) |
式中的r(t)>0表示无风险利率。其余m种资产为风险资产(如股票),其在t∈[0, T]时刻的价格过程P1(t), …, Pm(t)满足如下随机微分方程:
| $ d{P_i}\left( t \right) = {P_i}\left( {{t^ - }} \right)\left[ {{b_i}\left( t \right)dt + \sum\limits_{j = 1}^m {{\sigma _{ij}}\left( t \right)d{W_j}\left( t \right)} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {{\theta _{ijk}}\left( t \right)d{H_{jk}}\left( t \right)} } } \right],\;\;\;\;{P_i}\left( 0 \right) = {p_i} > 0 $ | (2) |
式中的bi(t)表示第i种风险资产的期望收益率,且bi(t)>r(t);σij(t)表示第j个Brown运动对第i种资产的价格所产生的波动率;θijk(t)表示第j个Lévy过程的跳跃对第i种风险资产的价格所产生的影响;假设对∀t∈[0, T],∃ε>0,使得
考虑一个初始资产为x0的投资者,其在t≥0时刻的资产记为x(t)。设u(t)=(u1(t), …, um(t))′为投资者的一个交易策略,其中ui(t)为t时刻投资到第i种风险资产上的资金,t时刻投资到无风险资产的资金为
| $ \begin{array}{l} dx\left( t \right) = \left[ {x\left( t \right) - \sum\limits_{i = 1}^m {{u_i}\left( t \right)} } \right]\frac{{d{P_0}\left( t \right)}}{{{P_0}\left( t \right)}} + \sum\limits_{i = 1}^m {{u_i}\left( t \right)\frac{{d{P_i}\left( t \right)}}{{{P_i}\left( t \right)}}} \\ \;\;\;\;\;\;\;\; = \left[ {r\left( t \right)x\left( t \right) + \tilde r\left( t \right)u\left( t \right)} \right]dt + \sum\limits_{j = 1}^m {u'\left( t \right){{\sigma '}_j}\left( t \right)d{W_j}\left( t \right)} \\ \;\;\;\;\;\;\;\; + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {u'\left( t \right){\theta _{jk}}\left( t \right)d{H_{jk}}\left( t \right)} } ,\;\;\;\;x\left( 0 \right) = {x_0} > 0, \end{array} $ | (3) |
其中
| $ {\rm{Var}}\;x\left( T \right) \equiv E{\left[ {x\left( T \right) - Ex\left( T \right)} \right]^2} = E{x^2}\left( T \right) - {\left[ {Ex\left( T \right)} \right]^2} $ | (4) |
定义1策略u称为允许策略,若对∀t∈[0, T],u(t)关于ft-循序可测,E∫0T‖u(t)‖2dt < ∞,且对任意的初始资产x0,随机微分方程(3)存在唯一解x(t)。所有允许策略组成的集合记为U。
定义2均值-方差投资组合优化问题记为
| $ \begin{array}{l} \min \;\;\left( {{J_1}\left( {u\left( \cdot \right)} \right),{J_2}\left( {u\left( \cdot \right)} \right)} \right) \equiv \left( { - Ex\left( T \right),{\rm{Var}}\;x\left( T \right)} \right)\\ s.t\left\{ \begin{array}{l} u\left( \cdot \right) \in U,\\ \left( {x\left( \cdot \right),u\left( \cdot \right)} \right)满足\left( 3 \right) \end{array} \right. \end{array} $ | (5) |
显然,该优化问题是一个双目标优化问题。
定义3允许策略u(·)称为有效的投资组合,如果不存在投资组合u(·)使得下列两个不等式至少有一个严格成立
| $ {J_1}\left( {u\left( \cdot \right)} \right) \le {J_1}\left( {\bar u\left( \cdot \right)} \right),\;\;\;\;{J_2}\left( {u\left( \cdot \right)} \right) \le {J_2}\left( {\bar u\left( \cdot \right)} \right) $ | (6) |
此时,称(J1(u(·)), J2(u(·)))∈ℝ2为有效点,有效点的全体构成了有效前沿。
根据多目标优化理论,若将多目标优化中的目标函数乘以一个权重,就可将多目标优化问题转化为一个单目标优化问题。因此,问题(5)可转化为下列的一个单目标最优化问题
| $ \begin{array}{l} \min \;\;{J_1}\left( {u\left( \cdot \right)} \right) + \mu {J_2}\left( {u\left( \cdot \right)} \right) \equiv - Ex\left( T \right) + \mu {\rm{Var}}\;x\left( T \right)\\ \quad \quad s.t\left\{ \begin{array}{l} u\left( \cdot \right) \in U,\\ \left( {x\left( \cdot \right),u\left( \cdot \right)} \right)满足\left( 3 \right) \end{array} \right. \end{array} $ | (7) |
其中μ>0。把上述问题记为P(μ),定义
| $ {\Pi _{P\left( \mu \right)}} = \left\{ {u\left( \cdot \right)\left| {u\left( \cdot \right)\;是\;P\left( \mu \right)\;的最优控制} \right.} \right\} $ | (8) |
把问题P(μ)嵌入到下述辅助问题中
| $ \begin{array}{l} \min \;\;J\left( {u\left( \cdot \right),\mu ,\lambda } \right) = E\left\{ {\mu {x^2}\left( T \right) - \lambda x\left( T \right)} \right\}\\ \;\;\;\;\;\;{\rm{s}}.\;\;{\rm{t}}.\left\{ \begin{array}{l} u\left( \cdot \right) \in U,\\ \left( {x\left( \cdot \right),u\left( \cdot \right)} \right)满足\left( 3 \right) \end{array} \right. \end{array} $ | (9) |
其中0 < λ < +∞。为表述方便,把上述问题记为A(μ, λ),定义
| $ {\Pi _{A\left( {\mu ,\lambda } \right)}} = \left\{ {u\left( \cdot \right)\left| {u\left( \cdot \right)\;是\;A\left( {\mu ,\lambda } \right)\;的最优控制} \right.} \right\} $ | (10) |
下述引理1给出了问题P(μ)与A(μ, λ)二者之间的关系。
引理1 对∀μ>0,若μ(·)∈ΠP(μ),
引理1的证明类似Zhou and Li(2000),囿于篇幅,这里不再给出详细的证明过程。
由引理1可知,通过解决A(μ, λ)可以得到P(μ)问题的最优解。
三、一般的随机LQ问题本节讨论一般情形下由Brown运动和Lévy过程共同驱动的随机LQ问题,而A(μ, λ)问题只是其中的一种特殊情况,我们将在下一节给出详细讨论。
考虑如下的随机微分方程描述的非齐次线性系统
| $ \left\{ \begin{array}{l} dx\left( t \right) = \left[ {A\left( t \right)x\left( t \right) + B\left( t \right)u\left( t \right) + f\left( t \right)} \right]dt + \sum\limits_{j = 1}^m {{D_j}\left( t \right)u\left( t \right)d{W_j}\left( t \right)} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {{F_{jk}}\left( t \right)u\left( t \right)d{H_{jk}}\left( t \right)} } , \hfill \\ x\left( 0 \right) = {x_0} \in {\mathbb{R}^n}, \hfill \\ \end{array} \right. $ | (11) |
其中,x0是系统的初始状态,W(t)≡(W1(t), W2(t), …, Wm(t))′为m-维Brown运动,{Hjk(t)}k=1∞为1维的Teugles鞅,u(t)∈Lf2(0, T; ℝm)是系统的控制输入。系数矩阵A(t)∈C(0, T; ℝn×n),B(t), Dj(t), Fjk(t),∈C(0, T; ℝn×m),f(t)∈Lf2(0, T; ℝn)。
对于每一个u(·)∈Lf2(0, T; ℝm),相应的性能指标取经典的线性二次型
| $ J\left( {u\left( \cdot \right)} \right) = E\int_0^T {\left\{ {\left[ {x'\left( t \right)Q\left( t \right)x\left( t \right) + u'\left( t \right)R\left( t \right)u\left( t \right)} \right]dt + x'\left( T \right)Hx\left( T \right)} \right\}} , $ | (12) |
式中的控制加权矩阵R(t)∈C(0, T; Sm);状态加权矩阵Q(t)∈C(0, T; S+n);H∈S+n。方程(11)的解x(·)称为控制u(·)的响应,(x(·), u(·))称为一个容许对。所谓的随机LQ问题就是在式(11)的约束下寻求最优控制u(·),使得式(12)的J(u(·))达到最小。
现在引入如下受限的随机Riccati方程和常微分方程:
| $ \left\{ \begin{array}{l} \dot P\left( t \right) = - P\left( t \right)A\left( t \right) - A'\left( t \right)P\left( t \right) - Q\left( t \right) + P\left( t \right)B\left( t \right){K^{ - 1}}\left( t \right)B'\left( t \right)P\left( t \right),\\ P\left( T \right) = H,\\ K\left( t \right) \equiv R\left( t \right) + \sum\limits_{j = 1}^m {{{D'}_j}\left( t \right)P\left( t \right){D_j}\left( t \right)} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {{{F'}_{jk}}\left( t \right)P\left( t \right){F_{jk}}\left( t \right)} } > 0, \end{array} \right. $ | (13) |
| $ \left\{ \begin{array}{l} \dot g\left( t \right) = - A'\left( t \right)g\left( t \right) + P\left( t \right)B\left( t \right){K^{ - 1}}\left( t \right)B'\left( t \right)g\left( t \right) - P\left( t \right)f\left( t \right),\\ g\left( T \right) = 0 \end{array} \right. $ | (14) |
定理1如式(13)和(14)存在解P(·)∈C(0, T; S+n)和g(·)∈C(0, T; Sn),则随机LQ问题(11)-(12)的最优反馈控制和最优性能指标分别为
| $ {u^ * }\left( {t,x} \right) = - {K^{ - 1}}\left( t \right)B'\left( t \right)\left( {P\left( t \right)x\left( t \right) + g\left( t \right)} \right), $ | (15) |
| $ {J^ * } = \int_0^T {\left[ {2f'\left( t \right)g\left( t \right) - g'\left( t \right)B\left( t \right){K^{ - 1}}\left( t \right)B'\left( t \right)g\left( t \right)} \right]dt} + x'\left( 0 \right)P\left( 0 \right)x\left( 0 \right) + 2x'\left( 0 \right)g\left( 0 \right) $ | (16) |
证明:假设P(·)∈C(0, T; S+n)和g(·)∈C(0, T; Sn)分别是式(13)和(14)的解,(x(·), u(·))称为一个容许对,利用Itô公式得
| $ \begin{array}{l} d\left( {x'Px + 2x'g} \right)\\ {\rm{ = }}\left\{ {x'\left( {\dot P + A'P + PA} \right)x + 2u'B'\left( {Px + g} \right) + u'\left( {\sum\limits_{j = 1}^m {{{D'}_j}P{D_j}} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {{{F'}_{jk}}P{F_{jk}}} } } \right)u} \right.\\ \;\;\left. { + 2x'\left( {Pf + A'g} \right) + 2f'g} \right\}dt + \sum\limits_{j = 1}^m {\left\{ \cdots \right\}d{W_j}\left( t \right)} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {\left\{ \cdots \right\}d{H_{jk}}\left( t \right)} } . \end{array} $ | (17) |
将式(17)从0到T上积分,并取期望得
| $ \begin{array}{l} E\left[ {x'\left( T \right)P\left( T \right)x\left( T \right) + 2x'\left( T \right)g\left( T \right)} \right] - x'\left( T \right)P\left( T \right)x\left( T \right) - 2x'\left( T \right)g\left( T \right)\\ = E\int_0^T {\left\{ {x'\left( {\dot P + A'P + PA} \right)x + 2u'B'\left( {Px + g} \right) + u'\left( {\sum\limits_{j = 1}^m {{{D'}_j}P{D_j}} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {{{F'}_{jk}}P{F_{jk}}} } } \right)u} \right.} \\ \;\;\;\;\;\left. { + 2x'\left( {Pf + A'g} \right) + 2f'g} \right\}dt. \end{array} $ | (18) |
将式(18)加到式(12),并结合式(13)和(14)得
| $ \begin{array}{l} J\left( {u\left( \cdot \right)} \right) = E\int_0^T {\left\{ {{{\left[ {u + {K^{ - 1}}B'Px + g} \right]}^\prime }K\left[ {u + {K^{ - 1}}B'Px + g} \right] + 2f'g - g'B{K^{ - 1}}B'g} \right\}dt} + x'\left( 0 \right)\\ P\left( 0 \right)x\left( 0 \right) + 2x'\left( 0 \right)g\left( 0 \right) \end{array} $ | (19) |
观察式(19)易知最优反馈控制和最优性能指标分别如式(15)和(16)所示。将最优反馈控制(15)代回式(11)得
| $ \left\{ \begin{array}{l} dx\left( t \right) = \left[ {A\left( t \right)x\left( t \right) - B\left( t \right){K^{ - 1}}\left( t \right)B'\left( t \right)\left( {P\left( t \right)x\left( t \right) + g\left( t \right)} \right) + f\left( t \right)} \right]dt - \sum\limits_{j = 1}^\infty {{D_j}\left( t \right){K^{ - 1}}\left( t \right)B'\left( t \right)} \\ \;\;\;\;\;\;\;\;\;\; + \left( {P\left( t \right)x\left( t \right) + g\left( t \right)} \right)d{W_j}\left( t \right) - \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {{F_{jk}}\left( t \right){K^{ - 1}}\left( t \right)B'\left( t \right)\left( {P\left( t \right)x\left( t \right) + g\left( t \right)} \right)d{H_{jk}}\left( t \right)} } ,\\ x\left( 0 \right) = {x_0}, \end{array} \right. $ | (20) |
式(20)是一个非齐次线性随机微分方程,由于P(t)∈C(0, T; S+n),g(t)∈C(0, T; Sn)和K-1(t)∈C(0, T; S+m),结合随机微分方程理论知式(20)存在唯一解。证毕。
四、辅助问题的解在本节中,我们将借助一般的随机LQ问题的结果求解A(μ, λ)问题。令γ=λ/2μ,y(t)=x(t)-γ,则A(μ, λ)等价于下述的随机LQ问题
| $ \left\{ \begin{array}{l} dy\left( t \right) = \left[ {A\left( t \right)y\left( t \right) + B\left( t \right)u\left( t \right) + f\left( t \right)} \right]dt + \sum\limits_{j = 1}^m {{D_j}\left( t \right)u\left( t \right)d{W_j}\left( t \right)} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {{F_{jk}}\left( t \right)u\left( t \right)d{H_{jk}}\left( t \right)} } , \hfill \\ y\left( 0 \right) = {x_0} - \gamma \in {\mathbb{R}^n}, \hfill \\ \end{array} \right. $ | (21) |
性能指标为J(u(·), μ, λ)=E{μx2(T)-λx(T)}=E{μy2(T)-μλ2}等价于minJ(u(·))=E{μy2(T)}。
写成标准二次型形式为
| $ J\left( {u\left( \cdot \right)} \right) = E\left\{ {\int_0^T {\left[ {x'\left( t \right)Q\left( t \right)x\left( t \right) + u'\left( t \right)R\left( t \right)u\left( t \right)} \right]dt + x'\left( T \right)Hx\left( T \right)} } \right\} $ | (22) |
在式(21)和(22)中,A(t)=r(t),
注意到式(22)中,控制加权矩阵R(t)=0,这说明在随机LQ框架下,均值-方差模型是一个奇异随机LQ问题。为了书写方便,记
| $ \rho \left( t \right) = B\left( t \right){\left[ {\sum\limits_{j = 1}^m {{D_j}\left( t \right){{D'}_j}\left( t \right)} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^\infty {{{F'}_{jk}}\left( t \right){F_{jk}}\left( t \right)} } } \right]^{ - 1}}B'\left( t \right) = B\left( t \right){\Sigma ^{ - 1}}B'\left( t \right) $ | (23) |
则Riccati方程(13)退化为
| $ \left\{ \begin{array}{l} \dot P\left( t \right) = \left( {\rho \left( t \right) - 2r\left( t \right)} \right)P\left( t \right),\\ P\left( T \right) = \mu ,\\ P\left( t \right)\Sigma \left( t \right) > 0,\;\;\;t \in \left[ {0,T} \right] \end{array} \right. $ | (24) |
常微分方程(14)退化为
| $ \left\{ \begin{array}{l} \dot g\left( t \right) = \left( {\rho \left( t \right) - r\left( t \right)} \right)g\left( t \right) - \gamma r\left( t \right)P\left( t \right),\\ g\left( T \right) = 0,\;\;\;\;\;t \in \left[ {0,T} \right] \end{array} \right. $ | (25) |
最优反馈控制为
| $ \bar u\left( {t,y} \right) \equiv {\left( {{{\bar u}_1}\left( {t,y} \right), \cdots ,{{\bar u}_m}\left( {t,y} \right)} \right)^\prime } = - {\Sigma ^{ - 1}}\left( t \right)B'\left( t \right)\left( {y + \frac{{g\left( t \right)}}{{P\left( t \right)}}} \right) $ | (26) |
令
| $ h\left( t \right) = \frac{{P\left( t \right)\dot g\left( t \right) - \dot P\left( t \right)g\left( t \right)}}{{{P^2}\left( t \right)}} = \frac{{r\left( t \right)P\left( t \right)g\left( t \right) - \gamma r\left( t \right){P^2}\left( t \right)}}{{{P^2}\left( t \right)}} = r\left( t \right)h\left( t \right) - \gamma r\left( t \right) $ | (27) |
由定解条件h(T)=0可得上述方程的解为
| $ \frac{{g\left( t \right)}}{{P\left( t \right)}} = h\left( t \right) = \gamma \left( {1 - {e^{ - \int_t^T {r\left( s \right)ds} }}} \right) $ | (28) |
将式(28)代入式(26)得
| $ \begin{array}{l} \bar u\left( {t,x} \right) = {\left( {{{\bar u}_1}\left( {t,x} \right), \cdots ,{{\bar u}_m}\left( {t,x} \right)} \right)^\prime } = - {\Sigma ^{ - 1}}\left( t \right)B'\left( t \right)\left[ {x - \gamma + \gamma \left( {1 - {e^{ - \int_t^T {r\left( s \right)ds} }}} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {\Sigma ^{ - 1}}\left( t \right)B'\left( t \right)\left[ {\gamma {e^{ - \int_t^T {r\left( s \right)ds} }} - x} \right] \end{array} $ | (29) |
建立在均值-方差基础上的投资组合选择理论,寻求的最优投资组合结果是在等方差的情况下收益的最大化, 或者在等收益的情况下方差的最小化。而这一结果可以通过均值-方差平面上的有效前沿来直观给出。因此,本节推到原均值-方差问题(5)的有效前沿。
将式(29)代回式(3),则投资者的财富方程变为
| $ \left\{ \begin{array}{l} {\rm{dx}}\left( t \right) = \left\{ {\left( {{\rm{r}}\left( {\rm{t}} \right) - {\rm{ \mathit{ ρ} }}\left( {\rm{t}} \right)} \right){\rm{x}}\left( {\rm{t}} \right) + {\rm{ \mathit{ γ} }}{{\rm{e}}^{ - \int_{\rm{t}}^{\rm{T}} {{\rm{r}}\left( {\rm{s}} \right){\rm{ds}}} }}{\rm{ \mathit{ ρ} }}\left( {\rm{t}} \right)} \right\}{\rm{dt}} + {\rm{B}}\left( {\rm{t}} \right){\mathit{\Sigma }^{ - 1}}\left( {\rm{t}} \right)\left[ {{\rm{ \mathit{ γ} }}{{\rm{e}}^{ - \int_{\rm{t}}^{\rm{T}} {{\rm{r}}\left( {\rm{s}} \right){\rm{ds}}} }} - {\rm{x}}} \right]\\ \left[ {{\rm{ \mathit{ σ} }}\left( {\rm{t}} \right){\rm{d}}W\left( {\rm{t}} \right) + \sum\limits_{{\rm{k}} = 1}^\infty {{{\rm{ \mathit{ θ} }}_{\rm{k}}}\left( {\rm{t}} \right){\rm{d}}{{\rm{H}}_{\rm{k}}}\left( {\rm{t}} \right)} } \right],\\ {\rm{x}}\left( 0 \right) = {{\rm{x}}_0} > 0 \end{array} \right. $ | (30) |
对x2(t)利用Itô公式,得
| $ \left\{ \begin{array}{l} d{x^2}\left( t \right) = \left\{ {\left( {2r\left( t \right) - \rho \left( t \right)} \right){x^2}\left( t \right) + {\gamma ^2}{e^{ - \int_t^T {r\left( s \right)ds} }}\rho \left( t \right)} \right\}dt + 2x\left( t \right)B\left( t \right){\mathit{\Sigma }^{ - 1}}\left( t \right)\\ \left[ {\gamma {e^{ - \int_t^T {r\left( s \right)ds} }} - x} \right]\left[ {\sigma \left( t \right)dW\left( t \right) + \sum\limits_{k = 1}^\infty {{\theta _k}\left( t \right)d{H_k}\left( t \right)} } \right],\\ {x^2}\left( 0 \right) = x_0^2 > 0 \end{array} \right. $ | (31) |
式(30)和(31)同时取数学期望,得Ex(t)和Ex2(t)满足如下两个非齐次线性常微分方程
| $ \left\{ \begin{array}{l} dEx\left( t \right) = \left\{ {\left( {r\left( t \right) - \rho \left( t \right)} \right)Ex\left( t \right) + \gamma {e^{ - \int_t^T {r\left( s \right)ds} }}\rho \left( t \right)} \right\}dt,\\ Ex\left( 0 \right) = {x_0} > 0, \end{array} \right. $ | (32) |
| $ \left\{ \begin{array}{l} dE{x^2}\left( t \right) = \left\{ {\left( {2r\left( t \right) - \rho \left( t \right)} \right)E{x^2}\left( t \right) + {\gamma ^2}{e^{ - 2\int_t^T {r\left( s \right)ds} }}\rho \left( t \right)} \right\}dt,\\ E{x^2}\left( 0 \right) = x_0^2 > 0 \end{array} \right. $ | (33) |
求解上述两个方程可得
| $ Ex\left( T \right) = \alpha {x_0} + \beta \gamma ,E{x^2}\left( T \right) = \delta x_0^2 + {\gamma ^2}, $ | (34) |
其中
| $ \alpha = {e^{\int_0^T {\left( {r\left( t \right) - \rho \left( t \right)} \right)dt} }},\beta = 1 - {e^{ - \int_0^T {\rho \left( t \right)dt} }},\delta = {e^{\int_0^T {\left( {2r\left( t \right) - \rho \left( t \right)} \right)dt} }} $ | (35) |
由引理1知,若问题P(μ)的最优控制存在,则可以通过选择下式所示的λ来求得
| $ \bar \lambda = 1 + 2\mu E\bar x\left( T \right) = 1 + 2\mu \left( {\alpha {x_0} + \beta \frac{\lambda }{{2\mu }}} \right) $ | (36) |
解上式得
| $ \bar \lambda = \frac{{1 + 2\mu \alpha {x_0}}}{{1 - \beta }} = {e^{\int_0^T {\rho \left( t \right)dt} }} + 2\mu {x_0}{e^{\int_0^T {r\left( t \right)dt} }},\gamma = \bar \gamma = \frac{{\bar \lambda }}{{2\mu }} $ | (37) |
将式(37)代回式(29)可得问题P(μ)的最优投资组合
| $ \bar u\left( {t,x} \right) = {\mathit{\Sigma }^{ - 1}}\left( t \right)B'\left( t \right)\left( {{x_0}{e^{\int_0^T {r\left( s \right)ds} }} - x + \frac{{{e^{\int_0^T {\rho \left( t \right)dt} - - \int_t^T {r\left( s \right)dt} }}}}{{2\mu }}} \right) $ | (38) |
相应地,终端财富的方差为
| $ \begin{array}{l} {\rm{Var}}\;\bar x\left( T \right) = E{{\bar x}^2}\left( T \right) - \left[ {{}^E\bar x\left( T \right)} \right]2\\ = \beta \left( {1 - \beta } \right){{\bar \gamma }^2} - 2\alpha \beta {x_0}\bar \gamma + \left( {\delta - {\alpha ^2}} \right)x_0^2 = \frac{{1 - \beta }}{\beta }\left[ {{\beta ^2}{{\bar \gamma }^2} - 2\frac{{\alpha {\beta ^2}{x_0}\bar \gamma }}{{1 - \beta }} + \frac{{\beta \left( {\delta - {\alpha ^2}} \right)}}{{1 - \beta }}x_0^2} \right] \end{array} $ | (39) |
将式(34)中的βγ=Ex(T)-αx0代入上式,并结合式(35)得
| $ \begin{array}{l} {\rm{Var}}\;\bar x\left( T \right) = \frac{{1 - \beta }}{\beta }\left[ {{{\left( {E\bar x\left( T \right)} \right)}^2} - 2\frac{\alpha }{{1 - \beta }}{x_0}E\bar x\left( T \right) + \frac{{\beta \delta + {\alpha ^2}}}{{1 - \beta }}x_0^2} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{1 - \beta }}{\beta }{\left[ {E\bar x\left( T \right) - {x_0}{e^{\int_0^T {r\left( t \right)dt} }}} \right]^2}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{{e^{ - \int_0^T {\rho \left( t \right)dt} }}}}{{1 - {e^{ - \int_0^T {\rho \left( t \right)dt} }}}}{\left[ {E\bar x\left( T \right) - {x_0}{e^{\int_0^T {r\left( t \right)dt} }}} \right]^2} \end{array} $ | (40) |
综合上述分析,可得如下结论。
定理2 对于双目标最优投资组合选择问题(5),如果它的有效前沿存在,则由式(40)确定。
式(40)揭示了投资者对于投资的均值(期望回报Ex(T))与其所承受的方差(风险水平varx(T))之间的关系。若记终端财富的标准差为σx(T),则由式(40)可得
| $ E\bar x\left( T \right) = {x_0}{e^{\int_0^T {r\left( t \right)dt} }} + \sqrt {\frac{{1 - {e^{ - \int_0^T {\rho \left( t \right)dt} }}}}{{{e^{ - \int_0^T {\rho \left( t \right)dt} }}}}} {\sigma _{\bar x}}\left( t \right) $ | (41) |
对于无Lévy过程情形下的均值-方差模型已在文献Zhou and Li(2000)中讨论过,对比该文可以发现,本文中所得的如式(40)所示的有效前沿与Zhou and Li(2000)中式(6.9)所得的有效前沿在形式上是一致的。在给定相同的期望回报(Ex(T))、相同的初始财富(x0)和相同的无风险利率水平(r(t))下,varx(T)主要受到ρ(t)的影响。而本文中由于Lévy过程的引入,使得式(23)中的Σ(t)增大,从而使得ρ(t)的取值比文献Zhou and Li(2000)中式(5.6)所示的ρ(t)的取值要小,这就使得
本节通过数值算例对比分析有Lévy过程和无Lévy过程两种情形下投资者的最优决策,从而得出Lévy过程的引入对投资者决策的影响。为了便于比较,我们沿用Zhou and Li(2000)中所使用的例子,考虑1种风险资产,它由一个Brown运动和一个Lévy过程共同驱动,假设模型中的各参数均为常数,取值如下表 1所示。
| 表 1 模型中所用的参数取值及初始值 |
在有Lévy过程的情形下,计算得Σ=σ2+θ2=0.0325,ρ=(b-r)2/Σ=0.1108,代入式(40)得
| $ {\rm{Var}}\bar x\left( 1 \right) = \frac{{{e^{ - 0.1108}}}}{{1 - {e^{ - 0.1108}}}}{\left( {E\bar x\left( 1 \right) - {e^{0.06}}} \right)^2} $ |
而在无Lévy过程的情形下,投资者对于期望回报(Ex(1))与其所承受的风险水平(varx(1))之间的关系如下式所示
| $ {\rm{Var}}\bar x\left( 1 \right) = \frac{{{e^{ - 0.1600}}}}{{1 - {e^{ - 0.1600}}}}{\left( {E\bar x\left( 1 \right) - {e^{0.06}}} \right)^2} $ |
下图 1给出了有Lévy过程和无Lévy过程两种情形下投资者的有效前沿。
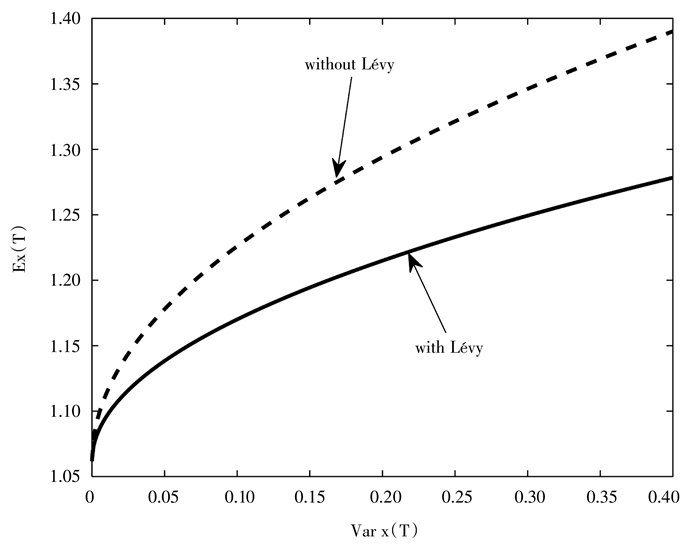
|
图 1 M-V平面内的有效前沿 |
从图 1可以看出,在相同的期望收益下,有Lévy过程情形下投资者承担的风险要比无Lévy过程情形下投资者承担的风险要高。出现这种情况的原因可能是,Lévy过程作为除布朗运动以外的不确定干扰,投资者已无额外的投资机会去对冲掉该风险,因而增加了投资者的投资风险。
接下来比较有Lévy过程和无Lévy过程两种情形下投资者的最优投资策略。
如Zhou and Li(2000)所示,假设投资者希望在这1年内取得20%的期望回报,即终端财富Ex(1)=1.2,将该值代入式(34)得
| $ \bar u\left( {t,x} \right) = 1.8462\left( {2.3792{e^{0.06\left( {t - 1} \right)}} - x} \right) $ |
而在无Lévy过程情形下的最优投资策略为
| $ \bar u\left( {t,x} \right) = 2.6667\left( {1.9963{e^{0.06\left( {t - 1} \right)}} - x} \right) $ |
为了直观地比较有Lévy过程和无Lévy过程两种情形下投资者的最优投资策略,不妨限定u(t, x)中的x取一个常值x0,下图 2给出了两种情形下的最优投资策略。
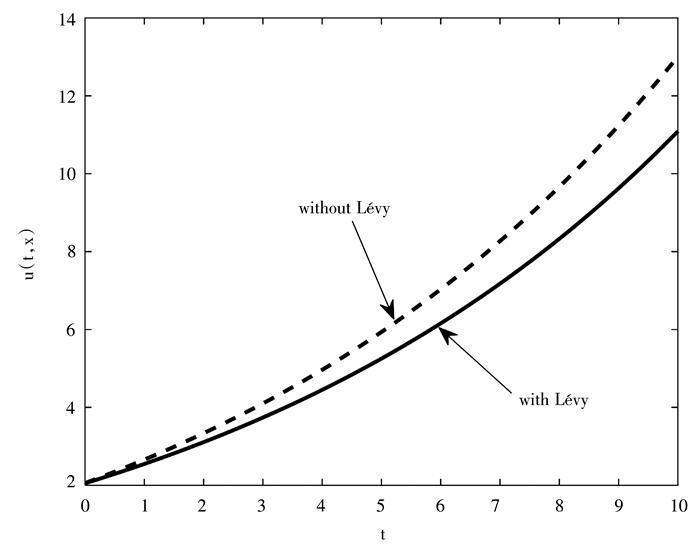
|
图 2 最优投资策略 |
从图 2可以看出,无Lévy过程情形下的最优投资策略曲线明显位于有Lévy过程情形下的最优投资策略曲线的上端,表明因为Lévy过程的存在,导致投资者在风险资产上的投资减少。
七、结语本文在连续时间框架下,研究了由Lévy过程和与之独立的多维Brown运动共同驱动的非齐次随机系统的LQ控制问题。利用Riccati方程法得到系统的最优反馈控制策略,并将所得理论结果应用于风险资产价格由Lévy过程和Brown运动共同驱动的均值-方差投资组合选择问题中,使用“嵌入”方法将其转化为随机LQ控制问题,在自融资的条件下,得到了最优证券组合的显式表达。最后通过数值算例对比分析有Lévy过程和无Lévy过程情形下投资者的最优投资策略和有效前沿,发现Lévy过程的存在增加了投资者的投资风险,使得投资者的投资都变得更加谨慎。本文推广了Zhou and Li(2000)的研究,因而所得的结论具有更广泛的用途。
| [] |
傅毅、张寄洲、周翠,
2017, “基于均值-方差模型的P2P债权投资策略与风险度量问题研究”, 《管理评论》, 第 7 期, 第 19-28 页。 |
| [] |
吴恒煜、朱福敏、温金明,
2014, “带杠杆效应的无穷纯跳跃Levy过程期权定价”, 《管理科学学报》, 第 8 期, 第 74-94 页。 |
| [] |
张伏、唐矛宁、孟庆欣,
2014, “Lévy过程驱动的正倒向随机系统的随机最大值原理”, 《数学年刊》, 第 1 期, 第 83-100 页。 |
| [] |
Markowitz H., 1952, "Portfolio Selection". Journal of Finance, 7(1), 77–91.
|
| [] |
Li D., Ng W. L., 2000, "Optimal Dynamic Portfolio Selection:Multiperiod Mean-Variance Formulation". Mathematical Finance, 10(3), 387–406.
DOI:10.1111/mafi.2000.10.issue-3 |
| [] |
Zhou X. Y., Li D., 2000, "Continuous-Time Mean-Variance Portfolio Selection:A Stochastic LQ Framework". Applied Mathematics & Optimization, 42(1), 19–33.
|
| [] |
Zhang M., Chen P., 2016, "Mean-Variance Asset-Liability Management under Constant Elasticity of Variance Process". Insurance:Mathematics and Economics, 70, 11–18.
DOI:10.1016/j.insmatheco.2016.05.019 |
| [] |
Chen P., Yang H. and Yin G., 2008, "Markowitz's Mean-Variance Asset-Liability Management with Regime Switching:A Continuous-Time Model". Insurance:Mathematics and Economics, 43(3), 456–465.
DOI:10.1016/j.insmatheco.2008.09.001 |
| [] |
Wei J., Wong K. C., Yam S. C. P. and Yung S. P., 2013, "Markowitz's Mean-Variance Asset-Liability Management with Regime Switching:A Time-Consistent Approach". Insurance:Mathematics and Economics, 53(1), 281–291.
DOI:10.1016/j.insmatheco.2013.05.008 |
| [] |
Christoffersen P., Elkamhi R., Feunou B. and Jacobs K., 2009, "Option Valuation with Conditional Heteroskedasticity and Nonnormality". The Review of Financial Studies, 23(5), 2139–2183.
|
| [] |
Andersen T. G., Bollerslev T., Diebold F. X. and Ebens H., 2001, "The Distribution of Realized Stock Return Volatility". Journal of Financial Economics, 61(1), 43–76.
DOI:10.1016/S0304-405X(01)00055-1 |
| [] |
Heston S. L., 1993, "A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options". The Review of Financial Studies, 6(2), 327–343.
DOI:10.1093/rfs/6.2.327 |
| [] |
Duffie D., Pan J. and Singleton K., 2000, "Transform Analysis and Asset Pricing for Affine Jump-Diffusions". Econometrica, 68(6), 1343–1376.
DOI:10.1111/ecta.2000.68.issue-6 |
| [] |
Barndorff-Nielsen O. E., Shephard N., 2001, "Non-Gaussian Ornstein-Uhlenbeck-Based Models and Some of Their Uses in Financial Economics". Journal of the Royal Statistical Society:Series B, 63(2), 167–241.
DOI:10.1111/rssb.2001.63.issue-2 |
| [] |
Bakkaloglu A., Aziz T., Fatima A., Mahomed F. M. and Khalique C. M., 2017, "Invariant Approach to Optimal Investment-Consumption Problem:the Constant Elasticity of Variance (CEV) Model". Mathematical Methods in the Applied Sciences, 40(5), 1382–1395.
DOI:10.1002/mma.v40.5 |
| [] |
Li D., Rong X., Zhao H. and Yi B., 2017, "Equilibrium Investment Strategy for DC Pension Plan with Default Risk and Return of Premiums Clauses under CEV Model". Insurance:Mathematics and Economics, 72, 6–20.
DOI:10.1016/j.insmatheco.2016.10.007 |
| [] |
Papapantoleon, A., 2008, An Introduction to Lévy Processes with Applications in Finance, Lecture Notes, TU Vienna.
|
| [] |
Carr P., Geman H., Madan D. B. and Yor M., 2002, "The Fine Structure of Asset Returns:An Empirical Investigation". The Journal of Business, 75(2), 305–332.
DOI:10.1086/jb.2002.75.issue-2 |
| [] |
Carr P., Wu L., 2004, "Time-Changed Lévy Processes and Option Pricing". Journal of Financial Economics, 71(1), 113–141.
DOI:10.1016/S0304-405X(03)00171-5 |
| [] |
De Vallière D., Kabanov Y. and Lépinette E., 2016, "Consumption-Investment Problem with Transaction Costs for Lévy-Driven Price Processes". Finance and Stochastics, 20(3), 705–740.
DOI:10.1007/s00780-016-0303-5 |
| [] |
Nowak P., Pawłowski M., 2017, "Option Pricing with Application of Levy Processes and the Minimal Variance Equivalent Martingale Measure under Uncertainty". IEEE Transactions on Fuzzy Systems, 25(2), 402–416.
DOI:10.1109/TFUZZ.2016.2637372 |
| [] |
Mitsui K., Yoshio T., 2008, "A Stochastic Linear-Quadratic Problem with Lévy Processes and Its Application to Finance". Stochastic Processes and their Applications, 118(1), 120–152.
DOI:10.1016/j.spa.2007.03.011 |
| [] |
Nualart D., Schoutens W., 2000, "Chaotic and Predictable Representations for Lévy Processes". Stochastic processes and their applications, 90(1), 109–122.
DOI:10.1016/S0304-4149(00)00035-1 |



