21世纪以来,我国居民收入大幅增长,2006至2015年,我国居民年均工资由21001元上升到62029元。然而,由于城乡、地区、行业分割造成的工资差距加大的现象也越发显著(HP. Chen, 2002; J.Knight, 2003; 陈钊, 2010)。2016年贵州省人均可支配收入为15121元,仅为上海的27.8%。过大的收入差距会破坏社会发展的稳定,因此,在保持工资增长的同时缩小不同群体间的收入差距,是国家十三五计划的一个重点。
经济集聚的规模效应和外部效应是收入增长与差距形成的重要原因(Combes,2003;J.Vernon Henderson, 2010)。地区平均人力资本水平提高能提高所有生产要素的生产率(Lucas, 1988),高技能工人的集聚使得知识、技术能够以较低的成本在特定范围内传播,团队间的交流与学习促进了城市扩大,经济增长以及工资提高(Romer,1989)。Puga(2010)、Glaeser and Resseger(2010)等学者对西方国家城市化的研究表明,城市中人力资本的集聚对工资溢价产生正向影响,对中国的研究也证明了相同的结论(柴国俊、邓国营,2012)。但也有学者发现,教育的社会收益率并不显著(Acemoglu, 2001)。在考虑选择偏差问题后,大城市中劳动者的收入优势甚至不再存在(宁光杰,2014)。
除内生性问题外,群体内部异质性也是影响平均效果的一个重要因素。由于性别、行业、地区、户籍的分割,城市人力资本对于不同群体有不同作用,从而间接影响了收入差距。Wheeler(2001), Adamson et al.(2004)和Lee(2010)认为城市人力资本产生的外部效应仅对特定技能劳动者有利,而对其他人影响不显著。Heuermann(2011)对于德国工人的数据研究表明,由于高技能区域劳动力市场匹配度更强,工人在高技能劳动力市场上实现行业内比行业间转换工作的可能性大一半,人力资本集聚更可能使高技能地区的工人获益。本文注意到城市的人力资本积累与高技术产业联系更为密切,将其作为重点因素研究。由于我国巨大的区域发展差异,2002年以来,对于男性、年长劳动者、东西部地区的群体来说,教育回报率持续提高,而对于女性、年轻劳动者和中部地区群体却出现停滞(刘泽云,2015)。因此,除了研究城市人力资本积累与工资的基本关系之外,本文将重点考察异质性影响,并分析收入差异的来源。
在前人研究的基础上,Fu(2007)提出了城市人力资本发挥外溢效应的四个渠道:人力资本深度、信息技术专业化水平、产业多样化程度、就业密度。人力资本深度指一个地区平均的教育水平,它的提高有利于推动创新、提升地区生产率,拉动企业对高技能人才以及其互补工人的需求,但同时也可能削弱替代工人的议价能力。马歇尔指出,经济集聚的专业化使得工人可以从当地相同职位、行业的同事中学习知识,从而对工资起到促进作用,且这种作用在高技术产业更显著(Rosenthal and Strange, 2004)。尽管有学者认为产业多样化有利于跨领域创新(Berliant, Reed, and Wang, 2002),但多样化造成的较高协调成本可能抵消了其积极作用,一些研究也表明其对于工资并无显著效果(Henderson, 2003;王海宁,2010;杨仁发,2013)。最后,劳动力市场密度越高,就业摩擦越小,工人越容易找到工作,但过高的就业密度可能会产生“拥塞”,削弱工人的竞争力。
目前,从这四个角度全面探究城市人力资本作用的文献尚不多,得出的结论也不相同。大部分研究者聚焦于平均效应,较少深入研究异质性关系,且多数模型都忽视了城市间和城市内的不同误差。本文采用分层线性模型(Hierarchical Linear Model)克服这一缺陷,运用跨层交互、分组回归以及分位数回归深入探究异质性影响,并用工具变量进行检验。文章安排如下:第二部分,理论框架和假设;第三部分,数据来源与计量模型;第四部分,基本模型实证分析;第五部分,异质性影响实证分析;第六部分,结论。
二、理论框架Acemoglu(1999)指出,有两种因素影响着职业结构:一、劳动力市场中高技术人员所占的比例,这种人员比重增加到临界点时,会使得厂商增加设置高技能岗位的数量,从而改变职业的结构。二、技术偏向性进步或者国际贸易使得对高技能劳动力需求的增加。考虑经济集聚的影响,当高技术人员比重提高时,与其互补的低技能工人的需求也将提高,因此对所有人的工资都有积极影响。另一方面,除人力资本程度提高、技术进步外,厂商寻找一个与空缺职位匹配的工人的成本、工人的议价能力大小也都会在不同程度上影响不同工人的工资。首先,本文借鉴Acemoglu的方法,通过一个静态模型进行分析。
假定有总量为1的风险中性的工人和同样数量的以利润最大化为目的的厂商。经济体只持续1个时期,且只包含2种类型的工人:受过高等教育者和未受过高等教育者(受过高等教育者倾向于从事高技术职业)。用ϕ来代表高技术工人所占比例,并将低技术者的人力资本存量或者说技术生产率正态化为h=1,则此时高技术者的h=η>1。假设一个拥有h的工人和拥有物质资本为k的工厂生产:
| $ y\left( {k,{\rm{ }}h} \right) = {k^{1 - \alpha }}{h^\alpha } $ |
事件的发生遵循以下顺序。首先,每个公司选择自己的资本(不可回收的),这个选择决定了公司设计的职位类型和商业方向。在这里,假定每寻找一个与空缺职位匹配的工人所耗费的成本占公司人均资本比例为Q(且Q对于不同类型的工人都相同)。此时,公司并不知道它会雇佣那种类型的工人。接下来,公司与工人匹配,并决定是否继续经营。若继续经营,则其耗费ck成本配置与工人相应的设备。最后,工资通过工人与厂商的谈判决定。考虑一个有摩擦的交易环境,厂商和工人随机匹配,即高资本与低资本厂商有相同的概率遇到高技术工人。一旦匹配成功,他们就会继续生产,并以一定比例分配产出y。这里,工资在不同资本水平公司的条件下有所不同。工资由工人的谈判能力β和产出y决定,而工厂的盈利则是除工资外的剩余与匹配所耗资本的差。为方便计算,将c、Q正态化为c≡1-β, Q≡q(1-β)
| $ \begin{array}{l} {w^H}\left( k \right) = \beta {k^{1 - \alpha }}{\eta ^\alpha },{w^L}\left( k \right) = \beta {k^{1 - \alpha }}\\ V({x^H},{x^L},k) = \phi {x^H}\left( {1 - \beta } \right)[{k^{1 - \alpha }}{\eta ^\alpha } - k] + \left( {1 - \phi } \right){x^L}\left( {1 - \beta } \right)[{k^{1 - \alpha }} - k] - q\left( {1 - \beta } \right)k \end{array} $ |
其中Xj是工厂结合j=L/H类型的工人的均衡可能性。在这个静态经济体中,工人是被动的:他们接受任何能够得到匹配。因此,均衡只是在H范围内,用F(k)代表的资产选择的分布。根据一阶条件,在混同均衡下,XH=XL=1, 解得:
| $ \begin{array}{l} {k^*} = {[\frac{{(\phi {\eta ^\alpha } + 1 - \phi )\left( {1 - a} \right)}}{{1 + q}}]^{1/\alpha }}\\ V({x^H} = 1,{x^L} = 1,{k^*}) = c{[\frac{{(\phi {\eta ^\alpha } + 1 - \phi )\left( {1 - a} \right)}}{{1 + q}}]^{\frac{{1 - \alpha }}{\alpha }}}a(\phi {\eta ^\alpha } + 1 - \phi )\\ = ac{\left( {\frac{{1 - a}}{{1 + q}}} \right)^{\frac{1}{a} - 1}}(\phi {\eta ^\alpha } + 1 - \phi ) \end{array} $ |
而在分离均衡情况下,满足V(xH=1, xL=0, k)>V(xH=xL=1, k*),即
| $ k\prime = {\left[ {\frac{{{\eta ^\alpha }\phi \left( {1 - a} \right)}}{{q + \phi }}} \right]^{1/\alpha }},V({x^H} = 1,{x^L} = 0,k = {k^{'}}) = a\phi c\eta {\left[ {\frac{{\phi \left( {1 - a} \right)}}{{q + \phi }}} \right]^{\frac{1}{a} - 1}} $ |
当技术人员的生产率与非技术人员之比并未超过这个临界值时,会形成混同均衡(pool equilibrium)。简单推理可知,当ϕ越大时,临界值η*越小,也越容易形成分离均衡。在混同均衡中,公司对两种员工采用相同的资本,因此低技能工人的物质-人力资本比高于高技术工人。而在分离均衡(separate equilibrium)中,工厂仅用较高的资本去匹配高技术工人,而拒绝低技术工人。
在两种情况下,对工资方程中的q, ϕ, η分别求导得,
高低技术工人技术生产率或人力资本之比为η,该因素容易受到当地高技术产业生产率的影响。因此,高技术产业专业化程度高地个体工资应该有促进作用。相关研究表明,产业多样化程度增加则会增加协调成本,使劳动力市场摩擦增加,限制劳动力流动从而降低工人的议价能力(黄思,2013),其产生的“就业补充效应”也会对工资起到抑制作用。但多样化同时也会对增加知识外溢、推动创新起到积极作用(Handerson, 2001)。这两种作用的大小不定,导致总体上对工资影响是模糊的。另外,在一个限定的地理区域内,劳动力市场密度越高,匹配成本越低(Carlino and Hunt, 2009),工人越可能在随机匹配中找到合适的工作。国外许多经验研究表明,空间密度导致累计回报增长(Ciccone and Hall, 1996),对工资有显著的正向效应(Mion, Naticchioni, 2005)。而对于我国的研究并未得到统一结论。范剑勇(2006)发现城市就业密度每提高1个百分点, 非农产业的劳动生产率提高8.8个百分点。刘修岩、殷醒民(2009)以地级行政区域为样本,发现在控制其他影响因素后,劳动力市场密度对工资水平的影响呈现非线性的关系,当就业密度达到某个“门滥”时,就业密度才能对工资水平呈现正向效应。综上,我们提出猜测:
H1:大学生比例提高对工资有积极影响,且对受教育程度高的群体影响较大;
H2:高技术产业生产率提高也会提高工资;
H3:产业多样化对工资的影响方向不确定;
H4:劳动力市场密度提高会提高工资。
三、数据来源与模型设定 (一) 数据和变量本文的微观数据来源于CHIP2013,CHIP2013的样本来自国家统计局2013年城乡一体化常规住户调查大样本库。考虑到人力资本积累范围基本集中于城镇内,本文采用了城镇住户的样本,并剔除了未工作的样本,且选择了年龄处于15-60岁之间的劳动就业人口。本文城市层面的数据来自于2014年《中国城市统计年鉴》。经过筛选、插补后,CHIP2013共9326个样本,其中男性5244名,女性4082名,一共来自14个省、直辖市的115个地级市。
1. 被解释变量本文的被解释变量为小时工资。原始数据中最高与最低工资者之间差距较大,而家户消费差距更大,为使因变量服从正态分布,本文进行了对数化处理。根据2016年全国小时工资最低标准,除极个别情况外,大部分最低工资标注都在10元/小时以上。因此本文在前面的分析中,先将取对数后小于0(即小时工资低于10元)的样本剔除,一共83名,占全样本的0.89%,剔除后样本有9243个。在其后的分析中,本文又将这些个体的工资视为0,纳入模型讨论。个体小时收入对数均值为2.6。进一步将样本根据个体特征分类可知,男性工资高于女性,体制内单位工资平均值高于体制外单位,但工资分布较为集中,而体制外单位工资容易出现极端值。
2. 主要解释变量本文从经济集聚的角度,将城市人力资本的来源分为4个部分:人力资本深度、高技术服务业专业化程度、产业多样化程度、劳动力市场密度。此外,还加入了各城市的人均GDP为控制变量。其中,人力资本深度为样本中拥有大专及以上人员的占比,劳动力市场密度主要指数学密度,为年鉴中除农林业以外就业人口与市辖区面积的比值①。计算信息服务业专业化以及产业多样化的指数如下:
① 尽管建成区面积可能更合适,但由于统计年鉴中相关数据有虚高的风险,因此未采用。
在个体层面,本文控制了性别、年龄、民族、政治面貌、户口、工作经历及其平方、教育年限、兄弟姐妹数量、健康状况等可能影响工资的因素,在城市层面控制了各市人均GDP以减轻未观察到的城市层面的异质性。
统计描述显示,男性占比超过一半,教育程度基本接近高中毕业水平,年龄分布较为均匀,而工作经历年数呈现右偏分布,在私营企业工作的略微偏少。从城市特征看,上大学比例均值为0.39,但极差、标准差较大,表明城市间受教育程度差距大。劳动力市场密度分布轻微右偏,产业多样化指数均值为0.53,城市间差异较小。①
| 表 1 城市层面变量描述统计 |
① 为节省空间,此处省略了其他变量的描述性统计,可向作者索取。
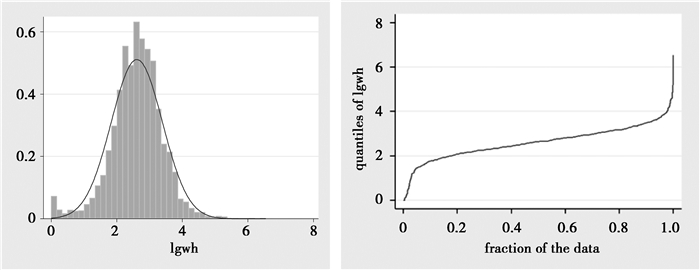
(二) 计量模型设定 1. 分层线性回归模型如图 1所示,城市人力资本的各渠道对于工资的影响并非一直是一个常数。也就是说,这些关系的部分差异可以被解释为不同城市间的不可观测的差别。针对这种可能性,基于嵌套的数据结构,本文运用分层线性模型(Hierarchical linear model)来识别个体与城市间的差异。分层线性模型允许不同城市的斜率和截距有所不同,符合图中的现象,无需满足方差齐性的假设,能够分离组间与组内的误差。同时与固定效应相比,随机效应允许本文研究高层次上变量的影响。此外,为保证结果的稳健,本文还运用工具变量法验证结果的可靠性。
|
图 1 对数小时工资的密度及分位数分布情况 |
第一层Xij为个体层面的变量组成的矩阵,第二层截距项中是表明人力资本变量,同时还包含人均GDP控制变量。此外,为尽量减少第一层变量与误差相关对结果造成影响,还对第一层面中的个体变量采用对中处理(即以原值减去所在城市的均值)以获得固定效应,并为减轻异方差性的影响计算了稳健标准误。本文还在斜率项加入了城市层面变量,以研究个体层面特征对城市人力资本外部性影响的调节效应。反映大学生比(PROCOL)、信息服务业专业化(SPECIAL)、产业多样化(DIVERSITY)以及劳动力市场密度(DENSITY)对因变量直接影响的参数分别为γ01, γ02, γ03,γ04, 反映通过个体特征起到调节作用的参数为γ11, γ12, γ13, γ14。
Level 1:
| $ {\rm{log}}\;wag{e_{ij}} = {\beta _0} + {\beta _k}({X_{ij}} - {{\bar X}_J}) + r $ |
Level 2:
| $ \begin{array}{l} {\beta _0} = {\gamma _{00}} + {\gamma _{01}}PROCO{L_j} + {\gamma _{02}}SPECIA{L_j} + {\gamma _{03}}DIVERSIT{Y_j} + {\gamma _{04}}DENSIT{Y_j}\\ + {\gamma _{05}}LOGPGD{P_j} + {u_{0j}}\\ {\beta _{1j}} = {\gamma _{j0}} + {\gamma _{11}}PROCO{L_j} + {\gamma _{12}}SPECIA{L_j} + {\gamma _{13}}DIVERSIT{Y_j} + {\gamma _{14}}DENSIT{Y_j} + {u_{1j}} \end{array} $ |
其中,level2种斜率项仅包含教育年限与性别。
2. 分位数回归另一方面,为进一步探究城市人力资本对于处于收入分布不同位置上的群体的作用,本文采用了分位数回归法进行研究。分位数回归放松了参数回归中对扰动项分布的假定,且与普通的均值回归相比, 分位数回归模型可以全面地描述解释变量对被解释变量的影响。对于该模型,本文不再详细介绍。为避免内生性影响,本文采用IVQR和CQIV法进行检验。
1.工具变量分位数回归(IVQR)
| $ Y = D\prime \alpha \left( \tau \right) + X\prime \beta \left( U \right),U|X,Z\sim Uniform\left( {0,1} \right) $ |
D=δ(X, Z, V)V依赖于U; D′α(τ)+Xβ(τ)随τ严格递增
我们将关注以下结构分位数回归, 它描述了根据固定D=d和抽样方差U得到的潜在结果变量Yd的形态:
| $ {S_Y}\left( {\tau |d,{\rm{ }}x} \right) = d\prime \alpha \left( \tau \right) + x\prime \beta \left( \tau \right) $ |
2.删截分位数回归工具变量法(Censored Quantile Instrumental Variable)
考虑到数据中小时工资低于10元的个体被归为0而产生删截问题(censoring),同时考虑数据内生性,本文还采用了Chernozhukov, Fernandez-Val and Kowalski (2010)提出的CQIV估计量。该方法采用控制变量法(control variable approach)进行两步估计,与Chernozhukov and Hansen(2008)提出的工具变量估计量相比,这个控制函数法不需要结构方程模型中排序不变条件。简化模型如下:
| $ Y = {\rm{max}}({Y^*},C)Y = {Q_Y}^*\left( {U|D,X,V} \right)D = {Q_D}\left( {V|X,Z} \right) $ |
U,V满足假设:
| $ U\sim U\left( {0,1} \right)\left| {D,X,Z,V,CV\sim V\left( {0,1} \right)} \right|C,X,Z $ |
其中,Y代表观察到的工资对数,Y*是连续的潜在响应变量,Y是由Y*被C截断的数据组成,这里C为0。D为我们重点关注的变量,即表示集聚效应的变量,X表示一系列协变量,而V则是造成D内生性的潜在未观测到的回归元,Z是工具变量,U是干扰项。干扰项V, U满足完全独立性假设(full independence),在文中指工具变量Z的变化仅通过影响城市人力资本集聚水平而影响工资,且工具变量满足相关条件假设。文中选取0.2,0.4,0.6,0.8这四个有代表性的分位点,其余控制变量与工具变量和1中的模型一样。重点关注代表人力资本外部效应的四个变量的系数在不同分位点的大小。
四、人力资本集聚对工资影响的微观机制 (一) 实证结果分析首先,在零模型的条件下,组内相关系数达到0.062/(0.062+0.466)=0.117, 可见有12%左右的工资差异是由城市间的差异引起的。控制其他变量的条件下,男性的收入高于女性,工作年限与收入呈现倒U型关系,个体教育水平与收入水平呈显著正相关关系,健康程度较低的人收入较低,党员工资较高,兄弟姐妹个数较多者工资也相对低一些。
从城市层面变量来看,上大学比例与个体工资呈现显著正相关,一个市上大学比例增加1%,个体工资增加0.63%,且在加入其它控制变量的情况下系数较稳定。第二、三列的结果说明信息服务业专业化程度与行业多样化程度对个体工资有相反作用,弹性系数分别为0.09、-0.52。就业密度对工资有微弱的促进作用。单独来看,加入大学生比例使得第一层残差减少(0.062-0.03)/0.062100=52%, 削减比例最大。第五列中本文加入了所有外部性的变量,采用随机截距模型,发现大学生比例的系数依然显著为0.6,劳动力市场密度系数略有下降,而多样化指数的效应依然显著为负,信息专业化程度的系数变为不显著,且第二层残差大幅度降低。由于不同城市对个体工资的影响不尽相同,第六列考虑了随机截距和斜率模型,与第五列相比,大学生比例系数降低至0.56,就业密度系数也明显降低,但第二层残差大幅减低并变得不显著,说明实际上可以通过这四种渠道解释工资的大部分变异。其中,大学生比例提高对个体工资有显著促进作用,就业密度也有一定正向影响,而多样化却与工资显著负相关,信息服务业专业化作用并不明显。
(二) 稳健性检验由于人口对工作地区的流动具有自选择性,聚集经济会带来大量且高质量的工作人员,从而使其对经济增长的效应被高估(Duranton,2010)。要对集聚效应对工资的影响做出相对准确的估计,选择合适的工具变量很重要。首先,需保证工具变量与内生变量的相关性,其次,必须有足够多的工具变量数,保证过度识别。但同时工具变量个数也不能太多,否则会影响推断准确性。
考虑到过去的历史对现今状况的直接相关,相关国内外文献中有采用有历史特征作为工具变量的先例(Ciccone and Hall, 1996; Fingleton and Longhi, 2013;吴晓怡、邵军,2016;孙三百,2016)。本文分别对四个自变量建立模型,在工具变量选择上借鉴他们的做法,对每个自变量都选择了两个具有历史特征的工具变量。对于模型1,本文相信2000年时各城市的大学生比例对现在各市的大学生比例有较为显著的影响,而2000-2013的时间间隔也足够长,使残差项与现在的工资不相关。此外,由于早期城市化率较高的城市教育普及较早、范围较大,市民文化程度普遍较高,因此2000年各市的城市化率与如今的大学生比例也有高度相关性。模型2中,多样化指数除采用历史数据外,还采用了2000年限额以上内资企业产值所占工业企业总产值的比重作为工具变量,考虑到2000年内资企业中国有与集体企业数量占比达到60%以上,产业结构相对单一,而由于路径依赖,迄今为止这些地区产业多样化增加程度通常也较低。而模型3、4则同理,采用信息专业化指数和就业密度的2000年历史数据作为工具变量,此外,考虑到历史上外商直接投资对地区就业密度、信息专业化程度的促进作用,本文还采用2000年FDI的对数分别作为两者的第二个工具变量。本文将个体层面变量对中后,再采用随机效应模型估计,以分离出个体异质性影响。经检验,工具变量与内生变量的相关性系数均较高。从表 3模型1的回归系数可以看出,大学生比例系数为0.58。模型2结果显示,多样化对工资的负向作用尽管为负,但是不再显著,说明产业多样化对工资的消极作用很大程度上来源于遗漏变量或误差项的干扰,其本身对于个体工资没有显著影响,符合假设3。模型3发现信息服务业专业化的系数为0.16,显著为正,映证高技术集聚对于个体工资有促进作用。基本模型中系数不显著可能是由于模型4以2000年房地产市场投资对数、外资流入对数作为劳动力市场密度的工具变量进行G2SLS回归,发现仍呈现显著正相关。验证了第二部分的假设内容。
| 表 2 分层线性模型回归结果 |
| 表 3 G2SLS回归结果 |
工资增长的同时伴随着不同群体之间收入差距的扩大,而城市的人力资本也对工资差距起到了一定程度的影响。考虑到不同渠道对工资的影响很可能随着性别及受教育程度不同而程度不同,本文将个体性别、受教育年限与四个表征经济集聚效果的变量进行交互,深入考察其中的调节效应。
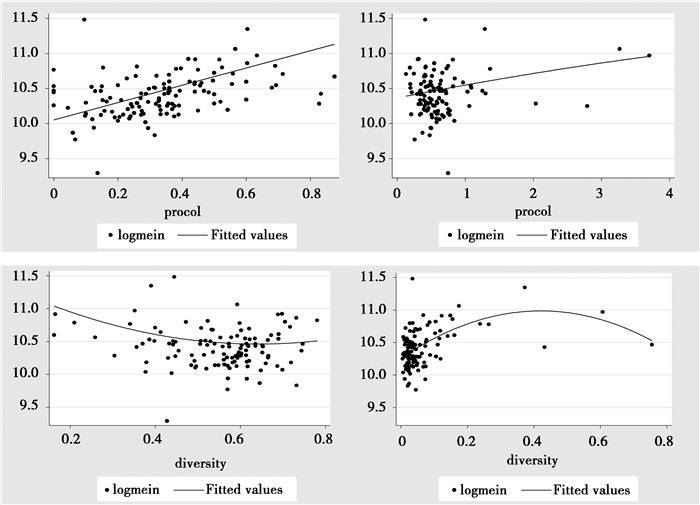
表 4结果表明,对于男性来说,本地大学生比例对他们的工资反而起到了负向调节效应,大学生比例每上升1%,他们的工资平均下降0.25%,但在总体上依然高于女性0.08%。在控制了城市层面的其他变化后,人力资本深度系数略有下降,但其他系数并未发生明显变化。样本中女性获得大学以上学历的占女性总体的69.2%,男性约占其总体的68.6%,由图 2也可以看出,尽管人力资本深度对男性工资的作用大于女性,但在大学生比例越高的地区,男女性之间工资差距越小。对于女性而言,地区人力资本深度的增加会减轻当地劳动力市场的性别歧视,对她们工资的促进作用比男性更加显著。
| 表 4 性别交互项的HLM回归 |
|
图 2 城市层面变量与城市平均工资的散点图 |
在不同性别群体中,信息化专业程度对其工资的影响也有所不同。信息专业化程度对男性工资的边际效应为-0.04,控制了其他城市层面变量后,该指数的主效应系数变为不显著,但从效应系数并未发生变化。和人力资本深度一样,尽管对于男性工资的促进更大,但随着该行业专业化程度提高,男女性之间工资逐渐缩小。不过从图中看,其缩小工资差距的效用不如人力资本深度强。考虑到更多男性从事与信息技术服务业相关的行业,这一专业化指数的提升会使男性职工在劳动力市场上竞争更为激烈,从而削弱他们的竞争力。
表 5探究了教育年限与四个微观渠道之间的交互效应。教育年限与大学生占比的交互项显著为正,边际效应系数为0.09,人力资本深度对受教育程度越高的人作用越明显。图 2左下方的图揭示了令人惊讶的现象:对于受教育年限处于较低水平的人群来说,地方人力资本深度提高反而会抑制他们的工资,在受教育水平最低的群体中,地方大学生占比的边际效应甚至为-0.46。另一方面,在人力资本深度较低地区,不同受教育程度者工资差别不大,而这一差距却随着地区教育程度提高而急剧增加。简而言之,教育溢出尽管会同时增加所有人的工资,但教育程度高者获益更大,假设其他变量都随机时,教育外部性甚至还抑制了受教育程度最低者的工资。虽然这种情况在现实中较少出现,但人力资本深度增加教育回报率的特征吸引了大量高学历人才,从而可能加剧了这些地区高低技能者之间的工资差距。
| 表 5 教育交互项的HLM回归 |
信息技术服务业专业化与个体受教育程度的交互项系数为0.017,作用也呈现相同的趋势,即随着个体教育程度提高,其对工资的积极作用凸显,而对于受教育程度较低者却起到消极作用。但与人力资本深度不同的是,在信息服务业专业化水平较低地区,受教育程度不同者之间的工资差距相差就比较大,因此该指数的边际效用没有人力资本深度强。其他两个变量的交互效应均不显著,可见它们对于工资的作用未随着性别与教育程度的不同发生显著变化。最后,本文将所有外部性变量分别对性别、教育进行跨层交互,结果显示,教育年限与人力资本深度、信息技术服务业专业化的交互项系数尽管有所减小,但依然显著为正。而性别与专业化指数交互项显著为正,但人力资本深度交互项的系数却变得不显著,推测应当是部分从效应被分解到了专业化指数的作用中。
| 表 6 全模型HLM回归 |
为验证结果稳健性,本文再次采用工具变量法进行分析。对于不同性别者,G2SLS回归系数的显著性与HLM模型一致,人力资本深度、信息服务业专业化程度的系数分别减小到-0.37、-0.06,放大了图 1中的效应,进一步验证了地区人力资本增加与信息服务业专业化度提高有助于缩小性别收入差距。而对于不同教育年限者,大学生比例交互项系数上升至0.17,接近原先的2倍,而信息专业化交互项系数也略有提高,印证了这两者增加反而会拉大不同受教育程度者的收入差距,从而吸引大量高学历人才向平均受教育程度高、信息技术就业需求大的地区转移。与HLM模型不同的是,G2SLS模型中教育与产业多样化、就业密度的交互项系数均显著,且产业多样化边际效应显著为-0.14。本文进一步采用了控制函数方法(Control Function Approach)进行验证,交互项系数甚至变为-0.15。经检验,G2SLS回归时教育年限与交互项的VIF值均高达55,而原模型中仅为14,这里出现严重的多重共线性,显著为负的交互项系数并不稳健。就业密度尽管为正,但系数很小,调节作用微弱。
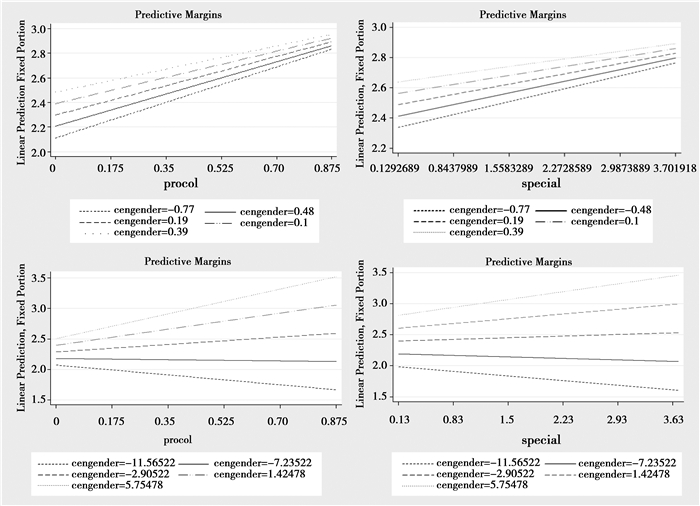
|
图 3 性别、教育与人力资本深度以及信息产业专业化的交互效应 注:图中为未控制其他变量的斜率,性别、教育均为对中后的结果,为处于改变量值域0%、20%、40%、60%、80%、100%处数值。在每节点处,系数均显著。 |
除了通过个体特征调节而产生的不同边际效应,劳动力市场分割也使得同一地区的人力资本对个体工资产生不同影响。本文按照单位所有制和地区的标准将样本划分成不同的子集,在保证每个子集样本量尽量接近的前提下运用G2SLS法分别对每个城市层面的变量进行回归,并利用费舍尔组合检验法比较不同子集之间系数是否有差异。
按单位所有制类型(党政机关、事业单位、国有控股、集体企业称为“体制内企业”,其他的归为“体制外企业”)划分的结果表明,大学生比例提高一个百分点,体制内员工工资上升1.51%,体制外的上升0.97%,都较为显著,经验P值为0.21,说明两者无明显区别。两者的信息服务专业化的弹性系数为0.3左右,而多样化系数仅对体制内员工的影响系数显著为-1.88,但经验P值为0.24,也说明两者之间并无显著差异。就业密度上两者系数也接近一致。
| 表 7 个体特征交互项的G2SLS回归 |
按照东、中、西部划分的结果表明,人力资本深度对工资的作用在东部地区显著优于中部和西部(P=0.07 < 0.1),大学生比例每上升1%,东部地区员工工资上升2.48%,中部上升1.05%,西部1.03%。而信息服务业专业化对工资的促进在东部显著为正,尽管经验P值显示东西部地区存在差异(P=0.06),但其作用在中部、西部地区都不明显。多样化指数对东部工资的抑制效果要显著大于中部和西部,可能是由于东部就业者对职业类型有较强的偏好性,而中西部地区工人专业性不强,且产业集聚现象不充分造成的。就业密度的作用在各地区都不存在显著差异。
(三) 工资差距的原因:收入分布的异质性影响 1. 城市人力资本在不同收入群体的分布表 9是将四个变量一次性全部放入模型进行分位数回归得到的结果, 同时我们对模型中各关键变量的回归系数估计结果进行了斜率相等检验(Slope Equality Test),结果表明,除了多样化程度外,其他三个系数都拒绝了各分位点上回归系数相等的原假设,意味着不同收入阶层间,人力资本深度、信息服务业专业化以及就业密度的外部性差异是显著的。从城市层面的变量来看,大学生比例对个体收入的促进作用随着收入分位数的提升而降低。当所在城市大学生比例提高1个百分点,20%的最高收入者小时工资增加0.636%,而20%的最低收入者收入增加达到0.776%,高于前者0.14%。人力资本深度的外部性效果随着收入分位数的提高而递减。多样化程度对于任意收入水平的群体都呈现显著负向效应,且随着收入分位数提高而递减。多样化每提高1个百分点,最高20%者工资降低0.26%,而最低20%降低了0.4%。信息技术专业化程度对收入处于不同分布位置的群体有着不同的效果:同一城市信息技术专业化程度提高1%,收入分位数处于最低40%的群体工资没有显著变化,而处于60%分位数者工资提高0.022%,最高80%者提高0.03%。
| 表 8 按不同标准划分的子样本回归与比较结果 |
| 表 9 全模型分位数回归结果 |
考虑到内生性,本文采用工具变量的方法对分位数回归结果进行检验。与表 9不同的是,为防止过多内生变量与工具变量造成共线性从而对估计产生影响,本文使用前文的工具变量,依次对四者进行回归。由于并未将四个变量一起放置于同一模型中,而是单独进行IVQR回归,因此系数估计上与表 9有出入,但根据全分位点检验图可以看出,除个别分位点上变化增幅突然加大,大部分系数的变动趋势都是相似的。但值得注意的是,大学生比例系数并未拒绝斜率相等检验,说明在不同收入阶层间大学生比例对工资的促进效果没有显著区别。而多样化程度则拒绝了斜率相等检验,它对收入分布底层20%者的系数为-0.69,而对最高20%几乎无负面影响,表现随着收入层次的上升而递减的倾向。低工资者议价能力相对较低,从事的职业大多处于供过于求的状态。在多样化程度低的情况下,一个地区的劳动力市场更容易分享劳动力储备从而形成企业集聚,根据通过调整价格实现区位均衡的原理,当孤立企业中对工人需求相对较低时为了使两个市场的工资具有无差异性,企业集群内的工资会提高。而产业多样化提高增加了他们辞职的机会成本,降低了劳动力市场流动性。信息服务业专业化水平对工资的促进作用仍然呈现随分位数而上升的趋势,且系数均显著,最高层次人群的信息技术业专业化强度是最低层次人群的2倍。就业密度系数的变化则呈现出更强的波动性,在40分位点处系数突然上升,但总体来说系数都小于0.001,促进作用很微弱。经过上述分析,可以看出,不同收入阶层并未从城市人力资本中均衡获益,除人力资本深度以外,其他变量都对收入层次越高者有更加积极的作用。
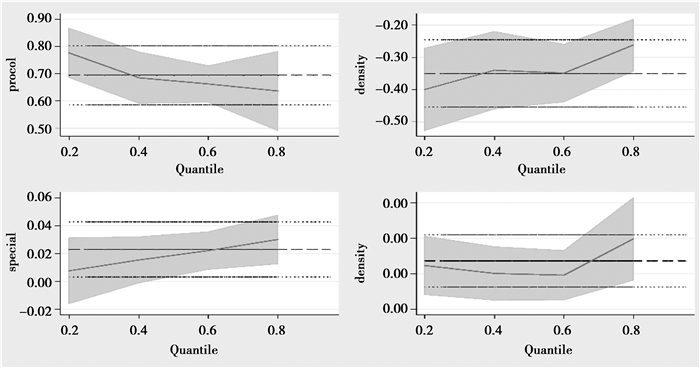
|
图 4 全模型全分位点检验 注:上下为95%置信区间。 |
由于以上分析中采用的样本剔除了小时工资在10元以下的个体,忽略了样本的一些信息,可能会对结论造成影响。为了确保结论正确以及上文分析的稳健性,本文将小时工资低于10元的个体替换为0,采用删截分位数回归模型(Censored Quantile Instrumental Variable)并用加权自助抽样法(weighed bootstrap)计算出置信区间(Chernozhukov,2010)。表 11的结果表明,大部分系数大小与IVQR法相差不大,但在20分位点处,各变量系数都出现了一定程度的膨胀,导致趋势在开始时出现拐点,这可能是由于删截变量造成的。总体而言,这些系数变化的趋势与之前的结果差不多,基本印证了先前的结论。
| 表 10 工具变量分位数回归估计结果 |
| 表 11 weighed-bootstrap CQIV回归结果 |
本文运用CHIP2013数据,从经济集聚的视角考察了城市人力资本对工资影响的微观机制。分层线性回归模型和工具变量法的结果显示:(1)地区人力资本深度有着显著的正外部性;(2)信息技术服务业专业化水平也有一定外溢作用,但与其他因素相关度较大;(3)产业多样化与工资之间有负向关系,但抑制作用并不稳健;(4)劳动力市场密度对工资起到轻微的促进作用。分类回归、交互项以及分位数回归的结果表明:(1)人力资本深度对工资的作用在东部地区显著优于中部和西部,人力资本深度提高同样单位,对于女性、教育程度高者的工资促进更大,且其对于不同分位数点收入的群体呈现边际效益用递减;(2)多样化指数对东部工资的抑制效果也要显著大于中部和西部,其对于收入较低群体负面影响最大;(3)信息服务业专业化与人力资本深度的调节效应方向相同,不过程度不及前者,且其对工资的促进作用随收入分位数上升而增加;(4)就业密度对不同收入群体的促进作用也呈现递增趋势。
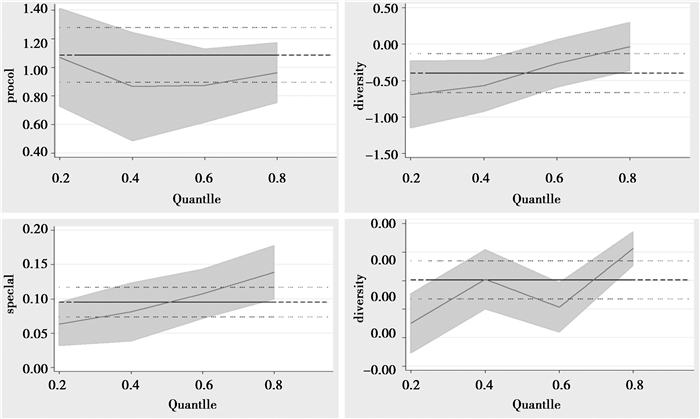
|
图 5 IVQR全分位点检验 |
这些结果说明,城市的人力资本积累从不同渠道对工资起到不同影响,甚至有些因素会起到双重效果。我国的劳动力市场分割在一定程度上阻碍了城市人力资本发挥积极作用,而个体特征的差别也使得同一渠道对不同个体的边际作用有所不同,例如个体受教育程度的不同就极大地影响了城市人力资本的作用,甚至会形成贫者愈贫的“马太效应”。当然,由于其他积极因素的影响,人力资本程度高的地区实际上收入差距是更小的;但提高落后地区的教育回报率应当是教育发展的当务之急。总体来说,政府应当加强当地教育水平,提高高技术产业专业化程度与就业密度,在制定城镇化政策时充分考虑群体之间的异质性,采用合理的配套措施打破分割、增强劳动力流动,使得政策在促进收入增长的同时能够缩小工资差距,兼顾公平与效率。
| [] |
白雪梅、李莹,
2014, “教育对中国居民收入的影响分析——基于分位数回归和收入分布的考察”, 《财经问题研究》, 第 4 期, 第 11-18 页。 |
| [] |
柴国俊、邓国营,
2012, “城市规模与大学毕业生工资溢价”, 《南方经济》, 第 10 期, 第 162-172 页。 DOI:10.3969/j.issn.1000-6249.2012.10.014 |
| [] |
陈钊、万广华、陆铭,
2010, “行业间不平等:日益重要的城镇收入差距成因”, 《中国社会科学》, 第 3 期, 第 65-76 页。 |
| [] |
范剑勇、李方文,
2011, “中国制造业空间集聚的影响:一个综述”, 《南方经济》, 第 6 期, 第 53-66 页。 |
| [] |
黄思, 2013, "产业集聚与工资: 机理分析与中国省际实证比较", 浙江大学博士论文.
|
| [] |
刘修岩、殷醒民,
2009, “空间外部性与地区工资差异:基于动态面板数据的实证研究”, 《经济学, 第8卷》, 第 1 期, 第 77-98 页。 |
| [] |
宁光杰,
2014, “中国大城市的工资高吗?”, 《经济学(季刊), 第13卷》, 第 3 期, 第 1021-1024 页。 |
| [] |
王海宁、陈媛媛,
2010, “产业集聚效应与地区工资差异研究”, 《经济评论》, 第 5 期, 第 72-81 页。 |
| [] |
谢小平、王贤彬,
2012, “城市规模分布演进与经济增长”, 《南方经济》, 第 6 期, 第 58-73 页。 |
| [] |
杨仁发,
2013, “产业集聚与地区工资差距”, 《管理世界》, 第 8 期, 第 41-51 页。 |
| [] |
岳昌君,
2004, “教育对个人收入差异的影响”, 《经济学(季刊), 第3卷》, 第 10 期, 第 135-149 页。 |
| [] |
Acemoglu D, 1996, "Changes in Unemployment and Wage Inequality:An Alternative Theory and Some Evidence". American Economic Review, 89(5), 1259–1278.
|
| [] |
Carlino G, Hunt R and Duranton G, 2009, "What explains the quantity and quality of local inventive activity?". Brookings-Wharton Papers on Urban Affairs, 65-123.
|
| [] |
Chen HP., 2002, "Urban externalities and city growth in Taiwan". The Annals of Regional Science, 36(4), 531–550.
DOI:10.1007/s001680200098 |
| [] |
Chernozhukov V, Fernández-Val I and Kowalski A E, 2011, "Quantile regression with censoring and endogeneity". Cowles Foundation Discussion Papers, 186(1), 201–221.
|
| [] |
Combes P P, Duranton G and Gobillon L, 2010, "The identification of agglomeration economies". Journal of Economic Geography, 11(2), 253–266.
|
| [] |
Combes, P. -P., G. Duranton, and L. Gobillon, 2003, "Wage Differences Across French Local Labor Markets: Endowments, Skills, and Interactions", Working Paper.
|
| [] |
Fu S, 2007, "Smart café cities:Testing human capital externalities in the Boston metropolitan area". Journal of Urban Economics, 61(1), 86–111.
DOI:10.1016/j.jue.2006.06.002 |
| [] |
Glaeser E L, Resseger M G, 2010, "The complementarity between cities and skills". Journal of Regional Science, 50(1), 221–244.
DOI:10.1111/jors.2010.50.issue-1 |
| [] |
Henderson V, Lee T and Lee Y J, 2001, "Scale externalities in Korea". Journal of Urban Economics, 49(3), 479–504.
DOI:10.1006/juec.2000.2202 |
| [] |
Henderson J V, 2010, "Cities and development". Journal of Regional Science, 50(1), 515–540.
DOI:10.1111/jors.2010.50.issue-1 |
| [] |
Knight J, Song L, 2003, "Increasing urban wage inequality in China". Economics of Transition, 11(4), 597–619.
DOI:10.1111/ecot.2003.11.issue-4 |
| [] |
Lucas R E, 1988, "On the mechanics of economic development". Journal of monetary economics, 22(1), 3–42.
DOI:10.1016/0304-3932(88)90168-7 |
| [] |
O'sullivan A, 2007, "Urban economics". McGraw-Hill/Irwin, 225-226.
|
| [] |
Puga D, 2010, "The magnitude and causes of agglomeration economies". Journal of Regional Science, 50(1), 203–219.
DOI:10.1111/jors.2010.50.issue-1 |
| [] |
Romer P, 1989, "Endogenous technological change". National Bureau of Economic Research.
|
| [] |
Henderson V., 2003, "Marshall's scale economies". Journal of Urban Economics, 53, 1–28.
DOI:10.1016/S0094-1190(02)00505-3 |