基本养老保险制度的发展目标为公平和可持续,可持续性主要体现为制度能够实现自我的长期收支平衡。基本养老保险统筹账户采用现收现付模式,人口年龄结构对统筹账户收支平衡的影响较大。我国目前的人口年龄结构呈现老年型,而且老龄化进程加快(刘书明、常硕,2017),制度抚养比已从2000年的3.30:1快速下降至2015年的2.87:1①,这意味着基本养老保险基金收入的相对减少和支出的相对增加。随着人口老龄化程度的不断加深,基本养老保险统筹账户将面临着严峻的收不抵支风险。基于此,国内学者提出延迟退休年龄、推行“全面二孩”政策、扩大制度覆盖率等配套完善措施(景鹏、胡秋明,2016;于洪、曾益,2015;林宝,2010)。
① 根据国家统计局的数据计算而得。
但是,在基本养老保险制度模式不发生变化、而且相关配套政策逐步完善的条件下,提高统筹账户缴费率和降低基础养老金替代率的参数调整应是应对人口老龄化,维持统筹账户长期可持续发展的必然选择。在引起人口年龄结构变动的因素中,预期寿命和生育率是关键,预期寿命延长、生育率降低将加剧人口老龄化(柳清瑞、苏牧羊,2016;耿志祥等,2016)。据此,以维持统筹账户自身收支平衡为目标,分析预期寿命和生育率变动与基本养老保险统筹账户调整的关系是本文的研究主线。
同时,根据目前的经济和社会发展需求,我国的政策选择是统筹账户缴费率的阶段性降低(彭浩然、陈斌开,2012),以及基础养老金替代率不能一味下降(李珍、王海东,2013)。所以,基于预期寿命和生育率变化对统筹账户收支平衡的影响,20%的缴费率能够阶段性下降到何种程度,35%的养老金目标替代率水平能够维持到何时,即统筹账户进行参数调整的临界点是本文的研究问题所在。
本文以三期世代交叠模型的构建为基础,采用《联合国:2015年全球人口发展报告》(以下简称《联合国人口报告》)数据,以2015-2100年为测算期,具体分析出预期寿命和生育率变动如何影响基本养老保险统筹账户收支,兼具分析经济发展和个体福利水平等的变化。
基于世代交叠模型,本文在实证分析中发现:老年期生存概率和人口增长率是影响机制中的关键参数,而预期寿命延长不仅会使个体的老年期生存概率增加,还会降低育龄妇女人数占比,在总和生育率一定的条件下,人口增长率将有所下降,对基本养老保险统筹账户收支平衡产生双重影响,这是以往大多数研究所忽视的(康传坤、楚天舒,2014;杨再贵,2007)。
本文的实证研究结果表明:第一,快速增长的预期寿命对基本养老保险统筹账户收支平衡发挥着绝对影响力,总和生育率的提高能够在一定程度上缓解收支失衡;第二,预期寿命为87.828岁且总和生育率为1.79(2086年左右)时,20%的统筹账户缴费率刚好维系35%的基础养老金目标替代率;第三,以经济发展和个体福利水平的变化为参照,临界点之前,阶段性降低统筹账户缴费率能够促进经济发展,而且可以维系统筹账户的收支平衡;临界点之后,必须通过提高缴费率或降低养老金替代率来保证制度平稳运行,降低基础养老金平均替代率的做法能够相对减少福利损失,加快经济发展。
需要说明的是,本文采用的《联合国人口数据》为全国人口数据,且假定养老保险参保率为100%,即并未考虑城镇化率、参保率等因素,仅考虑人口因素,旨在从宏观层面单独分析出预期寿命和生育率对基本养老保险统筹账户的影响,后续将进行完善分析。
二、文献综述基本养老保险统筹账户实行现收现付制,受人口年龄结构的影响较大。孙祁祥、朱俊生(2008)指出人口老龄化与现收现付制养老保险之间存在诸多矛盾,人口转变趋势使得基本养老保险统筹账户面临着难以持续发展的巨大挑战。关于人口年龄结构与基本养老保险的实证研究多以Diamond(1965)构建的世代交叠模型为基础;李军(2003)将人口老龄化因素引入模型中来研究养老保障问题;封进、宋铮(2006)运用世代交叠模型,并基于不同生育率假定比较分析了人口年龄结构与养老保险福利效应;张迎斌等(2013)基于跨期叠代模型的实证研究指出人口增长率、成年人存活至退休期的概率等在基本养老保险的均衡体系中具有重要作用。年轻化的人口年龄结构有利于制度的可持续发展,而少子老龄化的人口特征使得制度不得不因此进行参数和结构调整。
从制度参数调整视角来看,有效应对人口老龄化、提高基本养老保险制度可持续性的方法为“增收减支”,即提高统筹账户缴费率和降低养老金替代率。然而,许多学者的研究结果均表明我国目前20%的统筹账户缴费率实际属于高水平,未来应该降低统筹账户缴费率:李炜光、臧建文(2017)认为“五险一金”的缴费费率有下降空间;康传坤、楚天舒(2014)指出在预期寿命和人口增长率的共同影响之下,基本养老保险统筹账户最优缴费率变动区间为10.22%-19.04%;彭浩然、陈斌开(2012)的实证分析结果认为我国现收现付养老保险缴费率的阈值在15.6%左右。与此同时,在构建多层次养老保险体系时,基础养老金替代率应该下降,但是,李珍、王海东(2013)认为养老金替代率水平下降会削弱退休金的“保基本”功能,引起在职人员对退休生活的不安,不利于基本养老保险制度的公平发展。
在统筹账户缴费率应该下降以及养老金替代率不应下降的现实背景之下,为维持基本养老保险制度的公平可持续发展,扩大养老保险覆盖面、延迟退休年龄、实行“全面二孩”政策等配套政策改革受到了学界的一致推崇。林宝(2010)的研究表明随着预期寿命的增长,人口老龄化程度不断加深,养老保险综合覆盖率之比的变化将有效化解人口老龄化的冲击;景鹏、胡秋明(2016)的实证研究结果表明:0%-100%符合“全面二孩”政策的女性生育二孩,将使退休年龄为60岁时的最优社会统筹缴费率降到19.18%-19.63%;李晓鹤、殷俊(2016)认为延迟退休是应对养老保险基金缺口的现实选择;于洪、曾益(2015)指出在人口老龄化背景下,延迟退休年龄和实行生育政策转变可以缓解老龄化冲击,即使缴费率显著降低仍然可以使基本养老保险基金保持在略有盈余的状态。
与此同时,国外学者Haan and Prowse(2014)运用德国的微观数据构建包括退休、就业和消费结构在内的生命周期模型,研究认为若将退休年龄提高3.76岁将有利于保障德国公共养老金制度的财政稳定;Alfonso R. and Sánchez Martín(2010)研究在人口老龄化背景下,延长退休年龄等制度改革对西班牙养老保险制度的影响时发现:推迟法定退休年龄大幅减少了养老保险制度的隐性债务,同时使人口老龄化对制度造成的隐性成本均匀地分布在几代人之间。
基于以往研究可以看出,预期寿命和生育率变动所引致的人口年龄结构变化确实对基本养老保险统筹账户造成了巨大影响,但是我国的基本养老保险制度设计本身以及其它配套政策有较大的改善空间,可以基于此来促进制度的公平可持续发展,因此目前不需要进行制度参数的大幅调整。
但是,即使其它配套政策在逐渐完善,预期寿命和生育率变化对基本养老保险统筹账户的影响仍不可忽视,未来制度参数还是需要进行调整。综上,本文从统筹账户缴费率保持20%不变和基础养老金目标替代率保持35%不变这两个视角出发来研究预期寿命和生育率变化下的基本养老保险统筹账户参数调整问题,测算出统筹账户需要进行参数调整的临界点,并基于经济发展和个体福利视角提出了未来参数调整的具体建议。
三、世代交叠模型的构建贺菊煌(2002)构建了个人生命分为三期的世代交叠模型,汪伟、艾春荣(2015)基于世代交叠模型分析了人口老龄化和储蓄的关系,本文以此为参照构建三期世代交叠模型来分析个体行为。假设个体一生分为三期,分别是少年时期、成年时期和老年时期,少年时期的消费主要来源于借贷,成年时期通过劳动获得工资,并进行消费、储蓄、偿还少年时期的借贷,以及缴纳养老保险费,老年时期只消费不劳动,且资金来源为成年时期储蓄的积累以及政府发放的养老金,死亡时没有资金剩余。需要说明的是,统筹账户养老保险费虽然由企业进行缴纳,但其本质上仍属于职工工资,故模型中以个体作为统筹账户缴费主体并不与实际相悖。
同时,为进行预期寿命和生育率变化的影响分析,本文进一步假定个体三期的时间长度相同,且个体第三期的生存概率为m,即个体以m的概率生存到第三期期末,m取值越大,预期寿命越高。
(一) 个体行为个体在少年时期的消费主要来源于借贷,资金为s0, t-1,同时,由于后文设定的就业年龄低于一期长度,所以少年期将有占比为d的时间用于工作,获得总工资dAt-1wt-1,并按照工资的λ比例缴纳相应的养老保险费且0 < λ < 1;在成年时期提供一单位的劳动并获得工资报酬wt,同样按照工资的λ比例缴纳养老保险费,并偿还少年时期的借贷,剩余部分用作成年期的消费和储蓄;个体在老年时期只消费,资金来源于养老金pt+1和成年时期的储蓄积累,个体一生的预算约束为:
| $ {c_{0,t - 1}} = - {s_{0,t - 1}} + d\left( {1 - \lambda } \right){A_{t - 1}}{w_{t - 1}} $ | (1) |
| $ {c_{1,t}}{\rm{ = }}\left( {1 - \lambda } \right){A_t}{w_t} + \left( {1 + {r_t}} \right){s_{0,t - 1}} - {s_{1,t}} $ | (2) |
| $ {c_{2,t + 1}} = \frac{{\left( {1 + {r_{t + 1}}} \right){s_{1,t}} + {p_{t + 1}}}}{m} $ | (3) |
其中,c0, t-1、c1, t和c2, t+1分别代表个体在少年期、成年期和老年期的消费,d表示少年期工作时间占期间长度的比值,A表示劳动生产水平,s0, t-1和s1, t分别表示个体少年时期的借贷和成年时期的储蓄,rt表示资金从第(t-1)期积累到第t期的收益率,相应地,rt+1表示资金从第t期积累至第(t+1)期的收益率。个体一生的效用函数表示如下:
| $ U = Ln\left( {{c_{0,t - 1}}} \right) + \beta Ln\left( {{c_{1,t}}} \right) + {\beta ^2}m \cdot Ln\left( {{c_{2,t + 1}}} \right) $ | (4) |
其中,β表示个体的消费效用折现因子,在式(1)、(2)和(3)的预算约束下,根据拉格朗日函数可以求解个体一生的效用最大化问题,求解得到:
| $ \frac{{{c_{1,t}}}}{{{c_{0,t - 1}}}} = \beta \left( {1 - {r_t}} \right) $ | (5) |
| $ \frac{{{c_{2,t + 1}}}}{{{c_{1,t}}}} = \beta \left( {1 - {r_{t + 1}}} \right) $ | (6) |
假定生产技术为外生变量,根据柯布—道格拉斯函数可知企业的生产函数:
| $ {Y_t} = {A_t}{K_t}^\alpha {L_t}^{1 - \alpha } $ | (7) |
其中,Yt和Kt分别表示企业在第t期的总产出和总资本存量,At和Lt则分别代表第t期的劳动生产水平和劳动力投入量,而且At+1=(1+g)At,Lt+1=(1+n)Lt,g和n分别表示工资增长速度和人口增长速度,α代表资本产出的份额。为便于分析,可进一步将生产函数表示为人均生产函数的形式,即yt=Atktα,yt和kt表示第t期的人均产出和人均资本存量,且
| $ \pi = {Y_t} - {r_t}{K_t} - {w_t}{L_t} $ | (8) |
根据企业利润最大化原则,可求解得出:
| $ {r_t} = {A_t}\alpha {k_t}^{\alpha - 1} $ | (9) |
| $ {w_t} = {A_t}\left( {1 - \alpha } \right){k_t}^\alpha $ | (10) |
在三期世代交叠模型中,第(t+1)期共存在三类群体:少年、成年和老年,其中,第(t+1)期的老年人出生于第(t-1)期,获得人均养老金pt+1;第(t+1)期的成年人出生于第t期,缴纳养老保险费λAtwt;第(t+1)期的少年人出生于第(t+1)期,缴纳养老保险费dλAt+1wt+1。
在现收现付制下,养老保险实质上主要是由第(t+1)期存在的年轻人来赡养第(t+1)期的老年人,由于在三期世代交叠模型中,第(t+1)期的老年人出生于第(t-1)期,且老年期的生存概率为m,所以第(t+1)期的老年人口为mLt-1。政府在第(t+1)期获得的养老保险缴费主要为成年人缴纳的(λAtwtLt)和少年人缴纳的(dλAt+1wt+1Lt+1),养老金支出为(mLt-1pt+1)(不考虑老年死亡给付),故政府行为可具体表示为:
| $ \lambda {A_t}{w_t}{L_t} + d\lambda {A_{t + 1}}{w_{t + 1}}{L_{t + 1}} = m{p_{t + 1}}{L_{t - 1}} $ | (11) |
化简可得(稳态时wt-1=wt=wt+1):
| $ {p_{t + 1}} = \lambda {A_t}{w_t}\left( {1 + n} \right)\left[ {1 + d\left( {1 + n} \right)\left( {1 + g} \right)} \right]/m $ | (12) |
同时,第(t+1)期的社会平均工资为(dwt+1At+1Lt+1+wtAtLt)/(Lt+dLt+1),化简为Atwt[1+d(1+g)(1+n)]/[1+d(1+n)],由于养老金平均替代率为个体老年期养老金水平与当期社会平均工资之比,所以由式(11)和(12)可得平均替代率b1:
| $ {{\rm{b}}_1} = \frac{{{p_{t + 1}}\left[ {1 + d\left( {1 + n} \right)} \right]}}{{{A_t}{w_t}\left[ {1 + d\left( {1 + g} \right)\left( {1 + n} \right)} \right]}} = \lambda \left( {1 + n} \right)\left[ {1 + d\left( {1 + n} \right)} \right]/m $ | (13) |
养老金个体替代率为个体养老金水平与其退休前工资之比,个体替代率b2可表示为:
| $ {{\rm{b}}_2} = \frac{{{p_{t + 1}}}}{{{A_{t - 1}}{w_{t - 1}}}} = \frac{{\lambda \left( {1 + g} \right)\left( {1 + n} \right)\left[ {1 + d\left( {1 + n} \right)\left( {1 + g} \right)} \right]}}{m} $ | (14) |
另外,由式(13)和(14)可得:
| $ \lambda = \frac{{{b_1}m}}{{\left( {1 + n} \right)\left[ {1 + d\left( {1 + n} \right)} \right]}} = \frac{{{b_2}m}}{{\left( {1 + n} \right)\left( {1 + g} \right)\left[ {1 + d\left( {1 + n} \right)\left( {1 + g} \right)} \right]}} $ | (15) |
从式(13)可知:当b1和n为常数时,m增加则λ增加,即预期寿命提高则缴费率增加;当b1和m为常数时,n增加则λ减少,即人口增长率提高则缴费率减少。同理可从式(14)和(15)中分析得出老年期生存概率、人口增长率与平均替代率、缴费率之间的关系。
对政府而言,可通过式(11)实现当期的基本养老保险基金收支平衡,然而个体从基本养老保险制度中获得的养老金与缴费额却并不一定相等,个体一生的养老金收入与养老保险缴费之间的差额可表示为:
| $ s{z_{t + 1}} = m{p_{t + 1}}/\left( {1 + {r_{t + 1}}} \right)\left( {1 + {r_t}} \right) - \lambda {A_t}{w_t}/\left( {1 + {r_t}} \right) - d\lambda {A_{t - 1}}{w_{t - 1}} $ | (16) |
其中,szt+1表示个体一生在养老保险方面的收支差,本文称之为“制度福利”。由于个体在第三期的存活概率为m,因此在老年期的收入为mpt+1,并按照收益率r将其贴现至少年期。由于稳态时wt-1=wt=wt+1,rt-1=rt=rt+1,分别记做w*和r*,结合式(12),可将式(16)进一步化简为:
| $ s{z_{t + 1}} = \frac{{\lambda A{w^ * }}}{{{{\left( {1 + {r^ * }} \right)}^2}\left( {1 + g} \right)}}\left[ {\left( {1 + n} \right)\left( {1 + g} \right) + d{{\left( {1 + n} \right)}^2}{{\left( {1 + g} \right)}^2} - {{\left( {1 + {r^ * }} \right)}^2}\left( {1 + g} \right) - d{{\left( {1 + {r^ * }} \right)}^2}} \right] $ | (17) |
假定经济系统处于封闭状态,那么第(t+1)期的资本应为第t期的总财富值即所有个体的储蓄之和,Kt+1=s1, tLt,用人均资本可表示为:
| $ {k_{t + 1}} = {s_{1,t}}/\left( {1 + n} \right) $ | (18) |
未来我国预期寿命和生育率的预测数据来源于《联合国人口报告》,理由如下:其一,《联合国人口报告》的预测数据较为科学客观,使得本文研究结果的预测性具有一定参考价值;其二,本文在计算生育率与人口增长率之间的关系时,需要各年龄别人口占比的数据,《联合国人口报告》中具有该数据资源;其三,《联合国人口报告》预测我国人口的总和生育率将从2015年的1.55逐步提高至2100年的1.81,而我国人口总和生育率的正常值应为1.8①,二者相近,故可以基于此进行比较分析。
①《国家人口发展报告》认为我国的总和生育率应维持在1.8左右,过高和过低都不利于人口和经济的协调发展。
(二) 参数设定大多数学者将世代交叠模型的期间长度设为27~30年,本文将三期世代交叠模型的每期长度设定为30年,即少年期为0~30岁,成年期为30~60岁,老年期为60~90岁②。假定就业年龄为25岁,退休年龄为60岁,所以职工在少年期将有(1/6)③的时间用于工作,相应的参数d=1/6。同时,在现行制度下,我国男性职工的法定退休年龄为60岁,女性职工为55岁,女性工人为50岁,未来我国职工的法定退休年龄将延迟,本文将退休年龄设定为60岁符合未来发展趋势。另外,职工工作时间为25~60岁,总年限为35年,与基本养老保险制度设计的35%的目标替代率具有一定的吻合性。
② 由于本文需要分析生育率变化的影响效应,因此需要在模型中引入少年时期,用人口增长率来反映生育率变化;同时,由于我国人口的预期寿命增长较快,如果设置时期过短则难以较好体现预期寿命变化,因此本文将三期世代交叠模型的时间长度设定为30年。
③ 计算公式:1/6=(30-25)/30。
1. 效用折现因子β,资本产出份额α,技术水平A,工资增长率g简永军、周继忠(2012)将效用折现因子设定为0.95,康传坤、楚天舒(2014)设定折现因子取值为0.945,结合学者们的估算,本文将效用折现因子β设定为0.95。根据中国经济模拟中的常用参数值设定,本文将资本产出份额α设定为0.4,技术水平A设定为1,工资增长率设定为0.01,由于本文的时间长度为30年,所以工资增长率g的取值为0.3478④。
④ 计算公式:0.3478=0.01^30-1。
2. 基础养老金平均替代率b1和统筹账户缴费率λ⑤⑤ 需要说明的是,后文研究是从两方面着手进行分析,即分别假定养老金平均替代率不变和缴费率不变,因此当假定平均替代率不变时,缴费率将发生变化;而假定缴费率不变时,平均替代率将发生变化。
[国发(2005)38号]的规定表明我国基础养老保险金的目标替代率为35%,因此本文将基础养老金的平均替代率b1设定为35%;
《国务院关于建立统一的企业职工基本养老保险制度的决定》明确了企业的基本养老保险缴费率不超过20%,故将缴费率λ设定为20%。
3. 预期寿命与生存概率m本文通过预期寿命来测算未来老年期的生存概率变化,从《联合国人口报告》中可知我国人口的预期寿命(见表 1),生存概率与预期寿命的计算公式⑥如下,最终计算结果如表 1所示。
| 表 1 预期寿命和老年期生存概率 |
⑥ 计算公式解释:个体老年期从60岁开始,至90岁结束,共计30年。需要说明的是,在一些文献中,计算老年期生存概率的公式为预期寿命与计算期总期长之比,即预期寿命/90,本文认为由于假定个体均生存3期,即能够从成年期生存至老年期,因此计算期应该以老年期30年为基准。
| $ 老年期生存概率 = \frac{{预期寿命 - 60}}{{30}} $ |
从《联合国人口报告》中可知未来我国人口的总和生育率和各年龄别人口占比,通过这两个数据可估算出人口增长率,计算步骤如下:
(1) 计算生育率。计算公式为“生育率=总和生育率÷35”,其中育龄妇女岁数为15~49岁,共计35年;
(2) 计算育龄妇女占总人口的比重。已知15~59岁人口占比a,假设人口均匀分布,因此估算出15~49岁人口占比b为a的
(3) 计算人口出生率。由于人口出生率f为新增出生人口占总人口的比重,生育率为新增出生人口占育龄妇女人口数的比重,因此人口出生率f为生育率与e的乘积,由此计算出人口出生率;
(4) 计算人口增长率。由于世代交叠模型是以个体为研究对象,个体的死亡通过老年期生存概率反映,因此人口出生率即为人口增长率;
(5) 计算一期人口增长率。由于本文设定一期长度为30年,因此一期的人口增长率=f30-1。
总和生育率的数据如表 2所示,由于仅已知2015年、2050年和2100年的15~59岁人口占比分别为67.6%、50%和46.9%,因此先计算得出对应年份的育龄妇女人口占总人口的比重分别为26.29%、19.44%和18.24%①。为方便计算,假定育龄妇女人口占比在各已知年份(即2015-2020年、2020-2030年、2030-2050年、2050-2100年)之间服从均匀分布,因此可进一步计算得出2020年和2030年②的育龄妇女人口占比分别为25.31%和23.36%③,最终计算结果如表 2所示。另外,从表 2中可以看出:虽然人口的总和生育率在不断提高,但是由于育龄妇女占总人口的比重在下降,因此人口增长率总体呈下降趋势。在以往研究中,往往忽视人口老龄化背景下的育龄妇女人数占比降低的问题,其实,生育率的提高并不一定使得人口增长率上升。
| 表 2 生育率和人口增长率 |
① 计算公式:67.6%÷45×35÷2=26.29%,同样地,可计算而得19.44%和18.24%。另外,根据第六次人口普查的数据可知2010年我国育龄妇女总人数约为3.8亿,占总人口的比重约为28.5%,本文根据《联合国人口报告》计算2010-2015年育龄妇女占总人口比重为26.29%,计算结果可信度较高。
② 由于人口占比数据只有2015、2050和2100年,因此为简化计算,后文将预期寿命和总和生育率对应的年份2010-2015年、2015-2020年、2025-2030年、2045-2050年、2095-2100年间接假定为以2015、2020、2030、2050和2100年为准。
③ 计算公式:(19.44%-26.29%)÷(2050-2015)=-0.1956%,26.29%-0.1956%×(2020-2015)=25.31%,同理可计算而得23.36%。
五、数值模拟分析数值模拟中选取的制度指标包括缴费率λ、基础养老金平均替代率b1、个体替代率b2、基础养老金水平p。为便于比较分析,本文还选取了成年期储蓄s1、个体福利wel、制度福利sz这些指标。在进行数值模拟分析之前,本文先将各指标之间的相互作用机制予以说明:
(1) 生存概率增加或者人口增长率下降使得老年抚养比提高,为维持基本养老保险统筹账户自身的收支平衡,会引致制度缴费率上升或基础养老金平均替代率下降,本文称之为“人口效应”。
(2) 基于式(15)可知,个体替代率可由平均替代率和人口增长率计算而得,且与其呈正相关关系。
(3) 基于莫迪利安尼的“生命周期假说”,个体会均衡一生的收入以使个体福利最大化,当老年期生存概率增加时,个体会增加成年期储蓄以平衡一生的收入和消费,保障老年期的生存,即预期寿命提高会引致成年期储蓄增加,成年期消费减少, 本文称之为“生命周期效应”。
(4) 从式(18)可知,当储蓄增加或人口增长率降低时,社会资本存量增加,同时基于式(9)和式(10),社会资本存量的增加会导致利率下降、工资提高,本文称之为“经济效应”。
(5) 成年期和老年期的消费和储蓄变化。基于个体行为中的式(1)、(2)和(3)可知,工资水平提高,则成年期消费和储蓄增加;利率下降则老年期消费降低;成年期储蓄增加则老年期消费提高。
(6) 基础养老金水平变化。基于式(12),基础养老金水平与工资、缴费率、人口增长率呈正相关关系,与老年期生存概率呈负相关关系。
(7) 个体福利水平变化。个体福利取决于不同时期的消费水平,消费水平高则福利水平高。成年期消费与工资呈正相关,与成年期储蓄呈负相关;老年期消费与养老金水平、利率、成年期储蓄呈正相关,因此个体福利与工资、养老金水平、利率成正相关,与成年期储蓄之间的关系不确定。
(8) 制度福利水平变化。由式(17)可知,制度福利与人口增长率、工资水平、缴费率、利率等相关,式(17)中括号里的内容决定了制度福利的正负。在本文的人口增长率和缴费率设定下,式(17)中括号值为负,人口增长率下降则制度福利减少,制度福利与利率的关系不明确,工资水平提高则制度福利减少。
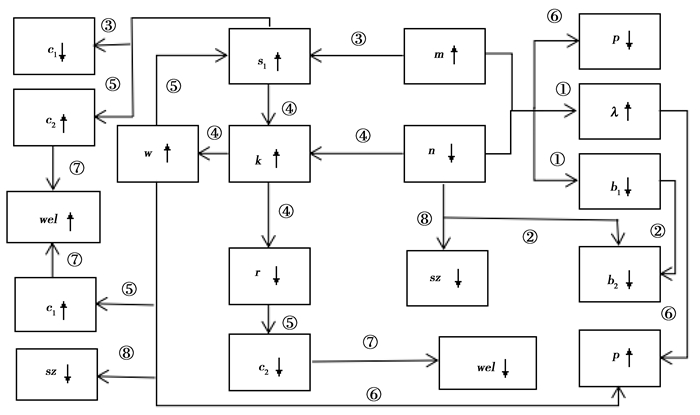
各指标间的相互作用机制可表示为图 1,图中标号分别对应说明中的序号。从图 1中可以看出:在各指标间的相互作用机制之下,老年期生存概率和人口增长率变化能够增加或者减少基础养老金水平、制度福利和个体福利,故而对这三者的影响方向不明晰;而且对其它制度指标的影响程度大小也难以准确测量,故而需要进行下文更为详细的数值模拟分析。
|
图 1 各指标间的相互作用机制 |
数值模拟中先单独分析了预期寿命和生育率对基本养老保险统筹账户的单独影响,而后将二者结合分析了共同影响,所采用数据均来源于《联合国人口报告》。单独分析预期寿命影响时,假定总和生育率保持不变为2010-2015年的1.55;单独分析生育率影响时,假定预期寿命保持不变为2010-2015年的75.4岁。另外,由于参数调整的途径主要是调整养老金水平和缴费率,因此本文在进行数值模拟分析时,分别假定养老金平均替代率不变和制度缴费率不变这两种情况,以便比较分析这两种情境下的经济和福利水平变化差异。另外,模拟1-5分别对应前文2010-2015年、2015-2020年、2025-2030年、2045-2050年、2095-2100年这五种情境。
(一) 预期寿命变动与基本养老保险统筹账户调整的数值模拟分析预期寿命通过改变老年期生存概率和人口增长率来对统筹账户收支平衡产生影响,进而引致统筹账户的参数调整:一方面,随着预期寿命提高,老年期生存概率增加;另一方面,预期寿命提高则人口结构趋于老化,育龄妇女占总人口的比重下降,在生育率不变的条件下,人口增长率随之下降。
本文在该部分仅详细分析预期寿命通过生存概率对统筹账户收支平衡的影响,原因如下:其一,从人口增长率这条作用机制进行分析缺少相关数据支持①;其二,预期寿命提高则人口增长率下降,生育率提高则人口增长率提高,二者的作用路径正好相反,因此预期寿命对人口增长率的影响机制可从生育率变化的影响机制中反推得出。预期寿命变化与基本养老保险统筹账户调整的模拟结果如表 3和表 4所示。表 3的假定条件为基础养老金平均替代率为35%保持不变,表 4的假定条件为基本养老保险缴费率为20%保持不变。从表 3和表 4可知:
| 表 3 预期寿命变动与基本养老保险统筹账户调整的模拟结果(养老金平均替代率不变) |
| 表 4 预期寿命变动与基本养老保险统筹账户调整的模拟结果(缴费率不变) |
① 一方面,大多数学者只关注到生存概率这个影响机制,研究预期寿命对人口增长率影响的文献较少;另一方面,《联合国人口报告》中各年龄别人口占比是在该年份特定的预期寿命和生育率数据之下预测而得的,无法得出生育率不变时的各年龄别人口占比,即无法单独计算出预期寿命对人口增长率的影响。
(1) 经济发展变化。随着预期寿命增长,老年期生存概率增加,成年期储蓄呈增加趋势,有利于社会资本积累和经济发展;在假定缴费率不变的情况下,储蓄增加更多。
(2) 福利水平变化。预期寿命提高使得制度福利和个体福利均不断降低,假定替代率不变的条件下二者降低的程度更大。
(3) 基本养老保险统筹账户调整。为维持基本养老保险统筹账户收支平衡,预期寿命从75.4岁提高至89.9岁时,缴费率需要从10.27%增长至19.94%以保证35%的目标替代率;在缴费率为20%的设定下,养老金平均替代率将从68.15%降至35.10%,个体替代率将从97.95%降至50.45%。
(4) 参数调整临界点。在总和生育率为1.55的情境下,预期寿命为89.985岁时正好可以维持20%的缴费率及35%的平均替代率,这也是基本养老保险统筹账户需要进行参数调整的临界点。
由此可见,目前20%的制度缴费率可以在相当长时期内保证统筹账户的平均替代率不低于35%,在总和生育率为1.55时,预期寿命提高至89.985岁为参数调整的临界点。在临界点前,维持35%的基础养老金目标替代率、逐步提高缴费率的方案可以使个体福利和制度福利的值相对大,同时有利于资本积累,促进经济发展。
(二) 生育率变动与基本养老保险统筹账户调整的数值模拟分析生育率通过改变人口增长率来影响基本养老保险统筹账户收支,当总和生育率提高时,人口增长率提高。为单独分析生育率变化对基本养老保险统筹账户收支的影响,假定预期寿命为2010-2015年的75.4岁,育龄妇女人数占总人口比重为26.29%保持不变①。由于表 2的人口增长率是在育龄妇女人数占比变化的条件下计算而得的,因此为单独分析生育率变化对人口增长率的影响,需再次计算人口增长率,计算方法同前文相同,故不再赘述,计算结果见表 5。生育率变化与基本养老保险统筹账户调整的数值模拟分析结果如表 6和表 7所示,从中可以得出:
| 表 5 生育率和人口增长率(育龄妇女人数占比不变) |
| 表 6 生育率变动与基本养老保险统筹账户调整的模拟结果(养老金平均替代率不变) |
| 表 7 生育率变动与基本养老保险统筹账户调整的模拟结果(缴费率不变) |
① 需要说明的是,在该部分虽然假定育龄妇女人口占比保持不变,并依此测定人口增长率。但是,在经济稳态时,总和生育率提高所引致的人口增长,会在一定程度上使得人口年龄结构趋于年轻化(假定预期寿命不变),育龄妇女人口占比可能会发生变化。由于生育率变化缓慢,故而影响不大,并未再进行深入探讨。
(1) 经济发展变化。生育率变动下的个体成年期储蓄呈小幅增加趋势,即生育率提高有利于经济发展,但作用有限,再结合表 3和表 4可知,生育率变动下的个体成年期储蓄基本不变,即生育率变动对国民储蓄的影响不大,再结合图 1可知,预期寿命在更大程度上决定了储蓄变化,对经济发展具有较大影响力。
(2) 福利水平变化。生育率水平提高,养老金替代率增加,但人均养老金实际水平下降,个体福利呈下降趋势;随着生育率水平提高,制度参保者所获取的制度福利不断增加。
(3) 基本养老保险统筹账户调整。在其它条件不变的情况下,总和生育率增加则人口增长率提高,维持缴费率不变可促进养老金替代率水平上升,维持平均替代率不变则可以促使缴费率下降,有利于基本养老保险制度的长期可持续发展。如果目前的总和生育率水平达到正常值1.8左右,则基础养老金的平均替代率将从68.85%提高至73.02%(表 4模拟2-模拟5)。
(4) 参数调整临界点。由于总和生育率变化缓慢,所以测算出参数调整临界点值过小,故不再分析。
由此可见,总和生育率水平的提高有利于基本养老保险统筹账户的可持续运行,但由于总和生育率的变化较为缓慢,其对统筹账户收支的影响也较小,对国民储蓄的影响也不大。同时,总和生育率增加使得个体福利水平降低,但是在一定程度上增加了参保者的制度福利。
(三) 预期寿命、生育率变动与基本养老保险统筹账户调整的数值模拟分析按照《联合国人口报告》的预测数据,我国人口预期寿命增长较快,而总和生育率增长缓慢,因此人口增长率总体仍呈下降趋势。在老年生存概率增加和人口增长率下降的共同作用下,各指标变化如表 8和9所示,其中表 8假定基础养老金平均替代率为35%保持不变,表 9假定制度缴费率为20%保持不变,关于预期寿命和生育率变化与统筹账户调整的作用机制前文已做详细分析,故不再赘述。另外,在测算制度参数调整临界点时,假设2050-2100年间的预期寿命和总和生育率变化服从均匀分布。从表 8和表 9中可知:
| 表 8 预期寿命、生育率变动与基本养老保险统筹账户调整的模拟结果(养老金平均替代率不变) |
| 表 9 预期寿命、生育率变动与基本养老保险统筹账户调整的模拟结果(缴费率不变) |
(1) 经济发展和福利水平变化。在未来预期寿命和生育率的共同影响之下,个体老年期生存概率增加,人口增长率降低。为应对老年长寿风险,国民储蓄增加,有利于资本积累和经济发展;然而,个体福利和制度福利都有所损失,维持平均替代率不变时的损失额相对较小。
(2) 基本养老保险统筹账户调整。在目前的预期寿命和生育率条件下(模拟2),20%的制度缴费率可以维系63.26%的基础养老金平均替代率,11.07%的缴费率可以维持最低35%的平均替代率,现期的统筹账户可实现制度目标下的收支平衡;在长期内,为维持基本养老保险统筹账户的收支平衡,制度缴费率需增加或者养老金平均替代率需减少,基础养老金水平在维持平均替代率不变的设定下呈增长趋势。
(3) 参数调整临界点。从模拟结果中可知预期寿命为87.828岁且总和生育率为1.79时为统筹账户进行参数调整的临界点,此时所对应的年份为2086年左右。
(4) 参数调整方案。一方面,从个体福利最大化的视角来比较分析表 8和表 9,保持平均替代率不变的方案在模拟1-4中具有较大福利水平,保持缴费率不变的方案在模拟5中具有较大福利水平,处于临界点时的二者福利水平最为相近,因此在临界点之前保持养老金平均替代率不变、临界点之后保持缴费率不变的方案可使得个体福利处于相对高的水平;另一方面,从经济发展的视角来看,通过比较分析,临界点前后分别维持平均替代率和缴费率不变的方案同样使得国民储蓄值相对较高,有利于经济发展。
基于模拟分析结果,在预期寿命和生育率的共同影响之下,为保证基本养老保险统筹账户的收支平衡,统筹账户需进行参数调整。2086年之前保持35%的养老金平均替代率水平不变,制度缴费率不高于20%;2086年后保持20%的缴费率不变,适当降低基础养老金平均替代率可以在最大程度保证经济和社会发展。
(四) 考虑灵活就业者参保人数增加的数值模拟分析为鼓励灵活就业者参加基本养老保险制度,落实相关社会保险补贴政策,《国务院关于完善企业职工基本养老保险制度的决定》中规定:灵活就业者参加基本养老保险制度的缴费比例为20%,其中8%划入个人账户,12%划入统筹账户。因此,与正规就业的企业职工相比,灵活就业者统筹账户缴费率相对较低。
随着灵活就业者参保人数的增加,灵活就业者参保对基本养老保险统筹账户公平可持续发展的影响将更加明显:一方面,灵活就业者参保人数增加有利于体现制度的互济性和公平性,增加基本养老保险基金收入,维系短期内的基金收支平衡;另一方面,灵活就业者低统筹账户缴费率在长期内容易造成基本养老保险基金收不抵支现象,统筹账户进行参数调整的临界点也将发生变化。
本文分别假定灵活就业参保者占总参保者的比例为0、25%、50%、75%和100%,并模拟分析这5种情境下的参数调整临界点。基于前文分析,在预期寿命和生育率变动对基本养老保险统筹账户收支的影响中,快速增长的预期寿命对统筹账户收支的影响程度远高于生育率,缓慢变化的生育率对基本养老保险统筹账户的影响较低,为简化分析,故而在测算参数临界点时仅基于预期寿命视角,测算结果如表 10所示。
| 表 10 灵活就业者参保与基本养老保险统筹账户调整的模拟结果 |
基于表 10并结合实际分析可知:(1)当灵活就业参保者人数占比为0时,在预期寿命为89.985岁时应进行基本养老保险制度的参数调整;当灵活就业参保者人数占比为100%时,预期寿命为77.991岁时就应进行参数调整,临界点提前近12岁;(2)2015年我国的预期寿命为76.34岁,最为接近灵活就业参保人数占比为100%的情况,这说明基本养老保险制度在目前可以“承受”的灵活就业参保者人数占比最高为100%。
需要说明的是,表 10的测算结果是基于基本养老保险制度参保率为100%的假定,目前我国灵活就业者参加基本养老保险制度的比例较低,将灵活就业者纳入到制度中可以提高制度参保率,有利于短期内的基金收入增加。但是,从长期发展来看,灵活就业参保者的低统筹账户缴费率并不利于统筹账户收支平衡。
(五) 实证结论基于前文分析,预期寿命和生育率变动对基本养老保险统筹账户收支的影响主要体现在以下三个方面:其一,预期寿命对老年期生存概率的影响;其二,预期寿命对人口增长率的影响;其三,生育率对人口增长率的影响,预期寿命、生育率变动对基本养老保险统筹账户收支的影响取决于这三方面作用大小。前文已分析出老年期生存概率和人口增长率与基本养老保险统筹账户调整的关系,汇总为表 11。其中,预期寿命引致人口增长率降低的影响反向参照生育率引致的人口增长率提高。由于我国目前处于快速老龄化阶段,且总和生育率增长速度较为缓慢,因此预期寿命对统筹账户收支的影响要显著大于生育率,二者对基本养老保险统筹账户的综合影响结果更加接近预期寿命影响的模拟结果(即表 11中④的结果更为接近①和②)。
| 表 11 预期寿命、生育率变动与基本养老保险统筹账户调整的汇总模拟结果 |
综合来看,从数值模拟分析中可得出以下几点结论:
(1) 预期寿命变动与基本养老保险统筹账户调整、经济和福利水平变化。未来预期寿命提高对基本养老保险统筹账户收支影响较大,造成缴费率提高或者基础养老金平均替代率下降,国民储蓄增加,个体福利和制度福利减少,因此预期寿命提高不利于基本养老保险统筹账户的可持续发展和个体福利水平的提高,但是可以促进资本积累和经济发展。
(2) 生育率变动与基本养老保险统筹账户调整、经济和福利水平变化。未来总和生育率变化缓慢,对基本养老保险统筹账户收支影响不大,引致制度缴费率降低或基础养老金平均替代率提高,国民储蓄小幅增加,个体福利减少,制度福利增加,所以生育率增加有利于基本养老保险统筹账户收支平衡,同时提高个体参加制度的“获得感”,但是个体一生的福利水平有所下降。
(3) 预期寿命、生育率变动与基本养老保险统筹账户调整、经济和福利水平变化。在预期寿命和生育率变动的共同作用下,为维持基本养老保险统筹账户收支平衡,制度缴费率在未来需要提高或者基础养老金平均替代率需要降低,同时,国民储蓄增加进而有利于经济发展,个体福利和制度福利总体上呈减少趋势。
(4) 基本养老保险统筹账户的参数调整临界点。仅考虑预期寿命影响,当预期寿命提高至89.985岁时,20%的制度缴费率刚好维系35%的基础养老金平均替代率;考虑预期寿命和生育率的共同影响,预期寿命为87.828岁且总和生育率为1.79(2086年左右)为基本养老保险统筹账户进行参数调整的临界点。
(5) 基本养老保险统筹账户的参数调整方案。基于我国目前的缴费和养老金水平,为促进经济发展和社会公平,参数调整临界点(2086年左右)之前应确保基础养老金平均替代率保持在35%,制度缴费率不高于20%;临界点之后可以适当降低基础养老金平均替代率以保证制度缴费率不高于20%。
(6) 灵活就业者参保与基本养老保险统筹账户的调整。在劳动者全部参保的假定下,结合当前的现实情境,基本养老保险制度目前可以“容纳”灵活就业者参保人数占总参保人数的比重最大为100%。随着灵活就业参保者人数占比增加,基本养老保险统筹账户进行参数调整的临界点将有所提前。
六、总结与启示基于前文的数值模拟分析与实证结论,本文得出以下几点总结与启示:
(一) 人口结构足以维系目前的基本养老保险统筹账户基金的当期收支平衡结合本文实证分析,在目前的预期寿命和生育率条件下,20%的缴费率可以保证63.26%的基础养老金平均替代率,35%的基础养老金平均替代率所需的缴费率仅为11.07%(表 8和表 9中的模拟情境2),均满足目前的制度参数规定。同时,从实际参保人数的角度进行分析,2015年我国参加基本养老保险的离退休职工人数占参保职工人数的比值为34.87%①,则20%的缴费率可以保证57.36%的平均替代率,保证35%的平均替代率所需的缴费率为12.2%②,也均满足目前的参数规定。由此可见,人口因素虽然会造成基本养老保险统筹账户基金的收入减少和支出增加,但在目前的人口结构和制度参数规定下,并不会引致基金收支失衡现象。然而,历史遗留债务、缴费基数不实、养老保险覆盖面窄、养老金上调机制不科学等均在一定程度上加大了基本养老保险统筹账户基金的收支失衡风险,目前应加大力度来规范制度运行,切实保障基本养老保险统筹账户的公平可持续发展。
① 人口数据来源于国家统计局网站。
② 制度抚养比=缴费率/养老金平均替代率,57.36%=20%÷34.87%,12.2%=35%×34.87%。
(二) 短期内可通过阶段性降低统筹账户缴费率来促进基本养老保险制度长远发展本文的实证分析认为参数调整临界点之前降低缴费率可最大化发展经济和避免福利损失,故短期内阶段性降低缴费率的做法是可取的。另外,虽然历史遗留债务、实际缴费基数过低等其它原因也造成基本养老保险统筹账户存在收不抵支风险,但仍可以阶段性降低缴费率,理由如下:首先,弥补历史遗留债务应该均衡各代之间的养老金权益,不可通过一味提高缴费率或者降低养老金替代率使历史债务由一代人或者几代人来承担;其次,部分企业降低实际缴费基数来减轻自身的税(费)负担,应该通过做实缴费基数而非提高整体缴费率来进行调整;最后,虽然在预期寿命和生育率变动影响下,未来缴费率应该提高,但目前的缴费率足以维持统筹账户收支平衡,故可在短期内降低缴费率;第四,降低缴费率可以减轻企业的税费负担,促进经济增长,提高工资增长率,进而促进基本养老保险制度的长远发展。
(三) 长期内需提高缴费率或降低养老金替代率来保证基本养老保险统筹账户收支平衡基于前文数值模拟,基本养老保险统筹账户在长期内需要通过参数调整来保证收支平衡,预期寿命为87.828岁且总和生育率为1.79(2086年左右)为参数调整临界点。由于本文的实证模拟是建立在相关配套政策完善的条件下,故结合制度运行现状和本文的实证结论,具体参数调整方案设计如下:
第一,参数调整临界点(2086年左右)之前,首先阶段性降低基本养老保险统筹账户缴费率,而且逐步调整基础养老金平均替代率保持在35%;其次,必须加快提高基本养老保险制度的参保率,构建多层次养老保险体系等,充分完善基本养老保险制度的配套政策,如退休政策、生育政策、低保政策等,以保证基本养老保险制度处于规范运行状态,个体养老风险分散于政府、企业和个体之间;最后,为维持基础养老金35%的平均替代率以及保证统筹账户长期收支平衡,需在阶段性降低缴费率的基础之上再逐步提高缴费率。
第二,参数调整临界点(2086年左右)之后,如果认为20%的缴费率为上限,则不应继续提高缴费率,此时需要逐步降低基础养老金平均替代率以确保制度平稳运行。但是,降低基础养老金替代率可能使低收入群体退休后的基本生活难以维系,为此,必须依靠多层次养老保险体系,或者建立全民参保的最低层次的“国民养老金”政策来予以应对。“国民养老金”政策旨在保障退休群体的最低生活水平,可由现有的基本养老保险统筹账户转变而来,或者在基本养老保险制度这一养老保险层次之下进行新建。
第三,进行基本养老保险制度内其它参数的调整也很有必要,如调整缴费基数上下限、调整养老保险缴费年限、领取年限等,使得基本养老保险统筹账户的参数设计能够与经济发展、国民收入分配、劳动力市场变化等相协调,充分调节高收入者收入,保障低收入者的基本生活,并促进基本养老保险统筹账户的可持续性发展,这能够在一定程度上减少统筹账户的收支失衡风险。
(四) 加快构建多层次养老保险体系,分散个体养老风险以应对人口老龄化预期寿命对基本养老保险统筹账户的影响日益加深,仅依靠政府举办的基本养老保险制度难以应对人口老龄化的冲击,必须借助企业、市场的力量来共同分担养老压力。具体地,第二层次的企业年金、职业年金的覆盖范围需要进一步扩大,政府需要为企业发展补充养老金提供足够的税收优惠等政策支持;同时,第三层次的商业养老保险可在一定程度上依靠政府力量来实现业务拓展等,设计差异化商业养老保险以确保个体的养老风险能够实现高效转移,充分满足不同个体的养老需求。依据前文数值模拟结果,基础养老金的平均替代率水平大概在2086年之后需要进行下调,在此之前必须加快构建多层次养老保险体系,以确保个体养老风险的最大程度转移。
(五) 出台家庭儿童福利相关政策以促进“全面二孩”政策落实,提高总和生育率总和生育率的提高可在一定程度上缓解基本养老保险统筹账户的收支失衡现象,而我国目前正处于“全面二孩”政策的初步实行阶段,必须完善相关配套政策,减轻家庭育儿负担以切实促进生育水平的提高,具体地:其一,拓宽生育保险覆盖范围、适时上调最高和最低生育津贴标准以减轻育儿家庭的生育成本;其二,参照国际社会的普遍做法,通过逐步制定且实行“家庭津贴”政策,稳步推行“父母带薪育儿假”等来分担育儿家庭在孩子出生至成年期的养育费用;其三,政府应该和企业共同负担生育津贴费用,以减轻劳动力市场的女性就业歧视问题,提高女性生育意愿以促进生育水平提高。
| [] |
封进、宋铮,
2006, “中国人口年龄结构与养老保险制度的福利效应”, 《南方经济》, 第 11 期, 第 22-33 页。DOI:10.3969/j.issn.1000-6249.2006.11.003 |
| [] |
耿志祥、孙祁祥、郑伟,
2016, “人口老龄化、资产价格与资本积累”, 《经济研究》, 第 9 期, 第 29-43 页。 |
| [] |
贺菊煌,
2002, “个人生命分为三期的世代交叠模型”, 《数量经济技术经济研究》, 第 4 期, 第 48-55 页。 |
| [] |
简永军、周继忠,
2011, “人口老龄化、推迟退休年龄对资本流动的影响”, 《国际金融研究》, 第 2 期, 第 4-13 页。 |
| [] |
景鹏、胡秋明,
2016, “生育政策调整、退休年龄延迟与城镇职工基本养老保险最优缴费率”, 《财经研究》, 第 42 期, 第 26-37 页。 |
| [] |
康传坤、楚天舒,
2014, “人口老龄化与最优养老金缴费率”, 《世界经济》, 第 4 期, 第 139-160 页。 |
| [] |
李军, 2003, "老龄化与养老保障宏观经济效应分析", 中国社会科学院研究生院博士论文.
|
| [] |
李炜光、臧建文,
2017, “中国企业税负高低之谜:寻找合理的企业税负衡量标准”, 《南方经济》, 第 2 期, 第 1-23 页。 |
| [] |
李晓鹤、殷俊,
2016, “延迟退休:个人理性与政府决策的冲突与平衡”, 《南方经济》, 第 2 期, 第 43-55 页。 |
| [] |
李珍、王海东,
2013, “养老金替代水平下降的制度因素分析及对策”, 《中国软科学》, 第 4 期, 第 50-59 页。 |
| [] |
林宝,
2010, “人口老龄化对企业职工基本养老保险制度的影响”, 《中国人口科学》, 第 1 期, 第 84-92 页。 |
| [] |
柳清瑞、苏牧羊,
2016, “少子老龄化、公共养老金支出与提高退休年龄——基于OECD国家的经验比较”, 《上海财经大学学报》, 第 3 期, 第 74-93 页。 |
| [] |
刘书明、常硕,
2017, “中国人口年龄结构特征与变化趋势分析——基于1995~2014年数据的实证研究”, 《西北人口》, 第 1 期, 第 1-11 页。 |
| [] |
彭浩然、陈斌开,
2012, “鱼和熊掌能否兼得:养老金危机的代际冲突研究”, 《世界经济》, 第 2 期, 第 84-97 页。 |
| [] |
孙祁祥、朱俊生,
2008, “人口转变、老龄化及其对中国养老保险制度的挑战”, 《财贸经济》, 第 4 期, 第 68-73 页。 |
| [] |
汪伟、艾春荣,
2015, “人口老龄化与中国储蓄率的动态演化”, 《经济研究》, 第 6 期, 第 47-62 页。 |
| [] |
杨再贵,
2007, “中国养老保险新制度与社会统筹养老金和个人账户本金”, 《中国人口科学》, 第 4 期, 第 74-79 页。 |
| [] |
于洪、曾益,
2015, “退休年龄、生育政策与中国基本养老保险基金的可持续性”, 《财经研究》, 第 6 期, 第 46-57 页。 |
| [] |
张迎斌、刘志新、柏满迎、罗淇耀,
2013, “我国社会基本养老保险的均衡体系与最优替代率研究——基于跨期叠代模型的实证分析”, 《金融研究》, 第 1 期, 第 79-91 页。 |
| [] |
Alfonso R., Sánchez Martín, 2010, "Endogenous Retirement and Public Pension System Reform in Spain". Economic Modelling, 27(1), 336–349.
DOI:10.1016/j.econmod.2009.09.013 |
| [] |
Diamond P. A., 1965, "National Debt in a Neoclassical Growth Model". American Economic Review, 55(5), 1126–1150.
|
| [] |
Haan P, Prowse V., 2014, "Longevity, Life-cycle Behavior and Pension Reform". Journal of Economet, 178(1), 582–601.
|



