密度依赖模型是组织生态学研究中应用得最为广泛的模型，密度依赖理论通过合法性(legitimacy)和竞争性(competition)来解释组织出生率、组织死亡率、组织种群密度和组织增长率的演变(Hannan and Carroll, 1992；Hannan and Freeman, 1993)。在组织发展的初级阶段，组织出生率低，组织死亡率尤其高，种群增长率很低。随着组织密度的增加，现有组织的数量能为相似组织的成立提供意识形态空间(the ideological space；Stretesky et al., 2011)，有利于组织形式被社会普遍性认可，达到“理所当然的地位”(social taken-for-grantedness；Hannan et al., 1995)，使组织收获更多资源(蔡宁、王发明，2006)。合法性随着密度增加，以递减的速度增强(Barron，1998)。瑞典IT行业的发展表明：行业的成长使得出生率上升，IT组织在资源提供者心目中的合法性逐步增强，组织更容易成立(Zaring and Eriksson, 2009)。组织出生率逐渐增加，死亡率减少，组织种群实现了整体的成长。当出生率达到最大值，死亡率接近最小值时，种群成长率达到最大值。之后，组织出生率下降，组织死亡率上升，组织成长率下降。最终，组织种群的规模稳定在环境承载力水平上(Wissen，2004)。

当资源充足时，出生率高，死亡率低，组织种群增殖扩展。资源稀缺时，新进入者会发现现有资源池(pool of resources)难以在短期内拓宽，保护组织生存的能量也有限，所以此阶段成立的组织实力羸弱。个体组织缺乏投资组织专业技能的激情，在组织生存存在诸多不确定因素的情况下，建立合作和信任的框架尤为困难(Lomi，1998)。Lomi研究了1846到1989年丹麦商业银行组织的出生率，发现：哥本哈根银行的出生率与银行密度负相关(Lomi，2000)，组织密度的增加意味着资源竞争益发激烈。对资源的竞争增加了死亡率，阻止了新企业进入，组织种群处于停滞或下降状态(Gómez et al., 2014)。Xu(2017)以报业组织成立微博账号作为组织在新媒体上的出生，结果发现：党报的微博出生率与当地、非当地党报和非党报的密度呈现倒U型关系，省外非党报密度对非党报出生率也存在影响。

在种群发展的初始阶段，随着种群中组织的数量增加，组织死亡率下降。其后，当组织密度达到最高临界值时，竞争性的作用增强(Lazzeretti，2017)，组织死亡率随着密度的增加而呈现上升趋势。种群中组织的大量死亡释放出环境不利于生存的信号(Messallam，1998)，所以当组织死亡率上升时，人们普遍认为组织出生率会下降。高出生率使许多企业家看到了未来有利的结果，良好的预期激励着企业家们，使得新出生者更有可能成功(Carroll and Khessina, 2005)。组织出生率上升时，人们普遍认为组织死亡率会下降。

以往研究一般认为密度依赖模型的组织出生率与组织死亡率函数呈反向关系。组织出生率上升时，组织死亡率下降；组织出生率下降时，组织死亡率上升。组织死亡率增长时，试图进入该行业种群的组织减少。组织死亡率下降时，试图进入该行业种群的组织增加。然而，实际情况是否如此？组织出生率与组织死亡率是否可能存在同向变动现象？

Hannan and Freeman假设t时刻的组织设立率λ(t)主要受合法性L_t和竞争性C_t影响，组织设立率λ(t)=a(t)· $\frac{{{L_t}}}{{{C_t}}}$。其中，合法性L_t=αN_t^β, α>0, 0 < β < 1，竞争性C_t=γe^δN_t2, γ>0, δ>0。合法性以递减的速度随密度增加而增加，竞争性则随密度增加而递增增长(彭璧玉、李熙，2014)，代入可得组织设立率λ(t)=a(t)· $\frac{\alpha }{\gamma }$N_t^βexp(－δN_t²)，求导可得$\frac{{{\rm{d}}\lambda t}}{{dN}}$=$\varphi $(t)N_t^β－1exp(－δN_t²)(β－2δN_t²)，N的极大值点N^*= $\sqrt {\frac{\beta }{{2\delta }}} $(Hannan and Freeman, 1993)。Hannan and Carroll在此基础上将设立率表示为普遍性尤尔模型(generalized-Yule model，GY)：λ(t)=$\frac{a}{\gamma }$N_t^β exp(kN_t²), κ=-δ，其中0 < β < 1，κ < 0(Hannan and Carroll, 1992)。Hannan和Freeman发现GY模型无法拟合美国工会组织的数据(1988)，于是采用对数二次方近似法(log-quadratic approximation，LQ)求取模型参数近似解，发现LQ法比GY模型更能拟合报业组织的出生率(Carroll and Hannan, 1989)。组织设立率密度依赖性的LQ近似值(Hannan and Carroll, 1992)具有如下形式：λ(t)=$\frac{a}{\gamma }$ exp (θ₁N_t+θ₂N_t²)。随着密度增加，出生率增长，直到N_λ^*=$\frac{{{\theta _1}}}{{2{\theta _2}}}$。当密度大于Ν_λ^*时，则出生率随密度增加而减少。

组织年龄为u时的组织倒闭率μ(u)=b(u)· $\frac{{{C_u}}}{{{L_u}}}$，其中L_u=νN^k, C_u=ξexp(λN²)。所以，μ(u)=$\frac{{\xi b(\mathit{u})}}{\nu }$N_u^－Kexp(λN_u²)。由于该模型难以得到收敛的参数估计，因此将其转换成参数解释力相同的：μ(u)=$\frac{{\xi b({u})}}{v}$exp(－θ₁N_u+θ₂N_u²)。将死亡率函数两边同时取log以方便计算，可得：lnμ(u)=ln$\frac{{\xi b(\mathit{u})}}{\nu }$－θ₁N_u+θ₂N_u²。求导可得，$\frac{{{\rm{d}}\mu {\rm{(}}\mu {\rm{)}}}}{{d{N_u}}}$=μ(u)·(－θ₁+2θ₂N_u)，密度最小值为N^*=$\frac{{{\theta _1}}}{{2{\theta _2}}}$(Hannan and Freeman, 1993)。

同理，将组织设立率求导可得$\frac{{d\lambda (\mathit{t})}}{{d{N_t}}}$=λ(t)· (θ₁+2θ₂N_t)。所以，当λ(t)>0时，如果θ₁+2θ₂N_t>0, 即N_t>－$ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，组织设立函数呈增长趋势；如果N_t < $ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，则组织设立率为下降趋势。当λ(t) < 0时, 如果N_t < $ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，则组织设立函数上升。组织设立率小于0时，如果N_t>$ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，则组织设立函数下降。

就组织倒闭率而言，当μ(u)>0时，如果-θ₁+2θ₂N_u>0, 即N_u>$\frac{{{\theta _1}}}{{2{\theta _2}}}$时，组织倒闭率函数呈增长态势；N_u < $\frac{{{\theta _1}}}{{2{\theta _2}}}$时，函数为下降趋势。当μ(u) < 0时, 如果-θ₁+2θ₂N_u < 0, 即N_u < $\frac{{{\theta _1}}}{{2{\theta _2}}}$时，函数上升；反之，组织死亡函数呈下降趋势。综上所述，组织设立和组织死亡函数的变动趋势如表 1所示。

表 1

表 1 组织设立和组织死亡函数的取值和变动趋势 出生率 死亡率 Nt和Nu的取值 变化趋势 λ(t)>0 μ(u)>0 ${N_t} > - \frac{{{\theta _1}}}{{2{\theta _2}}}, {N_u} > \frac{{{\theta _1}}}{{2{\theta _2}}}$ 组织设立和组织死亡函数同时上升 λ(t)>0 μ(u) < 0 ${N_t} > - \frac{{{\theta _1}}}{{2{\theta _2}}}, {N_u} < \frac{{{\theta _1}}}{{2{\theta _2}}}$ 组织设立和组织死亡函数同时上升 λ(t)<0 μ(u)>0 ${N_t} < - \frac{{{\theta _1}}}{{2{\theta _2}}}, {N_u} < \frac{{{\theta _1}}}{{2{\theta _2}}}$ 组织设立函数增长，组织死亡函数下降 λ(t)<0 μ(u)<0 ${N_t} > - \frac{{{\theta _1}}}{{2{\theta _2}}}, {N_u} < \frac{{{\theta _1}}}{{2{\theta _2}}}$ 组织设立函数下降，组织死亡函数上升 λ(t)<0 μ(u)>0 ${N_t} > - \frac{{{\theta _1}}}{{2{\theta _2}}}, {N_u} < \frac{{{\theta _1}}}{{2{\theta _2}}}$ 组织设立函数和组织死亡函数同时下降 λ(t)<0 μ(u)<0 \[{N_t} > - \frac{{{\theta _1}}}{{2{\theta _2}}}, {N_u} > \frac{{{\theta _1}}}{{2{\theta _2}}}\] 组织设立函数和组织死亡函数同时下降

表 1 组织设立和组织死亡函数的取值和变动趋势

本文沿用Hannan and Carroll设计的经典组织设立率模型(1992)，通过实证模型检验理论假设。

模型(1)中被解释变量λ(t)表示组织出生率，即新出生的组织数量占种群中现有组织数量(组织密度)的比重。N_t表示t时刻(1993≤t≤2017，单位：年)种群中的组织密度，如N₂₀₁₆即表示2016年广州市外资制造业种群的组织密度。市场主体退出市场的方式主要有两种：一是企业主动申请注销登记，二是工商行政管理部门依法吊销企业的营业执照。因此，本文将企业的注销和吊销这两种方式都定义为组织死亡。据此，统计1993年-2017年每年广州市出生和死亡的外资制造企业数量。用t－1年外资制造业的企业数量加上t年新成立的企业数量，再减去t年注销和被吊销营业执照的企业数量代表组织密度N_t。

Hannan and Freeman提出能得到收敛参数估计的死亡率函数(Hannan and Freeman, 1993)：

模型(2)的被解释变量μ(u)代表组织死亡率，本文的组织死亡率μ(u)等于每年注销和吊销的企业数量除以每年的组织密度。等式右边的解释变量N_u则表示：组织达到年龄u时，每年年初种群中组织的数量(彭璧玉、李熙，2014)。年龄为0岁，即在成立当年死亡。

本研究的数据来源于广州市工商行政管理局的企业数据库，涵盖了1993年1月1日到2017年5月12日广州市成立、注销和被吊销营业执照的外资制造业企业数据。企业类型包括外国法人独资有限责任公司、台港澳法人独资有限责任公司、台港澳自然人独资有限责任公司、台港澳与境内合资有限责任公司、台港澳与境内合作有限责任公司、外商合资有限责任公司、中外合资有限责任公司、中外合作有限责任公司、分公司、办事处、非公司台、港、澳企业、台港澳投资企业分支机构、外商投资企业分支机构等类型。行业门类包括机械制造、电子器件制造、电子元件制造、纺织业、服饰制造、机织服装制造、工艺美术品制造、设备制造业、计算机制造、金属制品制造、化学产品制造、塑料制品业、汽车制造业、食品制造业、医药制造业、石油加工、炼焦和核燃料加工业等制造业相关行业代码的所有制造业。企业状态包括已开业、注销、吊销、清算中和经营期限届满。因为2014年至2017年320个外资制造企业中仅有5个外资制造企业处于“清算中”状态。1993-2013年4338个外资制造开业企业中，仅有47个“经营期限届满”，110个“清算中”。所以，清算中和经营期限届满不具代表性，将涉及的企业数据剔除。再排除若干出生或死亡信息缺失的企业，共得到10328条企业数据。

根据收集到的数据，统计1993年到2017年每年新成立的外资制造企业数量，除以当年外资制造行业中的企业总数，作为组织出生率。本研究将每年主动注销和被吊销营业执照的企业组织视为组织死亡，统计每年死亡的组织数量，除以当年行业中的企业总数，作为组织死亡率。每年的组织密度N_t则用上一年外资制造业的企业总数N_t-1，加上当年新成立的企业数量，减去当年死亡的企业数量表示。

1993年-2017年广州市每年成立、注销和吊销的外资制造业企业数量如表 2所示。对1993年-2017年广州市外资制造企业的出生和死亡情况进行统计分析，描述统计量如表 3所示。经统计，广州市制造业企业从0岁到21岁不等，平均年龄为7.78岁。

表 2

表 2 1993年-2017年广州市成立、注销和吊销的外资制造业企业数量 年份 成立 注销 吊销 1993 302 1 0 1994 199 10 1 1995 240 12 48 1996 79 22 20 1997 105 35 18 1998 119 29 0 1999 149 73 120 2000 201 37 144 2001 218 50 141 2002 284 60 0 2003 315 63 1429 2004 389 68 456 2005 368 118 152 2006 303 179 0 2007 256 197 467 2008 177 170 285 2009 127 148 20 2010 149 143 1 2011 144 139 264 2012 115 119 83 2013 99 143 142 2014 111 40 0 2015 89 2 0 2016 77 16 0 2017 42 4 2

表 2 1993年-2017年广州市成立、注销和吊销的外资制造业企业数量

表 3

表 3 描述统计量 变量 平均值 标准差 最小值 最大值 中位数 出生的组织数量 186.28 97.42 42 389 149 死亡的组织数量 226.84 317.65 1 1492 168

表 3 描述统计量

本文运用stata 14.0分析软件对模型(1)和(2)进行回归，主要结果如表 4所示。两个模型的R²(R方，R-squared)均大于0.5，拟合优度较好。方程的显著性检验在5%的显著性水平上都非常显著。回归结果显示所有系数的t绝对值均大于2.58，表明系数在1%的显著性水平上显著，模型拟合效果较好。从表 4可知，$ - \frac{{{\theta _1}}}{{2{\theta _2}}}$=827.11。1993年到2002年出生率大于0，1993-2000年N_t < $ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，所以组织设立率为下降趋势。2001-2002年N_t>$ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，理论上组织设立函数增长。2003年-2017年出生率小于0，N_t < 827即N_t < $ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，理论上组织设立函数应呈上升趋势。

表 4

表 4 回归结果分析 模型 R2 θ1 θ2 θ1的t值 θ2的t值 P值 出生函数 0.7376 -0.0104051 6.29e-06 -3.50 2.89 0.010 死亡函数 0.5732 -0.3002622 -0.00119 2.60 -2.37 0.014

表 4 回归结果分析

最小二乘法(OLS回归)在拟合特异值的过程中容易损失样本案例，为减弱特异值的影响，提升拟合效率，本文应用stata软件中的rreg命令对灭绝率和密度、密度平方等变量进行稳健回归(Robust regression)。运用加权最小二乘法赋予异常值较小的权重，结合Huber函数和双权数函数，再按95%的高斯效率进行调整(汉密尔顿，2011)。稳健回归(Robust regression)的结果显示：θ₁=-0.0103239，θ₂== 6.23e-06，所以$ - \frac{{{\theta _1}}}{{2{\theta _2}}}$=828.56。1993年-2002年出生率λ(t)大于0，1993-2000年N_t < $ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，所以组织设立率为下降趋势；2001-2002年N_t>$ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，理论上组织设立函数增长。2003年-2017年出生率小于0，N_t < $ - \frac{{{\theta _1}}}{{2{\theta _2}}}$，理论上组织设立函数应呈增长趋势。两种方法进行的模型理论推导结果相同。

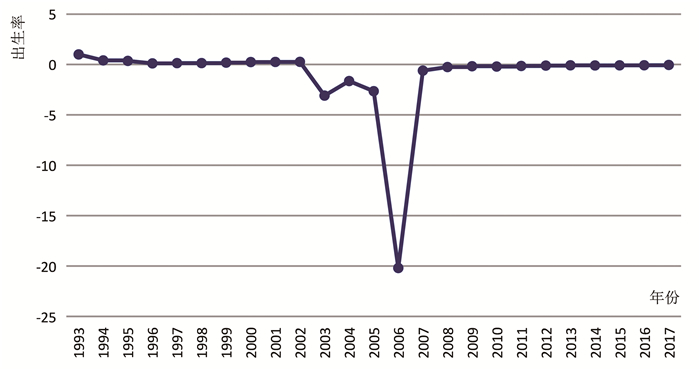
1993年到2017年实际出生率情况如图 1所示，可以看出：除了2001-2005年出生率有较大幅度下降外，其余年份的实际情况与理论推导大致相同。2001年广州市外资制造业组织出生率的较大幅度下降应与当时世界经济增长趋势放缓、外需拉动减弱^①有较大关联。

图 1

图 1 1993年到2017年广州市外资制造业企业实际出生率情况

① 广州年鉴编纂委员会, 2002, “2001年广州市国民经济和社会发展统计公报”，《广州年鉴》。

对模型(2)死亡率函数的回归结果显示：主要系数的t值均大于1.96，系数在5%的显著性水平上显著，拟合效果较佳。代入表 4数据可得，$\frac{{{\theta _1}}}{{2{\theta _2}}}$ =126.16。1993年-2002年μ(u)>0，1993年-1997年N_u> $\frac{{{\theta _1}}}{{2{\theta _2}}}$，理论上组织死亡函数应上升。1998-2002年N_u < $\frac{{{\theta _1}}}{{2{\theta _2}}}$，组织死亡函数下降。2003-2017年灭绝率μ(u)小于0、N_u < $\frac{{{\theta _1}}}{{2{\theta _2}}}$，理论上组织死亡函数应上升。稳健回归的R方和调整R方数值均未优于OLS回归结果。N_u的系数为-0.7478279，N_u²的系数为0.0027413，$\frac{{{\theta _1}}}{{2{\theta _2}}}$ =136.40。结合死亡率的数学推导结论与前面论述相同，不再赘述。

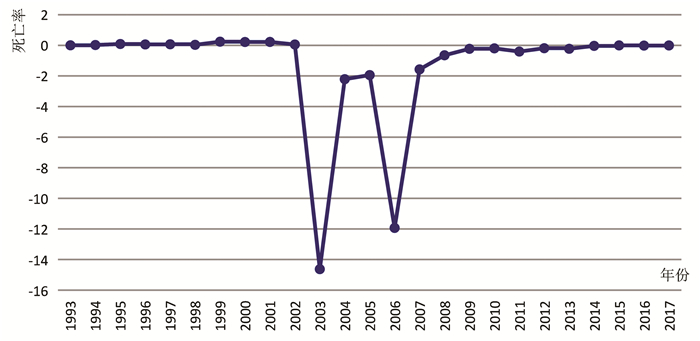
1993年到2017年实际死亡率情况如图 2所示，除2005-2006年死亡率有较大程度下降外，其余年份情况与理论推导相符。2004年广州市开始加快发展利用外资的制造业，其中交通运输设备制造业的合同利用外资金额增长幅度最大，增长了94.6%^①。外资的大幅涌入优化了广州市外资制造业企业的生存环境，使其组织死亡率下降。

图 2

图 2 1993年到2017年广州市外资制造业企业实际死亡率情况

① 广州市统计局, 2005, “2004年广州市国民经济和社会发展统计公报”。

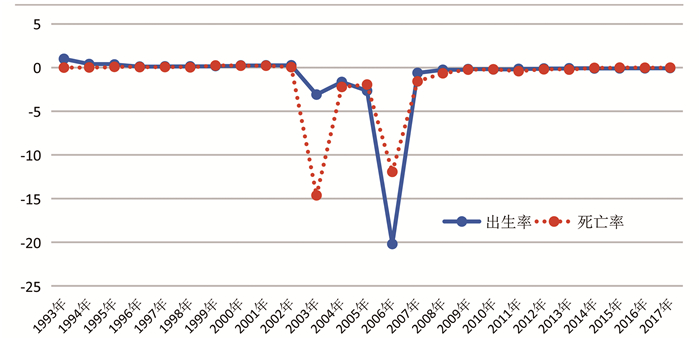
实际观察到的广州市外资制造业组织出生和组织死亡情况如图 3所示。

图 3

图 3 1993年到2017年广州市外资制造业的组织出生率和组织死亡率

由图可知，1993年-2017年广州市外资制造业组织设立和组织死亡的变化趋势大致相同。实际观察到的现象也与本文理论上的数学推导大体保持一致。

根据本文研究结果，可以推断：组织出生率与组织死亡率并非绝对呈现反向关系，当死亡率、出生率和组织密度形成一定组合时，组织设立函数和组织死亡函数会出现同时增加或者同时减少的同向变动现象。例如：死亡率大于0、组织设立率小于0时，如果N_t < － $\frac{{{\theta _1}}}{{2{\theta _2}}}$、N_u> $\frac{{{\theta _1}}}{{2{\theta _2}}}$，就会出现组织死亡函数增长时，组织设立函数同时增加的现象。当出生率λ(t)>0且死亡率μ(u)>0时，如果N_t>－ $\frac{{{\theta _1}}}{{2{\theta _2}}}$、N_u> $\frac{{{\theta _1}}}{{2{\theta _2}}}$，组织设立和组织死亡函数同时呈现上升趋势。当μ(u)>0时, 如果N_u < $\frac{{{\theta _1}}}{{2{\theta _2}}}$，则组织倒闭率函数下降。组织设立率小于0时，如果N_t>－ $\frac{{{\theta _1}}}{{2{\theta _2}}}$，则组织设立函数和组织死亡函数同时呈现下降趋势。

本文在密度依赖基础理论出生率和死亡率函数数学推导的基础上，结合1993年到2017年广州市外资制造业组织种群的实际情况，论证了组织设立和组织死亡的同向变动现象。组织的死亡可以释放更多资源到种群中，有利于种群现存组织获得新资源(Aldrich and Wiedenmayer, 1993)，使得组织的生存能力增强。种群可得资源的略微下降会使适应环境的种群在生态系统中的相对权重增加，敦促种群更有效率地开发和利用资源，反而有利于组织种群存活。所以，组织死亡率上升的同时，组织出生率反而会出现增长的现象。更多资源涌入反而会使效率的重要性减弱，不利于组织种群发展(Arthur et al., 2017)。过度丰裕的资源反而会使组织效率下降，不利于组织成长。因此，组织死亡率下降时，组织出生率反而会减少。资源充裕的时期，组织要专注于提升专业性和竞争力。资源有限的时期，组织则要实行多元化发展战略，寻求更多样的利润来源，全方位增强组织的综合实力。

本研究突破了对组织出生和死亡变化趋势的普遍认知，为密度依赖模型研究提供了新的研究视角，充实了现有的组织生态学研究。由于数据限制，本文只研究了1993年1月到2017年5月广州市外资制造种群的组织出生和组织死亡情况。如能从广州市制造行业种群诞生之日起进行追踪研究，将极大提升结论的科学性。未来可以尝试建立时间跨度更长的行业企业数据库，以进行更有效深入的研究。本文主要以企业数量作为组织密度的衡量，未来可以结合企业营业额、企业规模和企业市场份额对组织种群的发展情况做更透彻解读。除了对宏观数据的统计分析，还可以筛选出组织种群中具备代表性的企业，进行深入调研，作为分析案例。