一、问题的提出

2017年中央一号文件提出，要大力培育新型农业经营主体和服务主体，通过经营权流转、股份合作、代耕代种、土地托管等多种方式，加快发展土地流转型、服务带动型等多种形式规模经营。学界普遍关注流转，认为通过农地流转集中与规模经营，可以改变我国农地细碎化造成的低效率格局(钱忠好，2003；许庆等，2011)。但事实证明，尽管全国农地流转面积已经占到家庭承包耕地总面积的35%左右(截至2017年3月)，但不仅大大低于农业劳动力的外出比例，而且已经发生的流转主要发生在小农户之间，流转规模小，难以形成规模化经营(叶剑平等，2000；叶剑平等，2006；洪名勇、尚名扬，2013)。2013年对江苏、四川、山西、吉林和河北的农户调查显示，农户耕地经营面积在过去7年间仅平均增长了约0.03公顷(Ji et al., 2016)。因此，农地经营权流转并未有效促进农地规模化经营。

在农地流转市场发育滞后，且农业家庭经营仍将长期作为我国基本经营制度的阶段，发展农业服务规模经营无疑是转变农业经营方式，提高农业绩效的重要举措(罗必良，2016；胡新艳等，2016)。在罗必良等(2017)看来，农业经营虽然具有分散化、生产环节难以量化、雇工难以监督等天然不足，但借助农地产权细分，引入多元经营主体，发展农业社会化服务市场和分工经济，依然可以将小规模的农业家庭经营户卷入分工经济。从我国农业经营方式转型的大格局来看，农业分工和社会化服务已然成为一种大趋势(向国成、韩绍风，2007；王定祥、李虹，2016)。

发展农业社会化服务市场对于推动中国农业经营方式转型意义重大，但目前鲜有研究探讨农业社会化服务市场规模的形成和决定机制。尽管对如何构建农业服务经营体系进行了广泛的讨论，但却忽视了小农自主决策的关键性作用(关锐捷，2012；高强、孔祥智，2013；仝志辉、侯宏伟，2015)。为此，罗必良(2017)提出了交易半径和交易密度两个重要概念，在理论层面阐述了农业社会化服务市场容量的生成机理，具有重要的分类学价值。但应该强调，市场是由供需双方构成的(田国强，2016)，如果缺乏有效的市场需求以及与之相匹配的服务供给，农业的专业化和规模化的服务市场显然难以形成。为此，本文借助罗必良(2017)提出的两个概念，进一步探讨农业社会化服务市场的规模决定机理。重点在于：(1)从服务供给侧揭示农业生产性服务交易半径的决定机制；(2)从农户服务需求侧阐明其卷入分工经济，并形成农业生产性服务交易密度的内在逻辑；(3)进一步将两个独立模型纳入统一分析框架，并以种植业为例，探讨农业社会化服务规模决定的“时空”机制，以期为推进我国农业现代化和组织化提供理论依据。

二、服务商交易半径的决定机制

农作物种植包括多个生产环节。假定存在生产性服务的供给者i(本文统一简称为服务商)，它移动的速度为v，单位时间可服务的农地规模为s。同时假定：(1)在农作物的一个生产周期内，i只提供单一类型(生产环节)的服务，且其处理具体农事活动的时限为T；(2)一个农户需要服务的规模为s_j，农户在空间中均匀分布，且相邻农户的间距为d(即交易密度概念)。依据罗必良等(2017)的做法，引入交易半径概念，且假定i提供的服务集中在一个圆内，它只有将交易半径内所有农户需要的服务处理完，才会继续向外扩张。为了降低作业过程中的时间消耗，i按照圆周的方向逐渐向外扩张(可以证明，该做法的移动距离最短)。同时，我们也将农户经营的农地抽象为小圆，区别于服务商提供服务的大圆，这样便于将农户的间距做具体处理。此时相邻农户的距离就变成了相切圆圆心的距离。于是有：

$ \sqrt {\frac{{{s_j}}}{\pi }} \le \frac{d}{2} $

(1)

即相邻农户的间距不能小于单一农户作业规模的直径。

为了考察i会如何选择交易半径，可将交易半径设置为R^①，在交易半径为R的范围内可容纳的农户数量N可表示为一个经验函数形式^②：

① 为简化分析，可作如下抽象：将农户置于半径为d/2的圆内，其经营的农地则为半径为$\sqrt {{s_j}/\pi } $的圆，两圆同圆心。那么，交易容量可转变为，半径为R的圆可以包含多少个半径为d/2，且相互相切的圆的问题。

② 该经验函数的设置是根据圆的面积公式得出的。近期，业界有人提出大圆包含小圆的经验公式：N=0.83(4R²/d²)－1.9，但认可度并不高。为此，作者以圆的面积之比为基础，设置了一个包含参数的经验公式。当然，由于无法确定该形式的合理性，作者也尝试采用公式N=6R/d－2进行推导，但与本文的结论无显著差异。理论上说，这里可以设置N(R²/d²)和N(R/d)两类抽象函数，但后文涉及大量求解交易半径的公式，不做显式处理会造成模型无法求解。如果后期该经验公式得证，可重新论证本研究推论的稳健性。

$ N = {\kappa _1}\frac{{{R^2}}}{{{d^2}}} + {\kappa _2} $

(2)

其中，κ₁和κ₂为参数，且κ₁>0。那么交易半径内的市场容量可表示为：

$ Q = N{s_j} $

(3)

如前所述，i所提供的服务是受到农作物生命节律限制的，即i耗费在提供服务和空间转移上的时间之和不能超过T^③，即：

$ \frac{{Nd}}{v} + N\frac{{{s_j}}}{s} \le T $

(4)

③ 可以证明，服务商从大圆圆心出发，顺着圆周一圈一圈往外的运动半径最短。而且假定，服务商是按照从一个农户的圆心到另一个农户的圆心运动的。这类似于巴西一种长臂的耕作机械，其作业是在农户的耕地上伸缩机械臂，沿圆周往外旋转作业，其移动必然是从一个地块的圆心到另一个地块的圆心。

此外，i在交易半径内的服务收益可表示为：

$ {R_i} = Qr $

(5)

其中，r为单位面积作业收益。服务商所消耗的成本分为三部分：作业总成本C_w、移动总成本C_v和交易总费用TC(如与农户协商等)：

$ {C_w} = Q{c_w} $

(6)

$ {C_v} = Nd{c_v} $

(7)

$ TC = T\left( {{R^2},{d^2}} \right) $

(8)

其中，c_w为服务商的单位面积作业成本，c_v为服务商的单位移动成本。那么，i的目标函数可设置为：

$ Max\left( {Qr - Q{c_w} - Nd{c_v} - TC} \right) $

(9)

约束条件为式(4)，式(4)处理可得：

$ R \le \sqrt {\frac{{{d^2}}}{{{\kappa _1}}}\left( {\frac{T}{{d/v + {s_j}/s}} - {\kappa _2}} \right)} $

(10)

式(9)对R求偏导数可得：

$ \frac{{\partial Z}}{{\partial R}} = \frac{{2{\kappa _1}R}}{{{d^2}}}\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right) - 2R{{T'}_R}\left( {{R^2},{d^2}} \right) $

(11)

令式(11)等于0，有：

$ \frac{{2{\kappa _1}}}{{{d^2}}}\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right) - 2{{T'}_R}\left( {{R^2},{d^2}} \right) = 0 $

(12)

据式(12)是无法确定式(9)在式(10)确定的区间上的单调性的，为此需要将TC做显式处理，本文设立了三类交易费用函数。第一类是市场容量与交易费用满足线性关系。在杨小凯、黄有光(1999，P 257)的研究中，他们设置了交易费用系数，即单位交易的交易费用相等；第二类是市场容量与交易费用的关系满足分段凸函数。杨小凯、黄有光(1999)的处理方式是建立在交易同质的基础上，但在农业服务作业的过程中，本地的社会关系网络有助于降低交易的费用。但是，一旦超越熟人关系网络，信息的传递、价格的商量等成本就会提高，由此形成了一个交易“差序格局”(仇童伟等，2017)，可采用分段凸函数表达；第三类是市场容量与交易费用的关系满足凸函数。分段凸函数假定了农业服务作业的交易费用的变化存在严格的门槛，但这种假设过强。实际上，如果将任何向外拓展的交易都视为一个新的分段凸函数，并不断细分，可形成一个连续的凸函数。具体分析如下：

(一) 交易费用的形式：市场容量的线性函数

$ T\left( {{R^2},{d^2}} \right) = \delta N $

(13)

其中，δ为交易费用系数。式(13)对R求导，并带入式(12)：

$ F = \frac{{2{\kappa _1}}}{{{d^2}}}\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right) - \frac{{2{\kappa _1}}}{{{d^2}}}\delta $

(14)

由式(14)可知，当

$ {s_j}r - {s_j}{c_w} - {c_v} - \delta \ge 0 $

(15)

i选择的交易半径为：

$ {R^ * } = \sqrt {\frac{{{d^2}}}{{{\kappa _1}}}\left( {\frac{T}{{d/v + {s_j}/s}} - {\kappa _2}} \right)} $

(16)

相反，如果

$ {s_j}r - {s_j}{c_w} - {c_v} - \delta \le 0 $

(17)

那么i选择的交易半径为：R^*=0，即，i不会提供农业社会化服务。换句话说，如果从一开始，农业的分工收益就低于分工引致的交易费用，那么分工就难以形成，这与杨小凯、黄有光(1999)的观点一致。

当T(R², d²)与参与交易的农户数满足线性关系，且假定s_jr－s_jc_w－c_v－δ≥0，那么i会选择提供服务，而且其交易半径受到农作物生长周期、市场交易密度和服务商技术特征的限制。

(二) 交易费用的形式：市场容量的分段凸函数

$ T\left( {{R^2},{d^2}} \right) = \left\{ \begin{array}{l} {\delta _1}N,0 \le R \le \bar R\\ {\delta _2}N,\bar R \le R \le {R^ * } \end{array} \right. $

(18)

其中，δ₁和δ₂为交易费用系数，且有δ₁ < δ₂。R为交易半径的某一临界值，表明在交易半径的不同范围内，交易费用具有不同的函数形式。R^*同式(16)。从分段函数特征来看，当0≤R≤R，将T′_R(R², d²)带入式(12)

$ F = \frac{{2{\kappa _1}}}{{{d^2}}}\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right) - \frac{{2{\kappa _1}}}{{{d^2}}}{\delta _1} $

(19)

假设s_jr－s_jc_w－c_v－δ₁>0，那么在0≤R≤R -上，i将持续为农户提供服务。

当R≤R≤R^*时，将T′_R(R², d²)带入式(12)：

$ F = \frac{{2{\kappa _1}}}{{{d^2}}}\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right) - \frac{{2{\kappa _1}}}{{{d^2}}}{\delta _2} $

(20)

假设s_jr－s_jc_w－c_v－δ₂>0，在R≤R≤R^*，i将持续为农户提供服务。如果将分段凸函数的区间不断细分，那么当：

$ \frac{{2{\kappa _1}}}{{{d^2}}}\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right) - \frac{{2{\kappa _1}}}{{{d^2}}}{\delta _i} = 0 $

(21)

即当δ_i=s_jr－s_jc_w－c_v时，i的净收益达到最大值。即，随着交易半径的增加，如果交易系数δ_i也随之在增加，那么只要来自分工的报酬高于市场容量扩大造成的交易费用，那么农业分工就会进一步深化，直至分工的收益等于由其引致的交易费用。

(三) 交易费用的形式：市场容量的凸函数

$ T\left( {{R^2},{d^2}} \right) = {\delta _3}{N^m},\;\;\;\left( {m > 1} \right) $

(22)

其中，δ₃为交易费用系数。式(22)对R求导：

$ {{T'}_R}\left( {{R^2},{d^2}} \right) = \frac{{2{\kappa _1}{\delta _3}mR}}{{{d^2}}}{\left( {\frac{{{\kappa _1}{R^2}}}{{{d^2}}} + {\kappa _2}} \right)^{m - 1}} $

(23)

将式(23)带入式(12)：

$ F = \frac{{2{\kappa _1}}}{{{d^2}}}\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right) - \frac{{2{\kappa _1}{\delta _3}m}}{{{d^2}}}{\left( {\frac{{{\kappa _1}{R^2}}}{{{d^2}}} + {\kappa _2}} \right)^{m - 1}} $

(24)

令式(24)为0，有：

$ {R^ * } = \sqrt[2]{{\frac{{{d^2}}}{{{\kappa _1}}}\left[ {\sqrt[{m - 1}]{{\frac{{\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right)}}{{\delta m}}}} - {\kappa _2}} \right]}} $

(25)

式(24)进一步对R求导：

$ {{F'}_R} = - \frac{{\kappa _1^2R\delta m\left( {m - 1} \right)}}{{{d^4}}}{\left( {\frac{{{\kappa _1}{R^2}}}{{{d^2}}} + {\kappa _2}} \right)^{m - 2}} < 0 $

(26)

由式(26)可知，R^*为交易半径的极大值点。此时参与服务外包市场的农户数为：

$ N = \sqrt[{m - 1}]{{\frac{{\left( {{s_j}r - {s_j}{c_w} - {c_v}} \right)}}{{\delta m}}}} $

(27)

三、农户的生产决策过程

服务商的外包服务供给与农户的服务外包需求具有相互性。本部分进一步考察农业社会化服务的发展将如何影响农户的种植结构调整，进而讨论服务市场容量的生成机理。为便于分析，我们假定有潜在的服务商i会提供服务，且存在交易半径为R的区域^①。该区域存在n个农户，并假设只有当m个农户选择种植能进行服务外包的农作物时，农业的外包服务市场才会形成^②。换言之，只有当区域内种植同一类农作物(设定为A作物)的农户比重达到m/n，农业服务市场才可能出现。本部分的变量和参数设置如下：各农户经营的农地面积为s_j，可消耗的劳动力标准化为1。种植农作物A的单位产值为P_A，单位面积上的劳动消耗量为L_A，种植农作物B的单位产值为P_B，单位面积上的劳动消耗量为L_B。农户除了投入在农地上的劳动力外，其余劳动力均会到市场上去寻找工作，假定市场的平均工资为w，农户的劳动力在市场上找到工作的概率为$\varphi $。

① 在这部分，我们参照杨小凯、黄有光(1999)在《专业化与经济组织——一种新兴古典经微观经济学框架》第二章中关于交易费用的处理方式，先将潜在服务商的出现或交易半径作为先验因素处理，第四部分进一步将其内生化。实际上，在本部分的分析中，服务商是否进入市场取决于农业服务市场的容量，这本身也是其内生化的表现。

② 这里假定m个农户即使分布在圆周的最外沿，i提供服务的净收益也不小于0。余下部分的分析均假定这个约束成立，不予赘述。

进一步假定农作物A的生产环节可进行服务外包，但农作物B属于劳动密集型作物(如经济作物)而难以卷入农业分工。并且，农作物A一旦进行服务外包，单位农地上种植作物A的劳动消耗量由外包前的L_A变为ρL_A，从而使劳动消耗节省了(1－ρ)L_A，但单位面积农地的外包服务费为k。为了使我们的分析更接近现实，还需要设置如下约束条件：

$ {P_B}{s_j} \ge {L_B}{s_j}w\varphi $

(28)

$ {P_B}{s_j} < Lw\varphi $

(29)

$ {P_A}{s_j} - k{s_j} \le \left( {1 - \rho } \right){L_A}{s_j}w\varphi $

(30)

$ {P_A}{s_j} + \left( {1 - {L_A}{s_j}} \right)w\varphi < {P_B}{s_j} + \left( {1 - {L_B}{s_j}} \right)w\varphi $

(31)

$ {P_A}{s_j} + \left( {1 - \rho {L_A}{s_j}} \right)w\varphi - k{s_j} > {P_B}{s_j} + \left( {1 - {L_B}{s_j}} \right)w\varphi $

(32)

式(28)到式(32)表达的是：第一，当种植农作物B的劳动力不高于L_Bs_j时，种植农作物B的劳动产出率高于市场工资率，但农作物B的产值低于w$\varphi $；第二，在劳动力与农作物A的劳动需求匹配时，种植农作物A的劳动产出率低于劳动的市场工资率。但是，种植农作物A可以进行服务外包，且外包后，农作物A的产值加上家庭剩余劳动力的预期非农收入，大于农作物B的产值加上家庭剩余劳动力的预期非农收入。也就是说，种植农作物A释放的劳动力，可以提高家庭的总收入。但问题是，在面临潜在服务商是否出现的不确定性时，农户会如何选择农作物A和农作物B呢？为简化模型，本文将农户的选择设置为0或1，即只要选择某类农作物，那么农户经营的全部农地上均为该农作物。

当面临潜在服务商是否出现的不确定性时，农户选择种植什么农作物就主要取决于他们之间的示范效应和信息传递。因为种植农作物A的农户比例越高，服务商就越可能出现。而且这里只考虑一期的决策，否则就会出现农户多时期相机决策的情况。接下来，根据农户决策的信息传递方式，本文区分了信息完全不可传递和信息可传递两种信息传递机制^③。前者对应的决策机制为农户独立做决策，且所有农户的决策概率独立同分布。后者对应的是农户根据周围其他农户的选择来决定自身的农作物种植类型，且假定，随着农户之间距离的增加，信息的传递性呈指数形式下降(迪克西特，2007)。对两种情形的分析如下：

③ 本文做这样的区分，主要是为了便于比较分析。如读者感兴趣，可将信息的传递程度设置为一个参数引入模型，这并不会改变模型的结果。当然，本文式(38)所表达的就是一种信息传递可获性的空间衰减机制，一定程度上可避免作者的重复工作。

(一) 农户独立决策：信息完全不对称

在农户的决策互相独立的情况下，假定农户选择农作物A的概率为γ，那么农户j做决策的概率分布如下：

$ \gamma \left( {{A_j}\left| {{A_1},{A_2}, \cdots ,{A_{j - 1}},{A_{j + 1}}, \cdots ,{A_n}} \right.} \right) = \gamma \left( {{A_j}} \right) $

(33)

假设农户是同质的，那么式(33)的结果可表示为γ(A₀)(常数)。根据上文关于潜在服务商是否出现的约束条件：当n个农户中至少出现m个农户种植农作物A。那么这个概率可表示为：

$ {P_1} = \sum\limits_{J = m}^n {C_n^J\gamma {{\left( {{A_0}} \right)}^J}{{\left( {1 - \gamma \left( {{A_0}} \right)} \right)}^{n - J}}} $

(34)

由于单个农户决策的总收益是受制于其选择概率的，但这里我们希望从总得社会收益来看农户进行农作物选择的绩效变化。首先，在不存在社会化服务时，农户的总收益为：

$ {S_1} = n\left[ {{P_B}{s_j} + \left( {1 - {L_B}{s_j}} \right)w\varphi } \right] $

(35)

考虑农户可能存在普遍种植农作物A，并诱发服务商出现的可能性。那么，根据式(34)和农户家庭收入的构成方式，可得此时农户的总收益为：

$ \begin{array}{l} {S_2} = \sum\limits_{J = m}^n {C_n^J\gamma {{\left( {{A_0}} \right)}^J}{{\left( {1 - \gamma \left( {{A_0}} \right)} \right)}^{n - J}}} \left\{ {J\left[ {{P_A}{s_j} - k{s_j} + \left( {1 - \rho {L_A}{s_j}} \right)w\varphi } \right]} \right.\\ \;\;\;\;\left. { + \left( {n - J} \right)\left[ {{P_B}{s_j} + \left( {1 - {L_B}} \right)w\varphi {s_j}} \right]} \right\}\left( {1 - {P_1}} \right){S_1} \end{array} $

(36)

以农户家庭的总收益的大小为判断标准，只要存在：

$ {S_1} < {S_2} $

(37)

那么，农业外包服务市场就会发展起来，且按照“赢定输移”^①的资源竞争性配置约束机制，式(32)的约束条件必然使得种植农作物A成为农户的占优策略。当然，读者也可以将单个农户作为分析对象，但不会改变模型的最终推论。

①“赢定输移”策略可表述如下：如果我们在上一轮中都采取合作行为，那么我会再次选择合作。如果我们在上一轮中都采取背叛行为，那么我会以某一概率与对方合作。如果我们上一轮中采取不同的行为，那么我会选择背叛(马丁·诺瓦克，2010；马丁·诺瓦克、罗杰·海菲尔德，2013)。在本研究中，农户一旦因服务外包而获得更高的收益，他们将长期选择种植农作物A。因为与种植农作物B相比，种植农作物A，并进行服务外包是经济收益上的“赢”。

(二) 农户联合决策：信息交互影响

很显然，从众多的研究来看，农户的行为都具有“羊群效应”(杨唯一、鞠晓峰，2014；杨卫忠，2015)。也就是说，农户之间种植信息的传递会干扰他们选择种植的农作物品种。为此，依据迪克西特(2007)的处理方式，在以农户为圆心，且半径为χ的圆内^②，其他农户可以传递信息并影响农户种植类型决策的概率可设置为如下函数形式：

$ {P_2} = \frac{{a{e^{ - a\theta }}}}{{2\left[ {1 - {e^{ - a\chi }}} \right]}} $

(38)

② 这里假定，农户的信息传递是存在阈值的，一旦农户间距超过x，那么信息传递无法成功。这对于农村分散的居住格局和经营格局而言，无疑是合理的。

其中，a表示信息传递系数，θ为农户与其他农户的距离。为了便分析，假定：在每个农户周围存在s个农户种植农作物A，农户周围半径为R圆内种植作物A和作物B的农户均匀分布。那么农户通过其他农户的信息来决策自己的农作物种植类型的概率可表示为：

$ S{P_2} = \int_0^\chi {\frac{{a{e^{ - a\theta }}}}{{2\left[ {1 - {e^{ - a\chi }}} \right]}}d\theta } $

(39)

(1) 当$\frac{s}{n} \ge \frac{m}{n}$时，农户的预期收入为：

$ {I_1} = S{P_2}\left[ {{P_A}{s_j} - k{s_j} + \left( {1 - \rho {L_A}{s_j}} \right)w\varphi } \right] + \left( {1 - S{P_2}} \right)\left[ {{P_B}{s_j} + \left( {1 - {L_B}{s_j}} \right)w\varphi } \right] $

(40)

式(40)是否能够成为农户种植农作物A的充分条件呢？如果存在：

$ {I_1} > {P_B}{s_j} + \left( {1 - {L_B}{s_j}} \right)w\varphi $

(41)

那么，信息传递就能够带动农户种植农作物A。由于假定农户同质，则意味着所有农户均选择种植农作物A，由此形成连片种植。将式(41)简化可得：

$ {P_A}{s_j} - k{s_j} + \left( {1 - \rho {L_A}{s_j}} \right)w\varphi > {P_B}{s_j} + \left( {1 - {L_B}{s_j}} \right)w\varphi $

(42)

式(42)与式(32)的形式是一致的，这说明，在农户的农作物种植存在示范效应，且种植信息和收益信息可传递的决策环境中，只要存在农业的外包服务市场，农户种植农作物A的家庭预期总收益是要高于种植农作物B时的预期总收益的。此时，“赢定输移”策略将使得种植农作物A的农户比例迅速增加。当然，这里还存在一个隐含的假设：农户种植的农作物类型和家庭收入状况的信息是可以被识别的，且可传递。基于这个假设，那些因未种植农作物A而遭受“损失”的农户才会调整他们的种植结构。

(2) 当$\frac{s}{n} < \frac{m}{n}$时，农户的预期收入为：

$ {I_2} = S{P_2}\left[ {{P_A}{s_j} + \left( {1 - {L_A}{s_j}} \right)w\varphi } \right] + \left( {1 - S{P_2}} \right)\left[ {{P_B}{s_j} + \left( {1 - {L_B}{s_j}} \right)w\varphi } \right] $

(43)

很显然，从式(43)来看，此时农户的预期收入是小于完全种植农作物B时的收益的，参见式(31)。换句话说，一旦农户因种植农作物A而蒙受“损失”，那么他们就会重新选择种植农作物B。

四、农业外包服务市场的发展机制：从横向分工和连片专业化到纵向分工

在农业外包服务市场的发展过程中，纵向分工依赖于横向分工(罗必良等，2017；罗必良，2017)。因此，本节首先设置农户跨时期农作物选择(横向专业化和连片种植)的状态模型，然后与服务商的决策模型结合，进而探讨从横向分工和连片专业化到纵向分工的约束机制。

假设在某一期(如第1期)种植农作物A的农户比重达到m/n。农户选择种植农作物A的原因是，种植粮食作物的劳动消耗比经济作物要低，且生产环节的可分离性及其服务外包能够有效降低农业生产的机会成本(钟甫宁等，2016；仇童伟、罗必良, 2017, 2018)。进一步地，假定农业服务需求市场满足服务商的目标约束，且规定在服务商的决策方程中，交易费用为市场容量的凸函数(即式(22))，农户的信息传递模式为式(39)。那么各时期农业外包服务的需求者数量如下：

$ {N_1} = \frac{m}{n}N $

(44)

$ {N_2} = {N_1} + \left( {1 - \frac{m}{n}} \right)N\int_0^\chi {\frac{{a{e^{ - a\theta }}}}{{2\left[ {1 - {e^{ - a\chi }}} \right]}}d\theta } $

(45)

……

$ {N_n} = {N_{n - 1}} + \left( {N - {N_{n - 1}}} \right)\int_0^\chi {\frac{{a{e^{ - a\theta }}}}{{2\left[ {1 - {e^{ - a\chi }}} \right]}}d\theta } $

(46)

由式(44)到式(46)，可得：

$ {N_n} - {N_{n - 1}} = {\left( {1 - \int_0^\chi {\frac{{a{e^{ - a\theta }}}}{{2\left[ {1 - {e^{ - a\chi }}} \right]}}d\theta } } \right)^{n - 2}}\left( {{N_2} - {N_1}} \right) $

(47)

由式(47)变换可得：

$ {N_n} = \frac{{\left[ {1 - {{\left( {1 - \varepsilon } \right)}^{n - 1}}} \right]}}{\varepsilon }\left( {{N_2} - {N_1}} \right) + {N_1} $

(48)

其中，$\varepsilon = \int_0^\chi {\frac{{a{e^{ - a\theta }}}}{{2[1 - {{e}^{ - a\chi }}]}}} d\theta $。

式(48)表达的是在交易半径为R的区域内，第n期种植农作物A的农户比重。而且，为便于分析，假定按照式(32)的约束，接收信息后种植农作物A的农户，将在s_j种植面积上全部进行服务外包。为了与第二部分的分析结合起来，可将初始种植农作物A的农户比重设置为β，并满足如下条件：

$ \beta Qr - \beta Q{c_w} - Nd{c_v} - TC \ge \left( {\frac{{Nd}}{v} + \beta N\frac{{{s_j}}}{s}} \right)w\varphi $

(49)

这里将非农务工的单位时间的工资设置为w，且假定服务商依然需要按照原来的路径寻找农户，即他们的交易费用和机械空转的成本不变，但作业的时间可以节省下来。那么，按照现有设置，式(48)可表示为：

$ {N_n} = \left[ {1 - {{\left( {1 - \varepsilon } \right)}^{n - 1}}} \right]\left( {1 - \beta } \right)N + \beta N $

(50)

换言之，在时期n，单位面积上种植农作物A的农户密度为：

$ {\rho _n} = \frac{{\left[ {1 - {{\left( {1 - \varepsilon } \right)}^{n - 1}}} \right]\left( {1 - \beta } \right)N + \beta N}}{{\pi {R^2}}} $

(51)

式(51)表达的是，种植农作物A的农户在空间上是均匀分布的。那么按照第二部分服务商的目标函数和约束，现在的目标函数和约束分别为：

$ Max\left[ {{N_n}{s_j}r - {N_n}{s_j}{c_w} - Nd{c_v} - TC - \left( {\frac{{Nd}}{v} + {N_n}\frac{{{s_j}}}{s}} \right)w\varphi } \right] $

(52)

$ \frac{{Nd}}{v} + {N_n}\frac{{{s_j}}}{s} \le T $

(53)

按照拉格朗日法可得：

$ L = {N_n}{s_j}r - {N_n}{s_j}{c_w} - Nd{c_v} - TC - \left( {\frac{{Nd}}{v} + {N_n}\frac{{{s_j}}}{s}} \right)w\varphi + \lambda \left( {T - \frac{{Nd}}{v} - {N_n}\frac{{{s_j}}}{s}} \right) $

(54)

式(54)分别对R和λ求导：

$ \begin{array}{l} {{L'}_R} = \frac{{2{\kappa _1}R{s_j}r}}{{{d^2}}}\eta - \frac{{2{\kappa _1}R{s_j}{c_w}}}{{{d^2}}}\eta - \frac{{2{\kappa _1}R{c_v}}}{d} - \frac{{2{\kappa _1}R\delta m}}{{{d^2}}}{\left( {\frac{{{\kappa _1}{R^2}}}{{{d^2}}} + {\kappa _2}} \right)^{m - 1}}\\ \;\;\;\;\;\;\; - \frac{{2{\kappa _1}Rw\varphi }}{{dv}} - \frac{{2{\kappa _1}R{s_j}w\varphi }}{{{d^2}s}}\eta - \frac{{2{\kappa _1}R\lambda }}{{dv}} - \frac{{2{\kappa _1}R{s_j}\lambda }}{{{d^2}s}}\eta \end{array} $

(55)

$ {{L'}_\lambda } = T - \frac{{Nd}}{v} - \frac{{\eta N{s_j}}}{s} $

(56)

其中，η= [1-(1-ε)](1－β)+β。

令式(55)和式(56)为0，求出的极值点为：

$ {R^ * } = \sqrt[2]{{\frac{{{d^2}}}{{{\kappa _1}}}\left( {\frac{T}{{d/v + \eta {s_j}/s}} - {\kappa _2}} \right)}} $

(57)

从式(57)来看，服务商的交易半径是农作物生长和生产周期T的增函数，是相邻农户间距d的增函数^①，是初始种植农作物A的农户比重β的减函数，也是农户接受信息后转变种植行为概率ε的减函数。如果假定农户的分布和初始种植农作物是先验决定的，那么决定服务商交易半径的外生因素主要就是T和ε。对于前者，在特定区域内的某种农作物，其生长周期是无差异的，这就决定了沿着经度布局农作物种植结构会抑制服务商交易半径的扩大，最终形成多中心、小范围的服务区域(罗必良，2017)。对于后者，其涉及市场信息的传递和披露问题，一旦服务市场内的组织结构改善，信息传递融通，市场供给稳定，那么信息衰减的程度会大大下降，由此增加社会化服务潜在的市场需求。很显然，信息披露程度的增加表明，农户预期的收益是在增加的，那么农户横向专业化和连片种植的可能性也在增加，有利于促进纵向分工。但是，农业固有的节令特征和服务商的作业效率决定了，信息披露程度增加造成的交易密度的增加，会使得服务商的交易半径收缩。主要原因在于，服务能力决定了固定周期内服务商的作业量，为了降低交易费用，收缩交易半径更合乎经营效率。上述两方面的结合，则构成了农业社会化服务市场发育的“时空”概念。

① 相邻农户间距的增加无疑需要扩大交易半径才能获得正的预期净收益，这也是农业难以分工的主要原因。分散化的生产布局，使得初始的分工收益显著低于经营成本。如果在一个生产周期内，服务商无法获得正的净收益，自给自足将是农业的帕累托最优状态。本文是基于交易半径内出现分工正收益的前提展开的，故不需要考虑分工中交易效率和分工收益的两难问题，如读者感兴趣，可参考杨小凯、黄有光(1999)的研究。

五、一个延伸：农业服务市场的“时空”概念

随着农业劳动力非农转移规模的扩大，小规模、细碎化的农地家庭经营一定程度上抑制了农业经营绩效的改善。但作为农村基本的经营制度，家庭经营的基础性地位是被历史证明了的。在这种情况下，如何从农地规模经营转变为服务规模经营，成为当前政府和理论界普遍关注的话题(罗必良，2017)。虽然通过引入农业社会化服务，可以将农业家庭经营卷入分工经济，提高农业经营绩效。但是，农业固有的受限于农作物生命节律和分散化经营的特征，都使得它的分工程度要比工业小得多(杨小凯、黄有光，1999；罗必良，2008)。即使政府大力推进农业社会化服务市场的发育，但其固有的零碎化、服务组织的弱质化、农业经营周期的固定化导致的设备利用不充分、市场需求不足等，都使得农业服务市场的容量和细分程度难以改善。

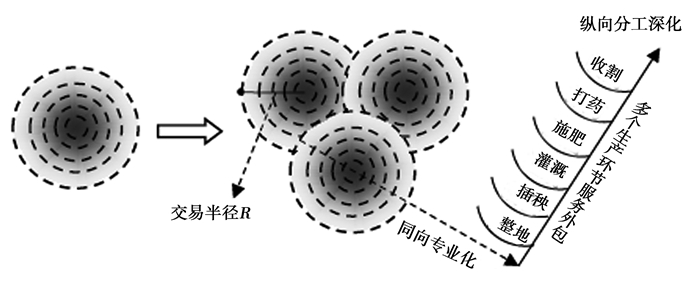
罗必良(2017)提出了农业外包服务市场的横向专业化和纵向专业化概念，由此构建了一个从连片经营到纵向专业化，以及两种专业化互动的理论模型。这一思路与本文的共同之处在于，农业外包服务市场供给的出现是建立在横向专业化基础之上的。如果特定交易半径内连片种植程度达不到最低进入规模，那么式(49)无法成立，潜在的服务商也不会出现。一旦连片种植规模达到阈值，市场的潜在盈利空间会诱发具有企业家精神的主体进入农业服务市场。反过来，服务规模或交易半径的增加，会使得那些未连片经营的农户会在其他农户的信息传递(如服务稳定信息、盈利信息和就业转移信息等)下，依照“赢定输移”策略，调整其种植结构，这又会进一步提高交易密度。随着市场容量的扩大，那些易于度量的生产环节将进一步实现分工，进而深化农业纵向分工(如图 1所示)。但按照上述理论模型，在当前农业社会化服务的发展过程中，很容易会出现多中心、多区域、碎片化的服务市场。这些市场往往集中在一个村，或者一个区域，难以形成组织化、规模化、系统化以及跨区域的市场布局。由此造成农业社会化服务的大市场概念难以形成，市场的运行仍然依赖于与工业的“迂回交易”得以维系，并缺乏自身的“造血”功能。

但从式(57)来看，农业外包服务市场的交易半径是可以改变的，至少从农作物的生长特性和节令的匹配上存在这种可能。在以往的研究中，学者们大多关心的是市场的空间概念。例如市场的细分、市场的价格歧视等，大多是基于空间的可分性来做文章的。与之不同的是，农业固有的必须根据生命节律及时处理作业信息的属性，使得其经营具有时间上的不可间断性。因此，农业外包服务市场的时间和空间概念是存在互动关系的。通过改变农作物的节令或生长周期与服务作业的匹配模式，有可能诱导农业服务市场交易半径的调整。

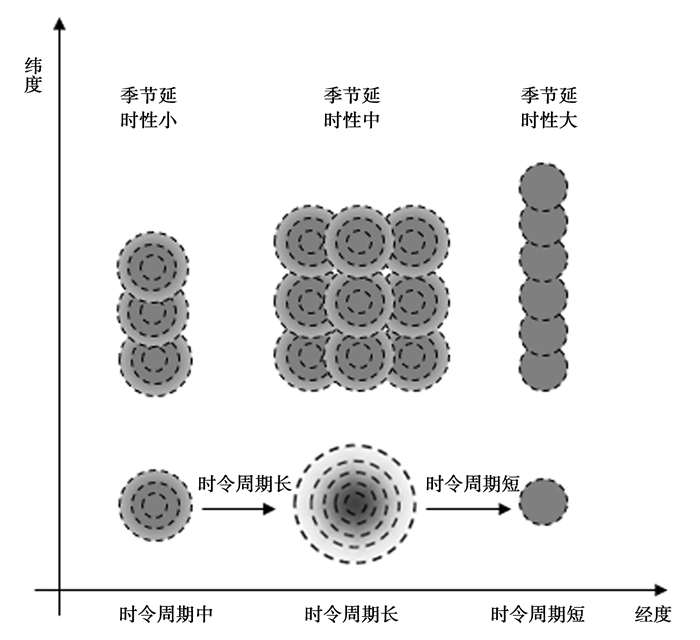
一方面，专业化服务商在东西经度上的跨区作业范围及其交易半径，与其生产环节的时令周期相关。该时令周期越长，其交易半径越大，且经度跨区作业的范围越大。

另一方面，专业化服务商在南北纬度上的跨区作业范围及其交易半径，既与其生产环节的时令周期相关，也与区际季节延时性相关。该时令周期越长，其交易半径越大；区际季节延时性越大，纬度跨区作业的范围越大。

可见，从我国农业的整体布局出发，应该寻求在空间和时间上的双向调整(图 2)^①。

① 当然，这里是从服务规模经济角度而言的。但从效率来说，有可能面临新的“两难冲突”：扩大时令周期，能够改善服务效率，但可能降低单位时间的生产量或时间效率。本文假定技术进步能够克服后者。

首先，目前我国种植业的布局是以东西走势为主，如玉米的种植就是以淮河以北为主，且主产区在东三省、内蒙、新疆一线。这样的布局符合按照等温线且最适合农作物生长气候的布局思路，但由此带来的结果是，玉米收获期内整体作业的难度增加，造成农业服务市场(如玉米征地、播种和收割等环节分工)呈现小范围、局部、多中心的特征。但随着农业技术的进步，长江、淮河中下游，以及东南沿海地区的玉米种植也成为了可能。其它的如小麦、稻谷等农作物，也基本上实现了可以在全国范围内种植。但所处温度带的不同，会使得农作物在成熟的时间上存在差异，这造成农业作业的周期从南到北被拉长了。换句话说，农业社会化服务的作业周期存在被延长的现实可能性。一旦在农业自然特征上存在调整种植业布局的可能，那么在技术层面上就存在实施的潜能。

其次，按照从南到北的种植业布局思路，在延长农业生产周期的同时也会增加交易半径。更为重要的是，由于作业周期延长，农业服务组织的固定资产投资和机器设备被闲置的频率就会下降。这一方面有利于提高农业服务组织的运作效率，另一方面也有助于引导农业服务组织加大后期投资，提高市场的深化程度。具体来说，农业外包服务市场的纵向分工程度会提高，作业的效率会改善，市场的组织化程度和规范化程度也会提升。而且，随着农业服务市场大格局和大信息的形成，会将更多从事传统家庭经营的小农户卷入分工经济。主要是在引导横向专业化的过程中，促使小农的连片种植，深化农业纵向分工和扩大市场容量，由此通过提高交易密度和减少单位作业的交易费用等来改善农业社会化服务的实施效率。因此，农业社会化服务市场的“时空”概念是改变当前市场发展慢、分散化、规模不经济等不足的重要方向，也是拓展市场容量、延长交易半径和提高交易密度的重要抓手，以此可以推动农业发展的横向专业化、连片种植以及纵向分工的深化。

六、结论与思考

发展农业社会化服务市场，是缓解我国农地细碎化经营固有效率不足的重要途径。虽然近年来，国家政策反复强调加快推进农业社会化服务市场的发育，但学界对有关理论性问题的研究严重滞后。在借鉴罗必良(2017)提出的农业服务市场的交易半径和交易密度理论概念的基础上，本文通过构建服务商交易半径决定理论模型、农户服务采纳的信息传递模型，并将二者的决策纳入统一模型，系统考察了农业社会化服务市场在空间和时间上的发展路径。研究表明：(1)初始农作物种植类型涨落所诱发的农业服务潜在市场的容量，对于农业社会化服务市场交易半径的后期增长具有正向激励作用。(2)随着服务市场信息的披露和传递速度的加快，基于“赢定输移”策略的农户会主动加入农业分工经济，由此提高市场的交易密度和交易半径。(3)虽然市场容量的增加会激励更多具有企业家精神的主体进入农业社会化服务市场，但囿于农业固有的节令特征和作业周期性，发展规模化、组织化、系统化的农业社会化服务市场必须立基于我国种植业“纬度布局”的调整，由此形成“大农业”与“大市场”概念。

虽然本文重点关注了交易半径和交易密度视角下农业社会化服务市场的规模决定机制，但其中无疑包含了交易费用的含义，且涵盖了社会化服务的组织建构、组织竞争和觅价等问题。首先，农业社会化服务市场始终面临分工水平和市场容量与交易费用的两难选择，虽然我们还无法确定服务商在扩大交易半径的过程中，到底面临怎样的交易费用增长模型。但很显然，交易费用会约束农业社会化服务的交易频率和交易半径。在张五常(2014)看来，讯息费用是交易费用的重要组成部分。随着觅价速度的增加，交易速度也会增加。这无疑说明，本文中农户信息传递机制的模型设置具有重要意义。反过来说，农业服务市场网络的形成，也会提高服务商的觅价速度，降低讯息费用。这有利于服务商在农业生产周期内扩大交易半径，提高横向专业化和纵向分工的程度。

其次，迪克西特(2007)认为，规范化、组织化的交易在市场发育的初始阶段都会面临规模不经济。这与Yang and Shi(1992)所表达的分工与交易费用的两难困境相似。在农业社会化服务市场的发展初期，服务商的沉淀成本在短期往往内难以收回，市场容量和交易预期不足也会显著抑制潜在竞争者的进入。造成上述情况的直接原因是，发展初期的市场呈现的碎片化、不连贯、价格信息机制不健全和竞争不足。进一步地，农业固有的生命节律性和分散化特征又是抑制服务市场规模化、组织化的重要原因。加之，农业的分工程度本来就低于工业，且大多依赖于与工业的“迂回交易”来自我支撑，工业对农业生产租值的吸纳使得农业社会化服务市场的发育面临“内忧外患”。

基于上述分析，本文认为，当前亟须调整我国农业布局并构建“大农业”和“大市场”概念，以发展农业分工经济并降低农业的自然约束。一方面，构建种植业“纬度布局”可以扩大市场容量，促进连片种植和纵向分工，提高农业服务组织的交易范围和交易频率，形成“大农业”概念。另一方面，“大市场”概念的形成会提高市场竞争主体数量和信息传递优势，提高交易速度并增加服务商获得的生产租值。很显然，农业社会化服务“大市场”的形成，不仅有助于加快农业现代化和组织化进程。而且，分工租值的积累还会提高农业服务组织应对市场和自然风险的能力。因此，中国农业的现代化和组织化，必然是与农业分工经济和种植业布局调整密切相关的。