21世纪以来, 中国经济发展迅猛, 并且中国产业正处于转型的关键阶段, 2016年全国工业增加值比上年增长6.0%, 制造业增加值同比增长6.8%, 为全国GDP实现6.7%的增速奠定了坚实基础。近年来, 中国制造业生产产值的增长率呈非规律性波动, 但整体表现上升趋势, 说明中国制造业在21世纪以来获得了较为快速地发展。
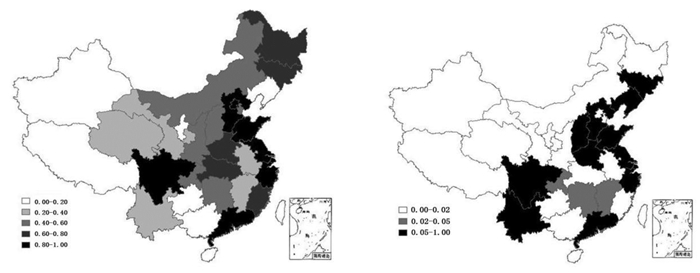
环渤海地区、珠三角和长三角是中国制造业发展的主要区域, 清晰指引的国家政策加上其特有的自然条件和人文因素, 刺激了该部分地区制造业的迅猛发展, 成为中国经济的支柱。从图 1(右)可以看出, 东部沿海地区的综合EG指数①要远大于中西部地区, 并且达到了产业高度集聚水平(大于0.05), 所以说东部沿海地区已经形成集聚经济, 但相对于国外发达国家的集聚水平而言, 东部地区集聚经济发展还不完善。图 1(左)显示, 东部地区效率显著高于中西部, 然而其与集聚分布还存在差异, 已经逐渐凸显出过度集聚现象(Ellison and Glaeser, 1997;范剑勇, 2004; 吉亚辉、李岩, 2011)。因为港口和国家政策支持, 中国制造业不断向东部沿海集聚, 并通过规模和学习效应产生正外部性。但近年来, 珠三角和长三角等主要集聚区都出现了产业同构、重复建设现象, 并导致了资源错配、生产成本上升和拥挤现象(杨礼琼、李伟娜, 2011; 魏守华等, 2013; 林灵等, 2015; 季书涵等, 2016)。行业的非均衡分布问题开始引起政府的重视, 优化产业结构的政策逐步付诸实施, 但西部大开发和产业转移等并没有有效促进西部产业快速发展, 而东部产业仍在不断集聚, 西部并没有很好的承接东部产业转移, 这种现实与理论的矛盾主要是政府产业布局具体目标的不明确。并且中国环境污染问题开始得到广泛关注, 这主要是因为产业的过度集聚引起部分厂商为了获取利益、占领市场份额等目的而进行不法生产(沈能等, 2014; 李晓萍等, 2015; 张云飞, 2014)。因此, 在考虑负外部性因素的前提下, 调整产业结构、平衡地区分布以及把握时机抉择是中国制造业结构升级的重中之重。
① 以工业总产值和在职人数分别求出各省不同行业2000-2013年的EG指数, 利用熵权法求出综合EG指数, 然后以不同行业产值为权重, 进行加权, 最后按照年份求出算术平均值。
|
图 1 中国各省效率(左)和综合EG指数(右)分布② |
② 图 1通过arcgis软件做出。
国内外大量研究表明集聚和效率之间存在着必然联系。国外产业发展起步早, 规模经济发展迅速, 首先出现集聚效应, 空间基尼系数、赫芬达尔指数和EG指数等测算集聚程度的指标不断出现(Krugman, 1991; Glaeser, 1997;Amiti, 1998)。中国的集聚产生在改革开放后, 主要出现在东部沿海地区, 大多数国内学者不断研究中国产生的集聚现象(文东伟、冼国明, 2014; 赵黎明、邢雅楠, 2011; 郝俊卿、曹明明, 2013)。而集聚和效率之间的关系到底如何, 是促进还是抑制了效率?部分学者认为集聚会形成规模经济, 吸引高素质人才和技术, 形成正外部性, 并影响着效率(陈得文、苗建军, 2010; 盛龙, 2013)。但是, 随着污染、拥挤和资源错配等现象的产生, 学者逐渐对集聚抱以怀疑, 关于集聚和效率呈负相关的研究不断出现。国外学者发现集聚和生产率之间的关系正在不断的减弱, 而且有时候线性关系不显著, 存在着非线性关系(Jones, 1995; Martínez, 2008; Rizov et al., 2012)。国内学者也发现了集聚和收益、生产率之间的负相关甚至得出呈倒“U”型关系, 并且通过建立传统非线性模型、传统门限模型等进行验证, 国内集聚和效率之间的负向作用存在且东部地区尤为明显, 在行业方面, 如制造业和服务业也出现了类似的现象(唐根年, 2009; 陈柳, 2010; 惠炜、韩先锋, 2016)。多数研究认为产生这种现象的一个原因是污染, 并且得出集聚促使环境污染的结论(张可、汪东芳, 2014; 张可、豆建民, 2015)。但集聚是否通过造成环境问题而影响生产率是值得思考的, 并且不同地区、不同类型制造业的特点不同, 这些特点是否影响集聚、环境污染和效率之间的关系也是值得关注的(沈能等, 2014)。
从上述文献看, 国内外学者对产业集聚和生产率的关系进行了较为丰富的研究, 且取得相应的成果。然而, 从指标、方法和内容看, 目前仍存在一些空缺。从指标看, 现有文献通常只使用单一的就业人数或销售产值等来测算集聚水平, 但这仅从单一视角反映了集聚, 并且数据往往会有缺失, 因此本文以熵权法为基础, 求出综合集聚指数, 以期能更全面的衡量集聚水平(陈雯, 2012); 在方法方面, 虽然相关文献对集聚和生产率之间的关系进行较为深入的探讨研究, 但环境污染、拥挤等负外部性尚未考虑进来, 因此本文引入非期望产出的DEA模型测算生产率。并且现有文献仅从上市公司或宏观数据测算集聚, 不能合理全面的反应微观特征, 本文采用工业企业数据库对不同地区不同行业集聚进行再测算(许余洁, 2011; 郭贯成、温其玉, 2014)。而且现有过度集聚的研究都是从集聚水平对生产率产生负向线性影响或传统不连续的STR模型进行说明(李胜会、章勇, 2011; 赵增耀, 2012), 为了能体现门限转换的平滑, 使结论更具现实性和科学性, 本文使用更为合理的PSTR模型; 最后, 在内容方面, 尽管有学者提出集聚效应存在明显的空间效应, 并且对相关行业进行研究, 但很少有文献同时从地区和要素密集度视角下分析集聚和生产率的关系, 中国不同地区、不同要素密集度制造业的特点和发展程度不同, 效率和集聚的关系也应该不同, 不同类型制造业的最优集聚水平也不同, 鉴于此, 本文从该视角进行比较分析, 以期能够从空间视角完善集聚水平和生产率关系的研究。
本文后续的结构安排如下:第二部分为理论分析; 第三部分为模型设定、变量选取和数据说明; 第四部分为实证检验和结果分析; 最后为主要结论和政策建议。
二、理论分析制造业的集聚与劳动力的集聚密切相关, 劳动力集聚是市场形成的必要条件及结果, 两者相互作用。这里定义区域系统效率为生产总值与劳动力福利和其他成本的差, 区域内企业的分布取决于区域内及区域间的交互作用, 即扩散和集聚作用, 本章依据中心外围理论和吴颖(2008)的研究进行理论推导, 引入资源有限的约束条件, 并且假定短期技术水平不变。
(一) 模型假设1.假设只有区域1和区域2, 区域1在集聚水平占有优势, 即单位劳动成本低, 并且熟练劳动力占绝大比例。
2.区域1和区域2的劳动力总和L固定, 其中包括即将就业的熟练劳动力和已经就业的劳动力。
3.资源有限, 技术短期不变。
(二) 参数选取1.Ti为贸易成本因子, 即不同地区集聚的基础条件, 并且不同区域的集聚随Ti的增大而减小。
2.区域集聚程度σ。当σ接近于1, 空间集聚程度越大; 当σ接近于0, 空间集聚程度越小。
3.Ai为生产损失因子。Ai越大, 越不利于集聚创造福利, 区域1指环境污染、拥挤等, 区域2指由于与区域1的地区差距扩大造成的社会成本。
(三) 模型设定区域系统生产模型。首先当Ti越低, 集聚水平越高, 熟练工人在某区域集聚使得该区域价格指数下降, 但其他区域相对价格指数上升, 所以两区域生产函数如下:
| $ G = \frac{{{Y_1}}}{{{P_1}^{ - {T_2}}}} + \frac{{{Y_2}}}{{{P_2}^{ - {T_1}}}} = {Y_1}{P_1}^{{T_2}} + {Y_2}{P_2}^{{T_1}} $ | (1) |
其中P是价格指数, Y是劳动L、资本K和人均资源耗费量ai的增函数, 设熟练工人数量占比为φi, 其他工人为1-φi, 区域i两类工人的生产率为Wis和Wir, 熟练工人可以提高非熟练工人的生产率。熟练工人总是向区域1转移, 这就会对区域2流动性差的非熟练劳动力造成负外部性, 所以把L1作为区域2非熟练劳动力的负向影响因素。短期技术水平不变, 则熟练工人生产率W1s和W2s不变, 则有:
| $ {Y_1} = {\phi _1}{W_{1s}}{L_1} + \left({1 - {\phi _1}} \right){W_{1r}}{L_1} $ | (2) |
| $ {Y_2} = {\phi _2}{W_{2s}}{L_2} + \left({1 - {\phi _2}} \right){W_{2r}}\left({{L_1}} \right){L_2} $ | (3) |
区域2的工人不断向区域1转移, 则对区域2造成负面影响, ∂ Y2/∂ L1 < 0。其他非熟练工人也会向区域2集聚, φ2不断减少。
区域效率函数为区域生产函数减去总成本, 用公式表示如下:
| $ U = G - C = G - [{{\bar c}_1}M\left({{L_1}, {S_1}, {F_1}} \right) + {{\bar c}_2}M({L_2}, {S_2}, {F_2})] $ | (4) |
其中S为流动资产, F为固定资产,
| $ U = G - C = G - \bar c[M\left({{L_1}, {S_1}, {F_1}} \right) + M({L_2}, {S_2}, {F_2})] $ | (5) |
① c的定义参考吴颖、蒲勇健(2008)。
又因为资源是一定的, 所以需要建立约束条件。假定ais和air为熟练和非熟练工人人均耗费资源量, 则有
| $ {\phi _1}{a_{1s}}{L_1} + \left({1 - {\phi _1}} \right){a_{1r}}{L_1} + {\phi _2}{a_{2s}}{L_2} + \left({1 - {\phi _2}} \right){a_{2r}}\left({{L_1}} \right){L_2} + {a_{2r}}\left({{L_1}} \right){L_3} \le R $ | (6) |
其中R为资源总量, L3为新进入的非熟练工人, 假定其只进入区域2, 因为相对已有非熟练工人, 其缺乏经验, 没有优势, 所以只会进入竞争压力相对小的区域2。非熟练工人的生产率随当地熟练工人的溢出效应而增加, 区域1的熟练工人增加意味着区域2熟练工人向区域1转移, 所以∂ a2r/∂ L1>0。区域1的技术短期不变, 所以熟练工人的流入不会对当地熟练工人和非熟练工人人均耗费资源产生影响。对(6)式求L1的导数, 有
| $ {\phi _1}{a_{1s}} + \left( {1 - {\phi _1}} \right){a_{1r}} + \left( {1 - {\phi _2}} \right){a_{2r}}^{'}\left( {{L_1}} \right){L_2} + {a_{2r}}^{'}\left( {{L_1}} \right){L_3} > 0 $ | (7) |
因为∂ Y2/∂ Y1 < 0, ∂ Y2/∂ L1 < 0, ∂ Y2/∂ L2>0, ∂2Y2/∂ L22 < 0, 则随着集聚水平上升, 资源消耗总量递增, 当集聚达到一定水平, 劳动力不再起决定作用, 取而代之的是资源, 过度集聚现象产生, 拉格朗日函数为:
| $ \begin{array}{l} LL = {Y_1}{P_1}^{{T_2}} + {Y_2}{P_2}^{{T_1}} - \bar c\left[ {M\left({{L_1}, {S_1}, {F_1}} \right) + M\left({{L_2}, {S_2}, {F_2}} \right)} \right]{\rm{ }}\\ \;\;\;\;\;\; + V[R - {\phi _1}{a_{1s}}{L_1} + \left({1 - {\phi _1}} \right){a_{1r}}{L_1} + {\phi _2}{a_{2s}}{L_2} + \left({1 - {\phi _2}} \right){a_{2r}}\left({{L_1}} \right){L_2} + {a_{2r}}\left({{L_1}} \right){L_3}] \end{array} $ | (8) |
一阶条件为∂ LL/∂ L1=∂ LL/∂ L2=0。中国现阶段各个区域只顾自身的发展, 国家和地方政府只重视短期利益, 所以某些地区高速发展, 而其他地区缓慢, 两极分化严重, 还造成了环境污染等问题。所以说, 各行业在发展的历程中和规模并不一定呈正的线性关系, 有可能导致负的非线性影响, 这也是本文要研究的, 下文将通过实证分析说明。
三、模型设定、变量选取与数据说明由于不同集聚水平下集聚和其他因素对制造业收益的影响不同, 可能是非线性的, 并存在门槛值, 而传统STR模型的转换是非平滑的, PSTR作为改进的非线性模型, 更符合现实的经济现状。公式表示如下:
| $ {y_{it}} = {u_i} + {b^{'}}_1{x_{it}} + {b^{'}}_2{x_{it}}g\left({{q_{it}};\gamma, c} \right) + {\varepsilon _{it}} $ | (9) |
其中γ为斜率, 表示从一个机制转换到另一个机制的转换速度或调整的平滑性, 决定转换的速度, c为平滑参数, qit为转换变量, 转换函数具体表示如下:
| $ g\left({{q_{it}};r, c} \right) = {\left[ {1 + {\rm{exp}}\left[ { - \gamma \prod\limits_{j = 1}^m {\left({{q_{it}} - {c_j}} \right)} } \right]} \right]^{ - 1}} $ | (10) |
其中γ>0, c1≤c2≤…≤cm, 0≤g(qit; r, x)≤1, xit的函数值将在b′1和b′1+b′2之间平滑。若γ=1且m=1时, PSTR只包含一个转换函数。PSTR是PTR模型和传统门限回归模型的延伸, 即当γ→+∞且qit>c时, limg(qit; r, c)=1;若γ→+∞并qit < c时, limg(qit; γ, c)=0。PSTR就变成两个转化机制的PTR模型。当γ=1且m=2时, PSTR转换为两机制模型。g(qit; γ, c)关于(c1+c2)/2对称, limg(qit; γ, c)=1。当qit=(c1+c2)/2时, g(qit; γ, c)最小(González A et al., 2005; 马薇、丰璐, 2010; Apergis N and Payne J E, 2014)。
本文根据上述的理论模型建立如下PSTR模型:
| $ {\rm{ln}}\theta = {\mu _{it}} + \sum \beta \times {x_{it}} + \sum \beta \prime g\left({{\rm{ln}}E{G_{it}};{\gamma _1}, {c_1}} \right) \times {x_{it}} + {u_{it}} $ | (11) |
其中xit=(lnEGit, PRit, lnFiit, FDIit, lnRoadit, Eit), β=(β1, β2.β3, β4, β5, β6), β′=(β′1, β′2, β′3, β′4, β′5, β′6), lnθ、lnFi、lnRoad和lnEG分别是θ、Fi、Road和EG的对数的相反数。因为变量取值都在(0, 1)之间, 相差不大, 不利于实证的稳定性, 所以取对数将其映射到[-∞, +∞], 但取对数后变为负值, 因此再对其取相反数, 保证为正, 方便解释。
(一) 变量选取与方法介绍 1. 效率变量的选取本文使用引入环境因素的非期望产出数据包络方法求生产率(唐根年, 2009; 李胜会, 2010; 许余洁, 2011), 其指标选取如下:
(1) 投入指标。将固定资产原价(亿元), 年末从业人数(万人), 流动资产总值(亿元), 主营业务成本(亿元)作为投入变量。
(2) 产出指标。即营业利润(亿元), 主营业务收入(亿元), 工业总产值(亿元)。
(3) 非期望产出指标。主要采用工业废水排放量(万吨), 工业粉尘排放量(万吨), 工业固体废弃物排放量(万吨), 工业烟尘排放量(万吨), 工业二氧化硫排放量(万吨)。采用熵权法, 构造综合污染指标。
2. PSTR模型变量的选取(1) 被解释变量
本文的被解释变量是效率(θ), 通过MATLAB进行编程, 使用上述变量计算得到的。
(2) 核心解释变量
本文的核心解释变量是综合EG指数。假设国家中某一行业的企业个数为N, 存在M个地区, 则EG指数表示如下:
| $ r = \frac{{G - \left({1 - \sum\limits_{i = 1}^M {{X_i}^2} } \right)H}}{{\left({1 - \sum\limits_{i = 1}^M {{X_i}^2} } \right)\left({1 - H} \right)}} = \frac{{\sum\limits_{i = 1}^M {{{\left({{S_i} - {X_i}} \right)}^2}} {\rm{ }} - \left({1 - \sum\limits_{i = 1}^M {{X_i}^2} } \right)\sum\limits_{j = 1}^N {{Z_j}^2} {\rm{ }}}}{{\left({1 - \sum\limits_{i = 1}^M {{X_i}^2} } \right)\left({1 - \sum\limits_{j = 1}^N {{Z_j}^2} } \right)}} $ | (12) |
其中
之前的文献都以单独的指标为研究对象, 部分产业指标数据可能缺失, 造成不可比性。本文通过求出以就业人数和销售产值两个要素为基础的EG指数, 然后利用熵权法计算综合EG指数。这里采用EG指数是因为它包含了赫芬达尔指数和空间基尼指数的优点, 既能够反映产业的集聚程度, 还能反映产业结构(范慧慧等, 2009)。本文的EG指数通过工业企业数据库微观企业数据和《中国统计年鉴》进行地区和行业分类求得。
(3) 控制变量
本文除了以上的变量外, 还加入了如下的控制变量:利息支出与销售收入的比, 即融资能力(Fi); 外商资本金作为外商参与度(FDI); 实有道路长度比省域面积, 即铁路密度(Road); 省能源消费数(E); 各省的专利数量和研发投入的自然对数之比来表示研发效率, 即PR=patent/lnR & D(冯照桢等, 2016)。
(二) 数据来源与描述性统计以上的数据都是通过《中国统计年鉴》、《中国工业经济统计年鉴》、《中国能源统计年鉴》和工业企业数据库搜集, 部分省份数据缺失, 譬如西藏等, 本文将其剔除。
本文所使用的制造业分类主要依据2002年制定的中国国民经济行业分类准则, 按照其专业化一种或者主要生产某种产品的所有单位集聚原则, 将制造业分为28个两位数行业。然后采取徐建荣(2008), 郭克莎(2005), 赵书华(2009)等分类方法, 计算生产要素的相对密集度来划分产业, 这里主要选取劳动、技术、资本和资源四个要素, 具体方法如下:先考虑资源密集型, 因为强烈的依赖资源, 使用存货占生产总值的比, 如果该数值超过所有行业的均值, 并且超过50%, 则为资源密集型; 资本与劳动是相互对立的, 所以使用人均固定资产占比来区分资本密集型和劳动密集型, 如果小于均值且超过50%, 则为劳动密集型; 如果该指标大于均值且超过50%, 则为资本密集型; 技术人员占所有员工的比例是区分技术密集型的主要变量, 对于其他没有划分的制造业, 如果该指标大于平均值且超过50%, 则将其划分为技术密集型; 此分法可能使部分制造业没有被划分, 回到第二步, 如果剩下的制造业人均固定资产占有额小于50%, 则划分为劳动密集型, 反之划分为资本密集型。于是所有的制造业行业就划分为了四类, 具体结果见表 1。
| 表 1 制造业按要素密集度分类 |
表 2是本文变量的描述性统计, 可以看出E(省能源消费数)的标准差最大, 为7.17, 变化波动最为明显; FDI(外商资本金)的标准差最小, 为0.06, 变化波动较小; 其他变量的标准差都在1附近。
| 表 2 描述性统计分析 |
PSTR模型回归前需要检验几个假设:一是检验模型的线性与非线性和转换函数的数量r; 二是在第一步的基础上确定模型位置参数的数量m; 三是在确定位置参数个数的基础上计算平滑参数γ和位置参数c的初始值。
(一) 非线性检验及门槛个数的选择面板数据的不平稳往往会造成分析结果的有偏性, 所以在进行实证分析之前要检验面板数据的平稳性, 从而保证结果的稳健性。而传统的单位根检验存在严格假定, 即各截面相互独立。但近年来的研究表明空间之间存在着溢出效应, 截面单位相互独立假设不成立, 传统检验会造成显著性偏差。下面首先对截面相关性进行检验, 如表 3所示, 可以看出除过变量FDI外, 其它变量均拒绝了截面相互独立的原假设①。
① 这里主要使用Pesaran(2004)采用的CD统计量来检验截面相关性, P为滞后期。
| 表 3 截面相关性检验 |
为了克服截面相关性问题并保证结果的科学性, 这里结合最新的研究成果, 分别采用CIPS、CZ检验方法, 检验平稳性①。如表 4所示, 与第一代面板单位根检验类似, 在不同的滞后阶数下, 不同变量的统计量均显著地拒绝存在单位根的原假设, 从而可以进行下面的检验。
① 第二代面板单位根检验主要是用Pesaran(2007)的CIPS、CZ和CP统计量, P为滞后期, 这里使用matlab编程所得。
| 表 4 第二代面板单位根检验 |
因为PSTR模型是非线性的, 传统的线性检验失效, 这里将原始PSTR模型进行一阶泰勒展开式, 转换成线性模型, 在原假设和备择假设情形下检验两种情况残差平方和的差异性, 一般使用LM、LMF和LRT指标进行检验②。下面对全国、东部、中部和西部关于(11)式进行线性与非线性检验, 将全国劳动型、全国资本型、全国技术型、全国资源型、东部劳动型、东部资本型、东部技术型、东部资源型、中部劳动型、中部资本型、中部技术型、中部资源型、西部劳动型、西部资本型、西部技术型和西部资源型简写为A1~A16, 结果如表 5所示。
② 三种非线性检验分别为
| 表 5 线性与剩余非线性检验 |
可以看出, 基本所有模型都关于原假设H0:r=0在1%下显著, 而在原假设H0:r=1的5%显著性水平下不显著, 也就是说都是非线性的, 并且转换函数个数都是一个, 即r=1。同时, 并不是所有模型m=1的AIC和BIC值都小于m=2的对应值, 可以得出全国资本密集型(A2)存在两个位置参数, 所以不同模型的最优位置参数值不同①。
① AIC全称最小信息量准则, BIC全称贝叶斯准则, 主要用于刻画用了某个模型后相对于真实模型的信息损失, 一般值越小, 说明该模型的形式最优。在本文, 首先对PSTR进行泰勒展开式, 然后对相应的m=1和m=2的模型进行该检验。
(二) 实证结果及分析本文的回归方法采用非线性最小二乘法(nls), 估计前需要确定参数γ和c的初始值。常用的求解方法是网格搜索法, 即将网格上每个(γ, c)代入模型进行估计, 并选取能使模型的残差平方和最小的初始值②。
② 网格搜索法、PSTR回归都通过MATLAB编程得到结果。
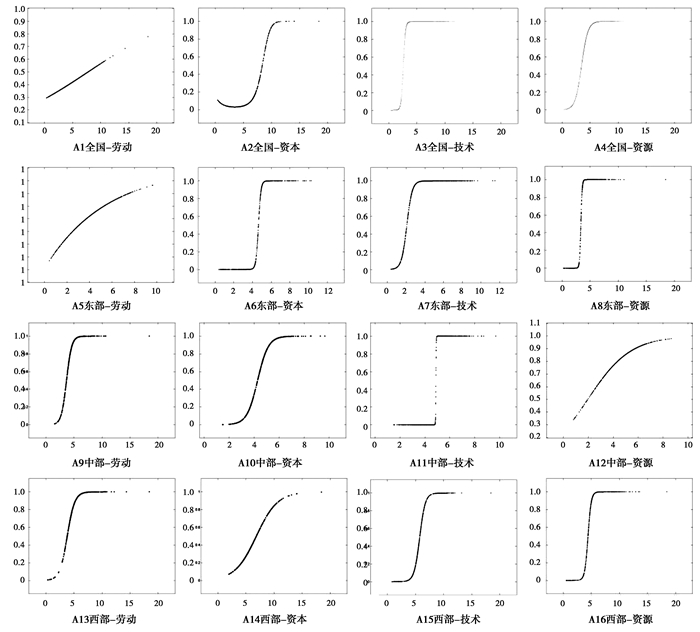
表 6为所有地区不同要素密集度制造业(A1~A16)的回归结果, 可以看出大多数变量的回归系数在1%显著性水平下显著, 说明了模型的可靠性。图 2为A1~A16回归结果的转换函数, 可以看出每个模型都存在部分观察值在高机制和低机制之间, 如果使用非平滑转换模型进行计量会产生偏误。下面首先分地区对实证结果进行分析。
| 表 6 模型的参数估计结果 |
|
图 2 不同模型回归结果的转换函数 |
从全国来看, 除过资本型制造业存在两个门限值, 其他类型制造业都只存在一个门限值。劳动密集型制造业效率和集聚之间存在一个转换机制EG=e-7.762, 当集聚水平低的时候, 集聚对效率呈正向关系, 随着集聚的增加并超过门槛值, 两者的关系开始转为负相关, 属于过度集聚型。资本密集型制造业的效率在前期与集聚的关系为正, 到达门槛值EG=e-8.342, 两者关系逐渐变为负, 但随着集聚继续增加到EG=e-1.434, 集聚又对效率产生正向作用, 但是正向关系没有集聚初期大, 属于过度集聚型。对于技术密集型制造业, 当集聚小的时候, 集聚对效率的作用为正, 但当达到门槛值EG=e-2.602时, 集聚的斜率突然变大, 属于集聚推进型。资源密集型制造业的门槛值是EG=e-3.482, 当集聚小于门槛值时, 集聚与效率为正向关系, 但是随后这种关系急剧变为负向, 说明资源密集型制造业属于过度集聚型。
东部地区劳动密集型制造业由于转换程度γ=0.184较小, 所以斜率变化平缓, 门限值为EG=e-3.390, 在集聚前期, 集聚和效率的关系为正, 但这种正向关系慢慢变为负, 属于过度集聚型。资本密集型制造业的转换程度γ=7.532很大, 所以斜率变化也很大, 门槛值为EG=e-4.639, 当小于门限值时, 集聚对效率的作用为正, 随着集聚水平的增加, 集聚的斜率突然变小, 但还为正, 属于集聚推进型。对于技术密集型制造业, 门槛值为EG=e-2.078, 集聚开始和效率呈负向关系, 当达到门槛值, 负向关系突然转为正向关系, 且斜率较大, 属于集聚推进型。而资源密集型制造业的门限值为EG=e-3.359, 当集聚小的时候, 集聚对效率产生正向作用, 但是这种作用小, 随着集聚的增加, 正向作用变大, 属于集聚推进型。
对于中部地区, 劳动密集型制造业门限值为EG=e-3.691, 当集聚水平低的时候, 集聚对效率的影响为正, 但达到门槛时, 这种作用突然降低, 但还处于比较小的正向关系, 属于集聚推进型。对资本密集型制造业, 其门槛值为EG=e-4.281, 期初集聚的系数为正, 但随着不断集聚, 系数不断减少为负值, 属于过度集聚型。而中部技术密集型制造业的门限值为EG=e-4.866, 转换程度为γ=73.7, 所以当集聚过小的时候, 其对效率的作用为正, 但当达到门限值时, 斜率变为负, 且这种变化特别突然, 属于过度集聚型。而对于资源密集型制造业来说, 其门槛值为EG=e-1.963, 当小于门限值的时候, 集聚水平和效率的关系为正, 当突破门限值时, 系数转为负, 并且该系数的绝对值比较大, 属于过度集聚型。
对西部地区来说, 劳动密集型制造业存在一个转换机制, 且为EG=e-3.817, 当集聚增加的时候, 其斜率开始为正, 但随后变为负值, 并且负值的绝对值比较大, 属于过度集聚型。对于资本密集型制造业来说, 其门限值为EG=e-6.840, 当集聚小于这个值时, 效率对集聚产生正向作用, 但是随着集聚水平的不断地增加, 其系数变为负数, 是过度集聚型制造业。对于技术密集型制造业, 因为本身没有人才和研发投入, 所以技术水平低下, 所以在集聚小的时候, 其对效率的作用为正, 但是这种正向关系非常小, 随着集聚不断增加并超过门限值EG=e-5.749, 其转变为负向关系, 属于集聚递减型。而对于资源密集型制造业, 这里的结果出乎意料, 其门限值为EG=e-4.399, 当集聚水平小的时候, 其对效率的作用是负向的, 但是当集聚水平不断的增加, 其对效率的作用慢慢转变为正, 说明西部资源密集型制造业的效率不断随着集聚增加而增加, 是集聚推进型。
下面对实证结果进行分析, 可以看出全国、东部和西部劳动密集型都属于过度密集型, 因为本文的研究时段是2000-2013年, 期间正是我国产业结构转型的重要时期, 劳动密集型制造业已经没有之前的优势, 规模的增加并不能带来显著的效益提升。东、西部地区早期的集聚对效率的正向作用比较小, 一方面是因为西部地区的劳动力外流和融资难问题以及东部地区逐渐转型为技术和资本密集型制造业, 所以随着集聚水平的提高, 其对效率的影响不断的下降。而中部城市发展水平比西部好, 虽然没有东部发达, 但也为其劳动密集型制造业发展提供了天然的避风港, 既没有激烈的竞争, 又能吸引大量劳动力、技术等资源, 虽然其对效率的作用也下降了, 但还保持在相对小的正向关系, 属于集聚推进型。
对于资本密集型制造业来说, 全国层面具有两个门限值, 与中部和西部同属过度集聚型, 但是随着集聚的增加, 全国和东部资本密集型制造业还是对效率产生正向关系。东部地区城市发展较快, 企业发展迅速, 吸引了很多的劳动力, 降低了成本。如此循坏, 企业越来越多, 规模也越来越大, 形成规模经济, 获得超额利润率, 效率不断增加。但是东部地区也会随着而来产生拥挤、竞争等问题, 这种正向关系会减弱。中、西部地区的资源不断外流, 企业发展到一定规模后, 内部劳动力、技术人员等辞职向东部聚集, 从而保证不了中、西部地区资本密集型企业规模的扩大, 提高不了效率, 无法与东部进行竞争, 甚至可能还会使效率下降。
中国资源型制造业不论地处什么位置, 其利用效率低下、结构单一和生态环境承受力弱。全国和中部地区都属于过度集聚, 其一旦发现资源, 资源所在地就会吸引企业, 获得高利润, 但达到一定规模, 资源耗尽时, 企业出现瓶颈, 企业倒闭或者迁移, 并且中部地区技术水平相对较弱, 污染带来的负影响就大于生产过程中带来的利益, 从而会使效率降低。而东部地区拥有着相对发达的资源利用技术, 虽然其资源相对稀缺, 但是却能高产出, 随着交通运输业的发展, 中、西部的资源也可以运送到东部进行生产, 从而随着集聚水平的提高, 对效率的影响有着显著的提升。西部地区在集聚小的时候对效率产生负向影响, 但是随着集聚水平提高, 影响变为正向, 因为西部有着大量的资源和劳动力, 会吸引大量技术和投资, 从而提高生产率, 前期的低效是因为技术水平不足和环境污染造成的。
技术型制造业的特点是技术人才比较多, 科研项目投入大。但是中国教育水平比较差, 企业创新能力低, 不能和其他该类型制造业竞争, 从而不能控制市场, 效率低下。不过企业成立时就存在新技术, 这是它能够立足于市场的保证。但是当规模不断的扩大, 技术被模仿, 迫使企业创新, 中部和西部尤为明显, 并且大量技术人员外流, 缺乏资本, 创新水平差, 效率降低。东部地区技术密集型企业比较多, 专利数非常多, 但有效专利的不足导致早期的负向关系, 随着集聚不断增加, 技术不断地被模仿, 企业要想存活和进入必须进行有效的创新, 而且东部教育水平比较高, 人才多, 加之政府补贴, 并且创新具有一定的滞后性, 从而慢慢开始对效率产生正向作用, 虽然期间可能会产生污染和拥挤等负外部性, 但是其会投入大量的资金和技术进行改善。
五、结论及政策建议产业集聚一般通过规模效应产生知识溢出, 使人们认为一个地区越集聚, 其正外部性越大, 但现实情况并非如此。本文的实证结果表明集聚对效率会产生正负两种效应, 并非单调递增, 不同地区不同要素密集度制造业差异很大, 部分地区已经出现过度集聚现象甚至集聚递减。当集聚达到一定水平时, 环境污染问题、生产要素拥挤现象以及要素错配等凸显而出, 严重抑制资源配置效率, 具体表现在以下几个方面:(1)中国绝大多数制造业集中在东部沿海地区, 表面上“极度东倾”现象严重, 但是东部过度集聚现象却不是很普遍, 而中、西部部分制造业过度集聚现象较为严重, 并且不同要素密集度制造业所表现出来的关系是不同的。(2)超过50%的制造业出现过度集聚现象, 并且部分地区要素密集度制造业集聚对效率产生负向作用, 说明中国制造业具有复杂性。(3)东、中、西部地区交通对效率都开始产生负向作用, 说明交通基础设施建设没有跟上产业集聚的增加。西部地区的专利和研发投入对生产率的影响为负, 说明其创新效率严重不足。东、中、西部地区随着集聚的增加, 外商投资对效率都产生很强的正向关系, 说明国外的管理模式和技术等对提高中国制造业的发展起着重要的作用。东、西部能源对效率的作用随着集聚的增加逐渐变为负的, 而中部地区则相反, 说明东部制造业的拥挤和西部资源利用效率不足抑制着当地的经济发展。
通过以上结论可以发现, 东南沿海地区处在高度集聚的发展阶段, 如何解决两极分化和产业分布失衡问题是解决社会问题的关键, 中国制造业已处在产业结构升级和调整的重要阶段。随着不断的国际化和市场化, 生产要素成本高、发展空间狭小以及技术水平不足使得传统制造业不断失去竞争优势, 当务之急是转型发展模式, 寻求新的增长点, 促进第三产业和高新技术产业的发展, 因此, 本文提出以下几点政策建议:(1)地区不能为了提高当地政府业绩而盲目追求产业集聚, 应该注意适度集聚原则, 保证资源优化配置, 避免资源错配和生产要素拥挤现象。国家应当制定相应的税收、补贴壁垒等政策, 适度调整和干预地方企业的发展, 避免过度集聚, 从而防止交通拥挤和环境污染等现象(郑丹, 2017)。(2)依靠廉价劳动力的传统发展模式已经不能长远立足于中国和国际市场上, 政府和企业应该提高其技术创新能力, 提升企业生产效率。虽然近年来中国制造业发展迅猛, 技术水平不断提高, 但远不足国外发达国家, 并且还是以高投入、高消耗为基础的, 核心技术依赖于国外, 无法获得价值链中的高收益。加强技术创新能力的主要方式有加大科研经费力度、提高当地教育水平、培养高素质人才、加强产学研联合、充分发挥院校的科研优势等, 并吸引外商投资和国外先进技术。(3)东、西部应该改善生产模式, 提高能源利用效率, 提高基础设施建设减轻拥挤现象, 使资源最大化利用。(4)中西部地域辽阔, 有着丰富的自然资源, 但还是无法满足对东部产业的承接。地区政府应当继续加大基础设施投入, 一方面提高交通质量, 另一方面保证交通数量的提高, 逐渐完善交通基础设施。同时, 还要建立健全良好的投资环境、金融市场和征信系统, 保证当地制造业获得相应的融资, 以此减少东部过度集聚现状, 促进中西部的产业结构优化升级, 建立具有中国中西部特色的经济发展模式。(5)中、西部地区高技术劳动力不断向东部转移, 严重抑制当地企业的发展。国家和政府应该提高其创新效率, 加大技术创新投资力度, 同时研发污染处理技术, 尽量减少非期望产出。国家和政府还应该提高补贴, 将高学历人才保留在当地企业中, 一方面保证个人的技能提升, 另一方面通过学习溢出效应促进其他劳动力的效率, 保证整个区域生产率的提升。
| [] |
陈得文、苗建军,
2010, “空间集聚与区域经济增长内生性研究—基于1995-2008年中国省域面板数据分析”, 《数量经济技术经济研究》, 第 9 期, 第 82–93 页。 |
| [] |
陈柳,
2010, “中国制造业产业集聚与全要素生产率增长”, 《山西财经大学学报》, 第 12 期, 第 60–66 页。 |
| [] |
陈雯,
2012, “基于熵权法的环境绩效与环境保护税费的灰色关联分析”, 《税务与经济》, 第 6 期, 第 81–85 页。 |
| [] |
范慧慧、王国栋、路正南,
2009, “熵权法下基金业绩的层次模糊评判”, 《经济管理》, 第 4 期, 第 130–135 页。 |
| [] |
范剑勇,
2004, “长三角一体化、地区专业化与制造业空间转移”, 《管理世界》, 第 11 期, 第 77–84 页。 |
| [] |
冯照桢、温军、刘庆岩,
2016, “风险投资与技术创新的非线性关系研究—基于省级数据的PSTR分析”, 《产业经济研究》, 第 2 期, 第 32–42 页。 |
| [] |
郭贯成、温其玉,
2014, “环境约束下工业用地生产效率研究—基于中国33个典型城市非期望产出的考量”, 《中国人口·资源与环境》, 第 6 期, 第 121–127 页。 |
| [] |
郝俊卿、曹明明、王雁林,
2013, “关中城市群产业集聚的空间演变及效应分析—以制造业为例”, 《人文地理》, 第 3 期, 第 96–100 页。 |
| [] |
惠炜、韩先锋,
2016, “生产性服务业集聚促进了地区劳动生产率吗”, 《数量经济技术经济研究》, 第 10 期, 第 37–56 页。 |
| [] |
吉亚辉、李岩,
2011, “甘肃省制造业产业集聚的实证研究—基于对EG指数修正后的指数分析”, 《工业技术经济》, 第 7 期, 第 17–21 页。 |
| [] |
季书涵、朱英明、张鑫,
2016, “产业集聚对资源错配的改善效果研究”, 《中国工业经济》, 第 6 期, 第 73–90 页。 |
| [] |
李胜会、李红锦,
2010, “要素集聚, 规模效率与全要素生产率增长”, 《中央财经大学学报》, 第 4 期, 第 59–66 页。 |
| [] |
李晓萍、李平、吕大国,
2015, “经济集聚、选择效应与企业生产率”, 《管理世界》, 第 4 期, 第 25–37 页。 |
| [] |
李耀新、石永清,
1989, “产业的生产要素密集形态演进的三个规律”, 《中国工业经济》, 第 5 期, 第 44–50 页。 |
| [] |
林灵、阎世平、曾海舰,
2015, “产业集聚与人力资本投资效益—来自中国工业企业的微观证据”, 《南方经济》, 第 2 期, 第 70–89 页。 |
| [] |
刘亦文、胡宗义,
2015, “中国碳排放效率区域差异性研究—基于三阶段DEA模型和超效率DEA模型的分析”, 《山西财经大学学报》, 第 2 期, 第 23–34 页。 |
| [] |
马薇、丰璐,
2010, “具有不同转换机制的非线性模型理论与应用研究”, 《统计研究》, 第 5 期, 第 96–100 页。 |
| [] |
沈能、赵增耀、周晶晶,
2014, “生产要素拥挤与最优集聚度识别—行业异质性的视角”, 《中国工业经济》, 第 5 期, 第 83–95 页。 |
| [] |
盛龙、陆根尧,
2013, “中国生产性服务业集聚及其影响因素研究—基于行业和地区层面的分析”, 《南开经济研究》, 第 5 期, 第 115–129 页。 |
| [] |
舒辉、周熙登、林晓伟,
2014, “物流产业集聚与全要素生产率增长—基于省域数据的空间计量分析”, 《中央财经大学学报》, 第 3 期, 第 98–105 页。 |
| [] |
唐根年、管志伟、秦辉,
2009, “过度集聚, 效率损失与生产要素合理配置研究”, 《经济学家》, 第 11 期, 第 52–59 页。 |
| [] |
王文声、易丹辉,
1988, “关于工业生产要素密集度研究的统计方法”, 《统计研究》, 第 1 期, 第 49–54 页。 |
| [] |
魏守华、李婷、汤丹宁,
2013, “双重集聚外部性与中国城市群经济发展”, 《经济管理》, 第 9 期, 第 30–40 页。 |
| [] |
文东伟、冼国明,
2004, “中国制造业产业集聚的程度及其演变趋势:1998-2009年”, 《世界经济》, 第 3 期, 第 3–31 页。 |
| [] |
吴雪花、杨蕙馨,
2004, “中国制造业产业集聚的实证研究”, 《中国工业经济》, 第 10 期, 第 36–43 页。DOI:10.3969/j.issn.1006-480X.2004.10.005 |
| [] |
吴颖、蒲勇健,
2008, “区域过度集聚负外部性的福利影响及对策研究—基于空间经济学方法的模拟分析”, 《财经研究》, 第 1 期, 第 106–115 页。 |
| [] |
徐建荣,
2009, “转型期中国制造业结构变动研究”, 《南京航空航天大学》。 |
| [] |
许余洁,
2011, “具有负外部性中间产出的两阶段网络DEA模型”, 《中国人民大学》。 |
| [] |
杨礼琼、李伟娜,
2011, “集聚外部性、环境技术效率与节能减排”, 《软科学》, 第 9 期, 第 14–19 页。 |
| [] |
张可、豆建民,
2015, “集聚与环境污染—基于中国287个地级市的经验分析”, 《金融研究》, 第 12 期, 第 32–45 页。 |
| [] |
张可、汪东芳,
2014, “经济集聚与环境污染的交互影响及空间溢出”, 《中国工业经济》, 第 6 期, 第 70–82 页。 |
| [] |
张云飞,
2014, “城市群内产业集聚与经济增长关系的实证研究—基于面板数据的分析”, 《经济地理》, 第 1 期, 第 108–113 页。 |
| [] |
赵黎明、邢雅楠,
2011, “基于EG指数的中国旅游产业集聚研究”, 《西安电子科技大学学报:社会科学版》, 第 2 期, 第 43–48 页。 |
| [] |
赵书华、张弓,
2009, “对服务贸易研究角度的探索—基于生产要素密集度对服务贸易行业的分类”, 《财贸经济》, 第 3 期, 第 90–95 页。 |
| [] |
赵增耀、夏斌,
2012, “市场潜能、地理溢出与工业集聚—基于非线性空间门槛效应的经验分析”, 《中国工业经济》, 第 11 期, 第 71–83 页。 |
| [] |
郑丹、TatsuakiKuroda,
2017, “城市基础设施水平如何影响居民工资收入:溢价还是折价”, 《南方经济》, 第 1 期, 第 66–85 页。 |
| [] |
Amiti M, 1998, "New trade theories and industrial location in the EU:a survey of evidence". Oxford review of economic policy, 14(2), 45–53.
DOI:10.1093/oxrep/14.2.45 |
| [] |
Apergis N, Payne J E, 2014, "Renewable energy, output, CO2, emissions, and fossil fuel prices in Central America:Evidence from a nonlinear panel smooth transition vector error correction model". Energy Economics, 42(1), 226–232.
|
| [] |
González A, Teräsvirta T and Dijk D, 2005, "Panel smooth transition regression models". SSE/EFI Working Paper Series in Economics and Finance..
|
| [] |
Jones C I, 1995, "R & D-based models of economic growth". Journal of political Economy, 759–784.
|
| [] |
Marinez-G J, Paluzie E and Pons J, 2007, "Agglomeration and labour productivity in Spain over the long term". Cliometrica, 2(3), 195–212.
|
| [] |
Pesaran M H, 2004, "General Diagnostic Tests for Cross Section Dependence in Panels". Social Science Electronic Publishing, 7, 1240.
|
| [] |
Pesaran M H, 2007, "A simple panel unit root test in the presence of cross-section dependence". Journal of Applied Econometrics, 22(2), 265–312.
DOI:10.1002/(ISSN)1099-1255 |
| [] |
Rizov M, Oskam A and Walsh P, 2012, "Is there a limit to agglomeration? Evidence from productivity of Dutch firms". Regional Science & Urban Economics, 42(4), 595–606.
|



