1978年土地相关法规调整以来,我国的房地产市场经历了近四十年的发展历程,尽管至今我们仍无法将中国的房地产市场定义为一个完全的竞争市场,但仍可以说我国的房地产市场确实朝着市场化方向迈进。2000年初,我国福利分房制度取消,住房制度改革又进入了一个新的平台,房地产价格也随之经历多轮上涨,以70个大中城市新建住房价格指数为例,除2014年4月至2015年7月期间出现较为持久下跌以外①,过去的十几年中房价整体保持着上升态势。另一方面,我国在实施2005年的“721”汇改之前,人民币基于持续的双顺差以及盯住美元的汇率制度而被长期低估,升值压力积蓄已久。2005年7月人民币汇率形成机制改革以来,人民币对美元汇率开始在更具市场化的有管理的浮动汇率制度下波动,并开启了长达近十年的升值之路,美元兑人民币汇率为例(美元直接标价法)在小幅波动中从2005年7月的8.22持续升值至2014年1月的6.05,升值幅度达到35.86%。
① 根据国家统计局提供数据,2014年4月至2015年7月期间,70个大中城市新建价格指数跌幅达到6.32%。
然而,人民币汇率升值预期在2014年1月开始扭转,贬值压力逐渐加大,并在2015年“811汇改”后加剧。升值预期的转变与美国宣布退出“量化宽松”政策不无关系,由于中美利差发生改变,出于套利目的的国际资本逐渐流出中国,直接导致人民币汇率的升值预期逆转以及小幅贬值出现(吴丽华,2014)。人民币贬值预期加大的压力下,许多基于套汇目的的“热钱”开始转而流出中国市场。与此同时,我国房价也相应出现跌势。一时间,关于“保房价”还是“保汇率”的声音开始频现金融界与学术界。那么,房价与汇率之间究竟存在怎么样的联系,二者是存在因果关系抑或是一个硬币的两面?
2017年末,中国人民银行首次在货币政策执行报告中提及金融周期的概念并强调其重要性①。古典经济学和凯恩斯主义就宏观经济中金融扮演的角色有所不同认知,前者认为经济增长由实体经济基本面决定,不强调金融的内生重要性,后者则认为金融与资源配置有着密不可分的关系。随着全球金融自由化程度的加深以及金融危机的出现,如何看待金融成为了一个愈发重要的问题,对金融周期的讨论也由此延伸而来。如明斯基所描述的“经济长期稳定时期信贷规模不断扩张,导致债务的不可持续以及资产价格的最终崩溃”的时刻,被称为“明斯基时刻”,体现了金融周期的拐点——金融危机。
① 参见2017年11月17日颁发的《2017年第三季度中国货币政策执行报告》。
不同于经济周期对经济增长、物价稳定以及失业率的关注,金融周期强调资产价格与信贷规模的相互作用,房地产价格和信贷是最核心的两个指标。其中,房地产是信贷抵押品,信贷是融资条件,二者相互强化体现顺周期性特征。从金融周期看,其上半场中房价与信贷相互促进,国内总需求得以支撑,投资增加抬高利率的同时也带来货币升值压力,国际资本净流入增加(彭文生,2017)。随着银行信贷规模的不断扩张,房地产价格脱离基本面程度逐渐加深,房地产泡沫增大,投资房地产的预期回报率降低,房地产行业出现拐点而进入调整,银行信贷随之收紧,金融周期转而进入下半场阶段②,投资的减少导致储蓄过剩,此时若国内资本流出向海外投资,加之国际资本的撤离造成货币的贬值压力。由此可见,房价与汇率在金融周期中表现出了上半场同涨、下半场同跌的相关性,这一相关性受到国际资本流动的作用得以加强,国际资本流动带来金融顺周期性。基于金融周期理论对房价与汇率关系的描述,本文提出以下问题:在我国逐步对外开放的基本国情下,国际资本流动是否对我国房地产价格与人民币汇率的相关性产生影响?试图解答我国国际资本流动是否产生金融顺周期性的问题。
② 徐荣等(2017)证明了房价的大幅攀升对于系统性金融风险有着促进的作用。
国外文献对房价与汇率的研究方面,Bowden(2004)在研究新西兰房价与汇率相关关系中,得到了房价即是影响汇率波动的因素,同时也受到汇率影响的结论。Abelson(2010)在对澳大利亚1970-2003年的房价进行研究时,通过分别对长期和短期影响房价的因素进行实证检验,发现汇率波动会显著影响房价。国内学者也对我国房价和人民币汇率之间的相关关系进行了研究讨论,王爱俭、沈庆劼(2007)从房地产供需两方面讨论了人民币汇率与我国房价的关系,他们认为房价的高涨是一种价格的错位对于汇率的错位的一种应对,部分缓解了人民币升值的压力。同时,文章也指出在人民币升值预期骤然上升的情况下,大批国际游资通过在汇市和房市建立多头头寸,进行套汇与套价获得双重收益,从而推动房价的上涨。朱孟楠等(2011)对2005年汇改后人民币汇率与中国房价的非线性动态关系进行研究,得出了房价上涨导致人民币兑美元实际汇率升值的结论,但二者相关性存在着明显的滞后效应。以上学者为代表的研究结果均表明,房地产价格作为一项重要的资产价格,与汇率存在着相关关系。
同时,也有许多文章指出,人民币汇率的上升通过资本流动为桥梁与房价上涨互相影响。研究认为流入中国的热钱涌向了股市、房地产等资本市场,推动资产价格的上涨,同时激发了国内资本的“羊群效应”,资产价格进一步被抬高(张中华,2007)。一方面,多数学者认为人民币汇率升值以及升值预期促进国际资本流入我国,而国际资本的流入又在外汇市场上加大了对人民币的需求,推动人民币汇率的进一步上升和升值预期的加强,国际资本流动和人民币汇率二者即存在着加强的正向相互作用。2005年汇改初期,曲凤杰(2005)便指出,在人民币大幅升值预期已形成的前提下,人民币的小幅升值不仅不会减少资本的流入,反而会促进投机性资本的流入。而当人民币升值预期消失后,资金的外流则在所难免。谷宇等(2008)在对人民币均衡汇率进行测算的过程中,通过构建包含中美利差的人民币汇率行为均衡汇率模型,指出了中美利差在长期将导致人民币贬值而在短期内会带来升值压力,因此如外商直接投资这类的长期资本流动和利差带来的短期套利资本对人民币汇率的长期变动趋势都有显著影响。
另一方面,房地产作为一项重要的投资资产,吸引国内外逐利资本的流入,在开放经济条件下,一国房价与国际资本的流动有着密切联系。国外学者通过对某些国家的经验进行观察以及研究分析,发现经历过房地产市场繁荣的国家都经历了资本流入的现象(S. Ludvigson et al., 2010)。Jansen (2003)分析了1998年金融危机之前,流入泰国的非FDI国际资本对股价和房价的影响,并认为其对房价的影响比对股价的影响更为显著。Kohli(2001)则以印度为例进行了相关研究,得到了境外资本与国内价格存在高度相关性的结论。类似的文献还包括Gete(2009)、Laibson and Mollerstrom (2010)以及Ferrero(2011)。国内研究方面,宋勃、高波(2007)利用1998-2006年的季度数据分析认为我国房价的上涨在短期内吸引外资流入,同时外资流入在长期对我国的住房价格产生影响。孟晓宏、李春吉(2006)指出国际资本通过直接途径和间接途径影响房地产价格,且长期而言其波动会影响房价的波动。刘莉亚(2008)构建了一个包含了热钱与资产价格的内生关系的理论模型,并进行实证研究,得到了热钱流入会显著抬高住宅价格,尤其是豪华住宅价格的结论。
最后,通过同时对汇率、资产价格以及国际资本流动建立联系,许多学者针对股价作为资产价格的代表做了以下研究,Hau and Rey(2005)建立了一个不完全外汇风险交易市场下的均衡模型,以研究汇率、股价以及资本流动如何被同时决定。国内学者则采用不同研究方法验证了汇率与股价通过资本流动这一桥梁产生了相互影响(张谊浩、沈晓华,2008;朱孟楠、刘林,2010;吴丽华、傅广敏, 2014)。以房价为资产价格代表的研究则相对较少,李芳、李秋娟(2014)基于2005-2012年月度数据采用MS-VAR模型对人民币汇率、短期国际资本流动与房地产价格进行了实证研究,文章结果表明在不同的经济状态下,三个变量之间存在不一样的动态关系,两区制下人民币升值与房价上涨之间存在双边促进的关系。袁东等(2015)利用了45个国家的面板数据研究实际有效汇率对房价的影响,其研究结果表明人民币实际有效汇率上升能够解释13%-25%的2005-2014年间我国房价的上涨。
已有的文献对于资产价格、短期国际资本流动以及人民币汇率的相关关系的研究取得了丰富的成果,大部分研究认为资产价格上涨、国际资本流入以及人民币升值存在相互促进的关系。然而已有模型多以股票价格作为资产价格的代表,对房地产价格的研究较少。在以房价为主要研究对象的文章之中,又少有对2015年“811汇改”后人民币贬值加剧以及国际资本流出情况的讨论。基于已有研究基础,本文建立一个带有时变参数的向量自回归模型,在汇率贬值以及资本流出的背景下,研究人民币汇率、短期国际流动与房价之间的动态关系。随着对外开放程度的逐步加大,资本管制的放松促进国际资本流动,从而加剧国内资产价格与汇率波动。金融周期上半场国际资本流入增加,房地产价格与汇率均受到来自国际资本的需求增加从而加大上涨幅度,下半场则呈相反表现,由此本文认为资本管制的放松(国际资本流动规模增加)具有金融顺周期性。本文的边际贡献包括:第一,在方法上本文通过构建一个包含人民币汇率、短期国际资本流动以及房价的理论模型,采用带有随机波动的时变参数向量自回归模型进行实证分析。引入随机性与时变性之后,本文发现人民币汇率、短期国际资本流动以及房价三者之间的影响关系并非单一不变的,在不同时代背景与政策影响下,三者互动关系有所不同;第二,在研究对象方面,本文加入了2015年“811汇改”后的数据,考察了“811汇改”对“房价-国际资本-汇率”关系的结构性影响;第三,在研究角度上,本文从金融周期的角度出发,考察了国际资本流动的金融顺周期性,即国际资本流动加剧房价与汇率的波动幅度,也是在房价与信贷相互促进的周期性阶段,国际资本流动对国内资产价格与汇率波动带来边际影响的研究。
二、理论模型本文的理论分析部分将房价、短期国际资本流动以及汇率三个变量置于同一个动态系统。首先考虑国际资本基于套汇以及套价动机在国家间流动,其次通过国际资本流动这一桥梁建立外汇市场和房地产市场的联系。其中,由于房地产既具有消费属性又具有投资属性的特殊性,本文在模型中假定其对于国外投资者而言不具消费属性。
本文在理论分析以及接下来的实证检验中均以“热钱”代替短期国际资本①,假设在套价动机驱使下,热钱主要受到以房地产为代表的资产吸引,因此本文提出以下模型:
① 本文认为影响汇率与房价之间相关性的短期国际资本主要为短期投机性资本,亦即通常所指的“热钱”。
| $ c{f_t} = {a_t} + {\beta _t}\left({e_{_t}^{^e} - {e_t}} \right) + {\gamma _t}\left({h_{_t}^{^e} - {h_t}} \right) $ | (1) |
其中,cft为热钱流动的对数值,at表示常数项,反映影响热钱流动的其他因素,et和ht分别表示即期汇率和房价,ete和hte分别为对数预期汇率和对数房价(对数化变量对应的大写字母表示变量值,分别以Et、Ete和Ht、Hte表示人民币即期汇率和预期汇率以及房价和房价预期, CFt表示热钱流动值)。βt和γt为参数,分别表示投资者对房价和汇率的预期值与实际值之差对热钱流动的影响程度。其中,由于汇率以直接标价法表示,故其数值的增大表示币值的下降,若ete < et,表明投资者预期人民币将升值,资本流入加大,因此βt < 0。
在房地产市场方面,借鉴价格调整函数的假设,本部分假设对数房地产价格的变化可以表达如下(假定房屋供给不变):
| $ {h_{t + 1}} = {h_t} + \alpha \left({D_{_t}^{^H} + D_{_t}^{^F}} \right), \alpha > 0 $ | (2) |
α为价格调整系数,DtH和DtF分别为国内投资者和国外投资者对房地产的需求,且本文假设国内投资者对房地产的需求出于消费性需求和投资性需求两方面,而国外投资者对房地产的需求仅出于投资性需求。国内投资者对房地产的需求表达为:
| $ D_{_t}^{^H} = D_{_t}^{^{H, C}} + D_{_t}^{^{H, I}} $ | (3) |
由于本文主要考虑房地产作为投资资产对于热钱流动的影响,此处不对国内投资者的消费性需求进行展开讨论,简单假设其占总消费的比例固定为μ,根据已有文献对汇率以及居民消费等宏观经济变量的检验研究,本文假定居民消费与汇率呈正相关关系:
| $ D_{_t}^{^{H, C}} = \mu {C_t}\left({{e_t}} \right), {C'}_t\left({{e_t}} \right) < 0 $ | (4) |
另一方面国内外投资者对房地产的投资性需求也受不同因素影响,假设国内投资者对房地产的投资性需求取决于对房价的预期,而国外投资者还需考虑汇率风险,二者分别表述如下:
| $ D_{_t}^{^{H, I}} = a\left({h_{_t}^{^e} - {h_t}} \right), a > 0 $ | (5) |
| $ D_{_t}^{^F} = b\left({e_{_t}^{^e} - {e_t}} \right) + c\left({h_{_t}^{^e} - {h_t}} \right), b < 0, c > 0 $ | (6) |
a、b、c分别为反应参数。故房价变动函数可以表示为:
| $ {h_{t + 1}} = {h_t} + \alpha [\mu {C_t}\left({{e_t}} \right) + \left({a + c} \right)\left({h_{_t}^{^e} - {h_t}} \right) + b\left({e_{_t}^{^e} - {e_t}} \right)] $ | (7) |
借鉴吴丽华等(2014)对短期资本流入流出股市比例随时间变化而改变的假设,本文同样假设热钱流动进入和离开房地产市场的比例具有时变性,若资本流入为正值,则:
| $ {H_t}D_{_t}^{^F} = {H_{t - 1}}D_{_{t - 1}}^{^F} + {\delta _t}exp(C{F_t}) $ | (8) |
外汇市场方面,根据Dieci and Westerhoff (2010),外汇市场本币的超额需求主要来源于国外股票投资者和外汇投资者的货币需求。本文根据我国热钱流入情况对上述描述进行修改,认为本币的超额需求一方面取决于外汇投资者,另一方面取决于国外投资者,而不仅仅是股票投资者。此处假设国外投资者中有占比为νt的是股票投资者,记其对本币需求为StF,(1-νt)比例的房地产投资者对本币需求为DtF。因此,在t时刻汇率可表达为:
| $ {e_{t + 1}} = {e_t} - \eta \left[ {{\nu _t}{P_t}S_{_t}^{^F} + \left({1 - {\nu _t}} \right){H_t}D_{_t}^{^F}} \right], \eta > 0 $ | (9) |
其中,η为反应参数,Pt为本国t期时的股价。
通过简单运算,可以得到短期资本对汇率、房价的影响以及汇率与房价之间的相互影响系数。
将(1)、(5)、(6)和(8)式代入(2)式可得:
| $ \begin{array}{l} {h_{t + 1}} = {h_t} + \alpha [D_{_t}^{^F} + 1/{H_t}\left({{H_{t - 1}}D_{_{t - 1}}^{^F} + {\delta _t}{\rm{exp}}\left({c{f_t}} \right)} \right)] = {h_t} + \alpha [\mu {C_t}\left({{e_t}} \right) + a\left({h_{_t}^{^e} - {h_t}} \right)\\ \;\;\;\;\; + 1/{H_t}\left({{H_{t - 1}}D_{_{t - 1}}^{^F} + {\delta _t}{\rm{exp}}\left({{a_t} + {\beta _t}\left({e_{_t}^{^e} - {e_t}} \right) + {\gamma _t}(h_{_t}^{^e} - {h_t})} \right)} \right)] \end{array} $ | (10) |
将(1)式和(8)式代入(9)式可得:
| $ \begin{array}{l} {e_{t + 1}} = {e_t} - {\eta _t}\left({{\nu _t}{P_t}S_{_t}^{^F} + \left({1 - {\nu _t}} \right)\left({{H_{t - 1}}D_{_{t - 1}}^{^F} + {\delta _t}{\rm{exp}}\left({c{f_t}} \right)} \right)} \right] = {e_t}\\ ~~~~~- {\eta _t}[{\nu _t}{P_t}S_{_t}^{^F} + \left({1 - {\nu _t}} \right)({H_{t - 1}}D_{_{t - 1}}^{^F} + {\delta _t}{\rm{exp}}({a_t} + {\beta _t}\left({e_{_t}^{^e} - {e_t}} \right) + {\gamma _t}(h_{_t}^{^e} - {h_t})))] \end{array} $ | (11) |
从(10)式和(11)式可通过计算分别得出三个变量的相互作用关系,其中汇率和房价对热钱流动的影响已于国际资本流动模型(1)式中给出。
从(10)式可得到热钱流动和汇率分别对房价的影响弹性:
| $ 热钱对房价的影响弹性系数为:d~{h_{t + 1}}/d\;c{f_t} = \alpha {\delta _t}{\rm{exp}}\left({c{f_t}} \right)/{H_t} $ | (12) |
| $ 汇率对房价的影响弹性系数为:d\;{h_{t + 1}}/d\;{e_t} = \alpha \mu C{'_t}\left({{e_t}} \right) - \alpha {\delta _t}{\beta _t}{\rm{exp}}\left({c{f_t}} \right)/{H_t} $ | (13) |
从(11)式可得到热钱流动和房价分别对汇率的影响弹性:
| $ 热钱对汇率的影响弹性系数为:d\;{e_{t + 1}}/d\;c{f_t} = - \eta \left({1 - {\nu _t}} \right){\delta _t}{\rm{exp}}\left({c{f_t}} \right) $ | (14) |
| $ 房价对汇率的影响弹性系数为:d\;{e_{t + 1}}/d\;{h_t} = \eta \left({1 - {\nu _t}} \right){\delta _t}{\gamma _t}{\rm{exp}}\left({c{f_t}} \right) $ | (15) |
由前面对反应参数的假定可知α>0, η>0, 同时在假设不存在资产泡沫以及外汇市场系统风险的情况下,可以认为βt < 0, γt>0, 因此以上四种影响弹性系数除汇率对房价的影响外,其余三者均取决于参数δt。如果δt < 0, 即在短期国际资本流入为正的情况下,国外投资者持有的房地产资产减少了,说明国际资本持有者在看好国内经济状况(或预期汇率上升)的情况下将资本注入如股票市场等其他资本市场里,也因此使得原本持有国内房地产资本的一部分国际投资者将资本转投至其他资本市场。换而言之,国际资本的流入并非受到房地产市场吸引而来,此时在国际资本流入股市等其他资本市场的带动下,房地产市场甚至可能出现资本流出的情形。在此情形下,房价与汇率的正相关性程度也出现下降。反之,只有当国际资本对房地产行业持有乐观态度的时期,热钱大量涌入房地产市场,国际资本的流入加大房价与汇率的正相关性。由(13)式可以看出,汇率对房价的影响取决于两个方面,一方面为汇率上升对居民整体消费的促进作用,一方面为汇率通过热钱对房价的影响。仅当δt < 0,且负的足够大时,汇率与房价呈数值上的正向关系,亦即人民币升值导致房价下跌。从金融周期角度来看,周期上半场,房价由于与银行信贷相互促进不断上涨,房地产行业的预期投资回报较高,受上半场货币升值预期驱动而流入的国际资本投向房地产市场,使得原本就处在上升通道的房地产价格进一步上涨,仍处于获利状态的国际资本带来羊群效应吸引更多国际资本流入,汇率上升压力增加。反映在模型中即δt表现为正,国际资本流入促进房价与汇率上升,房价与汇率表现出的正相关性在国际资本的作用下被加强,国际资本流动具有金融顺周期性。
三、时变参数向量自回归模型向量自回归模型(简称VAR模型),已经被广泛应用至多个内生变量动态关系的估计之中,是自回归模型(AR模型)向多个变量的拓展。作为一个静态模型,VAR模型假定其参数固定,从而降低了对经济变量之间存在的不稳定长期均衡关系的解释力(易晓薇,2015)。时变参数向量自回归模型(简称为TVP-VAR)的提出对解决这一问题起到了极为重要的作用,为研究具有时变特性的经济变量间相关性提供了有力工具①。本文的这一部分将简要介绍TVP-VAR模型以及其参数的分布假设。
① TVP-VAR模型被广泛运用于检验经济变量相关性的时变特性研究中,如陈宗义(2012)、齐红倩、席旭文(2015)、徐宁等(2017)等文献。
(一) VAR模型记yt为一个m*1维列向量,Γt-1=(yt-1, yt-2, …)为包含(t-1)期在内的之前所有期的t期信息集。VAR模型假定yt的条件期望仅与有限期过去的信息相关:
| $ E({y_t}\left| {{\Gamma _{t - 1}}) = E({y_t}} \right|{y_{t - 1}}, {y_{t - 2}}, \cdots, {y_{t - k}}) $ | (16) |
进一步地,线性VAR模型则假定yt条件期望与其有限个滞后项线性相关:
| $ E\left({{y_t}|{\Gamma _{t - 1}}} \right) = {a_0} + {A_1}{y_{t - 1}} + {A_2}{y_{t - 2}} + \cdots + {A_k}{y_{t - k}} $ | (17) |
Ai是m*m维的系数矩阵。定义误差项为et=ytE(yt|Γt-1), 我们可以得到VAR模型如下:
| $ {y_t} = {A_1}{y_{t - 1}} + {A_2}{y_{t - 2}} + \cdots + {A_k}{y_{t - k}} + {e_t} $ | (18) |
| $ E\left({{e_t}|{\Gamma _{t - 1}}} \right) = 0, E\left({{e_t}e{'_t}} \right) = \Sigma $ | (19) |
尽管VAR模型中存在着变量的不同阶滞后项,但是没有包括变量的当期联系,因此VAR模型被认为是对数据相关性的描述性检验,而缺乏了对变量间结构性关系的体现。另一方面,VAR模型的误差项通常存在自相关问题,而我们希望得到相互正交的冲击。结构向量自回归模型(SVAR模型)的提出解决了这一问题。
(二) SVAR模型SVAR模型中引入了变量间的当期相互作用:
| $ A{y_t} = {C_1}{y_{t - 1}} + {C_2}{y_{t - 2}} + \cdots + {C_k}{y_{t - k}} + B{u_t} $ | (20) |
其中,假设et=But, E(utu′t) =I。此时,我们需要估计的参数变为了A、B以及Ci。为使参数可被识别,通过Cholesky分解,我们假设A为一个下三角矩阵,而B=Σ。因此模型(20)可被改下为如下的简化式VAR模型:
| $ {y_t} = {B_1}{y_{t - 1}} + {B_2}{y_{t - 2}} + \cdots + {B_k}{y_{t - k}} + {A^{ - 1}}\Sigma {u_t}, {u_t} \sim N(0, {I_m}) $ | (21) |
其中,Bi=A-1Ci, i=1, …, k, Σ=diag(σ1, …, σm)。
进一步地,将Bi的行向量元素堆叠起来形成一个m2k*1维的列向量, 记为β, 另外记Xt=Im⊗(y′t-1, …, y′t-k), 则模型(21)可以被表示为:
| $ {y_t} = {X_t}\beta + {A^{ - 1}}\Sigma {u_t} $ | (22) |
相较于SVAR模型而言,TVP-VAR模型将非时变的参数假设为具有时变性。模型表达为:
| $ {y_t} = {X_t}{\beta _t} + A_{_t}^{^{ - 1}}{\Sigma _t}{u_t} $ | (23) |
参考Primiceri(2005),将At矩阵的下三角部分中元素进行堆叠,记为at,记hit=lnσit2, i=1, …, m, ht=(h1t, …, hmt)′, t=1, …, k+1。另外假设各个参数都服从随机游走: βt+1=βt+μβt,at+1=at+μat, ht+1=ht+μht, 且满足:
| $ \left({\begin{array}{*{20}{c}} {{\varepsilon _t}}\\ {{\mu _{\beta_t} }}\\ {{\mu _{a_t}}}\\ {{\mu _{h_t}}} \end{array}} \right) \sim N\left({0, \left({\begin{array}{*{20}{c}} I&0&0&0\\ 0&{{\Sigma _\beta }}&0&0\\ 0&0&{{\Sigma _a}}&0\\ 0&0&0&{{\Sigma _h}} \end{array}} \right)} \right) $ | (24) |
假设初值服从βk+1~N(μβ0, Σβ0), ak+1~N(μa0, Σa0), hk+1~N(μh0, Σh0), Σβ、Σa和Σh均为对角矩阵,随机扰动在不同参数间不相关。
(四) MCMC估计方法根据已有文献中TVP-VAR模型的应用,本文采用马尔科夫蒙特卡洛(MCMC)估计方法对参数进行估计。该算法的基本逻辑为首先通过先验分布初始化参数,然后通过MCMC方法抽取后验分布,估计参数的后验条件概率,最后进行时变脉冲响应分析。
参照Nakajima(2011),本文对参数初值赋值如下:
① 由于参数先验分布的设定带有一定主观性,本文对初值的赋值主要参照已有文献,包括Nakajima(2011)、Primiceri(2005)等,国内文献中也采取了类似的取值方法,如杨冬、张月红(2014)、刘一楠(2017)等。其中IW分布指的是Inverse Wishart分布。
四、数据选取与实证结果 (一) 数据选取为考察热钱流动对处在金融周期内的房价与汇率的相关性的影响,本文选取2005年8月至2016年12月为样本期,这一样本期内包含了2005年人民币汇改后人民币对美元名义汇率的长期上升时期以及2015年“811”汇改期间的下跌时期,是对三者动态关系的检验。汇率方面,由于国际投资者通常通过观测货币的名义汇率作为其产生升值或贬值预期的依据,故本文采取人民币兑美元汇率(直接标价法)作为汇率的样本数据,在下文中用cny表示,数据来源于外汇管理局。热钱的估算方面,本文利用公式:热钱=外汇储备增加量-外商直接投资金额-贸易顺差金额,其中等式右边的三个变量均可由wind数据库得到月度数据,通过公式计算即可得热钱的月度估计值,用hm表示。房价方面,本文选取70个大中城市新建住宅价格指数作为房价的代理变量,用hpi表示。三个变量中,热钱流动值为流量概念,而汇率和房价属于价格表现,难以界定其为流量或是存量概念。已有文献通过对短期资本流动量进行累积转化为存量概念,然后将三者取对数以解决可比性问题。然而本文选取的样本期包括了一段热钱流入为负值的时期,因此无法通过累积取对数进行处理。本文采取将汇率和房价通过差分方式,将二者转换为流量概念,然后降低计算所得热钱的数量级,本文将数值除以100,最后对三者进行比较研究。
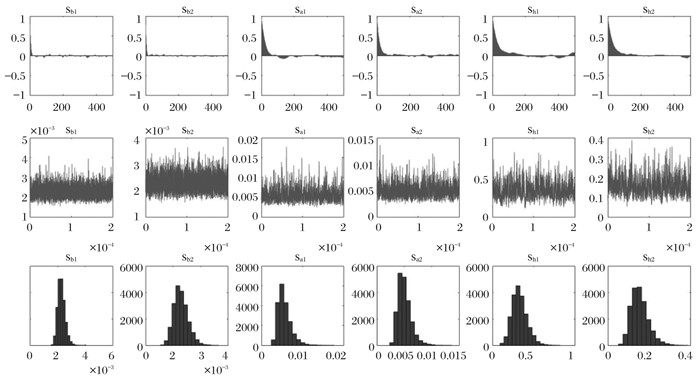
(二) 参数估计结果将TVP-VAR模型中的变量顺序定为房价、热钱、汇率,设定滞后期为2,MCMC抽样次数为20000,并剔除前2000次为预烧样本①。参数估计结果如下:由表 1可知,在5%的置信水平下,Geweke统计量均大于0.1,不能拒绝原假设,即马尔科夫链趋于集中,非有效因子均低于60,说明参数估计显著有效。图 1则包括了样本自相关函数、样本取值路径和后验分布密度函数。其中sb1、sb2、sa1、sa2、sh1、sh2分别对应矩阵Σβ、Σa和Σh的第一、二个对角元素。
① 本文实证检验部分根据Nakajima (2011)提供的Matlab代码进行修改,对模型进行处理。
| 表 1 参数估计结果 |
|
图 1 参数估计结果 |
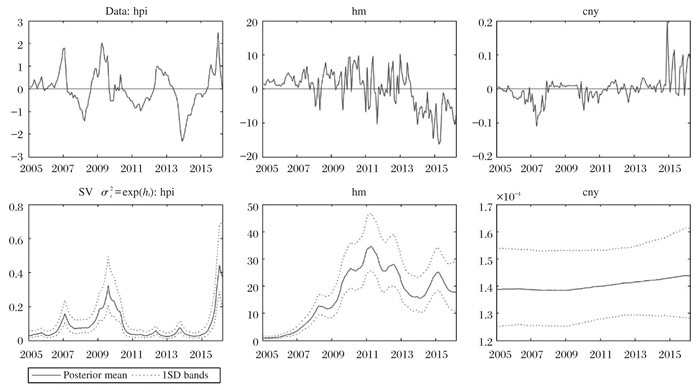
TVP-VAR模型通过设定时变参数与随机扰动得到房价变动量、热钱流动值以及汇率变动量的随机后验波动率。由图 2 ②所示,人民币兑美元汇率的变动量在样本期内波动性稳定,而房价变动量和热钱流动则分别出现了不一样的时变性。房价变动量的波动率在2009年末至2010年初达到一个峰值随后下降至2015年,之后波动率迅速提高,与此相对应的,房价分别对应了一段上涨期、平稳期以及下跌期。热钱流动的波动率则从样本初期开始小幅波动上涨至2011年中旬,随之出现下降,在2015年“ ‘811汇改’”时期达到第二个峰值。
|
图 2 数据变动及后验随机波动率 |
② 实证结果图 2、3、4中的时间横轴上,每个坐标点代表的是各年的6月。
|
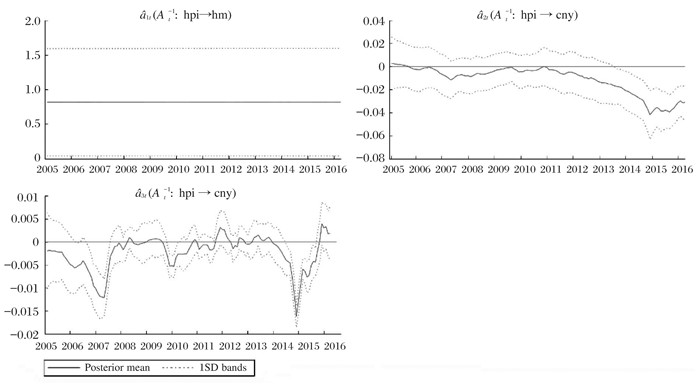
图 3 变量间时变影响系数 |
|
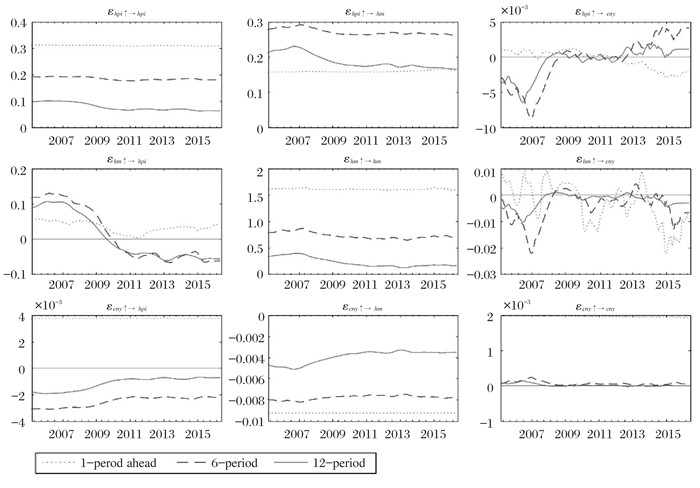
图 4 不同提前期形成的脉冲响应 |
图 3反映的是房价变动量、热钱流动量与人民币兑美元汇率变动量之间的系数随时间变动的特征。从第一个子图可以观察到,房价变动对热钱的影响保持稳定。第二个子图表明房价变动量对人民币汇率变动的影响在2011年8月之前较为稳定,且保持在接近0轴的下方(2007年初至2009年期间系数绝对值较大),而在此之后,这一影响系数的绝对值显著增大且保持为负值。这说明在2011年8月之后,房价对促进人民币汇率上升的影响程度越来越大。最后,从第三个子图中,我们可以观察到在样本期内,热钱流动量对人民币汇率变动的影响系数波动十分剧烈,其随时间的变化可以分为三个阶段,时间节点分别出现在2008年10月和2014年1月。在2005年8月到2008年10月期间以及2014年1月至2016年下半年之间(亦即第一、三阶段)影响系数明显为负,且在2007年底以及2015年中表现出最大的影响程度。而在中间阶段该影响系数保持在0值附近波动,影响系数的变化进入一个稳定期。
对比图 3中的三个子图可以发现,房价与人民币汇率之间通过热钱流动作为桥梁变量产生相互影响主要发生在2007年6月至2008年6月以及2014年6月至2015年6月期间。又结合样本数据可知,这两段时期内分别表现为人民币升值放缓-热钱流出-房价下跌以及人民币贬值-热钱流出-房价下跌。国际资本流动对房价与汇率相关性的影响在房价与汇率下降通道中更为显著,尽管目前难以将2007年6月-2008年6月以及2014年6月-2015年6月两段时期认定为金融周期的下半场(金融周期通常较经济周期更长,一个金融周期可能包含几个经济周期①),根据数据以及实证检验结果,本文认为就我国情况而言,短期国际资本的净流入对房价与汇率相关性的影响并不显著,亦即短期国际资本的流入并非导致房价上涨与汇率上升相互促进的主要因素,国际资本的顺周期性表现较弱;然而在短期国际资本净流出时期,房价与汇率的相关性受其影响增强,国际资本的顺周期性表现较强。对这一现象的解释也较为直观,具有逐利性的国际资本在全球范围内寻求投资回报高的货币及其计价的资产,短期国际资本的投机性又决定其对资产预期回报的敏感,因此对我国资产价格(房价和汇率)而言,受国际资本流出驱动下跌较受其流入的影响更大。表现在图 3中,即为房价、热钱与汇率的动态相关性在资本流入时期表现不显著,而在流出时期较为显著,国际资本流动带来的顺周期性呈现出不对称性。
① 参见彭文生,《渐行渐近的金融周期》第16页,导论第四节。
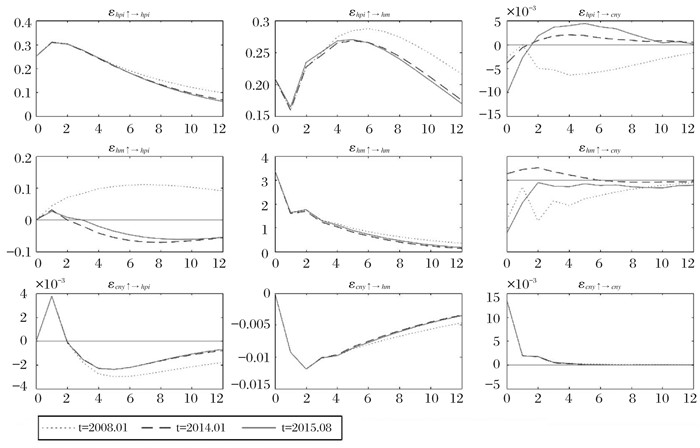
(四) 时变脉冲响应分析相较于VAR模型,TVP-VAR模型提供了具有随机时变特征的脉冲响应分析,参考Nakajima (2011),本文给出两种类型的脉冲响应分析,一种是不同提前期下的一单位标准正向冲击形成的脉冲响应,本文分别选取提前1个月、6个月以及一年;另一种是在不同时间点上产生的脉冲响应,本文选取了2008年1月、2014年1月以及2015年8月三个时间点,这三个时间分别对应了人民币汇率变动量最小、人民币汇率数值最小(币值最高)和汇率波动水平最高的时期,同时也与前一部分中的分析保持一致性。图 4反映了不同时间点上一单位标准正向冲击所产生的一个月、半年和一年滞后期的脉冲响应。图 4中的九个子图,分别体现了三个变量的正向冲击分别对其他变量产生怎样的滞后影响。
房价变动冲击对热钱流动产生的不同期滞后影响均为正值,且变动幅度较小。其中提前一个月产生的正向冲击带来的影响在不同时间基本保持一致,而提前半年和一年的正向冲击均在2005年8月至2007年8月之前有着相对较大且保持上升趋势的影响,随后两个不同期滞后影响小幅下降。房价变动的正向冲击对人民币汇率变动的不同期滞后影响出现了一定程度的差异,在提前一期的脉冲响应中,这一影响较小且保持相对稳定。在提前半年的脉冲响应中,房价变动的正向冲击在2009年6月之前都对汇率变动产生负向影响,且该负向影响在2007年8月达到最大,2009年6月之后一直在0值附近波动同时多数时期表现为负向影响,在2015年初再次出现增大的负向影响。这说明房价变动的正向冲击对半年后的汇率通常表现出了促进上升的影响,而这一影响程度在不同时期表现不同。提前一年的房价变动正向冲击有着与提前半年相似的走势,但是影响程度较小。
热钱流动的正向冲击对房价变动所产生的不同滞后期的影响也出现了较大程度的不同。其中,滞后一期的影响随时间变动较小,且均为正值。而滞后半年和一年的脉冲响应表现出了极高的相似性,二者均在2010年上半年之前表现为正值,之后表现为负。另一方面,汇率变动量对热钱流动的脉冲响应存在着不同的时滞性和波动性,其滞后一期的影响程度在不同时期差异很大,表现为一段时期为正值而一段时期为负值,而滞后半年的影响则大部分时间表现为负值,影响程度最大时期为2007年6月,滞后一年的影响程度总体较小,且波动较小。值得注意的是,本文因采取了差分法将汇率变为流量概念,故出现了对热钱流动的非正脉冲响应。
人民币汇率变动的正向冲击对房价变动量的不同滞后期脉冲响应同样出现了不一样的表现,滞后一期的脉冲响应表现为正而滞后半年和一年的脉冲响应则均表现为负,而影响程度上滞后一期的脉冲影响最大,滞后半年的影响其次,滞后一年的影响程度约为滞后半年期影响的一半。另一方面,热钱流动对人民币汇率变动冲击的滞后响应均为负值,且影响程度随滞后时间延迟而变小,汇率冲击带来的滞后一期响应程度最大,滞后一年的影响大大减小,且在2007年后这一影响进一步减弱。
由图 5可见,当模型在不同时间点施加相同的冲击时,大部分脉冲响应的变动趋势保持一致,但仍有几个子图展示了脉冲响应在不同时间节点的分化,类似地可以对三个变量的正向冲击所产生的脉冲响应作出以下分析:房价变动正向冲击的脉冲响应方面,热钱流动对房价变动正向冲击在不同时间的脉冲响应均表现为当期就产生正的影响,接着该正向脉冲响应在第一期出现一个下降后逐渐上升直到第五期或第六期达到最大(2008年1月的最大影响为第六期,且程度较大),随后逐渐减少。同样的,人民币汇率变动也在当期就对房价变动产生反应,表现为负向影响,然而在2015年8月这一影响较其他两个时间点程度更深,本文认为这与“811汇改”这一外生因素不无关系。“811汇改”使得人民币释放了大量的贬值压力,此时房价变动的正向冲击在短期内缓解了贬值压力,但是长期而言难以扭转人民币贬值预期。这也体现在不同时点脉冲响应的另一个不同之处--冲击发生第二期后,2008年1月的脉冲影响保持为负且程度加深,而2014年1月以及2015年8月所产生的脉冲影响转负为正,与图 4中房价下跌、热钱流出以及汇率贬值现象相对应。
|
图 5 不同时期产生的脉冲响应 |
热钱流动正向冲击的脉冲响应方面,房价变动对热钱流动在三个时间点上产生的正向冲击有着不一样的脉冲响应,其中在2008年1月,热钱流入的增加从第一期开始对房价的变动量产生正的影响,并随后逐渐加大,在后续的12期内都保持相对稳定的正向影响。而在2014年1月以及2015年8月,热钱的正向冲击都只在第一期产生一个较小的正向影响,随之转而为负,这说明在这两个时间点流入我国的短期国际资本较少进入到房地产行业,对应当时我国的资本流出情况,甚至可能是我国房地产行业的出现资本外流现象。不得否认的是,这与我国对房地市场的调控也有关系(信贷的作用),而短期内热钱流动又起着“推波助澜”的作用。人民币汇率的变动也对热钱流动产生了不同时间点上不一样的脉冲响应,其中2008年1月和2015年8月这两个时间点上所产生的脉冲响应均为负值,2008年的响应在当期达到最大值,随后出现了在下一期减弱而在第二期加强的现象,2015年的响应也在当期达到最大随后逐渐变小,并在第二期就几乎变为零。而在2014年1月产生的脉冲响应则出现了相反的结果,这一时期的热钱流动正向冲击在当期使得汇率变动出现了正向反应,尽管程度较小但是持续到第六期才消失,与这一时期人民币汇率表现为触顶下降的现象相一致。
最后,在讨论人民币汇率变动的正向冲击带来的脉冲响应时可以发现,在三个不同时间点上所产生的响应表现出极高的相似性。其中,房价变动在当期不对人民币汇率变动的冲击产生反应,而是在第一期出现一个正的影响又在第二期回落为零,随后一直保持一个负向的脉冲响应。热钱流动方面同样的在第一期不产生反应,而后出现一个一直为负的脉冲响应,且在第二期达到最大值。
五、结论与政策建议本文在人民币两次汇改的背景下,通过理论和实证两个部分研究了人民币汇率、热钱流动与中国房价之间的动态关系。理论部分,本文通过结合国际资本流动模型与房市汇市联动模型建立了一个包含我国房价、热钱与人民币汇率的动态系统;实证检验部分,本文采用了带有时变参数的向量自回归模型以检验不同时代背景下三者之间的动态关系有何变化。基于两个部分的研究,本文得到以下结论:
首先,通过理论部分的分析可知,国际资本流动具有金融顺周期性:房价可以通过短期国际资本流动作为桥梁变量与人民币汇率建立联系。在我国国际资本净流入的情况下,只有当国际资本流向了房地产市场时,其作为桥梁变量产生顺周期性,加大房价与汇率的相关性。相反,若进入国内的国际资本不选择房地产市场作为投资标的,此时顺周期性则体现得不显著。反之,在我国国际资本净流入的情况下,汇率相应出现下跌,此时若国际资本从房地产市场流出,房价下跌,国际资本顺周期性得以体现。因此,国际资本的流向与其投资标的资产对其顺周期性均有影响,即对房价与汇率的相关性的影响有所不同。
然后,通过实证检验可知,国际资本流动具有的金融周期性呈现不对称性特点:国际资本流出时期,房价与汇率二者的相关性受到显著影响,相关性增强;而国际资本流入时期二者相关性受国际资本影响不显著。由中TVP-VAR模型给出的时变系数结果可知,人民币汇率和我国房价通过热钱流动为桥梁建立联系主要发生在两个时期:2007年1月至2008年1月以及2014年6月至2015年6月。2005年人民币汇改后,人民币长期累积的升值压力得以释放,大量国际资本涌入我国,热钱基于套汇动机在外汇市场换取人民币,同时基于套价动机对我国重要资产进行投资,然而热钱的流向却不得而知。结合我国房地产市场的系列改革来看,2005年以来正是其向着市场化进程中的重要时期,为热钱成功涌入房地产市场提供有利条件。然而本文的实证结果没有给出显著的汇率上升-热钱流入-房价上涨的结论,反而是在2007年1月至2008年1月期间,我国房价与人民币汇率之间由于热钱的流出产生了相互加强的作用机制,这一时期由于次贷危机的发生,全球流动性紧缩造成的我国国际资本流出,我国房价受到影响出现下跌,人民币汇率也在这一时期出现升值速度放缓。汇率下降-热钱流出-房价下降的影响机制再次出现在2014年6月至2015年6月,由于美国的加息政策与美元升值,人民币相应贬值,国际资本流出我国。
最后,通过模型提供的不同时期脉冲响应分析可知,在模型提供的三个脉冲响应时点上,不同变量的正向冲击所产生的脉冲响应大部分保持趋势一致,也有个别脉冲响应函数出现了一定程度的分化。值得提出的是2015年8月时所产生的热钱正向冲击不再促使房价变动的正向增加,这一方面与热钱的长时期大量流出压力有关,另一方面也与热钱对我国房地产行业影响程度下降有关。结合房地产市场的整体发展历程来看,房市发展初期吸引国际资本涌入后,对国内资本产生羊群效应,房地产市场的蓬勃发展更多地受益于国内流动性和信贷环境的宽松。因此,在2015年“811汇改”释放了大量人民币贬值压力所导致的资本流出情行下,房价也未出现下跌。
本文认为出现上述不对称性的原因包括以下几点:在房价上涨与汇率上升时期,国际资本流入我国,而国际资本的流入通常伴随着国内的无风险偏好下降、风险资产配置上升,同时叠加土地财政、城市化进程等社会经济因素,国内流动性因素是决定房价上涨的主要动力,故在资本流入期内人民币汇率与房价的相互影响作用较小,国际资本并没有成为推动房价与汇率进一步上升的催化剂,房价更多的在金融周期上半场中受信贷规模扩张影响而被抬高,国际资本产生的顺周期性较小;而在汇率贬值预期加大、同时房地产市场受调控时期(房价上涨乏力),短期国际资本的投机性决定其敏感度较高、流出压力较大,国际流动性冲击将通过直接影响与加速影响(间接影响)两种渠道导致汇率与资产价格的下跌通道:从直接影响看,国际资本流出加大了人民币贬值预期,同时资本流出降低了国内流动性水平,打击投资者对人民币资产的信心,导致房价下降;间接影响方面,人民币贬值与房价下降存在显著的相互加速与相互强化机制,一方面,人民币贬值预期的强化进一步打击了国际资本的流入,投资者对人民币资产的需求减少,资产价格下降,另一方面,资产价格下降可能通过信贷抵押约束与金融加速器两种渠道导致企业海外融资利率上升,进一步降低流动性水平,促进汇率贬值。此时国际资本产生的顺周期性较大。
基于以上结论,本文提出以下政策建议:
(1) 关注经济周期的同时提高对金融周期的重视。房价与汇率作为重要的资产价格,在金融周期中呈现相关性;
(2) 关注国际资本流动带来的金融顺周期性及其不对称性特征,逐步实现资本项目对外开放。在金融周期上半场,对资本项目开放持较乐观态度,完善市场经济体制的同时吸引国际资本流入以提升经济活跃度和国际影响力,积极主动扩大对外开放程度;
(3) 在金融周期拐点和下半场期间,谨慎把控资本账户对外开放,完善国际资本流动监测预警机制,预防因大规模国际资本流出造成的资产价格暴跌。在周期下半场,房价与汇率均承受下跌压力,由于国际资本流动带来更为显著的顺周期性,有可能造成房价下跌与汇率下降的恶性循环,此时谨慎把控资本账户对外开放与国际资本流动情况对于防范金融危机的出现有着重要意义;
(4) 完善房地产投资资金来源监管机制,保证房地产行业稳定健康发展,防止投机性资本催生房地产业畸形发展,警惕经济脱实向虚的金融风险。
| [] |
邓燊、杨朝军,
2008, “汇率制度改革后中国股市与汇市关系——人民币名义汇率与上证综合指数的实证研究”, 《金融研究》, 第 1 期, 第 29–41 页。 |
| [] |
谷宇、高铁梅、付学文,
2008, “国际资本流动背景下人民币汇率的均衡水平及短期波动”, 《金融研究》, 第 5 期, 第 1–13 页。 |
| [] |
李芳、李秋娟,
2014, “人民币汇率与房地产价格的互动关系——基于2005-2012年月度数据的MS-VAR模型分析”, 《国际金融研究》, 第 3 期, 第 86–96 页。 |
| [] |
刘莉亚,
2008, “境外'热钱'是否推动了股市、房市的上涨?——来自中国市场的证据”, 《金融研究》, 第 10 期, 第 48–70 页。 |
| [] |
孟晓宏、李春吉,
2006, “国际资本流动对我国房地产价格的影响”, 《世界经济与政治论坛》, 第 6 期, 第 27–30 页。 |
| [] |
彭文生,
2017, 《《渐行渐近的金融周期》》. 北京: 中信出版社.
|
| [] |
齐红倩、席旭文,
2015, “资产价格具有通货膨胀指示作用吗——基于LT-TVP-VAR模型的实证研究”, 《南方经济》, 第 10 期, 第 33–48 页。 DOI:10.3969/j.issn.1000-6249.2015.10.003 |
| [] |
曲凤杰,
2005, “人民币汇率改革对资本流动的影响”, 《国际金融研究》, 第 9 期, 第 21–26 页。 |
| [] |
任泽平,
2016, “俄罗斯、日本和东南亚的启示:保房价还是保汇率”, 《股市动态分析》, 第 39 期, 第 16–17 页。 |
| [] |
宋勃、高波,
2007, “国际资本流动对房地产价格的影响——基于我国的实证检验(1998-2006年)”, 《财经问题研究》, 第 3 期, 第 55–61 页。 |
| [] |
王爱俭、沈庆劼,
2007, “人民币汇率与房地产价格的关联性研究”, 《金融研究》, 第 6 期, 第 13–22 页。 |
| [] |
吴丽华、傅广敏,
2014, “人民币汇率、短期资本与股价互动”, 《经济研究》, 第 49 期, 第 72–86 页。 |
| [] |
肖卫国、袁威,
2011, “股票市场、人民币汇率与中国货币需求”, 《金融研究》, 第 4 期, 第 52–64 页。 |
| [] |
徐荣、郭娜、李金鑫、何龄童,
2017, “我国房地产价格波动对系统性金融风险影响的动态机制研究——基于有向无环图的分析”, 《南方经济》, 第 11 期, 第 1–17 页。 |
| [] |
徐宁、刘金全、于洋,
2017, “理解我国名义利率传导机制有效性的时变特征——基于DSGE模型的理论分析与TVP-VAR模型的实证检验”, 《南方经济》, 第 7 期, 第 70–84 页。 |
| [] |
袁东、何秋谷、赵波,
2015, “实际有效汇率、热钱流动与房屋价格——理论与实证”, 《金融研究》, 第 9 期, 第 17–33 页。 |
| [] |
张谊浩、裴平、方先明,
2007, “中国的短期国际资本流入及其动机——基于利率、汇率和价格三重套利模型的实证研究”, 《国际金融研究》, 第 9 期, 第 41–52 页。 |
| [] |
张谊浩、沈晓华,
2007, “人民币升值、股价上涨和热钱流入关系的实证研究”, 《金融研究》, 第 11 期, 第 87–98 页。DOI:10.3969/j.issn.1003-4625.2007.11.028 |
| [] |
张中华,
2007, “汇率、国际资本流动与经济发展”, 《财贸经济》, 第 7 期, 第 73–77 页。 |
| [] |
周虎群、李育林,
2010, “国际金融危机下人民币汇率与股价联动关系研究”, 《国际金融研究》, 第 8 期, 第 69–76 页。 |
| [] |
朱孟楠、刘林,
2010, “短期国际资本流动、汇率与资产价格——基于汇改后数据的实证研究”, 《财贸经济》, 第 5 期, 第 5–13 页。 |
| [] |
朱孟楠、刘林、倪玉娟,
2011, “人民币汇率与我国房地产价格——基于Markov区制转换VAR模型的实证研究”, 《金融研究》, 第 5 期, 第 58–71 页。 |
| [] |
Abelson P., Joyeux R., Milunovich G. and Chung G, 2010, "Explaining House Prices in Australia:1970-2003". Economic Record, 81(s1).
|
| [] |
Bowden R.J., 2004, "McHouse Prices, Capital Hoovering, and Real Exchange Rate Exposures". New Zealand Economic Papers, 38(1), 119–139.
DOI:10.1080/00779950409544397 |
| [] |
Dieci R., Westerhoff F., 2010, "Heterogeneous Speculators, Endogenous Fluctuations and Interacting Markets:A Model of Stock Prices and Exchange Rates". Journal of Economic Dynamics & Control, 34(4), 743–764.
|
| [] |
Ferrero, A., 2011, "House Prices Booms and Current Account Deficits", Unpublished Paper, Federal Reserve Bank of New York.
|
| [] |
Gete, P., 2009, "Housing Markets and Current Account Dynamics", Dissertations & Theses-Gradworks.
|
| [] |
Guo F., Huang Y.S., 2010, "Does 'Hot Money' Drive China's Real Estate and Stock Markets?". International Review of Economics & Finance, 19(3), 452–466.
|
| [] |
Hau H., Rey H., 2006, "Exchange Rates, Equity Prices, and Capital Flows". Review of Financial Studies, 19(1), 273–317.
DOI:10.1093/rfs/hhj008 |
| [] |
Jansen W.J., 2003, "What Do Capital Inflows Do? Dissecting the Transmission Mechanism for Thailand, 1980-1996". Journal of Macroeconomics, 25(4), 457–480.
DOI:10.1016/j.jmacro.2002.06.003 |
| [] |
Kohli R., 2001, "Capital Flows and Their Macroeconomic Effects in India". Social Science Electronic Publishing, 01(192).
|
| [] |
Laibson D., Mollerstrom J., 2010, "Capital Flows, Consumption Booms and Asset Bubbles:A Behavioural Alternative To the Savings Glut Hypothesis". Economic Journal, 120(544), 354–374.
DOI:10.1111/(ISSN)1468-0297 |
| [] |
Nakajima J., 2011, "Time-varying Parameter Var Model with Stochastic Volatility:An Overview of Methodology and Empirical Applications". Jouchi Nakajima, 29, 107–142.
|




