由于招标采购将拍卖的竞争性引入采购环节,降低了采购成本,提高了采购的透明度和公平性,目前已经成为世界上标准化的采购手段,尤其广泛应用于政府采购、工程采购、企业物资等大型采购领域。具体实践中,招标机制种类繁多,最常见的方法为低价中标法①:潜在的供应商同时提交给招标方投标价格,投标价格最低者中标。但在实际履约过程中,常因设计变动、原材料价格浮动、天气变化等原因造成成本的不确定性,中标人在提交投标价格时如未考虑到这些成本变动风险,或因竞争激烈导致中标人在投标时低估了标的物的实际发生成本,则可产生“赢者诅咒”现象(Kagel and Levin, 2009)。“赢者诅咒”现象在实际生产生活和行为学实验中广泛存在(Crawford and Iriberri, 2007),可能会造成中标人无法完成合同、延期完成合同或低质量完成合同等不良风险,不但给中标人造成经济损失,也会给招标人带来巨大损害。
① 即密封第一价格低价中标法。
为解决该问题,现实中提出了很多其他招标采购机制,主要包括竞争性谈判、多属性逆向拍卖法与均价中标法。竞争性谈判包括多种类型,如和小范围供应商直接谈判采购合同(Gil and Oudot, 2009),招标后根据中标结果进行再谈判(Bajari,2006)等,竞争性谈判由于管理成本高更适用于合格供应商数量较少的小范围招标采购。多属性逆向拍卖改进于传统的单一价格属性拍卖,在评标过程中不但考虑投标人的价格属性,也纳入其他非价格属性,如质量、商誉、交货期和售后服务等,也被称为综合评分法招标。多属性逆向拍卖模型初始于只考虑价格和质量两个维度(Che,1993),后根据采购方的需求逐步扩展到多个维度,每个维度下制定不同的评分标准,根据设定合理的权重汇总成综合得分(David et al., 2006)。
均价中标法由于操作相对简便、管理费用较低而被广泛应用,标准的均价中标法下投标价格最接近所有投标价格均值的投标人中标, 在实际应用中存在多种衍生于标准均价中标法的变形,为简化表达,本文统一将后文提到的标准均价中标法及其衍生的各类中标法统称为均价中标法。直观上,相比最低投标价格,投标价格均值更能准确反映市场对标的物未来真实发生成本的估计,因此可避免“赢者诅咒”带来的损失(Chang, et al., 2014;Decarolis,2014)。均价中标法也可用作多属性逆向拍卖法中价格维度得分的计算方法,价格维度得分取决于投标价格与所有投标价格均值的接近程度。目前衍生于标准均价中标法的招标机制繁多,可概括为先按照一定的准则计算出评标基准价格,距离基准价格最近的投标人中标,基准价计算方式可表达为:
| $ BasePrice = [ReferencePrice \times \beta + \left({1 - \beta } \right)AveragePrice]\left({1 - \alpha } \right) $ | (1) |
式(1)中,ReferencePrice为招标人提供的参考中标价格,AveragePrice为投标人报价均值,该均值常为剔除部分极值报价后的均值①,β为基准价格计算时参考价格和报价均值的权重,β=0时只考虑报价均值。α为下浮系数且大于0,可以是固定值,也可以在评标时从分布[αL, αH]中随机抽取。此外招标人也可设置保留价格,也即中标价格的上限。当均价中标法作为多属性逆向拍卖中价格维度的衡量方法时,价格维度得分(满分100分)可表达为:
① 常用的剔除法有:剔除超过(低于)所有投标报价均值x%的报价、剔除投标报价从小到大排序,前(后)x%的报价等。
| $ {\rm{PriceScore}} = \left\{ \begin{array}{l} 100 - 100 \times a\frac{{{\rm{BasePrice}} - {\rm{BidPrice}}}}{{{\rm{BasePrice}}}}\;\;\;if\;\;{\rm{BidPrice}} \le {\rm{BasePrice}}\\ 100 - 100 \times b\frac{{{\rm{BidPrice}} - {\rm{BasePrice}}}}{{{\rm{BasePrice}}}}\;\;if\;\;{\rm{BidPrice}} > {\rm{BasePrice}} \end{array} \right. $ | (2) |
式(2)中,多属性逆向拍卖中价格维度得分取决于投标报价和基准价之间距离,a和b为扣分系数,通常0 < a < b,也即报价高于基准值的扣分惩罚更大。以上各种衍生的均价中标法则中,下浮系数α、扣分系数a < b都体现了标准均价中标法衍生出的一类对投标人有向下报价激励的均价中标法,这种带有向下激励的均价中标法是实际中最常见的招标机制。由于向下激励的手段繁多,为分析这一激励的影响且简化表述,我们将后文中所有这类带有向下激励的均价中标法统称为低于均价中标法。标准的低于均价中标法中,报价低且距离所有投标价格均值最近的投标人中标。
虽然已有研究(Chang et al., 2014;郑筱婷,2010)已通过行为学实验验证均价中标法确实可以降低“赢者诅咒”的发生频率,但在标准均价中标法下,由于所有投标人报完全相同的高价为一种均衡策略、报价不能反映真实成本,均价中标法被认为存在激励投标人串谋哄抬均价、中标人确定较为随机、无法有效选择出市场上真实成本最低的投标人等问题(Spagnolo et al., 2006;Decarolis,2013;郑筱婷,2010),在理论上并不被建议推广使用。然而与理论预测相反,现实中均价中标法被广泛使用,均价中标法是欧盟推荐的招标法则,用以控制不正常低价中标带来的损失(European Commission,2002)①,均价中标法也被广泛应用于意大利政府采购、美国纽约州政府采购等世界各地的公共采购领域。我国国务院办公厅2004年发布的《关于进一步规范招标活动的若干意见》[国办发[2004]56号]也指出要鼓励推行合理低价中标法②和无标底招标法,在我国广东,约有90%的工程招标采用均价中标法(郑筱婷等,2011)。意大利政府采购曾在2006年限制了均价中标法的使用范围,但又于2011年重新鼓励推广均价中标法。理论研究结论与现实应用的差异引发了使用均价中标法合理性的争议,既然均价中标法有如此多缺陷,为何现实中各领域仍在大范围使用呢?而争议的根本在于,均价中标法下投标人的投标价格是否可以反映投标人的真实成本(Chang et al., 2014),如果相比低价中标法,均价中标法下投标人投标行为改变导致投标价格不能反映真实成本,或者可以反映真实成本但将中标价格确定在一个非常高的位置,那么均价中标法即使可以解决“赢者诅咒”的问题,但由于给招标人带来采购成本的大幅提升而并不有效。验证低于均价中标法合理性要验证三个问题:一是投标人报价行为要和低于均价中标法下一致,也即投标人报价可以反映投标人真实成本;二是最后的中标价格不会被确定在一个非常高的位置,否则会给招标人带来采购成本损失;三是能够降低“赢者诅咒”的产生概率。本文正是基于低于均价中标法下投标人的投标行为对这三个特点进行一一验证。
① European Commission (2002) Prevention, detection and elimination of abnormally low tenders in the European construction industry. Report, Directorate Enterprise and Industry European Commission, Brussels.
② 合理低价中标在现实中的操作方式即为均价中标法,均价中标法选择的中标价格不是最低投标报价,因此该方法也被称为合理低价中标。
本文主要贡献有:目前学术上对均价中标法的实证多以实验数据(Chang et al., 2014;郑筱婷,2011)、意大利政府采购数据(Conley and Decarolis, 2016)为基础,国内只有郑筱婷(2010, 2011)系统讨论过我国工程招标里均价中标法的应用,而我国作为均价中标法使用最广泛的国家,对该方法在实践中的研究仍然较少。相比已有文献,理论上,本研究首次证明了标准低于均价中标法不存在随真实成本严格递增的贝叶斯纳什均衡。实证上,相比行为学实验为基础的研究无法纳入投标人的参标选择行为和串谋行为,本文采用中国实际部门招投标数据,在时间截面上基于投标人参标选择行为首次考察了投标人投标价格和真实成本间的关系,并分析了投标人的潜在串谋行为带来的不良影响;最后,已有基于工程招标数据的实证研究囿于工程间的异质性导致不同招标间价格和成本不可比,无法在时间趋势上比较低于均价中标法对投标价格绝对值产生的影响,本文以原材料市场价格为标杆,在时间尺度上验证了低于均价中标法促进了投标人市场产生稳定的低利润预期。结合低于均价中标法下投标人在时间截面上投标价格可以反映实际成本,时间趋势上采取稳定低利润的报价行为且可以降低“赢者诅咒”发生频率,本文回答了低于均价中标法在业界被广泛应用的原因。
内容上,本文首先从理论上讨论一种现实中最常见的标准均价中标法变形,标准低于均价中标法的均衡;再以某大型电力公司的物资招标采购数据为基础进行实证,探索低于均价中标法在实际应用中投标人的投标行为,这些行为包括投标人的参标行为、报价行为、经验学习行为和串谋行为;然后,将结合投标人时间截面上的报价行为、时间趋势上的报价行为以及对“赢者诅咒”控制的效果上对低于均价中标法的合理性进行讨论;最后,针对低于均价中标法的应用范围、应用特点、应用注意事项给出了管理建议,可作为招标人设计合理招标机制的参考。
文章余下部分安排如下:第二部分进行文献综述与理论假说;第三部分简要介绍数据背景并展开实证分析;第四部分为文章的结论和管理学建议。
二、文献综述与理论假说 (一) 文献综述针对均价中标法的研究主要集中在理论均衡、投标行为和招标机制效果三个方面。
理论均衡方面,Ioannou and Awwad(2010)采用蒙特卡洛模拟对低价中标法、标准均价中标法和标准低于均价中标法三种招标准则进行模拟,结果发现低于均价中标法下投标人的中标概率分布、最优报价、期望收益均介于低价中标法和标准均价中标法之间,且随着投标人数增大,低于均价中标法更接近于标准均价中标法。无论是共同价值(CV)还是私人价值(IPV)假设下,标准均价中标法的对称贝叶斯纳什均衡为所有的投标人报完全一样的高价k(k不低于所有投标人中的最高成本)已成为共识(Decarolis,2014;Conley and Decarolis, 2016;Chang et al., 2014;郑筱婷,2010),因为此时投标人如果偏离该均衡,则中标概率会由1/n(n为投标人数)下降为0。Chang et al.(2014)首次在共同价值假设下严格证明了标准均价法下不存在严格递增的对称贝叶斯纳什均衡,也即投标人的投标报价不会按照真实成本严格单调递增。只有3个投标人时,报完全相同的高价是唯一形式的非严格递增对称贝叶斯纳什均衡。但低于均价中标法下,这一均衡被打破,投标人有动机将报价降低至略低于完全一致的高价,以获得更高的中标概率(Spagnolo et al.,2006;Galavotti,2014;郑筱婷,2010)。当投标人大于3个时,由于均价中标法下投标人中标概率无法简单转换成概率分布函数或顺序统计函数,这为求解对称贝叶斯纳什均衡带来很大难度。
总结已有文献,均价中标法中下的投标行为常与低价中标法对比,可概况涵盖以下类型:投标人参标行为、报价行为、串谋行为和经验学习行为。参标行为方面,相比低价中标法,均价中标法下会有更多的投标人参与投标(Branzoli and Decarolis, 2015;Conley and Decarolis, 2016),原因是均价中标法吸引了低价中标法下很难中标的高成本投标人参标。报价行为方面,Chang et al.(2014)通过行为学实验,发现投标人报价行为与理论均衡预测不同,标准均价中标法下投标人报价行为和低价中标法下没有显著差异,也即投标人报价与成本信号呈递增关系,并通过最优反应理论(Best Response)解释了这一现象。然而也有针对意大利政府公共采购的研究发现,低价中标法下投标人报价和成本变量显著正相关,但均价中标法下投标人报价和成本变量失去显著关系(Conley and Decarolis, 2016)。串谋行为方面,Conley and Decarolis(2016)发现在意大利政府采用均价中标法进行招标采购时,投标人间会发生串谋、设立影子企业,共同参标操控均价,增大中标概率。文章同时提出了识别串谋企业的方法,但结果却反常识发现,由于投标人间存在多个串谋集团,各集团间形成了竞争关系,串谋集团反而倾向拉低均价而不是拉高均价。郑筱婷(2010)从投标人对成本预期和报价预期的角度在理论上说明了均价中标法对投标人有合谋的激励,并采用广东省建筑业招标数据中投标人报价离散程度随时间降低验证了这一理论。除均价中标法外,其他类型的招标机制下也同样存在投标人串谋问题,大量研究(Bajari and Ye, 2003;Porter and Zona, 1999;Zona,1993)讨论了低价中标法下,不同行业招标采购中法庭已确认过的合谋集团及其具体串谋方式。经验学习行为方面,Camerer et al.(2004)提出认知分层模型(Cognitive Hierarchy Model),理论认为博弈中各参与者的复杂度不同,参与人策略是一个迭代过程,复杂度高的参与人会根据复杂度低的参与人制定博弈策略。Galavotti(2014)根据这一理论,采用均价中标法下投标人的参与经验来量化认知分层模型中的参与人复杂度,以意大利公共采购数据进行验证,发现历史中标经验高的投标人可以从经验中学习,更好的预测招标基准价,并据此作出更有利于中标的招标决策。
招标机制效果方面,(Chang et al., 2014;郑筱婷,2011)均通过行为学实验验证了共同价值(CV)假设下均价中标法可以有效防止“赢者诅咒”现象的发生,但代价是将中标价格确定在了一个较高的水平。Decarolis(2013, 2014)通过对比意大利公共采购中低价中标法和均价中标法两种招标机制的中标结果,发现虽然均价中标法确定的中标人完成质量要高于低价中标法,但如果在低价中标法中纳入事后监控筛选,则可有效改善低质量问题,但需要比较事后监控的管理费用与均价中标法确定的高中标价格带来的损失才能判断何种招标机制更优。在中标后允许分包的情况下,(Branzoli and Decarolis, 2015)发现低价中标法下,中标价格过低会导致联合企业中标后在企业间分配标的物困难,无法保证标的物完成质量,而均价中标法则可将中标人看作招标方的市场委托代理,在中标后将标的物分包给市场上最有效的企业,研究认为即便不考虑投标人的投标策略,由于均价中标法在事后分包上的有效性可以确保标的物的高质量完成,也可解释均价中标法在现实中广泛采用的合理性。Ioannou and Awwa(2010)还提出均价中标法可以防止投标人行业内恶性竞争,有利于供应链上招标人与投标供应商的上下游关系。
从以上文献综述可以看出,已有理论表明均价中标法下严格的贝叶斯纳什均衡求解存在一定难度,因此基于实际投标数据探索投标人的投标行为有助于理解该招标机制的合理性。此外,实证上对投标人投标行为决策过程有所忽视,且缺乏分析低于均价中标法中对报价向下激励的影响。最后,已有文献以国外研究为主,而我国作为最广泛使用均价中标法的国家,近年来对该领域研究较少,本文正是以我国为背景的研究,探索该招标机制在我国推广应注意的问题。
(二) 理论假说在对标准低于均价中标法进行理论分析之前,首先假设投标人的成本分布。由于均价中标法的主要应用领域为公共采购、工程项目、大型企业招标,虽然这些领域成本分布采用关联价值①假设更为准确,但为了简化分析,鉴于均价中标法主要解决的是共同价值部分下的“赢者诅咒”问题,且这些领域在研究中也常以共同价值假设为基础(Hong and Shum, 2002),因此本文假设投标人成本分布符合共同价值。参考(Chang et al., 2014)研究标准均价中标法的招标环境:共有n个投标人参与采购招标,每个投标人的真实成本相同但未知,投标i∈{1, …, n}会接收到各自关于真实成本C的信号si,C未知但服从[CL, CH]上的均匀分布F,f为其概率密度函数,si间相互独立且服从[c-θ, c+θ],其中c为C在某次招标中的具体实现,θ>0,CH>CL>0,CH-CL>2θ,i个投标人同时提交密封报价bi,中标价格和报价相同。该假设下的低价中标法均衡已被严格证明(Lind and Plott, 1991),本文不再讨论,此时低于均价法中投标人的收益函数可表示为②:
① 最常用的关联价值模型参见(Levin, 2004),正向拍卖环境中,价值函数为
② 当出现n个相同报价中标时,随机分配标的物至n个投标人中的一个,也即每个投标人中标概率1/n。
| $ \prod\nolimits_{\rm{i}} {({b_i}, {b_{ - i}})\left\{ \begin{array}{l} {b_i} - c\;if\;i \in \arg \min \left| {{b_j} - \frac{1}{n}\sum\limits_{k = 1}^n {{b_k}} } \right., {\rm{其中}}j \in \left\{ {{b_j} < \frac{1}{n}\sum\limits_{k = 1}^n {{b_k}} } \right\}\\ 0\;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise}} \end{array} \right.} $ | (3) |
命题1:低于均价中标法不存在严格递增的贝叶斯纳什均衡。
证明:证明该命题只需找到反例即可。假设存在严格递增的贝叶斯纳什均衡,所有投标人的投标策略为,其中s∈[CL-θ, CH+θ],且保证b*{CH+θ} ≥CH,现考虑除了投标人M,其他投标人投标策略均为b*(s),当M收到成本信号s =CH+θ时,M可以推测出标的物真实成本为CH,如按照b*(CH+θ)报价,则其期望收益为零③,假设此时M按照接受信号为
③ 均匀分布下,至少还有一个投标人收到成本信号CH+θ的概率为0。
| $ \prod {\left({{b^*}\left({{C_H} - \frac{3}{8}\theta } \right);{\rm{\bar s}}} \right) = P\left({{b^*}\left({{C_H} - \frac{3}{8}\theta } \right)\left| {{\rm{\bar s}}} \right.} \right)} \left({{{\rm{b}}^*}\left({{{\rm{C}}_{\rm{H}}} - \frac{3}{8}{\rm{ \mathit{ θ} }}} \right) - {{\rm{C}}_{\rm{H}}}} \right) $ | (4) |
其中,
① 偶数情况下采用同样方法,同样可以找到反例。
| $ \begin{array}{l} P\left({{b^*}\left({{C_H} - \frac{3}{8}\theta } \right)\left| {\bar s} \right.} \right) > (n - 1)!{\left({\int_{{C_H} - \theta }^{{C_H} - \frac{1}{2}\theta } {\frac{{dt}}{{d\theta }}} } \right)^{\frac{{n - 1}}{2}}}{\left({\int_{{C_H} + \frac{1}{2}\theta }^{{C_H} + \theta } {\frac{{dt}}{{d\theta }}} } \right)^{\frac{{n - 1}}{2}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }}(n - 1)!{\left({\frac{1}{4}} \right)^{n - 1}} > 0 \end{array} $ | (5) |
上述不等式可表达为,我们可以找到一种M偏离b*(CH+θ)的报策略:M按照信号为CH-
② 由于投标策略b*(s)是单调递增函数,此时投标价格均值下限正比于
命题2:低于均价中标法中,所有投标人报完全相同的高价k(k≥CH),不再是对称的贝叶斯纳什均衡。
证明:此时,若所有投标人报完全的高价k,每个人的中标概率为1/n,对于投标人M,有动机向下偏离报价为k-ε(ε→0),此时M成为唯一低于均价投标人,从而中标概率从1/n上升为1。因此与标准均价法不同,所有投标人报完全相同的高价k不在是贝叶斯纳什均衡。
推论1:低于均价中标法中,若投标人不参与串谋,则有动机为了增大中标概率而降低投标价格。
证明:假设投标人M不参与串谋,其对某次招标中投标报价均值的预期为b,则当M报价为bm时,新的投标报价均值预期为
| $ \begin{array}{l} b{'_{(p)}} < {{\rm{b}}_m} < \overline {b'} < b{'_{(p + 1)}} \Leftrightarrow \\ b{'_{(p)}} < \frac{{(n - 1)\bar b + {{\rm{b}}_m}}}{n} < b{'_{(p + 1)}} \Leftrightarrow \\ b{'_{(p)}} < {{\rm{b}}_m} < b{'_{(p + 1)}} - (n - 1)(\bar b - b{'_{(p + 1)}}) \end{array} $ | (6) |
对于特定的投标报价序列b′(1)……b′(n-1),如果p>1,则区间(b′(p), b′(p+1)-(n-1)(b-b′(p+1)))不一定存在,但其存在的可能性仍为M提供了继续向下报价拉低投标均值进而提高中标概率的动机。
通过上述文献综述和理论分析,可以看出以低于均价中标法下的中标价格受整体投标报价影响,即使在简单的标准均价中标法假设环境下也无法得出其均衡策略,因此需要从实际数据出发对投标人的具体投标行为进行探索。基于已有研究和理论分析,本文对低于均价中标法中投标人行为提出以下假说。
假说1:参标行为上,投标人倾向于参加其真实成本更低的招标。
投标人参标行为的假设主要基于两个原因,一是参与真实成本更低的招标有利于提高利润率,二是从推论1可以看出,投标人有动机向下报价,参与真实成本更低的标包有更大的下拉报价空间。
假说2:报价行为上,投标人的投标报价和真实成本无关。
理论上,低于均价中标法不存在严格递增的贝叶斯纳什均衡,虽然在标准均价法中有研究发现投标人在行为学实验中会按照真实成本报价(Chang et al., 2014),但这里我们仍按照理论均衡分析命题1结果和已有对现实政府招标采购数据进行实证的研究结果(Conley and Decarolis, 2016),假设投标人报价和真实成本无显著关系。
假说3:串谋行为上,投标人有动机形成联盟,串谋哄抬均价,拉升中标价格。
相比低价中标法,均价法中投标人的串谋更容易达成,因为低价中标法中串谋联盟必须保证联盟外无更低成本的投标人,而均价中标法中只需要保证联盟人数足够多以达到操控均价目的即可(郑筱婷,2010)。
假说4:经验学习行为上,随时间推移,通过对历史经验学习,投标人整体对基准价的预期更加相似,招标整体报价离散程度降低。
投标人会根据中标经验不断优化自身的报价策略,随经验增多,投标人会获得更多真实的市场报价分布信息,对评标机制的理解程度也会随经验加深,在未来的投标过程中会做出更优的报价决策,在低于均价中标法中体现为投标人对即将形成的基准价预期更加准确,投标人整体对基准价的预期更加相似,招标整体报价离散度降低。
三、数据背景与实证分析 (一) 数据背景本文实证分析以国内某大型电力公司物资采购招标数据为例,由于电力工程项目关乎社会公共安全,一旦发生“赢者诅咒”现象会对社会安全和公众福利带来巨大损害。因此,该公司在评标过程中采用多属性逆向拍卖法,且价格维度评分采用均价中标法,以确保采购的产品和服务在质量和服务响应速度上可以保障工程项目的顺利进行。
电力物资种类繁多,本文仅选取220kV角钢铁塔一种物资进行研究。角钢铁塔主要应用于输电线路,属于电力物资中的重点物资,其多属性逆向拍卖规则中包含三部分,分别为技术、商务、价格,其中价格维度占比70%,由于角钢铁塔按照重量招标,不同招标项目内标的物单价可比较、成本易衡量、供应商技术水平平均、投标人是否中标主要取决于投标价格,使其成为本文良好的研究对象。为简便分析,我们将商务和技术维度归纳为技术质量维度。招标人每年进行6期招标,同期内同时进行多个招标项目,一个具体招标项目称为一个标包,不同标包的运输省份和标的物重量不同,投标人按总价报价。价格维度的具体评分规则如表 1所示,评分机制中具有下浮系数α、扣分系数a < b,体现了对投标人向下报价的激励,属于一种低于均价中标法。
| 表 1 角钢铁塔物资采购报价评分办法 |
① 下浮系数α范围为0-2.0%,以0.5%为级差设置5个浮动系数,评标现场随机抽取。
② 当投标人的评标总价≥基准价,a=1.8;当投标人的评标总价<基准价,a=0.3;当计算出的价格评审得分≤0时,价格部分得分为0分。
(二) 研究方法招标人发出招标公告即日起,投标人对投标决策分为两步:首先,投标人需要决策在哪些标包进行参标;其次,决定投标报价,并同时在评标过程中获得价格维度得分。投标人参标决策具有内生性(Bajari and Hortacsu, 2003),如果直接对投标报价进行分析,则会产生样本选择性偏误。为解决这一问题,本文参考(Pilehvar et al., 2016)的处理方式,采用Heckman样本选择模型(Heckman,1979)进行两阶段回归来避免参标决策内生对报价影响因素系数估计造成的影响。第一阶段,分析投标人参标的影响因素,第二阶段研究投标人决定参与投标后的报价和价格得分影响因素。
第一阶段,采用Probit模型分析投标人是否参与投标的选择问题。由于样本只能观察到各标包的实际参标结果,因此首先要构建潜在投标人样本。本文将在同期招标中参标至少一次、具备生产220kV铁塔生产资质的投标人作为该期中每个标包的潜在投标人,原因在于只要在同期中的一个标包参标,证明该投标人在该期通过了招标人初审,属于合格投标人,且是具有中标意愿的活跃投标人。本文采用Probit模型构建潜在投标人的参标行为模型:
| $ \begin{array}{l} Prob{\rm{(}}entr{y_{ki}} = 1|{Z_{ki}}) = \Phi (\delta '{Z_{ki}})\\ entr{y_{ki}} = \delta \prime {Z_{ki}} + {u_{ki}} \end{array} $ | (7) |
其中entryki表示第k个投标人是否参与了第i个标包的虚拟变量,如果投标人参标,entryki=1,如果投标人未参标则entryki=0。Zki代表了投标人k是否参与标包i的决策变量。根据(7)得到δ′的估计值,计算出逆米尔斯比率λi,Φ(δ′Zki)和φ(δ′Zki)分别表示Zki的标准正态密度函数和累计密度函数。
| $ {\lambda _i} = \frac{{\Phi (\delta '{Z_{ki}})}}{{\varphi (\delta '{Z_{ki}})}} $ | (8) |
第二阶段,利用参与投标的投标人样本,也即entryki=1的观测数据,加入逆米尔斯比率λi,进行如下回归:
| $ {Y_{ji}} = {\beta _0} + \beta '{X_{ij}} + {\alpha _{ji}}{\lambda _i} + {e_{ji}} $ | (9) |
Yji是为投标人j在标包i中的投标单价①BPij或按照表 1计算的价格维度得分PriceScoreij,Xij表示影响投标人报价或价格维度得分高低因素。Xij需是Zki的全子集,也即Zki中包含只影响投标人是否参标却不影响投标价格的因素,其中uki与eji满足经典假设中的二元正态分布(Maddala,1986)。
① 角钢铁塔招标时按照重量计算数量,单位:吨,投标企业虽然报价时按总价报价,但为对比不同标包,因变量采用单价,单位:元/吨。
(三) 实证模型对于时间点上投标人报价影响因素研究,第一阶段参标选择问题采用Probit模型如下:
| $ \begin{array}{l} entr{y_{ki}} = {\delta _0} + {\delta _1}DIST\_{N_{ki}} + {\delta _2}DIST\_{S_{ki}} + {\delta _3}LnCA{P_k} + {\delta _4}Product{H_k}\\ + {\delta _5}Package{N_t} \times C\_LnCA{P_k} + {\delta _6}Ln{Q_i} + {\delta _7}Are{a_i} + {\delta _8}Perio{d_t} + {u_{ki}} \end{array} $ | (10) |
第二阶段,利用选择样本,也即entryki=1的投标数据,对投标人投标报价影响因素进行分析,模型如下:
| $ \begin{array}{l} B{P_{ji}} = {\beta _0} + {\beta _1}DIST\_{N_{ji}} + {\beta _2}DIST\_{S_{ji}} + {\beta _3}LnCA{P_j} + {\beta _4}Product{H_j}\\ + {\beta _5}Ln{Q_i} + {\beta _6}Are{a_i} + {\beta _7}Perio{d_t} + {e_{ji}} \end{array} $ | (11) |
其中,因变量BPji为投标人j在标包i中的投标单价,对于投标人报价影响因素的自变量,已有文献(Bajari and Ye, 2003;Conley and Decarolis, 2016; Porter and Zona, 1999)对投标成本估计时选择的自变量主要包括原材料成本、运输距离、投标人产能等,本文收集到原材料市场价格SteelPt,为第t期招标市场上的角钢单价①,衡量原材料成本环境。DIST_Nji和DIST_Sji为投标人所处省份与招标地区是否为相邻省份②、是否为同一省份虚拟变量,用来衡量投标人的运输成本。由于铁塔成本主要由原材料成本构成,且投标人要承担将铁塔运输到施工现场的运费,铁塔重量大运输费用高,原材料成本和运输费用是成本中的最重要组成部分,但能观测到的市场原材料价格在t期对于所有投标人是一样的,已经在时间固定效应Periodt中控制,因此DIST_Nji和DIST_Sji是该部分研究代理投标人真实成本的主要自变量。LnCAPk为投标人年产能③对数④,也可衡量投标人真实成本,有研究表明高产能企业的边际生产成本更低(Zeynalian et al., 2013),当订单量接近产能临界点时生产成本则会提高(Bichler et al., 2011),且低价中标法中高产能投标人为了降低产能的闲置成本,会降低投标报价以获得更多的订单(Bajari and Ye, 2003),因此高产能通常代表了低成本。PackageNt是第t期招标人投放的标包总数,市场上的标包数量越多,投标人会提高参标概率,但PackageNt对不同规模的投标人参标概率有调节作用,研究纳入PackageNt和产能中心化⑤的交叉项PackageNt×C_LnCAPk来表示这种调节作用,高规模投标人由于有更多的人力和物力资源编制标书,当市场上的标包数量提高时,高规模投标人的参标概率提升会高于低规模投标人。尽管第t期总标包数对不同规模的投标人的参标概率有影响,但投标人一旦决定参与投标,标包总数将不对其报价产生影响,因此仅纳入式(10)作为只影响投标人参标决策但不影响报价决策的变量。
① 角钢铁塔主要成本由原材料市场价格决定,其市场期货价格为招标日当月的日均角钢单价,数据来源为上海有色网2012-2014年角钢(5#角钢)市场日价格。
② 同一省份DIST_Nji也记为1,因此β3+β4B[CL, CH]才是同省份投标人的距离因素影响估计值。
③ 角钢铁塔的交付期在2-3个月,和相邻两期招标时间间隔类似,因此本研究忽略投标人的剩余产能问题,用年度产能代理招标时间点的投标人剩余产能。
④ 由于投标人产能差异较大,为减少异方差带来的影响,取对数,下文标包重量取对数同理。
⑤ 中心化将减少交叉项和产能对数的相关性,减弱共线性对估计结果的影响。
控制变量方面,投标人层面,虽然铁塔招标结果主要由价格维度得分决定,但在多属性逆向拍卖中仍需控制质量维度得分能力对报价的影响,研究采用投标人是否可以生产高电压等级⑥角钢铁塔ProductHk代理投标人技术质量维度得分能力,具备高电压等级铁塔生产线的投标人技术更加先进,可以在技术质量维度获得更高得分,且高质量产品通常代表了高成本。标包层面研究控制了标包i项目所在地省份Areai和标包i内的铁塔重量对数LnQi,用来控制不同标包的特点,标包内招标重量越多,投标人会由于规模效应和批发价折扣(Chen,2011)而降低投标单价。此外还采用虚拟变量Periodt来控制第t期招标的时间固定效应。
⑥ 投标人可以生产750kV以上电压则ProductHk,否则为0。
与时间截面上的报价影响因素分析类似,时间趋势上,本文主要通过分析投标人在价格维度得分是否会随时间提升来研究投标人是否有经验学习能力。郑筱婷(2010)曾对建筑工程均价中标法下的投标数据分析,发现随着时间推移和投标人市场的成熟,投标人报价离差将会逐渐降低,本文的价格维度得分实则和离差类似,只是将均值换做表 1中计算出的基准价,随时间推进,价格维度得分越高,证明投标人对基准价的预期趋向于一致。模型仍分为两阶段,投标人仍首先做参标决策,报价时同时获得价格维度得分,第一阶段参标决策建模如下:
| $ \begin{array}{l} entr{y_{ki}} = {\delta _0} + {\delta _1}DIST\_{N_{ki}} + {\delta _2}DIST\_{S_{ki}} + {\delta _3}LnCA{P_k} + {\delta _4}Product{H_k} + \\ {\delta _5}Package{N_t} \times C\_LnCA{P_k} + {\delta _6}Ln{Q_i} + {\delta _7}Are{a_i} + {\delta _8}Dat{e_t} + {\delta _9}Dat{e_t}^2 + {u_{ki}} \end{array} $ | (12) |
第二阶段,利用选择样本,也即entryki=1的投标数据,对投标人价格维度得分影响因素进行分析,模型如下:
| $ \begin{array}{l} PriceScor{e_{ji}} = {\beta _0} + {\beta _1}DIST\_{N_{ji}} + {\beta _2}DIST\_{S_{ji}} + {\beta _3}LnCA{P_j} + \\ {\beta _4}Product{H_j} + {\beta _5}Ln{Q_i} + {\beta _6}Are{a_i} + {\beta _7}Dat{e_t} + {\beta _8}Dat{e_t}^2 + {e_{ji}} \end{array} $ | (13) |
其中PriceScoreji为按照表 1计算出的投标人j在标包i中的报价维度得分,由于下浮系数具有随机性,本文无法获得评标时具体抽取的α,因此本文以α取值范围均值α=1%进行计算,这一取值也符合投标人报价时对α的预期。其他自变量和控制变量同式(11),由于PriceScoreji是标包内投标人报价的相对值,在时间尺度上可比,因此不再纳入时间固定效应,而是直接加入时间趋势变量来分析投标人报价行为的动态变化,Datet为第t期的投标时间,Datet2是Datet的平方,2000年1月1日表示为14610,每增加一个单位增加一天,这一做法参考郑筱婷(2010)对时间变量的操作。模型(11)只考虑时间截面未考虑时间趋势变量的原因是研究时间范围内SteelPt有显著的时间趋势①,放入模型会和Datet产生严重的共线性,无法区分投标人报价变化是由于报价决策还是市场原材料价格变动导致。
① 研究时间段内,市场角钢价格恰好不断走低,有显著的时间趋势,与date相关性高达-0.93。
对于串谋行为,由于在均价中标法中投标人较容易通过串谋操控基准价,通常招标中形成联盟的方式是联盟内部首先选择“内部中标候选人”,联盟内的其他成员作为陪标投标人共同报出高价拉高均值,“内部中标候选人”投标价格略低于陪标报价以提高中标概率和中标利润。由于标准均价中标法的均衡情况是所有投标人报完全一样的高价(Chang et al., 2014),且对于陪标成员,报完全相同的高价②是最容易监控成员是否偏离合谋的方法,本文将采用投标人在同一标包内是否和其他投标人报价完全相同来代理投标人疑似串谋。Sameji表示在标包i内,是否有其他投标人投标报价和j完全相同的虚拟变量。SameNRji表示在标包i内,报价为BPji的投标人个数占标包投标人总数的比例,MaxSameRji表示同标包内SameNRji的最大值,用来代理标包i中最严重的串谋程度。在上述报价影响因素分析模型和价格维度得分影响因素分析模型后,研究将分别引入代理串谋程度的变量对对报价和价格维度得分的影响进行分析。
② 由于研究数据集的投标总价报价,单位:元,标包金额均为6位数以上,对数据检查发现投标人很少将后面位数全报为0,通常投标人会将价格报至个位数字,如果6位以上数字均报价完全相同,则有很强理由怀疑这些报价完全一样的投标人在进行串谋。
研究数据跨度2012-2014年,每年招标6期,因此共涉及18个时间点,831个标包,数据变量涉及市场层面、招标层面和投标人层面。主要变量描述性统计如表 2所示。
| 表 2 各主要变量的描述性统计 |
表 3为Heckman两步法估计投标人的参标行为与报价行为结果。所有模型的逆米尔斯比lambda皆显著说明了参标行为的确存在内生性,如果直接对报价行为分析存在样本选择偏误。表 3模型(2)结果可以看出投标人更倾向于参加招标重量大、距离自身地理位置近的标包。距离位置近意味着运输成本低,因此假设1得到验证。产能对投标人参标概率的影响来自两个部分LnCAP与PackageN×C_LnCAP,PackageN的最小值为28,因此产能对参标概率最小的影响仍为正向,当PackageN为28时,产能每提高10%,参标概率提高1.5%,且PackageN越高,参标概率随产能增大提升的越多,说明了市场上标包越多,高产能投标人参标概率越高于低产能投标人,低产能投标人的参标概率提升受到其自身资源限制。而高产能投标人可以生产更多的标的物,如有产能未被利用会产生闲置成本,因此倾向于参与更多的标包,高技术质量投标人由于在质量方面的优势也倾向于参与更多标包。模型(3)主要考察投标人报价是否与真实成本显著相关,结果发现投标人和招标项目处于相邻省份,投标单价将降低60元左右,同一省份将降低132元左右,运输成本是衡量投标人真实成本的关键变量,因此假设2并不成立,投标人报价可以反映自身的真实成本。年产能越高的投标人报价越低,和以往低价中标法研究结论类似(Bajari and Ye, 2003),这一方面说明高产能投标人报价反应了真实成本,另一方面也说明低于均价中标法下,高产能投标人也倾向于报低价来提高中标概率、减少产能空置带来的损失。而控制变量方面,高质量的投标人报价更高,这与多属性逆向拍卖结论一致,Che(1993)在包含价格和质量两个维度的多属性逆向拍卖提出了投标人报价会参考质量维度中的质量内生性因素,高质量产品通常会带来高成本,因此会报高价,而在质量维度的高得分会与价格维度的低得分相互弥补。LnQ系数显著为负,体现了规模效应和批发价折扣(Chen,2011)。对比模型(1),模型(3)变量系数方向没有改变,体现了模型的稳健性,但忽略了样本选择性偏误会导致估计系数偏低。至此,低于均价法合理性的第一个特点得到了验证,投标人报价行为和低价中标法下一致,可以反映投标人真实成本。
| 表 3 Heckman两阶段投标人参标与报价行为分析 |
模型(4)主要考察了投标人是否存在串谋行为,模型(4)在模型(1)基础上加入了变量Same和Same×SameNR,分别用来考察疑似参与串谋与未参与串谋投标人报价的区别和疑似串谋投标人数占总投标人数比例对疑似串谋人报价的影响。从回归结果可以看出,参与疑似串谋联盟(Same=1)的投标人报价要显著高于普通投标人37元左右,且高报价程度与疑似串谋联盟内投标人报价相同投标人个数比例SameNR正相关。SameNR每提高10%,疑似串谋价格将再提高82元/吨,表现了串谋投标人在联盟内人数更多的情况下,将以更高的陪标价格操控基准价。从表 2可以看出,数据集中SameNR最高可达48%,按照这一数字计算,疑似串谋投标人报价比其他普通投标人报价高出近433元/吨,可见严重的串谋行为可能给招标人带来巨大成本损失,疑似串谋具体对基准价的影响将在后文继续讨论。
表 4为Heckman两步法估计投标人的参标行为与价格维度得分影响因素结果,所有模型的逆米尔斯比lambda皆显著说明了参标行为的确存在内生性,如果直接对报价维度得分影响因素分析存在样本选择偏误。表 4中模型(2)结果和表 3模型(2)结果类似,相同的变量对投标人投标概率的影响方向不变,这里不再多做讨论。需要关注的是时间趋势变量系数,Date系数显著为正,Date2系数显著为负说明随时间推进,投标人的参标概率越来越大,且边际效应递减。
| 表 4 Heckman两阶段投标人参标与报价维度得分分析 |
表 4模型(3)与表 3模型(3)中相同的自变量系数方向全部相反,这说明了显著导致低投标价格的因素都同时导致了高价格维度得分,反应了招标机制对报低价的激励,正是由于低于均价中标法这种对投标人向下报价的激励,才使得投标人在时间截面上会按照真实成本报价,这与低价中标法非常相似。表 4模型(3)中需要重点关注的仍是时间趋势变量,由于价格维度得分是一个相对值,代表了投标人j报价相对于标包i基准价的位置,因此在时间趋势上可直接进行比较,Date系数显著为负,Date2系数显著为正说明随时间推进,投标人的价格维度得分越来越高,报价与基准价越来越接近,这说明整个投标人市场对基准价的预期通过经验学习也越来越准确,且存在边际递减效应,这和标准的均价中标法非常类似,即使没有串谋,投标人报价也会逐步趋同(郑筱婷,2011)。至此,假设4得到了验证,通过对历史经验学习,投标人整体对基准价的预期更加相似,招标整体报价离散程度降低。但需要注意,一致的市场基准价预期是针对不同时间截面时期t的基准价预期,而不是说市场基准价不随时间t变化,市场基准价的变化在下一节继续讨论。表 4中模型(4)进一步考察疑似串谋对报价维度得分的影响,疑似串谋投标人数占总投标人数比例SameNR越高,疑似串谋投标人价格维度得分则会显著降低,与表 3中模型(4)结果结合来看,说明通过报价一致识别出的疑似串谋投标人目标不在于中标而是陪标,类似“众星拱月”,其目的在于拉高标包基准价,提高联盟内部报略低于这一串谋价格的投标人的中标概率。至此,结合表 3中模型(4)结果,假说3得到验证,低于均价中标法容易激励投标人串谋哄抬均价。
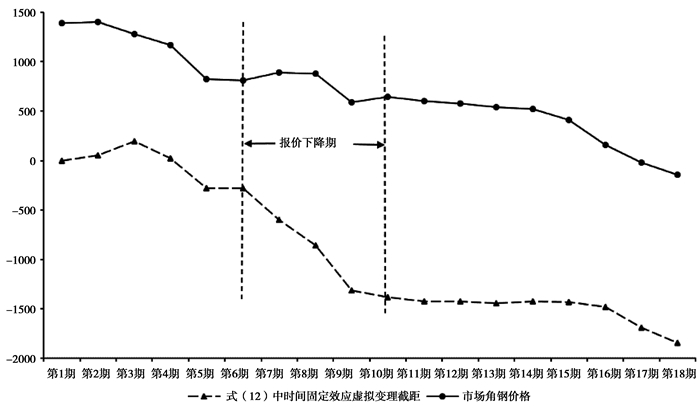
(五) 时间趋势上标包维度变量分析以上分析皆是对投标人i在标包j内的投标行为进行分析,下面将针对标包维度变量在时间趋势上的变化来进一步探索低于均价法的合理性。由于研究时间范围内,原材料市场角钢价格不断递减,形成时间趋势,一起纳入模型(11)会由于和时间趋势变量的强共线性(相关系数高达0.93)对回归结果造成影响。因此前文只分析了时间截面上投标人的报价影响因素,我们将式(11)、表 3模型(3)中的时间固定效应虚拟变量Periodt的系数与第t期市场角钢价格SteelPt进行作图比较,如果趋势一致则证明不同期的投标人整体报价变化主要由市场原材料价格导致,如果不一致,则在时间趋势上投标人可能发生报价策略的改变。
如图 1所示,在最初的3期内,投标人整体经验较少,如果我们用投标价格与市场角钢原材料价格的差异代理市场利润,整体行业预期利润还保持在一个较高的水平,且投标人报价分散,导致了初始时整体报价偏高,且没有体现和市场角钢原材料价格一样的走势,第4期至第6期内,投标人对市场利润的预期趋向稳定,报价和市场角钢价格走势相同,但通过经验学习,投标人学习到了低于均价中标法对报低价的激励,也即降低报价有助于提高价格维度的得分。第7期至第10期内,角钢市场价格较为稳定,招标机制未发生改变,但投标人整体报价发生了显著下降。在这一阶段,已经积累了足够多的投标人采取了推论1中的低价策略,市场利润被显著拉低,投标人整体对利润的预期将下降,投标人通过降低利润向新的市场利润预期靠拢,将进一步拉低市场利润预期,直到市场上大部分投标人的利润可以被压缩的空间变得很小,也即第10期,市场利润预期将重新趋于稳定,报价走势和市场角钢原材料价格走势再次相同。
|
图 1 投标人时间维度上的报价变化与市场角钢价格趋势 注:图内市场角钢价格为市场角钢价格减去3000元/吨。 |
为了验证图 1中的趋势是否显著,表 5研究采用OLS对标包维度变量的时间趋势进行简要分析。表 5中,模型(1)为带有时间固定效应的基准价影响因素分析,可以看出高重量标包的单价更低,招标人可以通过集中招标的方法获得批发价优势。MaxSameR是标包内报完全相同报价投标人数占总投标人数比例的最大值,代理了标包的串谋严重程度,回归结果显示,标包内疑似串谋程度越严重,标包基准价被拉升的幅度越高,MaxSameR每提高10%,标包基准价会被拉升63元左右,样本内MaxSameR最大值为0.48,估计该标包基准单价可以被拉升300元左右,可见串谋会给招标人带来严重损失。模型(2)为带有时间趋势的基准价影响因素分析,为了剔除原材料价格对报价的影响,因变量为基准价与原材料价格的差值T_Baseprice,代理市场利润,从图 1可以看出第7期起投标价格有显著的下跌,因此模型(2)将纳入虚拟变量Soph(期数t≤6),并加入Soph和Date以及Date2的交叉项,此外,为控制时期t其他因素可能对报价造成的影响,模型中将控制时期t市场上的竞争度,即市场上活跃投标人总数,以及时期t招标人投放的标包总数。
| 表 5 标包维度变量分析 |
模型(2)回归结果中,和模型(1)相同的自变量方向和大小均没有发生显著改变,说明了模型的稳健性。重点关注时间趋势,Soph=1也即前6期的T_Baseprice要显著高于后12期,其系数特别高是由于Date变量的取值范围导致。Date以及Date2的系数不显著,证明前6期内T_Baseprice变化无时间趋势,但Soph×Date系数显著为负,Soph×Date2系数显著为正,则说明了第6期后已有足够多的投标人采取了降价策略,引发了行业利润的下跌,但由于成本约束,投标人显然不会一直降价,Soph×Date2系数显著为正说明了降价幅度边际递减,逐渐趋于稳定,市场新的稳定利润预期形成。表 5模型(3)中的因变量为标包内投标报价的变异系数,衡量标包内报价的离散程度,回归结果可以看出,疑似串谋投标人比例越大,标包变异系数越大,由于变异系数是相对值在标包间可比,模型(3)中加入了时间趋势变量Date和Date2,Date系数显著为负,Date2系数显著为正说明了时间趋势上标包内报价的变异系数在不断降低,投标人报价离散度降低,投标人对市场基准价预期越来越趋向一致,该回归结果与表 4中模型(3)结果一致,说明了模型的稳健性,并再次验证了假设4内容,同时说明了低于均价中标法在投标人形成市场利润预期的过程中和标准均价中标法类似,但与标准均价中标法不同之处在于,低于均价法中由于投标人受到招标机制对报低价的激励,最后形成的稳定市场利润预期处于一个较低的位置,而不是标准均价中标法均衡下的高位。至此,低于均价法合理性的第二个特点得到了验证,最后的中标价格不会被确定在一个非常高的位置,而是在一个合理的低位。
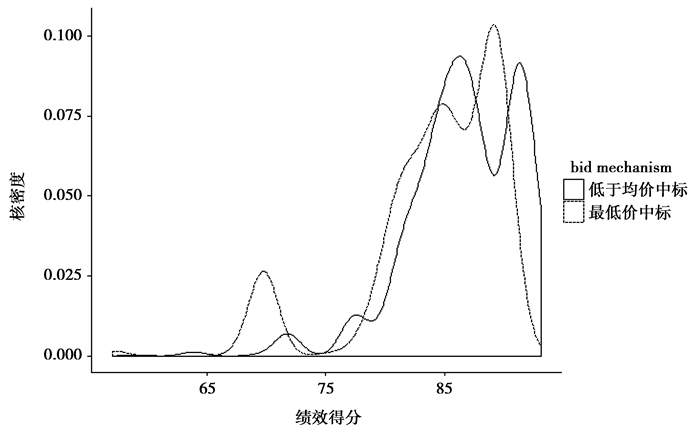
(六) 低于均价中标法下的“赢者诅咒”发生频率为验证低于均价中标法是否可以防止“赢者诅咒”发生的频率,本文搜集了2015年该大型电力企业对供应商的绩效评价得分,绩效评价得分衡量了供应商在投运角钢铁塔的产品质量、履约能力等方面的综合得分,可以一定程度上代理“赢者诅咒”程度,绩效得分越低,“赢者诅咒”程度越高。如图 2所示,分别为831次招标低于均价中标法下得分最高投标人与最低价的投标人的绩效表现分布情况,从非参数核密度分布可以看出,低于均价中标法下得分最高投标人的绩效得分相对最低价投标人要明显右移,说明低于均价中标法选择出的中标人产品质量和履约效果更优。另一方面,最低价投标人的绩效分布在65-75分之间有一个峰值,这种极低的绩效得分可以衡量“赢者诅咒”发生的频率,可以看出如果采用最低价中标法,在绩效得分极低区域,也即“赢者诅咒”发生的概率要远高于低于均价中标法。因此,可以看出相对于低价中标法,低于均价法可以在一定程度上降低“赢者诅咒”的概率,且选择出高绩效的供应商。
|
图 2 低于均价中标法下的中标人与最低价中标法下的中标人绩效分布对比 |
文章重点立足于一种常用的均价中标法的变形:低于均价中标法。理论上,本文在共同价值假设下严格证明了标准低于均价中标法不具备随真实成本严格递增的贝叶斯纳什均衡报价策略,同时与标准均价法不同,所有投标人报完全一样的价格不再是贝叶斯纳什均衡,在低于均价中标法下,投标人有动机向下报价以获得更高的中标概率。文章对某大型电力公司物资采购中角钢铁塔数据集进行分析,在该招标环境下一种低于均价中标法被用作多属性逆向拍卖中价格维度得分计算方法中,且价格维度得分主导了总得分,验证了低于均价中标法合理性需要满足的三个特点:一是投标人报价可以反映投标人真实成本;二是最后的中标价格在一个合理的低位;三是能够降低“赢者诅咒”的产生频率。本文针对低于均价中标法的主要结论如下:
(1) 参标行为上,投标人为获取更大的订单,更倾向于参加招标数量大的标包,且投标人倾向于参加具有成本优势的标包,也即本研究中投标人倾向于参加地理位置近、运输成本低的标包。
(2) 报价行为上,时间截面上投标人的投标报价可以反映投标人的真实成本,满足了低于均价中标法有效的第一个特点,也即本研究中投标人报价和市场上钢铁原材料价格、运输距离高度显著相关。这一现象不同于(Conley and Decarolis, 2016)研究结果中投标人报价与真实成本变量失去显著关系,其根本原因在于招标人在招标前对投标人资质进行初审,避免了Conley and Decarolis(2016)研究中存在的大量串谋行为——存在的大量的“影子企业”,也即只为陪标而参标的虚假企业。由于低于均价中标法对投标人报低价的激励,导致了时间截面上投标人报价行为和低价中标法下一样,可以反映投标人的真实成本,满足了低于均价中标法合理性的第一个特点。
(3) 时间趋势上的经验学习行为上,投标人从历史投标经验中学习,投标人整体对市场基准价预期、更具体来讲是市场利润的预期越来越接近,标包内报价变异系数减小,离散度降低,这和标准均价中标法类似,但不同之处在于由于低于均价中标法对报低价的激励,导致最终稳定的市场利润处于低位,投标人整体的预期利润被压缩,低于均价法并没有将中标价格确定在了一个高位,而是确定在了一个合理低位,满足了低于均价中标法合理性的第二个特点。
(4) 串谋行为上,和标准均价中标法一样,低于均价中标法下存在串谋投标人哄抬均价的现象。参与串谋的投标人会联盟足够人数的投标人,抬高报价操控基准价格,进而增加联盟中事先确定的被陪标对象中标概率和中标利润。本文实证中以投标人报完全相同的价格作为串谋的代理变量,研究发现随联盟人数增加,串谋投标人的抬价越高。虽然在任何一种招标模式下都存在串谋行为,但显然均价中标法下投标人串谋拉高基准价更加容易,其结果会给招标人带来巨大的采购成本损失。后文会具体针对这一现象提出解决方案。
(5) 机制效率上,低于均价中标法在使用前期更类似低价中标法,在时间截面上投标人会基于当期预期市场利润按照真实成本报低价,同时在时间趋势上激励投标人压低利润,当足够多的投标人采用降价策略时,会显著压低市场利润预期,但当行业整体利润已被压缩至低位时,低于均价中标法更类似于标准均价法,市场利润趋于稳定并很难继续被少数投标人压低,因此投标人没有动机报不理性的超低价造成“赢者诅咒”,只基于当期市场预期利润、按自身成本报价即可,也即将投标价格确立在了一个合理的低位。且通过对比和低价中标法确定的中标人的绩效分布,发现低于均价中标法可以降低“赢者诅咒”的发生频率,也即满足低于均价中标法合理性的第三个特点。而这正是均价中标法的设计初衷,指导投标人合理报价,避免恶性竞争、由于成本不确定性风险等因素带来的不理性超低报价,在降低采购成本的同时防止“赢者诅咒”的发生。
综上所述,低于均价中标法和低价中标法类似之处在于投标人报价在时间截面上可以反映其真实成本,在时间趋势上可以有效压缩投标人市场利润预期,而和标准均价法类似之处在于投标人可以从历史投标经验中学习、稳定这一较低市场利润的预期位置,采用报“合理低价”的策略防止“赢者诅咒”现象的发生,以上均说明了低于均价中标法在业界被广泛应用的合理性。
(二) 管理建议本文通过实证发现低于均价中标法既可以降低采购成本,又可以指导投标人合理报价降低“赢者诅咒”发生频率,因此本文认为低于均价中标法在实际中的普遍应用具备其合理性,且在一些领域具备很强的推广价值。本文针对低于均价中标法的使用提出以下建议:
(1) 该招标机制更适合竞争激烈、投标人数足够大的领域应用。均价中标法最大的缺陷即为投标人串谋难度降低,本文研究数据集中投标人竞争激烈,一次招标投标人数量平均达51个,在这种情况下串谋难度增大,串谋投标人需要找到足够联盟人数才能保证操控基准价成功,且串谋联盟内的陪标人显然有偏离动机。因此该方法对于投标人数量少、串谋联盟较易实现的领域并不适合。
(2) 设置下浮激励应足够明显。如在计算基准价前剔除高报价,增大下浮系数α、扣分系数a和b的距离。
(3) 对参标投标人在评标前进行初审,通过招标前对企业资质和既有业绩的审核,剔除虚假的、一类只为了陪标而存在的“影子企业”,这些企业通常没有历史业绩,由母公司设置的虚假企业,没有实际生产环境,招标人可以通过检查“既有业绩”、法人和管理人员同其他投标人是否存在交叉,进而实地考察厂房是否真实存在来检查这类“影子企业”的存在。
(4) 在标包的设置上,招标人应该继续深化集中招标的程度。增大标包内的招标数量,减少标包个数。从串谋投标人串谋方式可以看出,联盟内需要轮流进行“陪标”,因此需要参与足够多的标包保证联盟内投标人均能够成为被“陪标”的对象。因此深化集中招标一方面可以从规模效应、批发价优势的角度获得更低的采购成本,另一方面也可以增大串谋投标人“陪标”的机会成本,使得串谋投标人联盟难以稳定维持。
(5) 评标结束后,只公开中标人,不必公开中标人和其他投标人的报价。这一做法首先使得串谋投标人无法观察联盟内部是否有成员偏离“陪标”报价,减弱串谋联盟的稳定性;其次可以防止投标人市场过快形成较高的稳定市场利润预期,有利于市场预期利润的压低。
(6) 加大串谋投标人识别和惩罚力度。除“影子企业”外,绝大部分串谋企业是符合投标资格的真实企业,本文已经提供两种简单识别串谋投标人的方式,一是同标包内报价完全相同,二是标包内报价变异系数过高。我国颁布的《招标投标法实施条例》中39条-41条明确指出了串标投标的认定方式,招标人可以按照条例内容采取法律手段防治串谋投标人对招标人造成的损失。除法律维权外,招标人也可以对招标机制做细微调整,在事前对串谋进行预防,如:计算基准价时相同的报价只利用一次,减少多个相同报价对基准价格的影响;计算基准价时,投标价差在一定范围内的报价,只采用该范围内的均值等。此外,也可以对投标价格本身进行统计分析,如Padhi and Mohapatra(2011)提出对投标价格进行聚类,串谋投标人存在于投标价格显著更高的类别中。《招标投标法实施条例》40条规定“不同投标人的投标文件异常一致或者投标报价呈规律性差异”可认定为串谋,在之后的研究里,作者将针对“投标报价呈规律性差异”这一点,继续探讨均价中标法中如何识别串谋投标人的有效方式。
| [] |
郑筱婷,
2010, “BAMs的均衡报价性质及其对合谋的激励”, 《南方经济》, 第 3 期, 第 46–62 页。 |
| [] |
郑筱婷、张永刚、卢云锋,
2011, “建筑业招投标中'平均价中标'的实验研究”, 《产经评论》, 第 6 期, 第 52–63 页。 |
| [] |
Bajari P., Hortacsu A., 2003, "The Winner's Curse, Reserve Prices and Endogenous Entry:Empirical Insights from eBay Auctions". The RAND Journal of Economics, 34(99), 329–355.
|
| [] |
Bajari P., 2006, "Bidding for Incomplete Contracts:an Empirical Analysis". American Economic Review, 104(4), 1288–1319.
|
| [] |
Bajari P., Ye L., 2003, "Deciding Between Competition and Collusion". Review of Economics and Statistics, 85(4), 971–989.
DOI:10.1162/003465303772815871 |
| [] |
Bichler M., Schneider S., Guler K. and Sayal M, 2011, "Compact bidding languages and supplier selection for markets with economies of scale and scope". European Journal of Operational Research, 214(1), 67–77.
DOI:10.1016/j.ejor.2011.03.048 |
| [] |
Branzoli N., Decarolis F., 2015, "Entry and Subcontracting in Public Procurement Auctions". Management Science, 61(12), 2945–2962.
DOI:10.1287/mnsc.2014.2071 |
| [] |
Camerer C. F., Ho T. H. and Chong J. K., 2004, "A Cognitive Hierarchy Model of Games". The Quarterly Journal of Economics, 119(3), 861–898.
DOI:10.1162/0033553041502225 |
| [] |
Chang W. S., Chen B. and Salmon T. C., 2014, "An Investigation of the Average Bid Mechanism for Procurement Auctions". Management Science, 61(6), 1237–1254.
|
| [] |
Che Y. K., 1993, "Design Competition Through Multidimensional Auctions". The RAND Journal of Economics, 24(4), 668–680.
DOI:10.2307/2555752 |
| [] |
Chen, J., 2011, "Returns with wholesale-price-discount contract in a newsvendor problem", International Journal of Production Economics.
|
| [] |
Conley T. G., Decarolis F., 2016, "Detecting Bidders Groups in Collusive Auctions". American Economic Journal:Microeconomics, 8(2), 1–38.
|
| [] |
Crawford V. P., Iriberri N., 2007, "Level-k Auctions:Can a Nonequilibrium Model of Strategic Thinking Explain the Winner's Curse and Overbidding in Private Value Auctions?". Econometrica, 75(6), 1721–1770.
DOI:10.1111/ecta.2007.75.issue-6 |
| [] |
David E., Azoulay-Schwartz R. and Kraus S., 2006, "Bidding in Sealed-bid and English Multi-attribute Auctions". Decision Support Systems, 42(2), 527–556.
DOI:10.1016/j.dss.2005.02.007 |
| [] |
Decarolis, F., 2013, "Comparing Public Procurement Auctions", Boston University Department of Economics Working Paper.
|
| [] |
Decarolis, F., 2014, "Awarding price, Contract Performance, and Bids Screening:Evidence from Procurement Auctions", American Economic Journal:Applied Economics, 6(1):108-132.Galavotti, S. (n.d.). Sophistica-ted Bidders in Beauty-Contest Auctions, 1-37.
|
| [] |
Gil, R.and Oudot, J. M., 2009, "Competitive Bidding, Renegotiation and Relational Contracting:Evidence from French Defense Procurement", Working Paper.
|
| [] |
Heckman J., 1979, "Sample Specification Bias as a Selection Error". Econometrica, 47(1), 153–162.
DOI:10.2307/1912352 |
| [] |
Hong H., Shum M., 2002, "Increasing Competition and the Winner's Curse:Evidence from Procurement". The Review of Economic Studies, 69(4), 871–898.
DOI:10.1111/roes.2002.69.issue-4 |
| [] |
Ioannou P. G., Awwad R. E., 2010, "Below-Average Bidding Method". Journal of Construction Engineering and Management, 136(9), 936–946.
DOI:10.1061/(ASCE)CO.1943-7862.0000202 |
| [] |
Kagel, J. H.and Levin, D., 2009, Common value auctions and the winner's curse, Published by Princeton University Press.
|
| [] |
Lind B. B., Plott C. R., 1991, "The Winner's Curse:Experiments with Buyers and with Sellers". The American Economic Review, 81(1), 335–346.
|
| [] |
Maddala, G. S., 1986, Limited-dependent and qualitative variables in econometrics, Published by Cambridge University Press.
|
| [] |
Padhi S. S., Mohapatra P. K. J., 2011, "Detection of collusion in government procurement auctions". Journal of Purchasing and Supply Management, 17(4), 207–221.
DOI:10.1016/j.pursup.2011.03.001 |
| [] |
Pilehvar, A., Elmaghraby, W. J., and Gopal, A., 2016, "Market Information and Bidder Heterogeneity in Secondary Market Online B2B Auctions", Management Science, Articles in Advance:1-26.
|
| [] |
Porter R. H., Zona J. D., 1991, "Ohio School Milk Markets:An Analysis of Bidding". The RAND Journal of Economics, 30(2), 263–288.
|
| [] |
Spagnolo G., Albano G. L. and Bianchi M., 2006, "Bid Avarage Methods in Procurement". Rivista Di Politica Economica, 96(1), 41–62.
|
| [] |
Zeynalian M., Trigunarsyah B. and Ronagh H. R, 2013, "Quick Abnormal-Bid-Detection Method for Construction Contract Auctions". Journal of Construction Engineering and Management, 138(1), 51–60.
|
| [] |
Zona R. H. P., J.D. , 1993, "Detection of Bid Rigging in Procurement Auctions". Journal of Political Economy, 101(3), 518–538.
DOI:10.1086/261885 |



