自2012年召开中共十八大以来,党中央和国务院高度重视生态文明建设和绿色低碳发展,提出了政治、经济、文化、社会和生态文明建设“五位一体”的纲领性战略,2016年中美两国在G20杭州峰会上向联合国交存《巴黎协定》,标志着中国将在应对全球气候变化和保护生态环境方面担当大任。工业是中国经济的命脉和基石,也是能源消耗和环境污染大户。2007-2013年间中国工业增加值GDP贡献率平均为40%,而工业电力消费量占全国电力可供量73.27%,且工业电力消费量年均增长率为8.06%,工业二氧化硫和烟粉尘排放量分别占全国同类污染物排放量的87.59%和85.64%,同时二氧化碳和工业废气排放量分别以7.63%和10.14%的年均增长率不断增加,因此提升工业部门的绿色发展效率是首要任务。
现有关于工业绿色发展效率的研究主要将资源环境约束引入评估模型,如Watanabe and Tanaka(2007),Liu and Zhang(2012)和王兵、黄人杰(2014),或将非合意产出和合意产出引入评估模型,如Watanabe and Tanaka(2007),李艳军、华民(2014)和班斓、袁晓玲(2016)等。具体来看,已有文献对绿色发展效率测度及影响因素的研究范围主要涵盖区域、城市和产业三个层面,并从技术进步、能源环境、外资投入和产业结构等多方面考察了绿色发展效率的影响因素。在区域层面,按照东部、中部和西部三大区域划分方法考察区域绿色发展效率并对比区域间绿色发展效率差异,普遍结论是绿色发展效率在区域间存在明显差异,表现出东、中、西部地区呈递减分布特征。汪克亮等(2013)研究表明东部地区实现了全国潜在最优绿色生产技术的98%以上,而中西部地区则仅实现了11.38%和21.34%。钱争鸣、刘晓晨(2014)发现东部地区绿色经济效率水平最高,西部次之,中部最低。技术进步是效率改善的主要动力(汪克亮等,2013;钱争鸣、刘晓晨,2014;王兵、黄人杰,2014),另外环境管制、FDI、能源强度、教育投资、产业结构等也是影响绿色发展效率区域间差异的重要原因(钱争鸣、刘晓晨,2014;班斓、袁晓玲,2016;Yue et al., 2016)。在城市层面,李艳军、华民(2014)和聂玉立、温湖炜(2015)研究发现中部城市的绿色发展效率表现最差;王兵等(2014)研究表明东、中、西部地区绿色发展效率呈梯次下降趋势。影响城市绿色发展效率的因素更体现出城市间的“禀赋差异”,李艳军、华民(2014)和聂玉立、温湖炜(2015)认为经济水平和产业结构是影响城市绿色经济效率的关键原因,产业结构优化和升级、外资利用、科技投入提高对促进绿色经济效率有显著的积极影响,岳书敬等(2015a, 2015b)认为集聚对城市绿色发展效率的影响随集聚由弱变强呈先提高后降低的非线性变化趋势,除此之外,卢丽文等(2016)认为资源过度消耗和环境污染物过度排放是导致中部长江经济带绿色发展效率不高的主要原因。在行业层面,绿色发展效率的研究主要集中对工业绿色发展效率的研究,该类研究的共性是将能源消耗、环境污染、对外贸易、技术进步、工业结构等纳入工业绿色发展效率评价体系,如Watanabe and Tanaka(2007)和Liu and Zhang(2012)等,李静、倪冬雪(2015)从绿色生产和环境治理两个层面考察工业绿色发展效率。另外,部分学者还从可持续发展、全要素生产率和绿色技术等方面研究工业绿色发展,如陈诗一(2009, 2010)和景维民、张璐(2014)等人。通过对已有文献的梳理,发现对绿色发展效率的研究视点聚焦于能源耗费和环境污染。另外也有涉猎合意和非合意产出方面,但该类研究对绿色发展效率评估的维度狭窄,忽略了工业绿色发展效率在投入端和产出端的关联关系,没有同时考虑能源耗费、环境污染和合意产出的关系;其次对绿色发展效率评估维度的指标考虑不全面,如在资源维度中忽略工业用水、在生态维度中忽略二氧化碳,也没有将技术研发纳入评估体系;第三是指标测算不全面,主要是缺少对二氧化碳排放量和工业增加值的合理测算。
2016年国家发改委指出要全面推进输配电价改革试点,加快建立独立的输配电价体系,有序推进电价市场化改革。对电价的研究主要集中于合理定价和交叉补贴测算以及电价交叉补贴对社会福利的影响,如Kopsakangas-Savolainen(2004),Qi et al.(2008),Lin and Jiang(2011)等人采用拉姆齐定价模型,刘思强等(2015)从电压等级和用户类型方面;齐放等(2009)以及唐要家、杨健(2014)等人研究了电价交叉补贴对社会福利的影响。我国电力价格为承担社会目标而发生了水平扭曲和结构扭曲(唐要家、杨健,2014;谢品杰等,2015),电价交叉补贴的实施导致电力价格隐藏了电力市场的供需和竞争等重要信息,电价交叉补贴从要素投入和成本机制方面对工业绿色发展效率会有影响,并且该影响可能是多途径的。
综合分析现有文献发现,第一,已有关于绿色发展效率的研究未将研发强度纳入测算模型,很多研究亦未将二氧化碳和二氧化硫等重要污染指标纳入绿色效率指标体系;第二,测算电价交叉补贴程度的技术性障碍没有得到解决;第三,电价交叉补贴对绿色发展效率的影响途径尚未清晰。针对上述不足之处,本文拟将提出相应的解决办法:第一,从经济、资源和生态维度构建完整的工业绿色发展效率评估体系,构造包含研发强度的四要素生产技术函数;第二,用拉姆齐定价模型测算中国工业用电的理论电价,用价差法测算工业承担的电价交叉补贴程度;第三,在模型中设置交叉项,从要素投入和成本机制两方面探究电价交叉补贴对工业绿色发展效率的影响途径。
具体地,本文将从两个层面分三个步骤探究电价交叉补贴对中国工业绿色发展效率的影响。其一是总量研究,将各控制变量的实际值直接引入模型,考察电价交叉补贴对工业绿色发展效率的总量影响和地区间的绝对差异;其二是单位分量研究,考虑各地区经济水平差异显著,将各控制变量与相应变量的比例值引入模型;采用相同研究范式进行总量和单位分量研究,首先运用非径向方向距离函数数据包络(NDDF-DEA)技术评估中国工业绿色发展效率;其次结合拉姆齐定价模型和价差法从工业视角测算电价交叉补贴,并在控制环境管制、对外出口、外商资本等因素的基础上构建Tobit模型,采用归并最小离差法(CLAD,Censored Least Absolute Deviations)分析电价交叉补贴对工业绿色发展效率的影响和区域差异;最后探究了电价交叉补贴对全国、东部、中部和西部地区工业绿色发展效率的影响途径。
二、理论分析和研究假设工业承担的电价交叉补贴是对其实际供电成本的向上偏离,实质是工业用电的要素价格相对理论电价水平提高了。假定工业部门的规模报酬和要素投入比例保持不变,受电价交叉补贴影响而减少的电力要素投入会导致工业产出规模缩小,工业非期望产出和期望产出也随之增减变化,进而会导致工业绿色发展效率下降,因为工业企业电力要素的被替代性较低(Ma et al., 2008;于立宏、贺媛,2013;Wesseh et al., 2013)。如果工业企业不改变电力要素投入,那么就要承担由于电力要素替代性较低而导致企业成本增加的压力,如果工业企业为了控制成本而减少电力要素投入,那么在规模报酬不变的假设下,工业企业的产出会减少,此处规模报酬不变假设与NDDF-DEA测算的假设一致。为保持工业绿色发展效率水平至少不变的发展目标,工业期望产出也必须至少不变或提高,这实际是提高电价交叉补贴程度和提高工业绿色发展效率二者之间的矛盾,因此工业承担的电价交叉补贴引致期望产出减少的后果是绿色发展效率下降,电价交叉补贴通过要素投入和成本机制影响工业绿色发展效率。
(一) 要素投入电力价格相对终端消费者是外生的(Bjørner et al., 2001),由于中国电力行业承担着电力普遍服务等多任务社会目标(Lin and Jiang, 2011),电价结构的调整受非市场因素影响较大。当电价变化时终端用户会通过调整电力消费量以适应电价变化(Rodrigues and Linares, 2015),工业企业为控制生产成本,保护利润空间,在短期无法实现要素投入结构和生产技术改善的情况下,只能被动地通过调整电力消费量适应电价变化。在现实中,工业用户电力要素的被替代性很低,电价交叉补贴会导致工业减少电力消费量,在短期生产技术无法实现提升的情况下,电价交叉补贴将直接导致工业期望产出减少,通过经济维度对工业绿色发展效率产生消极影响,即电价交叉补贴可能对工业绿色发展效率产生不利影响。
再从对外出口视角分析,企业通过流通环节将电力要素价格增加部分转移到出口品价格上,将导致其失去出口价格的比较优势,故电价交叉补贴还有可能导致工业出口量下降,进而从经济维度影响工业绿色发展效率评估。另一方面,发展中国家环境管制力度较弱,生产技术水平较低,出口品生产通常表现出“非绿色”特征(景维民、张璐,2014),这从生态维度和资源维度对工业绿色发展效率评估产生不利影响。因此通过要素替代和对外出口缓冲电价交叉补贴对工业绿色发展绩效的影响可能成效甚微。基于上述分析,本文提出有待检验的理论假设:
假设1:电价交叉补贴不利于工业绿色发展效率提高,要素投入是电价交叉补贴影响工业绿色发展效率的途径之一。
(二) 成本机制电价交叉补贴既不利于工业企业实施成本控制,也不利于其实现利润最大化目标。电价交叉补贴承担的首要社会任务目标是电力普遍服务,对高耗能高污染行业征收环境税是电价交叉补贴的次要职能,电价交叉补贴对所有工业企业而言具有普遍性,但所有工业企业并不都是高耗能高污染,因此如果让电价交叉补贴完全承担征收环境税的职能将有失公平。但又不可置否地,电价交叉补贴确实承担了部分环境管制职能(唐要家、杨健,2014),从这个角度分析,工业企业承担的电价交叉补贴越高,说明工业为污染环境所承担的成本就越大,工业企业也可能因此减少对环境的污染,这对工业绿色发展效率产生积极影响。
但并不是所有工业企业都是高耗能高污染,如果通过普遍性的电价交叉补贴去履行环境管制职能,则有失效率和公平,这样电价交叉补贴就会从经济维度对低耗能低污染工业企业的绿色发展效率产生消极影响。上述积极影响和消极影响是通过不同维度对工业绿色发展效率产生影响的,但本文工业绿色发展效率涵盖经济维度、资源维度和生态维度,通过经济维度的消极效应和通过生态维度的积极效应不一定能“对冲”。因此,电价交叉补贴通过成本机制和环境管制强度影响工业绿色发展效率是可能的,基于上述分析,本文提出有待检验的理论假设:
假设2:电价交叉补贴通过成本机制影响工业绿色发展效率,电价交叉补贴通过环境管制强度对工业绿色发展效率产生影响。
三、工业绿色发展效率动态测算本文将工业产出划分为期望产出和非期望产出两类,电价交叉补贴通过要素投入和成本机制对工业期望产出和非期望产出有不同程度的影响,两种产出的增减变化极可能是不同比例。本文构建包含研发投入在内的四要素生产函数,结合非期望产出和期望产出不同比例变化的现实情况,借鉴Zhou et al.(2012)、Wang et al.(2013)、Zhang et al.(2014)、Wang et al.(2016)等的研究范式,本文选用NDDF-DEA方法考察中国工业绿色发展效率。
假定规模报酬不变,资本(K)、劳动(L)、能源(E)和技术(R)为投入要素,工业增加值为期望产出(Y),六类污染物(见表 1)为非期望产出(U),描述一个多投入多产出生产技术,且假定该技术满足生产理论的标准公理(Føre and Grosskopf, 2005;Zhang et al., 2014),一般地:
| $ T = \left\{ {K, L, E, R, Y, U:\left({K, L, E, R} \right)能生产\left({Y, U} \right)} \right\} $ | (1) |
| 表 1 中国工业绿色发展效率指标体系 |
令投入集为I(Y, U),产出集为P(K, L, E, R), 用产出集描述该生产技术写为:
| $ P(K, L, E, R) = \{ (Y, U):(K, L, E, R, Y, U)\} \in T $ | (2) |
根据Føre et al.(1989)、Føre et al.(2008)、王兵等(2008)、张可、丰景春(2016)的研究假定,上述生产技术应满足弱可处置性和零结合性,并且投入要素和期望产出具备强可处置性。如果存在N个决策单元,上述生产技术可被具体描述为:
| $ T = \left\{ \begin{array}{l} (K, L, E, R, Y, U){\rm{ }}:\sum\limits_{n = 1}^N {{z_n}{K_n} \le K, } \sum\limits_{n = 1}^N {{z_n}{L_n} \le \rm{L}, } \sum\limits_{n = 1}^N {{\rm{ }}{z_n}{E_n} \le E, } \\ \sum\limits_{n = 1}^N {{z_n}{R_n} \le R, } \sum\limits_{n = 1}^N {{z_n}{Y_n} \ge Y, } {\rm{ }}\sum\limits_{n = 1}^N {{z_n}{U_n} = U, {z_n} \ge 0, n = 1, 2, 3, ..., N} \end{array} \right\} $ | (3) |
对每个决策单元绿色发展效率的非径向方向距离函数定义如下:
| $ \overrightarrow D \left({K, L, E, R, Y, U:{\rm{g}}} \right) = {\rm{sup}}\left\{ {{w^T}B:\left({\left({K, L, E, R, Y, U} \right) + {\rm{g}} \times diag\left(B \right)} \right) \in T} \right\} $ | (4) |
其中,g=(-gK, -gL, -gE, -gR, +gY, -gU)为方向向量,符号表示各要素的期望方向,即“-”表示该要素越少越好,“+”表示该要素越多越好;B=(βK, βL, βE, βR, βY, βU)为松弛向量,表示各要素增减变化的比例;WT=(wK, wL, wE, wR, wY, wU, )为权重向量,权数大小表示各要素在生产技术中的相对重要性。借鉴Barros et al.(2012)、Zhou et al.(2012)、Zhang et al.(2014)等的做法,本文假设投入、期望产出和非期望产出对工业绿色发展效率同等重要,且投入的资本、劳动、能源和技术四类要素对期望和非期望两类产出也同等重要,故将四类要素和两类产出的权重矩阵取为
| $ {\overrightarrow D _T}\left({K, L, E, R, Y, U:{\rm{g}}} \right) = {\rm{max}}{w_K}{\beta _K} + {w_L}{\beta _L} + {w_E}{\beta _E} + {w_R}{\beta _R} + {w_Y}{\beta _Y} + {w_U}{\beta _U} $ | (5) |
| $ s.t.\sum\limits_{n=1}^{N}{{{z}_{n}}{{K}_{n}}\le K-{{\beta }_{Y}}{{g}_{Y}},}\sum\limits_{n=1}^{N}{{{z}_{n}}{{L}_{n}}\le \rm{L-}{{\beta }_{L}}{{g}_{L}},}\\\sum\limits_{n=1}^{N}{{{z}_{n}}{{E}_{n}}\le E-{{\beta }_{E}}{{g}_{E}},}\sum\limits_{n=1}^{N}{{{z}_{n}}{{R}_{n}}\le R-{{\beta }_{R}}{{g}_{R}},} $ |
| $ \sum\limits_{n = 1}^N {{z_n}{Y_n} \ge Y + {\beta _Y}{g_Y}, } \sum\limits_{n = 1}^N {{z_n}{U_n} = U - {\beta _U}{g_U}, {z_n} \ge 0, \\n = 1, 2, 3, ..., N;{\beta _K}, {\beta _L}, {\beta _E}, {\beta _R}, {\beta _Y}, {\beta _U} \ge 0} $ |
令方向向量
| $ \begin{array}{l} GEI = \frac{1}{5}\left[ \begin{array}{l} \frac{{{Y_m}/{K_m}}}{{({Y_m} + \beta _{mY}^*{Y_m})/({K_m} - \beta _{mK}^*{K_m}){\rm{ }}}} + \frac{{{Y_m}/{L_m}}}{{({Y_m} + \beta _{mY}^*{Y_m})/({L_m} - \beta _{mL}^*{L_m})}} + \frac{{{Y_m}/{E_m}}}{{({Y_m} + \beta _{mY}^*{Y_m})/({E_m} - \beta _{mE}^*{E_m})}}\\ \frac{{{Y_m}/{R_m}}}{{({Y_m} + \beta _{mY}^*{Y_m})/({R_m} - \beta _{mR}^*{R_m})}} + \frac{{{Y_m}/{U_m}}}{{{\rm{ }}({Y_m} + \beta _{mY}^*{Y_m})/({U_m} - \beta _{mU}^*{U_m})}} \end{array} \right]\\ = \frac{1}{5}\left[ {\frac{{(1 - \beta _{mK}^*) + (1 - \beta _{mL}^*) + (1 - \beta _{mE}^*) + (1 - \beta _{mR}^*) + (1 - \beta _{mU}^*){\rm{ }}}}{{1 + \beta _{mY}^*}}} \right]\\ = \frac{{1 - 1/5(\beta _{mK}^* + \beta _{mL}^* + \beta _{mE}^* + \beta _{mR}^* + \beta _{mU}^*)}}{{1 + \beta _{mY}^*}}, m = 1, 2, 3, ..., M. \end{array} $ | (6) |
需要明确指出的是“工业增加值”和“二氧化碳”的算法,本文根据工业增加值指数算法倒推出2008年后续年份的工业增加值。具体算法为:
| $ {Y_t} = {Y_{t - 1}} \times {I_t} $ |
其中Yt表示当期工业增加值,Yt-1前一期名义工业增加值,It表示当期工业增加值指数,本文将各期工业增加值以2002年为不变价格进行平减。
另外,能源投入根据《中国能源统计年鉴》中“各种能源折标准煤参考系数表”折算为标准煤单位,二氧化碳排放量根据IPCC碳排放系数测算,以2002年为不变价格。可参考陈诗一(2009)根据IPCC二氧化碳的计算方法:
| $ C{O_2} = \sum\limits_{i = 1}^n {C{O_{2, i}}} = \sum\limits_{i = 1}^n {{E_i} \times NC{V_i} \times CE{F_i} \times CO{F_i} \times \left({44/12} \right)} $ |
CO2表示二氧化碳排放总量,Ei表示各种能源消费量,NCVi表示各种一次能源平均低位发热量(净发热值),CEFi表示IPCC(2006)提供的碳排放系数,COFi表示碳氧化因子,44和12分别表示二氧化碳和碳的分子量,根据IPCC(2006)碳排放系数表,本文把各种能源的碳氧化因子均设定为1,具体测算结果如表 2所示。
| 表 2 中国工业碳排放系数 |
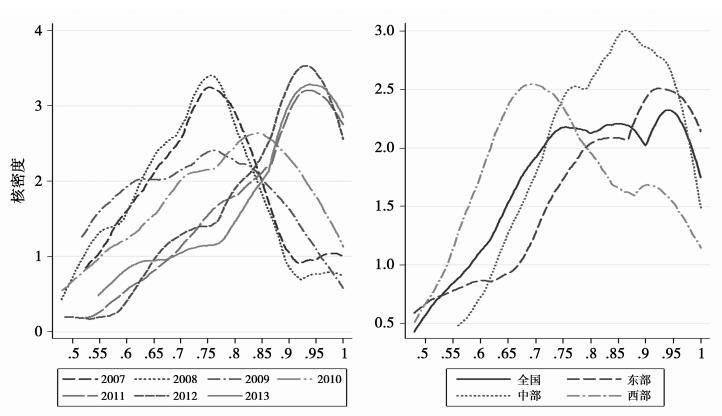
图 2为工业绿色发展效率核密度图,图 2(左)工业绿色发展效率介于0.8到0.85之间时,其概率密度出现明显分化,而0.8恰是工业绿色效率的全国平均水平,随后2011-2013年工业绿色发展效率的概率密度呈上升趋势,说明工业绿色发展效率密度在大于0.85的范围内分布密集,表明工业绿色发展效率有所提升。从图 2(右)可以看出全国工业绿色发展效率密集分布在0.75到0.85之间,而东部地区工业绿色发展效率相对密集分布在0.85至1区间内,且高于全国工业绿色发展效率水平,西部地区工业绿色发展效率密集分布在0.7至0.75,中部地区工业绿色发展效率密集介于0.75到0.85之间,说明东部地区工业绿色发展效率整体水平最高,中部地区次之,西部地区最低,这与实践经验和现有研究结果基本相符。
|
图 2 工业绿色发展效率核密度图 |
以2007-2013年中国除西藏、港澳台之外的30个省、直辖市和自治区为样本,数据来源于2008-2014年《中国工业统计年鉴》和《中国环境统计年鉴》。表 3中Panel A对总量研究(模型1、2)的各变量进行了描述,Panel B对作为稳健性检验的单位分量研究(模型1A、2A)进行了变量描述,在对数化处理过程中,当变量值小于1时,在弹性模型中用lnx′=ln(x+1)算法取对数。
| 表 3 变量的描述性统计 |
第一,核心解释变量。价差法是用参考价格与实际价格之差衡量能源价格补贴程度(IEA,1999),本文根据唐要家、杨健(2014)的做法,将拉姆齐价格作为参考价格。因为中国销售电价用户结构具有明显的“逆拉姆齐”现象(唐要家、杨健,2014),那么对中国工业部门承担的交叉补贴应该用“逆价差法”,即实际价格与参考价格之差。
借鉴Resende(1997)、Berry(2000)、Kopsakangas-Savolainen(2004)、席平建(2005),Qi et al.(2008, 2011)、唐要家、杨健(2014)等人的研究,拉姆齐定价公式可写为:
| $ \frac{{P\left(q \right) - MC\left(q \right)}}{{P\left(q \right)}} = \frac{\lambda }{{1 + \lambda }}{\rm{ }}\cdot{\rm{ }}\frac{1}{{e\left({P\left(q \right)} \right)}} $ | (7) |
P (q)为工业实际电价,MC (q)为电网企业边际成本,e(P (q))为工业电力需求价格弹性,令
| $ ({p_i} - M{C_i})\cdot{q_i} = \frac{{{k_i}\cdot\alpha }}{{{e_i}}}\cdot{\rm{ }}{({\rm{ }}\frac{{MC\cdot{e_i}}}{{{e_i} - \alpha }}{\rm{ }})^{1 - {e_i}}} = {\rm{F}} $ | (8) |
F为企业固定成本,qi和pi分别表示各地工业电力消费量和工业电价,ki为尺度项,MCi为边际成本,其中qi=ki·pi-e为得到拉姆齐价格需要进一步计算拉姆齐指数α和需求价格弹性ei,α由(8)式计算得到,ei由全弹性模型(9)计算得到。
| $ {\rm{ln}}{{\rm{q}}_{{\rm{i}},{\rm{t}}}} = {\beta _0} + {\beta _1} \times {\rm{ln}}\;{{\rm{y}}_{{\rm{i}},{\rm{t}}}} - {\beta _{\rm{2}}} \times {\rm{ln}}\;{{\rm{p}}_{{\rm{i}},{\rm{t}}}}{\rm{ + }}\sum\limits_{{\rm{i = 1}}}^{{\rm{30}}} {{\rm{ }}\left( {{{\rm{ \mathsf{ γ} }}_{\rm{j}}} \times {{\rm{D}}_{\rm{i}}}} \right)} {\rm{ + }}\sum\limits_{{\rm{i = 1}}}^7 {\left( {{{\rm{w}}_{\rm{j}}} \times {{\rm{T}}_{\rm{t}}}} \right){\rm{ + }}{{\rm{ \mathsf{ μ} }}_{{\rm{i}},{\rm{t}}}}} $ | (9) |
在(9)式中qi, t,yi, t,pi, t,Di和Tt分别表示各省工业电力消费量,工业增加值和实际电价,地区虚拟变量和年份虚拟变量,μi, t表示随机误差。(9)式得到工业电力消费需求模型结果的回归结果:
| $ {\rm{ln}}{q_{i, t}} = 8.734 + 0.502{\rm{ln}}{y_{i, t}} - 1.306{\rm{ln}}{p_{i, t}} + \sum\limits_{i = 1}^{30} {({\gamma _j} \times {D_i})} + \sum\limits_{t = 1}^7 {({\omega _j} \times {T_t}) + {\mu _{i, t}}} $ | (10) |
其中R2=0.6353,说明模型整体拟合度较好,F=23.52在10%的显著性水平上显著,估计结果显示中国工业电力需求价格弹性为-1.306,电力需求收入弹性为0.502。为了得到工业部门拉姆齐参考电价,可将拉姆齐定价模型描述为:
| $ R{P_i} = \frac{{{e_i}\cdot{M}{C_i}}}{{{e_i} - \alpha }} $ | (11) |
结合价差法算法,用EPi和RPi分别为实际电价和参考电价,工业承担的单位电价交叉补贴额为:
| $ P{G_i} = E{P_i} - R{P_i} $ | (12) |
第二,控制变量。在研究电价交叉补贴对工业绿色发展效率影响的模型中,本文还控制了可能影响该效率的其他因素:(1)电力消费量(Elec)。电力消费量反映工业要素需求,要素价格与要素需求呈反向关系,电价交叉补贴可能从投入端影响工业产出,进而影响工业绿色发展效率; (2)主营成本(Cost)。要素成本属于主营成本范畴,电价交叉补贴提高将直接导致要素成本上升,企业为控制成本可能会减少技术创新投资、节能减排设备更新和调整要素投入结构; (3)利润总额(Profit)。用利润总额衡量工业经营成果; (4)环境管制(Regulation)。中国环境管制机制尚未成形,排污费仅能反映环境污染的部分成本,根据Berman and Bui(2001)和Lanoie et al.(2008)做法,本文用工业治污总投资额与主营业务收入之比衡量环境管制强度; (5)对外出口(Export)。用出口交货值衡量工业对外出口情况,反映出口导向对工业绿色发展效率的影响; (6)外商资本(Forcapt)。用外商投资和港澳台投资总额衡量外商资本对工业的投资情况; (7)所有权结构(Ownstr)。不同所有权制度产生不同的激励机制,对企业生产效率、资源配置和利用效率有很大影响,本文用国家资本占实收资本比重衡量所有权结构; (8)集聚程度(Cluster)。工业集聚程度存在显著的区域性差异,反映该地区工业发展和基础设施环境,可能会促进工业绿色发展,借鉴Wen(2004)和金煜等(2006)以“各个地区工业产值占当年全国总的工业GDP的比重”作为度量工业集聚的变量,本文用各省工业总产值与全国工业总产值比值衡量集聚程度。
(三) 模型设计及检验考虑到工业绿色发展效率指数是介于0到1之间的截尾数据,借鉴Li and Wang(2014)和林伯强、刘泓汛(2015)的做法,本文以Tobit模型为基础模型,构建如下模型:
| $ {GEI_{i, t}^ * = \alpha + \beta \times Crosu{b_{i, t}} + \sum\limits_{k = 1}^K {} \left({{\gamma _i} \times X_{i, t}^j} \right) + {\omega _i} + {\lambda _t} + {\mu _{i, t}}{\rm{ }}\left({模型1, 1{\rm{A}}} \right)} $ |
| $ GEI_{i, t}^ * = {\rm{ }}\alpha + \beta \times Crosu{b_{i, t}} + \sum\limits_{k = 1}^K {} \left({{\gamma _i} \times X_{i, t}^j} \right) \\+ \sum\limits_{m = 1}^M {} {\delta _i} \times Crosu{b_{i, t}} \times A_{i, t}^m + {\omega _i} + {\lambda _t} + {\mu _{i, t}}\left({模型2,2{\rm{A}}} \right) $ |
| $ {其中有:{\rm{GE}}{{\rm{I}}_{{\rm{i, t}}}}{\rm{}}\left\{ \begin{array}{l} {\rm{GEI}}_{{\rm{i, t}}}^{\rm{*}}, if\;\;{\rm{GEI}}_{{\rm{i, t}}}^{\rm{*}} \in \left({0, 1} \right]\\ 1, \;\;if\;\;{\rm{GEI}}_{{\rm{i, t}}}^{\rm{*}} \in \left({1, + \infty } \right)\\ 0, \;\;if\;\;{\rm{GEI}}_{{\rm{i, t}}}^{\rm{*}} \in \left({ - \infty, 0} \right) \end{array} \right\}{{\rm{ \mathit{ μ} }}_{{\rm{i, t}}}}|{\rm{X}} \sim {\rm{N}}(0, {{\rm{ \mathit{ σ} }}^2})} $ |
Tobit模型中GEIi, t*是GEIi, t响应GEIi, t的潜变量,且满足经典线性模型假定,GEIi, t和Crosubi, t分别表示测算第i个省份第t年的工业绿色发展效率和单位电价交叉补贴,Xi, tj表示第j个控制变量,Ai, tm表示第m个中介变量ωi,λt和μi, t分别表示个体非观测效应,时间非观测效应和特异误差。
Tobit模型的随机扰动项不服从正态分布时,准极大似然估计(QMLE)不满足一致性要求,故首先应进行条件矩检验(Skeels and Vella, 1999)。表 4报告Tobit估计模型CM检验结果,检验结果表明在1%的显著性水平上拒绝“随机扰动项服从正态分布”原假设,故认为使用Tobit模型不稳健,不能使用Tobit回归方法分析电价交叉补贴对工业绿色发展效率的影响。然而,CLAD仅要求扰动项为独立同分布,在非正态分布情况下可以得到QMLE的一致估计(Powell,1984)。
| 表 4 CM检验结果 |
由于中国工业电价数据来源受限,原始样本只包含210观测值,根据Efron(1979)的研究和Cameron and Trivedi(2010)的建议,本文选择400为全样本自助样本进行估计,以“分样本占总样本的比例与400的乘积”作为分样本的自助样本选择,即东部、中部和西部地区自助样本选择分别为147、106和147,从而确保并模拟分样本与总样本之间的数量关系和重要程度,中心极限定理模拟显示基本符合正态分布。
五、实证结果分析表 5报告了电价交叉补贴对工业绿色发展效率影响的总量分析结果,其中模型1用CLAD估计了全样本、东部、中部和西部地区电价交叉补贴对工业绿色发展效率的影响,模型2通过引入交叉项分析了电价交叉补贴对各地区工业绿色发展效率的影响途径。
| 表 5 CLAD总量研究估计结果 |
表 5第1-4列是在未引入控制变量的条件下电价交叉补贴对工业绿色发展效率全样本和分地区影响的估计结果。第1列说明电价交叉补贴对中国工业绿色发展效率有消极影响,但不具有统计显著性,说明该直接消极影响作用甚微,这可能是电价交叉补贴对工业绿色发展效率主要通过成本机制和要素投入途径起间接影响作用。而电力消费量对工业绿色发展效率有显著积极影响,一方面,随着工业技术进步和企业节能环保意识增强,工业部门能源利用率得以显著提高,转变生产方式逐渐向集约型方向发展;另一方面,要素需求增加会使产出规模扩大,即使规模报酬保持不变,随着工业生产技术的提高产出规模也会扩大,这两点说明在控制其他因素不变的条件下,随着电力消费量的增加,工业绿色发展效率也会有所提高。这基本上验证了本文假设1提出的电价交叉补贴不利于工业绿色发展效率提高。
从分地区样本结果来看,表 5第2列和第4列表明电价交叉补贴和其他控制变量对东西部地区工业绿色发展效率的影响与全样本情况基本一致,对工业绿色发展效率有消极影响,但不具有统计显著性,说明电价交叉补贴对工业绿色效率的提高没有有益的影响,这与假设一内容基本相符。但需要指出的是,较多控制因素对西部地区工业绿色发展效率的影响不具有统计显著性,原因有二:一是西部地区工业绿色发展效率低于全国平均水平,且工业化水平相对东部和中部地区较低;二是政府为实现区域经济均衡发展,对西部地区工业发展实施相关优惠政策。表 5第3列结果显示电价交叉补贴对中部地区工业绿色发展效率有显著积极影响,而电力消费量对其有显著消极影响,这可能因为中部地区工业绿色发展效率值多集中在0.75-0.85,且处于全国平均水平以上,另外中国主要水电站分布在中部和西南地区,电力资源较为丰富,输配电成本较低。
从其他控制变量来看,环境管制对工业绿色发展效率有显著积极影响,污染治理投资是企业消除环境负外部性而承担的成本,强环境管制约束会督促工业企业提高能源效率,强调绿色发展技术,从而有利于工业绿色发展效率提高;成本和利润对绿色发展效率的影响是明显且直接的,高成本和低利润会制约企业实施有利于提高绿色发展效率的活动,如企业为控制成本会减少污染治理投资和新技术研发投资等;对外出口具有双重特征,中国出口品主要为劳动密集型和资源密集型产品,以环境污染和效率损失为代价,同时中国出口税收优惠政策鼓励出口,出口既拉动经济增长又降低绿色发展效率;外商资本投资会充分利用比较优势,发挥技术溢出效应,改进投资地企业生产技术,外商资本对中国工业绿色发展效率影响的区域差异明显,但总体有益于工业绿色发展;国有企业在政府补助、融资约束和资源配置等方面拥有比其他所有制企业更多的优势,但在激励机制、经营管理和创新动机等方面表现出低效率,所有权结构在一定程度上阻碍企业绿色发展效率;中国工业在布局和结构上的非均衡特征使集聚程度在地区和行业间有较大差异,并且张可、豆建民(2015)的研究表明集聚程度对工业污染物排放的影响与集聚程度的临界值有关,集聚通过生态维度对工业绿色效率的影响可能并不一致,本文实证结果也表明集聚程度与工业绿色发展效率负相关。
(二) 电价交叉补贴对工业绿色发展效率影响途径分析表 5第5-8列报告了在引入交叉项的条件下电价交叉补贴对工业绿色发展效率全样本和分地区影响途径的估计结果。表 5第5列表明电价交叉补贴对工业绿色发展效率有显著的消极影响,从影响机制上看,该影响作用通过成本机制和要素投入起作用。第5列显示电价交叉补贴通过电力消费量和对外出口对中国工业绿色发展效率有显著的消极影响,当电价交叉补贴程度增大时,工业企业会降低电力要素投入,工业期望产出也随之减少;当工业企业要素投入结构稳定时,其承担电价交叉补贴额越高,绿色发展效率就越低。另外,企业期望产出减少会导致其对外出口规模收缩,中国以劳动密集型和资源密集型为主的出口产品表现为“非绿色”特征,电价交叉补贴提高一方面会增加出口品生产成本,另一方面会加重对出口品的“非绿色”影响。由此可以看出,电价交叉补贴对工业企业电力要素投入的影响通过电力消费量和对外出口而对绿色发展效率有消极影响,这与假设一提出的要素投入是电价交叉补贴影响工业绿色发展效率的途径之一的观点基本相符。
表 5第5列显示成本和利润与电价交叉补贴交叉项对绿色发展效率均有显著影响,且二者互为反向关系,因为电价交叉补贴将直接导致工业生产成本增加,企业会通过要素结构调整和生产技术改进等活动实施成本控制与筹划,以实现成本最小化目标,当企业因实施成本控制与筹划活动而节约的成本大于因承担电价交叉补贴而增加的生产成本时,就可能对工业绿色发展效率有积极影响,从实证结果看,工业企业会通过成本机制“消化”部分电价交叉补贴对绿色发展效率的不利影响。环境管制是对工业环境负外部性成本的补偿,电价交叉补贴与环境管制交叉项对工业绿色发展效率有显著消极影响,从电价结构承担对高耗能高污染行业征收“环境税”职能的视角分析,电价交叉补贴越高,环境管制强度就越大,这侧面说明环境污染较为严重,而第1列显示环境管制对工业绿色发展效率有显著积极影响,然而这并不成为实证结果不稳健的证据。从效率视角分析,电价交叉补贴越高,环境管制强度就越大,环境污染就越严重,假设环境零污染与环境管制高强度并存,那么高强度环境管制则毫无疑问是非效率的;从公平视角分析,不可置否地,电价交叉补贴确实承担了部分环境管制职能,但并非所有工业企业都是高耗能高污染,只有对高耗能高污染企业征收高额环境税,对环保和绿色生产企业进行奖励,才是既公平又有效率的措施,如果忽略环境管制的公平与效率,那么电价交叉补贴提高会通过成本机制影响工业绿色发展效率。因此结合实证结果,本文认为当前电价交叉补贴承担环境管制职能的普遍性对工业绿色发展效率有消极影响,这验证了本文假设2的基本观点。
从分地区样本结果分析,表 5第6-8列分别显示了电价交叉补贴对东部、中部和西部地区工业绿色发展效率影响途径的估计结果。第6和7列显示电价交叉补贴与利润总额交叉项对中部地区工业绿色发展效率有显著积极影响,与环境管制交叉项对东部和中部地区工业绿色发展效率具有积极影响,因为中国工业企业密集分布在东部和中部地区,在推动东中部经济发展的同时也导致了严重的环境污染,增大环境管制强度和增加环境污染治理投资将有利于东中部地区的环境治理与改善,通过生态、资源和经济维度对工业绿色发展效率产生有利影响。分样本结果与全样本结果基本一致,说明在总量分析中,电价交叉补贴对中国工业绿色发展效率的影响途径基本一致,电价交叉补贴主要通过成本机制和要素投入影响工业绿色发展效率,也验证了本文假设1和假设2的观点。
六、稳健性检验表 8报告了稳健性检验结果,其中与模型1相对应的模型1A估计全样本、东部、中部和西部地区电价交叉补贴对工业绿色发展效率的影响,与模型2相对应的模型2A通过引入交叉项分析电价交叉补贴影响工业绿色发展效率的途径。
(一) 关于影响及区域差异的稳健性分析表 6第1列显示电价交叉补贴对工业绿色发展效率没有明显的积极影响,电价交叉补贴系数与表 5第1列相反,但二者均不具有统计显著性,说明电价交叉补贴对工业绿色发展效率没有显著的直接影响作用,系数符号相反可能由其他控制变量单位所导致,但这不是电价交叉补贴对工业绿色效率无影响的充分证据。从分地区样本结果来看,表 6第2和4列分别显示电价交叉补贴对东部和西部地区工业绿色发展效率的影响与全样本趋于一致,东部地区经济发展水平相对其他地区较高,但能源资源相对缺乏,输配电成本相对较高,另外东部和东北部以及华北地区环境污染严重,电价交叉补贴会起到调节电力平衡和征收环境污染成本的双重作用。表 6第3列说明电价交叉补贴对中部地区工业绿色发展效率有消极影响作用,与表 5第3列显示结果相反。因为总量分析中电价交叉补贴对中部工业绿色发展效率的积极影响是由于输配电成本相对较低,且中部地区工业绿色发展效率存在较大上升空间,电价交叉补贴对其的消极冲击不明显。
| 表 6 CLAD单位分量研究估计结果 |
其他控制变量的估计结果不在此赘述,需要注意的是表 5第1列显示电力消费量与工业绿色发展效率呈显著正相关关系,因为此处电力消费量表示要素投入含义,即使工业生产技术保持不变,规模报酬不变,要素投入增加也能使产出按产出比例增加,因此二者并不冲突,而且是一致的。
(二) 关于影响途径的稳健性分析表 6第5-8列报告了在引入交叉项条件下电价交叉补贴对工业绿色发展效率全样本和分地区影响途径的估计结果。表 6第5列显示电价交叉补贴对中国工业绿色发展效率有显著消极影响,这与表 5相应结果一致。电价交叉补贴与单位产出电力消费量的交叉项对中国绿色发展效率有积极影响。另外,表 6第5列还表明电价交叉补贴与出口率交叉项不利于工业绿色发展效率提高,其一是电价交叉补贴导致出口规模的相对下降,其二是出口品的“非绿色”特征。由此可以看出,电价交叉补贴导致的单位电力成本增加和通过成本机制影响出口规模缩小均不利于工业绿色发展效率,这与本文假设一和表 5总量分析描述的结果大致相符。表 6第5列显示单位产出成本和利润率与电价交叉补贴交叉项对绿色发展效率均有显著积极影响,利润率的提高也将从经济维度对工业绿色发展效率产生积极影响,这表明电价交叉补贴会通过产出端的成本控制机制对工业绿色发展效率产生影响。电价交叉补贴与治污投资率交叉项对工业绿色发展效率有显著消极影响,这与表 5第5列结果一致和本文假设2的观点基本一致,也说明总量分析结果的稳健性。
从分地区样本结果来看,表 6第6-8列分别表示了电价交叉补贴对东部、中部和西部地区工业绿色发展效率影响途径的估计结果。稳健分析结果与表 5结果一致。第6列结果显示电价交叉补贴对东部地区工业绿色发展效率的影响途径与全样本基本一致,第7列结果显示电价交叉补贴通过成本机制和要素投入对中部地区工业绿色发展效率的影响尤为明显,且与东部和中部地区差异显著。第8列结果显示电价交叉补贴通过成本机制不利于西部地区工业绿色的提高,而通过电力要素投入则对其绿色发展效率有显著提升影响,因为西部地区工业绿色发展效率低于全国平均水平,且工业生产技术水平较低,以重工业为主的工业结构和区域内非均衡的企业布局使得西部地区工业的整体效率较低,一定程度上制约了工业绿色发展效率提高。
总体来看,表 6单位分量研究的估计结果与表 5总量研究的估计结果基本一致。在不引入电价交叉补贴与中介变量交叉项的条件下,电价交叉补贴对中国工业绿色发展效率的影响具有不确定性,不具有统计显著性;引入电价交叉补贴与中介变量交叉项后,电价交叉补贴对全样本和东部地区工业绿色发展效率有显著的消极影响,而对中部和西部地区工业绿色发展效率有显著的积极作用。综上说明电价交叉补贴会阻碍中国工业绿色发展效率的提高,且表现出显著的区域差异,并主要通过成本机会和要素投入影响工业绿色发展效率,与本文假设1和假设2的观点内容基本符合。存在明显区域差异的原因,其一, 东部地区电力资源相对缺乏,输配电成本高昂,进而导致东部地区销售电价高企,另外,东部地区电力消费量在研究期内占全国电力消费总量的51.7%,输配电成本增加和电力消费量较大都会导致东部地区承担较大的电价交叉补贴;其二,工业结构和工业化程度的区域性失衡导致东部和东北部、华北地区环境污染严重,电价交叉补贴承担征收“环境税”的职能,较高的电价交叉补贴体现了环境管制力度的强化,同时为了考虑环境管制在区域间的公平和效率,承担环境管制职能的电价交叉补贴对工业绿色发展效率的影响必然会表现出区域性差异;其三,汪克亮等(2013)研究表明东部地区绿色发展效率基本实现了潜在最大值,而电价交叉补贴作为绿色发展效率的消极冲击,极有可能导致东部地区绿色发展效率下降,而中西部地区的绿色发展效率还有很大的上升空间,电价交叉补贴可能会影响其绿色发展效率提高的速度,但不会阻碍其绿色效率的提高;其四,本文测算东部地区承担的单位电价交叉补贴额为134.7272元/千千瓦时,中部地区147.6225元/千千瓦时,西部地区最低为109.9565元/千千瓦时,各地区工业承担的电价交叉补贴程度存在明显差异,电价交叉补贴对绿色发展效率的影响必然存在区域差异。
另外,电价交叉补贴对东部地区工业绿色发展效率的影响与全样本结果基本一致,电价交叉补贴主要通过成本机制影响东部地区工业绿色发展效率,通过成本机制和要素投入两条途径影响中部和西部地区工业绿色发展效率,对中部地区尤为明显,主要原因是,其一工业绿色发展效率是全部要素关系的结果,东部地区要素报酬和要素流动性较高,而电力要素的被替代性较低,电力要素与其他要素之间的结构关系较中西部地区更易改变;其二是东部地区以加工贸易为主的外向型经济导向,使多数外贸型企业更注重产出端效率,而非投入端的资源整合,这表明东部地区工业绿色发展效率更倚重产出端,因此要素投入机制并非电价交叉补贴影响工业绿色发展效率的主要途径,而中西部地区工业绿色发展效率存在很大的上升空间,受投入和产出两端综合影响较明显,因此电价交叉补贴会通过要素投入和成本机制影响中西部地区工业绿色发展效率。
七、结论与政策建议本文构建了资本、劳动、能源和技术的四要素非径向方向距离函数,并从资源、经济和生态维度构建中国工业绿色发展效率指标体系,以拉姆齐价格作为参考价格,运用价差法测算了电价交叉补贴,提供了测算电价交叉补贴的新思路,同时运用CLAD法从总量研究和单位分量研究两个层面考察了电价交叉补贴对工业绿色发展效率的影响、区域差异和影响途径。研究总结下述三点结论:一是总量研究和单位分量研究均表明在引入交叉项情况下电价交叉补贴对中国工业绿色发展效率有显著消极影响,明显阻碍了中国工业绿色发展效率的提高;二是电价交叉补贴对中国工业绿色发展效率影响的区域性差异明显,总量研究和单位分量研究均表明电价交叉补贴会削弱东部地区工业绿色发展效率,并且该消极影响较大,而对中部和西部地区工业绿色发展效率则有积极影响;三是电价交叉补贴主要通过成本机制和要素投入两个途径影响中国工业绿色发展效率,其中电价交叉补贴主要通过成本机制影响东部地区工业绿色发展效率,而从成本机制和要素投入两个途径影响中部和西部地区工业绿色发展效率。从其他影响因素来看,总量研究表明电力消费量、利润总额、环境管制和外商资本投资会促进工业绿色发展效率,对东部地区工业绿色发展效率的促进作用尤为明显;环境管制对中部地区工业绿色发展效率有显著促进作用,电力消费量和外商资本投资是促进西部地区工业绿色发展效率的重要因素,分量研究结果与此基本一致,佐证了总量研究结果的稳健性。
直接考察电价交叉补贴对工业绿色发展效率的影响时,发现电价交叉补贴对工业绿色发展效率没有显著影响,在探究电价交叉补贴对工业绿色发展效率的影响途径时,电价交叉补贴显著阻碍了工业绿色发展效率提高,并且表现出明显的区域差异。电价交叉补贴对工业绿色发展效率影响的区域间差异和其履行电力普遍服务的社会职能成为不可彻底消除电价交叉补贴的原因。为实现有效的电力能源保护和提高电力能源利用效率,让电价交叉补贴在发挥积极作用和调整消极作用的同时能充分反映电力市场价格信号和平衡电力市场供需,在实施电力价格机制改革和调整时,应注重三个方面:一是掌握好电价交叉补贴额度,既要保证工业企业对电力要素的正常投入需求,又要减轻企业成本负担,如试点成熟并推行大用户直购电、实施居民用电阶梯定价、建立电力普遍服务基金等;二是要制定实施与电价交叉补贴相配套的政策措施,如加强电力要素市场规范化建设、建立健全环境监测机构与管制制度、转变出口为技术密集型和资本密集型产品等;此外,考虑中国区域经济环境差异和工业绿色发展效率区域差异,实施符合区域经济协调发展的差异化电价结构,并且应从电力消费、环境管制、对外出口等多方面配合差异化电价结构,促进区域间协调发展。对工业企业而言,应该从技术和环保等方面着手:一是加强技术研发与创新,提高生产技术水平和电力能源利用效率;二是提高节能环保意识,树立可持续发展观念,加强环境污染治理与环保节能设备投资;三是依托区域比较优势,走经济、生态和资源相互协调的绿色发展之路。
| [] |
班斓、袁晓玲,
2009, “中国八大区域绿色经济效率的差异与空间影响机制”, 《西安交通大学学报(社会科学版)》, 第 第3期 期, 第 22–30 页。 |
| [] |
陈诗一,
2009, “能源消耗、二氧化碳排放与中国工业的可持续发展”, 《经济研究》, 第 第4期 期, 第 41–55 页。 |
| [] |
陈诗一,
2010, “中国的绿色工业革命:基于环境全要素生产率视角的解释(1980-2008)”, 《经济研究》, 第 第11期 期, 第 21–34+58 页。 |
| [] |
金煜、陈钊、陆铭,
2006, “中国的地区工业集聚:经济地理、新经济地理与经济政策”, 《经济研究》, 第 第4期 期, 第 79–89 页。 |
| [] |
景维民、张璐,
2014, “环境管制、对外开放与中国工业的绿色技术进步”, 《经济研究》, 第 第9期 期, 第 34–47 页。 |
| [] |
李静、倪冬雪,
2015, “中国工业绿色生产与治理效率研究——基于两阶段SBM网络模型和全局Malmquist方法”, 《产业经济研究》, 第 第3期 期, 第 42–53 页。 |
| [] |
李艳军、华民,
2014, “中国城市经济的绿色发展效率及其影响因素研究”, 《城市与环境研究》, 第 第2期 期, 第 36–52 页。 |
| [] |
林伯强、刘泓汛,
2015, “对外贸易是否有利于提高能源环境效率——以中国工业行业为例”, 《经济研究》, 第 第9期 期, 第 127–141 页。 |
| [] |
刘思强、姚军、叶泽,
2015, “我国销售电价交叉补贴方式及改革措施——基于上海市电力户控数据的实证分析”, 《价格理论与实践》, 第 第8期 期, 第 26–28 页。 |
| [] |
卢丽文、宋德勇、李小帆,
2016, “长江经济带城市发展绿色发展效率研究”, 《中国人口·资源与环境》, 第 第6期 期, 第 35–42 页。 |
| [] |
聂玉立、温湖炜,
2015, “中国地级以上城市绿色经济效率实证研究”, 《中国人口·资源与环境》, 第 第5期 期, 第 409–413 页。 |
| [] |
齐放、魏玢、张粒子、刘伟、李远卓,
2009, “我国销售电价交叉补贴问题研究”, 《电力需求侧管理》, 第 第6期 期, 第 16–19 页。 |
| [] |
钱争鸣、刘晓晨,
2014, “我国绿色经济效率的区域差异及收敛性研究”, 《厦门大学学报(哲学社会科学版)》, 第 第1期 期, 第 110–118 页。 |
| [] |
唐要家、杨健,
2014, “销售电价隐性补贴及改革的经济影响研究”, 《中国工业经济》, 第 第12期 期, 第 5–17 页。 |
| [] |
汪克亮、杨力、程云鹤,
2013, “异质性生产技术下中国区域绿色经济效率研究”, 《财经研究》, 第 第4期 期, 第 57–67 页。 |
| [] |
王兵、黄人杰,
2014, “中国区域绿色发展效率与绿色全要素生产率:2000-2010——基于参数共同边界的实证研究”, 《产经评论》, 第 1–16-35 页。 |
| [] |
王兵、唐文狮、吴延瑞、张宁,
2014, “城镇化提高中国绿色发展效率了吗?”, 《经济评论》, 第 第4期 期, 第 38–49 页。 |
| [] |
王兵、吴延瑞、颜鹏飞,
2008, “环境管制与全要素生产率增长:APEC的实证研究”, 《经济研究》, 第 第5期 期, 第 19–32 页。 |
| [] |
谢品杰、朱文昊、谭忠富,
2015, “中国电价扭曲与电力强度的影响因素”, 《技术经济》, 第 第10期 期, 第 75–83 页。 |
| [] |
于立宏、贺媛,
2013, “能源替代弹性与中国经济结构调整”, 《中国工业经济》, 第 第4期 期, 第 30–42 页。 |
| [] |
岳书敬、邹玉琳、胡姚雨,
2015a, “产业集聚对中国城市绿色发展效率的影响”, 《城市问题》, 第 第10期 期, 第 49–54 页。 |
| [] |
岳书敬、杨阳、许耀,
2015b, “市场化转型与城市集聚的综合绩效——基于绿色发展效率的视角”, 《财经科学》, 第 第12期 期, 第 80–91 页。 |
| [] |
张可、豆建民,
2015, “集聚与环境污染-基于中国287个地级市的经验分析”, 《金融研究》, 第 第12期 期, 第 32–45 页。 |
| [] |
张可、丰景春,
2016, “强可处置性视角下中国农业环境效率测度及其动态演进”, 《中国人口·资源与环境》, 第 第1期 期, 第 140–149 页。 |
| [] |
Barros C. P., Managi S. and Matousek R., 2012, "The technical efficiency of the japanese banks:non-radial directional performance measurement with undesirable output". Omega, 40(1), 1–8.
DOI:10.1016/j.omega.2011.02.005 |
| [] |
Berry S. K., 2000, "Stranded costs, access charges, and Ramsey pricing in the U.S. electric utility industry". Quarterly Review of Economics & Finance, 40(4), 503–517.
|
| [] |
Björner T. B., Togeby M. and Jensen H. H., 2001, "'Industrial companies' demand for electricity:evidence from a micropanel". Energy Economics, 23(5), 595–617.
DOI:10.1016/S0140-9883(00)00084-0 |
| [] |
Cameron A. C., Trivedi P. K., 2010, "Microeconometrics Using Stata, Revised Edition", Stata Press.
|
| [] |
Efron B., 1979, "Bootstrap methods:another look at the jackknife". The Annals of Statistics, 7(1), 1–26.
DOI:10.1214/aos/1176344552 |
| [] |
Føre R and S.Grosskopf, 2005, "New Directions:Efficiency and Productivity", Springer US.
|
| [] |
Føre R., Grosskopf S. and Jr C. A. P., 2008, "Environmental production functions and environmental directional distance functions". SSRN Electronic Journal, 32(7), 1055–1066.
|
| [] |
Føre R., Grosskopf S., Lovell C. A. K. and Pasurka C., 1989, "Multilateral productivity comparisons when some outputs are undesirable:a nonparametric approach". The Review of Economics and Statistics, 71(1), 90–98.
DOI:10.2307/1928055 |
| [] |
Kopsakangas-Savolainen M., 2004, "The welfare effects of different pricing schemes for electricity distribution in finland". Energy Policy, 32(12), 1429–1435.
DOI:10.1016/S0301-4215(03)00110-1 |
| [] |
Li M., Wang Q., 2014, "International environmental efficiency differences and their determinants". Energy, 78, 411–420.
DOI:10.1016/j.energy.2014.10.026 |
| [] |
Lin B., qiang J.Z., 2011, "Estimates of energy subsidies in china and impact of energy subsidy reform". Energy Economics, 33(2), 273–283.
DOI:10.1016/j.eneco.2010.07.005 |
| [] |
Liu R. J., Zhang Z. H., 2012, "Green-efficiency assessment of Chinese industry based on principal component analysis and super-efficiency data envelopment analysis". Advanced Materials Research, 490-495–2264-2268.
|
| [] |
Ma H., Oxley L. and Gibson J., 2008, "China's energy economy:Technical change, factor demand and interfactor/interfuel substitution". Energy Economics, 30(5), 2167–2183.
DOI:10.1016/j.eneco.2008.01.010 |
| [] |
Powell J. L., 1984, "Least absolute deviations estimation for the censored regression model". Journal of Econometrics, 25(3), 303–325.
DOI:10.1016/0304-4076(84)90004-6 |
| [] |
Qi, F., L.Zhang, B. Wei and G. Que, 2008, "An Application of Ramsey Pricing in Solving the Cross-subsidies in Chinese Electricity Tariffs"International Conference on Electric Utility Deregulation and Restructuring and Power Technologies.442-447.
|
| [] |
Resende M., 1997, "Ramsey Pricing and Regulator's Social Welfare Weights:An Empirical Application". Review of Industrial Organization, 12(3), 413–416.
DOI:10.1023/A:1007751816327 |
| [] |
Rodrigues R., Linares P., 2015, "Electricity load level detail in computational general equilibrium-part Ⅱ-welfare impacts of a demand response program". Energy Economics, 47, 52–67.
DOI:10.1016/j.eneco.2014.10.015 |
| [] |
Skeels C. L., Vella F., 1999, "A monte carlo investigation of the sampling behavior of conditional moment tests in Tobit and Probit models". Journal of Econometrics, 92(2), 275–294.
DOI:10.1016/S0304-4076(98)00092-X |
| [] |
Sueyoshi T., Goto M., 2011, "DEA approach for unified efficiency measurement:assessment of Japanese fossil fuel power generation". Energy Economics, 33(2), 292–303.
DOI:10.1016/j.eneco.2010.07.008 |
| [] |
Wang H., Zhou P. and Zhou D. Q., 2013, "Scenario-based energy efficiency and productivity in china:a non-radial directional distance function analysis". Energy Economics, 40(2), 795–803.
|
| [] |
Wang Q., Su B., Zhou P. and Chiu C. R., 2016, "Measuring total-factor CO2, emission performance and technology gaps using a non-radial directional distance function:a modified approach". Energy Economics, 56, 475–482.
DOI:10.1016/j.eneco.2016.04.005 |
| [] |
Watanabe M., Tanaka K., 2007, "Efficiency analysis of chinese industry:a directional distance function approach". Energy Policy, 35(12), 6323–6331.
DOI:10.1016/j.enpol.2007.07.013 |
| [] |
Wen M., 2004, "Relocation and agglomeration of Chinese industry". Economic Research Journal, 73(1), 329–347.
|
| [] |
Wesseh J. P. K., Lin B. and Appiah M. O., 2013, "Delving into Liberia's energy economy:Technical change, inter-factor and inter-fuel substitution". Renewable & Sustainable Energy Reviews, 24, 122–130.
|
| [] |
Yue S., Yang Y. and Hu Y., 2016, "Does foreign direct investment affect green growth? evidence from china's experience". Sustainability, 8(2), 158.
DOI:10.3390/su8020158 |
| [] |
Zhang N., Kong F., Choi Y. and Zhou P., 2014, "The effect of size-control policy on unified energy and carbon efficiency for Chinese fossil fuel power plants". Energy Policy, 70(4), 193–200.
|
| [] |
Zhou P., Ang B. W. and Wang H., 2012, "Energy and co 2, emission performance in electricity generation:a non-radial directional distance function approach". European Journal of Operational Research, 221(3), 625–635.
DOI:10.1016/j.ejor.2012.04.022 |




