近年来,我国的房地产市场发展十分迅速,住房市场改革不断推进,而房地产价格也在随之而步步攀升。2016年,房地产市场迎来了本轮周期的高点,据国家统计局数据显示,2016年8月,全国70个大中城市中有64个城市新建商品住宅销售价格同比上涨,其中,北京、上海、广州三大一线城市新建商品住宅销售价格同比涨幅均在20%-40%之间,深圳新建商品住宅销售价格同比涨幅甚至高达43.01%,房价涨幅屡创新高。全年的成交量创下了历史新高,最具有代表性的五十个城市全年月均成交约3710万平方米,同比增长逾两成,成交量绝对额突破历史同期最高记录。为了抑制房价的过快上涨,自2017年3月16日北京颁布最严限购令开始,全国多地楼市调控政策密集出台,市场环境收紧,价格出现一定程度的回落。为了防止房价泡沫破灭所造成的系统性金融风险,2016年12月中央经济工作会议中强调:“要把防控金融风险放到更加重要的位置,并进一步明确住房的居住定位,在支持居民自住购房的同时更加注重抑制投资投机性需求,以防止热点城市的泡沫风险及市场出现大起大落”。
房地产行业的繁荣发展离不开金融方面的大力支持,我国的金融体系以银行为中心就决定了房地产业的融资需求更多地依靠商业银行等金融机构来满足,因此,房地产价格水平的波动在很大程度上会对一国金融业乃至整个金融体系的稳定产生影响。历史上,房地产价格波动引发金融危机的现象时有发生,如日本、美国、东南亚都曾因为房地产泡沫导致金融危机的爆发,严重破坏本国甚至全球的金融系统稳定性,造成全球经济的衰退和金融秩序的混乱。目前,面对处于高位的房地产市场,我国政府开始担忧房价泡沫破灭对金融系统稳定造成的冲击,并开启了新一轮严苛的房地产调控政策。目前,我国房价高涨是否会对系统性金融风险造成直接的影响?其动态影响程度如何?何种调控手段更为有效?关于这些问题的正确回答,对于保障我国金融体系稳定和改善房地产市场调控手段有着十分重要的理论和实践意义。因此,本文将采用基于有向无环图(DAG)的结构向量自回归(SVAR)模型和预测误差方差分解的方法,在系统梳理房地产价格波动对系统性金融风险影响传导机制的基础上,实证研究了房价波动对我国系统性金融风险造成的动态影响,定量给出了影响程度的大小,并在此基础上讨论房地产市场调控手段的有效性问题,以期能够为维护我国金融稳定和政府进一步实施有效的房地产市场调控政策提供依据。
本文接下来主要包括:第二部分即文献综述;第三部分说明了房价波动对系统性金融风险的传导机制;第四部分介绍了采用的研究方法和样本数据的构成及来源;第五部分是实证分析;第六部分为本文的研究结论和政策建议。
二、文献综述前期关于房地产价格水平波动与金融体系稳定的研究主要以Bernanke and Gertlrter(1995)以及Allen and Gale(2000)等为代表,这些研究成果大多注重探讨房地产价格水平波动对银行体系是否产生影响以及这种影响的传导机制。Collyns and Senhadji(2002)采用了VAR模型研究了国际上四个国家和地区的房价与银行信贷的相关性,并得出结论:房地产价格的波动与银行贷款变动之间具有显著的相关性和一致性。Goodhart and Hofmann(2007)实证得出,短期而言,实际利率对房地产价格存在显著负相关性,长期来说,房地产价格波动对银行信贷变动产生的影响更大。美国金融危机的爆发又开始让学者们聚焦到房价与金融稳定的议题上,Crowe et al.(2011)该轮房价的上涨伴随着金融杠杆化的增加,一旦实行信贷紧缩政策将可能导致房价下跌,并伴随着系统性金融风险的增大,有可能造成宏观经济的不稳定。Pouvelle (2012)基于法国数据,认为房地产周期或价格波动与银行体系的稳健及金融稳定密切相联。Shen et al.(2015)采用面板误差修正模型对我国27个省及4个直辖市的银行信贷和房地产价格水平之间的关系进行研究,实证结果表明,我国房地产价格水平对银行信贷的影响大于银行信贷对房地产价格水平的影响。
国内有关房地产价格影响金融稳定研究方面,张晓晶、孙涛(2006)重点研究了房地产周期对金融体系稳定的影响,他们提出房地产周期对金融体系稳定产生影响的重要渠道是期限错配风险、政府担保风险和房地产信贷风险暴露,并且据此提出了努力解决银行业问题和规范政府行为等政策建议。段忠东等(2007)在理论上解释了房地产价格与银行信贷之间的作用机制,并通过实证分析表明,从短期来看,房地产价格水平对银行信贷所产生的影响是有限的,但从长期来看,房地产价格水平和银行信贷增长之间存在着互为因果的关系。强林飞等(2010)通过协整分析、格兰杰因果关系检验发现我国房地产价格、银行信贷和宏观经济三者之间存在两两的互动关系。郭娜、梁琪(2011)通过对房地产市场周期与金融稳定以及房地产市场周期的影响因素进行了相关度分析,认为经济状况和政策因素会很大程度上导致经济周期的产生,而且金融稳定面临着来自房地产行业的冲击。赵园(2015)选取了股票市值、房地产价格波动、金融稳定指数作为变量,构建了一个三变量的VAR模型,得到以房地产价格为代表的资产价格波动与金融稳定指数的变化两者互为因果关系的结论。
国内外学者已经分别从各个层面各个角度比较全面地深入研究了房地产价格水平与银行体系乃至一国宏观金融稳定之间的关系问题,但前期研究成果并未讨论房地产价格上涨对系统性金融风险产生的重要影响,系统性金融风险是本次金融危机暴露出来的全球性金融体系新问题,许多国家因此开始构建满足自身需求的逆周期宏观审慎监管框架,从而降低由房地产市场失衡引发系统性风险并对实体经济的造成不利影响。因此,讨论系统性金融风险与房价波动的关系问题,在现阶段更具有现实意义。另外,前期文献在对金融稳定的指标选取中只采用银行贷款额或贷款/国内生产总值等指标来替代度量,使得结果的准确性和可靠性下降,也就无法为政策的进一步有效实施提供理论依据。有鉴于此,本文采用基于DAG的结构向量自回归方法来对分析房价波动对系统性金融风险的动态影响,从而为政策实施提供有益的参考依据。
在系统性风险指标选取上,本文采用了陶玲、朱迎(2016)的研究方法构建的系统性金融风险指数。近年来,系统性金融风险度量方法主要有:(1)研究风险传染性和金融机构关联程度的方法,包括网络分析法、共同风险模型法、困境依赖矩阵法和违约强度模型法;(2)评估系统性风险损失及损失概率的方法,包括在险价值和条件在险价值法、边际期望损失法和系统性期望损失法、Gray and Jobst(2010)在Merton模型基础上提出的或有权益分析法、Huang et al.(2009)提出的困境保费法;(3)国际组织以及各国中央银行金融监管机构分别开发的监测预警工具,如欧洲央行采用的改进的综合指数法、IMF系统性风险早期预警系统、英国系统性机构风险评估系统、韩国央行的宏观审慎政策系统性风险评估模型等。陶玲、朱迎(2016)在采用马尔科夫状态转换方法对综合指数进行实证分析的基础上,构建了包含七个维度的系统性金融风险综合指数。其方法上的优势为:第一,对历史上是否发生过金融危机不做强制要求,因此对于我国这种数据量有限且金融市场不完善的发展中国家来说非常适合;第二,综合指数法不关注系统性风险发生的具体原因,而是按照各类金融指标与金融危机之间的相关性大小来选择风险指标构建综合指数,再根据综合指数的现状和走势判断系统性金融风险的水平和发展趋势;第三,综合指数法表达简洁,可以和很多复杂的模型方法结合使用,例如在风险指标确定权重等方面可以由模型来决定,此外还可以运用模型构建复杂指标作为综合指数的原始指标等。另外,在基础指标选取上,我们选取了金融机构风险股票市场风险、债券市场风险、货币市场风险、外汇市场风险、房地产市场风险及政府部门风险7个维度作为基础指标池,指标涵盖了全面的经济信息来测度系统性金融风险,然后通过统计综合评价技术构造出系统性金融风险综合指数。
从研究方法来看,前期成果大多选择采用预测误差方差分解方法、格兰杰因果关系检验和VAR(或VECM)模型来进行研究,但这些研究方法都有较大的局限性。首先,格兰杰因果关系描述的仅仅是时间概念上的“先于”关系,而不是具有真正意义的因果关系,此外它还忽略了变量之间的同期因果关系;其次,VAR模型滞后阶数的选择对格兰杰因果关系的影响较大,不同的滞后阶数有可能得到截然相反的结论;更重要的是,格兰杰因果关系所检验的变量之间的显著性并不具有真正的经济意义,而是仅从统计角度来考虑的显著性,然而,前者却是研究者更应该关注的。因此,仅仅通过格兰杰因果关系来研究我国货币政策与房地产价格调控之间的关系是不够的。另外,现有国内外对货币政策与房地产价格相关研究成果中,多数文献采用乔利斯基(Cholesky)分解法,该方法对变量先后顺序十分敏感,或者在相关经济理论的基础上再结合作者的先验判断来限制随机误差项的同期因果关系,同样具有一定的主观性。
然而,Spirtes et al.(2000)提出了“有向无环图”(Directed Acyclic Graphs,DAG)研究方法,该方法成功突破了上述方法的局限性。DAG不需要任何先验判断和理论假设,只需要分析残差的方差协方差矩阵(或者相关系数矩阵),就能对扰动项之间存在的同期因果关系进行正确地识别,同时为SVAR的结构方差分解和结构关系设定提供依据。目前,这种数据驱动的研究方法已经被应用到经济相关研究领域中,并受到了国内外学者的广泛重视。鉴于此,为了突破传统VAR模型研究的局限性,本文将运用基于有向无环图(DAG)的结构向量自回归模型对系统性金融风险的影响因素进行了深入细致的分析,克服了传统VAR模型研究的缺陷,以期得出更加准确且富有政策启示意义的结论,提高研究成果的准确性和稳健性。
三、房价波动对系统性金融风险影响的传导机制分析本文在对国内外文献分析与总结的基础上概括出房地产价格波动对系统性金融风险影响的金融体系传导渠道和宏观经济传导渠道,具体内容如下:
(一) 金融体系传导渠道房地产价格波动风险通过银行体系直接与金融系统相关联,银行危机往往会引发整个金融系统的危机。银行直接或间接参与投资大量高风险高收益的房地产开发项目,面临较大的风险暴露。当房价急剧下跌容易引发银行产生大量的坏账使得银行陷入流动性危机,更进一步诱发大量借贷资本外逃,影响人民币汇率稳定。与此同时大量房地产公司面临破产,致使银行产生巨额不良资产,加剧了银行危机,诱发了系统性金融风险。如上世纪八九十年代发生的美国储贷危机、日本房地产泡沫危机、东南亚金融危机等都存在着房地产价格迅速攀升使得风险不断累积,泡沫破裂后房地产价格急剧下跌,使得银行陷入流动性危机,进一步产生连锁反应最终演变为金融危机的现象。
我国房价波动风险向金融体系传导机制主要如下:(1)抵押品机制。银行贷款除少数基于借款人的信誉发放之外,大部分是要求债务人提供抵押品的,根据抵押品价值确定贷款金额。房地产按揭贷款的数额较大,要求房屋购买人在向银行按揭时候必须将其购买的房屋抵押给银行。当房价上升的时候,抵押品价值上升,导致贷款人获贷款的数量增加,抵押贷款数量的增加会使贷款人的负债率进一步上升,负债率的上升会对金融稳定性造成影响。当房地产价格下降时候,抵押品价值下降。首先,会导致贷款人的财富值下降,极端情况下,购房者会放弃抵押品而选择违约,这时候银行会对抵押房屋进行拍卖,但仍然会有一定的损失,银行流动性会面临压力,造成风险上升。其次,银行不良贷款率的上升会使银行的贷款环境恶化,个人或者企业从银行获得贷款的可行性降低,导致经济总产出下降,宏观经济下行,影响系统性金融风险。(2)资本金机制。资本金的作用机制和抵押品机制有点类似,抵押品机制是从购房者的角度来说,而资本金机制主要从银行角度来考虑,当房地产价格上升时候,贷款者的财富值上升,房地产抵押品价值也会随之上升,因此,购房者的违约概率会下降,银行在这种情况下一般会选择扩大信贷规模以增加利润,进而影响到金融稳定。当房地产价格下降时候,贷款人的财富水平下降,下降程度越大,贷款人的违约概率越高,银行的资本金减少,银行会相应的收缩信贷规模,不仅仅是房地产行业的贷款,对实体经济的贷款也会随着减少,导致缺血的实体企业的融资更加困难,取得资金的成本更加高。企业在这种情况下的积极性会受到打击,资金不充足会导致社会总产出下降,增加系统性金融风险。(3)流动性机制。房地产价格上涨时候,房地产开发商贷款和房地产按揭贷款都会有所增加。目前,由于理财方式增多,我国居民和企业定期储蓄和存款的倾向降低,大部分都是短期储蓄和存款,而房地产行业的贷款的期限通常较长。因此,随着房地产行业贷款的规模的不断扩大,银行可能会产生流动性错配的问题。当房地产价格上涨时,房地产类贷款增多,期限错配问题更加严重,在遇到大额取现或者挤兑的情况时,银行会面临很大的风险,影响金融稳定性。当房地产价格下降时,一方面银行的净资产值会缩水,另一方面房屋所有人的违约率会增加,这两种结果都会导致银行的流动性减少甚至不足的情况发生,为了补充流动性,银行或选择出售风险资产(抵押房屋),进一步导致资产(房屋)价格下跌,或者选择清理其投资头寸进而影响资本市场的流动性,这导致系统性金融风险的积累。
另外,我国的影子银行发展较为迅速,在金融市场中起着越来越重要的作用。影子银行在房地产市场上一定程度上也在补充着房地产企业的信贷需求。当房地产价格上升时,房地产企业倾向于扩大规模,因此需要更多的资金。房地产开发商从商业银行获得贷款的规模是有限的,因此他们会寻求影子银行的信贷支持。影子银行的理财产品收益率在房价高涨的情况下通常会高于普通理财产品,因此会吸引大量的资金流入,部分居民储蓄和企业定期存款等也会流出商业银行进入影子银行,增加了商业银行存款量的波动幅度,导致商业银行期限错配的问题更加严重。当房地产价格下降时,影子银行有关房地产的理财产品也会面临问题,收益率下降,严重时甚至会出现违约,影子银行可能会面临兑付危机、资金紧张。这种情况下,影子银行会出售风险资产或者会提高资本金,出售风险资产会造成房价进一步下跌,影响宏观金融稳定。
(二) 宏观经济传导渠道房地产行业作为国民经济的基础产业,与其他各实体产业息息相关,房地产价格波动会影响到我国宏观经济各部门。风险传导机制如下:(1)财富效应机制。房地产的财富效应指的是当房地产价格发生变化的时候,房地产所有者会认为其所拥有的财富水平也会随着房屋价格的变化而发生变化,最终导致购买者的消费发生变化,消费的变化又会影响到社会的总产出水平和宏观经济,对金融稳定造成影响。具体来说,当房价上涨时候,房屋所有者对自己的消费计划做出调整,增加消费的边际倾向,从而增加企业的积极性,企业便会有动力继续扩大产能,促进经济总产出水平上升,影响宏观经济,造成对金融稳定的影响。当房地产价格下跌时候,房屋所有者的净财富值减少,他们会根据自己的财富水平对自己的消费支出做出一定的调整,减少非生活必须品的支出,导致市场需求减少,使得社会总产出也随之下降,影响宏观经济,造成对系统性金融风险的影响。(2)房地产价格还会通过托宾Q效应对金融稳定造成影响。“托宾Q”系数指的是资本的市场价值与其重置成本的比值。托宾Q理论是建立在有调整成本的新古典投资模型的基础之上的一种新古典投资理论。我们可以将房地产价格理解为托宾Q理论中的企业股票价值,将新房屋的建造成本理解为托宾Q理论中的资产重置成本。当房地产价格上升时,房屋的Q值会增大即房屋价格会大于或者远远大于房地产建造成本,这会刺激房地产开发商增加对房地产市场的投资增加,以追求更高的利润,投资增加带动了总需求的扩大,影响到社会总产出,进而影响到金融稳定。而当房地产价格下降时候,房地产行业的利润会被压缩,Q值会接近于1甚至出现小于1的情形,此时房屋建造成本会大于或者等于房屋价格,开发商会削减投资,投资的减少会造成社会总需求和总产出减少,影响到宏观经济发展,从而增大国家宏观层面的系统性金融风险水平。
四、研究方法与样本数据 (一) 结构向量自回归模型本文采用的VAR模型可表述为式(1):
| $ {X_t} = \mu + \sum\limits_{i = 1}^p {{\Phi _i}{X_{t - i}} + {e_t}, t = 1, 2..., T} $ | (1) |
由式(1)中可以看出,Xt表示列向量所构成的内生变量,p表示VAR模型中的滞后阶数,μ为常数项列向量,T是为样本容量。Φ1,…,Φp表示系数矩阵。et是表示随机误差项列向量,Σ表示et的协方差矩阵。
传统的研究方法经常使用格兰杰因果关系检验来分析变量之间的关系,但是格兰杰因果关系检验存在无法克服的缺陷。预测方差分解方法对于解释变量之间的关系更有意义,但是,应用此方法前提是必须对公式(2)中的矩阵A和B进行限制,即设定扰动项et之间的同期因果关系,对VAR模型结构进行识别,在此基础之上建立结构向量自回归模型(SVAR)。
| $ A{e_t} = {v_t} = B{u_t}, {u_t} \sim N\left({0, {I_k}} \right) $ | (2) |
式(2)中的A矩阵表示K阶方阵,B矩阵与A矩阵一样都表示K阶方阵,ut为结构扰动项。乔利斯基正交化分解实际上是对变量设定了一个恰好识别的递归结构,即设定矩阵A是下三角矩阵,主对角线元素为1,矩阵B为对角矩阵,这种递归的同期因果关系无疑是一种非常强的假设,而且不同的变量顺序往往会带来不同的分析结果。研究者大多依据以往的研究成果和自己的主观判断建立结构向量自回归模型(SVAR)模型,变量之间的同期因果关系一般很难依靠经济理论指导,因此主观色彩较为强烈,导致模型分方差分解结果也存在一定的主观性,不能更好地解释其经济意义。
以前的文献研究大都是基于以上所描述的方法,因此,设定扰动项结构成为了关键性难题。“有向无环图”技术有效克服了传统研究方法的这一缺陷,DAG完全基于数据,不需要先验的经验或者理论假设,使得实证结果更稳健,更具有现实意义。
(二) 有向无环图的分析方法有向无环图能够识别变量之间的同期因果关系,它通过两个步骤来完成:第一,分析变量之间的无条件相关系数;第二,对变量之间的偏相关系数进行分析,通过这两步来完成识别,是一种新型的数据驱动方法。变量之间的同期因果关系是否存在以及存在什么方向的同期因果关系会以图形的方式表示出来。有向无环图由变量和“边”构成,如果两个变量之间存在“边”,则表明二者之间存在同期因果关系,两个相互独立的变量之间则没有“边”。带有箭头的边表示变量之间同期因果关系的方向性。具体来讲,假设存在两个变量,分别为X和Y,他们之间存在五种相关性:(1)“X→Y”,表示在其他变量不变时,X的变化直接导致Y的变化,而Y对X无影响。(2)“Y→X”,表示在其他变量不变时,Y的变化直接导致X的变化,而X对Y无影响。(3)“X
在有向无环图的实际操作中,主要有两个步骤,首先要对无向完全图进行“去边”,之后进行“定向”。凭借这两部完成对变量之间同期因果关系的识别,主要借助PC算法。在去边的过程中,我们首先从一个初始的关联图出发,图中各变量之间均有一个无向边相连。通过PC算法分析无条件相关系数,对于无条件相关系数显著为0的无向边采用去除的方式。然后,对于不能去掉边的变量再进行偏相关系数分析,首先分析其1阶偏相关系数,然后2阶、3阶……,依次类推,假如模型中存在N个变量,则对偏相关系数的分析要持续到N-2阶。另外,PC算法采用了Fisher’s z统计量①,检验偏相关系数是否显著为0,进行“去边”,然后在“定向”步骤中,PC判别两个变量之间同期因果关系。
① 关于Fisher’s z统计量的相关细节见Spirtes et al.(2000)。
(三) 样本数据本文的原始数据来源于中经网中国经济统计数据库,结合我国的经济实际和数据的可获性,本文的样本区间设定为2001年第一季度到2016年第四季度。系统性金融风险指数本文采用了陶玲、朱迎(2016)的研究方法构建的系统性金融风险指数;随着我国利率市场化进程的不断推进,银行间的同业拆借利率的市场化程度也不断提高,因而本文将以银行间市场的7天同业拆借利率作为代理变量来替代市场利率;由于房地产价格没有公开的原始数据,本文采用了中经网统计数据库公布的全国商品房销售额除以全国商品房销售面积计算得到。由于存在通货膨胀等因素,为了使研究结论更加符合现实经济状况,本文根据中经网统计数据库公布的消费物价指数指标,对名义变量(国内生产总值、房地产平均销售价格)进行了消涨处理,并对其进行了季节调整,调整方法为美国商务部国势普查局最新推出的X-13ARIMA-SEATS方法。然后采用H-P滤波方法对其进行了去势处理,最后对两者取了对数值。系统性金融风险指数、房地产价格、国内生产总值和实际利率分别采用FS、HP、GDP和SHIBOR来表示。
五、实证分析 (一) 单位根检验为了对模型中每个变量的稳定性进行判断,我们对模型中采用的各个变量进行了ADF检验,检验结果如表 1所示。
| 表 1 各变量的平稳性检验结果 |
由表 1我们可知,模型中变量均在5%的显著水平下拒绝了变量平稳的备择假设,然后用一阶差分后的时间序列再次进行ADF检验,发现各个变量的一阶差分后的新序列均在5%的显著水平下拒绝了非平稳的原假设,则可以据此判断各个变量均为一阶单整的I(1)过程。对于一阶单整I(1)过程,要建立VAR模型,必须保证原序列之间存在协整关系,否则无法建立模型。因此,接下来要对各原时间序列进行Johansen协整关系检验,协整检验的关系如表 2所示,模型四个变量之间存在两个协整关系,符合建立VAR模型的条件。
| 表 2 Johansen协整关系检验结果 |
根据AIC和FPE最小化原则,我们建立了一个2阶四变量的向量自回归(VAR)模型,公式(3)给出了各变量的残差相关系数矩阵:
| $ {\rm{corr = }}\left( \begin{array}{l} \;\;\;HP\;\;\;\;\;\;\;\;GDP\;\;\;\;\;\;\;\;SHIBOR\;\;\;\;\;\;\;FS\\ \;\;\;\;\;1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ - 0.0697\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ - 0.2184\;\; - 0.1175\;\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\;\;\;\;\\ 0.3450\;\;\;\;\;0.1600\;\;\;\;\;\; - 0.1769\;\;\;\;\;\;\;\;\;1 \end{array} \right) $ | (3) |
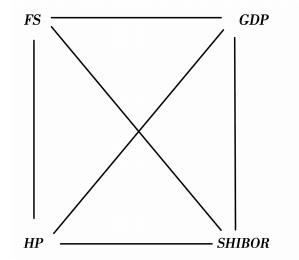
接下来,我们运用DAG分析方法对系统性金融风险指数(FS)、房地产价格(HP)、国内生产总值(GDP)和实际利率(SHIBOR)之间的同期因果关系进行了分析。首先,我们从无向完全图开始进行分析,如图 1所示,在起始阶段并不能判断各变量之间是否有同期因果关系存在,因此变量之间都用一条无方向的边连接。接下来,进行“去边”工作,首先分析各变量之间的无条件相关系数,去掉无条件相关系数为0的边;之后对没有去掉边的变量观察其偏相关系数,去掉偏相关系数为0的边,以此类推。然后再通过“隔离集”的概念确定变量之间同期因果关系的方向性。
|
图 1 无向完全图 |
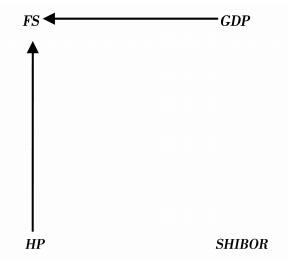
首先,我们通过无条件相关系数可知,房地产价格与实际利率的相关系数为-0.2184(p=0.3384),这说明房地产价格和实际利率之间在20%的显著水平下表现为同期独立变量,二者之间不存在同期因果关系,因此可移去图中二者之间的连线。同理,国内生产总值与实际利率的相关系数为-0.1175(p=0.3621),这说明国内生产总值和实际利率之间在20%显著水平下也表现为同期独立变量,同理可以将二两者之间的无向边去掉;系统性金融风险与实际利率的相关系数为-0.1769(p=0.4626),这说明系统性金融风险与实际利率之间在20%显著水平下也是同期独立变量,可移去二者之间的无向边。在无条件相关系数分析完之后,我们在考虑变量之间的偏相关系数,进而通过偏相关系数大小进行下一步的去边步骤。当系统性金融风险为条件变量时,国内生产总值与房地产价格之间的偏相关系数为0.2239(p=0.2956),由此可知国内生产总值与房地产价格之间也表现为同期独立,两者之间的连线也可以去除。由此,在无向完全图去掉四条连线后,只有房地产价格与系统性金融风险指数以及国内生产总值与系统性金融风险指数之间存在表示同期因果关系的连线,可以表示为房地产价格-系统性金融风险指数-国内生产总值,这样房地产价格与系统性金融风险指数“相邻”,国内生产总值与系统性金融风险指数“相邻”。在确定了各变量之间关系的存在性后,我们要对存在同期因果关系的各变量之间方向性进行确定,通过上文偏相关系数结果可以判断,系统性金融风险不属于房地产价格和国内生产总值的“隔离集”,因此根据PC算法的准则,我们可以推知房地产价格-系统性金融风险指数-国内生产总值三者之间的同期因果关系应为房地产价格→系统性金融风险指数←国内生产总值。综合以上过程,我们可以知道各个变量之间的同期因果关系和因果关系方向(如图 2),存在着房地产价格到系统性金融风险指数的同期因果关系;国内生产总值到系统性金融风险指数的同期因果关系。下一步,我们将根据上文的分析结论,建立基于有向无环图的结构向量自回归模型,然后进行脉冲响应函数与预测方差分解分析。为了检验有向无环图的分析结果是否合理,以及扰动项机构设置是否具有可靠性,本文采用了似然比检验对其进行验证。检验结果表示,LR检验统计量在5%的显著水平下接受了“过度约束为真”的原假设,因此,我们上文中有向无环图的分析结构以及扰动项结构的设置均具有合理性和可靠性。
|
图 2 有向无环图 |
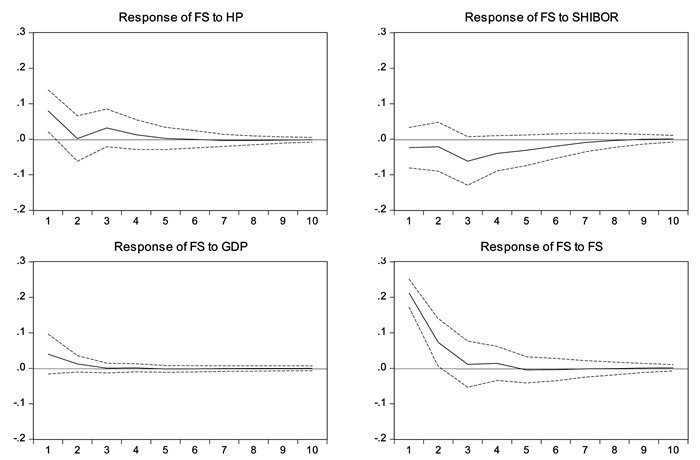
接下来,我们基于以上DAG分析结果,建立了结构向量自回归(SVAR)模型,并进行了脉冲响应函数分析,以此探究各个变量对系统性金融风险的影响作用,刻画房价波动对系统性金融风险影响的动态特征。图 3是各个变量对系统性金融风险冲击的脉冲响应函数图。
|
图 3 系统性金融风险指数的脉冲响应函数图 |
图 3中第一幅图代表了系统性金融风险指数对房地产价格冲击的脉冲响应函数,由图中可以看出,对于一个单位标准新息的房地产价格冲击,系统性金融风险指数始终表现为正向响应,最开始第一期达到最大值0.0798,然后在第二期下降到0.0017,并在第三期达到了另一个高点0.0317,随后便一直向0收敛。由此可知,房价冲击会对系统性金融风险产生正向影响,大幅上涨的房地产价格确实会推动我国系统性金融风险的上升,房地产价格上升会通过财富效应机制、银行信贷机制、托宾Q机制和影子银行机制四种传导机制影响到金融稳定,从而导致系统性金融风险累积,然而这种影响会随着时间推移逐渐缩小;第二幅图代表系统性金融风险指数对实际利率冲击的脉冲相应函数图,由图中可以看出,对于一个单位标准新息的实际利率冲击,系统性金融风险指数始终表现为负向的响应,响应时间较短而且响应深度较大,在第四期便达到了最大影响-0.0618,随后渐进收敛到0值附近。这表明中央银行提高利率在短期内确实能够使系统性金融风险指数下降,是调控房价并维护金融系统稳定的重要手段,然而长期其调控效果会逐渐减弱,这似乎也与我国历次房地产市场调控事实相符①;第三幅图代表系统金融风险指数对国内生产总值冲击的脉冲响应函数图,由图中可以看出,系统性金融风险指数对国内生产总值的动态响应最开始表现为正向,在第一期便达到了最大值0.0398,随后快速下降,第三期便下降到0值附近,随后稳定收敛到0。这表明,国内生产总值的变化对系统性金融风险的影响相对较小,在长期这种影响逐渐减弱并消失。由此可见,经济基本面状况似乎并未对虚拟经济风险产生较大影响,这源于多年来我国大量资金流向房地产市场、股票市场、大宗商品交易市场等进行投机活动,资金存在离实向虚的现象,因此我国系统性金融风险一定程度上脱离实体经济状况而存在;第四幅图代表了系统性金融风险指数对自身冲击的脉冲响应函数,由图中可以看出,对于一个单位标准新息的系统金融风险指数冲击,其自身最初保持着正向响应,在一开始达到最大值0.2121,第二期开始逐渐下降,在第五期的变为负值-0.0048,随后逐渐趋向于0。这表明我国的金融系统稳定性最开始容易受到自身惯性的影响,但是自身惯性的影响程度在随时间不断减小,外部冲击对其影响变得越来显著。
① 如2006年2次加息,3次上调存准率,2011年出台新国八条等房地产调控政策,结果均是房价短期出现下跌随后长期出现房价的上涨。
(四) 基于DAG的预测方差分解分析我们对上文建立的SVAR模型进行了预测方差分解,来进一步深入分析房地产价格、国内生产总值、实际利率三种因素对我国系统性金融风险的动态影响机制,表 3为基于有向无环图的预测方差分解实证结果。
| 表 3 基于DAG的预测方差分解(%) |
通过表 3我们可以看出,系统性金融风险指数波动主要由其自身解释大部分都由系统性风险自身来解释,第一期中达到84.06%的解释比例,到第八期仍然有74.61%的解释比例,说明我国系统性金融风险受其自身惯性的影响较大。金融系统性风险具有传染性,金融体系在自身出现不平衡的情况时,风险会迅速传导,并在预期的作用下不断扩大,同时信息不对称以及金融脆弱性的存在都会导致金融系统性风险在金融体系内快速传导,因此系统性金融风险存在惯性。在其他三种影响因素中,房地产价格波动相对于其他变量来说拥有对系统性金融风险指数波动更大的解释力,自始至终始终保持在10.00%-13.00%之间。说明房地产价格波动能够对系统性金融风险起到基础性作用,房地产价格冲击会通过前文所述的四种传导机制影响到金融稳定;其次为实际利率,由最开始的0迅速上升到第六期的11.67%,随后逐渐稳定在11.60%附近,这说明我国实际利率对系统性金融风险的解释力是逐渐上升的。这是因为利率水平的变化会直接影响到经济体系中的可用资金规模,提高利率会使得金融市场的资金供求成本上升,抑制房地产投资和投机需求,从而降低系统性金融风险的生成;最后是国内生产总值变量,由第二期的3.65%逐渐下降并稳定在第八期的2.67%,这说明我国经济基本面对系统性风险的解释力较弱,目前我国资金偏重于从事投机活动,并未真正流入到实体经济,是导致国内生产总值波动对系统性金融风险的解释力较弱的关键原因。
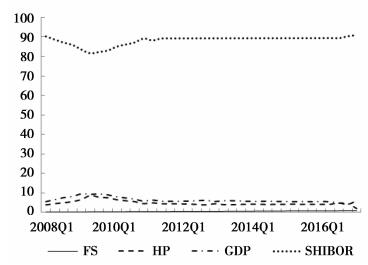
预测方差分解结果还显示,在其他三种影响因素中,房地产价格波动的解释力都较强。首先,房地产价格波动对自身的影响最大,第一期中完全由自身解释,然后下降到第二期的92.38%,直到第八期的68.75%,这说明我国的房地产价格波动主要受其自身惯性的推动,一方面我国城镇化水平的提高和我国人口数量增长所形成的住房刚性需求一直推动着我国房地产价格的不断上涨(郭娜、吴敬,2015),另一方面房地产价格的升值预期和投机行为也是引起房价不断上涨的重要原因(赵胜民等人,2011);其次,是房地产价格波动对国内生产总值的影响,从第一期的0快速上升到第八期的11.74%,仅次于国内生产总值自身的影响力(79.26%),这说明我国国内生产总值上升最主要还是源于国内经济的成长性,房地产行业对我国经济的带动作用十分显著,牵动着各行各业的发展,例如:钢铁、水泥甚至石油化工等行业,对经济发展以及就业影响巨大。最新数据显示2016年我国房地产增加值占整个国内生产总值的比重达到了6.5%,其价格波动必然会对国内生产总值起到至关重要的推动作用;最后,是房地产价格波动对实际利率的影响,从第一期的0一直上升到第八期的6.05%,这说明房地产价格波动对实际利率的解释力很弱,我国货币政策制定并没有在很大程度上盯住房地产价格波动,这也与我国稳定物价和促进经济增长的货币政策目标相一致。现阶段,人民银行对资产价格最准确的说法是关注,房地产价格并不是制定和执行货币政策的直接依据。
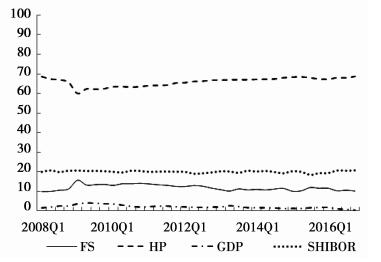
(五) 采用递归的预测方差分解进行稳健性分析为了进一步得出我国房地产价格波动对系统性金融风险的动态影响,同时检验本文研究结论的稳健性,我们采用了递归方差分解方法来进行分析。我们从2008年第一季度开始作为基准期,每增加一期,做一次方差分解结果,同时提取第八期的方差分解结果作为一个样本点,直至到样本期的最末端2016年第四季度。递归的方差分解结果见下图。
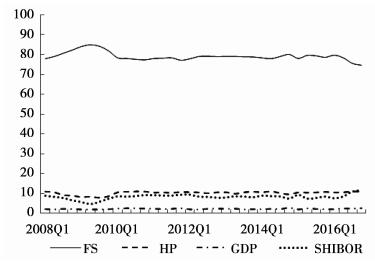
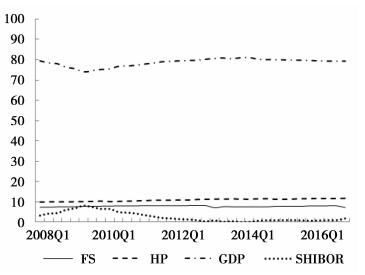
由图 4-图 5的递归预测方差分解结果,我们可以知道系统性金融风险指数变化大部分波动(70%-85%)由其自身进行解释,这表明系统性金融风险的惯性因素一直是推动我国风险积累的重要原因。房地产价格对系统性金融风险的解释力在整个递归期内基本保持与上文预测方差分解一致的结果,保持在10%左右;实际利率对系统性金融风险的影响一直保持在9%左右;国内生产总值的平均解释力也徘徊在2%附近,与上文预测方差分解结果保持一致。然而,我们观察到在2009年第2季度,系统性金融风险有一个陡然的上升随后慢慢下降,房地产价格却恰恰相反,在突然的下降之后开始了缓慢地回升。这充分证明了我国房地产市场由于受到了来自金融危机的强烈外部冲击,使自身的发展路径产生了改变,同时使系统性风险出现了显著的上升。另外,在金融危机以后,房地产价格冲击对实际利率的解释力有着十分明显的上升,这也从侧面反映出,我国中央银行在制定货币政策时开始愈发地关注房地产价格波动,货币政策调整和规则制定开始在更大程度上参考房地产市场因素,央行意图通过货币政策工具调控房地产价格的目标也愈加明显。根据以上递归预测方差分解可知即使改变样本期间,本文的分析结果依然不会改变,因而证明本文得出的是十分稳健的实证研究结果。
|
图 4 系统性金融风险的递归预测方差分解 |
|
图 5 房地产价格的递归预测方差分解 |
|
图 6 国内生产总值的递归预测方差分解 |
|
图 7 实际利率的递归预测方差分解 |
本文基于目前我国房价上涨的现实情况,本文通过选取系统性金融风险指数、房地产价格、国内生产总值和同业拆借利率,建立基于有向无环图(DAG)的结构向量自回归(SVAR)模型,研究房地产价格波动对系统性金融风险的影响机制和动态效应,得出了如下结论:第一,有向无环图的检验表明我国存在房地产价格对系统性金融风险指数的同期影响,国内生产总值对系统性金融风险指数的同期影响,其他变量之间不存在同期因果关系;第二,通过脉冲响应函数结果得到我国房地产价格的快速上涨确实会推动我国系统性金融风险的上升,为了应对该种情况,我国中央银行一般采取提高利率这种货币政策工具手段来调控房价并维护金融系统稳定,然而长期看,政策效果微弱;另外,由于多年来我国资金存在离实向虚的现象,导致我国系统性金融风险一定程度上脱离实体经济状况而存在;第三,预测方差分解结果显示,自身惯性的推动作用是我国房地产价格水平不断上升的主要原因,房地产价格波动相较于其他变量来说拥有对系统性金融风险更大的解释力,房价对金融稳定起到至关重要的基础作用,且由于金融系统性风险具有传染性,信息不对称以及金融脆弱性的存在都会导致金融系统性风险在金融体系内快速传导,使得系统性金融风险也存在惯性。
为了维护我国金融稳定和政府进一步实施有效的房地产市场调控政策,结合本文实证分析结论,我们提出如下政策建议:第一,房地产价格波动与金融系统性风险之间有着紧密的内在联系,政府要加强土地市场调控,合理控制土地的供应,合理控制房地产开发投资,防止其加剧房地产价格的波动,建立多元化房地产融资机制,防止风险集聚。总的来说,政府实施房地产价格调控需遵循“宏观审慎”的原则,把阻绝房价剧烈波动作为先决条件,对金融系统的风险概况进行严密监管;第二,人民银行的应该密切关注房地产价格的变化,尤其在房地产价格波动对金融系统性风险产生重要影响时,可以适时合理地运用货币政策工具,譬如调整货币供应量,推动利率市场化改革灵活使用利率政策等,来对房地产市场进行调控,降低房地产价格波动导致可能导致的金融系统性风险;第三,政府应通过降低税收、提高金融市场效率等举措降低企业经营成本;加大基础设施投资和基础科学研究和技术创新的投入来提高企业劳动生产率;继续推进国际市场开拓和全球化战略,提升中国产品竞争力和需求;切实提升实体企业回报率,从而引导社会资金“脱虚入实”,我国应当不断推进经济结构优化进程、加快经济结构调整步伐,打造资金、技术、资源、劳动密集型行业均衡发展的可持续经济增长模式,从根源上防止系统性金融风险的出现和蔓延。
| [] |
巴曙松、居姗、朱元倩,
2013, “我国银行业系统性违约风险研究——基于Systemic CCA方法的分析”, 《金融研究》, 第 9 期, 第 71–83 页。 |
| [] |
段忠东,
2007, “房地产价格波动与银行信贷增长实证研究”, 《金融论坛》, 第 2 期, 第 40–45 页。 |
| [] |
郭娜、李政,
2013, “我国货币政策工具对房地产市场调控的有效性研究——基于有向无环图的分析”, 《财贸经济》, 第 9 期, 第 130–137 页。 |
| [] |
郭娜、梁琪,
2011, “我国房地产市场周期与金融稳定——基于随机游走滤波的分析”, 《南开经济研究》, 第 4 期, 第 98–107 页。 |
| [] |
强林飞、贺娜、吴诣民,
2010, “中国银行信贷、房地产价格与宏观经济互动关系研究——基于VAR模型的实证分析”, 《统计与信息论坛》, 第 9 期, 第 75–80 页。 |
| [] |
齐讴歌,
2015, “房地产价格波动对金融体系的传导效应研究”, 《统计与决策》, 第 16 期, 第 44–48 页。 |
| [] |
梁琪、李政,
2014, “系统重要性、审慎工具与我国银行业监管”, 《金融研究》, 第 8 期, 第 55–69 页。 |
| [] |
陶玲、朱迎,
2016, “系统性金融风险的监测和度量——基于中国金融体系的研究”, 《金融研究》, 第 6 期, 第 18–36 页。 |
| [] |
谢正发、饶勋乾,
2016, “金融脆弱性指数构建的测度与实证分析”, 《统计与决策》, 第 5 期, 第 152–156 页。 |
| [] |
杨子晖,
2008, “财政政策与货币政策对私人投资的影响研究——基于有向无环图的应用分析”, 《经济研究》, 第 5 期, 第 81–93 页。 |
| [] |
张晓晶、孙涛,
2006, “中国房地产周期与金融稳定”, 《经济研究》, 第 1 期, 第 23–33 页。 |
| [] |
赵园,
2015, “房价波动、信贷结构与金融稳定——基于1998-2012年数据的实证分析”, 《武汉金融》, 第 12 期, 第 60–62 页。 |
| [] |
赵胜民、方意、王道平,
2011, “金融信贷是否中国房地产、股票价格泡沫和波动的原因——基于有向无环图的分析”, 《金融研究》, 第 12 期, 第 62–76 页。 |
| [] |
Allen F., Gale D., 2000, "Bubbles and Crises". Economic Journal, 110(460), 236–255.
DOI:10.1111/ecoj.2000.110.issue-460 |
| [] |
Bernanke B. S., Gertle M., 1995, "Inside the Black Box:The Credit Channel of Monetary Policy Transmission". Journal of Economic Perspective, 9(4), 27–48.
DOI:10.1257/jep.9.4.27 |
| [] |
Crowe C., Ariccia G. and Igan D., 2011, "How to Deal with Real Estate Booms:Lessons from Country Experiences". Journal of Financial Stability, 9(3), 300–319.
|
| [] |
Collyns C., Senhadji A., 2002, "Lending Booms Real Estate Bubbles and the Asian Crisis". IMF Working Paper(No. 20).
|
| [] |
Shen CH, Lee YH, Wu MW and Guo N, 2015, "Does Housing Boom Lead to Credit Boom or Is It the Other Way Around? The Case of China". International Review of Economics and Finance, 42, 349–367.
|
| [] |
Diebold F. X., Ylmaz K., 2014, "On the Network Topology of Variance Decompositions:Measuring the Connectedness of Financial Firms". Journal of Econometrics, 182(1), 119–134.
DOI:10.1016/j.jeconom.2014.04.012 |
| [] |
Drehmann M., Tarashey N., 2013, "Measuring the Systemic Importance of Interconnected Banks". Journal of Financial Intermediation, 22(4), 586–607.
DOI:10.1016/j.jfi.2013.08.001 |
| [] |
Goodhart B., Hofmann B., 2007, "House Prices and the Macroeconomy:Implications for Banking and Price Stability", Published by Oxford University Press.
|
| [] |
Pouvelle C., 2012, "Bank Credit Asset Prices and Financial Stability:Evidence from French Banks". IMF Working Paper(No. 103).
|
| [] |
Sprites P., Glymour C. and Scheines R., 2000, "Causation Prediction and Search", Published by MIT Press.
|




