随着我国经济的不断增长,环境污染问题变得日益严重,尤其是近年来许多大中城市出现的严重雾霾现象,使得解决城市环境问题显得尤为迫切。城市集聚大量的人口,是人类经济活动的主要空间场所。城镇化作为近年来经济发展的主要推手,在不断促进经济增长的同时也深刻地影响环境。因此,了解经济增长、城镇化与环境污染之间的关系显得尤为重要。
经济增长与环境污染之间的关系,最为经典的研究是Grossman和Krueger发现的环境库兹涅茨曲线(Environmental Kuznets Curve,EKC)。EKC假说认为,随着经济的发展,环境污染逐渐增大,到达某个顶点后会逐渐下降,呈现出先上升后下降的倒U型关系。围绕EKC假说,出现了大量的结论迥异的实证文献,如关于EKC曲线就存在倒U型、U型、N型等不同的结果(Dinda,2005;李文玉等,2005;周国富等,2012)。关于EKC的内在机制,多数文献没有考虑环境污染的内生性,因而得出单向的EKC关系,即经济增长使得环境污染出现倒U型曲线。事实上环境污染具有内生性(黄菁,2009;汪笑云等,2013),因此,单向的EKC曲线可能不能准确说明经济增长与环境污染之间的关系。
以往的研究主要关注于经济增长与环境污染之间直接关系,而对环境污染的主要空间场所城市关注不够。城市聚集着生产要素,推动着经济增长,使得其成为环境污染的主要空间场所。我国目前整体的城镇化水平不高,且城镇化发展长期滞后经济增长,因此,在未来很长一段时间内,城镇化仍将处于快速推进的阶段,但不同的城镇化道路会导致不同的环境后果。显然,若再走发达国家那种先污染后治理的老路,面临的资源与环境压力将使之难以为继。
受自然作用,污染排放物会在空间范围内扩散,与此类似,某个城市的经济增长与城镇化发展受到周边城市影响,因此,在研究济增长、城镇化与环境污染之间的关系必须考虑空间因素。基于以上原因,本文将城镇化纳入EKC假设的研究中,考虑环境污染的内生性及空间溢出效应建立联立方程模型,以此分析经济增长、城镇化与环境污染之间的相互关系。
二、文献回顾与理论分析 (一) 文献回顾现有的文献主要侧重经济增长与环境污染之间的研究,基于经典的EKC假说来验证其是否存在。一些学者对个别城市进行检验(吴玉萍等,2003;陈华文,2004),还有学者运用全国数据(黄菁,2010;王成飞等,2014)验证环境库兹涅茨曲线(EKC)在中国城市似乎成立。近期部分文献开始将城镇化纳入经济增长与环境污染之间分析框架中,如李姝(2011)、汪笑云等(2013)、李鹏飞等(2014)。关于城镇化对环境污染的影响,学者们认为城镇化是影响EKC的机制之一,表现为城镇化会改善环境污染,但不同的地方存在差异。一些学者认为,全国总体城镇化与东部地区城镇化的提高能减少环境污染,但中西部地区城市化的上升对环境污染的影响并不显著,如丁翠翠(2014)、李鹏飞等(2014)。
在EKC的基础上,环境污染的空间效应,也得学者们的关注。Hossin and Kaneko(2013)认为不同国家间环境污染具有空间溢出效应。张可等(2014)、东童童等(2015)发现在我国环境污染也存在空间溢出效应。
在研究方法上,早期的文献主要运用时间序列进行分析。近期的文献虽以面板数据分析为主,但这些研究,忽略了环境污染对经济增长或城镇化之间的反馈作用,没能消除变量的内生性影响,使得模型的估计存在偏误。近年来有部分学者尝试运用联立方程来刻画经济增长、城镇化与环境污染之间的影响机制(包群等,2006;黄菁,2010;汪笑云等,2013)。不过这些学者在建立联立方程时,使用的控制变量过少,不能全面反映经济发展或城镇化与环境污染之间的关系,而且忽略了环境污染的空间溢出效应,其结论的适用范围受限。因此,本文利用误差修正模型及空间联立方程模型对经济增长、城镇化与环境污染的相互关系进行实证研究,以期深入探索它们之间的内在联系及其决定机制。
(二) 理论分析经济增长主要通过产业结构调整与资源集聚效应影响城镇化。经济增长推动着产业结构调整,劳动力由第一产业向第二、三产业转移;城镇化水平随着劳动力向非农产业的集聚而提高。经济增长同时带动着资源向城市集中,生产资源与各种生活服务资源在城市的集中使得人口向城市集聚,也提高了城镇化。另一方面,城镇化也影响着经济增长。一是资源支持效应,由于城市拥有人力资源、基础设施等各种资源,这些资源的集聚推动着经济增长。二是分工效应,城镇化带来分工的专业化,降低企业的交易成本与交易时间,提高了经济效益也推动着经济增长。
经济增长对环境污染有两个影响途径。一是在国内通过规模效应、结构效应与技术效应对环境污染产生影响。规模效应是指在技术条件、环保政策与其他条件没有发生变化的情况下,经济增长意味着经济规模的扩大,必然带来更多的污染物;经济增长推动产业结构优化升级从而减少污染,产生结构效应(蔡濛萌、尹秀芳,2017);经济增长会带来更为环保的技术,产生正的技术效应而减少污染,改善环境(包群等,2006;黄菁,2009)。二是经济增长使得国际间贸易更为开放,发达国家通过贸易与投资将污染企业或产品向发展中国家转移,会带来环境污染。正因这四类效应的共同作用,使得经济增长与环境质量之间存在倒U型的环境库兹列茨曲线。环境污染也会反作用于经济增长。一是环保成本上升阻碍经济增长。随着经济增长,更多的污染物排出,当环境污染到达一定程度时,其会严重影响公众健康,使得政府采取严厉的环保政策,增加厂商的成本(施美程等,2016),从而降低生产规模,阻碍着经济增长。二是生产方式改变影响经济增长。政府的环保监管会促使企业采用先进技术,减少污染,提高生产效率,推动经济增长。三是消费偏好改变影响经济增长。环境污染的增加导致消费者对绿色环保的健康产品需求增多从而拉动经济增长。
城镇化主要通过以下方式影响环境污染。一是人口的聚集效应。大量人口迁移到城镇会使得人口的密度增大,消耗大量的物质,造成废物排放增多,带来环境污染;城镇化水平的提高会带来消费结构的变化,产生更多的生活垃圾,进而恶化环境质量(Poumanyvong and Kaneko, 2010)。二是生产能耗效应。城镇化的生产方式为大规模工业生产,耗费大量石化能源,会带来严重的工业污染;城镇的扩大,机动车辆的增多,也会消耗更多能源导致环境污染。三是市政效应。城镇的扩大使得城市有能力对污染进行大规模处理,降低单位环保成本,从而减少环境污染;城镇化会增加居民受教育的机会和层次,改变生活方式进而减少环境污染(张腾飞,2016);高度城镇化会改变居民出行的方式,增加公共交通的利用率,降低环境污染。反之,环境污染也会影响城镇化的进程。一是环境污染影响居民健康从而迟滞城镇化。一方面污染会导致居民健康下降,使得人口外流;另一方面由于污染损害居民健康,使得医疗支出增加,损害社会经济福利,不利于城镇化的进一步深化。二是污染会影响居住环境,阻碍城镇化。环境恶化排斥居住人口,使得城市对人口的吸引力下降,导致人口外流。三是环境污染对劳动力供给机制产生影响而作用于城镇化。污染会影响劳动者的健康人力资本与劳动时间,抑制劳动者参与劳动的积极性,可能造成劳动力供给下降(杨俊等,2012),从而影响城镇化。四是环境污染降低资源的承载力,抑制城镇化。固体污染物的增多占用大量的土地资源,制约了城镇化对土地的需求;废水的污染与处理,减少了水资源,提升了水价格,增加了生产与生活成本。
空间地理因素作为重要的外生变量对经济增长、城镇化与环境污染都有着重要影响。一个区域经济的增长不但受自身发展状况的影响而且受临近地区经济发展的影响,所以,空间溢出效应是影响我国区域经济增长的重要因素(潘文卿,2012),其随时间会推移整体增强,并且随地理距离的增加而减弱(王雪辉等,2016)。空间溢出效应使得经济增长对周边地区产生影响,进而影响周边地区的城镇化水平与环境污染。
城镇化是各种资源要素在城镇的空间集聚,它的空间效应表现为通过一定的方式影响经济增长的空间格局。城镇在发展过程中,通过交通、物流等因素与周边地区进行交流,经济强势城市对周边地区产生辐射效应,带动周边地区技术进步,促进经济增长,也影响着周边地区的环境污染。
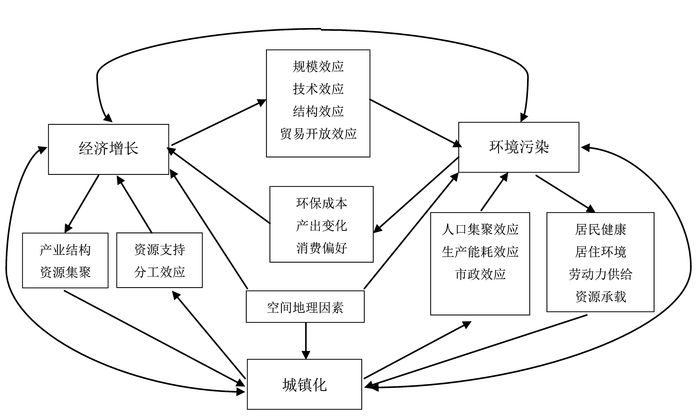
环境污染的空间溢出效应有三个途径。一是污染排放物通过空间扩散对周边地区产生影响,形成跨界污染。二是由于一些城市的环保标准提升,其污染产业向周边地区转移,会加重周边地区的环境污染。三是一些城市的先进环保技术因产业链或其他渠道向周边地区输出,这有利于周边地区环境得到改善。环境污染的空间溢出效应使得其对周边环境可能产生影响,进而影响周边地区的经济增长与城镇化。经济增长、城镇化与环境污染之间的相互作用机理见图 1。
|
图 1 经济增长、城镇化与环境污染相互影响机理 |
由理论分析可知,经济增长、城镇化与环境污染相互影响,为此,对其进行面板格兰杰因果检验,以证实其内生性。对于面板格兰杰因果检验,张清勇、郑环环(2012)认为不能用VAR模型验证,而需用面板VECM模型进行检验,为此本文构建三个误差修正模型(VECM):
| $\left[ {\begin{array}{*{20}{l}} {Dp{o_{it}}}\\ {Drgd{p_{it}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\gamma _1}}\\ {{\gamma _2}} \end{array}} \right]{e_{i,t - 1}} + \sum\nolimits_{j = 1}^l {\left( {\begin{array}{*{20}{l}} {{\beta _{11,j}}}&{{\beta _{12,j}}}\\ {{\beta _{21,j}}}&{{\beta _{22,j}}} \end{array}} \right)} \left[ {\begin{array}{*{20}{l}} {Dp{o_{i,t - 1}}}\\ {Drgd{p_{i,t - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{\varepsilon _{1i}}}\\ {{\varepsilon _{2i}}} \end{array}} \right]$ | (1) |
| $\left[ {\begin{array}{*{20}{l}} {Dp{o_{it}}}\\ {Durba{n_{it}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\gamma _1}}\\ {{\gamma _2}} \end{array}} \right]{e_{i,t - 1}} + \sum\nolimits_{j = 1}^l {\left( {\begin{array}{*{20}{l}} {{\beta _{11,j}}}&{{\beta _{12,j}}}\\ {{\beta _{21,j}}}&{{\beta _{22,j}}} \end{array}} \right)} \left[ {\begin{array}{*{20}{l}} {Dp{o_{i,t - 1}}}\\ {Durba{n_{i,t - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{\varepsilon _{1i}}}\\ {{\varepsilon _{2i}}} \end{array}} \right]$ | (2) |
| $\left[ {\begin{array}{*{20}{l}} {Drgd{p_{it}}}\\ {Durba{n_{it}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\gamma _1}}\\ {{\gamma _2}} \end{array}} \right]{e_{i,t - 1}} + \sum\nolimits_{j = 1}^l {\left( {\begin{array}{*{20}{l}} {{\beta _{11,j}}}&{{\beta _{12,j}}}\\ {{\beta _{21,j}}}&{{\beta _{22,j}}} \end{array}} \right)} \left[ {\begin{array}{*{20}{l}} {Drgd{p_{i,t - 1}}}\\ {Durba{n_{i,t - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{\varepsilon _{1i}}}\\ {{\varepsilon _{2i}}} \end{array}} \right]$ | (3) |
上式中D为差分,poit为单位非农产出的污染排放量。rgdpit为人均GDP表示经济增长。urbanit为城镇化率,表示城镇化的水平。ei, t-1为误差修正项,γi为误差修正项系数,βik, j为差分项系数,εki为随机扰动项。(1)式是经济增长与环境污染互为格兰杰因果关系的检验,相应地转化为检验β12, 1=β12, 2…=γ1=0、β21, 1=β21, 2…=γ2=0,这可利用F检验进行。(2)式与(3)分别为环境污染与城镇化,经济增长与城镇化的格兰杰因果检验,其原理与(1)式相同。
(二) 空间联立方程模型设定在VECM模型验证经济增长、城镇化与环境污染之间存在相互影响的基础上,本文再用空间联立方程模型来估计各影响因素的大小及空间溢出效应。(4)式为污染方程,(5)式为经济增长方程,(6)式为城镇化方程。wij为空间权重矩阵①,当城市地理相邻时取值为1,不相邻时取值为0。Xit和Yit、Zit为控制变量。uit、ηit、θit表示地区个体效应,εit、νit、ξit为随机误差扰动项。在污染方程中加入rgdpit的平方项gdpit,以验证是否存在环境的库兹涅茨曲线;在经济增长方程中加入污染的平方项poll,以验证污染增加大时其对经济增长的作用是否会发生变化。
① 本研究删掉了一些数据缺乏与城镇化率较高的城市,使得个别城市没有临近单元,又因我国地级城市的行政区域面积相差较大,故难以用地理距离等空间权重矩阵。
| $p{o_{it}} = {\alpha _0} + {\alpha _1}{w_{ij}}p{o_{it}} + {\alpha _2}rgd{p_{it}} + {\alpha _3}rgd{p_{it}} + {\alpha _4}urba{n_{it}} + {\alpha _5}urba{n_{it}} + \sum\limits_{i = 1}^k {{\alpha _i}{X_{it}}} \\ + {\mu _i} + {\varepsilon _{it}}$ | (4) |
| $rgd{p_{it}} = {\beta _0} + {\beta _1}{w_{ij}}rgd{p_{it}} + {\beta _2}p{o_{it}} + {\beta _3}{w_{ij}}p{o_{it}} + {\beta _4}urba{n_{it}} + {\alpha _5}{w_{ij}}urba{n_{it}} + \sum\limits_{i = 1}^k {{\beta _i}{Y_{it}}} \\ + {\eta _i} + {\nu _{it}}$ | (5) |
| $urba{n_{it}} = {\delta _0} + {\delta _1}{w_{ij}}urba{n_{it}} + {\delta _2}rgd{p_{it}} + {\delta _2}{w_{ij}}rgd{p_{it}} + {\delta _4}p{o_{it}} + {\delta _5}{w_{ij}}p{o_{it}} + \sum\limits_{i = 1}^k {{\delta _i}{Z_{it}}} \\ + {\theta _i} + {\xi _{it}}$ | (6) |
1.内生变量。环境污染强度(po):用单位非农产出的污染排放量来测度,采用GDP平减指数调整为2003年不变价格。根据数据的可得性,选取工业废水(FW)、工业粉尘(FD)、二氧化硫(SO2)三种污染物来度量环境污染,并比较三者与经济增长与城镇化之间关系可能存在的差异。经济增长(rgdp)用人均GDP表示;城镇化(urban)用户籍非农人口占总户籍人口的比重来度量①。
① 由于2009年后中国城市年鉴不再提供非农人口数据,为保障数据的连续性,所有非农人口与总人口数据均取自各省统计年鉴,一些省份城市的城镇人口数据相应调整为非农人口。
2.控制变量。污染方程的控制变量主要有第二产业占比(sec)、贸易开放因素(fdi)、环保规则(rule)与技术进步(tech)。其中二产业占比(sec)用第二产业产值占GDP的比重来衡量。第二产业主要由工业组成,工业污染是环境污染主要来源(张可等,2014)。贸易开放使得发达国家可能通过对外投资转移环境污染(王碧,2013;史青,2013)。贸易开放因素(fdi)用FDI占城市GDP的比重来衡量。加强环境管治能抑制污染,通过加大环境治理投资可降低污染排放(黄贸兴等,2013;史青,2013),因此,环保规则(rule)用环境治理的投资来度量。在我国技术进步直接表现为单位产值的耗电量降低(马磊,2012;李斌等,2014),因此,技术进步(tech)用工业用电与城市GDP的之比来衡量,由于其为逆向指标,改用其倒数来测度。
经济增长方程的控制变量有劳动人数(labor)、资本(capital)与技术进步(tech)。劳动人数(labor)用万人中从业人数来衡量;资本的存量对经济产出有较大的影响,但每年变化的是新增资本(张可等,2014;候淑霞等,2014),所以,资本(capital)用万元GDP所用的固定资产投资额来衡量,采用GDP平减指数调整为2003年不变价格。城镇化方程的控制变量有第二产业占比(sec)与第三产业占比(third)、贸易开放因素(fdi)、人口自然增长率(popg)与教育程度(edu)。第三产业占比(third)用第三产业产值占GDP比重来衡量;人口自然增长率(popg)为各城市人口自然增加数与该时期内平均人数之比来衡量;教育程度(edu)用各城市中万人大学生在校人数来衡量(王立新,2014)。
3.数据来源。本文选取2003~2014年中国地级城市作为研究样本,数据来于同期的《中国城市统计年鉴》和各省份的统计年鉴。考虑行政区域的变化、各指标的数据的完整性,以及将城镇化率非常高的城市剔除②,最终选取了253个地级城市作为研究对象。部分指标的缺失值通过指数平滑法进行补齐。除人口自然增长率外,所有数据均取自然对数以消除异方差影响。
② 深圳、珠海等城市从2005年开始其人口城镇化率一直为100%,不适合做计量分析,因此,将其从样本中删去。
四、实证结果分析 (一) 面板格兰杰因果关系分析对内生变量进行平稳性分析,各变量均为一阶单整,变量间存在协整关系,限于篇幅,单整及协整检验报告表格予以省略,仅报告格兰杰因果检验报告(见表 1)。表 1中所有滞后l至6期时的F值表明,其在1%的显著性水平下均拒绝原假设,即经济增长、城镇化与环境污染互为格兰杰因果成因, 这为空间联立方程建模提供了依据。
| 表 1 格兰杰因果检验结果 |
对于空间联立方程模型,Kelejian and Prucha(2004)给出广义空间三阶段最小二乘法(GS3SLS)估计方法,Baltagi and Ying(2015)对空间面板联立方程给出EC3SLS估计步骤。GS3SLS方法考虑了内生变量的潜在的空间相关性,也对各方程的随机扰动项的相关性进行处理。本文参考李胜兰等(2014)方法,利用虞义华(2015)的程序,运用广义空间三阶段最小二乘法(GS3SLS)对(4)~(6)式进行估计,结果见表 2。为了对比分析,本文同时给出3SLS的估计结果(见表 3),以便更好地了解内生变量的空间溢出效应。
| 表 2 2003—2014年经济增长、城镇化与环境污染的GS3SLS估计结果 |
| 表 3 2003—2014年经济增长、城镇化与环境污染的3SLS估计结果 |
由表 2可知,在污染方程中经济增长的估计系数显著为正,经济增长每增加1%,工业废水、工业粉尘与二氧化硫的排放强度分别会增加0.19%、0.42%与0.41%。改革开放以来,我国经济增长主要以粗放式工业化发展为主,而这种发展方式加剧了环境污染。在污染方程中城镇化的估计系数都显著为负,城镇化率每增加1%,工业废水、工业粉尘与二氧化硫的排放强度分别会降低1.29%、1.8%与2.32%。目前我国的城镇化已处于城镇化中后期阶段,其生产与生活方式向环保节能方向转变,大部分城市对加大了对污染物的处理,因此,城镇化的发展会降低环境污染。污染排放与经济增长的空间滞后项系数均显著为正,而城镇化的空间滞后项系数为显著为负,说明污染排放、经济增长与城镇化的发展与周边城市有关。以工业废水方程为例,周边城市的污染排放强度、经济增长每增加1%,本城市的工业废水将会分别增加0.29%和0.27%,而周边城市的城镇化率每增加1%时,本城市的工业废水会减少1.64%。当然,对于不同的污染物方程,经济增长与城镇化对其影响是不一样的,如经济增长对工业粉尘方程(0.43%)的影响大于工业废水方程(0.19%)与二氧化硫方程(0.41%)。污染的空间相关主要是由于临近地区的自然因素影响,也可能由于周边城市之间的经济联系与产业关联的影响。
由表 2可知,人均GDP与其平方项分别为正与负,其中工业废水与二氧化硫方程中人均GDP与其平方项都十分显著。而工业粉尘空间方程中人均GDP的平方项不显著,在3SLS回归中,则人均GDP不显著。可以认为随着经济的发展,环境污染会出现先增加后减少的倒U型的关系,环境库兹列茨曲线是客观存在的。但这并不意味着所有的污染物都会在相同的时间内同时出现显著的倒U型的关系,某些污染物可能受自身的特点与各种条件限制使得其倒U型的关系并不显著,或者倒U型的关系延期出现。我国不同区域的城市经济发展存在较大差异,其污染排放物也相差较大。以2014年为例,东部样本城市的人均GDP已达到6万元,中部样本城市的GDP接近5万元,而西部样本城市的人均GDP为4万元,东部与西部相差近2万元;样本东部城市的废水、二氧化硫与工业烟尘排放物,其占总体比例分别为54.18%、40.56%、44.80%,中部城市占比为31.2%、32.41%、34.77%,西部城市占比为14.62;27.03%、20.43%。因此,随着经济的增长,不同城市不同污染物先增后减达到临界点时间并不一致。而像工业烟尘这类污染排放物可能由于某些自然属性等原因,其并不存在明显的临界点。第二产业的估计系数显著为正,第二产业每增加1%时,工业废水、工业烟尘与二氧化硫会相应增加0.41%、0.60%与1.00%。第二产业主要由工业组成,工业发展导致其排放的工业污染物会大量增加。外商直接投资在1%显著性水平上对二氧化硫的排放影响为正,在10%显著性水平上对工业废水的排放影响为正,对工业烟尘的影响为正但不显著。总体来说,外商直接投资增加了环境污染,这与是史青(2013)、王碧芳(2013)的研究类似。发达国家向发展中国家进行投资时,可能将其高污染高耗能的产业会向发展中国家转移,因而FDI也会带来环境污染。环保规则估计系数在3SLS方程中为负,除在工业烟尘方程的影响显著外,其余不显著;在空间联立方程中却都为正,但都不显著,说明我国环保政策目前并没显著抑制环境污染,其原因是环保政策没有得到有效的执行(张卫东、汪海,2007)。包群等(2013)指出,单纯环保立法不能有效抑制污染,只有严格环保执法力度,环保立法才能有效改善环境。技术进步的估计系数在3SLS方程中除对工业烟尘不显著外,工业废水与二氧化硫排放都通过了1%的显著性水平,但考虑空间效应后,都变得不显著。本地的技术进步能显著抑制本地污染排放,但周边城市的技术进步可能导致落后的技术向本市转移,因而周边地区的技术进步会增加本地环境污染,这两种因素的共同作用使得技术进步对环境排放的影响不明显。
(三) 经济增长方程的估计结果分析在经济增长方程中,三种污染排放物对经济增长的影响都显著为正,工业废水、工业烟尘与二氧化硫排放强度每增加1%,可使得经济增长分别增加0.26%、0.73%与0.72%。环境污染作为工业生产的副产品,随工业生产的增加而不断上升,因此,工业生产越多,意味着环境污染排污物也越多,经济也就不断增长。在空间联立方程与3SLS方程中污染排放物的平方项的系数均显著为负,其中工业废水与二氧化硫的平方项均为在1%的显著性水平通过检验,工业烟尘的平方项在10%显著性水平通过检验。以上实证结果说明,当经济发展处于较低的水平时候,工业化发展推动着经济增长,污染物随之上升,但当经济发展一定程度时,由于环境污染对公众健康的影响,以及环保成本的上升都会使得其阻碍经济增长。因此,环境污染的库兹涅茨曲线EKC是一个双向的到U型曲线,既包括经济增长影响环境污染的倒U型曲线,也包括环境污染影响经济增长的倒U型曲线。
污染排放物的空间滞后系数均不显著,说明周边城市的污染对本地经济的发展基本没有影响。但经济增长与城镇化的空间滞后项都显著为正,且它们在三个经济增长方程中的系数都通过了1%显著性水平检验。这说明周边城市的经济增长与城镇化水平的提升会拉动本地的经济增长。周边城市的经济增长会通过产业集聚与产业结构等经济联系而加快本地的经济增长。周边城市的城镇化提高,一方面通过促进周边城市的经济增长而影响本地经济增长,另一方面通过交通等因素带动本地经济增长。技术进步的估计系数不管在空间联立方程中还是在3SLS方程中,都通过1%的显著性水平为正。技术进步导致对资源的利用效率提高,产出增加,推动着经济增长。在三个经济增长方程中,劳动的估计系数为负且不显著,说明劳动的增加对经济增长几乎没有影响。与此相反,资本的估计显著为正,其都通过了1%显著性检验。在样本的研究期间,我国经济增长得益于我国民间与政府的投资不断增加。以废水的经济增长方程为例,投资每增长1%,经济增长将会加0.28%。
(四) 城镇化方程的估计结果分析在3SLS方程中,污染排放物对城镇化的影响为负,但不显著,而在空间联立方程中,污染排放物的影响为正也不显著,污染排放物空间滞后项的影响也不显著。分析发现,在东部地区污染排放物的影响为负且通过1%显著性水平检验,而在西部地区,污染排放物的影响为正也通过5%的显著性检验。这说明在城镇化发展的不同阶段,污染排放物对环境的影响是不一样的,这与丁翠翠(2014)的研究结果类似。我国幅员辽阔,城镇化的发展存在巨大差异(蓝庆新等,2017),当城镇化发展处于较低水平的时候,工业化发展推动经济增长进而提高了城镇化水平。因此,随着污染排放物的增加,城镇化水平也在上升;而当城镇化水平处于较高水平时,城市的经济增长主要由第三产业带动。环境污染通过影响居民健康、居住环境恶化、劳动力供给减少以及资源承载能力下降进而阻碍第三产业发展,使得就业人口向周边城市流失,因而会出现随着污染排放物的增加,城镇化水平下降。
经济增长的估计系数为正,以废水方程为例,经济每增长1%,城镇化率会增长0.15%。但经济增长的空间滞后项的影响并不显著,说明周边城市的经济增长对本地的城镇化的影响并不显著。周边城市的经济增长一方面会通过产业结构等经济关系对当地的经济产生正向影响,但同时也可能对当地劳动力产生吸引,因而其总的影响并不显著。城镇化的空间滞后项的估计系数为正且通过1%的显著性检验。说明周边城市的城镇化对本城市的城镇化的影响为正。周边城市的城镇化发展一方面通过经济联系带动本市的城镇化的深化,另一方面也可能由于城市圈的发展带动本市的城镇化率提升。
在城镇化3SLS方程中,第二产业、第三产业的估计系数都为正且都通过1%的显著性检验,而在空间方程中,两者都通过10%的显著性检验。本地产业结构的变化对于当地的城镇化发展有显著影响,而考虑空间因素后,这种作用有所下降。其他控制变量如FDI、人口自然增长率以及教育对城镇化的影响都不显著。
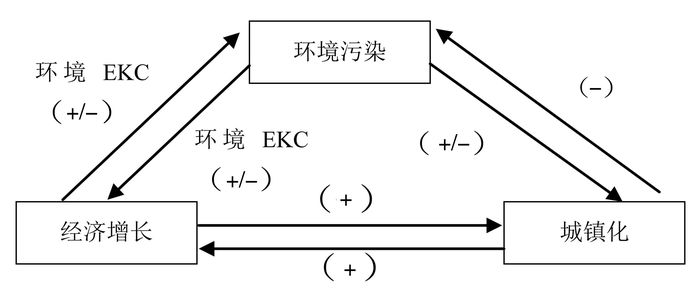
经济增长、城镇化与环境污染之间的相互关系实证结果可由图 2来表示。
|
图 2 经济增长、城镇化与环境污染相互影响实证结果 |
由于污染物主要由工业排放的,而工业是第二产业最主要的组成部分,参考高宏霞等(2012)做法,将单位非农产出的污染排放量改为第二产业人均污染排放量,重新对模型进行估计,具体结果见表 4。从表 4中可以看出,各变量的估计系数、符号与显著性均无较大变化,说明估计的结果较为稳健。
| 表 4 第二产业人均污染排放强度的GS3SLS估计结果 |
本文通过建立空间面板联立方程对经济增长、城镇化与环境污染之间的关系进行实证研究,得到如下结论:
环境库兹列茨曲线是客观存在的,但这并不意味着所有的污染物都会在相同的时间内同时出现显著的倒U型的关系,某些污染物可能受自身属性与各种条件限制使得其倒U型的关系并不显著,或者倒U型的关系延期出现,因此,不同城市不同污染物达到临界点时间并不一致。
经济增长通过国内国际两方面影响环境污染,环境污染对经济增长也有反向作用。当环境污染达到一定程度时,会增加企业的环保成本而阻碍经济增长,因此,经济增长与环境污染之间的关系应该是双向倒U型关系:随着经济的增长,环境污染会先上升后下降;随着环境污染的增加,经济增长也会先上升后下降。
城镇化的发展会降低环境污染。环境污染也反作用于城镇化。当城镇化发展处于较低水平的时候,随着污染排放物的增加,城镇化水平会上升;但当城镇化达到较高水平时,环境污染会影响第三产业的发展进而阻碍城镇化发展。
经济增长、城镇化与环境污染均存在空间溢出效应,它们的发展均与周边城市密切相关。周边城市的经济增长与环境污染会加剧本地环境污染,周边城市的城镇化发展会降低本地的环境污染。
一般说来,中国的工业化是导致环境污染的主要原因;发达国家向发展中国家进行投资时,可能将其高污染高耗能的产业会向发展中国家转移,因此,外商直接投资可能会增加环境污染;目前我国的环保政策并没能显著抑制环境污染,主要由于环保政策的执行力度不够。由于在空间溢出效应,技术进步对环境污染的影响并不明显。
| [] |
包群、彭水军,
2006, “经济增长与环境污染:基于面板数据的联立方程估计”, 《世界经济》, 第 11 期, 第 48–58 页。 |
| [] |
包群、邵敏、杨大利,
2013, “环境管制抑制了污染排放吗?”, 《经济研究》, 第 12 期, 第 42–54 页。DOI:10.3969/j.issn.1002-5863.2013.12.019 |
| [] |
蔡濛萌、尹秀芳,
2017, “产业结构调整与环境质量优化的协动关系研究——基于我国省级面板数据的分析”, 《江西社会科学》, 第 8 期, 第 59–67 页。 |
| [] |
丁翠翠,
2014, “FDI, 城市化与环境污染关系的实证检验”, 《统计与决策》, 第 14 期, 第 143–145 页。 |
| [] |
陈华文、刘康兵,
2004, “经济增长与环境质量:关于环境库兹涅茨曲线的经验分析”, 《复旦学报(社会科学版)》, 第 2 期, 第 87–94 页。 |
| [] |
东童童、李欣、刘乃全,
2015, “空间视角下工业集聚对雾霾污染的影响——理论与经验研究”, 《经济管理》, 第 9 期, 第 29–41 页。 |
| [] |
侯淑霞、王雪瑞,
2014, “生产性服务业集聚与内生经济增长——基于空间联立模型的经验研究”, 《财经论丛》, 第 5 期, 第 3–8 页。 |
| [] |
高宏霞、杨林、付海东,
2012, “中国各省经济增长与环境污染关系的研究与预测——基于环境库兹涅茨曲线的实证分析”, 《经济学动态》, 第 1 期, 第 52–57 页。 |
| [] |
黄菁,
2009, “环境污染、人力资本与内生经济增长:一个简单的模型”, 《南方经济》, 第 4 期, 第 3–11 页。 |
| [] |
黄菁,
2010, “环境污染与城市经济增长:基于联立方程的实证分析”, 《财贸研究》, 第 5 期, 第 8–16 页。 |
| [] |
李斌、李拓,
2014, “中国空气污染库兹涅茨曲线的实证研究——基于动态面板系统GMM与门限模型检验”, 《经济问题》, 第 4 期, 第 17–22 页。 |
| [] |
蓝庆新、刘昭洁、彭一然,
2017, “中国新型城镇化质量评价指标体系构建及评价方法——基于2003-2014年31个省市的空间差异研究”, 《南方经济》, 第 1 期, 第 111–126 页。 |
| [] |
李鹏飞、吴利学、田野,
2014, “中国城镇化路径的环境效应分析”, 《城市与环境研究》, 第 2 期, 第 65–82 页。 |
| [] |
李玉文、徐中民、王勇,
2005, “环境库兹涅茨曲线研究进展”, 《中国人口资源与环境》, 第 5 期, 第 7–14 页。 |
| [] |
李胜兰、初善冰、申晨,
2014, “地方政府竞争、环境规制与区域生态效率”, 《世界经济》, 第 4 期, 第 88–110 页。 |
| [] |
李炫榆、宋海清、李碧珍,
2015, “集聚与二氧化碳排放的空间交互作用——基于空间联立方程的实证研究”, 《山西财经大学学报》, 第 5 期, 第 1–13 页。 |
| [] |
李姝,
2011, “城市化、产业结构调整与环境污染”, 《财经问题研究》, 第 6 期, 第 38–43 页。 |
| [] |
马磊,
2010, “中国城市化与环境质量研究”, 《中国人口科学》, 第 2 期, 第 73–81 页。 |
| [] |
潘文卿,
2012, “中国的区域关联与经济增长的空间溢出效应”, 《经济研究》, 第 1 期, 第 54–65 页。 |
| [] |
史青,
2013, “外商直接投资、环境规制与环境污染——基于政府廉洁度的视角”, 《财贸经济》, 第 1 期, 第 193–103 页。 |
| [] |
施美程、王勇,
2016, “环境规制差异、行业特征与就业动态”, 《南方经济》, 第 7 期, 第 48–62 页。 |
| [] |
苏素、贺娅萍,
2011, “经济高速发展中的城镇化影响因素”, 《财经科学》, 第 11 期, 第 93–100 页。 |
| [] |
江笑云、汪冲,
2013, “经济增长, 城市化与环境污染排放的联立非线性关系”, 《经济经纬》, 第 5 期, 第 1–6 页。 |
| [] |
王飞成、郭其友,
2014, “经济增长对环境污染的影响及区域性差异——基于省际动态面板数据模型的研究”, 《山西财经大学学报》, 第 4 期, 第 14–26 页。 |
| [] |
王立新,
2014, “经济增长、产业结构与城镇化——基于省级面板数据的实证研究”, 《财经论丛》, 第 4 期, 第 3–8 页。 |
| [] |
王碧,
2013, “经济增长、外商直接投资与环境污染——基于面板数据联立方程分析”, 《经济与管理》, 第 8 期, 第 5–13 页。 |
| [] |
王雪辉、谷国锋,
2016, “市场潜能、地理距离与经济增长的溢出效应”, 《财经论丛》, 第 11 期, 第 3–10 页。 |
| [] |
吴玉萍、董锁成、宋键峰,
2002, “北京市经济增长与环境污染水平计量模型研究”, 《地理研究》, 第 2 期, 第 239–246 页。 |
| [] |
虞义华, 2015, 《空间计量经济学理论在中国的实践应用》, 经济科学出版社.
|
| [] |
杨俊、盛鹏飞,
2012, “环境污染对劳动生产率的影响研究”, 《中国人口科学》, 第 5 期, 第 56–65 页。 |
| [] |
张清勇、郑环环,
2012, “中国住宅投资引领经济增长吗?”, 《经济研究》, 第 2 期, 第 67–79 页。 |
| [] |
张卫东、汪海,
2007, “我国环境政策对经济增长与环境污染关系的影响研究”, 《中国软科学》, 第 12 期, 第 32–38 页。 |
| [] |
张可、汪东芳,
2014, “经济集聚与环境污染的交互影响及空间溢出”, 《中国工业经济》, 第 6 期, 第 70–82 页。 |
| [] |
张腾飞、杨俊、盛鹏飞,
2016, “城镇化对中国碳排放的影响及作用渠道”, 《中国人口资源与环境》, 第 2 期, 第 47–57 页。 |
| [] |
周国富、李时兴,
2012, “偏好、技术与环境质量——环境库兹涅茨曲线的形成机制与实证检验”, 《南方经济》, 第 6 期, 第 85–95 页。 |
| [] |
Brückner M., 2012, "Economic growth, size of the agricultural sector, and urbanization in Africa". Journal of Urban Economics, 71(1), 26–36.
DOI:10.1016/j.jue.2011.08.004 |
| [] |
Baltagi B H, Deng Y, 2015, "EC3SLS estimator for a simultaneous system of spatial autoregressive equations with random effects". Econometric Reviews, 34(6-10), 659–694.
DOI:10.1080/07474938.2014.956030 |
| [] |
Dinda S. A, 2005, "Theoretical basis for the Environmental Kuznets Curve". Ecological Economics, 53(3), 403–413.
DOI:10.1016/j.ecolecon.2004.10.007 |
| [] |
Grossman G M, Krueger A B, 1992, "Environmental Impacts of a North American Free Trade Agreement". Social Science Electronic Publishing, 8(2), 223–250.
|
| [] |
Henderson J.V, 2003, "Urbanization and economic development". Annals of Economics and Finance(4), 275–342.
|
| [] |
Hosseini H M, Kaneko S, 2013, "Can environmental quality spread through institutions?". Energy Policy, 56(2), 312–321.
|
| [] |
Kelejian H H, Prucha I R, 2004, "Estimation of simultaneous systems of spatially interrelated cross sectional equations". Journal of Econometrics, 118(1), 27–50.
|
| [] |
Panayotou T., 1993, "Empirical tests and policy analysis of environmental degradation at different stages of economic development", Working Paper, No. W 3914, Technology and Employment Program. Geneva.
|
| [] |
Poumanyvong P, Kaneko S, 2010, "Does urbanization lead to less energy use and lower CO2, emissions? A cross-country analysis". Ecological Economics, 70(2), 434–444.
DOI:10.1016/j.ecolecon.2010.09.029 |




