中国经济在过去30多年的时间内取得了令世界瞩目的增长奇迹,但在经历了金融危机与全球经济低迷后,中国经济进入新常态,甚至面临“中等收入陷阱”的困境(蔡昉,2008;郑秉文,2011)。如何转换经济发展模式、保持经济增长、成功跨越“中等收入陷阱”成为中国经济发展面临的重大议题。Todaro and Smith(2011)指出,教育和健康作为广义的人力资本是现代经济发展的核心。对于发展中国家,如果想进一步推进技术进步、维持经济增长,一个重要的途径就是发展教育(刘生龙等,2016)。
中国的教育发展经历了两次重大的变革:第一次是1986年《中国人民共和国义务教育法》通过,标志着中国开始推行义务教育。根据国家统计局的数据显示,1982年中国的文盲率为22.81%,而到2010年这一数字下降到4.08%,面对这一成绩,义务教育法的实施可谓功不可没。中国教育发展的第二次变革是1999年教育部实施的《面向21世纪教育振兴行动计划》,该计划标志着中国开始进行大规模的高等教育扩张。姚先国等(2013)指出,从1999年到2009年,中国高校招生规模提高近4倍,相当于此前22年(1978-1999年)的增幅。在教育大发展的同时,中国经济发展也经历了“中国奇迹”,在这一过程中,教育作为现代经济发展的核心为中国经济发展提供了重要的人力资本支撑。
在教育发展对经济影响的研究文献中,教育回报率这一主题具有重要的理论价值和政策意义。在宏观层面,劳动力市场的结构变化可以通过教育回报率的变化得以反映。蔡昉、都阳(2011)通过对农民工教育回报率的变化进行研究发现,不同教育水平的农民工教育回报率趋同,而这一特征的出现是劳动力市场“刘易斯拐点”到来的重要标志之一。在微观层面,教育作为促进个人收入的一个重要影响因素,对于提高居民生活质量,缓解收入不平等起到了重要的作用(徐舒,2010;Hu and Hibel, 2014;张驰、叶光,2016)。
总结现有研究中国教育回报率的文献我们发现:在20世纪80年代及以前,无论是城镇还是农村,教育回报率都呈现出偏低的水平,甚至个别研究得出了教育对个人收入没有显著影响的结论(Meng,1994;Psacharopoulos,2004;Fleisher and Wang, 2005)。然而,随着中国经济市场化改革的推进与劳动力市场各项机制的逐步完善,教育回报率自1990年后开始逐年攀升。Zhang et al.(2005)的研究显示,中国城镇居民的教育回报率在2000年左右已达到世界平均水平。与此同时,由于中国特有的城乡二元体制,教育回报率呈现显著的城乡差异,并且这一差异逐渐成为阻碍劳动力自由流动与人力资本有效提高的重要因素。毫无疑问,随着中国面临如何保证经济平稳发展等经济问题,以及城镇化、人口老龄化等人口问题,对教育回报率这一主题仍有进行深入研究的必要。
本文的研究主要着眼于以下两个方面:首先,估计高校扩招政策对城乡居民受教育年限以及教育回报率的影响;其次,考察教育回报是否在外部存在城乡“马太效应”,以及在城乡居民内部是否存在贫富“马太效应”。在估计方法上,我们采用断点回归设计(Regression Discontinuity Designs)。在Angrist and Lavy(1997)、Duflo(2000)、雷晓燕(2010)以及邹红、喻开志(2015)等一系列重要的政策评估文献中,断点回归设计发挥了巨大作用。该方法可以在没有随机性的情况下对政策效果进行评估,是当前较为流行的“准实验”方法。
文章接下来的部分安排如下:第二部分进行文献综述,对已有相关研究进行梳理并提出创新点;第三部分对数据和计量模型进行说明;第四部分进行实证检验并对结果进行解读,同时对结论的稳健性进行检验;第五部分对全文进行总结。
二、文献综述作为劳动经济学研究的一个重要方向,教育回报率一直是学者关注的焦点。自明瑟1974年提出明瑟工资方程对教育回报率进行了开创性的研究后,关于教育回报率研究的相关文献开始大量涌现。在针对中国教育回报率的研究中,大多数学者在早期着眼于考察教育回报率水平及变化趋势。多数研究显示,20世纪80年代及以前,中国的教育回报率水平较低,城镇地区的教育回报率在0.75%-11.5%的区间内,平均水平在6%左右(邵利玲,1994;孙志军,2004;Zhang et al., 2005)。农村地区的教育回报率在0.7%-6.4%的区间内,平均水平在5%左右(Jamison and Gaag, 1987;Li and Aselia, 2002)。而在同一时期,世界平均教育回报率为10.1%,亚洲为9.6%(Psacharopoulos,2004; 张车伟,2006)。随着改革开放以及一系列推进中国经济市场化政策的推行,中国劳动力市场逐渐发育。作为劳动力的主要流入地,城镇地区的教育回报率开始出现大幅上涨。李实、丁赛(2003)采用1990-1999年全国住户调查数据研究发现城镇居民教育回报率呈逐年上升趋势,十年间上涨了近3倍。Zhang et al.(2005)采用1988-2001年中国城镇住户调查数据(CUHS)的研究显示,城镇地区的教育回报率1988年为4%,而到2001年则上升到10.2%。利用同样的数据,姚先国等(2013)的研究也得出了相似的结论。与之相对,研究表明农村地区的教育回报率并未出现上涨,其平均水平始终维持在5%左右,甚至有些学者得到了更低的结果(侯风云,2004;姚先国、张海峰,2004;张兴祥,2012;孟凡强、熊家财,2015)。
随着研究的进一步深入,越来越多的学者意识到,由于中国特有的城乡二元结构,教育回报率可能存在较大的城乡差异。部分学者利用微观数据进行考察,发现教育回报率在城乡间存在4%左右的差异(姚先国、张海峰,2004;Liu,2012;张兴祥,2012)。更进一步地,一些学者对这一现象的成因进行了研究。姚先国、张海峰(2004)认为,城乡间教育质量的差异是导致教育回报率差异的主要原因。杜两省、彭竞(2010)认为劳动力市场存在人才进入壁垒和对“低端”劳动力的强制退出机制,使得劳动力无法充分流动,导致教育回报率在城乡地区间存在显著差异。徐舒(2010)通过对不同收入群体进行考察发现,低收入群体中教育回报率的城乡差异较大,而在高收入群体中这种差异并不明显,进而得出结论认为,城乡间的收入差距可能是导致教育回报率城乡差异的原因。
除了上述两个角度,估计教育回报率时存在的内生性问题也一直是学界关注的焦点。在经典的明瑟工资方程框架下,最常使用的教育回报率估计方法就是OLS。但是由于个体的异质性,以及个体的一些特质与教育程度存在一定的反向因果关系,导致教育回报率的估计存在一定的内生性问题,如果直接使用OLS进行估计难免会产生一定的偏差(Card,1999)。于是,学者们开始采用不同的估计方法来解决这一内生性问题。Li et al.(2005)应用双胞胎数据对个体的家庭背景与个人能力进行了控制,结果发现固定效应模型下的教育回报率为2.7%,远低于OLS的估计结果。李雪松、赫克曼(2004)在处理效应模型下,对异质性与选择偏差进行了控制,认为在20世纪末中国大学的教育回报率约为11%。除了对个体异质性进行控制,更多的文献采用了工具变量的方法(Angrist,1991;Card,1993)。尹志超、甘犁(2014)以配偶特征变量作为工具变量,得出结论认为在1989-2000年间,中国城镇居民教育回报率大约为7%左右。张巍巍、李雪松(2014)将母亲教育水平作为工具变量,认为城镇居民大学教育的回报率在2000年为9.9%,2009年为11.4%,并且其结论还显示相对于Ⅳ估计,OLS会产生低估的问题,Chen and Hamori(2009)的研究也得出了类似的结论。近年来,一些研究开始采用制度变量作为工具变量来对教育回报率进行估计。例如Fang et al.(2012)将中国1986年实施的义务教育法作为工具变量对教育回报率进行了估计。在此基础上,La(2014)还加入了以劳动法规定的最低工作年龄作为工具变量与义务教育法作为工具变量进行了对比。
目前关于教育回报率的文献可谓汗牛充栋,但在以下几个方面仍有待丰富:首先,在研究视角上,现有文献对教育回报率城乡差异的研究仍较为缺乏,仅有少数几篇文献对这一领域进行了关注,但也仅是对教育回报率城乡差异的简单数值对比,没能在一个统一的框架下对教育回报率的城乡差异水平及其成因作出分析;其次,在研究方法上,一方面,尽管现有文献开始将政策作为工具变量进行回归,但已有文献大多以“义务教育法”作为工作变量。随着时间推移,这一政策的效果正逐渐减弱,而高等教育扩招政策对劳动力市场的影响逐渐显现(Gao and Smyth, 2015;Kuo and Shiu, 2016)。另一方面,在使用工具变量时,少有文献关注样本选择范围。实际上,政策的实施存在局部处理效应(LATE),如果直接用政策变量进行Ⅳ估计极易使回归结果产生偏差(Duflo,2000)。
鉴于以上问题,本文将主要贡献如下:第一,在断点回归设计(RDD)的框架下对教育回报率的城乡差异进行考察。通过细致的考察高校扩招对城乡教育回报率的影响,以及对城乡居民内部不同收入群体的影响,来进一步深化理解高校扩招对城乡外部发展差异以及对不同收入群体的影响。第二,选取高校扩招政策作为影响断点的主要政策变量,采用RDD方法对中国的教育回报率进行因果推断与参数估计。相对于Ⅳ估计,除了对内生性问题的缓解,RDD的优势还在于:一方面,当制度变量不能够完全被个体所影响时,其回归结果更具有“准实验”的特征;另一方面,RDD可以通过对带宽(Bandwidth)的控制,对政策冲击产生的局部处理效应(LATE)进行更精确的度量(Lee and Lemieuxa, 2010;刘生龙等,2016)。实际上,除了教育制度的变迁,劳动力市场的制度变迁以及许多宏观经济因素均对中国教育回报率有着重要的影响。因此,采用RDD得出的LATE能够很好的将高校扩招对居民受教育程度的影响进行估计,从而进一步准确对中国的教育回报率进行估计。
三、数据与计量模型 (一) 数据本文使用的数据来自由澳大利亚国立大学、北京师范大学与国家统计局等机构联合实施的中国家庭收入调查项目(Chinese Household Income Project,CHIP),其中我们选取了2007年与2013年得到的调查数据。该项目在数据调查过程中,采取了分层线性随机抽样的方式来获得样本,其要求访谈员入户并询问相关的人口学特征、户籍、收入等信息。
首先,参照以往文献的做法,我们筛除了在读学生、失业退休人员、从未从事过生产性劳动以及没有工资信息的样本。其次,在样本选择范围上,由于高校扩招于1999年6月开始实施,考虑到参加高考的年龄一般为18周岁,所以本文认为出生于1981年及以后的个体会受到扩招政策的影响。更具体地,根据我国小学入学时间规定,只有1981年9月以后出生的个体才会受到扩招政策的影响。但刘德寰、李雪莲(2015)指出,由于7、8月份处于规定的“灰色”地带,家长为了孩子能够早上学往往采取各种措施“帮助”孩子入学。基于此,我们将1981年7月及以后出生的孩子作为受扩招政策影响的群体。另外我们注意到,在1970年之前出生的个体可能没有受到义务教育法的影响,为了尽可能使数据保持准确性,在断点回归的设计下,本文选取的样本仅包含受扩招政策影响前后10年左右的样本,即出生于1970年1月至1990年1月之间的个体。再者,对于被解释变量个人收入的处理上,由于我们选取的是2007年与2013年的数据,不同年份的个体收入不能直接简单对比,所以我们按照国家统计局公布的年度消费者物价指数对收入进行调整。最后,由于CHIP采用城镇与农村分别入户调查,所以在城乡居民划分标准上,我们主要以城乡不同数据集作为划分标准,同时为了使数据尽可能地准确,我们还将城镇数据集中农村户口以及农村数据集中城镇户口的个体进行了筛除与转换。经过上述处理后,我们得到农村样本4678个,城镇样本6485个。
表 1显示了本文主要所需变量的描述性统计。从被解释变量对数小时收入来看,城镇居民大于农村居民。从受教育年限来看,城镇居民显著高于农村居民,农村居民的受教育年限平均为9.39年,这说明大多数农村居民可能仅完成义务教育。相对地,城镇居民的受教育年限平均为13.18年,这说明大多数城镇居民能够接受高等教育。从年龄分布来看,在劳动力市场的农村居民平均年龄为25岁左右,而城镇居民平均年龄为30岁左右,这意味着相对于城镇居民,农村居民进入劳动力市场的年龄更小。从工作经验来看,城镇居民的平均工作经验高于农村居民。性别分布上,城镇居民男性所占比例为57%,农村居民男性所占比例为52%。婚姻结构上,农村居民已婚比例较大,城镇居民已婚比例略高于未婚比例。民族分布和健康分布上,农村居民与城镇居民均是汉族与健康比例居多。
| 表 1 描述性统计 |
在基准回归部分我们采用OLS方法,回归方程以拓展的明瑟工资方程作为基准方程:
| $ln{{y}_{i}}=\alpha +{{\beta }_{1}}\cdot Ed{{u}_{i}}+{{\beta }_{2}}\cdot Ex{{p}_{i}}+{{\beta }_{3}}\cdot Exp_{i}^{2}+\varphi \cdot {{Z}_{i}}+{{\varepsilon }_{i}}$ | (1) |
其中lnyi是个体i小时收入的对数形式,在本文的研究中作为被解释变量。Ddui代表个体i的受教育年限,是本文主要关注的解释变量。Expi与Expi2是个体i的工作经验与工作经验的平方项。Zi一系列控制变量,包括:性别(Gender)、婚姻(Marry)、民族(Nation)、健康(Healthy)、地区(Reign)、个人工作所在行业(Industry)。
2. RDD估计断点回归设计有两种主要形式,一种是尖锐断点回归设计(Sharp RDD), 一种是模糊断点回归设计(Fuzzy RDD)。高校扩招政策与义务教育法的最大区别在于:一方面,这项政策并没有直接通过法律的形式规定下来,从而使其不具有“强制性”,因此这项政策对居民受教育程度的影响主要在于提供更多的高等教育“机会”与改善人们对高等教育获得的预期; 另一方面,高校扩招是一个渐进的过程,从政策实施以来高校扩招的脚步一直没有停止。正如李春玲(2010)的研究显示,自1999-2006年,高校扩招幅度以年均20%的水平增加,按照这样的水平计算,在2006年受到政策影响的群体是1999年的1.4倍。鉴于以上两个原因,本文采用模糊断点回归设计(Fuzzy RDD)。
假设扩招政策为expansion, 个体受到扩招政策影响时取1,否则为0。y1表示受到扩招政策影响个体的收入水平,y0表示未受到扩招政策影响个体的收入水平,于是,个体的收入水平可以表达为:Y=yi*expansion+y0*(1-expansion),进一步的,在明瑟方程的基础上我们假定:个体收入水平由教育程度(Edui(expansion))以及其他因素(U)共同决定,其中,受到扩招政策影响个体的教育程度为Edui(1), 未受到扩招政策影响个体的教育程度为Edui(0)。于是,个体的收入水平的表达式拓展为:y1=f[Edui(1), U], y0=f[Edui(0), U]。最后,我们将个体在扩招前后的收入总结为一个表达式:Y=f[Edui(1)*expansion, U]+f[Edui(0)*(1-expansion), U]=f[Edui(1-expansion), U]。
Fuzzy RDD的基本思想是居民i是否受到政策影响部分取决于驱动变量(running variable)在断点两侧的取值情况,驱动变量是影响居民收入Y的重要变量,一般我们假定这一影响是平滑的,但是扩招政策的实施会使得个体受教育年限在断点处出现一个外生的跳跃。同时,在Fuzzy RDD的框架下,我们假设发生这一跳跃的概率不完全为1,即个体从控制组到实验组的概率在断点处存在一个概率在(0,1)的跳跃,我们用Xi代表代表驱动变量,e表示可能的断点。公式表示为:
| $\underset{x\downarrow e}{\mathop{lim}}\,Pr\{f[Ed{{u}_{i}}\left( 1 \right),U]\ {{X}_{i}}=x\}\ne \underset{x\downarrow e}{\mathop{lim}}\,Pr\{f\left[ Edui\left( 1 \right),U \right]|{{X}_{i}}=x\}$ |
Lee(2010)指出,在Fuzzy RDD框架下,实验的平均效应可以看作是两个差值的比,即:被解释变量个体收入Y对协变量的回归在断点处之差除以分配变量Edui(expansion)对协变量的回归在断点处之差,即:
| ${{\tau }_{FRDD}}=\frac{\underset{x\downarrow e}{\mathop{lim}}\,E\left( Y|X=x \right)-\underset{x\downarrow e}{\mathop{lim}}\,E\left( Y|X=x \right)}{\underset{x\downarrow e}{\mathop{lim}}\,E(Ed{{u}_{i}}\left( expansion \right)|X=x)-\underset{x\downarrow e}{\mathop{lim}}\,E(Ed{{u}_{i}}\left( expansion \right)|X=x)}$ |
上述效应是在假设个体无异质性下的结果,当个体存在异质性时,根据Hahn et al(2001)的做法,我们只需要再加上一个单调性假设就可以对Fuzzy RDD的试验效应进行解释。同样的,与Imbens and Angrist(1999)的LATE思路类似,我们可以得到:
| $\begin{align} &{{\tau }_{FRDD}}=\frac{\underset{x\downarrow e}{\mathop{lim}}\,E\left( Y|X=x \right)-\underset{x\uparrow e}{\mathop{lim}}\,E\left( Y|X=x \right)}{\underset{x\downarrow e}{\mathop{lim}}\,E(Ed{{u}_{i}}\left( expansion \right)|X=x)-\underset{x\uparrow e}{\mathop{lim}}\,E(Ed{{u}_{i}}\left( expansion \right)\left| X=x) \right.} \\ &=E[y\left( 1 \right)-y\left( 0 \right)\left| {{X}_{i}}=e] \right. \\ \end{align}$ |
需要注意的是,当个体存在异质性时,以上结果得到的是“顺从者”(compliers)的试验效应,所谓“顺从者”是指扩招政策实施后“愿意”接受政策影响的个体。在中国自古以来“万般皆下品,唯有读书高”的传统文化理念影响下,能够接受高等教育是每个家庭的愿望,所以我们认为在人群中顺从者应该占主要部分。
上述分析框架一个重要的前提就是高校扩招政策能否作为受教育程度有效的工具变量。沿用Lee and Lemieux(2010)的思想,我们认为:扩招政策的实施增加了个体接受高等教育的机会,并且会改变父母对子女获得高等教育难易的预期,从而增大家庭中的教育投入。这样一来,在个体接受高等教育机会增加与家庭教育投入增加的双重作用下,个体的教育程度毫无疑问会产生一定幅度的增加。另一方面,在现有文献中很难找到高校扩招政策实施与个人收入直接相关的证据。鉴于此,我们认为扩招政策实施是个体受教育程度合适的工具变量。进一步地,为了更好的控制年龄效应,我们在LATE的思路下,把样本限定在受扩招政策影响附近的群体。
以上的估计思路可以采用参数估计与非参数估计两种方法,根据Imbens and Lemieux(2008)的讨论,两种估计方法具有一致性,在本文中,我们采取了参数估计的方法。在Fuzzy RDD框架下,参数估计的标准做法是2SLS(Meng,2013;刘生龙等,2016)。具体方程设定如下:
| $\text{ln}{{y}_{i}}={{\partial }_{0}}+{{\partial }_{1}}\cdot expansion+h\left( cutoff \right)+{{\varepsilon }_{i}}$ | (2) |
| $Ed{{u}_{i}}{{\beta }_{0}}+{{\beta }_{1}}\cdot expansion+g\left( cutoff \right)+{{\gamma }_{i}}$ | (3) |
上述(2)和(3)为简化式,教育回报率方程的结构式为:
| $\text{ln}y={{\delta }_{0}}+{{\tau }_{FRDD}}\cdot Ed{{u}_{i}}+f\left( cutoff \right)+{{\mu }_{i}}$ | (4) |
其中,h(·)、g(·)、f(·)为分界点cutoff(个体出生日期与1981年7月的差)两边的低阶多项式模型,多项式的阶次选择通过AIC准则判断。另外,当影响简化式的误差项与影响结构式的误差项相同时,方程(4)中工具变量的估计系数为(2)式与(3)式估计系数的比值,即:τFRDD=α1/β1。按照前文所述,我们认为1981年7月及以前出生的个体不会受到扩招政策的影响,并将其定义为控制组(control group)。相应地,我们把1981年7月及以后出生的个体作为实验组(treatment group)。当个体出生在1981年7月及以后时,我们将扩招政策的虚拟变量(expansion)定义为1,反之则为0。
四、实证结果 (一) 教育回报率:OLS基准回归估计我们在表 2中报告了城乡全体居民以及城乡居民中高收入50%与低收入50%群体教育回报率的OLS回归结果,首先来看第(1)列与第(4)列的结果。其中第(1)列代表农村全体居民,回归结果显示其教育回报率为5.1%。在控制变量对收入的影响中,工作经验、性别以及婚姻特征对个体收入均有显著的正向影响,而健康和民族特征对个体收入影响不显著。为了与农村居民进行对比,我们来观察第(4)列城镇居民的相关回归结果。其中,教育回报率为8.1%。在控制变量中,工作经验、男性、以及健康均对个人收入具有正向的显著影响,而婚姻与民族特征对收入的影响则不显著。通过对表(1)与表(4)的对比,我们发现城镇居民的教育回报率显著高于农村居民。
| 表 2 OLS基准回归结果 |
为了更细致考察这一问题,我们接下来借鉴张车伟(2006)和刘生龙等(2016)的做法,对城乡居民中高收入50%的群体与低收入50%的群体分别进行回归。其中第(2)列与第(5)列分别代表农村与城镇50%低收入群体,我们发现农村50%低收入群体的教育回报率为1.2%,城镇50%低收入群体的教育回报率为2.4%。同样的,第(3)列与第(6)列分别代表农村与城镇50%高收入群体, 在这部分群体中,农村居民的教育回报率为2.6%,城市居民的教育回报率为3.6%。通过以上对比我们可以发现,无论是全体样本,还是50%高收入或50%低收入群体中,城镇居民的教育回报率都高于农村居民。同样的,我们还发现城乡群体中50%高收入者的教育回报率都高于50%低收入者。这意味着教育回报不仅存在“穷者愈穷,富者愈富”的贫富马太效应,可能还存在着“农村愈穷,城市愈富”的城乡马太效应。那么,很自然的我们考虑到,旨在促进人力资本提升与教育机会均等化的高校扩招政策对上述问题会产生何种影响,以及影响的途径是什么?为了更细致的对这一问题进行考察,我们在下一部分将采用断点回归的方法对这一问题进行研究。
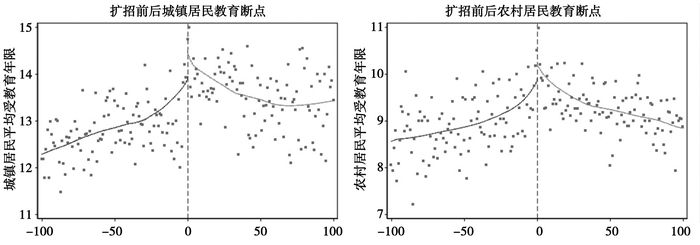
(二) 教育回报率:Fuzzy RDD估计 1. 扩招政策产生的LATE在进行断点回归之前,按照惯常做法,我们首先需要观察由扩招政策所产生的断点情况。图 1展示了扩招政策对城乡居民受教育程度的影响。其中,左右两侧的垂直虚线是代表受到扩招政策影响人群的分割线。我们可以发现,无论是城市居民还是农村居民,在断点处均存在一个明显的“跳跃”。对城镇居民来说,平均受教育年限经历了扩招政策产生的显著“跳跃”后出现了下降的趋势,随后又开始逐渐上涨。可能的原因是在高校扩招初期,实行扩招的大部分是高职、专科等初级高等教育形式,所以在这一阶段,城镇居民所得到的高等教育年限相对有所下降。随着扩招政策的逐步实施,正规本科形式的高等教育开始扩张,城镇居民逐渐得到了相对时间更长的高等教育形式。对农村居民来看,在高校扩招政策实施初期,农村居民的平均教育年限经历了显著的“跳跃”,但是随后平均受教育年限开始下降并逐渐趋于平稳。出现这一现象的可能原因是,一方面,随着距离分割线距离越远,意味着越靠近调查年份,这就导致会“遗漏”一些正在接受教育的个体。另一方面,李春玲(2010)等的研究认为,中国的高校扩招带来的高等教育机会在城乡间存在明显的分配不平等现象,高等教育机会的增加越来越多的被城镇居民获得。于是我们会发现,农村居民的平均受教育年限在经历初期的增长后,逐渐降低并在平均教育年限为9年处趋于平稳。
|
图 1 扩招前后城乡居民教育断点 |
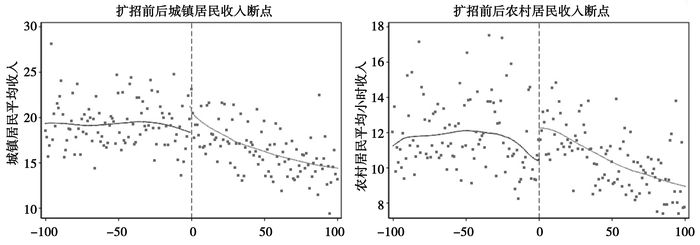
进一步地,我们在图 2展示了扩招政策对城乡居民收入的影响。与图 1相类似,城乡居民收入在扩招政策前后也存在一个显著的“跳跃”。与前文相结合,教育程度和收入水平在扩招政策前后均存在显著的“跳跃”,这意味着教育与收入存在一定的因果关系,在下一小节的实证结果部分我们将进行详细的分析。
2. Fuzzy RDD估计结果表 3展示了Fuzzy RDD的估计结果。其中第(1)列到第(4)列是对农村居民的回归结果,第(5)列到第(8)列是对城镇居民的回归结果。Panel A表示对数工资简化式方程(方程(2)),其含义是表明高校扩招政策对个体收入的影响。首先,对农村居民来说,扩招政策对个体收入有正向影响且都至少在5%的显著性水平上显著。其中第(4)列是加入了控制变量与驱动变量平方项的回归结果,我们发现高校扩招政策对农村居民的对数收入影响为0.074。其次,对城镇居民来说,扩招对个体收入同样均产生了正向的影响,且都通过了5%的显著性水平检验。从加入了控制变量与驱动变量平方项的回归结果(第(8)列)来看,高校扩招政策对城镇居民的对数收入影响为0.071。通过对比我们发现高校扩招政策对城乡居民的收入均有正向影响,且对农村居民影响更大。产生这一现象的原因可能是因为早期农村居民的收入水平较低,且工农业长期存在“剪刀差”的情况。伴随着高校扩招政策的实施,大量的高素质人才不断涌入劳动力市场,人力资本得到了迅速的积累,这也在一定程度上促使了劳动力市场不断向市场化发育,从而促进了农村居民个人收入的增加。
| 表 3 Fuzzy RDD估计结果 |
Panel B的回归结果(方程(3))表示高校扩招对个体受教育年限的影响。从加入了控制变量与驱动变量平方项的回归结果来看,扩招政策对农村居民的影响为0.565,对城镇居民的影响为0.857,两者均在在1%的水平性上显著。我们发现,高校扩招政策对城镇居民的影响显著大于对农村居民的影响。这在一定程度上印证了李春玲(2010)、邢春冰(2014)等研究结论,即高校扩招政策对不同特征群体间具有差异化的影响,城镇居民相对于农村居民更容易获得高校扩招政策带来的高等教育机会。
在Panel C部分,我们展示了工具变量的回归结果,结果显示,受教育年限对城乡居民收入均有正向影响。对农村居民来说,未加入任何控制变量时其教育回报率约为12.7%,仅加入个体特征控制变量后,教育回报率略有变化。当加入驱动变量平方项时,教育回报率的估计结果为11.3%,与之前相比略有下降。最后,当加入控制变量与驱动变量平方项时,得到的教育回报率为13%。这与OLS的估计值相比有了显著的提高。进一步的,我们对城镇居民的回归结果进行解读:未加入任何控制变量时城镇居民的教育回报率为7.5%,当加入驱动变量平方项时教育回报率略有下降。当加入个体特征后,教育回报率升高至8.5%。当同时加入驱动变量平方项与个体特征时,教育回报率的估计结果达到了8.2%。这与OLS的估计值相比略有提高。与OLS的估计结果不同,Fuzzy RDD的估计结果显示,平均来看农村居民的教育回报率略高于城镇居民,这意味着教育回报率的的城乡“马太效应”是不存在的。
|
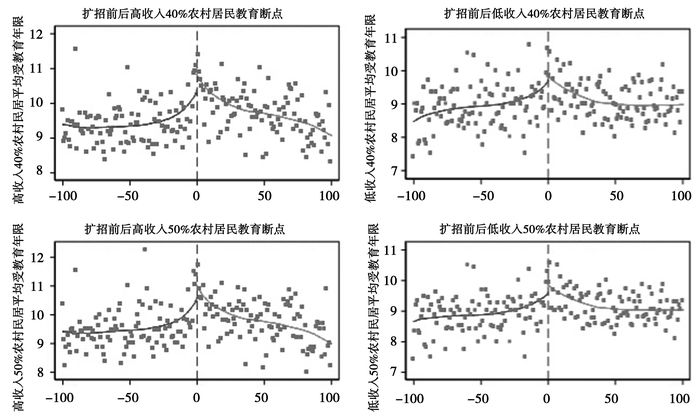
图 3 不同收入分位数农村居民教育断点 |
与此同时我们还注意到,Fuzzy RDD的估计结果显示就个体收入来说,高校扩招对城乡居民均有显著的正向影响,其中对农村居民的影响更大。对居民教育程度来说,高校扩招显著促进了城乡居民的受教育年限,并且对城镇居民的促进作用显著大于对农村居民的促进作用。结合上述Panel C部分的结果,为了更好的高校扩招对城乡居民教育回报率的影响,我们在下一部分对收入在不同分位数的城乡居民进行进一步细致的研究。
(三) 教育回报率:在不同收入分位点上的Fuzzy RDD估计 1. 扩招政策对不同收入分位点的LATE在分位点的选取上,我们参考张车伟(2006)与刘生龙等(2016)的做法,选取50%以上高收入、50%以下低收入、40%以上高收入以及40%以下低收入四个分位点作为分析的根据。与前文做法类似,在进行断点回归前,我们首先利用图形观察扩招政策对城乡居民在不同收入分位点上的影响。首先,对农村居民在不同收入分位点群体的平均受教育年限变化进行观察。如表 3所示,40%以上高收入农村居民在分割线附近有一个较明显的“跳跃”,随后出现了下降的趋势,并在大约10年出趋于平稳。40%以下低收入农村居民在分割线附近也有小幅度的上升,但是并不明显,并且在扩招前后平均受教育年限基本都稳定在9年左右。对50%以上高收入农村居民进行观察我们发现,其平均教育年限变化趋势与40%以上高收入农村居民类似。同样的,我们发现50%以下低收入农村居民的平均教育年限变化与40%以下低收入农村居民的变化趋势类似,而且其变化幅度更小。通过这部分的观察我们认为高校扩招政策带来的高等教育机会在农村居民的分布中更多的被高收入群体占据。
|
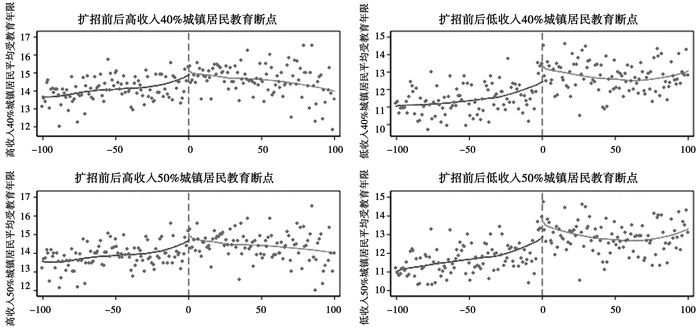
图 4 不同收入分位数城镇居民教育断点 |
其次,我们对在不同收入分位点城镇居民的平均受教育年限进行观察。如表 4所示,对40%以上高收入城镇居民来说,扩招政策实施后这部分群体的平均受教育年限略有提高,随后逐步稳定在14年-15年之间。对40%以下低收入城镇居民来说,扩招政策实施后其平均受教育年限出现了显著的向上“跳跃”,随后出现略有下降后又逐渐上升的的变化趋势。进一步的,50%以上高收入城镇居民的平均受教育年限在扩招政策实施前后并未出现明显的变化,其变化趋势与40%以上高收入城镇居民类似。50%以下低收入城镇居民的平均受教育年限在扩招前后出现了显著的“跳跃”,其变化趋势与40%以下低收入城镇居民类似,但是变化幅度更大。通过这部分的观察我们发现高校扩招带来的高等教育机会在城镇居民中更多的被低收入群体获得。
| 表 4 不同收入分位点Fuzzy RDD估计结果 |
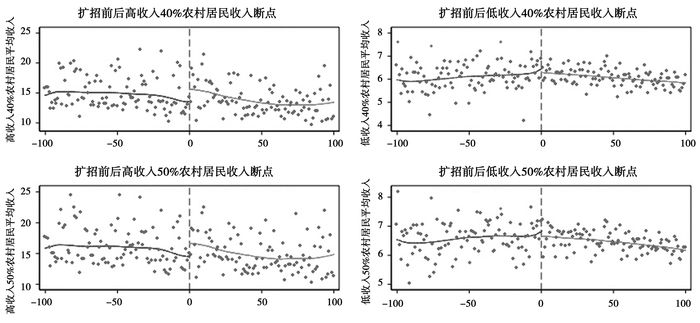
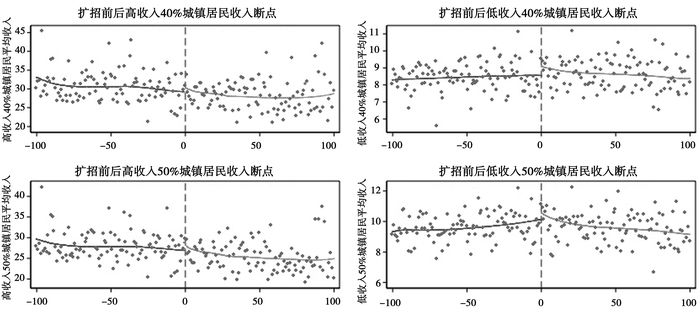
最后,我们对不同收入分位点城乡居民的平均收入变化进行观察。通过表 5我们可以发现,对农村居民来说,无论是50%以上或是40%以上高收入农村居民在扩张政策事实前后均产生了显著的“跳跃”,而50%以下或是40%以下低收入农村居民在扩招政策前后则无明显的变化。与此相对,表 6展示了城镇居民平均收入变化情况。我们可以发现,无论是50%以上或是40%以上高收入城镇居民在扩招政策前后并无明显变化,而50%以下或是40%以下低收入城镇居民的平均收入则在扩招前后出现了显著的“跳跃”。
| 表 5 不同带宽下Fuzzy RDD估计结果 |
| 表 6 控制变量平滑性检验 |
通过以上描述我们认为,高校扩招政策对城乡居民的影响不仅存在外部的城乡差异,在城乡内部还存在由于收入水平不同所导致的差异。在下一小节我们将利用数据与计量模型对这一问题进行实证检验。
|
图 5 不同收入分位数农村居民收入断点 |
|
图 6 不同收入分位数城镇居民收入断点 |
表 4给出了城乡居民在不同分位点下的断点回归结果。首先,对50%与40%高收入群体进行观察。在高收入组中,高校扩招政策显著促进了农村居民的收入与受教育程度,而对城镇居民仅仅是促进了其教育程度的提升。Panel C中得出的教育回报率显示,在50%高收入组中,农村居民的教育回报率为6.4%,且在10%的显著性水平上显著。城镇居民的教育回报率为2.7%且未通过10%水平的显著性检验。在40%高收入组中,农村居民的教育回报率为11.1%,且在5%的显著性水平上显著,而城镇居民的教育回报率仅为1.7%,且不显著。
其次,对50%与40%低收入群体进行观察。在这两个收入低分位群体中,扩招政策对城乡居民的影响与高收入群体相反:扩招政策显著的提高了低收入城镇居民的收入与受教育程度,而对低收入农村居民的影响则并不显著。进一步结合Panel C中的教育回报率回归结果,我们发现低收入组中城镇居民的教育回报率显著为正,平均约为5%。农村居民的教育回报率也为正,但并不显著。
上述现象在一定程度上解释了为何OLS估计结果与断点回归估计结果产生了差异。一方面,OLS估计本身存在“低估”的可能(刘生龙等,2016)。另一方面,对城镇居民来说高校扩招使高收入群体与低收入群体的教育回报率差异变小,而对农村居民来说却出现了教育回报的贫富“马太效应”。这就导致了表面上教育回报率在城乡居民间差异不大,但是在城乡内部不同收入群体间的教育回报率却存在较大差异的现象。
(四) 稳健性检验为了使结果更加稳健,我们在这一节对方法的有效性做一些必要的检验。首先,在前文回归中我们没有刻意设定带宽,这是因为我们将样本本身限定在了LATE框架下。为了使结果更加稳健,我们根据Calonico et al.(2014)提出的带宽估计方法,重新估计了在IK准则下带宽的回归结果,并将其展示在表 5中。在IK准则下,农村居民的教育回报率为16.4%,城镇居民的教育回报率为11.8%。在CV准则下,农村居民的教育回报率为15.8%,城镇居民的教育回报率为6.9%。可以发现,两种准则下的城乡居民教育回报率估计值有所提高,但是无论哪种准则下,农村居民的教育回报率都是高于城镇居民的,这也在一定程度上印证了前文结果的稳健性。
其次,我们检验了平滑性假定,即控制变量在断点处也是平滑的。表 6给出了工作经验、性别、民族和地区四个控制变量可观察到的证据。最后一列是这些变量在断点处的局部瓦尔德(Lwald)估计量,我们可以发现这些变量在断点处不存在明显的“跳跃”,满足平滑性假定。
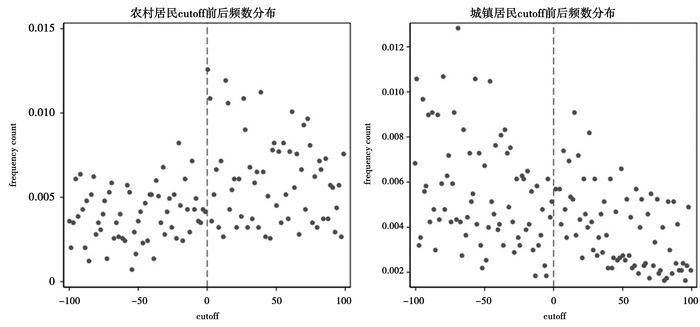
最后,RDD的有效性还取决于驱动变量(个体的出生年月)连续性假定。这一假定要求驱动变量在断点附近出现的概率不能出现大的波动,即要满足非随机排序的要求。图 7给出了驱动变量的核密度函数分布图,可以看出无论是农村居民还是城镇居民在截断点附近都没有出现明显的断点。
|
图 7 cutoff核密度函数分布图 |
本文利用中国家庭收入调查项目数据(2007年与2013年),采用断点回归设计方法对中国城乡地区的教育回报率进行了实证研究,实证结果显示:第一,高校扩招政策对城乡居民的平均受教育年限与收入均有正向的影响。从平均受教育年限来看,农村居民的提升幅度约为0.59年,城镇居民的提升幅度约为0.85年。从平均收入来看,农村居民的收入提升了约8%,城镇居民的收入提升了约7%。总的来看,高校扩招政策对中国提升人力资本有着重要的正向意义。第二,教育回报率并未出现城乡马太效应。农村居民的教育回报率大约为11%,城镇居民的教育回报率大约为8%。这同时意味着,中国的教育回报率水平与发达国家相当。第三,高校扩招政策在城乡居民中仍存在显著的差异化作用,具体的:首先,对城镇居民而言,高校扩招政策起到了促进公平的作用,教育机会更多的被低收入群体获得,同时低收入群体与高收入群体的教育回报率逐渐趋同,这将有助于缩小城镇居民的贫富差异。其次,对农村居民而言,高校扩招带来的教育机会更多的被高收入群体获得,这进一步导致了高收入群体与低收入群体间的教育回报率差异的增大,从而出现了贫富差异扩大的“马太效应”。
更深层次的,虽然断点回归的结果显示教育回报率在城乡间不存在显著差异,甚至出现了农村居民教育回报率高于城镇居民的结果。但是这并不意味者高校扩招带来的教育机会与公平效应在城乡间平等的分配,实际上扩招政策虽然提升了农村居民的平均受教育年限与收入,但是与城镇居民相比差距依然很大,并且教育回报在农村居民内部出现的贫富马太效应更加值得我们关注。
最后,需要指出的是,本文利用RDD方法对教育回报率的估计也存在一定的局限性,这是由于RDD方法本身的缺陷所导致。RDD方法只能得出在LATE的框架下的估计结果,这与以全体劳动力为样本的估计结果存在一定差异。在当前中国面临经济结构转型以及城镇化与人口老龄化的背景下,如何通过发展教育事业来提高教育回报率,促进城乡间合理协同发展以提升中国人力资本存量是实现中国经济与社会进一步发展的关键。因此,关于中国教育回报率的研究议题仍然具有重要的现实意义。
| [] |
蔡昉,
2008, “中国经济如何跨越'低中等收入陷阱'?”, 《中国社会科学院研究生院学报》, 第 1 期, 第 13–18 页。 |
| [] |
蔡昉、都阳,
2011, “工资增长、工资趋同与刘易斯转折点”, 《经济学动态》, 第 9 期, 第 9–16 页。 |
| [] |
杜两省、彭竞,
2010, “教育回报率的城市差异研究”, 《中国人口科学》, 第 5 期, 第 85–94 页。 |
| [] |
侯风云,
2004, “中国农村人力资本收益率研究”, 《经济研究》, 第 12 期, 第 75–84 页。 |
| [] |
李实、丁赛,
2003, “中国城镇教育收益率的长期变动趋势”, 《中国社会科学》, 第 6 期, 第 58–72 页。 |
| [] |
李雪松、詹姆斯·赫克曼,
2004, “选择偏差、比较优势与教育的异质性回报:基于中国微观数据的实证研究”, 《经济研究》, 第 4 期, 第 91–99 页。 |
| [] |
李春玲,
2010, “高等教育扩张与教育机会不平等——高校扩招的平等化效应考查”, 《社会学研究》, 第 3 期, 第 82–113 页。 |
| [] |
雷晓燕、谭力、赵耀辉,
2010, “退休会影响健康吗?”, 《经济学(季刊)》, 第 4 期, 第 1539–1558 页。 |
| [] |
刘生龙、周绍杰、胡鞍钢,
2016, “义务教育法与中国城镇教育回报率:基于断点回归设计”, 《经济研究》, 第 2 期, 第 154–167 页。 |
| [] |
刘德寰、李雪莲,
2015, “'七八月'的孩子们——小学入学年龄限制与青少年教育获得及发展”, 《社会学研究》, 第 6 期, 第 169–192 页。 |
| [] |
孟凡强、熊家财,
2015, “中国人力资本回报率的城乡差异-基于中国综合社会调查数据的分析”, 《贵州财经大学学报》, 第 4 期, 第 94–102 页。 |
| [] |
孙志军,
2004, “中国教育个人收益率研究:一个文献综述及其政策含义”, 《中国人口科学》, 第 5 期, 第 67–74 页。 |
| [] |
邵利玲, 1994, "国有企业内部职工个人收入差异的因素", 载于杜海燕主编: 《管理效率的基础: 职工心态与行为》, 上海: 上海人民出版社, 第156-172页.
|
| [] |
邢春冰,
2014, “教育扩展、迁移与城乡教育差距-以大学扩招为例”, 《经济学(季刊)》, 第 1 期, 第 207–232 页。 |
| [] |
徐舒,
2010, “技术进步、教育收益与收入不平等”, 《经济研究》, 第 9 期, 第 79–92 页。 |
| [] |
姚先国、方昕、张海峰,
2013, “高校扩招后教育回报率和就业率的变动研究”, 《中国经济问题》, 第 2 期, 第 3–11 页。 |
| [] |
姚先国、张海峰,
2004, “中国教育回报率估计及其城乡差异分析-以浙江, 广东, 湖南、安徽等省的调查数据为基础”, 《财经论丛》, 第 6 期, 第 1–7 页。 |
| [] |
尹志超、甘犁,
2014, “非货币收益、工资差异和教育回报”, 《经济学报》, 第 3 期, 第 1–11 页。 |
| [] |
张车伟,
2006, “人力资本回报率变化与收入差距:'马太效应'及其政策含义”, 《经济研究》, 第 12 期, 第 59–70 页。 |
| [] |
张驰、叶光,
2016, “中国教育回报率的分布特征与收入差距——基于分位数回归的经验证据”, 《经济经纬》, 第 1 期, 第 78–83 页。 |
| [] |
张巍巍、李雪松,
2014, “中国高等教育异质性回报的变化:1992~2009-基于MTE方法的实证研究”, 《首都经济贸易大学学报》, 第 3 期, 第 63–77 页。 |
| [] |
邹红、喻开志,
2015, “退休与城镇家庭消费:基于断点回归设计的经验证据”, 《经济研究》, 第 1 期, 第 124–139 页。 |
| [] |
郑秉文,
2011, “'中等收入陷阱'与中国发展道路-基于国际经验教训的视角”, 《中国人口科学》, 第 1 期, 第 2–15 页。 |
| [] |
章莉、李实,
2016, “中国劳动力市场就业机会的户籍歧视及其变化趋势”, 《党政视野》, 第 3 期, 第 61。 |
| [] |
张兴祥,
2012, “我国城乡教育回报率差异研究-基于CHIP2002数据的实证分析”, 《厦门大学学报(哲学社会科学版)》, 第 6 期, 第 118–125 页。 |
| [] |
Angrist J. D., 1991, "Does Compulsory School Attendance Affect Schooling and Earnings?". Quarterly Journal of Economics, 106(3), 979–1014.
|
| [] |
Angrist J. D., Lavy V., 1997, "Using Maimonides' Rule to Estimate the Effect of Class Size on Scholastic Achievement". Quarterly Journal of Economics, 106(2), 533–575.
|
| [] |
Chen G., Hamori S., 2009, "Economic Returns to Schooling in Urban China:OLS and the Instrumental Variables Approach". China Economic Review, 20(2), 143–152.
DOI:10.1016/j.chieco.2009.01.003 |
| [] |
Calonico S., Cattaneo M.D. and Titiunik R., 2014, "Robust Nonparametric Confidence Intervals for Regression-Discontinuity Designs". Econometrica, 82(6), 2295–2326.
DOI:10.3982/ECTA11757 |
| [] |
Card, D., 1993, "Using Geographic Variation in College Proximity to Estimate the Return to Schooling", NBER Working Papers:1127-1160.
|
| [] |
Card D., 1999, "Chapter 30-The Causal Effect of Education on Earnings". Handbook of Labor Economics, 3(99), 1801–1863.
|
| [] |
Duflo E., 2000, "Schooling and Labor Market Consequences of School Construction in Indonesia:Evidence from an Unusual Policy Experiment". American Economic Review, 91(4), 795–813.
|
| [] |
Fleisher B. M., Wang X., 2005, "Returns to Schooling in China Under Planning and Reform". Journal of Comparative Economics, 33(2), 265–277.
DOI:10.1016/j.jce.2005.03.006 |
| [] |
Fang, H., K. Eggleston, J. Rizzo, S. Rozelle and R. Zeckhauser, 2012, "The Returns to Education in China:Evidence from the 1986 Compulsory Education Law", NBER Working Paper, No.18189.
|
| [] |
Gao W., Smyth R., 2015, "Education Expansion and Returns to Schooling in Urban China, 2001-2010:Evidence from Three Waves of the China Urban Labor Survey". Journal of the Asia Pacific Economy, 20(2), 178–201.
DOI:10.1080/13547860.2014.970607 |
| [] |
Hu A., Hibel J., 2014, "Changes in College Attainment and the Economic Returns to a College Degree in Urban China, 2003-2010:Implications for Social Equality". Social Science Research, 44(2), 173–186.
|
| [] |
Imbens G. W., Lemieux T., 2008, "Regression Discontinuity Designs:A Guide to Practice". Journal of Econometrics, 142(2), 615–635.
DOI:10.1016/j.jeconom.2007.05.001 |
| [] |
Jamison D. T., Gaag J.V.D., 1987, "Education and earnings in the People's Republic of China". Economics of Education Review, 6(2), 161–166.
DOI:10.1016/0272-7757(87)90049-5 |
| [] |
Kuo M.Y., Shiu J.L., 2016, "A Dynamic Quantitative Evaluation of Higher Education Return:Evidence from Taiwan Education Expansion". Journal of the Asia Pacific Economy, 21(2), 1–25.
|
| [] |
Lee D.S., Lemieuxa T., 2010, "Regression Discontinuity Designs in Economics". Journal of Economic Literature, 48(2), 281–355.
DOI:10.1257/jel.48.2.281 |
| [] |
La, V., 2014, "Does Schooling Pay? Evidence from China", Mpra Paper.
http://econpapers.repec.org/RePEc:pra:mprapa:54578 |
| [] |
Li H., Liu P.W., Ma N. and Zhang J., 2005, "Does Education Pay in Urban China? Estimating Returns to Education Using Twins". Discussion Papers, 97(2), 494–504.
|
| [] |
Liu, E., 2013, "A Meta-Analysis of the Estimates of Returns to Schooling in China", Working Papers.
|
| [] |
Li, H. and A. Urmanbetov, 2002, "The Effect of Education and Wage Determination in China's Rural Industry", Working Papers, School of Economics, Georgia Institute of Technology.
|
| [] |
Li H., Loyalka P., Rozelle S. and Xie J., 2015, "Unequal Access to College in China:How Far Have Poor, Rural Students Been Left Behind?". China Quarterly, 221, 185–207.
DOI:10.1017/S0305741015000314 |
| [] |
Meng L., 2013, "Evaluating China's Poverty Alleviation Program:A Regression Discontinuity Approach". Journal of Public Economics, 101(1), 1–11.
|
| [] |
Mccrary J., 2008, "Manipulation of the Running Variable in the Regression Discontinuity Design:A Density Test". Journal of Econometrics, 142(2), 698–714.
DOI:10.1016/j.jeconom.2007.05.005 |
| [] |
Psacharopoulos G., 2004, "Returns to Investment in Education:A Global Update". Social Science Electronic Publishing, 12(2), 111–134.
|
| [] |
Todaro M. P., Smith S. C., 2011, "Economic Development". New York:Prentice Hall.
|
| [] |
Meng X., 1994, "An Examination of Wage Determination in China's Rural Industrial Sector". Applied Economics, 28(6), 715–724.
|
| [] |
Zhang J., Zhao Y., Park A. and Song Y., 2005, "Economic Returns to Schooling in Urban China, 1988 to 2001". Journal of Comparative Economics, 33(4), 730–752.
DOI:10.1016/j.jce.2005.05.008 |