加入WTO以来,中国制造业全员劳动生产率呈现逐年增长的趋势,由2001年的1.7万元上升到2014年的10.9万元①。制造业在中国经济增长过程中发挥着不可替代的作用。制造业劳动生产率的提升有利于整个社会福利水平的提高及经济增长方式的转变,因此,如何提高制造业劳动生产率就成为学界研究和关注的焦点问题。
① 数据来源:2015年《中国统计年鉴》并经作者计算所得。
从现有研究文献看,国外研究者一般都将资本深化和技术进步作为制造业劳动生产率提升的源泉和动力(Kumar and Russell, 2002;Los and Timmer, 2005;Madsen,2010)。就国内学者而言,大都采用国外的研究方法,基于中国的数据,实证检验中国制造业劳动生产率增长的源泉和动力。比如,涂正革、肖耿(2006)在Kumar and Russell(2002)研究的基础之上,利用中国大中型工业企业数据,实证检验了1995-2002年制造业劳动生产率增长的原因,结果表明,相对于技术进步而言,资本深化对样本期内中国制造业劳动生产率增长的贡献更大,贡献率高达81%。进一步的研究发现,资本深化对劳动生产率的贡献在逐年下降。杨文举(2006)则基于Los and Timmer(2005)的研究方法,从中国省际数据入手,考察了20世纪90年代以来,中国各省劳动生产率的变化,经验研究发现,资本深化是劳动生产率提升的重要因素,且比技术进步和技术效率的贡献还要大。黄先海、刘毅群(2006)从物化性技术进步(embodied technical change)的角度,探讨了改革开放以来中国工业部门劳动生产率的变化情况,其研究进一步证实了资本深化在劳动生产率提升和经济增长方面的重要影响。吴海民(2013)利用中国民营上司公司的经营数据,从更微观的数据角度来检验企业劳动生产率增长的源泉,实证研究发现,资本深化对劳动生产率的促进作用在企业层面依然存在。
基于国外和国内的研究文献都充分肯定了资本深化在劳动生产率提升中的作用,但未就资本深化由何种力量引致这一问题做出进一步探讨。一般而言,在资本深化进程中存在两种力量:一种是来自市场,另一种是来自政府。其中在市场上,资本的波动相对平稳,工资变动则相对比较大,劳动力的相对价格引发资本深化,而政府方面则是因为产业升级引发资本深化。就转型期的中国而言,资本深化不完全是一种市场选择行为,更多的体现为政府行为,地方政府投资在资本深化过程中扮演着重要的角色(李小平、朱钟棣,2005)。朱轶、涂斌(2011)基于中国式分权的视角,探讨了中国工业部门资本深化形成的内在机理。他们认为,各地方政府面临着两个方面的激烈竞争:一是地区经济绩效的竞争,二是地方政府政治绩效的竞争。因此,出于政治和经济层面的考虑,政府干预投资,以资本驱动经济增长的做法助长了过度投资行为,造成了制造业部门普遍的资本深化。段国蕊、臧旭恒(2013)也认为,对于处于经济转轨时期的中国经济而言,地方政府对于企业投资行为的干预将会导致过度投资行为的发生,从而促使制造业部门出现了长期的、持续的资本深化趋势。
同已有研究相比,本文主要在以下几个方面有所创新:第一,基于市场选择和政府行为的视角,将工资上涨引致的资本深化和政府投资引致的资本深化同时纳入分析框架。在已有的文献中,国外的研究主要集中在由工资上涨引致的资本深化层面,而国内的研究则主要集中在由政府投资引致的资本深化层面,割裂了两者之间的相互联系。事实上,对于转型期的中国而言,由工资上涨引致的资本深化和由政府投资引致的资本深化共同存在于经济体系之中,且两者之间有着密切的联系。厘清这些问题对制造业自身的发展及效率的提升显得尤为重要。第二,采用非线性的分析方法。现有研究分析框架都是基于线性条件下的,而相对忽略了由政府投资引致的资本深化对中国制造业劳动生产率提升可能存在的非线性影响。投资作为拉动中国经济增长的“三驾马车”之一,在经济发展过程中扮演着重要的角色。但我国学者Zhang(2003)的研究发现,相对于劳动来说,中国固定资产总投资过快。魏楚、沈满洪(2008)进一步认为,过度的资本深化可能使得经济偏离资源禀赋路径,导致资源配置效率下降。Qin and Song(2009)也发现,与计划经济相伴随的资本过度投资(Over-investment)(即所谓的投资饥渴(investment hunger)),在当今中国依然存在。陈诗一等(2010)在以上研究的基础之上发现,不管是地区分解还是行业剖析,这种根植于计划经济时代的过度资本深化现象仍然伴随着中国经济转轨始终。第三,利用制造业28个分行业的数据,来分析转型期中国资本深化对制造业劳动生产率的影响。现有文献关于资本深化对制造业劳动生产率影响的实证研究大都是基于省级面板数据,不能更为详细的反映制造业部门内部行业之间的关系。
本文余下部分结构安排为:第二部分对中国转型期的工资水平、资本深化及劳动生产率的特征事实进行描述性分析;第三部分是模型的设定;第四部分为指标构建与数据说明;第五部分为实证结果分析;最后是结论及政策建议。
二、特征事实 (一) 制造业工资状况分析充足而廉价的劳动力供应一直是我国制造业在国际市场上的主要竞争优势,依靠这种比较优势我国从一个贸易小国一跃成为世界上最大的货物贸易出口国。近年来制造业部门劳动力成本的上升呈愈演愈烈之势。招工难、招工荒、劳动力市场摩擦以及工资上涨等问题成为我国劳动力市场的新常态。对于这一现象,蔡昉(2008;2010) 认为中国劳动力供给无限弹性的优势已经发生逆转,中国开始进入“刘易斯拐点”,制造业“人口红利”逐渐消失。图 1给出了2000以来中国制造业名义工资和实际工资①的变化情况,从名义工资的变化情况来看,2000年的名义工资水平为8836元,2014年增加到了51369元,十四年间增长了4.81倍,年均增长率为13.40%。从实际工资的变化情况来看,2000年的实际工资水平为8836元,2013年增加到了36737元,十二年间增长了3.16倍,年均增长率为10.71%。从发展趋势来看,尽管工资增长率(包括名义工资增长率和实际工资增长率)在2011达到峰值之后开始下降,但仍保持在高位运行,名义工资增长率保持在10%以上,实际工资增长率保持在8%以上。
① 实际工资水平以2000年为基期的实际工资指数进行平减。
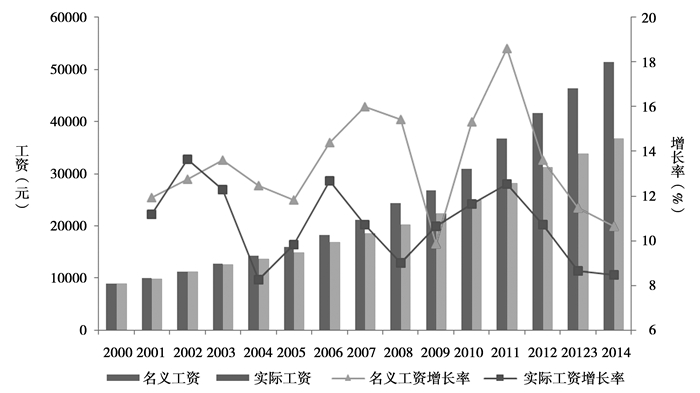
|
图 1 2000年以来中国制造业的工资水平状况 |
理论上,要素相对价格的变动是资本深化的直接原因,正如新古典经济理论所强调的,在完全竞争的市场经济条件下,企业以利润最大化为经营目标,工资上涨将促使企业以资本替代劳动。Hicks (1932)认为要素相对价格改变会诱使企业家进行技术创新,使用相对价格较低的要素。Madsen (1998)在马歇尔的均衡工资理论基础上建立了劳动力供求模型,分析结果显示,工资上涨能够促进资本深化,进而促进劳动生产率提升。然而,对于转型期的中国而言,2000年以来制造业工资水平的快速上升是否是促使制造业资本深化以及劳动生产率提升的主要原因?这需要我们进行更为严格的计量分析。
(二) 制造业资本深化问题分析伴随着工业经济的发展和大规模的固定资产投资,中国工业行业经历了持续的、快速的资本深化(张军,2002;蔡昉,2005;张军等,2009)。为了刻画这一发展趋势,本文采用永续盘存法测算中国制造业的物质资本存量①,并在此基础之上,测算制造业的资本劳动比,如图 2所示,从资本劳动比的绝对值来看,资本劳动比呈现逐年上升的趋势,特别从2008年开始,这种上升趋势更为明显。从资本劳动比的增长率来看,2001-2004年资本劳动比的增长率相对较低,且比较平缓,但从2005年开始,资本劳动比平均增长率显著上升。
① 具体各个指标的测算见第四部分。
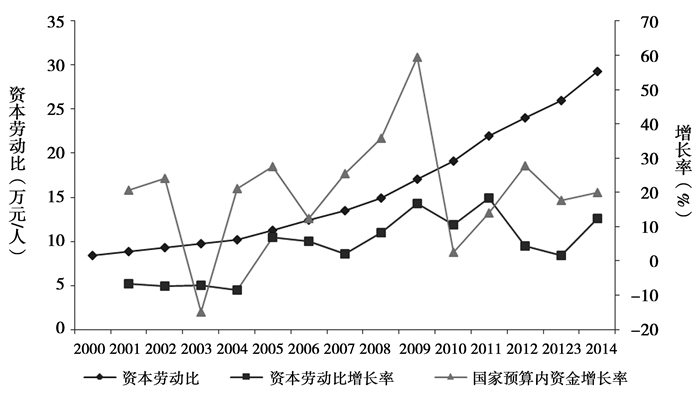
|
图 2 2000年以来中国制造业的资本深化 |
Burmeister and Turnovsky(1972)指出,基于市场竞争机制的资本劳动比的提高,可以促进劳动生产率的提高。但国内大多数学者认为中国的资源配置不是基于市场选择行为,而是基于政府行为。特别是从1997年亚洲金融危机以来,中国经济的持续、高速发展在很大程度上依靠政府投资的快速增长。因此,政府在资本深化中扮演了重要的角色。图 2的统计数据可以进一步佐证政府投资和资本深化之间的密切关系。2000年以来政府投资年均增长率为19.89%。尤其是2008年,为了应对国际金融危机,政府推出四万亿的刺激方案,使得2009年的政府投资比2008年增长了59.47%,之后随着中国经济的企稳回升和产能过剩的逐渐累积,政府投资增长率开始回落,并在2012年经济进入新常态的背景下,维持在17%-20%之间的水平。另外,从图中可以看出,虽然不同年份的政府投资增长率波动较大,但政府投资增长率与资本劳动比增长率存在着很强的相关性,并具有一定的时滞效应。也就是说,在政府投资增长率较高的年份,资本劳动比的增长率也出现了快速增长;在政府投资增长率较低的年份,资本劳动比的增长率也呈现出了下降态势。
结合图 1和图 2可以初步得出工资上涨、政府投资以及资本深化三者之间的内在联系。特别是中国加入WTO以来,实际工资、政府投资年均增长率以及资本劳动比增长率均较高,这符合我们的逻辑。但对于转型期的中国制造业而言,究竟哪种因素作用下的资本深化对劳动生产率产生的作用更大,这需要我们接下来进行更为严格的实证检验。为了进一步分析其中的作用机理,本文第三部分借助CES生产函数,构建符合转型期中国发展的实证模型,并运用2000-2014年制造业面板数据进行实证分析。
三、模型设定工资上涨促进劳动生产率提升的一个重要途径是资本对劳动的替代。为了从实证上检验这种替代关系,我们沿用Naastepad and Kleinknecht(2004)的CES生产函数:
| $ Y = \gamma {\left[ {\delta {L^{ - \rho }} + \left({1 - \delta } \right){K^{ - \rho }}} \right]^{ - \frac{h}{\rho }}} $ | (1) |
其中,1<ρ<∞; 0<δ<1; γ>0; h>0且
Y是实际GDP, K是资本存量, L是就业人口, w是名义工资率,r是资本存量的名义租赁价格; ρ衡量了资本和劳动的替代性, σ是替代弹性, γ是所谓的效率参数(efficiency parameter),δ是分布参数,h是规模参数。值得注意的是,如果h=1, 那么生产函数表现为规模报酬不变;如果h>1 (h<1), 则生产函数表现为规模报酬递增(或递减)。利用利润最大化的一阶条件:
| $ L = {\left[ \begin{array}{l} \underline {h\delta } \\ {\gamma ^{\frac{\rho }{h}}} \end{array} \right]^\sigma }{\left[ {\frac{w}{p}} \right]^{ - \sigma }}{Y^{\frac{{h + \rho }}{{h\left({\rho + 1} \right)}}}} $ | (2) |
| $ K = {\left[ {\frac{{h\left({1 - \delta } \right)}}{{{\gamma ^{\frac{\rho }{h}}}}}} \right]^\sigma }{\left[ {\frac{r}{\rho }} \right]^{ - \sigma }}{Y^{\frac{{h + \rho }}{{h\left({\rho + 1} \right)}}}} $ | (3) |
其中,p是GDP平减指数。用(3) 式除以(2) 式就可以得到如下的资本-劳动比或资本深化:
| $ \frac{K}{L} = {\left[ {\frac{\delta }{{\left({1 - \delta } \right)}}} \right]^{ - \sigma }}{\left[ {\frac{w}{r}} \right]^\sigma } $ | (4) |
上式表明,资本-劳动比(K/L)依赖于劳动价格相对于资本价格之比、替代弹性σ和分布参数δ。为了分析的方便,将等式(4) 表示成增长率的形式,对等式(4) 进行全微分,并除以K/L, 整理得:
| $ \frac{{\dot K}}{L} = \sigma \frac{{\dot W}}{r} $ | (5) |
等式(5) 表明,资本深化的增长率依赖于相对要素价格比的增长率;其影响规模取决于替代弹性的大小。相应地,资本深化增长率的提高将对劳动生产率的增长产生正向的促进作用。为了表明这种效应,把等式(1) 写成劳动生产率(Y/L)的函数:
| $ \frac{K}{L} = {\gamma ^{\frac{1}{h}}}{\left[ {\delta + \left({1 - \delta } \right){{\left[ {\frac{K}{L}} \right]}^{ - \rho }}} \right]^{ - \frac{1}{\rho }}}{Y^{\frac{{h - 1}}{h}}} $ | (6) |
从等式(6) 中能够得出:
| $ \left[ {\frac{{\dot K}}{L}} \right] = \frac{1}{h}\dot \gamma + \sigma \left[ {\frac{{\left({1 - \delta } \right){{\left({K/L} \right)}^{ - \rho }}}}{{\delta {\rm{ + }}\left({1 - \delta } \right){{\left({K/L} \right)}^{ - \rho }}}}} \right]\left[ {\frac{{\dot W}}{r}} \right] + \left[ {\frac{{h - 1}}{h}} \right]\dot Y $ | (7) |
把(5) 式代入(7) 式得:
| $ \left[ {\frac{{\dot Y}}{L}} \right] = \frac{1}{h}\dot \gamma + \sigma \left[ {\frac{{\left({1 - \delta } \right){{\left({K/L} \right)}^{ - \rho }}}}{{\delta {\rm{ + }}\left({1 - \delta } \right){{\left({K/L} \right)}^{ - \rho }}}}} \right]\left[ {\frac{{\dot w}}{r}} \right] + \left[ {\frac{{h - 1}}{h}} \right]\dot Y $ | (8) |
Naastepsd and Kleinknecht(2004)认为,大多数关于劳动生产率的实证分析中,都采用规模报酬不变的生产函数,即假定h=1。但卡尔多-凡登定律表明:制造业本身规模的扩大将促进其劳动生产率的提升(Harris and Eunice, 1998;Wells and Thirlwall, 2003)。基于此,本文设定如下的基本计量模型,即劳动生产率的增长取决于技术进步γ (由于本文主要研究资本深化对中国制造业劳动生产率的影响,因此,假定γ为常数,且外生给定)、行业规模报酬递增效应scale、资本深化和其他控制变量:
| $ {y_{it}}{\rm{ = }}{\beta _{\rm{1}}}scal{e_{it}}{\rm{ + }}{\beta _2}{\left({\frac{K}{L}} \right)_{it}} + {\beta _3}{\left({\frac{K}{L}} \right)_{it}} + {\varepsilon _{it}} $ | (9) |
另外,Naastepsd and Kleinknecht(2004)将资本深化的原因完全归于市场选择的工资上涨,而忽略了政府行为在资本深化形成中的作用。基于此,本文在改进Naastepsd and Kleinknecht (2004)研究的基础之上,将模型扩展为:
| $ {y_{it}}{\rm{ = }}{\beta _{\rm{1}}}scal{e_{it}}{\rm{ + }}{\beta _2}{\left({\frac{K}{L}} \right)_{it}} \times {\left({\frac{w}{r}} \right)_{it}} + {\beta _3}{\left({\frac{K}{L}} \right)_{it}} \times gover{n_{it}} + {\beta _4}{X_{it}} + {\varepsilon _{it}} $ | (10) |
其中,yit为制造业i行业t年的全员劳动生产率,scaleit为制造业各行业的规模报酬递增效应,
依靠要素投入,特别是大规模的固定资产投资,支撑了中国三十多年来近两位数的高速增长。但政府的强势介入,势必会影响和干扰要素市场的正常运行,造成要素价格的扭曲和资源错配。体现在资本市场上,一方面会造成政府投资挤压市场力量投资,另一方面会产生资本的边际报酬递减现象。也就是说,由政府投资引致的资本深化必须控制在一定的区间之内,如果超出这个区间,反而会对劳动生产率产生不利的影响。进一步地,我们可以假定政府投资引致的资本深化与中国制造业劳动生产率可能存在非线性关系,而门限回归模型(Threshold Regression Model,Hansen,2000)是检验这一门限非线性关系的合意方法。由于本文考察的是政府投资引致的资本深化对制造业劳动生产率的非线性影响,因此将政府投资引致的资本深化设定为其自身的门限变量,门限回归模型设定如下:
| $ \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{y_{it}}{\rm{ = }}}\\ {\left( {{\alpha _1}scal{e_{it}} + {\alpha _2}{{\left( {\frac{K}{L}} \right)}_{it}} \times {{\left( {\frac{w}{r}} \right)}_{it}} + {\alpha _3}{{\left( {\frac{K}{L}} \right)}_{it}} \times gover{n_{it}}I\left( {{{\left( {\frac{K}{L}} \right)}_{it}} \times gover{n_{it}} \le \tau } \right) + {\alpha _4}{X_{it}}} \right){\rm{ + }}} \end{array}}\\ {\left( {{\beta _1}scal{e_{it}}{\rm{ + }}{\beta _2}{{\left( {\frac{K}{L}} \right)}_{it}} \times {{\left( {\frac{w}{r}} \right)}_{it}} + {\beta _3}{{\left( {\frac{K}{L}} \right)}_{it}} \times gover{n_{it}}I\left( {{{\left( {\frac{K}{L}} \right)}_{it}} \times gover{n_{it}} \le \tau } \right) + {\beta _4}{X_{it}}} \right)}\\ { + {\varepsilon _{it}}} \end{array} $ | (11) |
其中,τ为门限值,I(·)为示性函数,当括号中条件满足时,I(·)取值为1,否则为0。
其他变量同(10) 式。
四、指标构建与数据说明 (一) 劳动生产率作为单要素生产率的一种,关于劳动生产率的测度一般采用两种方法:一是劳均产出(总产值或增加值);二是在特殊函数的设定下扣除要素贡献后劳均产出增长的残差。然而,在相关研究中,一般都直接将劳均产出(总产值或增加值)作为劳动生产率的变量指标,几乎没有用残差式的生产率作为劳动生产率的测度(唐东波,2014)。一方面,由于在实际应用中,劳均产出数据相对容易获得,而残差式的劳动生产率不仅需要较为复杂的计算,而且对函数形式设定的依赖较强,在较为一般化的函数设定下得到的全要素生产率并不等同于劳动生产率。事实上,满足完美理论要求的劳动生产率很难从现实数据中估算得到。另一方面,已有研究发现,劳均产出与严格意义上的劳动生产率之间的正相关性极强(Hall and Jones, 1999)。因此,和既有研究保持一致,本文采用样本期内各制造业行业的增加值与各制造业行业的平均就业人数之比来测度劳动生产率,并用2000年为基期的生产者价格指数对增加值进行平减。
(二) 资本存量在经验研究中,大多数学者(张军等,2004;徐现祥等,2007;单豪杰,2008)都采用永续盘存法来测度资本存量,其具体的估算公式为:
| $ {K_t} = {K_{t - 1}}\left({1 - {\delta _t}} \right) + {I_t} $ | (12) |
为了准确测度中国制造业资本存量,我们需要知道以下几个内容:一是基期资本存量K的确定(K0);二是制造业实际投资序列(It);三是折旧率(δt)的确定。
1. 基期资本存量的估计沿用Hall and Jones(1999)的做法,我们采用2000-2014年间中国制造业各行业投资的平均增长速度(gi2000)来估算制造业各行业的资本存量。即:制造业各行业2000年投资除以2000-2014年制造业各行业投资的平均增长速度与折旧率之和,得到制造业各行业以2000年为基期的资本存量。用公式表示为:
| $ {K_{i2000}} = \frac{{{I_{i2000}}}}{{{g_{i\left({2000 - 2014} \right)}} + {\delta _{i2000}}}} $ | (13) |
关于实际投资的构造,本文借鉴张军等(2009)的方法,其计算公式如下:
| $ in{v_{it}} = ovf{a_{it}} - ovf{a_{i\left({t - 1} \right)}};\;\;\;\;{I_{it}} = \frac{{in{v_{it}}}}{{{P_{K, t}}}} $ | (14) |
其中,ovfa表示固定资产原值,inv以当年价格衡量的新增投资。PK是固定资产投资价格指数,I表示经过固定资产价格指数平减后的2000年价格水平的可比价新增投资。下标t和t-1代表当前和前一期,i代表制造业行业。
3. 折旧率的确定关于折旧率的确定,不同的学者基于不同的研究方法,得出的结论也不尽相同(黄勇峰等,2002;张军等,2004;Perkins,1988;Wang and Yao, 2003)。本文沿用张军等(2009)的计算方法,其原理是利用制造业分行业固定资本累计折旧、当年折旧、固定资本原值和净值的内在联系,进而确定折旧率。计算公式如下:
| $ \begin{array}{l} c{d_t} = ovf{a_t} - nvf{a_t}\\ C{D_t} = c{d_t} - c{d_{t - 1}}\\ {\delta _t} = C{D_t}/ovf{a_{t - 1}} \end{array} $ | (15) |
按照以上分析的方法和数据,我们可以根据等式(12)、(13)、(14) 和(15) 计算出中国制造业分行业的资本存量。
(三) 资本深化指标关于资本深化指标的选择,从现有研究文献来看,主要存在着以下两种:一种采用资本-产出比,一种采用资本-劳动比。然而,卡尔多典型事实(Kaldor stylized facts)指出,稳态经济增长的资本-产出比大致保持不变。且Romer(2001)的研究进一步发现,这一比例大致为3。因此,本文认为资本-产出比指标并不是衡量资本深化的理想指标。另外,Burmeister and Turnovsky(1972)将资本深化定义为物质资本-劳动比的上升(Increase in the physical capital-labor ratio),这就意味着在生产过程中,相对于劳动要素的投入,资本要素的投入增长要更快一些。鉴于此,本文选择资本-劳动比作为衡量资本深化的指标。
在前文,我们已经通过永续盘存法测算了制造业分行业的资本存量水平,从而作为生产过程中资本要素(K)的投入。因此,我们还需要进一步找到劳动要素(L)的投入。根据数据的完整性、连续性和可比性,本文选取制造业按行业分组的规模以上企业的全部从业人员年平均人数作为衡量劳动投入要素的指标。
(四) 要素价格指标劳动力价格w,本文采用制造业分行业平均工资这一指标,并用2000年为基期的实际工资指数进行平减。对于资本价格,通常可以用市场利率来表示,但对于转型期的中国而言,金融市场发展不完善,市场化化程度不高,利率水平很大程度上受到政府管制,因此,基于供求关系的市场化利率水平难以形成。在这种情况下,本文借鉴段国蕊和臧旭恒(2013)的做法,选取实际贷款利率作为反映资本价格的指标。用rKt表示资本价格,it表示1年期的法定贷款基准利率①,pt表示消费者价格指数(CPI)的变动率,则资本的价格可以近似的表示为:
① 若本年度内1年期法定贷款基准利率进行调整,则取数次调整后的平均值作为本年度1年期法定贷款基准利率。
| $ {r_{Kt}} = {i_t} - {P_t} $ | (16) |
为了刻画政府投资对中国制造业劳动生产率的影响,本文参考樊纲和王小鲁(2011) 的做法,用制造业分行业国家资本金与行业总产值的比值来测算政府投资的作用。该变量旨在捕捉制造业行业中政府与市场的力量对比变化及政府在资本深化中的作用。
(六) 其他控制变量对于规模报酬递增效应指标(scale),本文采用样本期内各制造业行业主营业务收入变动与主营业务成本变动之比来表示;人力资本(human)采用样本期内各制造业行业研发人员的全时当量与本行业的就业人数的比值来表示;研发投入(rd)采用样本期内各制造业行业的研发支出与主营业务收入之比来表示;外商直接投资(fdi)采用样本期内各制造业行业中外资企业(不包括港澳台)的固定资产净值年平均余额与整个行业的固定资产净值年平均余额之比来表示;出口(export)采用样本期内各制造业行业的出口交货值与总产值的比值来表示。其中,研发支出和固定资产净值采用以2000年为基期的固定资产价格指数进行平减,主营业务收入、出口交货值、增加值和总产值采用以2000年为基期的生产者价格指数进行平减。
表 1提供了变量的描述性统计,表 2提供了各个解释变量的相关系数矩阵,并计算了相应的方差膨胀因子(Variance Inflation Factor,简记为VIF)。我们发现,解释变量之间的相关性较弱,最大的为0.69,低于0.7的临界值,因此,可以认为不存在严重的多重共线性问题。通过对方差膨胀因子(VIF)的考察,发现VIF值都在1-4之间,远远小于10的临界值,进一步确认了变量间不存在多重共线性问题。
| 表 1 变量的统计描述 |
| 表 2 变量间的相关系数 |
计量检验的研究样本为2000-2014年间28个制造业行业的数据①,选取的行业是根据统计局公布的两位数分类法,除了工艺品及其他制造业。计量中所使用的数据都来自各年《中国工业经济统计年鉴》、《中国劳动统计年鉴》、《中国科技统计年鉴》、《中国统计年鉴》、中国人民银行官方网站和中国统计局官方网站。
① 自2008开始《中国工业统计年鉴》取消了对各制造业行业增加值的统计,因此,本文2008-2014年的增加值是采用增加值月度累计增长率计算而来的。
五、实证结果与分析 (一) 基准模型分析结果表 3为(9) 式的估计结果,其中,第(1) 列、第(2) 列和第(3) 列分别汇报了以全员劳动生产率为被解释变量的OLS回归模型、随机效应(RE)回归模型和固定效应(FE)回归模型的估计结果。这一设定主要为了考察回归结果的稳健性。上述三个模型的回归结果均显示,核心解释变量工资上涨引致的资本深化的估计系数都为正,且都至少在1%的统计水平显著成立。这表明工资上涨引致的资本深化可以促进中国制造业劳动生产率的提高。这一研究结果与现有的理论模型和实证分析相一致。Solow(1957)的古典增长模型指出,劳动生产率会随着资本产出比的提高而上升。新古典经济理论也认为,工资上涨将促使企业在生产中更多使用相对廉价的资本进而促进劳动生产率的提升。Naastepad and Kleinknecht(2004)利用荷兰1970-1997年的数据分析了1984年以后荷兰劳动生产率下降的原因,他们的研究发现,荷兰的工资节制(wage moderation)政策引起工资-资本相对要素价格的下降,工资-资本相对要素价格的下降又引致资本劳动比的下降,进而带来劳动生产率的下降。李平等(2011)认为,在要素市场完善的条件下,工资上涨将促使企业在生产中多使用资本,进而促进劳动生产率的提升。并利用中国1995-2009年的省际面板数据进行了实证检验,结果表明,工资与人均物质资本交互项的估计系数显著为正,进一步印证了我们回归结果的正确性和适用性。
| 表 3 基准模型回归结果 |
规模报酬递增效应的估计系数在三个回归模型中都为正,且都至少在1%的水平上显著,这表明制造业行业规模的扩大可以促进制造业劳动生产率的提升,这也进一步印证了卡尔多-凡登定律的正确性,并也从实证上验证了卡尔多-凡登定律在我国制造业的适用性。这一研究结果与辛永容、陈圻(2009)的相一致,他们的研究发现,中国制造业至少在1995-2006年间,存在生产率增长的规模递增效应,且产出增长率每上升1%,劳动生产率就上升大约0.3%。
由于变量之间可能存在潜在的内生性问题:一方面,外资企业通过提供资本、管理和技术的方式促进制造业劳动生产率提升;出口通过扩大市场规模的方式提高制造业劳动生产率。另一方面,制造业劳动生产率的提高,吸引更多的外资企业进入,并有利于出口规模的扩大。因此,外商直接投资、出口与制造业劳动生产率存在一定的逆向因果关系,基准模型中的外商直接投资和出口可能是内生的,OLS、固定效应和随机效应的估计量的有效性受到一定的影响。而广义矩估计(GMM)能比较好的处理模型的内生性问题,GMM估计有效性的前提条件是新增工具变量是有效的。Arellano and Bover(1995)建议使用Sargan统计值检验以确定工具变量有效性。另外,GMM动态面板估计方法需要检验εit是否序列相关,本文实证结果分别给出了Sargan统计量对应的p值和检验εit自相关的AR(1)、AR(2) 统计量对应的P值以衡量GMM估计的有效性。
表 3中的第(4) 列汇报了GMM的回归结果,核心解释变量工资上涨引致的资本深化和规模报酬递增效应都显著为正,这进一步表明了工资上涨引致的资本深化和规模报酬递增效应对中国制造业劳动生产率提升的作用具有相当的稳健性。人力资本和研发投入的估计系数也显著为正,这说明加大人力资本投资和研发投入可以促进中国制造业劳动生产率的提升。外商直接投资的估计系数显著为正,这说明改革开放以来,我国以市场换技术的开放战略是有效的和成功的。出口的估计系数为负,且在1%的统计水平上显著,这表明出口不利于中国制造业劳动生产率提升。Melitz(2003)的理论分析表明企业生产率越高则越有利于出口,本文的检验发现与传统理论预期有差异。但是,这却与中国企业出口的“生产率悖论”有相似之处。Lu(2010)认为中国企业在国内销售的成本不一定比出口成本低,这取决于具体的行业特征。就多数行业而言,国内竞争比国外竞争可能更激烈。因此,出口企业未必比非出口企业的生产率高。
(二) 考虑中国转型期政府行为的模型分析结果李小平、朱钟棣(2005)的研究发现,在中国经济转型过程中,政府投资在中国资本深化过程中发挥着重要作用。接下来本文对(10) 式进行回归分析,进而检验政府投资引致的资本深化对中国制造业劳动生产率的影响。从表 4的第(5) 列和第(6) 列的回归结果来看,无论是固定效应模型还是GMM模型,政府投资引致的资本深化的估计系数都为负,且都至少在1%的水平上显著,这表明政府引致的资本深化不利于中国制造业劳动生产率的提升。从表 4的第(7) 列和第(8) 列的回归结果来看,当把由工资上涨引致的资本深化和由政府投资引致的资本深化同时纳入回归模型中去的时候,由政府投资引致的资本深化对中国制造业劳动生产率的这种不利影响依然存在,且和表 3的回归结果相比,由工资上涨引致的资本深化对中国制造业劳动生产率的提升作用也出现了明显下降,这也进一步表明,由政府引致的资本深化除了对制造业劳动生产率产生不利影响之外,还对由工资上涨引致的资本深化对制造业劳动生产率的促进作用产生不利影响。
| 表 4 考虑中国转型期政府行为的模型回归结果 |
这一研究结果也得到了现有文献的支持,张军(2002)认为,正是由于政府的力量在资本的形成中扮演着重要的角色,才导致资本的形成在很大程度上对经济增长的变动不太敏感,且过度的资本深化可能是20世纪90年代中期以来中国经济增长持续下滑的主要原因。朱钟棣和李小平(2005)运用面板数据对中国制造业行业的全要素生产率进行了估算,发现工业行业资本深化和全要素生产率变动显著负相关。袁云峰等(2012)通过建立空间计量模型检验了地区资本深化对经济效率的影响,发现地区政府对金融干预的强化导致地区资本过度深化,最终降低了经济效率。
另外,我们的实证检验结果也与我国当下的经济形势相一致。2012年以来,煤炭、钢铁、电解铝、石化产业等产业产能过剩十分严重,企业利润大幅下滑,大量员工下岗或转岗,“去产能、去库存、去杠杆”成为时下最为时髦的中国经济改革名词。而背后的深层次原因就是非市场经济条件下地方政府的投资饥渴和投资冲动,导致非理性的、扭曲的投资盲目性、重复性和巨大的浪费性,进而引致资本边际报酬递减和劳动生产率下降。
正是由于中央集权的计划经济(Centrally planned economy)思维和惯性导致的政府过度投资,使得过度的资本深化导致资源错配和配置效率下降,进而不利于制造业劳动生产率的提升。但经济发展的国际经验表明,现在比较发达的经济体在经济发展初期和工业化进程中都经历了投资规模和投资速度的急剧扩张。这就表明了投资对一国经济的发展存在门限效应,当低于某个门限值时,投资规模的扩张可以促进经济的发展;当高于这个门限值时,反而会对经济发展带来不利的影响。进一步地,由政府投资引致的资本深化对制造业劳动生产率的影响可能也存在着门限效应,当然了,这只是我们的推测,需要我们接下来进行更为严格的计量检验。
(三) 政府投资引致的资本深化促进劳动生产率提升的门限效应表 5为(11) 式的估计结果,从第(9) 列的回归结果可以看出,政府投资引致的资本深化的一次方项系数显著为正,二次方项系数显著为负,可以初步推断政府投资引致的资本深化对中国制造业劳动生产率的影响效应存在显著的“倒U型”特征,即当政府投资引致的资本深化低于某个临界值时,政府投资引致的资本深化对中国制造业劳动生产率提升产生有利的影响,但当政府投资引致的资本深化高于这个临界值时,政府投资引致的资本深化对中国制造业劳动生产率提升却产生了不利的影响。由表 5中的第(10) 列门限效应检验结果可知,政府投资引致的资本深化对中国制造业劳动生产率的影响存在显著的单一门限值。最优门限值为0.051。这进一步验证了政府投资引致的资本深化和中国制造业劳动生产率之间“倒U型”关系的存在,政府投资引致的资本深化在拐点(0.051) 前后对于中国制造业劳动生产率分别表现出显著的促进和抑制作用。
| 表 5 门限回归结果 |
和前面的分析保持一致,为了克服变量之间可能存在的内生性问题,基于Caner and Hanse(2004)的方法,我们利用GMM方法对门限回归模型(11) 式重新进行估计。AR(1)、AR(2) 统计量对应的p值分别为0.006和0.381,表明随机扰动项不存在自相关性。Sargan统计量对应的p值为0.890,表明工具变量的选择是有效的。估计结果如表 5中的第(11) 列所示,可以看到,在控制了变量之间的内生性问题之后,政府投资引致的资本深化与中国制造业劳动生产率之间的“到U型”关系依然显著成立,最优门限值略有提高,从0.051变为0.057。但是,无论在基准模型还是在GMM模型估计中,上述两个最优门限值都在1%的统计水平上通过检验,说明我们的模型具有相当的稳健性。
其中,未跨过门限值的行业包括:纺织业,纺织服装、鞋帽、羽毛(绒)及其制品业,木材加工及木、竹、藤、棕、草制品业,家具制造业,造纸及纸制品业,印刷业和记录媒介的复制,文教体育用品制造业,塑料制品业。这些都属于轻工业。而跨过门限值的行业除了烟草业和食品加工业之外,大都属于重化工业制造业,这一研究结果也得到了现有研究文献的支持。蔡昉(2005)的研究发现,目前中国重化工业的条件仍不成熟,这主要表现在过早的资本深化。结合我们的实证结果,说明在中国制造业行业中,重化工业制造业普遍存在着过度资本深化的现象,且这种过度的资本深化已经跨过临界值,对中国制造业劳动生产率的提升产生了不利的影响。这是因为,重化工业既属于资本密集型工业又属于技术密集型工业。一方面,根据新古典增长理论,随着人均资本拥有量(资本深化)的增加,投资的边际收益率呈现出递减规律;另一方面,根据附加值高低和要素配置两个标准,可以将重化工业阶段分为“重化工业阶段上半场”和“重化工业阶段下半场”,其中上半场发展主要依赖于资本投入,而下半场主要依赖于知识和技术。近年来,化工、钢铁、有色等重化工业出现的生产经营困境表明,中国重化工业阶段上半场正在退出。在此背景下,加快产业结构优化升级,发展知识和技术密集型重化工业,才能促进中国制造业劳动生产率提升,而过度的资本深化只会造成生产效率下降,过剩产能进一步累积,不利于中国制造业劳动生产率提升和供给侧结构性改革的推进。
六、结论及政策建议资本深化是制造业劳动生产率提升的重要因素。本文基于转型期中国所特有的发展特性,从市场选择和政府行为的角度,将资本深化分解为由工资上涨引致的资本深化和由政府投资引致的资本深化,并利用2000-2014年中国制造业28个分行业的面板数据,实证检验了资本深化对中国制造业劳动生产率提升的影响。研究结果表明,工资上涨引致的资本深化能显著促进中国制造业劳动生产率的提升,但政府投资引致的资本深化对中国制造业劳动生产率的提升产生了不利的影响。进一步的研究发现,政府投资引致的资本深化与中国制造业劳动生产率之间呈显著的“倒U型”关系,其临界值为政府投资引致的资本深化达到0.0567左右。目前跨过该临界值的制造业行业有20个,且大都集中在重化工业行业。未跨过该临界值的制造业行业有8个,都分布于轻工业行业。上述研究结果具有重要的政策涵义。
在经济新常态背景下,随着中国人口红利消失,工资上涨,企业通过资本深化提升劳动生产率,抵消工资上涨的不利影响,这为产业政策的制定、产业结构的优化升级和供给侧结构性改革提供了有利的支撑。而本文的实证结果表明,在政府层面上,政府推动的资本深化对轻工业行业劳动生产率的提升产生了有利的影响,而对重化工业行业产生了不利的影响,为此,政府在这方面应当做出以下调整:第一,密切监控政府对重化工业行业的投资方法和投资规模,加大对医药、仪器仪表、专用设备等技术含量高的知识和技术密集型重化工业行业的投资,限制和减少对化工、钢铁、有色等技术含量较低的资源和劳动密集型重化工业行业的投资,促进重化工业行业的产业结构优化升级。第二,通过制定相关产业支持政策,引导资本在轻工业行业和重化工业行业之间合理配置,促进轻工业行业和重化工业行业协调和可持续发展。第三,防范部分重化工业行业化解过剩产能过程中所出现的风险,这主要体现在资源和劳动密集型重化工业行业向知识和技术密集型行业转变过程中所累积的债务风险,如果不能及时化解,就会引发金融风险。
| [] | 陈诗一、严法善、吴若沉, 2010, “资本深化、生产率提高与中国二氧化碳排放变化”, 《财贸经济》, 第 12 期, 第 111–119 页。 |
| [] | 陈勇、李小平, 2006, “中国工业行业的面板数据构造及资本深化评估: 1985-2003”, 《数量经济技术经济研究》, 第 10 期, 第 57–68 页。DOI:10.3969/j.issn.1000-3894.2006.10.006 |
| [] | 蔡昉, 2005, “发展阶段判断与发展战略选择—中国又到了重化工业化阶段吗?”, 《经济学动态》, 第 9 期, 第 15–19 页。 |
| [] | 段国蕊、臧旭恒, 2013, “中国式分权、地方政府行为与资本深化”, 《南开经济研究》, 第 6 期, 第 37–53 页。 |
| [] | 黄先海、刘毅群, 2006, “物化性技术进步与我国工业生产率增长”, 《数量经济技术经济研究》, 第 4 期, 第 52–60 页。 |
| [] | 单豪杰, 2008, “中国资本存量K的再估计”, 《数量经济技术经济研究》, 第 10 期, 第 17–31 页。 |
| [] | 唐东波, 2014, “垂直专业分工与劳动生产率:一个全球化视角的研究”, 《世界经济》, 第 11 期, 第 25–52 页。 |
| [] | 涂正革、肖耿, 2006, “中国工业增长模式的转变”, 《管理世界》, 第 10 期, 第 27–39 页。 |
| [] | 吴海民, 2013, “资本深化带来了劳动生产率下降吗?”, 《财经科学》, 第 9 期, 第 40–50 页。 |
| [] | 辛永容、陈圻, 2009, “我国制造业劳动生产率增长源泉研究”, 《商业经济与管理》, 第 7 期, 第 52–60 页。 |
| [] | 徐现祥、周吉梅、舒元, 2007, “中国省区三次产业资本存量估计”, 《统计研究》, 第 5 期, 第 6–13 页。 |
| [] | 杨文举, 2006, “技术效率、技术进步、资本深化与经济增长—基于DEA的经验分析”, 《世界经济》, 第 5 期, 第 73–83 页。 |
| [] | 袁云峰、贾康、徐向东, 2012, “金融竞争、相对资本深化与地区经济效率”, 《统计研究》, 第 3 期, 第 45–53 页。 |
| [] | 张军, 2002, “改革以来中国的资本形成与经济增长:一些发现及其解释”, 《世界经济文汇》, 第 1 期, 第 20–29 页。 |
| [] | 张军、吴桂英、张吉鹏, 2004, “中国省际物质资本存量估计:1952-2000”, 《经济研究》, 第 10 期, 第 35–44 页。DOI:10.3969/j.issn.1004-7778.2004.10.038 |
| [] | 张军、陈诗一、JeffersonG.H., 2009, “结构改革与中国工业增长”, 《经济研究》, 第 7 期, 第 4–20 页。 |
| [] | 朱轶、涂斌, 2011, “财政分权、投资失衡与工业资本深化—基于中国区域特征的经验检验”, 《宏观经济研究》, 第 11 期, 第 28–36 页。 |
| [] | 朱钟棣、李小平, 2005, “中国工业行业资本形成、全要素生产率变动及其趋异化—基于分行业面板数据的研究”, 《世界经济》, 第 9 期, 第 51–62 页。 |
| [] | Arellano M., Bover O., 1995, "Another Look at the Instrument Variable Estimation of Error-Component Model". Journal of Econometrics, 68(2), 29–51. |
| [] | Burmeister E., Turnovsky S. J., 1972, "Capital Deepening Response in an Economy with Heterogeneous Capital Goods". The American Economic Review, 62(5), 842–853. |
| [] | Caner M., Hansen B., 2004, "Instrumental Variable Estimation of a Threshold Model". Econometric theory, 20(5), 813–843. |
| [] | Duo Qin, Haiyan Song, 2009, "Sources of investment inefficiency: The Case of fixed asset investment in China". Journal of Development Economics, 90(1), 94–105. DOI:10.1016/j.jdeveco.2008.06.001 |
| [] | Hall R. E., Jones C. I., 1999, "Why Do Some Countries Produce So Much More Output than Others?". The Quarterly Journal of Economics, 114(1), 83–116. DOI:10.1162/003355399555954 |
| [] | Hansen B. E., 2000, "Sample Splitting and Threshold Estimation". Econometrica, 68(3), 575–603. DOI:10.1111/ecta.2000.68.issue-3 |
| [] | Hicks J. R., 1932, "The Theory of Wages.London: MacMillan Press. Kumar S. and R. R. Russell.2002. Technological Change, Technological Catch-up, and Capital Deepening: Relative Contributions to Growth and Convergence.". The American Economic Review, 92(3), 527–548. |
| [] | Los B., Timmer M. P., 2005, "The 'Appropriate Technology' Explanation of Productivity Growth Differentials: An Empirical Approach". Journal of Development Economics, 77(2), 517–531. DOI:10.1016/j.jdeveco.2004.04.001 |
| [] | Lu J., Lu Y and Tao Z., 2010, "Exporting Behavior of Foreign Affiliates: Theory and Evidence". Journal of International Economics, 81(2), 197–205. DOI:10.1016/j.jinteco.2010.03.002 |
| [] | Madsen J. B., 1998, "General Equilibrium Macroeconomic Models of Unemployment: Can They Explain the Unemployment Path in the OECD". The Economic Journal, 108(448), 850–867. DOI:10.1111/ecoj.1998.108.issue-448 |
| [] | Madsen J. B., 2010, "Growth and Capital Deepening since 1870: Is It All Technological Progress?". Journal of Macroeconomics, 32(2), 641–656. DOI:10.1016/j.jmacro.2009.10.004 |
| [] | Melitz M., 2003, "The Impact of Trade on Intra-industry Reallocations and Aggregate Industry Productivity". Econometrica, 71(6), 1695–1725. DOI:10.1111/ecta.2003.71.issue-6 |
| [] | Naastepsd C. W., Kleinknecht A., 2004, "The Dutch Productivity Slowdown: The Culprit at Last?". Structural Change and Economic Dynamics, 15(2), 137–163. DOI:10.1016/j.strueco.2003.10.001 |
| [] | Perkins D, 1998, "Reforming China's economy system". Journal of Economic Literature, 26(2), 601–645. |
| [] | Solow R, 1957, "Technical Change and the Aggregate Production Function". Review of Economics and Statistics, 39(3), 312–320. DOI:10.2307/1926047 |
| [] | Wang Y., Yao Y., 2003, "Source of China's Economic Growth: Incorporating Human Capital Accumulation". China Economic Review, 14(1), 32–52. DOI:10.1016/S1043-951X(02)00084-6 |
| [] | Zhang Jun, 2003, "Investment, Investment Efficiency, and Economic Growth in China". Journal of Asian Economics, 14(5), 713–734. DOI:10.1016/j.asieco.2003.10.004 |



