2007年美国次贷危机爆发引发的全球性金融危机猛烈地冲击了世界经济, 同时造成传统经济理论备受质疑。在此之前, 每次经济遭遇负面冲击时, 政府都会祭出宏观经济刺激政策这一利器, 就像一剂灵丹妙药似的能拯救经济于水火之中, 并在屡试不爽之后将其奉为一条铁的经济准则。这次也不另外, 甚至将其过度信奉。面对这次金融危机, 全世界主要经济体默契地通过前所未有的大规模宏观调控政策刺激经济, 意欲避免金融危机的冲击, 回到危机前的经济状态。然而, 刺激政策的效果并非想象那般令人满意。即便如此也没有影响人们对"经济衰退→宏观经济刺激政策"这一铁律的信奉, 反而将不如意的结果归结于宏观刺激政策不够猛烈。随后, 许多国家都陆续推出一系列的经济刺激政策, 但刺激政策依然效果不佳。即便是自从1978年改革开放以来经济增长保持30年左右高速增长、一枝独秀的中国面对这次金融危机以及随后的经济刺激政策, 也没有特别的表现。人们开始认识到, 此次危机并非经济周期所致, 而是经济结构发生了改变, 呈现出经济发展的新阶段。这一新阶段被称作为"新常态"。新常态的突然出现, 并带来的全局性、长期性、深刻性影响, 突显了对这一新经济状态认识的紧迫性和必要性。
在中国, 习近平总书记在2014年5月于河南考察时首次应用了新常态一词并判断中国
经济已经处于新常态, 并在同年随后的APEC工商领导人峰会、中央经济工作会等多个场合进一步诠释了中国经济新常态的表现形式、特征以及新常态下国家的战略发展。新常态以国家最高领导人身份提出及随后的详细阐释迅速引发了大量研究者从学术角度对新常态展开了多层次、多视角的解读。大批文献的涌现为人们迅速接触、消化这一新概念提供了素材, 也为深入研究新常态提供了研究基础。
然而, 现有研究主要从理论分析层面来探讨新常态。基于新常态是当前及未来很长一段时间内中国甚至全世界的经济状态形式, 有必要突破理论层面的理解, 从经验分析角度以更为深入认识新常态。而这一需求满足的一个前提条件是, 我国经济何时进入了新常态?对此问题的明确回答才能更好地展开经验分析。
基于此, 本文尝试从以下两个方面拓展现有的研究:第一, 基于对新常态的严格定义, 通过条件马尔可夫状态转移模型将自从改革开放以来的中国经济进行划分, 界定中国经济进入新常态的时刻; 第二, 应用时变参数模型从要素禀赋的视角量化分析我国新常态形成的驱动因素, 丰富现有对"新常态"和"大稳健"的解释。本文其余的章节安排如下:第二部分为文献综述; 第三部分为新常态内涵的解读, 以为量化识别中国经济新常态奠定基础; 第四部分为条件马尔可夫状态转移模型的说明以及解释其在量化识别新常态这一目的上的恰当性; 第五部分为实证结果; 第六部分则从要素禀赋角度探讨了中国经济新常态形成的原因; 最后为本文的结论。
二、文献综述新常态较早出现于西方媒体报道中, 并于2009年被太平洋投资管理公司的El-Erian进一步诠释, 其主要概括了2008年全球金融危机之后以美国为代表西方世界的经济发展状态, 阐述了当前的经济下滑与以往的经济衰退有着本质区别, 其不仅仅是一次经济周期运行的表现, 而是经济秩序的重构(El-Erian, 2009; Davis, 2009)。
虽然新常态一词源自于国外, 但是国内和国外的新常态概念基本上是相对独立形成的(李扬、张晓晶, 2015)。新常态在国内有着不同的内涵。余斌、吴振宇(2014)突出了中国经济新常态下经济放缓的核心特征, 故而将其定义为, 我国将进入与高速增长阶段不同的中高速增长阶段。李智(2014)指出, "新"是指它在中国经济发展历程中刚刚出现, 与过去的发展特征有所差别; "常态"是指它会在中国经济发展新阶段形成相对的稳定, 不同于经济周期中的阶段性状态或经济波动中的临时性状态。易淼、赵晓磊(2015)认为, "常态"是"统一体的相对的平衡", 新常态即为新的"相对的平衡"。齐建国等(2015)则更多将新常态定义为动态过程, 即经济发展的环境、发展阶段发生变化, 使经济发展特征从一种状态转向另一种状态。
由此可见, 虽然国内文献"新常态"的定义存在些许差别, 但是对"常态"的定义较为统一。"常态"这一概念与国外学者对美国经济在80年代中期之后的"大稳健(Great Moderation)"较为接近。"大稳健"由Stock and Watson(2002)提出, 其核心含义是, 经济波动的微波化。Bernanke(2004)在东部经济协会的会议上发表了以"大稳健"为题的演讲, 此后这一词语也成为通用术语。此后, "大稳健"现象成为了过去近二十年宏观经济研究的主题之一。研究者还尝试从运气、政策、产业结构等多个角度解释美国经济"大稳健"的原因。
在定义新常态的基础上, 现有文献还从新常态的表现特征、形成机制以及新常态下宏观调控政策调整等多方面深入研究了新常态。El-Erian(2010)、Davis(2009)、Arnott(2012)等通过观测2008年金融危机之后的经济表现, 发现新常态的新特征主要由造成经济低增长的原因和经济低增长相伴随的现象所构成, 如高失业率、"滞胀"隐患出现、政府角色上升、金融杠杆率低等。李扬(2013)、汪红驹(2014)、刘伟、苏剑(2014)、金碚(2015)等则分析了我国进入新常态后出现的新特征, 主要从经济增长速度、产业结构、要素禀赋结构、行为等方面概况了中国经济新常态的表现形式。
在宏观调控政策方面, 余斌、吴振宇(2014)从增长目标、经济增长动力、社会保障制度三个方面探讨了新常态下宏观调控政策取向。李扬、张晓晶(2015)则提出了宏观调控新常态的概念, 并概括了宏观调控新常态的九大特征。张晓晶(2015)在讨论中国经济新常态下新矛盾与新挑战的基础上指出了新常态下经济的增长动力源泉。金碚(2015)基于长期视角审视了经济发展新常态, 藉此思考了中国经济新常态的特征, 并指出了新常态下的改革动力与发展动力。此外, 齐建国等(2015)从中国经济新常态的形成机制探讨了中国经济新常态。
由此可知, 现有研究从多个层次探讨了中国经济新常态, 对深入理解新常态提供了广阔视野。由于新常态一词提出时间不长而在我国出现的时间则更短, 对新常态仍需进一步研究。从前文可知, 现有研究对新常态内涵的理解尚未达成一致, 同时现有文献都是从理论分析或简单的数据描述对新常态进行了探讨, 尚未对新常态进行严格的经验分析。经验分析的缺乏主要源自于现有研究尚未对新常态进行量化界定与经济进入新常态的起点判断。
基于此, 本文将在定义中国经济新常态内涵的基础上, 通过经验分析尝试划分中国经济发展阶段, 界定中国经济进入新常态的时刻, 并从要素禀赋的角度量化分析我国经济新常态的形成原因。
三、中国经济新常态的内涵为了量化识别中国经济新常态, 有必要对中国经济新常态的内涵进行严格定义。从字面来看, "常态"意为, 通常的状态、固定的形态。换而言之, 常态表示事物长期处于一种均衡、稳定的状态。但是一种常态并非始终不变和永远存在下去, 而是具有时空性。当外界环境、事物内部等发生较大改变以至于破坏事物原有的均衡状态时, 事物将不能维持原有的常态, 进入一种不稳定的状态, 直至新均衡的形成, 即"新常态"。新常态亦是常态的一种, 只是有别于以往的常态。
中国经济新常态首先是一种稳定的状态, 即从数理角度来讲就是经济发展平稳、波动较小的时期。其次, 新常态还强调了"新"这一前缀。当前, 国际经济形势的限制、自身经济发展的瓶颈、经济发展阶段的制约等因素, 改变了中国经济的微观运行机制与宏观经济表现, 使得经济发展呈现出诸多新特征, 而这些诸多新特征则集中体现在中国经济增长速度的下滑, 经济增长速度的放缓是刻画新常态区别旧常态的核心特征。2014年11月10日习近平在亚太经合组织的演讲中提出中国经济新常态的主要特点是:"从高速增长转为中高速增长"。李扬、张晓晶(2015)同样认为, 中国经济新常态的一个突出特征是结构性减速。因此, 中国经济新常态可定义为, 中国经济增长速度出现了转变, 并呈现新的稳态形式。根据此定义, 中国经济新常态可分解为两个方面:第一, "新"度量了经济增长速度的改变; 第二, "常态"度量了经济运行较为平稳。
然而, 经济并不会一直处于稳定的发展状态, 在某些时期将存在大起大落、不稳定, 这一时期预示着旧常态的结束, 又孕育着新常态, 暂且称之为"过渡期"。进而, 经济发展将存在三种状态:旧常态、过渡期、新常态。
四、模型设定与估计方法在定义中国经济新常态的基础上, 我们将对中国经济新常态进行量化识别, 以界定中国经济何时进入了新常态。根据以上的定义, 中国经济新常态是一个发展较为平稳且发展速度有别于以往增长速度的时期。对于这一时期的刻画, Bai and Wang(2011)提出的条件马尔可夫状态转移模型是恰当的分析方法。Bai and Wang(2011)将数据生成过程设定如下:
| $ {{y}_{t}}=\mu \left({{A}_{t}}, {{s}_{t}} \right)+\sigma \left({{A}_{t}} \right)\cdot {{e}_{t}} $ | (1) |
其中et~N(0, 1); At为状态变量, 存在两种状态, 记为A1与A2, 即σ(At)存在两种状态{ σ1, σ2 }, 对应于高方差与低方差; st也是状态变量和存在两种状态, 记为s1和s2, 对应于高均值与低均值, 但是均值变量μ同时依赖于At与st, 存在4种状态{ μ(A1, s1), μ(A1, s2), μ(A2, s1), μ(A2, s2) }, 即为{高方差时高均值, 高方差时低均值, 低方差时高均值, 低方差时低均值}。
Bai and Wang(2011)进一步将At与st设定为马尔可夫状态转移过程:
| $ {\rm{Pr}}\left({{A_{t{\rm{ + 1}}}}|{A_t}{\rm{, }}{s_t}{\rm{, }}{A_{t - {\rm{1}}}}{\rm{, }}{s_{t - {\rm{1}}}}{\rm{, }} \cdots {\rm{, }}{A_{\rm{0}}}{\rm{, }}{s_{\rm{0}}}} \right){\rm{ = Pr}}\left({{A_{t{\rm{ + 1}}}}|{A_t}} \right) $ | (2) |
| $ {\rm{Pr}}\left({{s_{t{\rm{ + 1}}}}|{A_{t + 1}}{\rm{, }}{A_t}{\rm{, }}{s_t}{\rm{, }}{A_{t - {\rm{1}}}}{\rm{, }}{s_{t - {\rm{1}}}} \cdots {\rm{, }}{A_{\rm{0}}}{\rm{, }}{s_{\rm{0}}}} \right){\rm{ = Pr}}\left({{s_{t{\rm{ + 1}}}}|{A_{t + 1}}, {s_t}} \right) $ | (3) |
其中假定At转移过程只依赖自身历史信息, 而st转移过程不仅依赖于自身历史信息, 还依赖于当前的At。因而, 前者也被称之为外生马尔可夫状态转移过程, 而后者被称之为条件马尔可夫状态转移过程。
由式可知, 在At存在两种状态的情况下, Pr(At+1At)的取值存在四种可能, 用矩阵形式可表示为:
| $ {P^A} = \left(\begin{array}{l} \;\;\;p\;\;\;\;\;1 - q\\ 1 - p\;\;\;\;\;q \end{array} \right) $ | (4) |
式(4)表述了方差从上一期的状态At转移至本期状态At+1四种情形的概率:(1) p度量了上一期的状态At为高方差A1和本期继续保持高方差A1的概率; (2) 1-p度量了上一期的状态At为高方差A1, 本期转变为低方差A2的概率; (3) q度量了上一期的状态At为低方差A2和本期继续保持低方差A2的概率; (4) 1-q度量了上一期的状态At为低方差A2, 本期转变为高方差A1的概率。
由式(3)可知, st+1同时依赖于At+1与st。在At+1=A1和At+1=A2不同状态下, 均值从st转移至st+1的可能性可分别表示为①:
① 矩阵内概率的含义与PA类似, 在此不再赘述。
| $ {P^1} = \left(\begin{array}{l} \;\;{p_1}\;\;\;\;1 - {q_1}\\ 1 - {p_1}\;\;\;\;{q_1} \end{array} \right), {P^2} = \left(\begin{array}{l} \;\;{p_2}\;\;\;\;1 - {q_2}\\ 1 - {p_2}\;\;\;\;{q_2} \end{array} \right) $ | (5) |
在给定初始状态(A0, s0)的联合分布Pr(A0, s0)时, 即可对模型进行估计。Bai and Wang(2011)认为, 由于At与st信息不可得, 进而将视为缺失数据, 并应用EM(expectation-maximization)算法对模型进行估计, 具体估计过程可参考此文。
根据常态的含义, 当经济发展波动较小、长期处于低方差A2时, 经济发展较为平稳, 处于常态式发展。换而言之, 此时q数值较大, 经济处于低方差A2时自我维持能力较强。而当经济发展处于高方差A1时, 经济发展波动较大, 处于"过渡期"。通过观察经济是否长期处于低方差A2以判断经济是否处于常态, 这一测算方法也体现了常态的核心含义。
在识别常态的基础上, 通过比较各常态下低均值与高均值分布的差异, 严格检验不同常态内的经济增长速度是否存在不同, 可判断各常态之间的差异, 识别是否存在"新常态"以及"新常态"的起点。
五、实证结果分析 (一) 数据来源及处理本文以中国实际GDP增长率作为中国经济的代理指标, 并以1979年第1季度至2015年第2季度为研究样本。其中, 1992年第1季度以后的数据来源于国家统计局网站, 而1979年第1季度至1991年第4季度的数据则参考Abeysinghe and Gulasekaran(2004)、王成勇、艾春荣(2010)、林建浩、王美今(2013)等的做法, 将1979年至1991年的年度GDP数据进行季度分解, 并得到全样本数据。
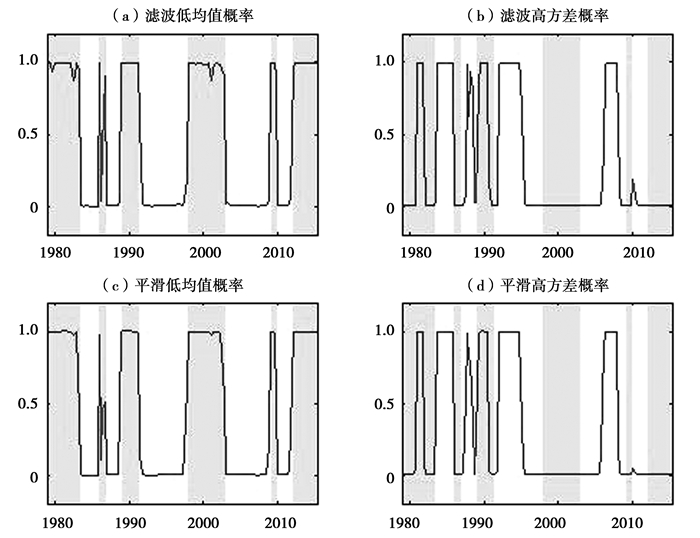
(二) 中国经济新常态的量化识别由以上模型介绍可知, Bai and Wang(2011)的方法是基于经济状态的概率变化来描述经济发展状态的改变, 一般以0.5的概率作为临界点。在实现估计模型参数的基础上, 我们可得到滤波概率与平滑概率, 前者的概率是在基于历史和当前信息下获得的, 后者的概率则是基于全样本信息下得到。图 1描述了整个样本期间低均值与高方差的滤波概率和平滑概率, 其中(a)与(b)为滤波概率, 而(c)与(d)为平滑概率。由于两种概率的估计结果非常接近, 本文以平滑概率来分析中国经济新旧常态的存在、过渡、转变等研究问题。
|
图 1 1979Q1-2015Q2中国GDP增长率的滤波概率与平滑概率 |
1.经济常态与过渡期。
中国自从改革开放以来有相当一段时间处于不稳定时期, 即经济发展处于过渡期。从具体时段来看, 中国经济在1979年第1季度至1995年第1季度以及2006年第1季度至2007年第4季度两个时段内大多数时间处于高波动、过渡式的发展状态。高波动时期经济增长率方差为1.9124。这一测算结果与林建浩、王美今(2013)在探讨中国经济是否进入"大稳健"时的结果很接近。
从历史背景来看, 1978年十一届三中全会以后, 为了修补国有经济改革停滞不前而提出的增量改革, 使得非国有经济发展取得了政治支持。与此同时, 财政与银行体系的分权化改革又使得非国有经济发展有了经济基础。在此时代背景下, 非国有经济得以迅速发展, 进而带动经济高速增长。然而, 中央政府为了避免高通货膨胀而采取收回信贷管理权、消减投资等行政手段进行宏观经济调控。由于直接的宏观调控较难把握力度, 往往导致经济过度下滑。正如林毅夫等(1999)所概括, 经济发展处于"一活就乱、一乱就收、一收就死、一死就放"的循环。而2006年第1季度至2007年第4季度这一短暂的经济剧烈波动更多是自从2003以来高投资、高贸易顺差等问题积聚而成。
与过渡期不同的是, 自从上个世纪90年代中以来, 中国经济波动出现了明显的稳定化趋势。根据前文的定义, 经济发展处于较为平稳的时期可将其定义为处于常态。由图 1中(d)可以看出, 中国经济长期处于稳定发展、波动较小的时期, 即高方差概率很小的时期, 有1995年第2季度至2005年第4季度, 以及2008年第1季度至2015年第2季度。中国经济在两个时期都长期处于平稳发展状态, 前期长达10年, 后者也有8年, 并大有延续之势。期间经济增长率的方差0.6291, 只为高波动时期方差的1/3。经济波动在常态下与过渡期下存在明显差异。
上个世纪90年代以后, 中央政府为了避免经济继续进入"一活就乱、一乱就收、一收就死、一死就放"的循环, 对经济进行了一系列改革, 如分税制改革、金融体制改革、存量改革、市场化的宏观经济调控体系的建立等。正是这些微观经济结构的改变与宏观经济调控方式的转变共同促使了中国经济呈现平稳化发展态势。
2.经济新常态与旧常态。
2006年第1季度至2007年第4季度经济的异常波动将自从1995年以来的中国经济切断为两个稳定时期, 那么2006年第1季度至2007年第4季度经济的异常波动是经济常态的短暂插曲, 还是新常态的前奏曲?为了论证中国经济是否进入新的常态, 需要检验两个大稳定时期的均值是否存在显著差异。首先, 在简单的统计上, 中国GDP增长率在1995年第2季度至2005年第4季度期间均值为9.44%, 而在2008年第1季度至2015年第2季度期间均值为8.80%。GDP增长率在第一时期比第二时期高出0.64%。此外, 在第一段稳定时期, 高增长率占据的比例较高, 为53.49%, 而第二段稳定时期此比例为40%, 明显低于第一段稳定时期。
进一步, 我们通过严格的计量检验发现:当假定两个时期均值相等时, 学生分布t=1.927, 即在10%的显著性水平上拒绝两个时期均值相等, 两个时期均值存在显著差异。而这一差异在2012年进入7%的时代之后表现的更为明显。从2012年第1季度至2015年第2季度的GDP增长率平均为7.53%, 比第一时期低了近2%。而均值相等的检验结果为t=5.8795, 更为显著地拒绝两个时期均值相等的假设, 经济增长出现了大幅、显著地下滑。
概而言之, 简单的统计描述和计量分析结果都表明, 中国经济当前处于一个稳定的发展状态, 呈现出常态式的增长形态, 而这种常态与过去的常态存在显著差异, 经济增长出现了显著地下滑, 中国经济进入了新常态。
六、中国经济新常态的形成原因根据前文中对中国经济发展状态的区段划分, 通过对比不同区段下经济结构的不同形态, 我们可揭示中国经济新常态的产生原因。本文主要从要素禀赋的视角, 观测不同区段下各要素的演变方式, 对比各要素和经济增长的相对变化, 并应用时变参数模型分析各要素对经济增长作用强度的变化, 综合判断各要素在中国经济新常态形成过程的作用大小。
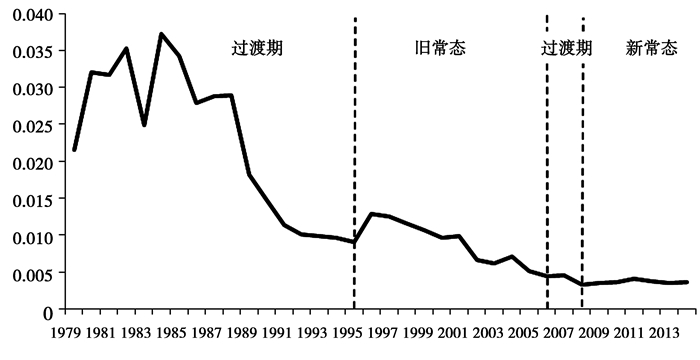
(一) 人口要素改革开放以来, 我国经济高速增长很大程度上得益于劳动力快速增长与释放形成的人口红利。虽然20世纪80年代初实行的计划生育政策抑制了人口的出生率, 但之前的高出生率人口在80年代及之后逐步形成劳动力, 并带来了高就业人口增长率, 进而造就了中国经济高增长率。然而, 随着计划生育政策的持续执行, 就业人口发生了明显变化(见图 2)。
|
图 2 1978年以来我国就业人口增长率② |
② 就业人口增长率数据根据国家统计局网就业人口水平数据对数差分得到。此外, 由于1990年我国就业人口的统计口径发生改变而使得1990年的就业人口增长率发生重大改变(高达15.72%), 因此本文以1989年和1991年的就业人口增长率平均值代替。
由图 2可知, 我国就业人口增长率呈现以下特征:第一, 就业人口增长率总体上呈现下降趋势。就业人口在20世纪80年代与90年代平均增长率分别为2.99%和1.12%, 而本世纪以来就业人口平均增长率才为0.53%。第二, 经济处于过渡期时也是就业人口增长率高波动时期, 尤其是1995年以前。1979年至1994年经济处于过渡期, 就业人口增长率的波动率为0.0099, 而1995年至2005年和2008年至2014年经济处于常态时期, 就业人口增长率的波动率分别为0.0026与0.0003①。前者远远高于后两者。第三, 旧常态就业人口增长率远大于新常态就业人口增长率。旧常态时就业人口平均增长率为0.92%, 而新常态就业人口平均增长率为0.36%, 前者是后者近3倍。
① 由于第二段过渡期期较短, 所以我们没有将其与其他经济形态对比。
(二) 资本要素资本是经济增长的另一个基本要素。改革开放以来, 以我国长期高储蓄率为保障, 以政府主导为特征, 依靠高投资拉动一直是我国驱动经济增长重要方式。然而, 在分析资本变动对经济发展形态变化的影响时存在一个难题——资本存量的估计。
对于资本存量的估计, 现有研究目前主要采用永续盘存法:
| $ {K_t}{\rm{ = }}{I_t}{\rm{ + }}\left({1 - {\delta _t}} \right){K_{t - 1}} $ | (6) |
其中It为第t年的实际投资额; Kt为第t年的实际资本存量; δt为第t年的资本折旧率。给定初始的资本存量, 根据各年的实际投资额和折旧率便可测算出各年的实际资本存量。然而, 国家统计部门并未统计或公布这些经济数据。基于此, 现有研究根据不同方法尝试估计我国各年的资本存量(Chow, 1993; 王小鲁、樊纲, 2000; 张军等, 2004; 郭庆旺、贾俊雪, 2005; 等等)。
首先, 实际投资额的测度。虽然国家统计部门会公布投资额, 但是各年的投资额都是基于当年的价格来计价的。因而, 实际投资额的测度关键因素是将名义投资额转换为实际投资额, 其中核心的问题就是价格指数的度量。国家统计局只公布了1990年之后的投资价格指数, 而1990年之前的投资价格指数则需要估算。我们将1990年之前的投资价格指数根据张军等(2004)的方法得到, 即:
| $ \begin{array}{l} \ \ \ \ \ \ {\rm{1985年的固定资本形成总额指数{\left({{\rm{1978=1}}} \right)}}}\\ {\rm{ = }}\frac{{{\rm{1985年的固定资本形成总额}}\left({{\rm{当年价格}}} \right){\rm{/1985年的投资隐含平减指数}}\left({{\rm{1978 = 1}}} \right)}}{{{\rm{1978年的固定资本形成总额}}\left({{\rm{当年价格}}} \right)}} \end{array} $ | (7) |
其中投资隐含平减指数是我们需要测算的投资价格指数, 而各年的固定资本形成总额指数和固定资本形成总额来自《中国国内生产总值核算历史资料:1952—1995》。
其次, 资本折旧率的选择。根据统计年鉴上国有企业在1978年之后采取大约5%左右的折旧率, 大量文献选择了5%的折旧率, 本文也遵循这一做法。
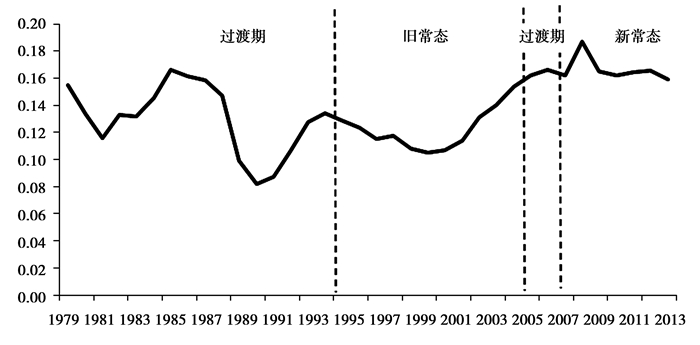
最后, 初始资本的估算。现有研究对初始资本的估算差别较大:在1978年, 张军、章元(2003)估算的资本存量为12361.96亿元(按1952年价格计算), 根据前面方法计算得到投资价格指数换算成1978年时为12458.68亿元; 郭庆旺、贾俊雪(2004)固定资产净值为3837亿元(以1978年为基期); 贺菊煌(1992)将资本分为生产性资本和非生产性资本, 其中生产性资本在1978年为16297亿元(按1990年价格计算), 换算成1978年时为8820.94亿元。由于我们更多关注于资本总量的波动与增长率而不是具体数值, 因此初始资本的选择对于本文所需说明的问题影响并不大。当选择郭庆旺、贾俊雪(2004)中1978年的固定资本净值作为本文的初始资本时, 我们可估计我国固定资本存量, 并进一步可计算固定资本存量的增长率(如图 3)。
|
图 3 1979年以来我国资本存量增长率① |
① 1980年之后的全社会固定资产投资额数据来自于国家统计局网站, 而1979年全社会固定资产投资额源自郭庆旺和贾俊雪(2004)。
与人口要素相比, 资本存量增长率并没有明显的趋势。但在不同经济形态下, 资本存量增长率依然存在些许差别:第一, 经济在常态下资本存量增长率比过渡期下资本存量增长率稳定, 1979年至1994年经济处于过渡期, 资本存量增长率的波动率为0.026, 而1995年至2005年和2008年至2014年经济处于常态时期, 资本存量增长率的波动率分别为0.02与0.009。第二, 资本存量增长率的波动率在新常态下要比旧常态下更小, 并且资本存量平均增长率在新常态下要明显高于旧常态, 前者为17%而后者为12%。
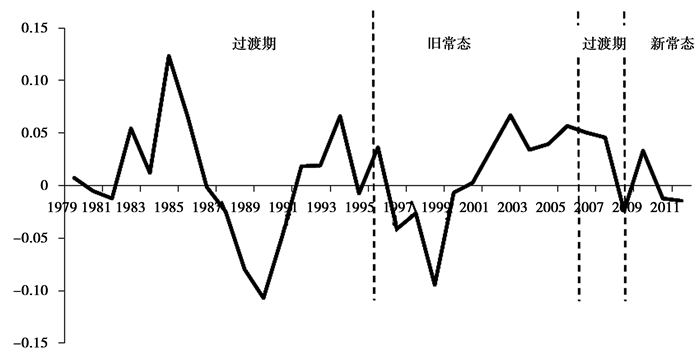
(三) 技术要素技术创新是经济增长的内生力量, 是确保经济保持持续增长的关键因素, 也是当前中国经济面临环境约束、投资效率低下、人口红利降低等约束下稳定经济增长的重要途径。一般来讲, 度量技术进步速度的主要是全要素生产率增长率。自从改革开放以来, 我国全要素生产率增长率见图 4。
|
图 4 1979年以来我国全要素生产率增长率 数据来源:http://www.rug.nl/research/ggdc/data/pwt/pwt-8.0。 |
由图 4可知, 自从改革开放以来, 我国全要素生产率增长率波动幅度较大, 尤其是过渡期:全要素生产率增长率的波动在1979年至1994年过渡期为0.0567, 而在旧常态和新常态下分别为0.0481和0.0258。从水平值来看, 全要素生产率平均增长率在1979年至1994年过渡期为0.0052, 而在旧常态和新常态下分别为0.0095和-0.0042。由此可是, 全要素生产率增长率在旧常态下最高并且波动并不大, 而在新常态下, 虽然全要素生产率增长率波动较小, 但是全要素生产率平均增长率为负值。新旧常态下全要素生产率增长率相差高达1.37%。根据C-D生产函数:
| $ \mathit{\Delta Ln}\left({GDP} \right) = \mathit{\Delta }Ln\left({TFP} \right) + \alpha \mathit{\Delta }Ln\left(L \right) + \beta \mathit{\Delta }Ln\left(K \right) $ | (8) |
其中TFP、L和K分别为全要素生产率、就业人口和资本存量。由此可知, 新常态下全要素生产率增长率的下降将同幅度降低GDP增长率。
(四) 实证分析通过以上描述发现, 各要素的变化对我国经济增长具有明显的影响。这从量上解释了我国经济新常态形成的原因。由于改革开放以来, 我国经济结构、经济水平等都发生了较大改变, 各要素与经济增长之间的作用机制可能随之改变。因此, 接下来, 我们将分析各要素对经济增长率的作用强度是否发生变化。
为刻画各要素对经济增长率的作用强度是否存在变化, 需要将模型设定为参数时变的:
| $ \mathit{\Delta Ln}\left({GDP} \right) = \mathit{\Delta }Ln\left({TFP} \right) + {\alpha _t}\mathit{\Delta }Ln\left(L \right) + {\beta _t}\mathit{\Delta }Ln\left(K \right) + {\varepsilon _t} $ | (9) |
其中αt和βt分别代表了就业人口增长率和资本存量增长率对经济增长率的时变贡献度; εt为随机扰动项, 满足εt~N(0, Ωt)。通过简单转变, 可得:
| $ \mathit{\Delta Ln}\left({GDP} \right) = \mathit{\Delta }Ln\left({TFP} \right) + {\alpha _t}\mathit{\Delta }Ln\left(L \right) + {\beta _t}\mathit{\Delta }Ln\left(K \right) + {\varepsilon _t} $ | (10) |
对于此类单方程、时变参数的模型, 由于参数维度较大, 研究中一般偏向于应用卡尔曼滤波方法降低待估的维度并实现估计。基于Koop and Korobilis(2012)方法计算上的简便与良好表现, 本文参考Koop and Korobilis(2012)的方法来估计式, 优化了传统卡尔曼滤波方法中参数递归的过程①。
① 具体估计过程备索。
在进一步估计之前, 我们需要说明的是:第一, 数据平稳性的检验。为了更为稳健地判断各变量的平稳性, 我们应用了常用的ADF、DF GLS和KPSS三种方法综合检验变量的平稳性。检验结果发现, 当选择5%的显著性水平时, GDP增长率、全要素生产率增长率和就业人口增长率在三种方法下都通过了平稳性检验, 而资本存量增长率在ADF检验下并没有决绝存在单位根, 但是DF GLS和KPSS两种方法都通过了平稳性检验。因此综合来讲, 这些变量都满足平稳性条件。第二, 系数显著性的判断。为判断参数的显著性, 本文通过Bootstrap方法进行10000次抽样估计, 模拟参数分布, 选择模拟分布的中位数作为结果的估计, 并借鉴Doan(2004)等以[0.16, 0.84]分位数作为置信区间, 判断参数显著性。
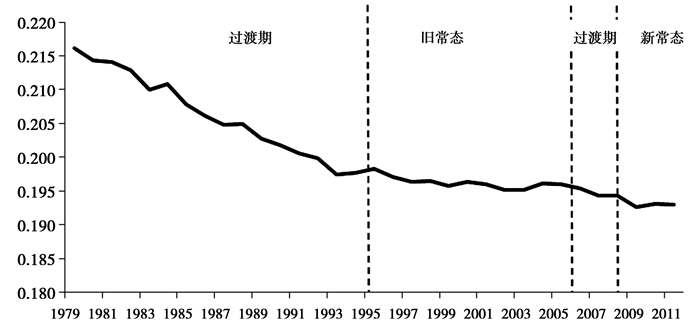
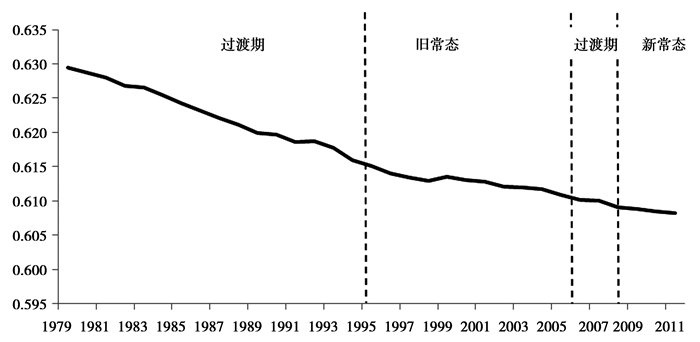
就业人口对经济增长率的作用强度见图 5。就业人口对经济增长率的作用呈现轻微的下降趋势, 就业人口增长率上升1%将带来GDP增长率上升大约0.21%左右。这与Maddaloni等(2006)对欧洲地区估计的0.19%较为接近。而资本存量对经济增长率的作用强度见图 6。与就业人口对经济增长率的作用趋势一样, 资本存量对经济增长率的作用强度呈现轻微的下降趋势, 资本存量增长率上升1%将带来GDP增长率上升大约0.61%左右。资本存量增长对GDP的贡献远高于就业人口对GDP的贡献。同时由于就业人口快速增长短期内难以实现, 资本存量具有短期拉动较快的特征。因此, 这也较好地说明了, 为何我国政府偏向于以政府主导型的投资拉动来刺激经济, 这突出体现在2008年全球性金融危机后的救市政策。
|
图 5 αt的时变性 |
|
图 6 βt的时变性 |
从图 2至图 4来看, 各要素展示了不同的增长路径, 与GDP增长率路径存在不同程度的差异, 甚至截然相反的发展路径。人口要素和技术要素与GDP增长率的增长路径较为一致, 在经济处于过渡期就业人口增长率、全要素生产率增长率与GDP增长率都处于波动较大时期, 而旧常态下三者平均增长率也高于新常态时平均增长率。然而, 资本存量与GDP的增长路径存在显然不同, 虽然在过渡期下资本存量增长率波动亦是较高时期, 但是新常态下资本存量增长率却明显高于旧常态下资本存量增长率, 与GDP的增长路径相反。
由图 5-图 6可知, 虽然就业人口与资本存量对经济增长的贡献大小随着时间发展略有下降, 但是新旧常态下各要素对经济增长的贡献变化并不明显。因此, 综合来讲, 我国新常态的形成主要是各要素的增长率变化带来的, 其中主要是就业人口增长率下降和全要素生产率增长率下降造成的。
而如何避免经济增长速度进一步下降则是我们需要考虑的问题。虽然从图 6来看, 投资拉动具有较好的经济刺激效果, 依靠投资拉动能够避免经济增长速度的下降, 但是近年来, 我国各地出现的"民工荒"而突显的低劳动力成本优势在逐渐消失、存贷款利率得以放开带来的企业融资成本上升、土地价格不断地上升等都造成了投资回报率下降。资金大规模转向了房地产、股票等高投资回报率的金融市场, 脱离了实体经济。这一方面对实体经济增长速度造成了一定影响, 另一方面带来了高房价、股市动荡等经济与社会问题。此外, 以政府主导的投资表现出重复建设、盲目竞争性投资等造成了资源极大浪费。
在此背景下, 中国未来经济增长引擎将从人口要素和全要素生产率两者中寻找。从人口要素方面来讲, 虽然我国在2016年开始全面放开了二胎, 但是新生儿要形成劳动力还需二十年左右, 短期并不能产生效果。而上个世纪50、60年代高出生率的一代在不久的未来将逐步退休。因而, 未来很长一段时间内依赖就业人口增长来维持经济的可能性并不大。此外, 我国是世界人口第一大国家, 进一步的人口快速增长将考验我国环境承受力与资源承受力, 并带来诸多的社会与经济问题。依赖就业人口增长来维持经济的必要性值得质疑。
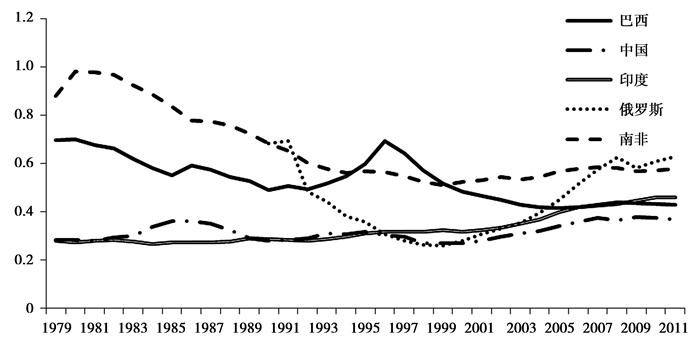
因此, 我国新常态下稳定经济增长将主要依赖于全要素生产率的提高。由于我国全要素生产率迄今依然较低, 即便与我国经济发展水平相当的"金砖五国"相比亦是如此(见图 7), 依靠提高全要素生产率来促进经济增长将有很大的空间。图 7显示, 自从改革开放以来, 我国全要素生产率远低于"金砖五国"其他四国的全要素生产率, 尤其是改革开放初期。虽然近年来我国全要素生产率有所改善和其他四国全要素生产率出现下降, 但是其他四国全要素生产率依然远高于我国全要素生产率。这表明, 一方面我国与其他国家技术依然存在较大差距, 依靠后发优势与技术引进的技术进步模式是我国未来经济增长的重要引擎, 另一方面由于我国现有的全要素生产率并不高, 企业通过自主创新改进技术带来的生产力提高将较为显著。不管是技术引进方式还是企业自主创新的方式, 都可以弥补我国与其他国家之间的技术差距, 改善我国全要素生产率低下的现状, 并进一步带动经济增长。
|
图 7 1979年以来"金砖五国"全要素生产率 数据来源:http://www.rug.nl/research/ggdc/data/pwt/pwt-8.0。 |
本文首先定义了新常态的经济状态形式, 并将经济划分为过渡期、旧常态与新常态三种发展形态。在此基础上, 本文通过条件马尔可夫状态转移模型量化了自从改革开放以来中国经济状态形式的改变, 识别了经济处于过渡期、旧常态与新常态的历史时段, 并从要素禀赋的角度探讨了中国经济新常态的形成原因。
根据实证分析, 自从改革开放以来, 我国经济发展可分为四个阶段:1979年第1季度至1995年第1季度是中国经济大起大落、波动较大时期, 为过渡期; 1995年第2季度至2005年第4季度阶段, 中国经济保持高速增长的同时并没有带来剧烈波动, 反而保持高位、平稳增长, 此一时期为中国的旧常态时期; 2006年第1季度至2007年第4季度时期为中国经济从旧常态转向新常态的过渡时期, 亦是经济较大幅度波动时期, 为过渡期; 2008年第1季度至2015年第2季度为中国经济新常态时期。
进一步, 我们依据中国经济状态形式阶段性划分, 对比了各阶段人口要素、资本要素和技术要素的变化趋势, 并观测各要素变化趋势与GDP变化趋势的吻合度, 发现:就业人口增长率和全要素生产率增长率的降低与GDP增长率变化较为契合, 而资本要素变化与GDP变化呈现相反变化趋势, 以高投资的方式避免了中国经济过度下滑。此外, 本文应用时变参数模型, 分析了各要素对经济增长的作用是否随着时间发生改变。结果显示, 就业人口和资本要素对GDP的贡献呈现下降趋势, 但是变化微乎其微。因此, 我国经济状态的转变主要源自于各要素增长速度的变化, 尤其是人口要素和资本要素。
由于我国现存庞大的人口存量, 并且近期放开二胎伴随的高出生率形成高就业人口增长率仍需时日, 我国通过提高就业人口增长率促进经济增长的方式在不远的未来并不可行。另一方面, 我国近年来以政府为主导的高投资带来的重复建设, 投资效率低下, 这一方式难以持续。因此, 在新常态下, 我国经济增长的稳定将主要依靠全要素生产率的提高。基于我国现有的全要素生产率依然较低, 通过引进国外技术、先进管理方式等仍可作为我国未来经济增长的重要方式。但从长远来看, 依靠自主创新, 以创新驱动的方式促进经济增长才是长远之计。因此, 政府需营造自主创新的政策环境, 激发社会各界创新的欲望, 提高创新转化为产出的能力, 并保障各经济主体自主创新带来的利益。
| [] | 国家统计局国民经济核算司, 1997, 《中国国内生产总值核算历史资料:1952—1995》. 东北财经大学出版社. |
| [] | 郭庆旺、贾俊雪, 2005, “中国全要素生产率的估算:1979 —2004”, 《经济研究》, 第 6 期, 第 51–60 页。 |
| [] | 贺菊煌, 1992, “我国资产的估算”, 《数量经济与技术经济研究》, 第 8 期, 第 24–27 页。 |
| [] | 金碚, 2015, “中国经济发展新常态研究”, 《中国工业经济》, 第 1 期, 第 5–18 页。 |
| [] | 李扬, 2013, “中国经济发展的新阶段”, 《财贸经济》, 第 11 期, 第 5–12 页。 |
| [] | 李扬、张晓晶, 2015, “'新常态':经济发展的逻辑与前景”, 《经济研究》, 第 5 期, 第 4–19 页。 |
| [] | 李智, 2014, “新常态下中国经济发展态势和结构动向研究”, 《价格理论与实践》, 第 11 期, 第 7–12 页。 |
| [] | 林建浩、王美今, 2013, “中国宏观经济波动的'大稳健'——时点识别与原因分析”, 《经济学(季刊)》, 第 1 期, 第 577–604 页。 |
| [] | 林毅夫、蔡昉、李周, 1999, 《中国的奇迹:发展战略与经济改革(增订版)》. 上海三联出版社. |
| [] | 刘伟、苏剑, 2014, “'新常态'下的中国宏观调控”, 《经济科学》, 第 4 期, 第 5–13 页。 |
| [] | 齐建国、王红、彭绪庶、刘生龙, 2015, “中国经济新常态的内涵和形成机制”, 《经济纵横》, 第 3 期, 第 7–17 页。 |
| [] | 王成勇、艾春荣, 2010, “中国经济周期阶段的非线性平滑转换”, 《经济研究》, 第 3 期, 第 78–90 页。 |
| [] | 汪红驹, 2014, “防止中美两种'新常态'经济周期错配深度恶化”, 《经济学动态》, 第 7 期, 第 4–11 页。 |
| [] | 王小鲁、樊纲, 2000, 《中国经济增长的可持续性——跨世纪的回顾与展望》. 经济科学出版社. |
| [] | 易淼、赵晓磊, 2015, “利益视域下的中国经济发展新常态”, 《财经科学》, 第 4 期, 第 81–88 页。 |
| [] | 余斌、吴振宇, 2014, “中国经济新常态与宏观调控政策取向”, 《宏观经济》, 第 11 期, 第 17–25 页。 |
| [] | 张军、吴桂英、张吉鹏, 2004, “中国省际物质资本存量估算:1952—2000”, 《经济研究》, 第 10 期, 第 35–44 页。DOI:10.3969/j.issn.1002-9605.2004.10.015 |
| [] | 张军、章元, 2003, “对中国资本存量K的再估计”, 《经济研究》, 第 7 期, 第 35–43 页。 |
| [] | 张晓晶, 2015, “试论中国宏观调控新常态”, 《经济学动态》, 第 4 期, 第 12–22 页。 |
| [] | Abeysinghe T., Gulasekaran R., 2004, "Quarterly Real GDP Estimates for China and ASEAN4 with a Forecast Evaluation". Journal of Forecasting, 23, 431–447. DOI:10.1002/(ISSN)1099-131X |
| [] | Arnott, R., 2012, "What's New about the 'New Normal'?", The Journal of Portfolio Management, Fall:1-2. |
| [] | Bai J., Wang P., 2011, "Conditional Markov Chain and its Application in Economic Time Series Analysis". Journal of Applied Econometrics, 26(5), 715–734. DOI:10.1002/jae.1140 |
| [] | Bernanke B., 2004, "The Great Moderation. Meetings of the Eastern Economic Association", Washington: DC. |
| [] | Chow, G.C., 1993, "Capital Formation and Economic Growth in China", Quarterly Journal of Economics, August:809-842. |
| [] | Davis, L., 2009, "The New Normal", The McKinsey Quarterly, March. |
| [] | Doan, T., 2004, Rats Manual, version 6, Evanston. |
| [] | El-Erian, M. A., 2009, "A New Normal", PIMCO Economic Outlook, May. |
| [] | El-Erian, M. A., 2010, "Navigating the New Normal in Industrial Countries", International Monetary Fund, (Dec. 15), Retrieved October. |
| [] | Koop G., Korobilisi D., 2012, "Forecasting Inflation Using Dynamic Model Averaging". International Economic Review, 53(3), 867–886. DOI:10.1111/iere.2012.53.issue-3 |
| [] | Maddaloni, A., Musso, A., Rother, P., Ward-Warmedinger, M., and Westermann, T., 2006, "Macroeconomic Implications of Demographic Developments in the EURO Area. ECB", Occasional Paper, No. 51. |
| [] | Stock, J. H., and Watson, M. W., 2002, "Has the Business Cycle Changed and Why? ", NBER Working Paper, No. w9127. |



